Effect of Pre-Heating and Post-Heating on Electron Beam Welding of Reduced Activation Ferrite/Martensite Steel
Abstract
:1. Introduction
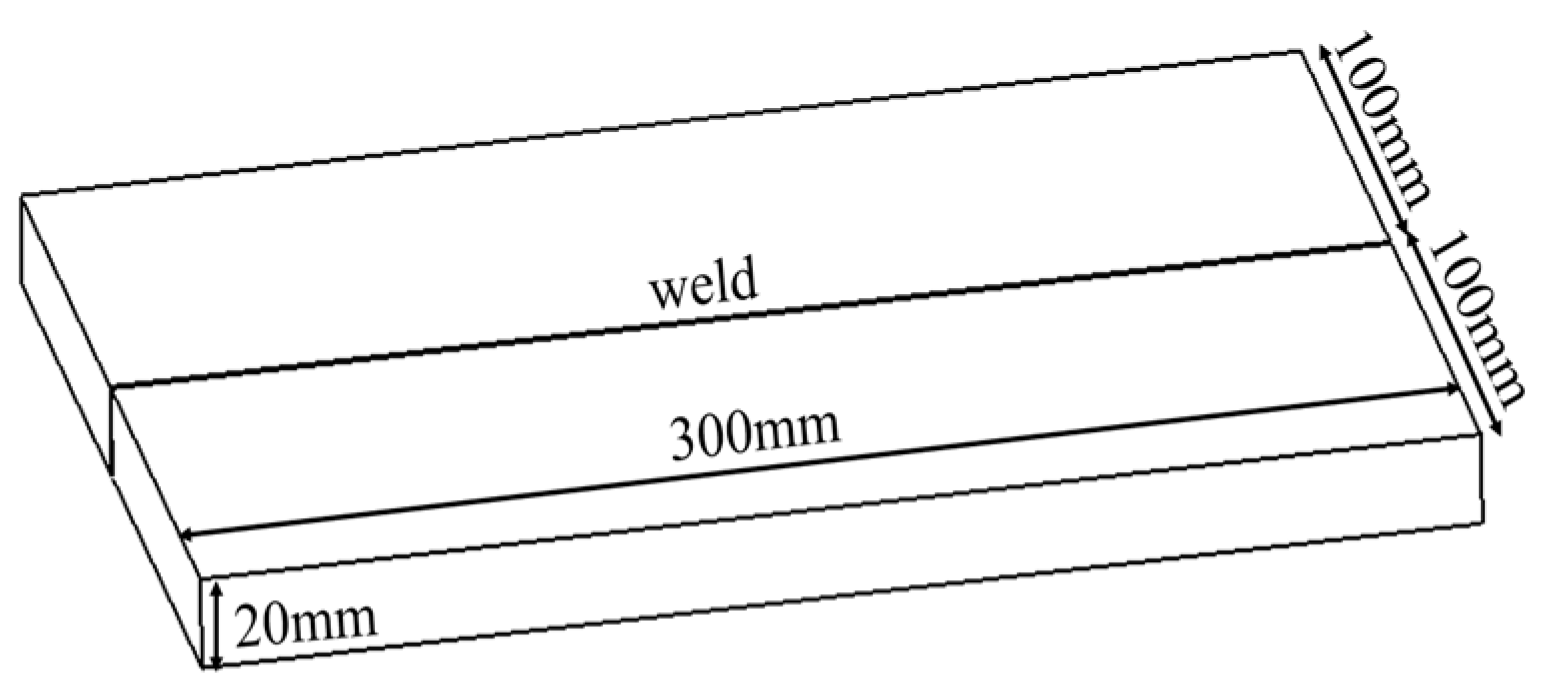
2. Experimental Conditions
3. Finite Element Modeling
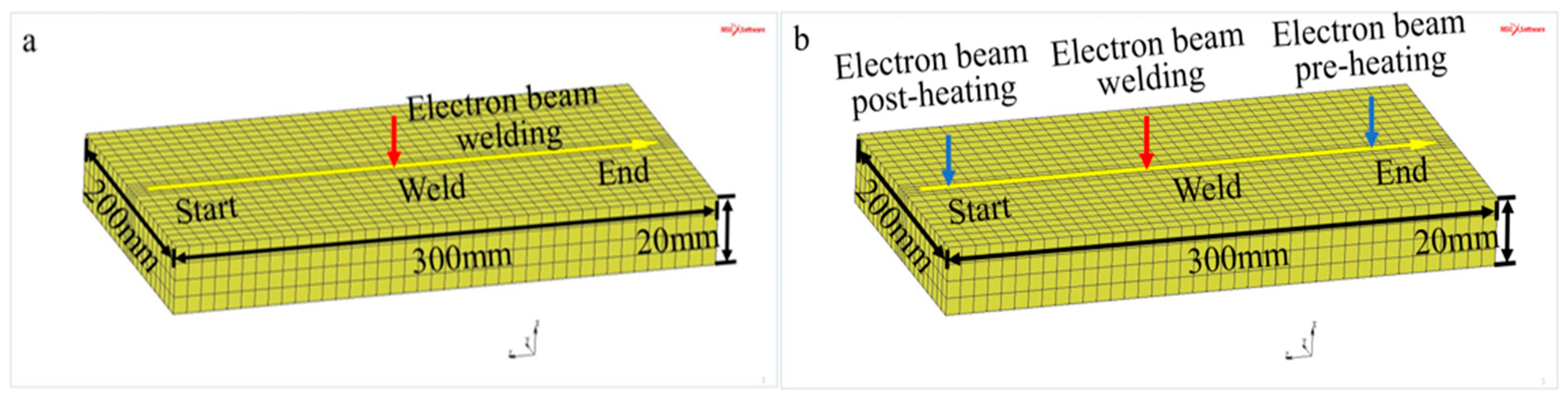
3.1. Finite Element Model
3.2. Heat Conduction Equation
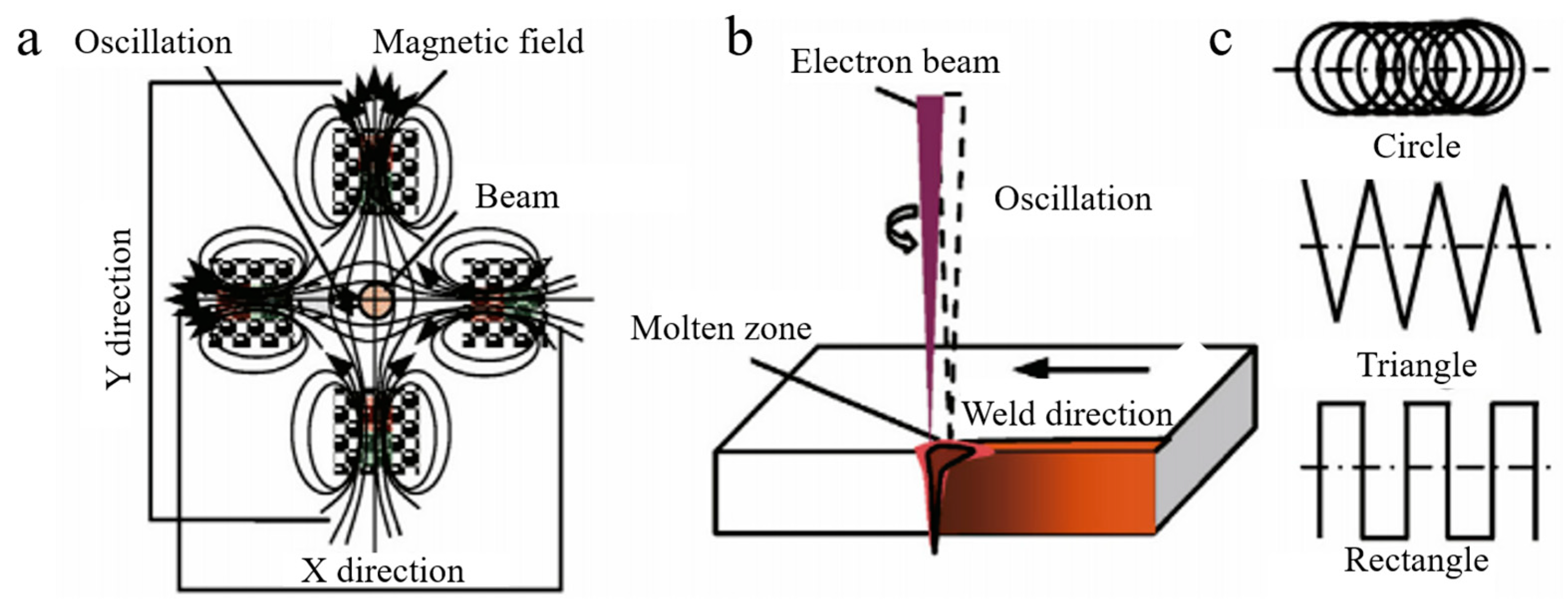
3.3. Heat Source Model
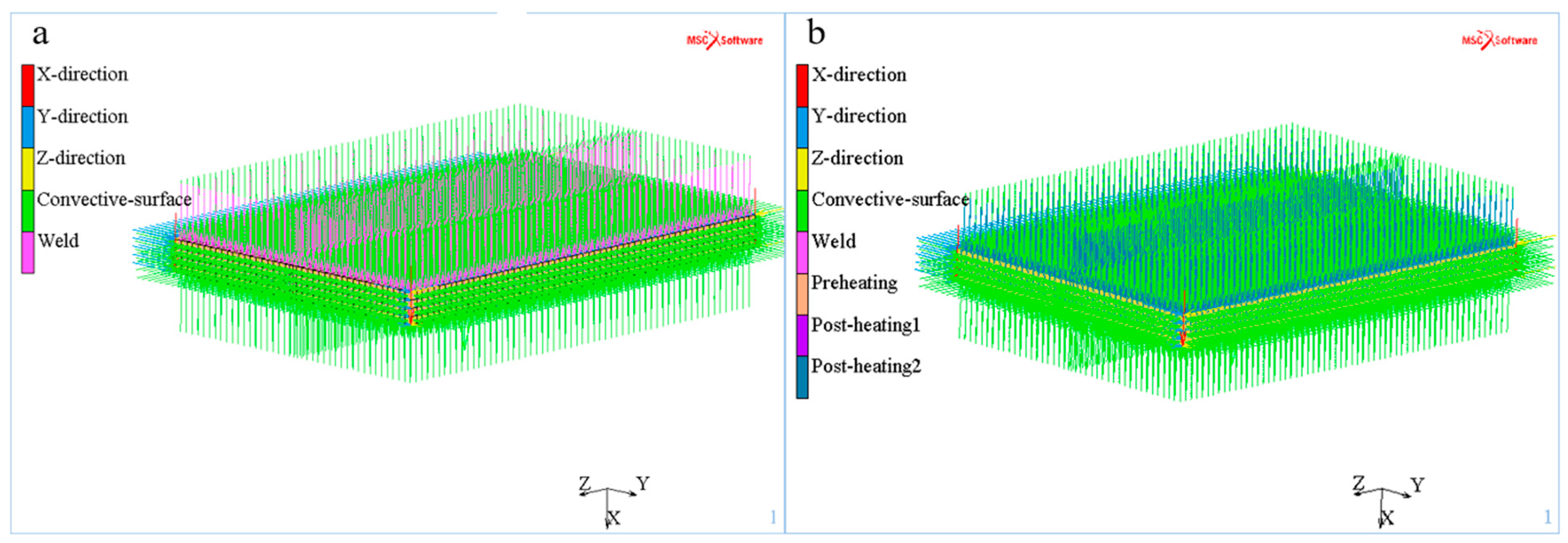
3.4. Boundary Conditions
4. Results and Discussion
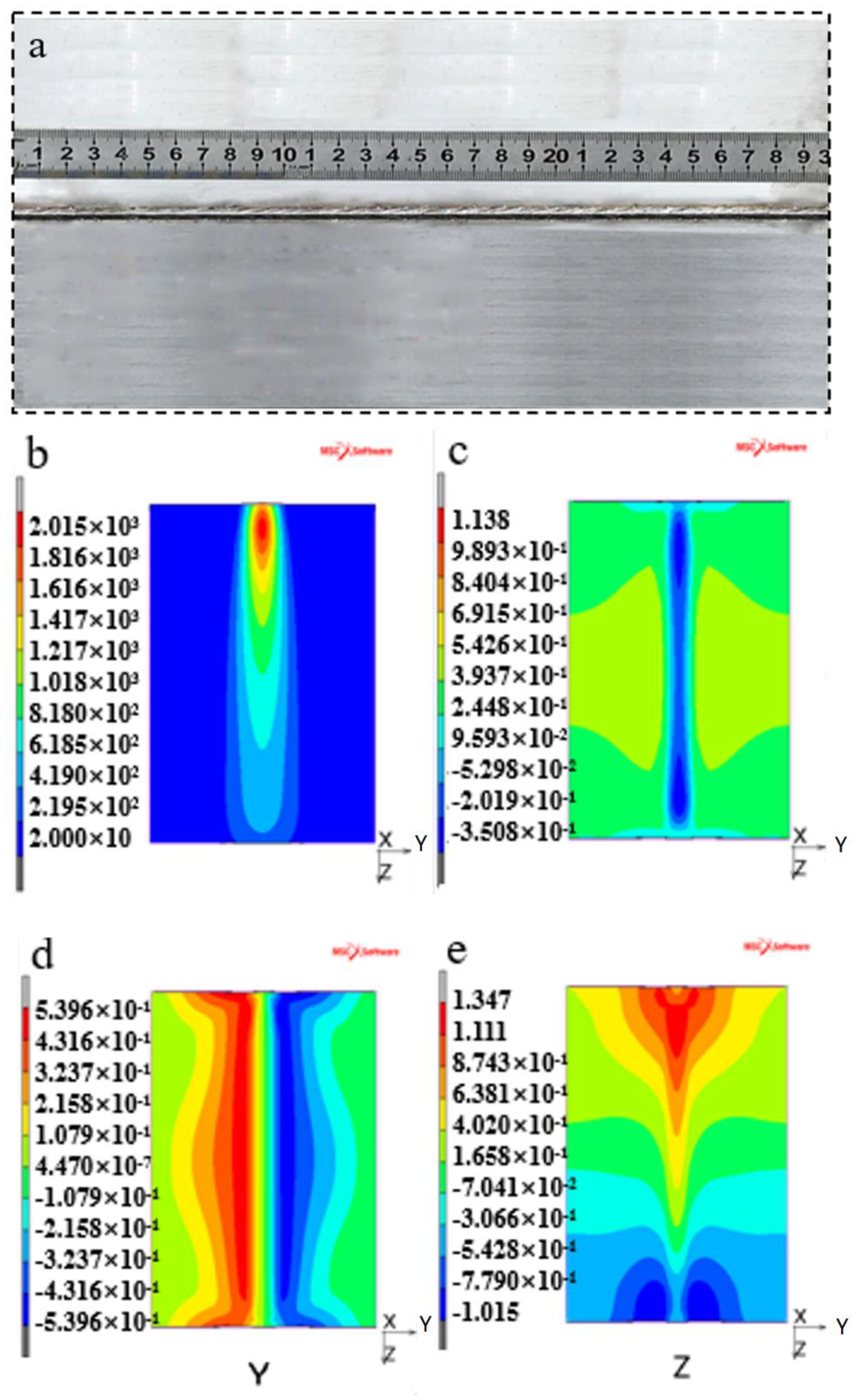
4.1. Verification of Heat Source Model
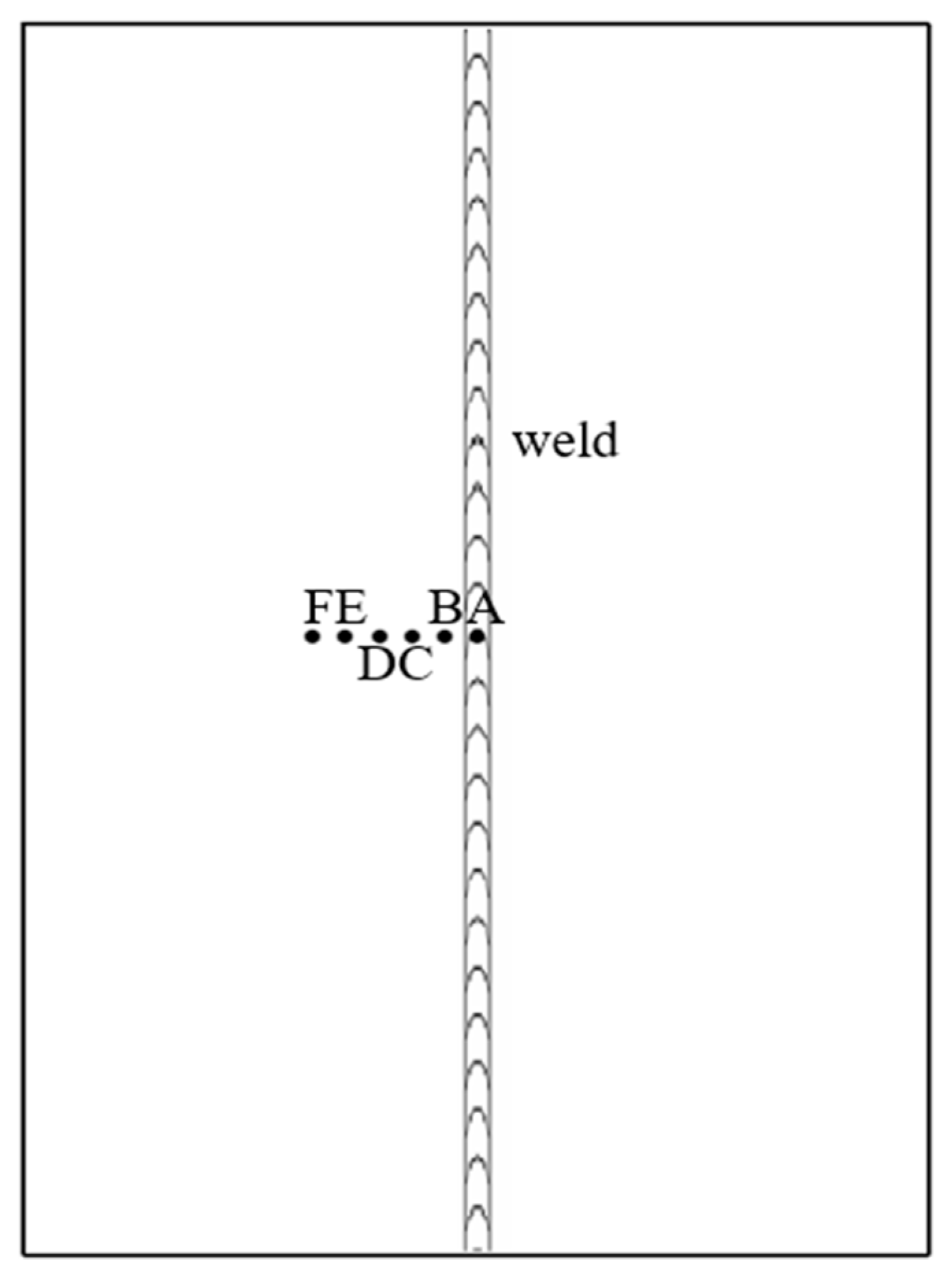
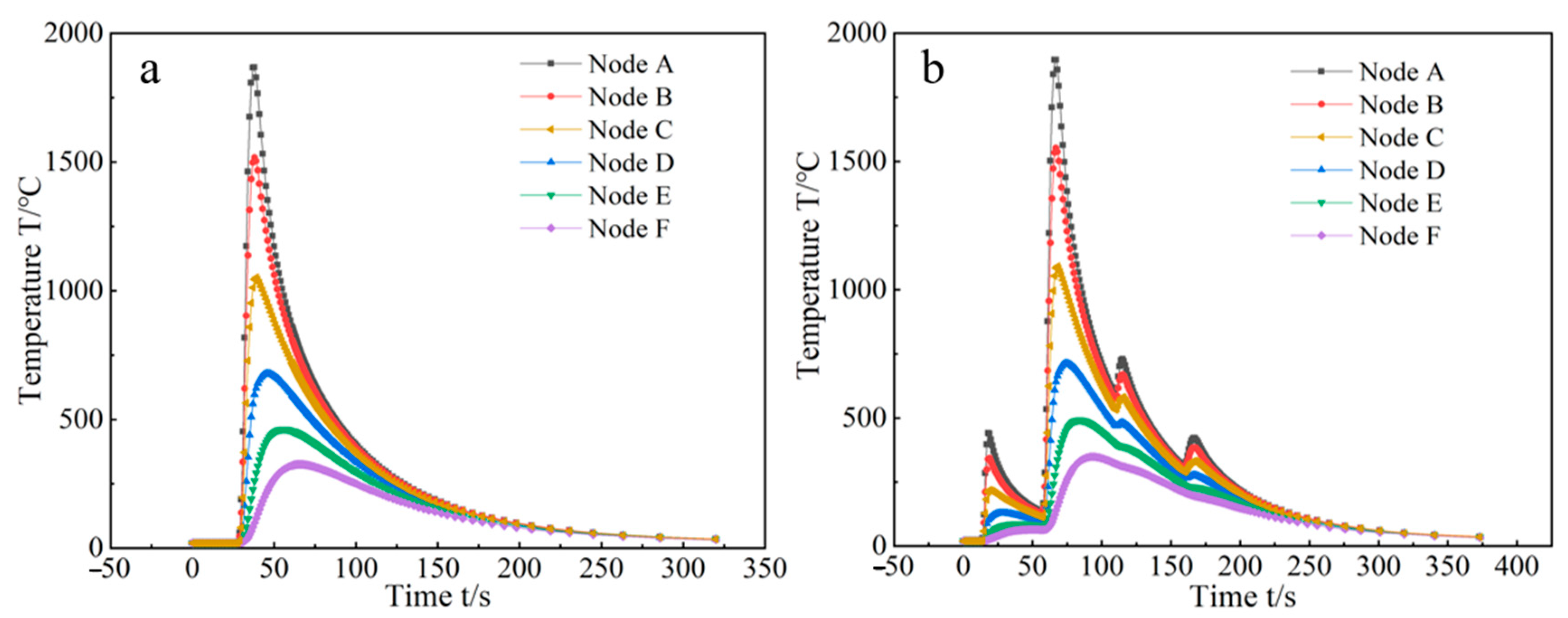
4.2. Welding Temperature Field
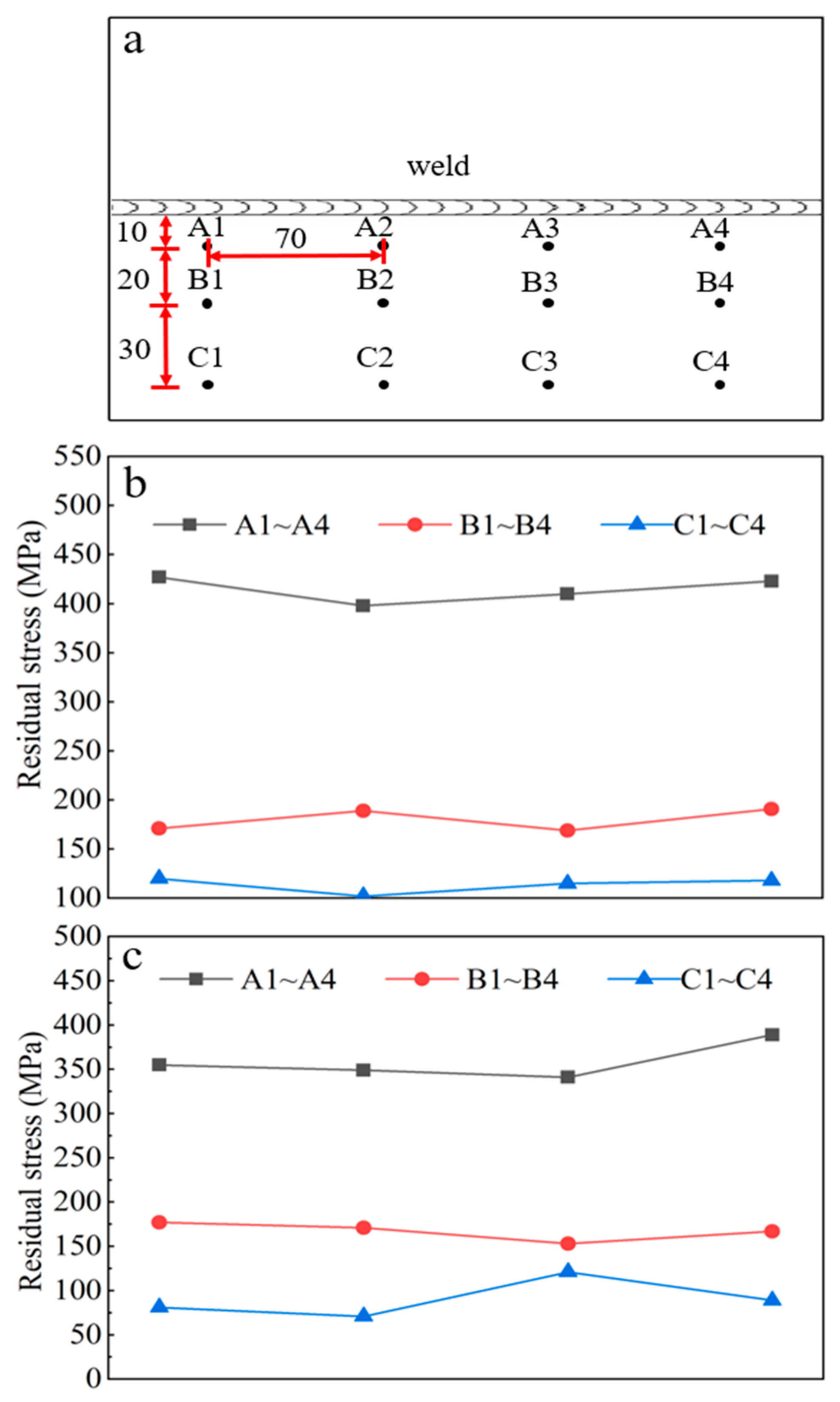
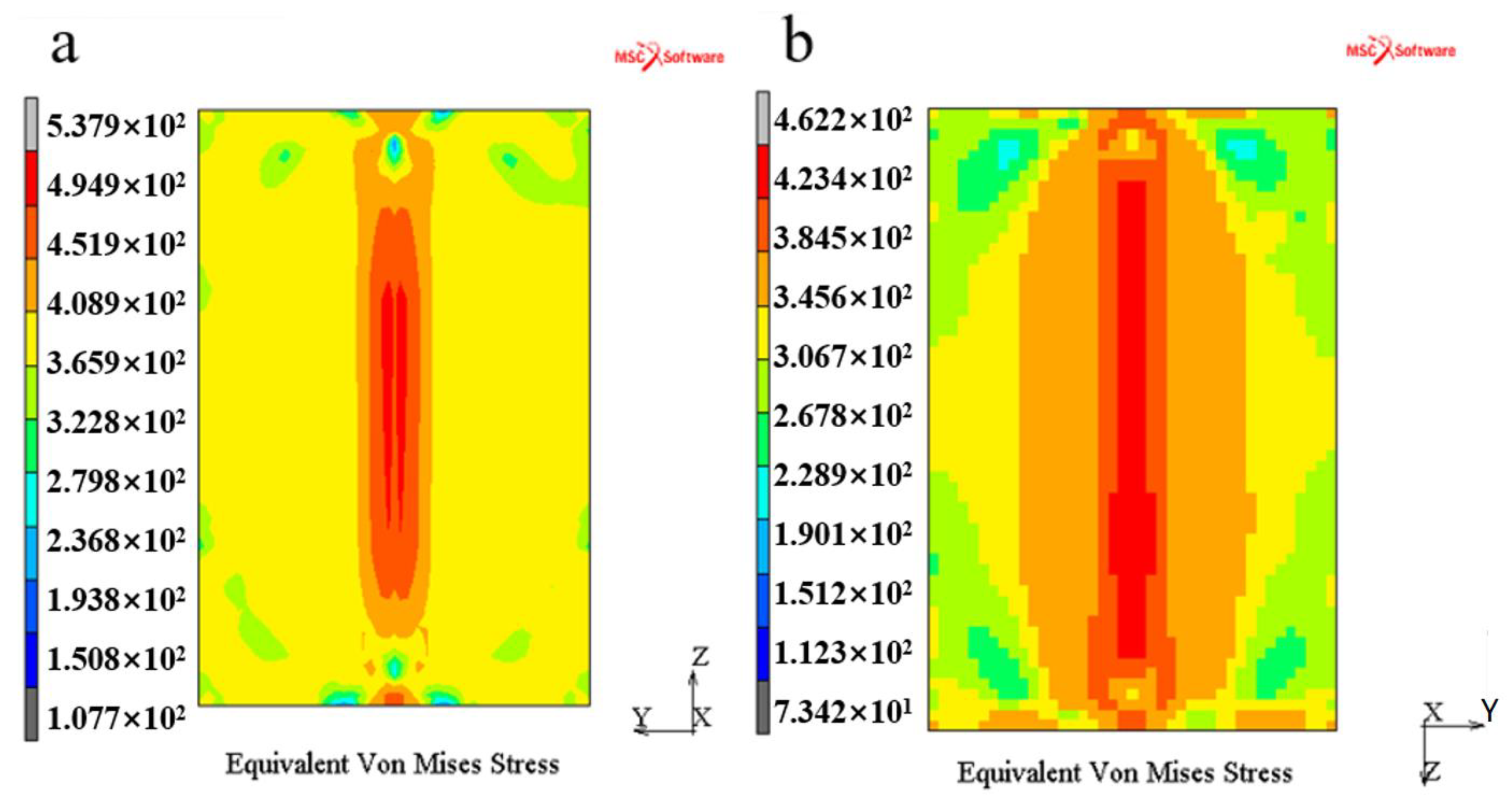
4.3. Residual Stress
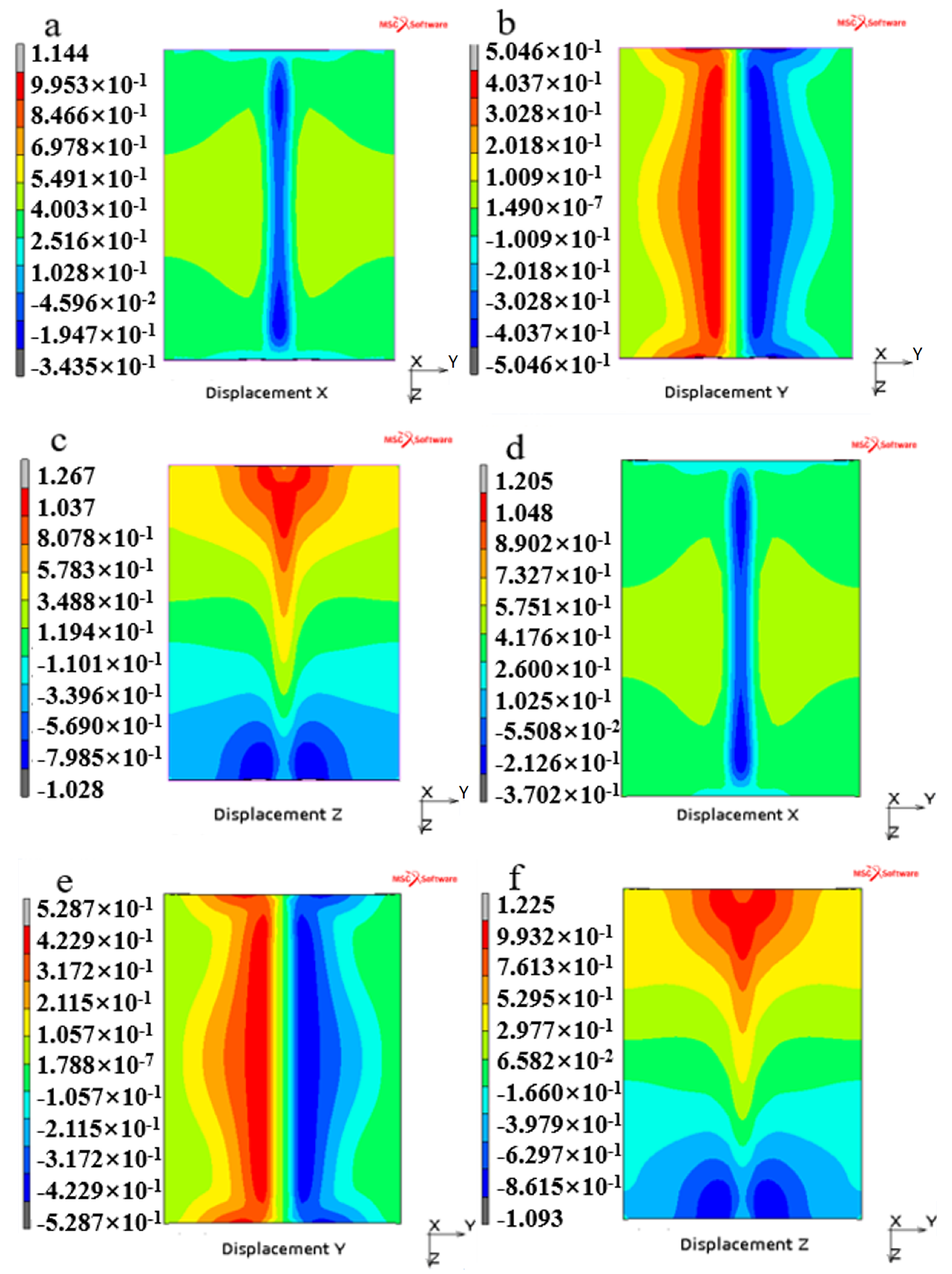
4.4. Welding Deformation
4.5. Properties of Electron Beam Welding (EBW) Joint
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, J. Nuclear fusion energy-clean energy in the future. Sci. Technol. West. China 2012, 11, 55–56. [Google Scholar]
- Huang, Q.; Wu, Y.; Li, J.; Wan, F.; Chen, J.; Luo, G.; Liu, X.; Xu, Z.; Zhou, X.; Ju, X.; et al. Status and strategy of fusion materials development in China. J. Nucl. Mater. 2008, 30, 400–404. [Google Scholar] [CrossRef]
- Zheng, S.; Wu, Q.; Huang, Q.; Liu, S.; Han, Y. Influence of different cooling rates on the microstructure of the HAZ and welding CCT diagram of CLAM steel. Fusion Eng. Des. 2011, 86, 2616–2619. [Google Scholar] [CrossRef]
- Liu, S.; Li, X.; Ma, X.; Jiang, K.; Li, M.; Huang, K.; Lei, M.; DelNevo, A.; Agostini, P. Updated design of water-cooled breeder blanket for CFETR. Fusion Eng. Des. 2019, 146, 1716–1720. [Google Scholar] [CrossRef]
- Lei, M.; Wu, Q.; Xu, S.; Xu, K.; Ma, X.; Liu, S. Design and analysis of the equatorial inboard WCCB blanket module for CFETR. Fusion Eng. Des. 2020, 161, 111889. [Google Scholar] [CrossRef]
- Hu, J.; Jiang, Z.Z.; Huang, J.H.; Chen, S.H.; Zhao, X.K.; Zhang, H. Effects of heat treatment processes on microstructure and impact toughness of weld metal of vacuum electron beam welding on CLAM steel. J. Trans. China Weld. Inst. 2012, 33, 67–71. [Google Scholar]
- Hishinuma, A.; Kohyama, A.; Klueh, R.; Gelles, D.; Dietz, W.; Ehrlich, K. Current status and future R&D for reduced-activation ferritic/martensitic steels. J. Nucl. Mater. 1998, 258–263, 193–204. [Google Scholar] [CrossRef]
- Kano, S.; Yang, H.; McGrady, J.; Hamaguchi, D.; Ando, M.; Tanigawa, H.; Abe, H. Study of radiation-induced amorphization of M23C6 in RAFM steels under iron irradiations. J. Nucl. Mater. 2020, 533, 152088. [Google Scholar] [CrossRef]
- Dulieu, D.; Tupholme, K.; Butterworth, G. Development of low-activation martensitic stainless steels. J. Nucl. Mater. 1986, 141–143, 1097–1101. [Google Scholar] [CrossRef]
- Polekhina, N.A.; Litovchenko, I.Y.; Almaeva, K.V.; Bulina, N.V.; Korchagin, M.A.; Tyumentsev, A.N.; Chernov, V.M.; Leontyeva-Smirnova, M.V. Features of Phase Transformations of Low-activation 12%-Chromium Ferritic-Martensitic Steel Ek-181. Russ. Phys. J. 2020, 62, 2314–2318. [Google Scholar] [CrossRef]
- Rai, R.; Burgardt, P.; Milewski, J.O.; Lienert, T.J.; DebRoy, T. Heat transfer and fluid flow during electron beam welding of 21Cr–6Ni–9Mn steel and Ti–6Al–4V alloy. J. Phys. D Appl. Phys. 2009, 42, 025503. [Google Scholar] [CrossRef]
- Huang, Q.; Li, C.; Li, Y.; Chen, M.; Zhang, M.; Peng, L.; Zhu, Z.; Song, Y.; Gao, S. Progress in development of China low activation martensitic steel for fusion application. J. Nucl. Mater. 2007, 367–370, 142–146. [Google Scholar] [CrossRef]
- Li, C.; Huang, Q.; Wu, Q.; Liu, S.; Lei, Y.; Muroga, T.; Nagasaka, T.; Zhang, J.; Li, J. Welding techniques development of CLAM steel for test blanket module. Fusion Eng. Des. 2009, 84, 1184–1187. [Google Scholar] [CrossRef]
- Zhang, X.L.; Li, R.F.; Liu, Q.Z.; Du, H.H. Welding procedure test of P91 heat resistant steel. Metalworking (Hot Work) 2011, 16, 39–41. [Google Scholar]
- Sun, X.; Wang, H.H. Martensite in weld metal of new heat resistant steel P91. Welding 2010, 4, 7–12. [Google Scholar]
- Lindau, R.; Klimenkov, M.; Jäntsch, U.; Möslang, A.; Commin, L. Mechanical and microstructural characterization of electron beam welded reduced activation oxide dispersion strengthened—Eurofer steel. J. Nucl. Mater. 2011, 416, 22–29. [Google Scholar] [CrossRef]
- Jiang, Z.; Huang, J.; Chen, S.; Ju, X. Microstructure transformation and mechanical properties of electron beam welded joints of fusion CLAM steel. Trans. China Weld. Inst. 2011, 32, 45–48. [Google Scholar]
- Lundback, A.; Runnemalm, H. Validation of three-dimensional finite element model for electron beam welding of Inconel 718. Sci. Technol. Weld. Join. 2013, 10, 717–724. [Google Scholar] [CrossRef]
- Li, C.W.; Wang, Y. Three-dimensional finite element analysis of temperature and stress distributions for in-service welding process. Mater. Des. 2013, 52, 1052–1057. [Google Scholar] [CrossRef]
- Lacki, P.; Adamus, K. Numerical simulation of the electron beam welding process. Comput. Struct. 2011, 89, 977–985. [Google Scholar] [CrossRef]
- Kiyoshima, S.; Deng, D.; Ogawa, K.; Yanagida, N.; Saito, K. Influences of heat source model on welding residual stress and distortion in a multi-pass J-groove joint. Comput. Mater. Sci. 2009, 46, 987–995. [Google Scholar] [CrossRef]
- Kim, Y.-C.; Hirohata, M.; Inose, K. FEM Simulation of Distortion and Residual Stress Generated by High Energy Beam Welding with Considering Phase Transformation. Open J. Met. 2014, 4, 31–39. [Google Scholar] [CrossRef] [Green Version]
- Joshi, S.; Hildebrand, J.; Aloraier, A.S.; Rabczuk, T. Characterization of material properties and heat source parameters in welding simulation of two overlapping beads on a substrate plate. Comput. Mater. Sci. 2013, 69, 559–565. [Google Scholar] [CrossRef]
- Bonakdar, A.; Molavi-Zarandi, M.; Chamanfar, A.; Jahazi, M.; Firoozrai, A.; Morin, E. Finite element modeling of the electron beam welding of Inconel-713LC gas turbine blades. J. Manuf. Process. 2017, 26, 339–354. [Google Scholar] [CrossRef]
- Anca, A.; Cardona, A.; Risso, J.; Fachinotti, V.D. Finite element modeling of welding processes. Appl. Math. Model. 2011, 35, 688–707. [Google Scholar] [CrossRef]
- Davis, J.W.; Smith, P.D. ITER Materials Properties Handbook (MPH); ITER Doc. G 74 MA 16 04-05-07 R0.1 (Internal Project Document Distributed to the ITER Participants); U.S. Department of Energy Office of Scientific and Technical Information: Oak Ridge, TN, USA, 1996.
- Fu, P.; Mao, Z.; Zuo, C.; Wang, Y.; Wang, C. Microstructures and fatigue properties of electron beam welds with beam oscillation for heavy section TC4-DT alloy. Chin. J. Aeronaut. 2014, 27, 1015–1021. [Google Scholar] [CrossRef] [Green Version]
- Xia, X.; Wu, J.; Liu, Z.; Shen, X.; Ma, J.; Liu, Z. Study of microstructure difference properties of electron beam welds with beam oscillation of 50 mm 316L in CFETR. Fusion Eng. Des. 2019, 138, 339–346. [Google Scholar] [CrossRef]
- Mathar, J. Determination of inherent stress by measuring the deformations around drilled holes. Tech. Rep. Arch. Image Libr. 1934, 56, 245–254. [Google Scholar]
- Tian, Y.; Wang, C.; Zhu, D.; Zhou, Y. Finite element modeling of electron beam welding of a large complex Al alloy structure by parallel computations. J. Mater. Process. Technol. 2008, 199, 41–48. [Google Scholar] [CrossRef]
- Goldak, J.; Chakravarti, A.; Bibby, M. A new finite element model for welding heat sources. Metall. Trans. Trans. A 1984, 15, 299–305. [Google Scholar] [CrossRef]
- Wu, H.; Feng, J.; He, J.; Zhang, B. Three-dimensional calculation of temperature and stress field in Al-Li alloy during electron beam welding by finite element analysis. Weld. Tech. 2004, 6, 10–12. [Google Scholar]






| Cr | C | W | V | Ta | Mn | Si | O | N | P | Ti |
|---|---|---|---|---|---|---|---|---|---|---|
| 8.96 | 0.093 | 1.48 | 0.16 | 0.10 | 0.48 | 0.042 | <0.01 | <0.02 | <0.005 | <0.01 |
| Temperature (K) | Specific Heat (J/(kg K)) | Thermal Conductivity (W/(m K)) | Coefficient of Thermal Expansion (10−6/K) | Yang’s Modulus (GPa) |
|---|---|---|---|---|
| 298 | 443.8 | 17.7 | 11.8 | 214.7 |
| 373 | 474.0 | 18.9 | 12.0 | 211.2 |
| 473 | 512.4 | 20.9 | 12.4 | 205.2 |
| 673 | 608.7 | 24.6 | 13.1 | 187.3 |
| 873 | 803.2 | 26.5 | 13.8 | 162.6 |
| 1073 | 785.4 | 27.2 | 14.6 | 133.6 |
| 1273 | 623.3 | 29.4 | 15.3 | 103.2 |
| 1473 | 658.3 | 31.8 | 16.0 | 74.5 |
| 1673 | 885.3 | 33.7 | 16.7 | 50.6 |
| Voltage Ua (kV) | Beam Current Ib (A) | Focusing Current If (A) | Velocity V (m/s) | Working Distance (m) | Oscillation Shape | Oscillation Frequency fp (Hz) |
|---|---|---|---|---|---|---|
| 150 | 0.05 | 2.448 | 0.005 | 0.42 | circular | 500 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Y.; Wu, J.; Liu, Z.; Liu, S.; Lei, M.; Atif, M.; Liu, Z.; Ma, J. Effect of Pre-Heating and Post-Heating on Electron Beam Welding of Reduced Activation Ferrite/Martensite Steel. J. Nucl. Eng. 2021, 2, 225-238. https://doi.org/10.3390/jne2030021
Zhang Y, Wu J, Liu Z, Liu S, Lei M, Atif M, Liu Z, Ma J. Effect of Pre-Heating and Post-Heating on Electron Beam Welding of Reduced Activation Ferrite/Martensite Steel. Journal of Nuclear Engineering. 2021; 2(3):225-238. https://doi.org/10.3390/jne2030021
Chicago/Turabian StyleZhang, Yong, Jiefeng Wu, Zhihong Liu, Songlin Liu, Mingzhun Lei, Muhammad Atif, Zhenfei Liu, and Jianguo Ma. 2021. "Effect of Pre-Heating and Post-Heating on Electron Beam Welding of Reduced Activation Ferrite/Martensite Steel" Journal of Nuclear Engineering 2, no. 3: 225-238. https://doi.org/10.3390/jne2030021
APA StyleZhang, Y., Wu, J., Liu, Z., Liu, S., Lei, M., Atif, M., Liu, Z., & Ma, J. (2021). Effect of Pre-Heating and Post-Heating on Electron Beam Welding of Reduced Activation Ferrite/Martensite Steel. Journal of Nuclear Engineering, 2(3), 225-238. https://doi.org/10.3390/jne2030021






