Distributional Trends in the Generation and End-Use Sector of Low-Carbon Hydrogen Plants
Abstract
1. Introduction
2. Data
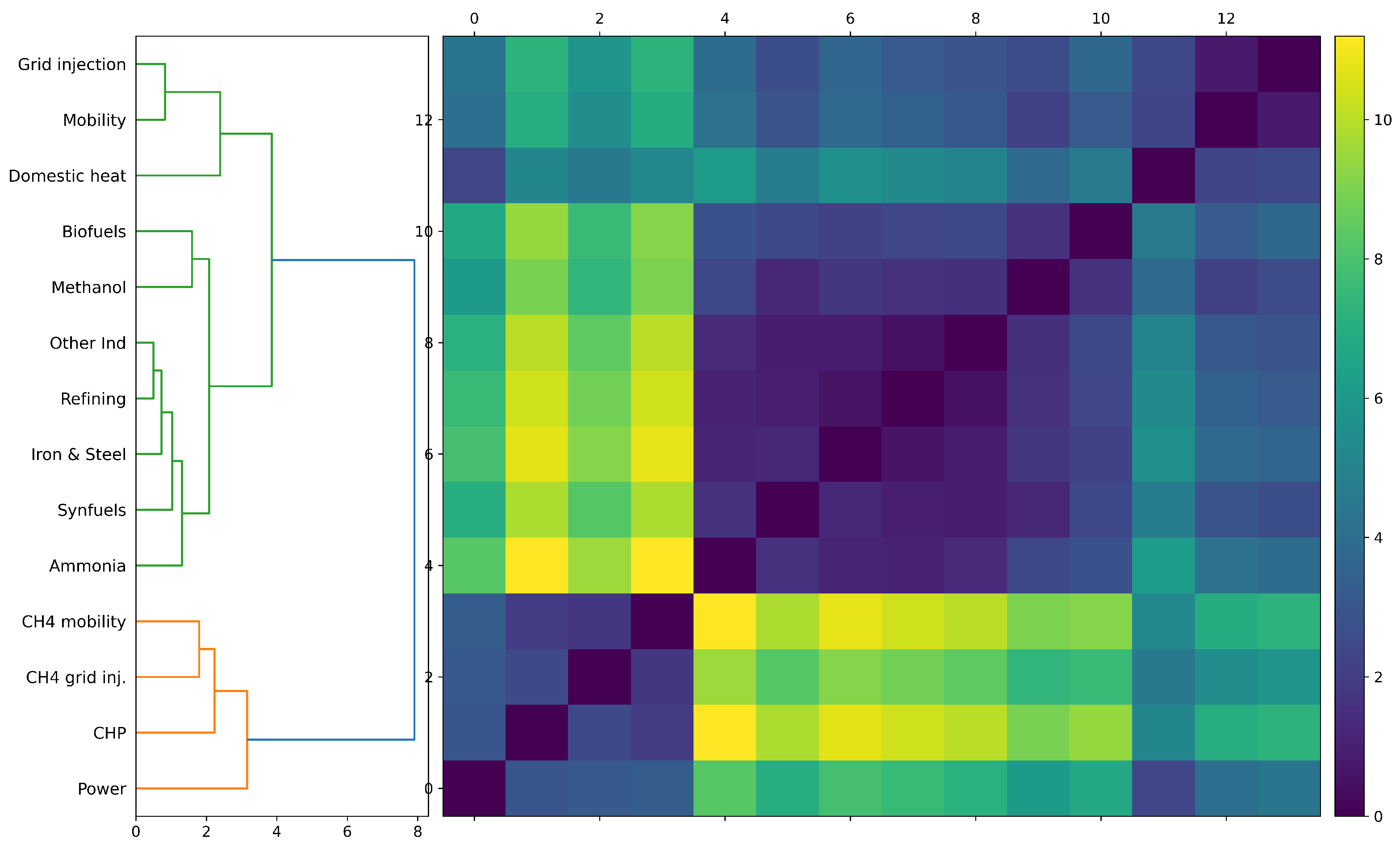
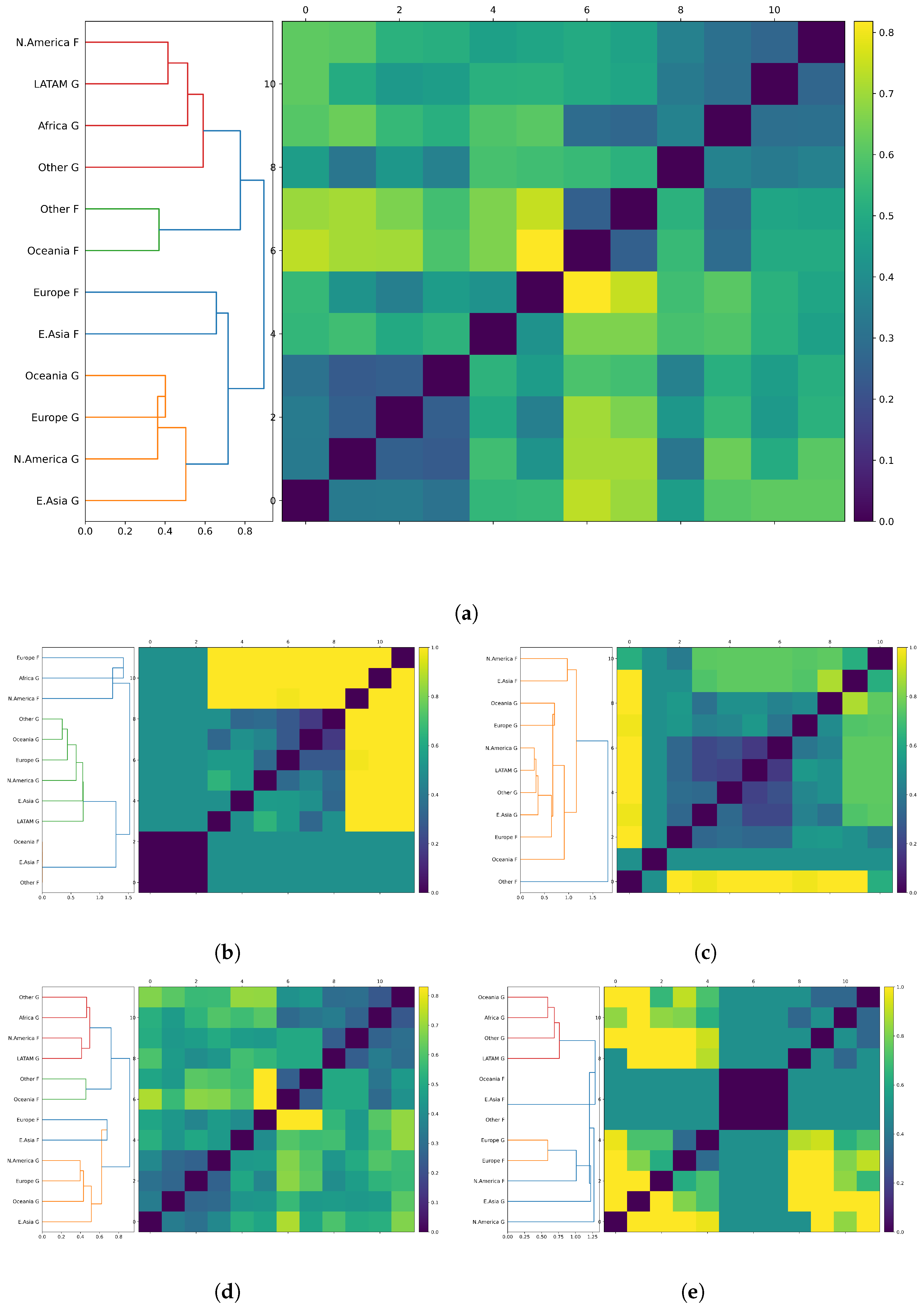
3. Distributions of End-Use Sector Over Time
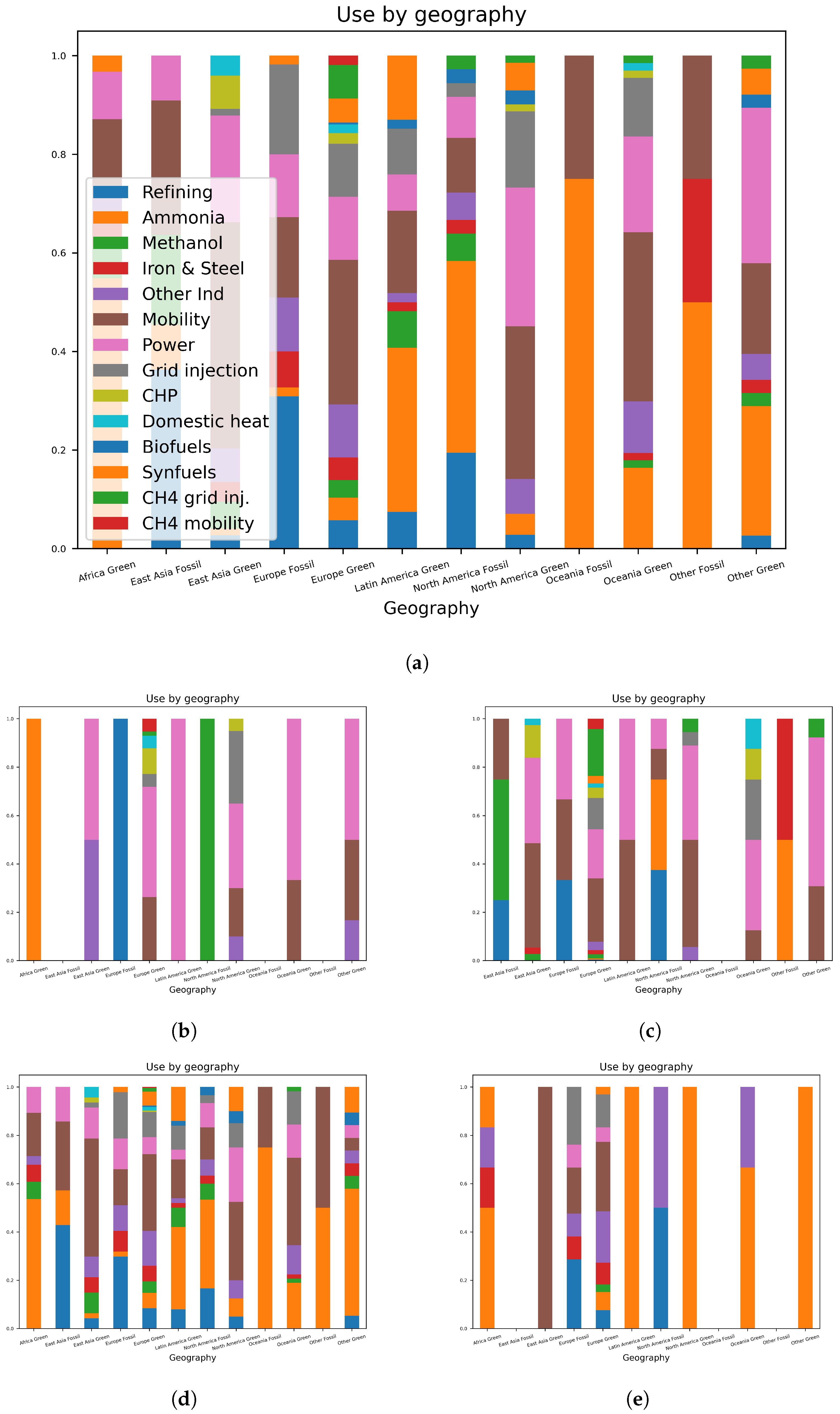
4. Usage Distributions
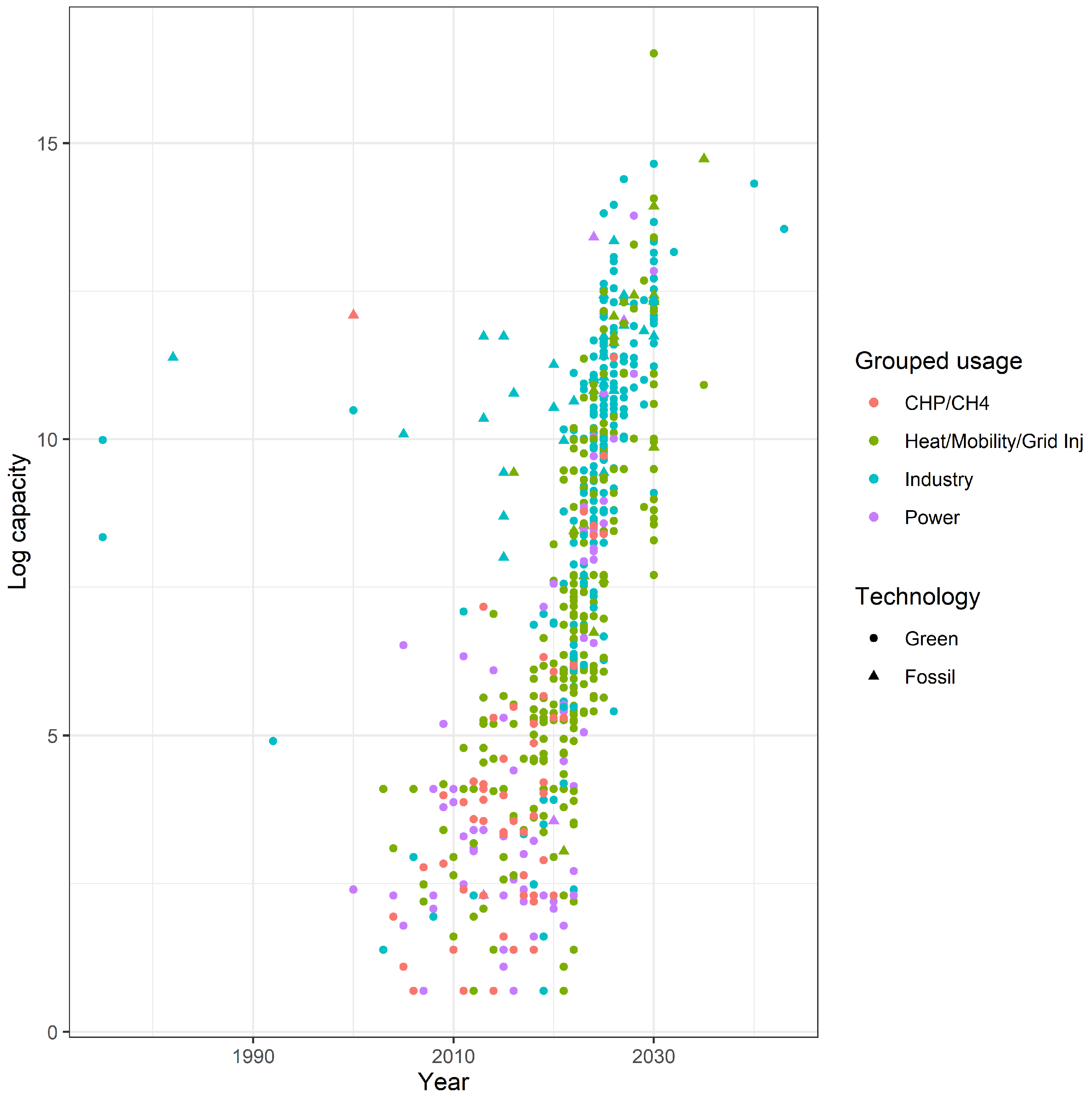
5. Trends in Capacity over Time and Relative to Technology and End-Use Sector
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Probability Distribution Distance
References
- Anandakugan, N.; U.S. Energy Information Administration. Coal Explained: Coal and the Environment. 2022. Available online: https://www.eia.gov/energyexplained/coal/coal-and-the-environment.php (accessed on 26 November 2022).
- Doenitz, W.; Schmidberger, R.; Steinheil, E.; Streicher, R. Hydrogen production by high temperature electrolysis of water vapour. Int. J. Hydrog. Energy 1980, 5, 55–63. [Google Scholar] [CrossRef]
- Wendt, H.; Plzak, V. Hydrogen production by water electrolysis / Wasserstoffproduktion durch Elektrolyse von Wasser. Kerntechnik 1991, 56, 22–28. [Google Scholar] [CrossRef]
- Khaselev, O. High-efficiency integrated multijunction photovoltaic/electrolysis systems for hydrogen production. Int. J. Hydrog. Energy 2001, 26, 127–132. [Google Scholar] [CrossRef]
- Ursua, A.; Gandia, L.M.; Sanchis, P. Hydrogen Production From Water Electrolysis: Current Status and Future Trends. Proc. IEEE 2012, 100, 410–426. [Google Scholar] [CrossRef]
- Chi, J.; Yu, H. Water electrolysis based on renewable energy for hydrogen production. Chin. J. Catal. 2018, 39, 390–394. [Google Scholar] [CrossRef]
- Zeng, K.; Zhang, D. Recent progress in alkaline water electrolysis for hydrogen production and applications. Prog. Energy Combust. Sci. 2010, 36, 307–326. [Google Scholar] [CrossRef]
- Barbir, F. PEM electrolysis for production of hydrogen from renewable energy sources. Sol. Energy 2005, 78, 661–669. [Google Scholar] [CrossRef]
- Grigoriev, S.; Porembsky, V.; Fateev, V. Pure hydrogen production by PEM electrolysis for hydrogen energy. Int. J. Hydrog. Energy 2006, 31, 171–175. [Google Scholar] [CrossRef]
- Bessarabov, D.G.; Wang, H.; Li, H.; Zhao, N. (Eds.) PEM Electrolysis for Hydrogen Production: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Guo, Y.; Li, G.; Zhou, J.; Liu, Y. Comparison between hydrogen production by alkaline water electrolysis and hydrogen production by PEM electrolysis. IOP Conf. Ser. Earth Environ. Sci. 2019, 371, 042022. [Google Scholar] [CrossRef]
- Yilmaz, C.; Kanoglu, M. Thermodynamic evaluation of geothermal energy powered hydrogen production by PEM water electrolysis. Energy 2014, 69, 592–602. [Google Scholar] [CrossRef]
- Rozendal, R.; Hamelers, H.; Euverink, G.; Metz, S.; Buisman, C. Principle and perspectives of hydrogen production through biocatalyzed electrolysis. Int. J. Hydrog. Energy 2006, 31, 1632–1640. [Google Scholar] [CrossRef]
- Call, D.; Logan, B.E. Hydrogen Production in a Single Chamber Microbial Electrolysis Cell Lacking a Membrane. Environ. Sci. Technol. 2008, 42, 3401–3406. [Google Scholar] [CrossRef] [PubMed]
- Rai, C.; Bhui, B.; V, P. Techno-economic analysis of e-waste based chemical looping reformer as hydrogen generator with co-generation of metals, electricity and syngas. Int. J. Hydrog. Energy 2022, 47, 11177–11189. [Google Scholar] [CrossRef]
- Wang, M.; Wang, Z.; Gong, X.; Guo, Z. The intensification technologies to water electrolysis for hydrogen production—A review. Renew. Sustain. Energy Rev. 2014, 29, 573–588. [Google Scholar] [CrossRef]
- Chakik, F.E.; Kaddami, M.; Mikou, M. Effect of operating parameters on hydrogen production by electrolysis of water. Int. J. Hydrog. Energy 2017, 42, 25550–25557. [Google Scholar] [CrossRef]
- Wu, L.; Zhou, Z.; Xiao, Y.; Xu, Z.; Li, X. Hydrogen evolution reaction activity and stability of sintered porous Ni-Cu-Ti-La2O3 cathodes in a wide pH range. Int. J. Hydrog. Energy 2022, 47, 11101–11115. [Google Scholar] [CrossRef]
- Ikeda, H.; Misumi, R.; Kojima, Y.; Haleem, A.A.; Kuroda, Y.; Mitsushima, S. Microscopic high-speed video observation of oxygen bubble generation behavior and effects of anode electrode shape on OER performance in alkaline water electrolysis. Int. J. Hydrog. Energy 2022, 47, 11116–11127. [Google Scholar] [CrossRef]
- Zhang, H.; Lin, G.; Chen, J. Evaluation and calculation on the efficiency of a water electrolysis system for hydrogen production. Int. J. Hydrog. Energy 2010, 35, 10851–10858. [Google Scholar] [CrossRef]
- Shit, S.; Bolar, S.; Kolya, H.; Kang, C.W.; Murmu, N.C.; Kuila, T. Assisting the formation of S-doped FeMoO4 in lieu of an iron oxide/molybdenum sulfide heterostructure: A unique approach towards attaining excellent electrocatalytic water splitting activity. Int. J. Hydrog. Energy 2022, 47, 11128–11142. [Google Scholar] [CrossRef]
- Tong, L.; Liu, Y.; Song, C.; Zhang, Y.; Latthe, S.S.; Liu, S.; Xing, R. (Fe, Ni)S2@MoS2/NiS2 hollow heterostructure nanocubes for high-performance alkaline water electrolysis. Int. J. Hydrog. Energy 2022, 47, 11143–11152. [Google Scholar] [CrossRef]
- Liang, S.; Sui, G.; Li, J.; Guo, D.; Luo, Z.; Xu, R.; Yao, H.; Wang, C.; Chen, S. ZIF-L-derived porous C-doped ZnO/CdS graded nanorods with Z-scheme heterojunctions for enhanced photocatalytic hydrogen evolution. Int. J. Hydrog. Energy 2022, 47, 11190–11202. [Google Scholar] [CrossRef]
- Khasanah, R.A.N.; Lin, H.C.; Ho, H.Y.; Peng, Y.P.; Hsiao, H.L.; Wang, C.R.; Chien, F.S.S. Photoelectrocatalytic hydrolysis of ammonia borane by electrochemical deposited cuprous oxide on titanium dioxide nanotube arrays. Int. J. Hydrog. Energy 2022, 47, 11203–11210. [Google Scholar] [CrossRef]
- Liu, Y.; Shi, X.; Liu, X.; Li, X. Facile synthesis of C-Ta4+ co-doped NaTaO3 and rGO nanocomposites with enhanced visible light photocatalytic performance. Int. J. Hydrog. Energy 2022, 47, 11211–11223. [Google Scholar] [CrossRef]
- Ulate-Kolitsky, E.; Tougas, B.; Huot, J. First Hydrogenation of TiFe with Addition of 20 wt.% Ti. Hydrogen 2022, 3, 379–388. [Google Scholar] [CrossRef]
- He, J.; Han, X.; Xiang, H.; Ran, R.; Wang, W.; Zhou, W.; Shao, Z. Aluminum Cation Doping in Ruddlesden-Popper Sr2TiO4 Enables High-Performance Photocatalytic Hydrogen Evolution. Hydrogen 2022, 3, 501–511. [Google Scholar] [CrossRef]
- Sołowski, G.; Shalaby, M.; Özdemir, F.A. Plastic and Waste Tire Pyrolysis Focused on Hydrogen Production—A Review. Hydrogen 2022, 3, 531–549. [Google Scholar] [CrossRef]
- Shelepova, E.V.; Maksimova, T.A.; Bauman, Y.I.; Mishakov, I.V.; Vedyagin, A.A. Experimental and Simulation Study on Coproduction of Hydrogen and Carbon Nanomaterials by Catalytic Decomposition of Methane-Hydrogen Mixtures. Hydrogen 2022, 3, 450–462. [Google Scholar] [CrossRef]
- Vedyagin, A.A.; Mishakov, I.V.; Korneev, D.V.; Bauman, Y.I.; Nalivaiko, A.Y.; Gromov, A.A. Selected Aspects of Hydrogen Production via Catalytic Decomposition of Hydrocarbons. Hydrogen 2021, 2, 122–133. [Google Scholar] [CrossRef]
- Lys, A.; Fadonougbo, J.O.; Faisal, M.; Suh, J.Y.; Lee, Y.S.; Shim, J.H.; Park, J.; Cho, Y.W. Enhancing the Hydrogen Storage Properties of AxBy Intermetallic Compounds by Partial Substitution: A Short Review. Hydrogen 2020, 1, 38–63. [Google Scholar] [CrossRef]
- Heinemann, N.; Wilkinson, M.; Adie, K.; Edlmann, K.; Thaysen, E.M.; Hassanpouryouzband, A.; Haszeldine, R.S. Cushion Gas in Hydrogen Storage—A Costly CAPEX or a Valuable Resource for Energy Crises? Hydrogen 2022, 3, 550–563. [Google Scholar] [CrossRef]
- Pistidda, C. Solid-State Hydrogen Storage for a Decarbonized Society. Hydrogen 2021, 2, 428–443. [Google Scholar] [CrossRef]
- Ekhtiari, A.; Flynn, D.; Syron, E. Green Hydrogen Blends with Natural Gas and Its Impact on the Gas Network. Hydrogen 2022, 3, 402–417. [Google Scholar] [CrossRef]
- Lattin, W.; Utgikar, V. Transition to hydrogen economy in the United States: A 2006 status report. Int. J. Hydrog. Energy 2007, 32, 3230–3237. [Google Scholar] [CrossRef]
- Park, S. The country-dependent shaping of ‘hydrogen niche’ formation: A comparative case study of the UK and South Korea from the innovation system perspective. Int. J. Hydrog. Energy 2013, 38, 6557–6568. [Google Scholar] [CrossRef]
- Yuan, K.; Lin, W. Hydrogen in China: Policy, program and progress. Int. J. Hydrog. Energy 2010, 35, 3110–3113. [Google Scholar] [CrossRef]
- Collera, A.A.; Agaton, C.B. Opportunities for production and utilization of green hydrogen in the Philippines. Int. J. Energy Econ. Policy 2021, 11, 37–41. [Google Scholar] [CrossRef]
- Ramirez-Salgado, J.; Estrada-Martinez, A. Roadmap towards a sustainable hydrogen economy in Mexico. J. Power Sources 2004, 129, 255–263. [Google Scholar] [CrossRef]
- Touili, S.; Alami Merrouni, A.; Azouzoute, A.; El Hassouani, Y.; Amrani, A.i. A technical and economical assessment of hydrogen production potential from solar energy in Morocco. Int. J. Hydrog. Energy 2018, 43, 22777–22796. [Google Scholar] [CrossRef]
- Apak, S.; Atay, E.; Tuncer, G. Renewable hydrogen energy regulations, codes and standards: Challenges faced by an EU candidate country. Int. J. Hydrog. Energy 2012, 37, 5481–5497. [Google Scholar] [CrossRef]
- James, N.; Menzies, M. Spatio-temporal trends in the propagation and capacity of low-carbon hydrogen projects. Int. J. Hydrog. Energy 2022, 47, 16775–16784. [Google Scholar] [CrossRef]
- Bridgeland, R.; Chapman, A.; McLellan, B.; Sofronis, P.; Fujii, Y. Challenges toward achieving a successful hydrogen economy in the US: Potential end-use and infrastructure analysis to the year 2100. Clean. Prod. Lett. 2022, 3, 100012. [Google Scholar] [CrossRef]
- Saeedmanesh, A.; Kinnon, M.A.M.; Brouwer, J. Hydrogen is essential for sustainability. Curr. Opin. Electrochem. 2018, 12, 166–181. [Google Scholar] [CrossRef]
- Dawood, F.; Anda, M.; Shafiullah, G. Hydrogen production for energy: An overview. Int. J. Hydrog. Energy 2020, 45, 3847–3869. [Google Scholar] [CrossRef]
- Pleshivtseva, Y.; Derevyanov, M.; Pimenov, A.; Rapoport, A. Comprehensive review of low carbon hydrogen projects towards the decarbonization pathway. Int. J. Hydrog. Energy 2023, 48, 3703–3724. [Google Scholar] [CrossRef]
- Manchein, C.; Brugnago, E.L.; da Silva, R.M.; Mendes, C.F.O.; Beims, M.W. Strong correlations between power-law growth of COVID-19 in four continents and the inefficiency of soft quarantine strategies. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 041102. [Google Scholar] [CrossRef] [PubMed]
- James, N.; Menzies, M.; Bondell, H. Comparing the dynamics of COVID-19 infection and mortality in the United States, India, and Brazil. Phys. D Nonlinear Phenom. 2022, 432, 133158. [Google Scholar] [CrossRef]
- Li, H.J.; Xu, W.; Song, S.; Wang, W.X.; Perc, M. The dynamics of epidemic spreading on signed networks. Chaos Solitons Fractals 2021, 151, 111294. [Google Scholar] [CrossRef]
- Blasius, B. Power-law distribution in the number of confirmed COVID-19 cases. Chaos Interdiscip. J. Nonlinear Sci. 2020, 30, 093123. [Google Scholar] [CrossRef]
- James, N.; Menzies, M. Estimating a continuously varying offset between multivariate time series with application to COVID-19 in the United States. Eur. Phys. J. Spec. Top. 2022, 231, 3419–3426. [Google Scholar] [CrossRef]
- Perc, M.; Miksić, N.G.; Slavinec, M.; Stožer, A. Forecasting COVID-19. Front. Phys. 2020, 8, 127. [Google Scholar] [CrossRef]
- Machado, J.A.T.; Lopes, A.M. Rare and extreme events: The case of COVID-19 pandemic. Nonlinear Dyn. 2020, 100, 2953–2972. [Google Scholar] [CrossRef] [PubMed]
- James, N.; Menzies, M. Global and regional changes in carbon dioxide emissions: 1970–2019. Phys. A Stat. Mech. Appl. 2022, 608, 128302. [Google Scholar] [CrossRef]
- Khan, M.K.; Khan, M.I.; Rehan, M. The relationship between energy consumption, economic growth and carbon dioxide emissions in Pakistan. Financ. Innov. 2020, 6, 1. [Google Scholar] [CrossRef]
- James, N.; Menzies, M. Equivalence relations and Lp distances between time series with application to the Black Summer Australian bushfires. Phys. D Nonlinear Phenom. 2023, 448, 133693. [Google Scholar] [CrossRef]
- Drożdż, S.; Kwapień, J.; Oświęcimka, P. Complexity in Economic and Social Systems. Entropy 2021, 23, 133. [Google Scholar] [CrossRef] [PubMed]
- James, N.; Menzies, M.; Gottwald, G.A. On financial market correlation structures and diversification benefits across and within equity sectors. Phys. A Stat. Mech. Appl. 2022, 604, 127682. [Google Scholar] [CrossRef]
- Liu, Y.; Cizeau, P.; Meyer, M.; Peng, C.K.; Stanley, H.E. Correlations in economic time series. Phys. A Stat. Mech. Appl. 1997, 245, 437–440. [Google Scholar] [CrossRef]
- Basalto, N.; Bellotti, R.; Carlo, F.D.; Facchi, P.; Pantaleo, E.; Pascazio, S. Hausdorff clustering of financial time series. Phys. A Stat. Mech. Appl. 2007, 379, 635–644. [Google Scholar] [CrossRef]
- Wątorek, M.; Kwapień, J.; Drożdż, S. Financial Return Distributions: Past, Present, and COVID-19. Entropy 2021, 23, 884. [Google Scholar] [CrossRef]
- Prakash, A.; James, N.; Menzies, M.; Francis, G. Structural Clustering of Volatility Regimes for Dynamic Trading Strategies. Appl. Math. Financ. 2021, 28, 236–274. [Google Scholar] [CrossRef]
- Drożdż, S.; Grümmer, F.; Ruf, F.; Speth, J. Towards identifying the world stock market cross-correlations: DAX versus Dow Jones. Phys. A Stat. Mech. Appl. 2001, 294, 226–234. [Google Scholar] [CrossRef]
- James, N.; Menzies, M.; Chin, K. Economic state classification and portfolio optimisation with application to stagflationary environments. Chaos Solitons Fractals 2022, 164, 112664. [Google Scholar] [CrossRef]
- Gębarowski, R.; Oświęcimka, P.; Wątorek, M.; Drożdż, S. Detecting correlations and triangular arbitrage opportunities in the Forex by means of multifractal detrended cross-correlations analysis. Nonlinear Dyn. 2019, 98, 2349–2364. [Google Scholar] [CrossRef]
- James, N.; Menzies, M. A new measure between sets of probability distributions with applications to erratic financial behavior. J. Stat. Mech. Theory Exp. 2021, 2021, 123404. [Google Scholar] [CrossRef]
- Sigaki, H.Y.D.; Perc, M.; Ribeiro, H.V. Clustering patterns in efficiency and the coming-of-age of the cryptocurrency market. Sci. Rep. 2019, 9, 1440. [Google Scholar] [CrossRef] [PubMed]
- Drożdż, S.; Kwapień, J.; Oświęcimka, P.; Stanisz, T.; Wątorek, M. Complexity in Economic and Social Systems: Cryptocurrency Market at around COVID-19. Entropy 2020, 22, 1043. [Google Scholar] [CrossRef]
- James, N.; Menzies, M. Collective correlations, dynamics, and behavioural inconsistencies of the cryptocurrency market over time. Nonlinear Dyn. 2022, 107, 4001–4017. [Google Scholar] [CrossRef]
- Drożdż, S.; Minati, L.; Oświęcimka, P.; Stanuszek, M.; Wątorek, M. Competition of noise and collectivity in global cryptocurrency trading: Route to a self-contained market. Chaos: Interdiscip. J. Nonlinear Sci. 2020, 30, 023122. [Google Scholar] [CrossRef] [PubMed]
- Wątorek, M.; Drożdż, S.; Kwapień, J.; Minati, L.; Oświęcimka, P.; Stanuszek, M. Multiscale characteristics of the emerging global cryptocurrency market. Phys. Rep. 2021, 901, 1–82. [Google Scholar] [CrossRef]
- James, N.; Menzies, M. Dual-domain analysis of gun violence incidents in the United States. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 111101. [Google Scholar] [CrossRef]
- Perc, M.; Donnay, K.; Helbing, D. Understanding Recurrent Crime as System-Immanent Collective Behavior. PLoS ONE 2013, 8, e76063. [Google Scholar] [CrossRef]
- James, N.; Menzies, M.; Chok, J.; Milner, A.; Milner, C. Geometric persistence and distributional trends in worldwide terrorism. Chaos Solitons Fractals 2023, 169, 113277. [Google Scholar] [CrossRef]
- Ribeiro, H.V.; Mukherjee, S.; Zeng, X.H.T. Anomalous diffusion and long-range correlations in the score evolution of the game of cricket. Phys. Rev. E 2012, 86, 022102. [Google Scholar] [CrossRef]
- James, N.; Menzies, M. Optimally adaptive Bayesian spectral density estimation for stationary and nonstationary processes. Stat. Comput. 2022, 32, 45. [Google Scholar] [CrossRef]
- Merritt, S.; Clauset, A. Scoring dynamics across professional team sports: Tempo, balance and predictability. EPJ Data Sci. 2014, 3, 4. [Google Scholar] [CrossRef]
- James, N.; Menzies, M.; Bondell, H. In search of peak human athletic potential: A mathematical investigation. Chaos Interdiscip. J. Nonlinear Sci. 2022, 32, 023110. [Google Scholar] [CrossRef]
- Clauset, A.; Kogan, M.; Redner, S. Safe leads and lead changes in competitive team sports. Phys. Rev. E 2015, 91, 062815. [Google Scholar] [CrossRef]
- International Energy Agency. Hydrogen Projects Database. 2022. Available online: https://www.iea.org/data-and-statistics/data-product/hydrogen-projects-database (accessed on 1 November 2022).
- Ward, J.H. Hierarchical Grouping to Optimize an Objective Function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Szekely, G.J.; Rizzo, M.L. Hierarchical Clustering via Joint Between-Within Distances: Extending Ward’s Minimum Variance Method. J. Classif. 2005, 22, 151–183. [Google Scholar] [CrossRef]
- Müllner, D. Fastcluster: Fast Hierarchical, Agglomerative Clustering Routines forRandPython. J. Stat. Softw. 2013, 53, 1–18. [Google Scholar] [CrossRef]
- James, N.; Menzies, M.; Bondell, H. Understanding spatial propagation using metric geometry with application to the spread of COVID-19 in the United States. Europhys. Lett. 2021, 135, 48004. [Google Scholar] [CrossRef]
- James, G.; Witten, D.; Hastie, T.; Tibshirani, R. An Introduction to Statistical Learning; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. Carbon Dioxide Capture and Storage. 2005. Available online: https://www.ipcc.ch/site/assets/uploads/2018/03/srccs_wholereport-1.pdf (accessed on 26 November 2022).
- Kantorovich, L.V.; Rubinstein, G. On a space of completely additive functions. Vestn. Leningr. Univ. 1958, 13, 52–59. [Google Scholar]

| Adjusted | No Separation by Tech | Stratified by Tech | ||
|---|---|---|---|---|
| Grouped Sectors | All Sectors | Grouped Sectors | All Sectors | |
| Capacity | 0.0255 | 0.0204 | 0.0273 | 0.0226 |
| Log capacity | 0.569 | 0.587 | 0.607 | 0.622 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
James, N.; Menzies, M. Distributional Trends in the Generation and End-Use Sector of Low-Carbon Hydrogen Plants. Hydrogen 2023, 4, 174-189. https://doi.org/10.3390/hydrogen4010012
James N, Menzies M. Distributional Trends in the Generation and End-Use Sector of Low-Carbon Hydrogen Plants. Hydrogen. 2023; 4(1):174-189. https://doi.org/10.3390/hydrogen4010012
Chicago/Turabian StyleJames, Nick, and Max Menzies. 2023. "Distributional Trends in the Generation and End-Use Sector of Low-Carbon Hydrogen Plants" Hydrogen 4, no. 1: 174-189. https://doi.org/10.3390/hydrogen4010012
APA StyleJames, N., & Menzies, M. (2023). Distributional Trends in the Generation and End-Use Sector of Low-Carbon Hydrogen Plants. Hydrogen, 4(1), 174-189. https://doi.org/10.3390/hydrogen4010012






