Cushion Gas in Hydrogen Storage—A Costly CAPEX or a Valuable Resource for Energy Crises?
Abstract
1. Introduction
- Open saline aquifers are mostly hydrostatically pressured; as such, injecting in an open system leads to a pressure build-up. This can initially restrict injection rates, but will equilibrate with time, depending on how well the aquifer is hydraulically connected to the regional geology. When gas is injected into a saline aquifer, two-phase flow of hydrogen and brine can be expected.
- Open saline aquifers are often poorly characterised because their exploration has, so far, been of little commercial value. However, the low well density reduces the risk of leakage via abandoned wells, which is considered to be a major threat to gas storage containment [14].
- Saline aquifers are geologically connected to sedimentary basins, which occur worldwide. The size of individual anticlines, potential storage targets, can also be significant, such as the Bunter Sandstone dome structures in the Southern North Sea [15].
- Saline aquifer storage sites (in comparison to depleted gas fields) will most likely require infrastructure investment. The cost of expensive infrastructure required for the storage operation could be significantly reduced by storage in sites close to already existing infrastructure; however, legacy infrastructure would require certification to be hydrogen compatible.
2. Methodology
2.1. Hydrogen Storage Demand Scenario
2.2. Reservoir Model
2.3. Scenario Schedule
- CG is injected during the first year and is controlled by a maximum allowed BHP, and, hence, the amount of CG injected depends on the duration of CG injection. The maximum CG injection time is one year.
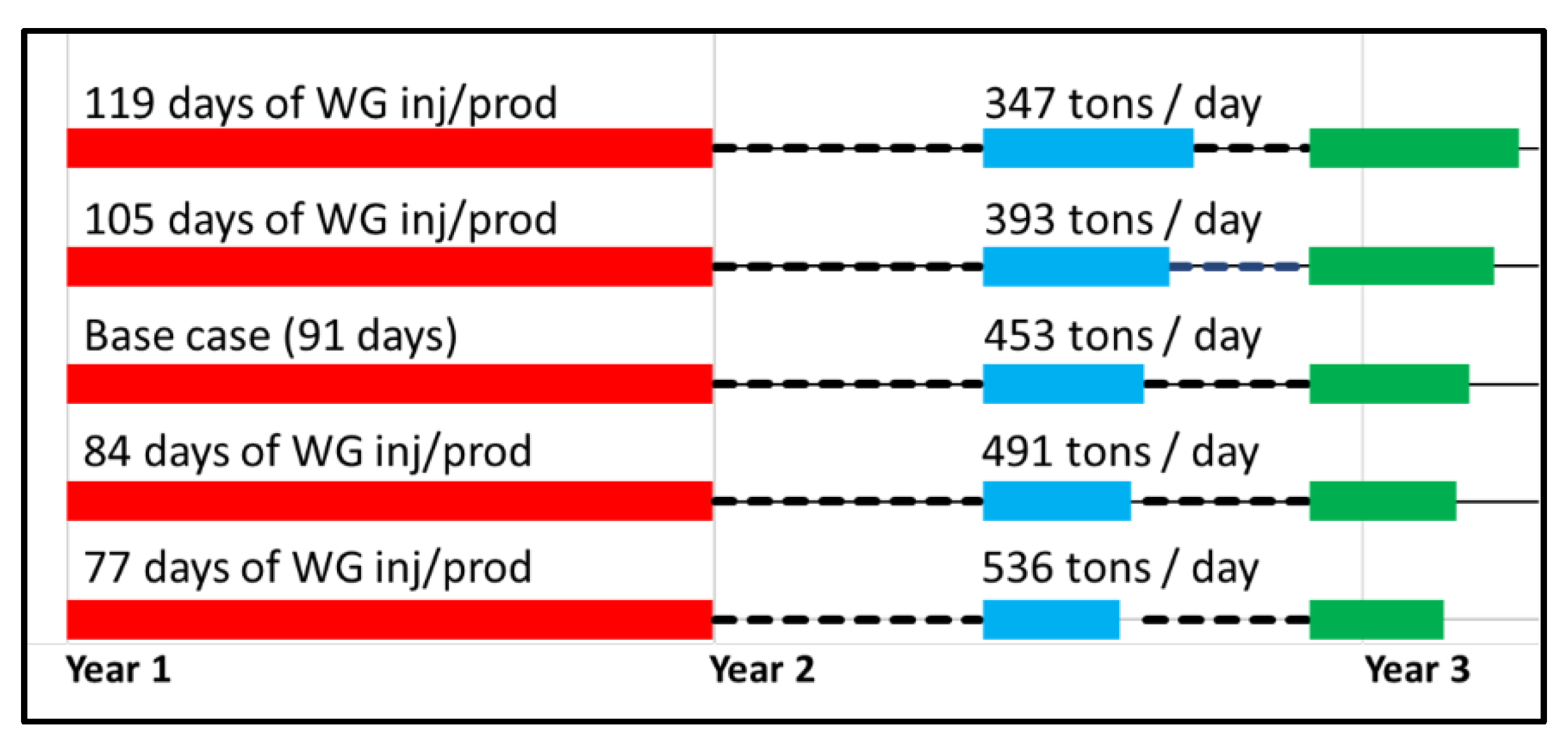
- The second year of operation starts with a rest phase of five months (January–May) for the CG injection pressure to equilibrate.
- After the rest phase, the three-month WG injection period (June–August) commences and is succeeded by a rest phase of three months (September–November).
- WG production starts at the beginning of December and lasts for 91 days, until the beginning of March.
2.4. The Base Case
2.5. Technical Optimisation Tests
- (1)
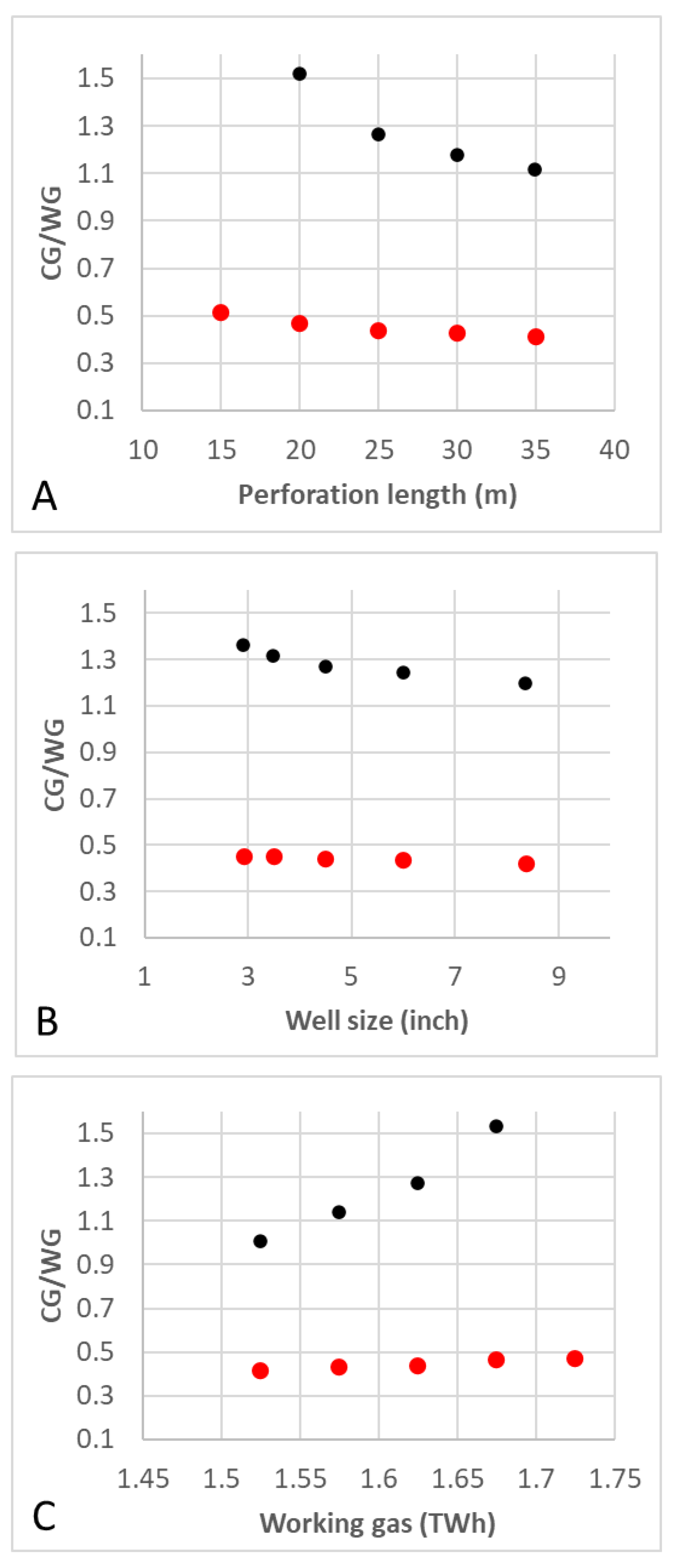
- The perforation length: The perforation length determines how deep the open well penetrates the reservoir from the roof of the reservoir. The base case has a perforation of 25 m, and the sensitivity tests investigate a length between 15 m and 35 m.
- (2)
- The well diameter: The well diameter determines the size of the injection and production well and, hence, how much fluid can travel through the well for a fixed pressure gradient. The base case well had a diameter of 4.5″, and the sensitivity tests investigate a well diameter between 2.925″ and 8.378″.
- (3)
- WG target: This simulation tests if a change in the WG target will change the CG/WG ratio, essentially evaluating whether smaller or bigger scenarios are preferable in terms of CG requirements. The base case WG target was 1.625 TWh worth of hydrogen, and the sensitivity tests investigate WG targets between 1.525 TWh and 1.725 TWh.
- (4)
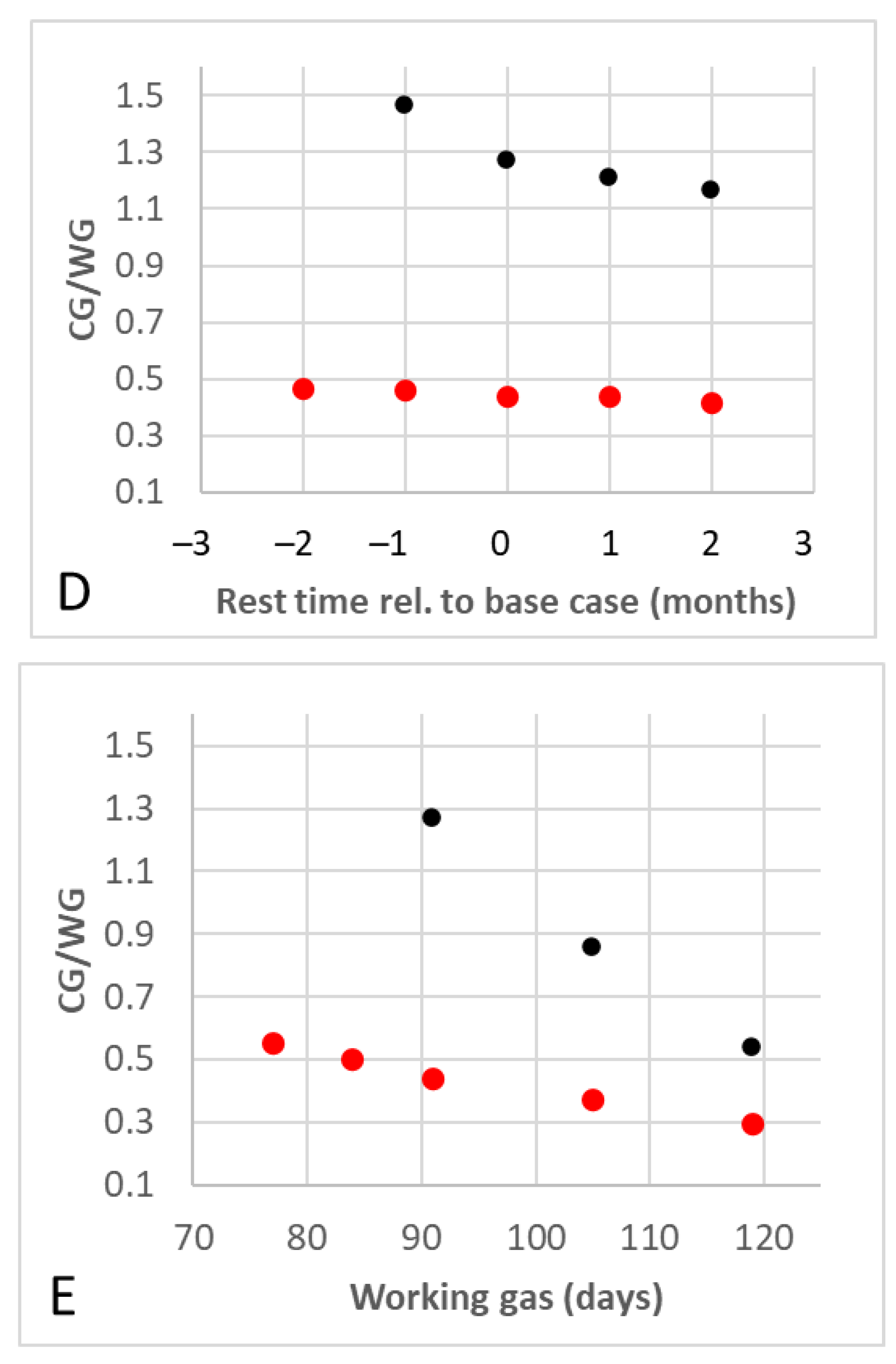
- Rest time after CG injection: The rest time is the time the reservoir is given to equilibrate after the CG injection. For the base case, the rest time is at least 5 months, following a CG injection period lasting the entire first year. The rest time is longer than 5 months for scenarios with shorter CG injection periods. The sensitivity tests investigate a rest time of at least 3 to 7 months.
- (5)
- WG inj/prod duration (Figure 2): The base case injects and produces WG for 91 days with a 91-day rest period in between. This sensitivity test increases or decreases the duration of the injection, while decreasing and increasing the injection and production rate target accordingly to maintain the 1.625 TWh target, respectively, at the expense of the rest time between WG injection and production. The production duration is also adjusted in the same way, by extending or shortening the production period and increasing or decreasing the production rate target.
3. Results and Discussion
3.1. Base Case Scenario
3.2. Sensitivity Tests
- Firstly, gas dependent countries would have a national strategic gas reserve. Strategic reserves are known from oil; they act as emergency resources if, for political or other reasons, oil supply is hindered. National, or international, strategic gas reserves will most likely be discussed in Europe soon, as Russia as the main supplier has started reducing gas supply as a political measure.
- Secondly, the implementation of natural gas storage projects would become cheaper, and, hence, more gas storage projects will be installed, increasing energy security and reducing gas cost spikes, as recently seen.
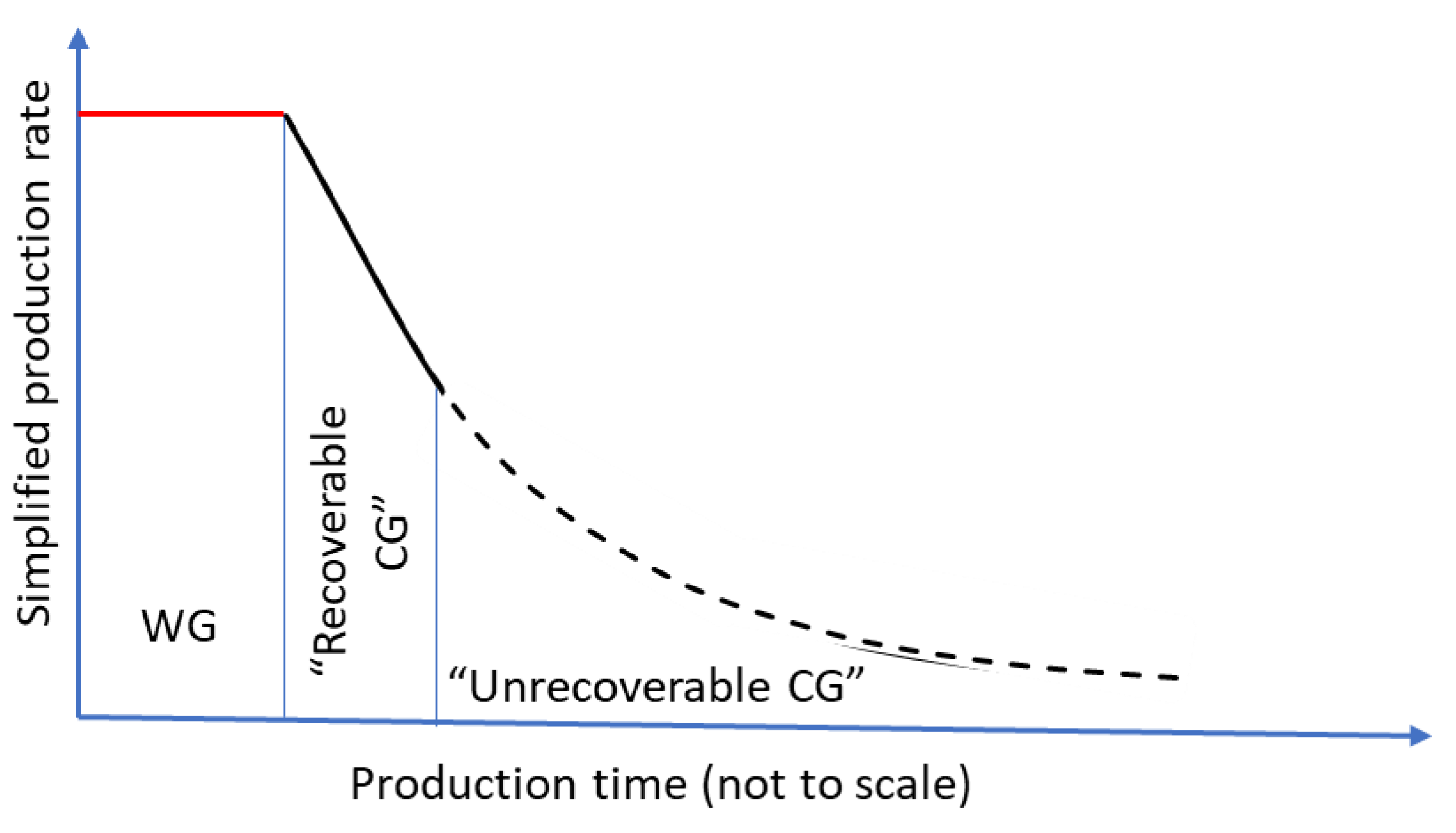
- Thirdly, the incentive to invest into hydrogen storage would also increase. As hydrogen is a valuable commodity, the usage of vast amounts of hydrogen as essential, but ordinarily unused (i.e., not produced to the surface) CG, is an obstacle for the implementation of large-scale hydrogen storage. If classified as “recoverable CG” and paid for by national governments, hydrogen storage would become cheaper for a site operator, and the decarbonisation of energy supply could make a big step forward.
4. Summary and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Miocic, J.M.; Heinemann, N.; Edlmann, K.; Scafidi, J.; Molaei, F.; Alcalde, J. Underground hydrogen storage: A review. In Miocic, Heinemann, Edlmann, Alcalde, Schultz: Enabling Secure Subsurface Storage in Future Energy Systems; Geological Society of London Special Publication: London, UK, 2022; p. 528. [Google Scholar] [CrossRef]
- Tarkowski, R.; Uliasz-Misiak, B. Towards underground hydrogen storage: A review of barriers. Renew. Sustain. Energy Rev. 2022, 162, 112451. [Google Scholar] [CrossRef]
- Engeland, K.; Borga, M.; Creutin, J.D.; Francois, B.; Ramos, M.H.; Vidal, J.P. Space-time variability of climate variables and intermittent renewable electricity production—A review. Renew. Sustain. Energy Rev. 2017, 79, 600–617. [Google Scholar] [CrossRef]
- Sun, X.; Alcalde, J.; Bakhtbidar, M.; Elío, J.; Vilarrasa, V.; Canal, J.; Ballesteros, J.; Heinemann, N.; Haszeldine, S.; Cavanagh, A.; et al. Hubs and clusters approach to unlock the development of carbon capture and storage–Case study in Spain. Appl. Energy 2021, 300, 117418. [Google Scholar] [CrossRef]
- Cavanagh, A.; Wilkinson, M.; Haszeldine, S. Deliverable D2.1 Report: Methodologies for Cluster Development and Best Practices for Data Collection in the Promising Regions. Part 2: Bridging the Gap Storage Resource Assessment Methodologies. 2020. Available online: https://www.strategyccus.eu/sites/default/files/STRATCCUSWP21-PART2-SRAM-v1.pdf (accessed on 2 December 2022).
- Hassanpouryouzband, A.; Joonaki, E.; Edlmann, K.; Haszeldine, R.S. Offshore Geological Storage of Hydrogen: Is This Our Best Option to Achieve Net-Zero? ACS Energy Lett. 2021, 6, 2181–2186. [Google Scholar] [CrossRef]
- Mouli-Castillo, J.; Heinemann, N.; Edlmann, K. Mapping geological hydrogen storage capacity and regional heating demands: An applied UK case study. Appl. Energy 2021, 283, 116348. [Google Scholar] [CrossRef]
- Kanaani, M.; Sedaee, B.; Asadian-Pakfar, M. Role of Cushion Gas on Underground Hydrogen Storage in Depleted Oil Reservoirs. J. Energy Storage 2022, 45, 103783. [Google Scholar] [CrossRef]
- Wang, G.; Pickup, G.; Sorbie, K.; Mackay, E. Scaling analysis of hydrogen flow with carbon dioxide cushion gas in subsurface heterogeneous porous media. Int. J. Hydrog. Energy 2022, 47, 1752–1764. [Google Scholar] [CrossRef]
- Scafidi, J.; Schirrer, L.; Vervoort, I.; Heinemann, N. An open-source tool for the calculation of field deliverability and cushion gas requirements in volumetric gas reservoir storage sites. Geol. Soc. Lond. Spec. Publ. 2022, 528, SP528-2022. [Google Scholar] [CrossRef]
- Heinemann, N.; Scafidi, J.; Pickup, G.; Thaysen, E.M.; Hassanpouryouzband, A.; Wilkinson, M.; Satterley, A.K.; Booth, M.G.; Edlmann, K.; Haszeldine, R.S. Hydrogen storage in saline aquifers: The role of cushion gas for injection and production. Int. J. Hydrog. Energy 2021, 46, 39284–39296. [Google Scholar] [CrossRef]
- Matos, C.R.; Carneiro, J.F.; Silva, P.P. Overview of Large-Scale Underground Energy Storage Technologies for Integration of Renewable Energies and Criteria for Reservoir Identification. J. Energy Storage 2019, 21, 241–258. [Google Scholar] [CrossRef]
- Wallace, R.L.; Cai, Z.; Zhang, H.; Zhang, K.; Guo, C. Utility-scale subsurface hydrogen storage: UK perspectives and technology. Int. J. Hydrog. Energy 2021, 46, 25137–25259. [Google Scholar] [CrossRef]
- Alcalde, J.; Flude, S.; Wilkinson, M.; Johnson, G.; Edlmann, K.; Bond, C.E.; Scott, V.; Gilfillan, S.M.V.; Ogaya, X.; Haszeldine, R.S. Estimating geological CO2 storage security to deliver on climate mitigation. Nat. Commun. 2019, 9, 2201. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.D.O.; Jin, M.; Bentham, M.; Pickup, G.E.; Hannis, S.D.; Mackay, E.J. Modelling carbon dioxide storage within closed structures in the UK Bunter Sandstone Formation. Int. J. Greenh. Gas Control. 2013, 18, 38–50. [Google Scholar] [CrossRef]
- Thaysen, E.M.; McMahon, S.; Strobel, G.J.; Butler, I.B.; Ngwenya, B.T.; Heinemann, N.; Wilkinson, M.; Hassanpouryouzband, A.; McDermott, C.; Edlmann, K. Estimating Microbial Growth and Hydrogen Consumption in Hydrogen Storage in Porous Media. Renew. Sustain. Energy Rev. 2021, 151, 111481. [Google Scholar] [CrossRef]
- Gregory, S.P.; Barnett, M.J.; Field, L.P.; Milodowski, A.E. Subsurface microbial hydrogen cycling: Natural occurrence and implications for industry. Microorganisms 2019, 7, 53. [Google Scholar] [CrossRef]
- CMG. ‘GEM’. 2021. Available online: https://www.cmgl.ca/gem (accessed on 2 December 2022).
- Bentham, M. An assessment of carbon sequestration potential in the UK—Southern North Sea case study. Tyndall Cent. Clim. Change Res. Work. Pap. 2006, 85. [Google Scholar]
- Gammer, D.; Green, A.; Holloway, S.; Smith, G. The Energy Technologies Institute’s UK CO2 Storage Appraisal Project (UKSAP). In SPE 148426, Proceedings of the SPE Offshore Europe Oil and Gas Conference and Exhibition, Aberdeen, UK, 6–8 September 2011. [Google Scholar]
- Gluyas, J.G.; Hichens, H.M. The United Kingdom Oil and Gas Fields Commemorative Millennium Volume; Gluyas, J.G., Hichens, H.M., Eds.; Memoirs of the Geological Society of London: London, UK, 2003. [Google Scholar]
- Yekta, A.E.; Manceau, J.-C.; Gaboreau, S.; Pichavant, M.; Audigane, P. Determination of Hydrogen–Water Relative Permeability and Capillary Pressure in Sandstone: Application to Underground Hydrogen Injection in Sedimentary Formations. Transp. Porous Media 2018, 122, 333–356. [Google Scholar] [CrossRef]
- Fetkovitch, M.J. A simplified approach to water influx calculations—Finite aquifer systems. J. Pet. Technol. 1971, 23, 814–828. [Google Scholar] [CrossRef]
- Carden, P.O.; Paterson, L. Physical, chemical and energy aspects of underground hydrogen storage. Int. J. Hydrog. Energy 1979, 4, 559–569. [Google Scholar] [CrossRef]
- Amid, A.; Mignard, D.; Wilkinson, M. Seasonal storage of hydrogen in a depleted natural gas reservoir. Int. J. Hydrog. Storage 2016, 41, 5549–5558. [Google Scholar] [CrossRef]
- Jossi, J.A.; Stiel, L.I.; Thodos, G. The viscosity of pure substances in the dense gaseous and liquid phases. Am. Inst. Chem. Eng. J. 1962, 8, 59–63. [Google Scholar] [CrossRef]
- Stiel, L.I.; Thodos, G. The viscosity of nonpolar gases at normal pressures. Am. Inst. Chem. Eng. J. 1961, 7, 611–615. [Google Scholar] [CrossRef]
- Peaceman, D.W. Interpretation of well-block pressures in numerical reservoir simulation with nonsquare grid blocks and anisotropic permeability. SPE J. 1983, 23, 531–543. [Google Scholar] [CrossRef]
- Peaceman, D.W. Interpretation of well-block pressures in numerical reservoir simulation: Part 3: Off-center and multiple wells within a well-block. In SPE 16976, Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 27–30 September 1987. [Google Scholar]
- Aziz, K.; Govier, G.W. Pressure drop in wells producing oil and gas. J. Can. Pet. Technol. 1972, 11, 3. [Google Scholar] [CrossRef]
- Dodds, P.E.; Demoullin, S. Conversion of the UK gas system to transport hydrogen. Int. J. Hydrog. Energy 2013, 38, 18. [Google Scholar] [CrossRef]
- Miocic, J.M.; Alcalde, J.; Heinemann, N.; Marzan, I.; Hangx, S. Toward Energy-Independence and Net-Zero: The Inevitability of Subsurface Storage in Europe. ACS Energy Lett. 2022, 7, 2486–2489. [Google Scholar] [CrossRef]

| Reservoir thickness | 100 m |
| Water depth | 100 m |
| Horizontal permeability | 200 mD |
| Vertical permeability | 50 mD |
| Porosity | 20% |
| Brine salinity | 3.13 gmol NaCl/L |
| Hydrostatic gradient | 10.07 MPa/km |
| Lithostatic gradient | 22.7 MPa/km |
| Fracture pressure | 18 MPa/km |
| Temperature gradient | 3.65 °C/km |
| Surface temperature | 4 °C |
| Technical Parameter | Base Case | Additional Scenario Ranges |
|---|---|---|
| Perforation length | 25 m | 15–35 m |
| Well diameter | 4.5 | 2.925–8.375 |
| Working gas target | 1.625 TWh | 1.525–1.725 TWh |
| Rest time | 5+ months | 3+–7+ months |
| Working gas inj/prod duration | 91 days | 77–119 days |
| Scenario | Optimal Injection | Optimal Production | Best Case |
|---|---|---|---|
| (CG/WG) | (CG/WG) | (CG/WG) | |
| Base case | 1.27 | 0.44 | 1.27 |
| Perforation length | |||
| 15 m | failed | 0.52 | failed |
| 20 m | 1.52 | 0.47 | 1.52 |
| 30 m | 1.18 | 0.43 | 1.18 |
| 35 m | 1.12 | 0.42 | 1.12 |
| Well size | |||
| 2.925″ | 1.36 | 0.45 | 1.36 |
| 3.5″ | 1.32 | 0.45 | 1.32 |
| 6″ | 1.24 | 0.44 | 1.24 |
| 8.375″ | 1.20 | 0.42 | 1.20 |
| Working gas volume | |||
| 1.525 TWh | 1.00 | 0.41 | 1.00 |
| 1.575 TWh | 1.14 | 0.43 | 1.14 |
| 1.675 TWh | 1.53 | 0.46 | 1.53 |
| 1.725 TWh | failed | 0.47 | failed |
| Rest time | |||
| 2 months shorter | failed | 0.46 | failed |
| 1 month shorter | 1.46 | 0.46 | 1.46 |
| 1 month longer | 1.21 | 0.44 | 1.21 |
| 2 months longer | 1.17 | 0.42 | 1.17 |
| Working gas injection/production duration | |||
| 77 days | failed | 0.55 | failed |
| 84 days | failed | 0.50 | failed |
| 105 days | 0.86 | 0.37 | 0.86 |
| 119 days | 0.54 | 0.29 | 0.54 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heinemann, N.; Wilkinson, M.; Adie, K.; Edlmann, K.; Thaysen, E.M.; Hassanpouryouzband, A.; Haszeldine, R.S. Cushion Gas in Hydrogen Storage—A Costly CAPEX or a Valuable Resource for Energy Crises? Hydrogen 2022, 3, 550-563. https://doi.org/10.3390/hydrogen3040035
Heinemann N, Wilkinson M, Adie K, Edlmann K, Thaysen EM, Hassanpouryouzband A, Haszeldine RS. Cushion Gas in Hydrogen Storage—A Costly CAPEX or a Valuable Resource for Energy Crises? Hydrogen. 2022; 3(4):550-563. https://doi.org/10.3390/hydrogen3040035
Chicago/Turabian StyleHeinemann, Niklas, Mark Wilkinson, Kate Adie, Katriona Edlmann, Eike Marie Thaysen, Aliakbar Hassanpouryouzband, and Robert Stuart Haszeldine. 2022. "Cushion Gas in Hydrogen Storage—A Costly CAPEX or a Valuable Resource for Energy Crises?" Hydrogen 3, no. 4: 550-563. https://doi.org/10.3390/hydrogen3040035
APA StyleHeinemann, N., Wilkinson, M., Adie, K., Edlmann, K., Thaysen, E. M., Hassanpouryouzband, A., & Haszeldine, R. S. (2022). Cushion Gas in Hydrogen Storage—A Costly CAPEX or a Valuable Resource for Energy Crises? Hydrogen, 3(4), 550-563. https://doi.org/10.3390/hydrogen3040035









