Supercriticality, Glassy Dynamics, and the New Insight into Melting/Freezing Discontinuous Transition in Linseed Oil
Abstract
1. Introduction
2. Materials and Methods
3. Comments on Critical Phenomena, Supercriticality, and Melting/Freezing Discontinuous Transition
4. Results and Discussion
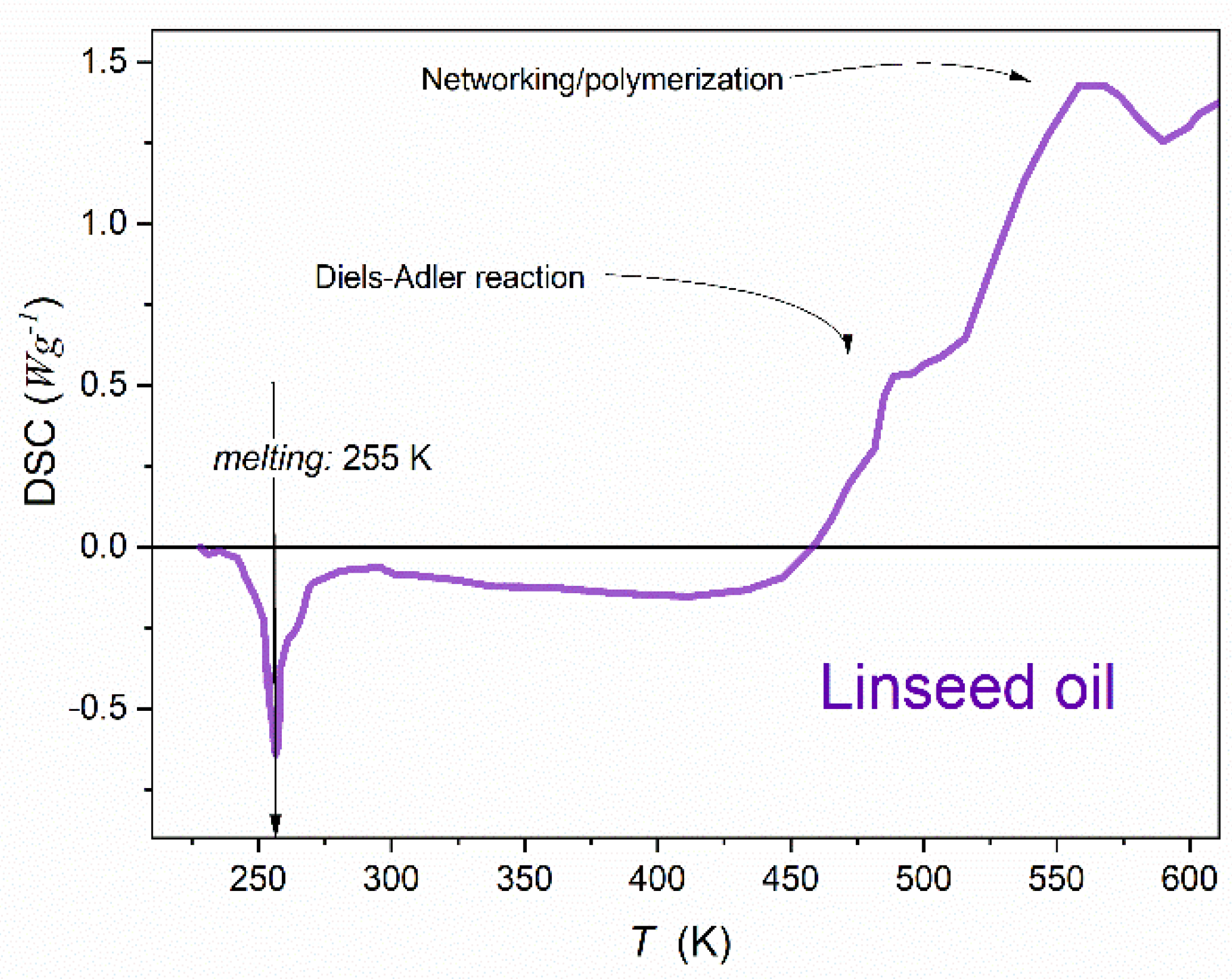
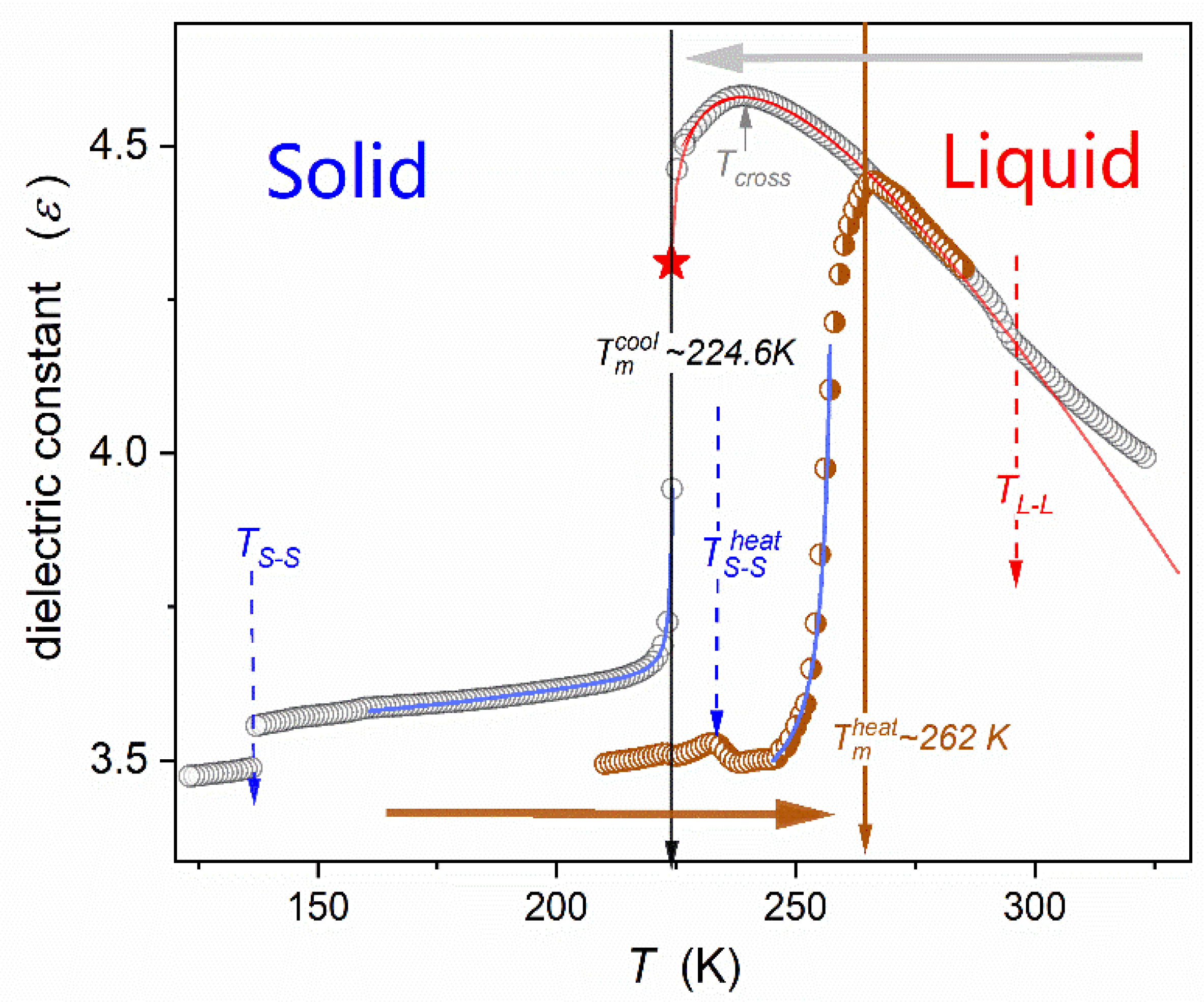
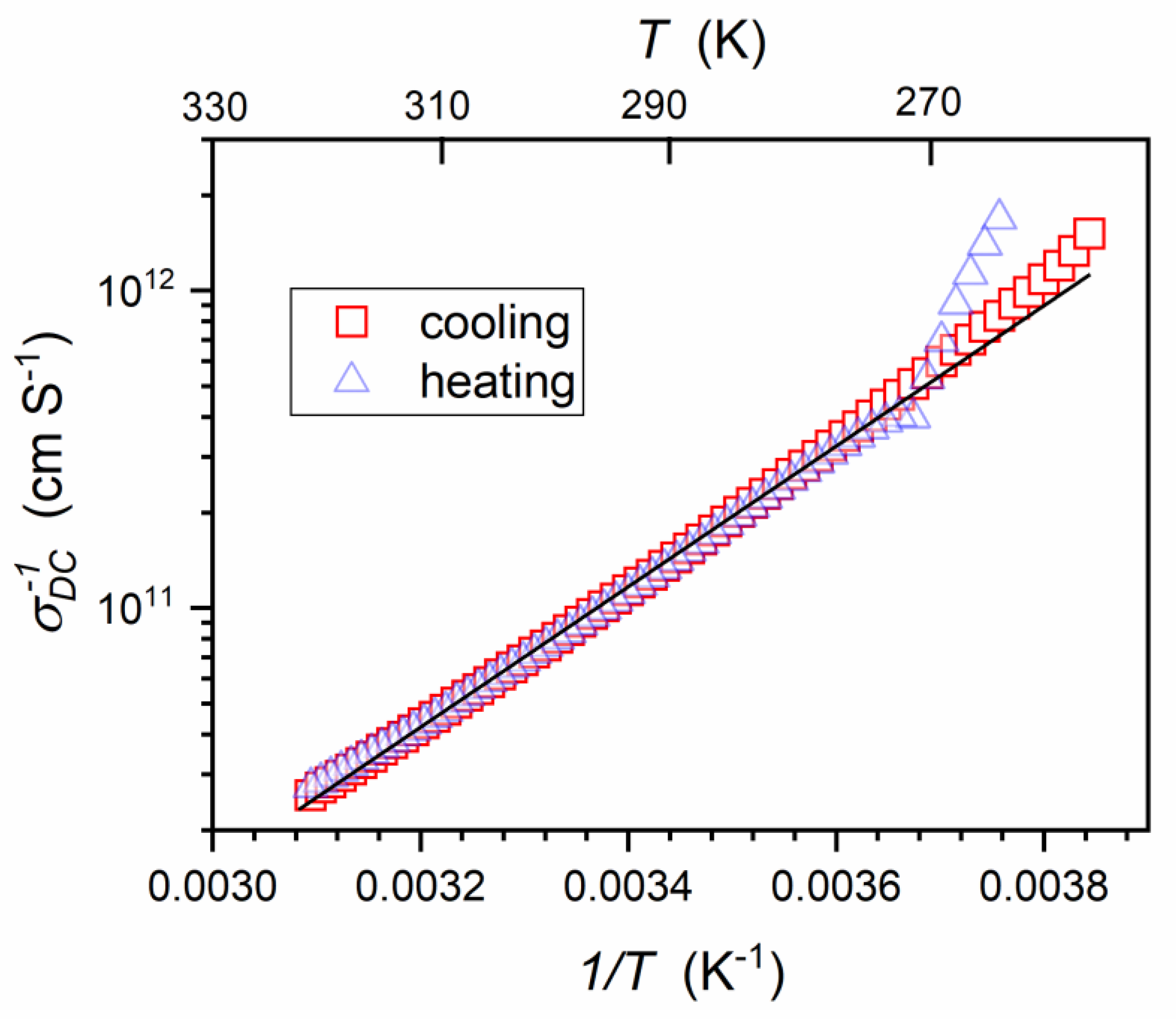
4.1. The Static Domain: Supercriticality and the Solid State Premelting and Post-Freezing Effect
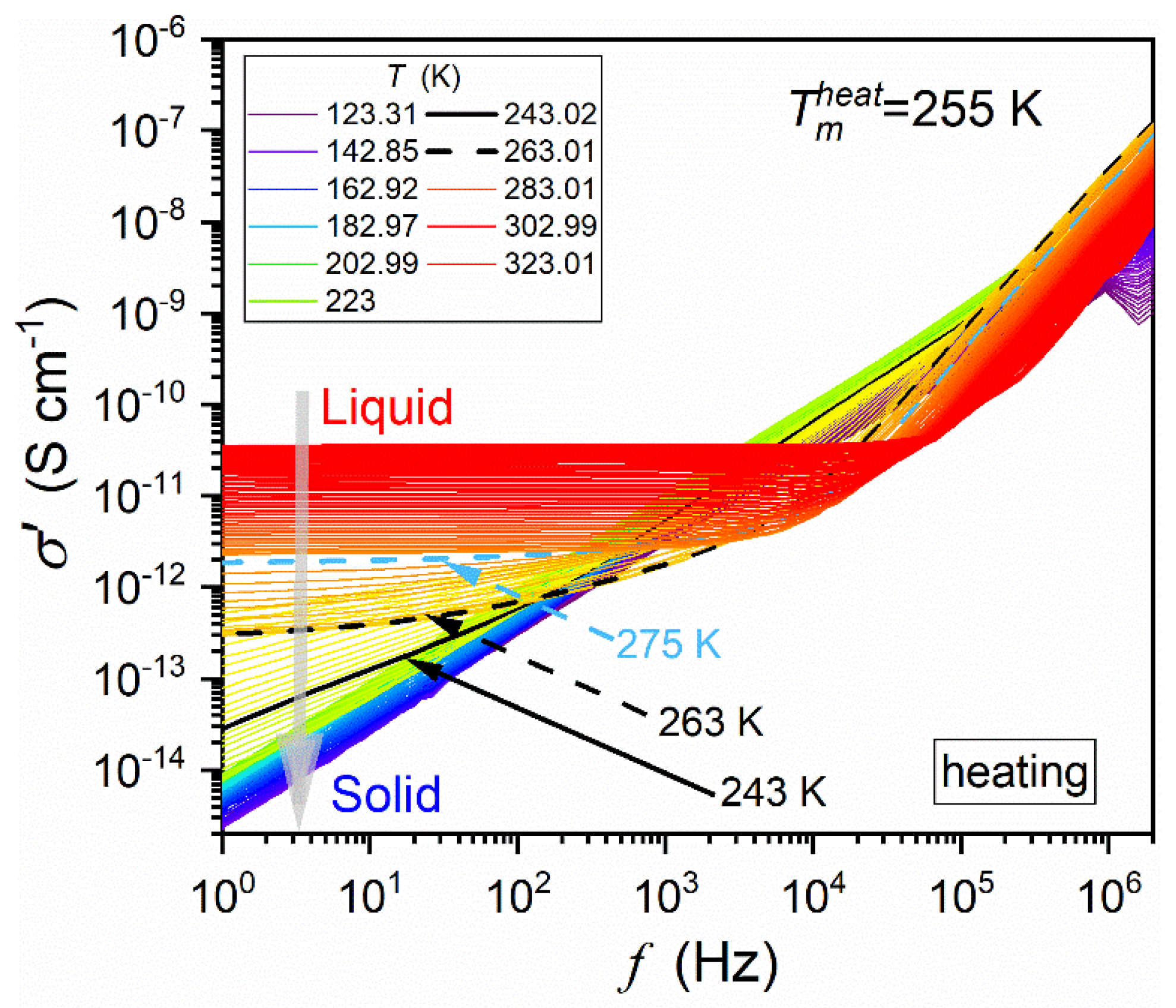
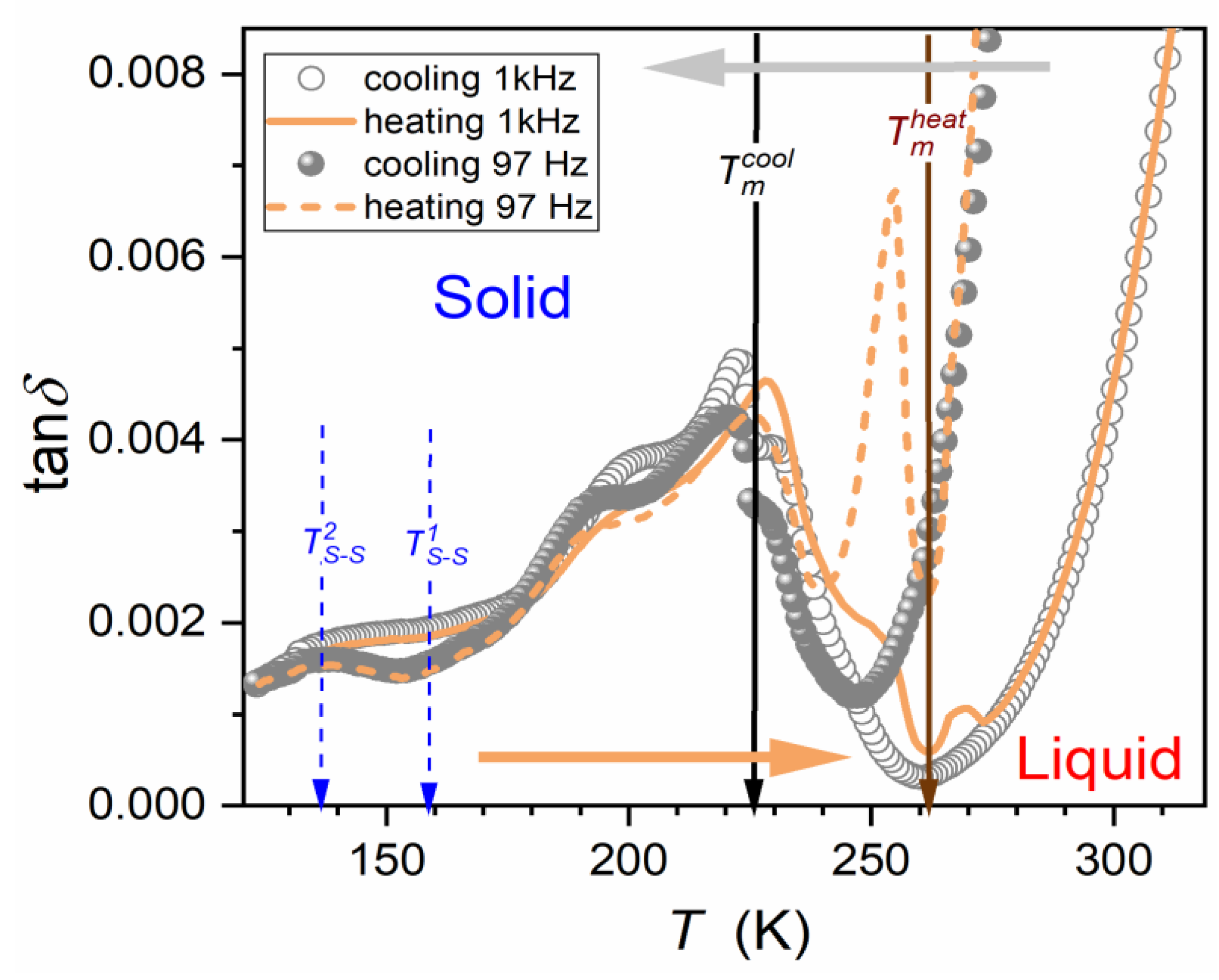
4.2. The Low-Frequency Domain: Supercriticality and Premelting/Post-Freezing Effects
4.3. Unique Glassy Dynamics
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Flashar, H. Meister der Heilkunst. Leben und Werk; Beck: Berlin, Germany, 2016; ISBN 3406697461. [Google Scholar]
- Chamberlin, E.R. The Emperor Charlemagne; Sapere Books: Ilkley, UK, 2020; ISBN 1913518817. [Google Scholar]
- Fisher, L. The Life of Mahatma Gandhi; Vintage Publishing: New York, NY, USA, 2015; ISBN 1784700401. [Google Scholar]
- Johnston, I.M.; Johnston, J.R. Flaxseed (Linseed) Oil and the Power of Omega 3; Keats Pub. Inc.: New York, NY, USA, 1995. [Google Scholar]
- Neukam, K.; De Spirt, S.; Stahl, W.; Bejot, M.; Maurette, J.-M.; Tronnier, H.; Heinrich, U. Supplementation of flaxseed oil diminishes skin sensitivity and improves skin barrier function and condition. Ski. Pharmacol. Physiol. 2011, 24, 67–74. [Google Scholar] [CrossRef]
- Piłat, B.; Zadernowski, R. Physicochemical characteristics of linseed oil and flour. Pol. J. Nat. Sci. 2010, 25, 106–113. [Google Scholar] [CrossRef]
- Patterson, H.B.W. Hydrogenetion of Fats and Oils; Springer: Berlin, Germany, 2011. [Google Scholar]
- de Souza, E.; Franco, C.M.; de Aquino, F.; Lys de Medeiros, P.; Evencio, L.B.; da Silva Goes, A.J.; de Souza Maia, M.B. Effect of a semisolid formulation of Linum usitatissimum L. (linseed) oil on the repair of skin wounds. Evid.-Based Complement. Altern. Med. 2012, 2012, 270752. [Google Scholar]
- Tripathi, V.; Abidi, A.B.; Marker, S.; Bilal, S. Linseed and linseed oil: Health benefits—A review. Int. J. Pharm. Bio. Sci. 2013, 3, 434–442. [Google Scholar]
- Bartkowski, L. Linseed—A natural source of health and beauty. Chemik 2013, 67, 186–191. [Google Scholar]
- Goyal, A.; Sharma, V.; Upadhyay, N.; Gill, S.; Sihag, M. Flax and flaxseed oil: An ancient medicine & modern functional food. J. Food Sci. Technol. 2014, 51, 1633–1653. [Google Scholar]
- Szymczyk, B.; Szczurek, W. Effect of dietary pomegranate seed oil and linseed oil on broiler chickens performance and meat fatty acid profile. J. Anim. Feed Sci. 2016, 25, 37–44. [Google Scholar] [CrossRef]
- Duran, D. The pharmacological evaluation of flax seed oil. J. Curr. Med. Res. Opin. 2020, 3, 2589. [Google Scholar] [CrossRef]
- Kiryluk, A.; Kostecka, J. Pro-environmental and health-promoting grounds for restitution of flax (Linum usitatissimum L.) cultivation. J. Ecol. Eng. 2020, 21, 99–107. [Google Scholar] [CrossRef] [PubMed]
- Patel, G.; Naik, R.K.; Patel, K.K. Studies on Some Physical and Engineering Properties of Linseed. Biol. Forum-Int. J. 2021, 13, 303–308. [Google Scholar]
- Tang, Z.-X.; Ying, R.-F.; Lv, B.-F.; Yang, L.-H.; Xu, Z.; Yan, L.-Q.; Bu, J.-Z.; Wei, Y.-S. Flaxseed oil: Extraction, health benefits and products. Qual. Assur. Saf. Crops Foods 2021, 13, 1–19. [Google Scholar] [CrossRef]
- Li, X.; Chen, Q.; Li, Q.; Li, J.; Cui, K.; Zhang, Y.; Kong, A.; Zhang, Y.; Wan, M.; Mai, K.; et al. Effects of high levels of dietary linseed oil on the growth performance, antioxidant capacity, hepatic lipid metabolism, and expression of inflammatory genes in large yellow croaker (Larimichthys crocea). Front. Physiol. 2021, 12, 631850. [Google Scholar] [CrossRef]
- Lewandowska, H.; Eljaszewicz, A.; Poplawska, I.; Tynecka, M.; Walewska, A.; Grubczak, K.; Holl, J.; Hady, H.R.; Czaban, S.L.; Reszec, J.; et al. Optimization of novel human acellular dermal dressing sterilization for routine use in clinical practice. Int. J. Mol. Sci. 2021, 22, 8467. [Google Scholar] [CrossRef] [PubMed]
- Skórkowska-Telichowska, K.; Mierziak-Darecka, J.; Wrobel-Kwiatkowska, M.; Gebarowski, T.; Szopa, J.; Zuk, M. Wound coverage by the linen dressing accelerates ulcer healing. Postep. Derm. Alergol 2021, 38, 827–841. [Google Scholar]
- Friend, J.N. The Chemistry of Linseed Oil; Legare Press: London, UK, 2022; ISBN 978-016378017. [Google Scholar]
- Langyan, S.; Yadava, P.; Khan, F.N.; Sharma, S.; Singh, R.; Bana, R.S.; Singh, N.; Kaur, V.; Kalia, S.; Kumar, A. Trends and advances in pre- and post- harvest processing of linseed oil for quality food and health products. Crit. Rev. Food Sci. Nutr. 2023; epub ahead of print. [Google Scholar]
- There, U.; Gour, N.; Shrikant, S.; Choudhary, V.; Kandasamy, R. Development of skincare formulations using flaxseed oil and mucilade. J. Pharmacogn. Phytochem. 2023, 12, 33–39. [Google Scholar] [CrossRef]
- Al-Madhagy, S.; Ashmawy, N.S.; Mamdouh, A.; Eldahshan, O.A.; Farag, M.A. A comprehensive review of the health benefits of flaxseed oil in relation to its chemical composition and comparison with other omega-3-rich oils. Eur. J. Med. Res. 2023, 28, 240. [Google Scholar] [CrossRef] [PubMed]
- Arai, Y.; Sako, T.; Takebayashi, Y. Supercritical Fluids: Molecular Interactions, Physical Properties and New Applications; Springer: Berlin, Germany, 2002. [Google Scholar]
- Drozd-Rzoska, A.; Rzoska, S.J. The super- and sub-critical effects for dielectric constant in diethyl ether. J. Chem. Phys. 2016, 144, 224506. [Google Scholar] [CrossRef] [PubMed]
- Marszałek, K.; Doesburg, P.; Starzonek, S.; Szczepańska, J.; Woźniak, Ł.; Lorenzo, J.M.; Skąpska, S.; Rzoska, S.J.; Barba, F.J. Comparative effect of supercritical carbon dioxide and high pressure processing on structural changes and activity loss of oxidoreductive enzymes. J. CO2 Util. 2019, 29, 46–56. [Google Scholar] [CrossRef]
- Hong Geow, C.; Ching, M.; Tan, S.; Yeap, P.; Chin, N.L. A review on extraction techniques and its future applications in industry. Europ. J. Lipid Sci. Technol. 2021, 123, 2000302. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Drozd-Rzoska, A. Criticality-related fundamental bases for new generations of gas-liquid, liquid-liquid, and liquid (LE) extraction technologies. Eur. Phys. J. E 2022, 45, 67. [Google Scholar] [CrossRef]
- Anisimov, M.A. Critical Phenomena in Liquids and Liquid Crystals; Gordon and Breach: Reading, UK, 1992. [Google Scholar]
- Drozd-Rzoska, A.; Rzoska, S.J.; Kalabiński, J. Impact of pressure on low molecular weight near-critical mixtures of limited miscibility. ACS Omega 2020, 5, 20141–20152. [Google Scholar] [CrossRef] [PubMed]
- Proctor, J.E. The Liquid and Supercritical Fluid. States of Matter; CRC Press: Boca Raton, FL, USA, 2020; ISBN 9781138589735. [Google Scholar]
- Talevi, A.; Ruiz, M.E. Drug Dissolution: Fundamental Theoretic Models. In The ADME Encyclopedia; Talevi, A., Ed.; Springer: Berlin, Germany, 2022. [Google Scholar]
- Dokoumetzidis, A.; Macheras, P. A century of dissolution research: From Noyes and Withney to the biopharmaceutics classification system. Int. J. Pharm. 2006, 321, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Kremer, F.; Schönhals, A. Broadband Dielectric Spectroscopy; Springer: Berlin, Germany, 2002. [Google Scholar]
- Drozd-Rzoska, A.; Rzoska, S.J.; Starzonek, S. New scaling paradigm for dynamics in glass-forming systems. Prog. Mater. Sci. 2023, 134, 101074. [Google Scholar] [CrossRef]
- Agrawal, S.; Bhatnagar, D. Dielectric studies of binary mixtures of edible unsaturated oils. Indian J. Pure Appl. Phys. 2005, 43, 624–629. [Google Scholar]
- Mathew, T.; Vyas, A.D.; Tripathi, D. Dielectric properties of some edible and medicinal oils at microwave frequency. Can. J. Pure Appl. Sci. 2009, 3, 953–957. [Google Scholar]
- Palummo, L.; ·Bearzotti, A. Analysis of the electrical of linseed oil films exposed humidity. Appl. Phys. A 2009, 97, 835–839. [Google Scholar] [CrossRef]
- Shah, H.; Tahir, Q.A. Dielectric properties of vegetable oils. J. Sci. Res. 2011, 3, 48–492. [Google Scholar] [CrossRef]
- Pecovska-Gjorgjevich, M.; Andonovski, A.; Velevska, J. Dielectric constant and induced dipole moment of edible oils subjected to conventional heating. Maced. J. Chem. Chem. Eng. 2012, 31, 285–294. [Google Scholar] [CrossRef][Green Version]
- Spohner, M.; Frk, M.; Liedermann, K. Study of electrical and rheological properties of natural and other oils. In Proceedings of the 2012 IEEE International Symposium on Electrical Insulation, San Juan, PR, USA, 10–13 June 2012; pp. 30–33. [Google Scholar]
- Chetty, L.; Serukenya, W.I.; Ijumba, N.M. Vegetable oil based liquid nanocomposite dielectric. S. Afr. J. Sci. 2013, 109, 6. [Google Scholar] [CrossRef]
- Khandelwal, V.; Sahoo, S.K.; Kumar, A.; Manik, G. Electrically conductive green composites based on epoxidized linseed oil and polyaniline: An insight into electrical, thermal and mechanical properties. Compos. Part B Eng. 2018, 136, 149–157. [Google Scholar] [CrossRef]
- Xu, B.; Wei, B.; Ren, X.; Liu, Y.; Jiang, H.; Zhou, C.; Ma, H.; Chalamaiah, M.; Liang, Q.; Wang, Z. Dielectric pretreatment of rapeseed 1: Influence on the drying characteristics of the seeds and physico-chemical properties of cold-pressed oil. Food Bioprocess Technol. 2018, 11, 1236–1247. [Google Scholar] [CrossRef]
- Kumar, A.V.P.; Goel, A.; Kumar, R.; Ojha, A.K.; John, J.K.; Joy, J. Dielectric characterization of common edible oils in the higher microwave frequencies using cavity perturbation. J. Microw. Power Electromagn. Energy 2019, 53, 48–56. [Google Scholar]
- Woo, Y.S.; Kim, M.-J.; Lee, J.H. Prediction of oxidative stability in bulk oils using dielectric constant changes. Food Chem. 2019, 279, 216–222. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Chen, J.; Jing, B.; Dong, Y.; Yu, X. New method for the discrimination of adulterated flaxseed oil using dielectric spectroscopy. Food Anal. Methods 2019, 12, 2623–2629. [Google Scholar] [CrossRef]
- Blyagaz, A.I. Improvement of quality control methods for linseed oils. Novye Technol. (MAJKOP) 2019, 1, 11–18. [Google Scholar]
- Teseme, W.B.; Weldeselassie, H.W. Review on the study of dielectric properties of food materials. Am. J. Eng. Technol. Manag. 2020, 5, 76–83. [Google Scholar] [CrossRef]
- Valantina, S. R Measurement of dielectric constant: A recent trend in quality analysis of vegetable oil—A review. Trends Food Sci. Technol. 2021, 113, 1–11. [Google Scholar] [CrossRef]
- Doganer, M.; Dincer, S.; Dincer, M.S.; Duzkaya, H.; Tezcan, S.S. Statistical investigation of AC dielectric strength of flaxseed oil. In Proceedings of the 2022 IEEE 21st International Conference on Dielectric Liquids (ICDL), Sevilla, Spain, 29 May–2 June 2022; pp. 1–4. [Google Scholar]
- Radojčić, D.; Hong, J.; Petrović, Z.S. From natural oils to epoxy resins: A new paradigm in renewable performance materials. J. Polym. Environ. 2022, 30, 765–775. [Google Scholar] [CrossRef]
- Sudhakar, A.; Chakraborty, S.K.; Mahanti, N.K. Varghese, Advanced techniques in edible oil authentication: A systematic review and critical analysis. Crit. Rev. Food Sci. Nutr. C 2023, 63, 873–901. [Google Scholar] [CrossRef]
- Sabnis, S.M.; Rander, D.N.; Kanse, K.S.; Joshi, Y.S.; Kumbharkhane, A.C. Spectroscopic measurement and dielectric relaxation study of vegetable oils. Inf. Process. Agric. 2023; in press proof. [Google Scholar] [CrossRef]
- Agaev, S.G.; Baida, A.A.; Georgiev, O.V.; Maiorova, O.O.; Mozyrev, A.G. Dielectric spectroscopy of vegetable oils. Russ. J. Appl. Chem. 2020, 93, 748–756. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A.; Rzoska, S.J.; Zioło, J. Critical behaviour of dielectric permittivity in the isotropic phase of nematogens. Phys. Rev. E 1996, 54, 6452–6456. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A.; Rzoska, S.J.; Zioło, J. The quasi-critical behavior of dielectric permittivity in the isotropic phase of smectogenic n-cyanobiphenyls. Phys. Rev. E 2000, 61, 5349–5354. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A.; Rzoska, S.J.; Czupryński, K. Phase transitions from the isotropic liquid to liquid crystalline mesophases studied by “linear” and “nonlinear” static dielectric permittivity. Phys. Rev. E 2000, 61, 5355–5360. [Google Scholar] [CrossRef] [PubMed]
- Drozd-Rzoska, A.; Rzoska, S.J.; Pawlus, S.; Zioło, J. Complex dynamics of supercooling n-butylcyanobiphenyl (4CB). Phys. Rev. E 2005, 72, 031501. [Google Scholar] [CrossRef] [PubMed]
- Łoś, J.; Drozd-Rzoska, A.; Rzoska, S.J. Critical-like behavior of low-frequency dielectric properties in compressed liquid crystalline octyloxycyanobiphenyl (8OCB) and its nanocolloid with paraelectric BaTiO3. J. Mol. Liq. 2023, 377, 121555. [Google Scholar] [CrossRef]
- Drozd Rzoska, A.; Rzoska, S.J.; Zioło, J.; Jadżyn, J. Quasi-ciritical behavior of the low-frequency dielectric permittivity in the isotropic phase of n-pentylcyanobiphenyl. Phys. Rev. E 2001, 63, 052701–052704. [Google Scholar] [CrossRef]
- Mei, Q.S.; Lu, K. Melting and superheating of crystalline solids: From bulk to nanocrystals. Prog. Mater. Sci. 2007, 52, 1175–1262. [Google Scholar] [CrossRef]
- Starzonek, S.; Rzoska, S.J.; Drozd-Rzoska, A.; Pawlus, S.; Biała, E.; Martinez-Garcia, J.C.; Kistersky, L. Fractional Debye-Stokes-Einstein behaviour in an ultraviscous nanocolloid glycerol and silver nanoparticles. Soft Matter 2011, 11, 5554–5562. [Google Scholar] [CrossRef]
- Kaisersberger, E. DSC investigations of the thermal characterization of edible fats and oils. Thermochim. Acta 1989, 151, 83–90. [Google Scholar] [CrossRef]
- Wang, C.; Erhan, S. Studies of thermal polymerization of vegetable oils with a differential scanning calorimeter. J. Am. Oil Chem. Soc. 1999, 76, 1211–1216. [Google Scholar] [CrossRef]
- Zhang, Z.-S.; Li, D.; Zhang, L.-X.; Liu, Y.-L.; Wang, X. Heating effect on the DSC melting curve of flaxseed oil. J. Therm. Anal. Calorim. 2014, 115, 2129–2135. [Google Scholar] [CrossRef]
- Tomaszewska-Gras, J.; Islam, M.; Grzeca, L.; Kaczmarek, A.; Fornal, E. Comprehensive thermal characteristics of different cultivars of flaxseed oil (Linum usittatissimum L.). Molecules 2021, 26, 1958. [Google Scholar] [CrossRef] [PubMed]
- Murray, C. Ferroelectric Materials: Science and Technology; States Academic Press: Cambridge, UK, 2022; ISBN 978-1639891986. [Google Scholar]
- Rzoska, S.J.; Drozd-Rzoska, A.; Bulejak, W.; Łoś, J.; Starzonek, S.; Szafran, M.; Gao, F. Critical insight into pretransitional behavior and dielectric tunability of relaxor ceramics. Materials 2023, 16, 7634. [Google Scholar] [CrossRef] [PubMed]
- Mierzwa, M.; Paluch, M.; Rzoska, S.J.; Zioło, J. The liquid-glass and liquid-liquid transitions of TPP at elevated pressure. J. Phys. Chem. B 2008, 112, 10383. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, H. Liquid-liquid transition and polyamorphism. J. Chem. Phys. 2020, 153, 130901. [Google Scholar] [CrossRef] [PubMed]
- Kalabiński, J.; Drozd-Rzoska, A.; Rzoska, S.J. Giant premelting effects for solid-liquid discontinuous transition in nitrobenzene under compression. Crystals 2023, 13, 247. [Google Scholar] [CrossRef]
- Rzoska, S.J.; Paluch, M.; Pawlus, S.; Drozd-Rzoska, A.; Jadzyn, J.; Czupryński, K.; Dąbrowski, R. Complex dielectric relaxation in supercooling and superpressing liquid-crystalline chiral isopentycyanobiphenyl. Phys. Rev. E 2003, 68, 031705. [Google Scholar] [CrossRef]
- Massalska-Arodz, M.; Williams, G.I.; Smith, K.C.; Conolly, G.; Aldridge, R.A. Dabrowski. Molecular dynamics and crystallization behaviour of isopentyl cyanobiphenyl as studied by dielectric relaxation spectroscopy. J. Chem. Soc. Faraday Trans. 1998, 94, 387–394. [Google Scholar] [CrossRef]
- Kryuchkov, N.P.; Dmitryuk, N.A.; Li, W.; Ovcharov, P.V.; Han, Y.; Sapelkin, A.V.; Yurchenko, S.O. Mean-field model of melting in superheated crystals based on a single experimentally measurable order parameter. Sci. Rep. 2021, 11, 17963. [Google Scholar] [CrossRef]
- Riegler, H.; Köhler, R. How pre-melting on surrounding interfaces broadens solid–liquid phase transitions. Nat. Phys. 2007, 3, 890–894. [Google Scholar] [CrossRef]
- Mishin, Y.; Boettinger, W.; Warren, J.; McFadden, G. Thermodynamics of grain boundary premelting in alloys. I. Phase-field modeling. Acta Mater. 2009, 57, 3771–3785. [Google Scholar] [CrossRef]
- Yang, Y.; Asta, M.; Laird, B.B. Solid-liquid interfacial premelting. Phys. Rev. Lett. 2013, 110, 096102. [Google Scholar] [CrossRef] [PubMed]
- Spatschek, R.P.; Adland, A.; Karma, A.S. Structural short-range forces between solid-melt interfaces. Phys. Rev. B 2013, 87, 024109. [Google Scholar] [CrossRef]
- Samanta, A.; Tuckerman, M.E.; Yu, T.-Q.; Ee, W. Microscopic mechanisms of equilibrium melting of a solid. Science 2014, 346, 729–732. [Google Scholar] [CrossRef] [PubMed]
- Rad, M.T.; Boussinot, G.; Apel, M. Dynamics of grain boundary premelting. Sci. Rep. 2020, 10, 21074. [Google Scholar]
- Pocheć, M.; Niu, H.; Ren, L.; Bai, S.; Orzechowski, K. Premelting phenomena in n-alcohols from nonanol to dodecanol. J. Phys. Chem. C 2020, 124, 21013–21017. [Google Scholar] [CrossRef]
- Tian, X.-L.; Zhao, Y.-H.; Peng, D.-W.; Guo, Q.-W.; Guo, Z.; Hou, H. Phase-field crystal simulation of evolution of liquid pools in grain boundary pre-melting regions. Trans. Nonferrous Met. Soc. China 2021, 31, 1175–1188. [Google Scholar] [CrossRef]
- Azad, M.; Groulx, D.; Donaldson, A. Melting of phase change materials in horizontal annuli. J. Energy Storage 2021, 42, 103096. [Google Scholar] [CrossRef]
- Pocheć, M.; Orzechowski, K.; Rutkowski, K. Indicators of premelting in 1-decanol and 1-nonanol studied by FTIR spectroscopy. Surf. Interfaces 2022, 28, 101676. [Google Scholar] [CrossRef]
- Pocheć, M.; Krupka, K.M.; Panek, J.J.; Orzechowski, K.; Jezierska, A. Inside out Approach to Rotator State in Hydrogen-Bonded System-Experimental and Theoretical Cross-Examination in n-Octanol. Int. J. Mol. Sci. 2022, 23, 2138. [Google Scholar] [CrossRef]
- Vachier, J.; Wettlaufer, J.S. Biolocomotion and premelting in ice. Front. Phys. 2022, 10, 904836. [Google Scholar] [CrossRef]
- Vachier, J.; Wettlaufer, J.S. Premelting controlled active matter in ice. Phys. Rev. E 2022, 105, 024601. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.I.; Li, W.; Qiao, K. Surface premelting and melting of colloidal glasses. Sci. Adv. 2023, 9, eadf1101. [Google Scholar] [CrossRef] [PubMed]
- Cui, S.; Chen, H. Transition dynamics and metastable states during premelting and freezing of ice surfaces. Phys. Rev. B 2023, 108, 045413. [Google Scholar] [CrossRef]
- Lipowsky, R. Critical surface phenomena at first-order bulk transitions. Phys. Rev. Lett. 1982, 49, 1575–1578. [Google Scholar] [CrossRef]
- Lipowsky, R. Melting at grain boundaries and surfaces. Phys. Rev. Lett. 1986, 57, 2876. [Google Scholar] [CrossRef] [PubMed]
- Lipovsky, T. Surface critical phenomena at first-order phase transition. Ferroelectrics 1987, 73, 69–81. [Google Scholar] [CrossRef]
- Mossotti, O.F. Discussione analitica sull’influenza che l’azione di un mezzo dielettrico ha sulla distribuzione dell’elettricità alla superficie di più corpi elettrici disseminati. Mem. Mat. Fis. Soc. Ital. Sci. Resid. Modena 1850, 24, 49–74. [Google Scholar]
- Clausius, R. Die Mechanische Behandlung der Electricität; Vieweg + Teubner Verlag: Wiesbaden, Germany, 1878. [Google Scholar]
- Böttcher, C.J.F. Theory of Electric Polarization; Elsevier: Amsterdam, The Netherlands, 1973. [Google Scholar]
- Chełkowski, A. Dielectric Physics; PWN-Elsevier: Warsaw, Poland, 1990. [Google Scholar]
- von Hippel, A. Dielectrics and Waves; Artech House: New York, NY, USA, 1954. [Google Scholar]
- Raju, G.G. Dielectric in Electric Field; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Talebian, E.; Talebian, M. A general review on the derivation of Clausius–Mossotti relation. Optik 2013, 124, 2324–2326. [Google Scholar] [CrossRef]
- Eremin, L.E.; Neschimenko, V.V.; Shcherbam, D.S.; Fomin, D.V. System modification of the equation Lorenz–Lorentz–Clausius Mossotti. Optic 2021, 231, 166327. [Google Scholar] [CrossRef]
- Chen, X.; Nijhuis, C.A. The Unusual Dielectric Response of Large Area Molecular Tunnel Junctions Probed with Impedance Spectroscopy. Adv. Electron. Mat. 2021, 8, 2100495. [Google Scholar] [CrossRef]
- Trainer, M. Ferroelectrics and the Curie–Weiss law. Eur. J. Phys. 2000, 21, 459–464. [Google Scholar] [CrossRef]
- Hoffmann, M.; Ravindran, P.V.; Kha, A.I. Why Do Ferroelectrics exhibit negative capacitance? Materials 2019, 12, 3743. [Google Scholar] [CrossRef]
- Mugiraneza, S.; Hallas, A.M. Tutorial: A beginner’s guide to interpreting magnetic susceptibility data with the Curie-Weiss law. Commun. Phys. 2022, 5, 95. [Google Scholar] [CrossRef]
- Drozd-Rzoska, A. Universal behavior of the apparent fragility in ultraslow glass forming systems. Sci. Rep. 2019, 9, 6816. [Google Scholar] [CrossRef] [PubMed]
- Hill, R. Characterisation of dielectric loss in solids and liquids. Nature 1978, 275, 96–99. [Google Scholar] [CrossRef]
- Kim, T.; Yong, H.; Kim, B.; Kim, D.; Choi, D.; Park, Y.T.; Lee, S. Energy-loss return gate via liquid dielectric polarization. Nat. Commun. 2018, 9, 1437. [Google Scholar] [CrossRef] [PubMed]
- Morsalin, S.; Phung, T.B.; Danikas, M.; Mawad, D. Diagnostic challenges in dielectric loss assessment and interpretation: A review. IET Sci. Meas. Technol. 2019, 13, 767–782. [Google Scholar] [CrossRef]
- Huang, Z.; Wang, F.; Wang, Q.; Yao, W.; Sun, K.; Zhang, R.; Zahao, J.; Lou, Z.; Li, J. Significantly enhanced electrical performances of eco-friendly dielectric liquids for harsh conditions with fullerene. Nanomaterials 2019, 9, 989. [Google Scholar] [CrossRef]
- Nadolny, Z. Determination of dielectric losses in a power transformer. Energies 2022, 15, 993. [Google Scholar] [CrossRef]
- Havran, P.; Cimbala, R.; Kurimský, J.; Dolník, B.; Kolcunová, I.; Medved, D.; Király, J.; Kohanmm, V.; Šárpataky, L. Dielectric properties of electrical insulating liquids for high voltage electric devices in a time-varying electric field. Energies 2022, 15, 391. [Google Scholar] [CrossRef]
- Omonov, T.S.; Patel, V.R.; Curtis, J.M. Biobased thermosets from epoxidized linseed oil and its methyl esters. ACS Appl. Polym. Mater. 2022, 4, 6531–6542. [Google Scholar] [CrossRef]
- Ruwoldt, J.; Toven, K. Alternative wood treatment with blends of linseed oil, alcohols and pyrolysis oil. J. Bioresour. Bioprod. 2022, 7, 278–287. [Google Scholar] [CrossRef]
- Bonaduce, I.; Carlyle, L.; Colombini, M.P.; Duce, C.; Ferrari, C.; Ribechini, E.; Selleri, P.; Tiné, M.R. New insights into the ageing of linseed oil paint binder: A qualitative and quantitative analytical study. PLoS ONE 2012, 7, e49333. [Google Scholar] [CrossRef]
- Gorrée, M.; Guinée, J.B.; Huppes, G.; van Oers, L. Environmental life cycle assessment of linoleum. Int. J. Life Cycle Assess. 2002, 7, 158–166. [Google Scholar] [CrossRef]
- Martin, D.; Saha, T.; Mcpherson, L. Condition monitoring of vegetable oil insulation in in-service power transformers: Some data spanning 10 years. IEEE Electr. Insul. Mag. 2017, 33, 44–51. [Google Scholar] [CrossRef]
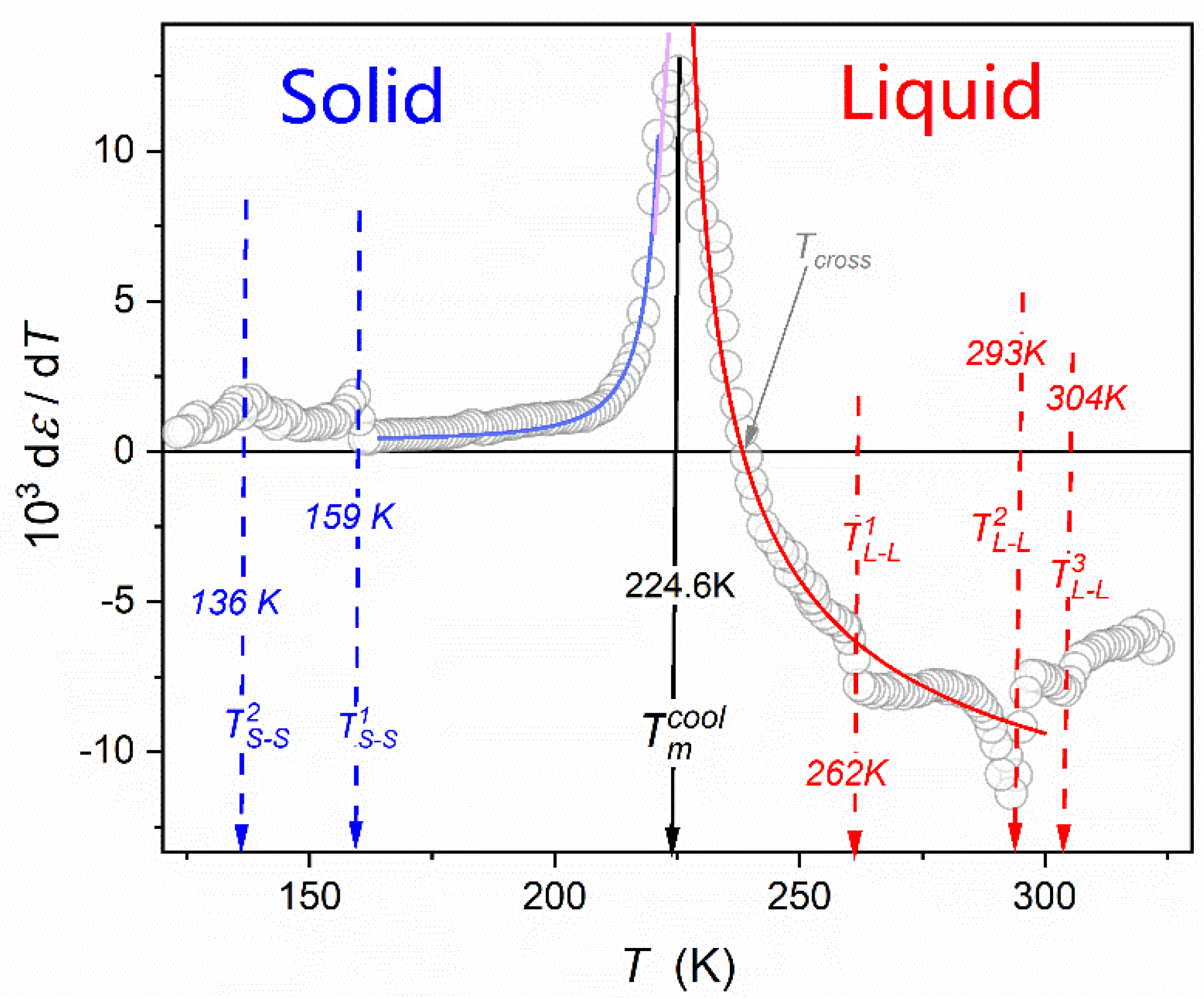
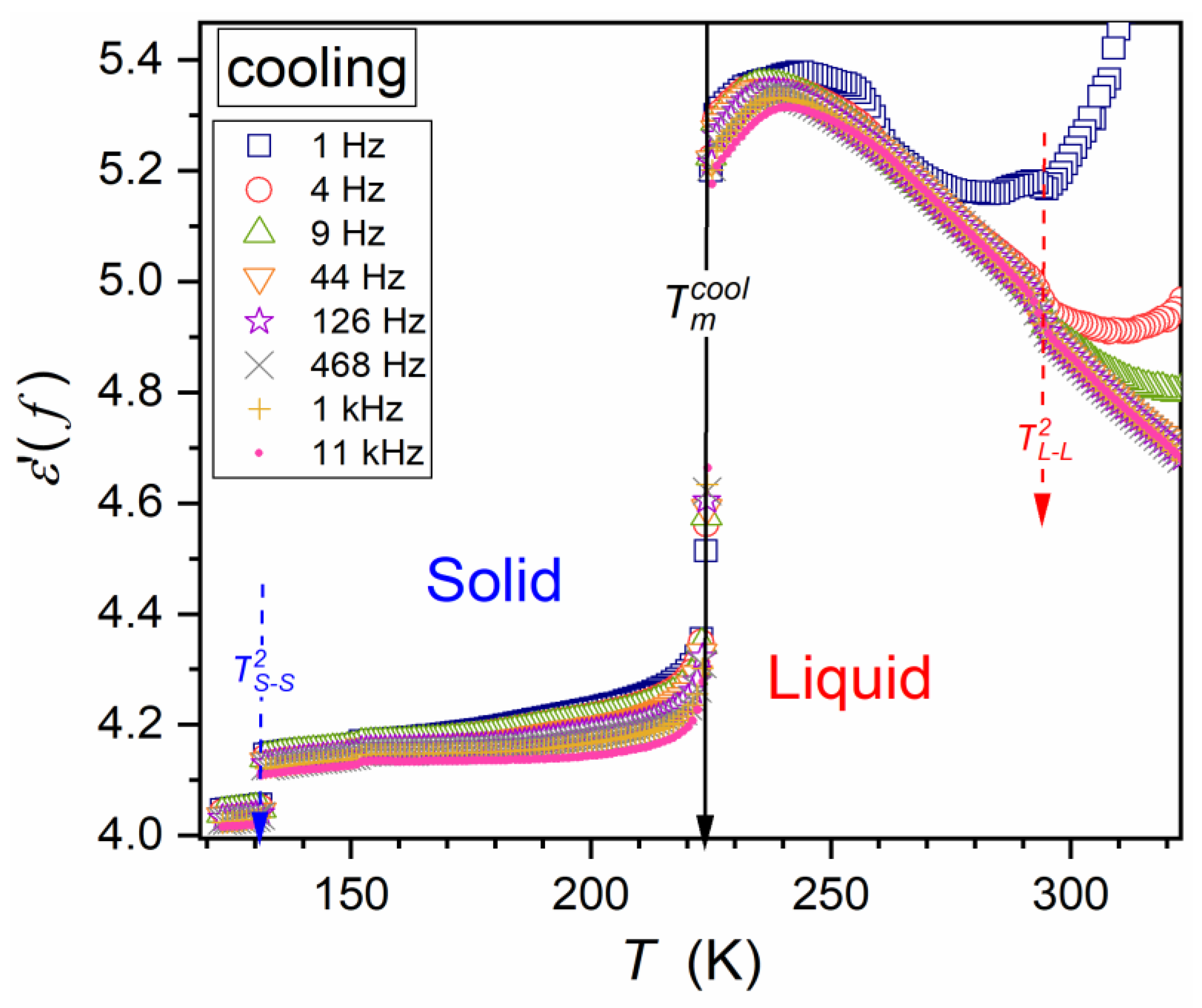

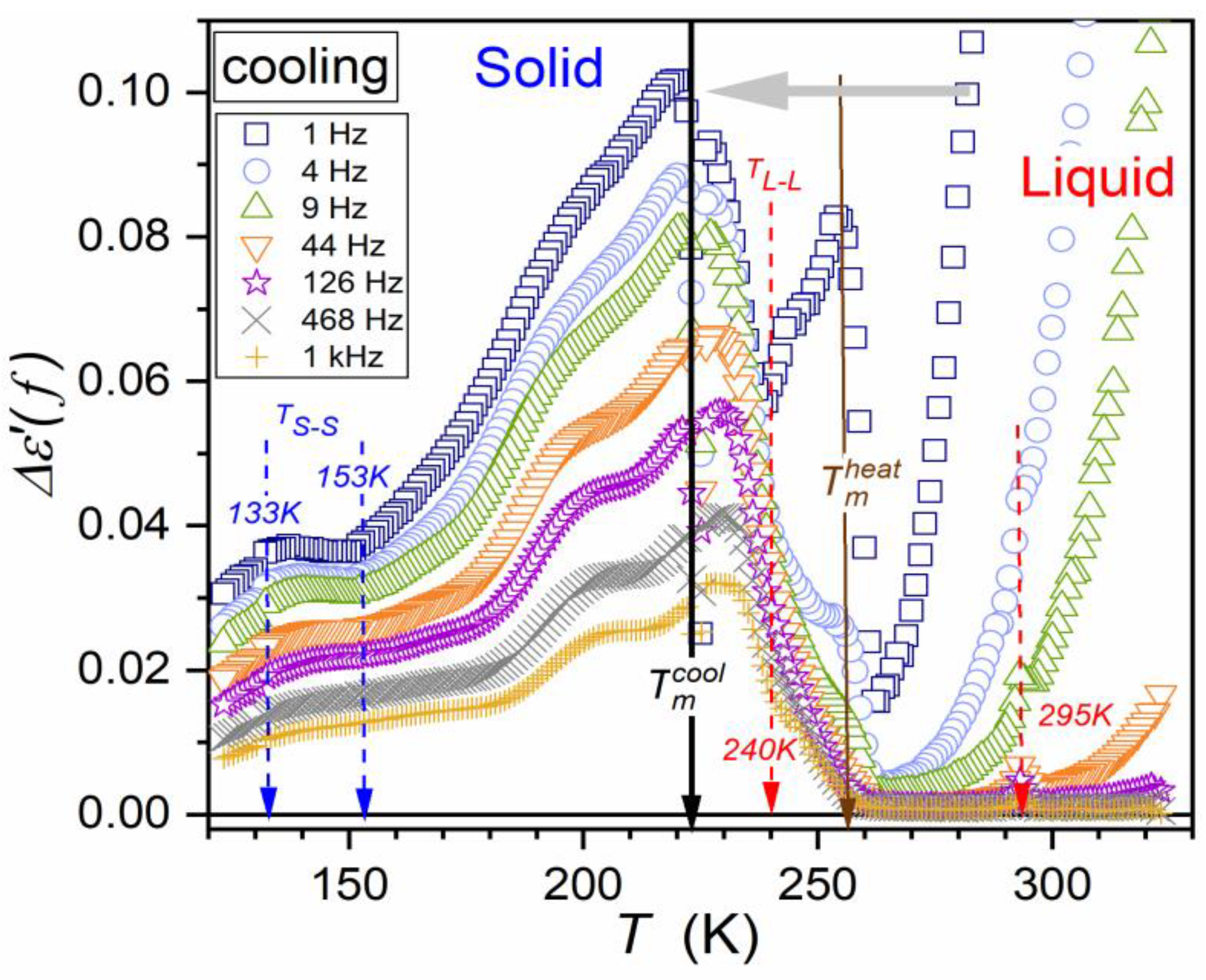
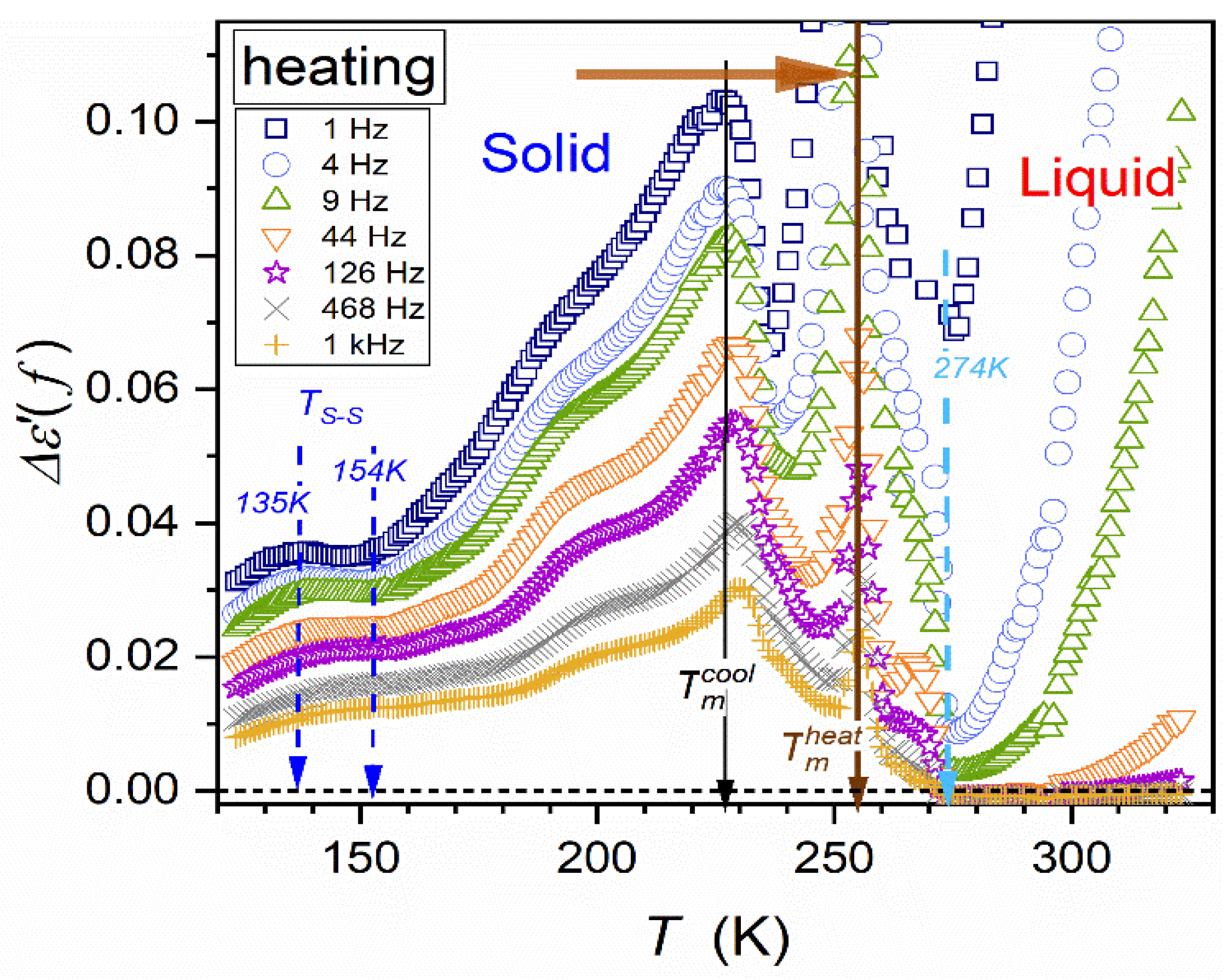


| Parameter | |||||||
|---|---|---|---|---|---|---|---|
| Value | 4.310 | −16.4 | 125 | 0.50 | 224 | 224.6 | 0.6 |
| Parameter | a (K−1) | M (K−1) | T** (K) | ||||
|---|---|---|---|---|---|---|---|
| Value | 9.3 × 10−4 | 3.83 | 0.159 | 1.0 | 224.75 | 224.6 | 0.15 |
| Parameter | Ω | (K) | (K) | (K) | |
|---|---|---|---|---|---|
| Process 1 | −31.1 | 9.85 | 204.0 | 204.5 | 0.5 |
| Process 2 | −22.0 | 4.8 | 204.0 | 206 | 2 |
| Process 3 | −22.2 | 3.0 | 204.0 | 210 | 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drozd-Rzoska, A.; Rzoska, S.J.; Łoś, J. Supercriticality, Glassy Dynamics, and the New Insight into Melting/Freezing Discontinuous Transition in Linseed Oil. Biophysica 2024, 4, 34-57. https://doi.org/10.3390/biophysica4010003
Drozd-Rzoska A, Rzoska SJ, Łoś J. Supercriticality, Glassy Dynamics, and the New Insight into Melting/Freezing Discontinuous Transition in Linseed Oil. Biophysica. 2024; 4(1):34-57. https://doi.org/10.3390/biophysica4010003
Chicago/Turabian StyleDrozd-Rzoska, Aleksandra, Sylwester J. Rzoska, and Joanna Łoś. 2024. "Supercriticality, Glassy Dynamics, and the New Insight into Melting/Freezing Discontinuous Transition in Linseed Oil" Biophysica 4, no. 1: 34-57. https://doi.org/10.3390/biophysica4010003
APA StyleDrozd-Rzoska, A., Rzoska, S. J., & Łoś, J. (2024). Supercriticality, Glassy Dynamics, and the New Insight into Melting/Freezing Discontinuous Transition in Linseed Oil. Biophysica, 4(1), 34-57. https://doi.org/10.3390/biophysica4010003






