The Dynamic Behavior of a Single Semiflexible Ring Chain in a Linear Polymer Matrix
Abstract
:1. Introduction
2. Model and Method
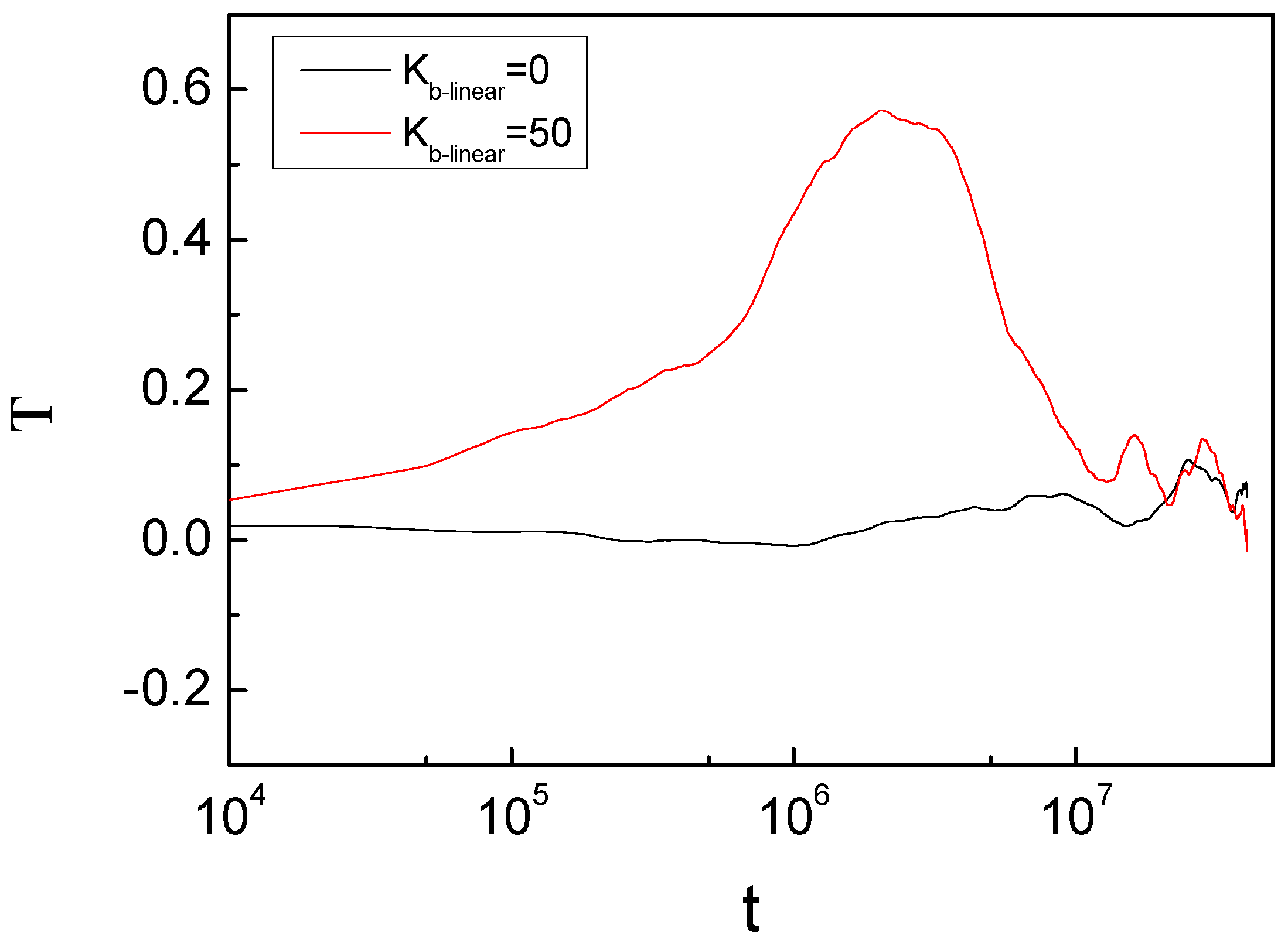
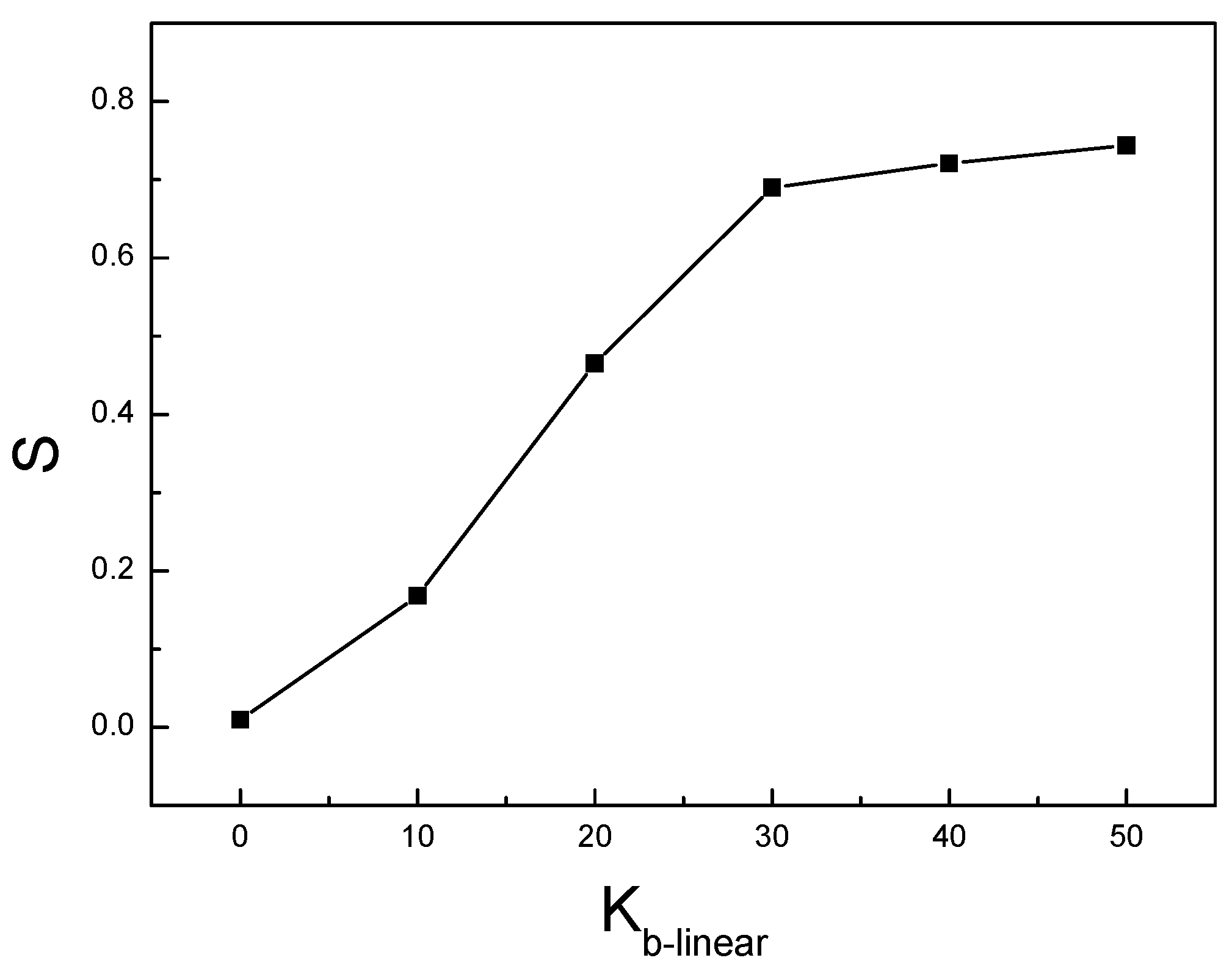
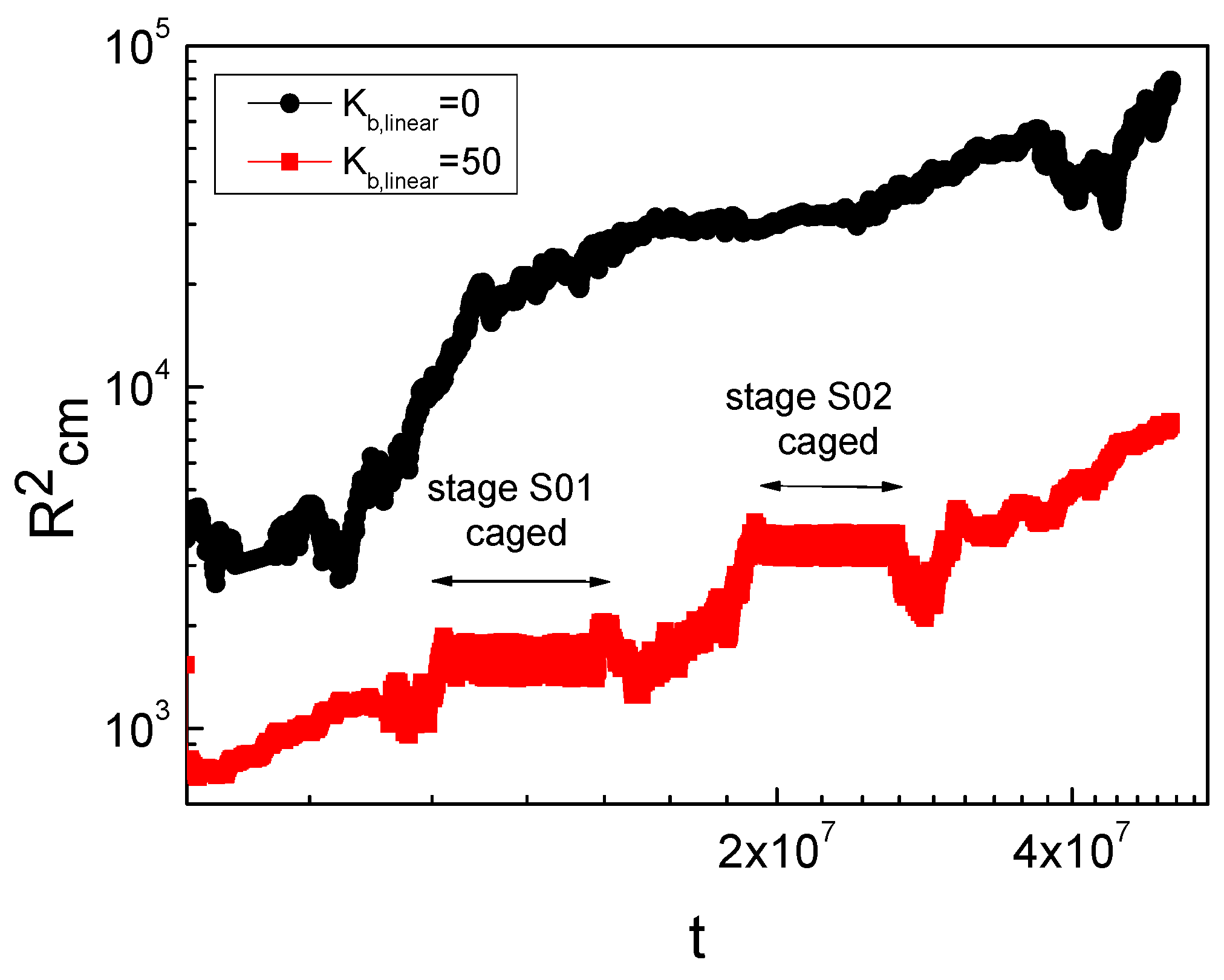
3. Result and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Craig, I.R.; Manolopoulos, D.E. Quantum statistics and classical mechanics: Real time correlation functions from ring polymer molecular dynamics. J. Chem. Phys. 2004, 121, 3368–3373. [Google Scholar] [CrossRef]
- Pioper, P.; Likos, C.N.; Moreno, A.J.; Blaak, R. An anisotropic effective model for the simulation of semiflexible ring polymers. Macromolecules 2015, 48, 4983. [Google Scholar]
- Narros, A.; Likos, C.N.; Moreno, A.J.; Capone, B. Multi-blob coarse graining for ring polymer solutions. Soft Matter 2014, 10, 9601. [Google Scholar] [CrossRef] [Green Version]
- Slimani, M.Z.; Bacova, P.; Bernabei, M.; Narros, A.; Likos, C.N. Cluster glasses of semiflexible ring polymers. ACS Macro. Lett. 2014, 3, d611. [Google Scholar] [CrossRef] [PubMed]
- Narros, A.; Moreno, A.J.; Likos, C.N. Effects of knots on ring polymers in solvents of varying quality. Macromolecules 2013, 46, 3654. [Google Scholar] [CrossRef] [Green Version]
- Richardson, J.O.; Althorpe, S.C. Ring-polymer molecular dynamics rate-theory in the deep-tunneling regime: Connection with semiclassical instanton theory. J. Chem. Phys. 2009, 131, 214106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Halverson, J.D.; Lee, W.B.; Grest, G.S.; Grosberg, A.Y.; Kremer, K. Molecular dynamics simulation study of nonconcatenated ring polymers in a melt. II. Dynamics. J. Chem. Phys. 2011, 134, 204905. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Michieletto, D.; Turner, M.S. A topologically driven glass in ring polymers. Proc. Natl. Acad. Sci. USA 2016, 113, 5195. [Google Scholar] [CrossRef]
- Obukhov, S.P.; Rubinstein, M.; Duke, T. Dynamics of a ring polymer in a gel. Phys. Rev. Lett. 1994, 73, 1263–1266. [Google Scholar] [CrossRef]
- Reigh, S.Y.; Yoon, D.Y. Single-molecule Imaging reveals topology dependent mutual relaxation of polymer chains. ACS Macro Lett. 2013, 2, 296. [Google Scholar] [CrossRef]
- Trabi, M.; Craik, D.J. Circular proteins: No end in sight. Trends Biochem. Sci. 2002, 27, 132–138. [Google Scholar] [CrossRef]
- Dobay, A.; Dubochet, J.; Millett, K.; Stasiak, A. Scaling behavior of random knots. Proc. Natl. Acad. Sci. USA 2003, 100, 5611–5615. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, T.; Kulic, I.M.; Dogic, Z. Circularization, photomechanical switching, and a supercoiling transition of actin filaments. Phys. Rev. Lett. 2010, 104, 4. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Greene, J.; Baird, A.M.; Brady, L.; Lim, M.; Gray, S.G.; McDermott, R.; Finn, S.P. Circular RNAs: Biogenesis, Function and Role in Human Diseases. Front. Mol. Biosci. 2017, 4, 11. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lasda, E.; Parker, R. Circular RNAs: Diversity of form and function. RNA 2014, 20, 1829–1842. [Google Scholar] [CrossRef] [Green Version]
- Liang, X.G.; Chen, H.; Li, L.; An, R.; Komiyama, M. Ring-Structured DNA and RNA as Key Players In Vivo and In Vitro. Bull. Chem. Soc. Jpn. 2021, 94, 141–157. [Google Scholar] [CrossRef]
- Deutsch, J.M. Equilibrium size of large ring molecules. Phys. Rev. E 1999, 59, R2539–R2541. [Google Scholar] [CrossRef] [Green Version]
- Meaburn, K.J.; Misteli, T. Cell biology— Chromosome territories. Nature 2007, 445, 379–381. [Google Scholar] [CrossRef]
- Farihah, M.H.; Scott, M.G. The synthesis, properties and potential applications of cyclic polymers. Nat. Chem. 2020, 12, 433–444. [Google Scholar]
- Jacob, F.; Wollman, E.L. Les épisomes, éléments génétiques ajoutés. Seances Acad. Sci. 1958, 247, 154. [Google Scholar]
- Nasongkla, N.; Chen, B.; Macaraeg, N.; Fox, E.; Fréchet, J.M.J.; Szoka, F.C. Dependence of pharmacokinetics and biodistribution on polymer architecture: Effect of cyclic versus linear polymers. J. Am. Chem. Soc. 2009, 131, 3842. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Poelma, J.E.; Ono, K.; Miyajima, D.; Aida, T.; Satoh, K.; Hawker, C.J. Cyclic block copolymers for controlling feature sizes in block copolymer lithography. ACS Nano 2012, 6, 10845. [Google Scholar] [CrossRef] [PubMed]
- Bennour, H.; Fildier, A.; Chatti, S.; Kricheldorf, H.R.; Zina, M.S.; Medimagh, R. Biosourced cyclic and multicyclic polyesters based on 1, 4: 3, 6-dianhydrohexitols: Application to metal ions uptake in aqueous media. Macromol. Chem. Phys. 2015, 216, 1081. [Google Scholar] [CrossRef]
- Roovers, J.; Toporowski, P.M. Synthesis of high molecular weight ring polystyrenes. Macromolecules 1983, 16, 843–849. [Google Scholar] [CrossRef]
- McKenna, G.B.; Hadziioannou, G.; Lutz, P.; Hild, G.; Strazielle, C.; Straupe, C.; Rempp, P. Dilute solution characterization of cyclic polystyrene. Macromolecules 1987, 20, 498–512. [Google Scholar] [CrossRef]
- Kapnistos, M.; Lang, M.; Vlassopoulos, D.; Pyckhout-Hintzen, W.; Richter, D.; Cho, D.; Chang, T.; Rubinstein, M. Unexpected power-law stress relaxation of entangled ring polymers. Nat. Mater. 2008, 7, 997–1002. [Google Scholar] [CrossRef]
- Gooβen, S.; Krutyeva, M.; Sharp, M.; Feoktystov, A.; Allgaier, J.; Pyckhout-Hintzen, W.; Wischnewsiki, A.; Richter, D. Sensing polymer chain dynamics through ring topology: A neutron spin echo study. Phys. Rev. Lett. 2015, 115, 148302. [Google Scholar]
- Wang, Z.W.; Mei, L.; Guo, C.X.; Huang, S.; Shi, W.Q.; Li, X.W.; Feng, W.; Li, X.P.; Yang, C.; Yuan, L.H. Supramolecular shish kebabs: Higher order dimeric structures from ring-in-rings complexes with conformational adaptivity. Angew. Chem. Int. Ed. 2023, 62, e202216690. [Google Scholar] [CrossRef]
- Zhou, Y.C.; Young, C.D.; Lee, M.; Banik, S.; Kong, D.; McKenna, G.B.; Robertson-Anderson, R.M.; Sing, C.E.; Schroeder, C.M. Dynamics and rheology of ring-linear blend semidilute solutions in extensional flow: Single molecule experiments. J. Rheol. 2021, 65, 729–744. [Google Scholar] [CrossRef]
- Yang, Y.B.; Sun, Z.Y.; Fu, C.L.; An, L.J.; Wang, Z.G. Monte Carlo simulation of a single ring among linear chains: Structural and dynamic heterogeneity. J. Chem. Phys. 2010, 133, 064901. [Google Scholar] [CrossRef] [Green Version]
- Bernabei, M.; Bacova, P.; Moreno, A.J.; Narros, A.; Likos, C.N. Fluids of semiflexible ring polymers: Effective potentials and clustering. Soft Matter 2013, 9, 1287–1300. [Google Scholar] [CrossRef] [Green Version]
- Poier, P.; Bačová, P.; Moreno, A.J.; Likos, C.N.; Blaak, R. Anisotropic effective interactions and stack formation in mixtures of semiflexible ring polymers. Soft Matter 2016, 12, 4805–4820. [Google Scholar] [CrossRef] [PubMed]
- Halverson, J.D.; Lee, W.B.; Grest, G.S.; Grosberg, A.Y.; Kremer, K. Molecular dynamics simulation study of nonconcatenated ring polymers in a melt. I. Statics. J. Chem. Phys. 2011, 134, 204904. [Google Scholar] [CrossRef] [Green Version]
- Lee, E.; Jung, Y.J. Segregated structures of ring polymer melts near the surface: A molecular dynamics simulation study. Soft Matter 2015, 11, 6018–6028. [Google Scholar] [CrossRef] [Green Version]
- Smith, J.S.; Bedrov, D.; Smith, G.D.; Compos, G.D. A molecular dynamics simulation study of nanoparticle interactions in a model polymer-nanoparticle composite. Composites Sci. Technol. 2003, 63, 1599. [Google Scholar] [CrossRef]
- Liu, J.; Cao, D.; Zhang, L. Molecular dynamics study on nanoparticle diffusion in polymer melts: A test of the Stokes-Einstein Law. J. Phys. Chem. C 2008, 112, 6653. [Google Scholar] [CrossRef]
- Weeks, J.D.D.; Andersen, H.C. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237. [Google Scholar] [CrossRef]
- Plimpton, S. Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef] [Green Version]


| Lring | Nring | Llinear | Nlinear | Kb-ring | Kb-linear | Pressure | Side Length of Simulation Box Lx/Ly/Lz | rc |
|---|---|---|---|---|---|---|---|---|
| 30 | 1 | 30 | 2082 | 50 | 0 | 0.381 | 50.23 | 21/6 |
| 10 | 0.418 | 51.57 | ||||||
| 20 | 0.426 | 50.82 | ||||||
| 30 | 0.435 | 51.43 | ||||||
| 40 | 0.441 | 50.56 | ||||||
| 50 | 0.451 | 50.90 |
| Kb-linear | τorientation | τnormal |
|---|---|---|
| 0 | 17,295 | 113,378 |
| 10 | 18,642 | 561,797 |
| 20 | 20,000 | 572,100 |
| 30 | 22,000 | 579,100 |
| 40 | 23,000 | 582,400 |
| 50 | 24,026 | 590,000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Qin, Y. The Dynamic Behavior of a Single Semiflexible Ring Chain in a Linear Polymer Matrix. Biophysica 2023, 3, 476-484. https://doi.org/10.3390/biophysica3030031
Zhou X, Qin Y. The Dynamic Behavior of a Single Semiflexible Ring Chain in a Linear Polymer Matrix. Biophysica. 2023; 3(3):476-484. https://doi.org/10.3390/biophysica3030031
Chicago/Turabian StyleZhou, Xiaolin, and Yifan Qin. 2023. "The Dynamic Behavior of a Single Semiflexible Ring Chain in a Linear Polymer Matrix" Biophysica 3, no. 3: 476-484. https://doi.org/10.3390/biophysica3030031
APA StyleZhou, X., & Qin, Y. (2023). The Dynamic Behavior of a Single Semiflexible Ring Chain in a Linear Polymer Matrix. Biophysica, 3(3), 476-484. https://doi.org/10.3390/biophysica3030031






