Nervous Activity of the Brain in Five Dimensions
Abstract
:1. Introduction
2. Materials and Methods
2.1. EEG Traces
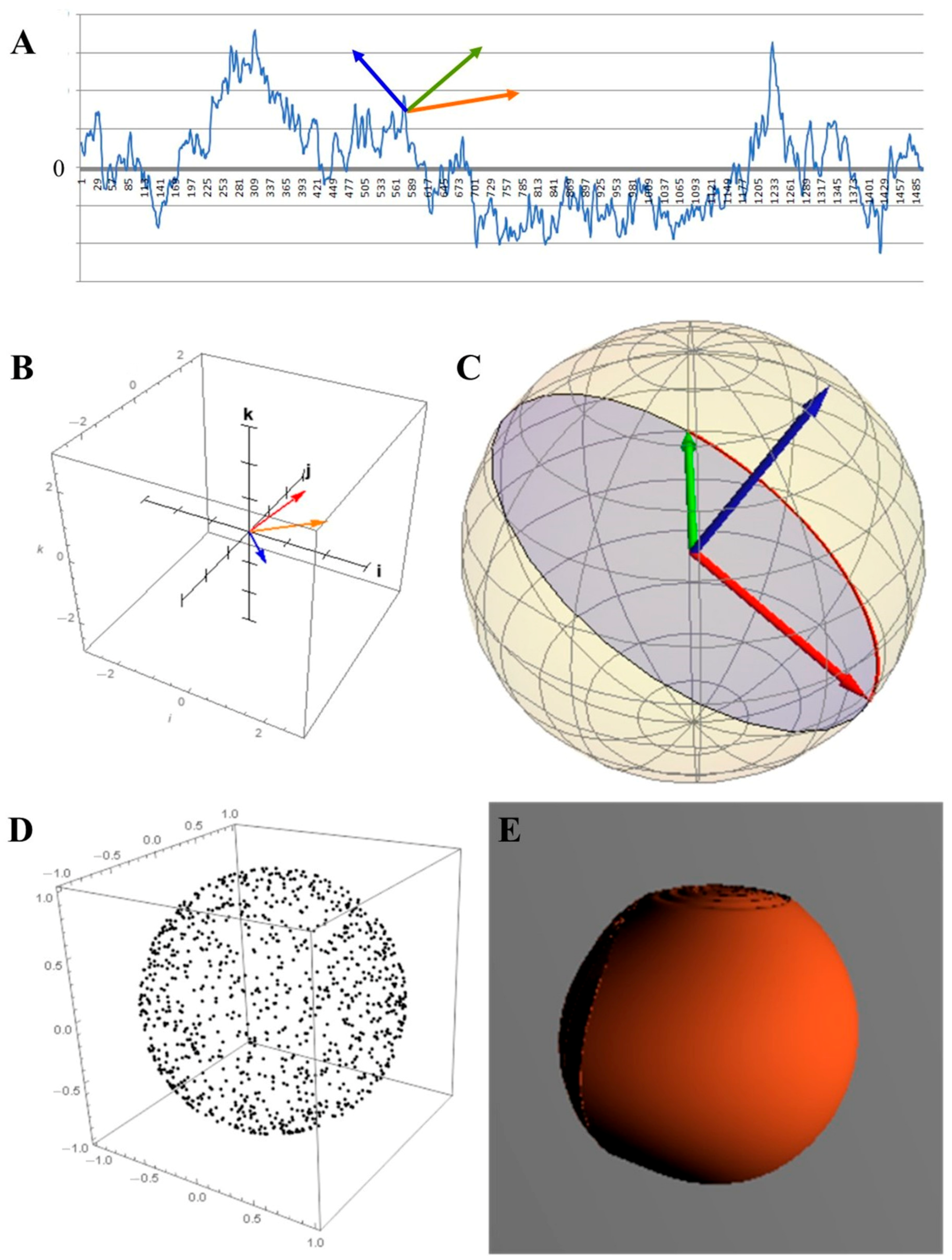
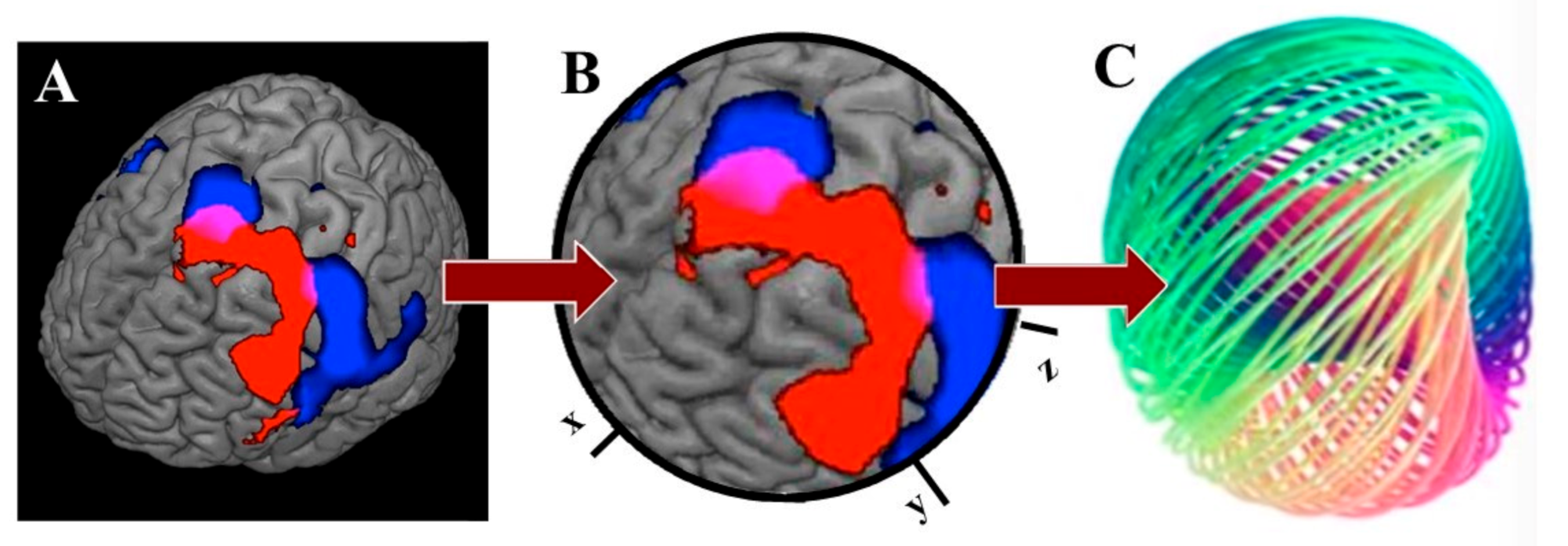
2.2. Quaternion Maps
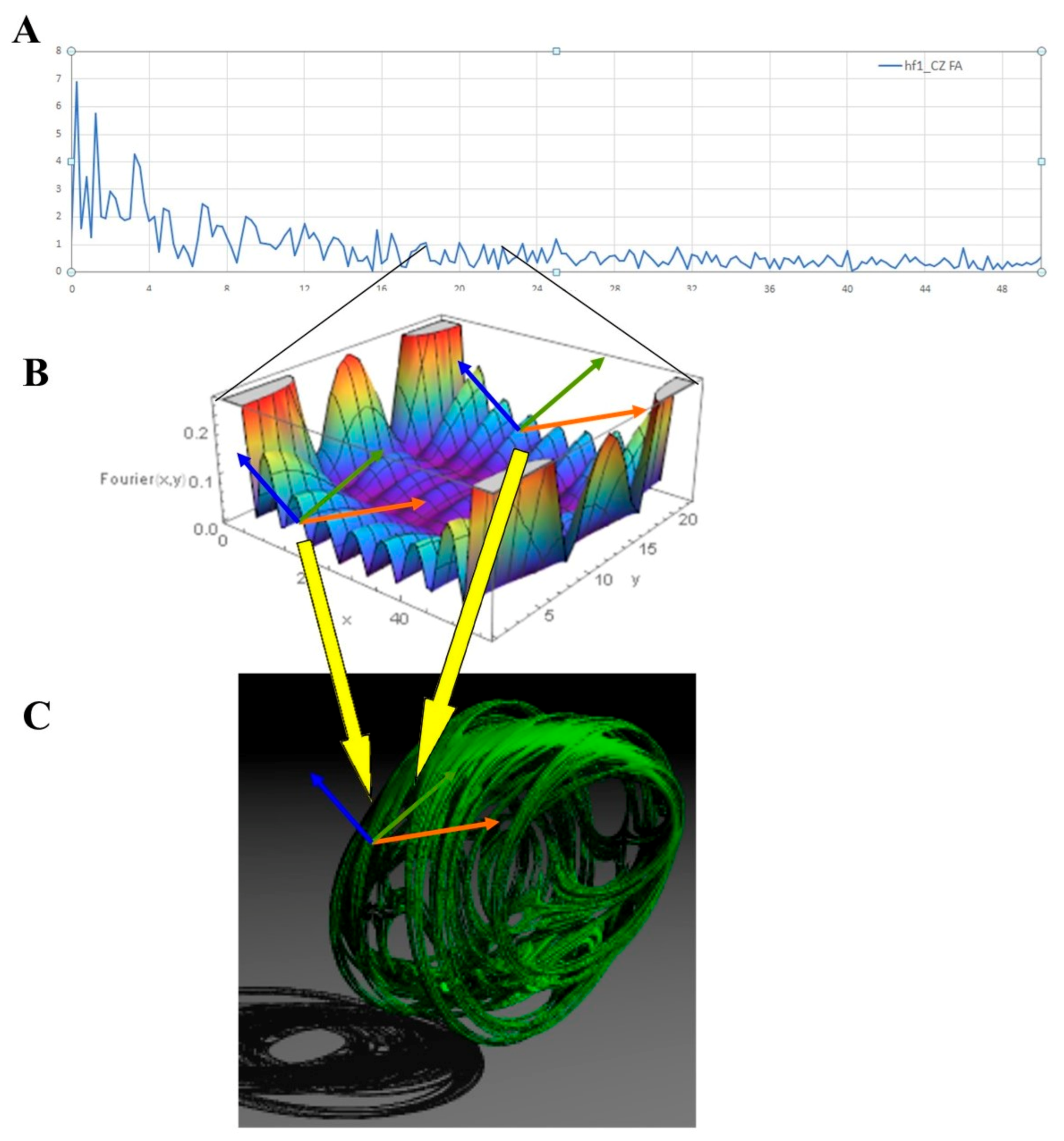
2.3. Fourier Analysis
3. Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Reimann, M.W.; Nolte, M.; Scolamiero, M.; Turner, K.; Perin, R.; Chindemi, G.; Dłotko, P.; Levi, R.; Hess, K.; Markram, H. Cliques of Neurons Bound into Cavities Provide a Missing Link between Structure and Function. Front. Comput. Neurosci. 2017, 11, 48. [Google Scholar] [CrossRef] [Green Version]
- Bellmund, J.L.S.; Gardenfors, P.; Moser, E.I.; Doeller, C.F. Navigating cognition: Spatial codes for human thinking. Science 2018, 362, eeat6766. [Google Scholar] [CrossRef] [Green Version]
- Chariker, L.; Shapley, R.; Young, L.-S. Rhythm and Synchrony in a Cortical Network Model. J. Neurosci. 2018, 38, 8621–8634. [Google Scholar] [CrossRef] [Green Version]
- Tozzi, A. The multidimensional brain. Phys. Life Rev. 2019, 31, 86–103. [Google Scholar] [CrossRef] [PubMed]
- Friston, K. The Emperor’s new topology: Comment on “Topodynamics of metastable brains” by Arturo Tozzi et al. Phys. Life Rev. 2017, 21, 26–28. [Google Scholar] [CrossRef]
- Tozzi, A.; Peters, J.F. Towards a Fourth Spatial Dimension of Brain Activity. Cogn. Neurodyn. 2016, 10, 189–199. [Google Scholar] [CrossRef] [PubMed]
- Peters, J.F.; Ramanna, S.; Tozzi, A.; İnan, E. Bold-Independent Computational Entropy Assesses Functional Donut-Like Structures in Brain fMRI Images. Front. Hum. Neurosci. 2017, 11, 38. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, W.R. On Quaternions; or on a new System of Imaginaries in Algebra (letter to John T. Graves). Philos. Mag. 1844, 25, 489–495. [Google Scholar]
- Tate, P.G. An Elementary Treatise on Quaternions; Clarendon Press: Oxford, UK, 1867. [Google Scholar]
- Hosny, K.M.; Khedr, Y.M.; Khedr, W.I.; Mohamed, E.R. Robust Color Image Hashing Using Quaternion Polar Complex Exponential Transform for Image Authentication. Circuits Syst. Signal Process. 2018, 37, 5441–5462. [Google Scholar] [CrossRef]
- Ayzenberg, A. Torus action on quaternionic projective plane and related spaces. arXiv 2019, arXiv:1903.03460. [Google Scholar]
- Batres-Mendoza, P.; Montoro-Sanjose, C.R.; Guerra-Hernandez, E.I.; Almanza-Ojeda, D.L.; Rostro-Gonzalez, H.; Romero-Troncoso, R.J.; Ibarra-Manzano, M.A. Quaternion-Based Signal Analysis for Motor Imagery Classification from Electroencephalographic Signals. Sensors 2016, 16, 336. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, H. Almost periodic synchronization of quaternion-valued shunting inhibitory cellular neural networks with mixed delays via state-feedback control. PLoS ONE 2018, 13, e0198297. [Google Scholar] [CrossRef] [Green Version]
- Enshaeifar, S.; Kouchaki, S.; Took, C.C.; Sanei, S. Quaternion Singular Spectrum Analysis of Electroencephalogram with Application in Sleep Analysis. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 57–67. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hanson, A.J.; Thakur, S. Quaternion maps of global protein structure. J. Mol. Graph. Model. 2012, 38, 256–278. [Google Scholar] [CrossRef] [PubMed]
- Hart, V.; Segerman, H. The Quaternion Group as a Symmetry Group. arXiv 2014, arXiv:1404.6596v1. [Google Scholar]
- Giblin, P. Graphs, Surfaces and Homology; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Weeks, J.R. The shape of space: How to visualize surfaces and three-dimensional manifolds. Pure Appl. Math. 1985, 96, 197–210. [Google Scholar]
- Hopf, H. Collected Papers/Gesammelte Abhandlungen; Springer: Berlin, Germany; New York, NY, USA, 2001. [Google Scholar]
- Johnson, N. A Visualization of the Hopf Fibration. 2015. Available online: https://nilesjohnson.net/hopf.html (accessed on 22 September 2020).
- Ozdemir, F.; Özekes, H. On the Homomorphisms of the Lie Groups SU(2) and S3. Abstr. Appl. Anal. 2013, 2, 1–5. [Google Scholar] [CrossRef]
- Pritchard, W.S. The brain in fractal time: 1/f-like power spectrum scaling of the human electroencephalogram. Int. J. Neurosci. 1992, 66, 119–129. [Google Scholar] [CrossRef]
- Fingelkurts, A.A.; Fingelkurts, A.A.; Neves, C.F.H. Natural world physical, brain operational, and mind phenomenal space-time. Phys. Life Rev. 2010, 7, 195–249. [Google Scholar] [CrossRef] [Green Version]
- Buzsáki, G.; Watson, B.O. Brain rhythms and neural syntax: Implications for efficient coding of cognitive content and neuropsychiatric disease. Dialogues Clin. Neurosci. 2012, 4, 345–367. [Google Scholar]
- Van de Ville, D.; Britz, J.; Michel, C.M. EEG microstate sequences in healthy humans at rest reveal scale-free dynamics. Proc. Natl. Acad. Sci. USA 2010, 107, 18179–18184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jirsa, V.K.; Stacey, W.C.; Quilichini, P.P.; Ivanov, A.I.; Bernard, C. On the nature of seizure dynamics. Brain 2014, 137 Pt 8, 2210–2230. [Google Scholar] [CrossRef] [Green Version]
- de Arcangelis, L.; Herrmann, H.J. Learning as a phenomenon occurring in a critical state. Proc. Natl. Acad. Sci. USA 2010, 107, 3977–3981. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oliveros-Muñoz, J.M.; Jiménez-Islas, H. Hyperspherical path tracking methodology as correction step in homotopic continuation methods. Chem. Eng. Sci. 2013, 97, 413–429. [Google Scholar] [CrossRef]
- Tozzi, A.; Ahmad, M.Z.; Peters, J.F. Neural computing in four spatial dimensions. Cogn. Neurodyn. 2020. [Google Scholar] [CrossRef]
- Lohse, M.; Schweizer, C.; Price, H.M.; Zilberberg, O.; Bloch, I. Exploring 4D quantum Hall physics with a 2D topological charge pump. Nature 2018, 553, 55–58. [Google Scholar] [CrossRef]
- Zilberberg, O.; Huang, S.; Guglielmon, J.; Wang, M.; Chen, K.P.; Kraus, Y.E.; Rechtsman, M.C. Photonic topological boundary pumping as a probe of 4D quantum Hall physics. Nature 2018, 553, 59–62. [Google Scholar] [CrossRef]
- Di Concilio, A.; Guadagni, C.; Peters, J.F.; Ramanna, S. Descriptive proximities, properties and interplay between classical proximities and overlap. Math. Comp. Sci. 2018, 12, 91–106. [Google Scholar] [CrossRef]
- Peters, J.F. Computational Geometry, Topology and Physics of Digital Images with Applications. Shape Complexes, Optical Vortex Nerves and Proximities; Springer Nature: Cham, Switzerland, 2020; p. xxv+440. [Google Scholar] [CrossRef]
- von Wegner, F. Partial Autoinformation to Characterize Symbolic Sequences. Front. Physiol. 2018, 9, 1382. [Google Scholar] [CrossRef]
- von Wegner, F.; Laufs, H.; Tagliazucchi, E. Mutual information identifies spurious Hurst phenomena in resting state EEG and fMRI data. Phys. Rev. E 2018, 97, 022415. [Google Scholar] [CrossRef]
- Fruchart, M.; Zhou, Y.; Vitelli, V. Dualities and non-Abelian mechanics. Nature 2020, 577, 636–640. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tozzi, A.; Peters, J.F.; Jausovec, N.; Don, A.P.H.; Ramanna, S.; Legchenkova, I.; Bormashenko, E. Nervous Activity of the Brain in Five Dimensions. Biophysica 2021, 1, 38-47. https://doi.org/10.3390/biophysica1010004
Tozzi A, Peters JF, Jausovec N, Don APH, Ramanna S, Legchenkova I, Bormashenko E. Nervous Activity of the Brain in Five Dimensions. Biophysica. 2021; 1(1):38-47. https://doi.org/10.3390/biophysica1010004
Chicago/Turabian StyleTozzi, Arturo, James F. Peters, Norbert Jausovec, Arjuna P. H. Don, Sheela Ramanna, Irina Legchenkova, and Edward Bormashenko. 2021. "Nervous Activity of the Brain in Five Dimensions" Biophysica 1, no. 1: 38-47. https://doi.org/10.3390/biophysica1010004
APA StyleTozzi, A., Peters, J. F., Jausovec, N., Don, A. P. H., Ramanna, S., Legchenkova, I., & Bormashenko, E. (2021). Nervous Activity of the Brain in Five Dimensions. Biophysica, 1(1), 38-47. https://doi.org/10.3390/biophysica1010004







