Blast Wave Simulator for Laminated Glass Panels Experimental Evaluation
Abstract
1. Introduction
2. Experimental Apparatus and Test Setup
2.1. Preliminary Tests Using Only Tube and Piston
2.2. Tests Using Steel Fluid Chamber and Rigid Plate Sample
3. Tests of Laminated Glass Samples Using the Fluid Chamber
4. Tests of Flexible Aluminum Plate Using the Fluid Chamber
5. Results and Discussion
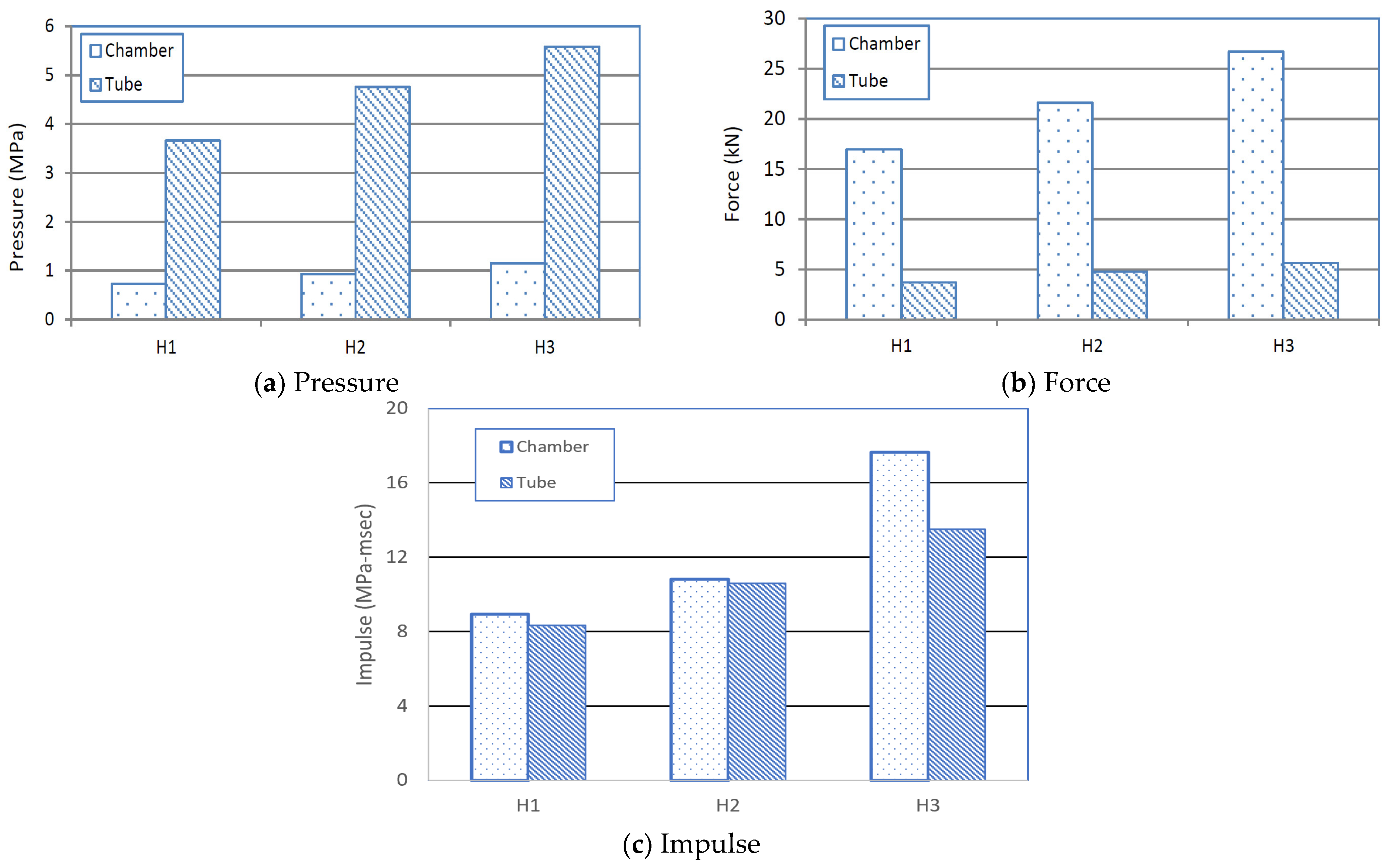
5.1. Piston Tube and Fluid Chamber with 6.35 mm Steel Base Plate
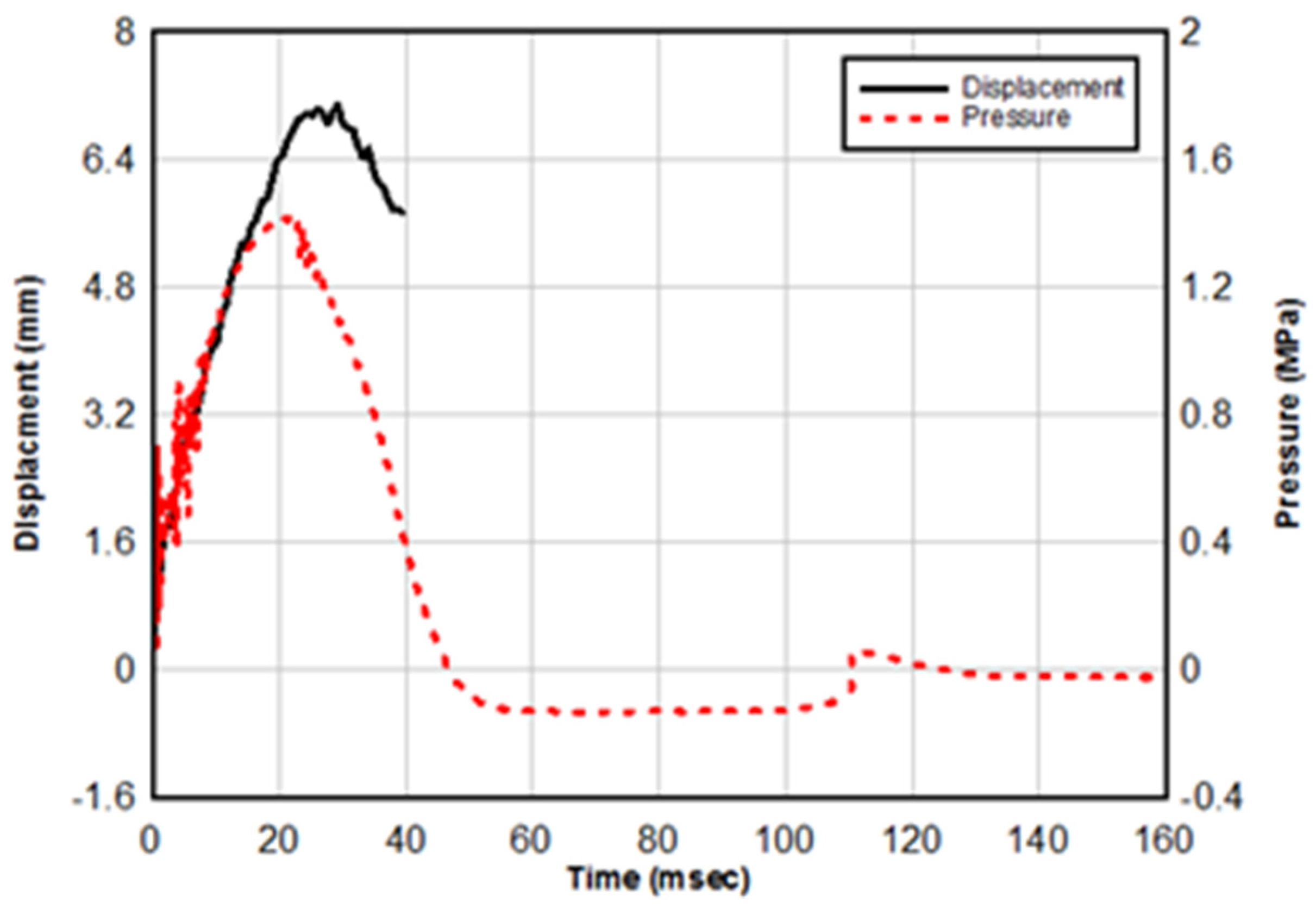
5.2. Aluminum Plate Sample
5.3. Four Tested LG Samples
5.3.1. Test of LG Panel #1
5.3.2. Test of LG Panel #2
5.3.3. Test of LG Panel #3
5.3.4. Test of LG Panel #4
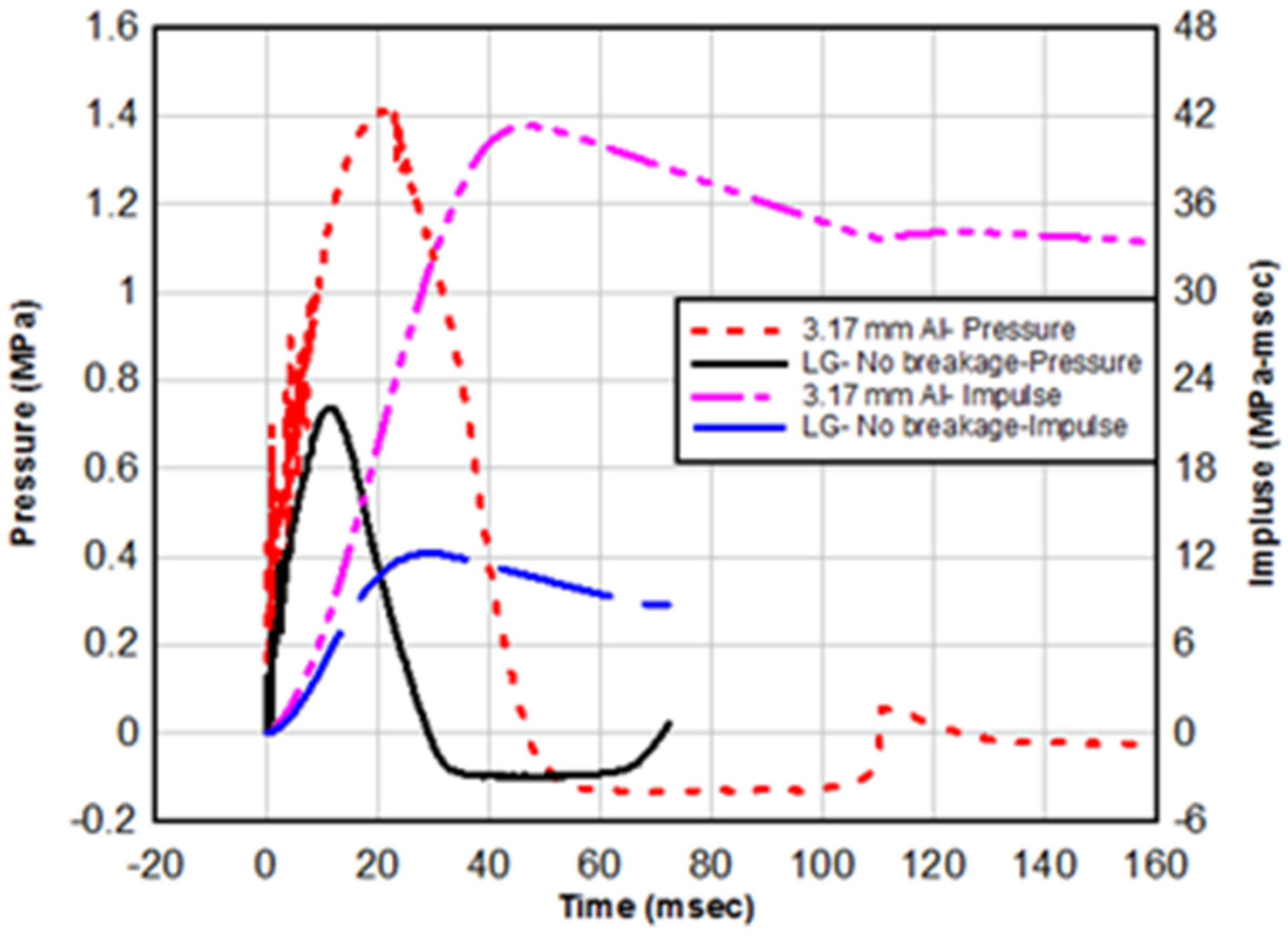
5.4. Behavior Comparisons of the Aluminum and LG Samples
5.5. The Speed of the Glass Splinters
6. Conclusions
- The high variation in the results can be attributed to the effect of the presence of flaws at the surface of glass samples.
- The breakage of the glass allowed the test panes to absorb the generated energy and drop the pressure value instantaneously for the three sample panes tested.
- It was observed that the initial velocities for randomly selected flying shards were 3 m/s to 4 m/s, and they can be assumed as medium hazards based on the current standard, UFC.
- The induced impulse inside the fluid chamber for the case of the aluminum plate was almost 3.4 times the induced impulse for the case of an unbroken LG pane.
- The results of this novel apparatus and research can be used to efficiently design and test a full-scale shock wave simulator for cost-efficient testing of specimens for blast design.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shirbhate, P.A.; Goel, M.D. A Critical Review of Blast Wave Parameters and Approaches for Blast Load Mitigation. Arch. Comput. Methods Eng. 2021, 28, 1713–1730. [Google Scholar] [CrossRef]
- Nawar, M.; Salim, H.; Newberry, M.; El-Sisi, A. High strain rate response of laminated glass interlayer materials. Constr. Build. Mater. 2021, 299, 123934. [Google Scholar] [CrossRef]
- Martín, M.; Centelles, X.; Solé, A.; Barreneche, C.; Fernández, A.I.; Cabeza, L.F. Polymeric interlayer materials for laminated glass: A review. Constr. Build. Mater. 2020, 230, 116897. [Google Scholar] [CrossRef]
- Nawar, M.; Salim, H.; Lusk, B.; Kiger, S. Numerical Simulation and Verification of Curtain Wall Systems under Shock Pressure. Pract. Period. Struct. Des. Constr. 2014, 19, 04014008. [Google Scholar] [CrossRef]
- Nawar, M.; Salim, H.; Lusk, B.; Perry, K.; Kiger, S.; Miller, G. Modeling and testing of laminated curtain wall systems under blast loading. In Structures Congress 2013: Bridging Your Passion with Your Profession: Proceedings of the 2013 Structures Congress, Pittsburgh, PA, USA, 2–4 May 2013; American Society of Civil Engineers: Reston, VA, USA, 2013; pp. 170–180. [Google Scholar] [CrossRef]
- Lusk, B.; Salim, H.; Perry, K.; Nawar, M.; Wedding, W.C.; Kiger, S.; Ibrahim, A. Modeling and Testing of Laminated Window Systems under Blast Loading. In Proceedings of the Structures Congress 2011, Las Vegas, NV, USA, 14–16 April 2011; pp. 1552–1560. [Google Scholar] [CrossRef]
- Hidallana-Gamage, H.D.; Thambiratnam, D.P.; Perera, N.J. Influence of interlayer properties on the blast performance of laminated glass panels. Constr. Build. Mater. 2015, 98, 502–518. [Google Scholar] [CrossRef]
- Biolzi, L.; Simoncelli, M. Overall response of 2-ply laminated glass plates under out-of-plane loading. Eng. Struct. 2022, 256, 113967. [Google Scholar] [CrossRef]
- Ranocchiai, G.; Andreozzi, L.; Zulli, F.; Fagone, M. Effects of Interlayer Weathering on the Structural Behaviour of Laminated Glass Structures. In Proceedings of the Challenging Glass 5—Conference on Architectural and Structural Applications of GlassBelis, Gent, Belgium, 16–17 June 2016. [Google Scholar]
- Inaba, K.; Shepherd, J.E. Flexural waves in fluid-filled tubes subject to axial impact. J. Press. Vessel. Technol. 2010, 132, 021302. [Google Scholar] [CrossRef]
- Skews, B.W.; Kosing, O.E.; Hattingh, R.J. Use of a liquid shock tube as a device for the study of material deformation under impulsive loading conditions. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2004, 218, 39–51. [Google Scholar] [CrossRef]
- Espinosa, H.D.; Lee, S.; Moldovan, N. A novel fluid structure interaction experiment to investigate deformation of structural elements subjected to impulsive loading. Exp. Mech. 2006, 46, 805–824. [Google Scholar] [CrossRef]
- Deshpande, V.S.; Heaver, A.; Fleck, N.A. An underwater shock simulator. Proc. R. Soc. A Math. Phys. Eng. Sci. 2006, 462, 1021–1041. [Google Scholar] [CrossRef]
- Ando, K.; Sanada, T.; Inaba, K.; Shepherd, J.E.; Colonius, T.; Brennen, C.E. Shock Theory of a Bubbly Liquid in a Deformable Tube. In Proceedings of the 7th International Conference on Multiphase Flow, Tampa, CA, USA, 30 May–4 June 2010. [Google Scholar]
- Chao, T.W.; Shepherd, J.E. Comparison of fracture response of preflawed tubes under internal static and detonation loading. J. Press. Vessel. Technol. 2004, 126, 345–353. [Google Scholar] [CrossRef]
- Schiffer, A.; Tagarielli, V.L. The response of rigid plates to blast in deep water: Fluid–structure interaction experiments. Proc. R. Soc. A Math. Phys. Eng. Sci. 2012, 468, 2807–2828. [Google Scholar] [CrossRef]
- Perotti, L.; Deiterding, R.; Inaba, K.; Shepherd, J.; Ortiz, M. Elastic response of water-filled fiber composite tubes under shock wave loading. Int. J. Solids Struct. 2013, 50, 473–486. [Google Scholar] [CrossRef]
- Shepherd, J.E.; Inaba, K. Shock loading and failure of fluid-filled tubular structures. In Dynamic Failure of Materials and Structures; Springer: Boston, MA, USA, 2010. [Google Scholar] [CrossRef]
- Wei, J.; Shetty, M.S.; Dharani, L.R. Stress characteristics of a laminated architectural glazing subjected to blast loading. Comput. Struct. 2006, 84, 699–707. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, H.; Wang, Z. Experimental study of laminated glass window responses under impulsive and blast loading. Int. J. Impact Eng. 2015, 78, 1–19. [Google Scholar] [CrossRef]
- Zhang, X.; Hao, H. Experimental and numerical study of boundary and anchorage effect on laminated glass windows under blast loading. Eng. Struct. 2015, 90, 96–116. [Google Scholar] [CrossRef]
- Marchand, K.A.; Conrath, E.J.; Stevens, D.J.; Meyer, S.B. Blast Induced Glass Hazards: A Comparison of Design Approaches and Recent Research. In WIT Transactions on the Built Environment; WIT Press: Southampton, UK, 2006; Volume 87. [Google Scholar] [CrossRef]
- UFC 3-340-02. DoD Structures to Resist the Effects of Accidental Explosions, U.S. Army Corps of Engineers, USA. 5 December 2008. Available online: https://www.wbdg.org/FFC/DOD/UFC/ARCHIVES/ufc_3_340_02.pdf (accessed on 3 June 2024).
- DoD. UFC 4-010-01. DoD Minimum Antiterrorism Standards for Buildings. Unified Facilities Criteria, U.S. Army Corps of Engineeers, USA. 12 December 2018. Available online: https://www.wbdg.org/ffc/dod/unified-facilities-criteria-ufc/ufc-4-010-01 (accessed on 3 June 2024).








| Test | Mass (kg) | Height (mm) | Pressure (MPa) | Max. Impulse (MPa-ms) | Positive Phase Duration (ms) | Rising Time (ms) | Total Force at Steel Plate (kN) |
|---|---|---|---|---|---|---|---|
| 1 | 2.54 | 152.4 | 2.63 | 6.53 | 9.4 | 0.6 | 2.649 |
| 2 | 2.54 | 304.8 | 3.66 | 8.34 | 7.3 | 0.22 | 3.687 |
| 3 | 2.54 | 609.6 | 4.75 | 10.6 | 8.9 | 0.3 | 4.785 |
| 4 | 2.54 | 914.4 | 5.58 | 13.5 | 9.3 | 0.23 | 5.621 |
| 5 | 7.94 | 152.4 | 7.2 | 17.67 | 5 | 0.3 | 7.253 |
| Test | Mass (kg) | Height (mm) | Pressure (MPa) | Time to Max. Pressure (ms) | Max. Impulse (MPa-ms) | Positive Phase Duration (ms) | Total Force at Steel Plate (kN) |
|---|---|---|---|---|---|---|---|
| W1-H1 | 4.35 | 304.8 | 0.98 | 13 | 18.47 | 30.3 | 22.761 |
| W1-H2 | 4.35 | 609.6 | 1.05 | 7.74 | 9.87 | 15.1 | 24.387 |
| W1-H3 | 4.35 | 914.4 | 1.377 | 9.5 | 17.3 | 21.2 | 31.982 |
| W2-H1 | 2.54 | 304.8 | 0.73 | 9.5 | 8.93 | 24 | 16.955 |
| W2-H2 | 2.54 | 609.6 | 0.93 | 7.5 | 10.8 | 15.8 | 21.600 |
| W2-H3 | 2.54 | 914.4 | 1.15 | 10.61 | 17.65 | 22.62 | 26.710 |
| Sample | Frist Breakage Data | Measured Displacement | |||
|---|---|---|---|---|---|
| Max. Pressure (MPa) | Time to Max. Pressure (ms) | Impulse (MPa-ms) | Max. Displacement (mm) | Time for Max. Displ. (ms) | |
| LG1 | 0.36 | 4.2 | 0.97 | 10.4 | 40 |
| LG1 * | 0.2 | 9.7 | 1.81 | - | - |
| LG2 | 0.56 | 4.9 | 1.55 | 9.27 | 33.5 |
| LG3 | 0.76 | 9.1 | 4.51 | 9.77 | 23.4 |
| Property | Annealed Glass | AL 5052-H32 | |
|---|---|---|---|
| Properties | Density (kg/m3) | 2500 | 2680 |
| Young’s modulus, GPa | 69 | 70.3 | |
| Poisson ratio | 0.22 | 0.33 | |
| Elastic limit, MPa | - | 193 | |
| Failure strain | 0.0012 | 0.12 | |
| Failure stress, MPa | 84.8 | 228 | |
| Results | Max. Pressure (kPa) | 0.74 | 1.43 |
| Max. Pressure Time (ms) | 11.8 | 22.4 | |
| Max. Impluse (MPa-ms) | 12.25 | 41.3 | |
| Positive Phase (ms) | 29.1 | 46.9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nawar, M.T.; El-Zohairy, A.; El-Sisi, A.; Salim, H.; Aldoshan, A.A. Blast Wave Simulator for Laminated Glass Panels Experimental Evaluation. CivilEng 2024, 5, 576-590. https://doi.org/10.3390/civileng5030031
Nawar MT, El-Zohairy A, El-Sisi A, Salim H, Aldoshan AA. Blast Wave Simulator for Laminated Glass Panels Experimental Evaluation. CivilEng. 2024; 5(3):576-590. https://doi.org/10.3390/civileng5030031
Chicago/Turabian StyleNawar, Mahmoud T., Ayman El-Zohairy, Alaa El-Sisi, Hani Salim, and Abdelhakim A. Aldoshan. 2024. "Blast Wave Simulator for Laminated Glass Panels Experimental Evaluation" CivilEng 5, no. 3: 576-590. https://doi.org/10.3390/civileng5030031
APA StyleNawar, M. T., El-Zohairy, A., El-Sisi, A., Salim, H., & Aldoshan, A. A. (2024). Blast Wave Simulator for Laminated Glass Panels Experimental Evaluation. CivilEng, 5(3), 576-590. https://doi.org/10.3390/civileng5030031








