Butt Jointing of Prefabricated Concrete Columns
Abstract
1. Introduction
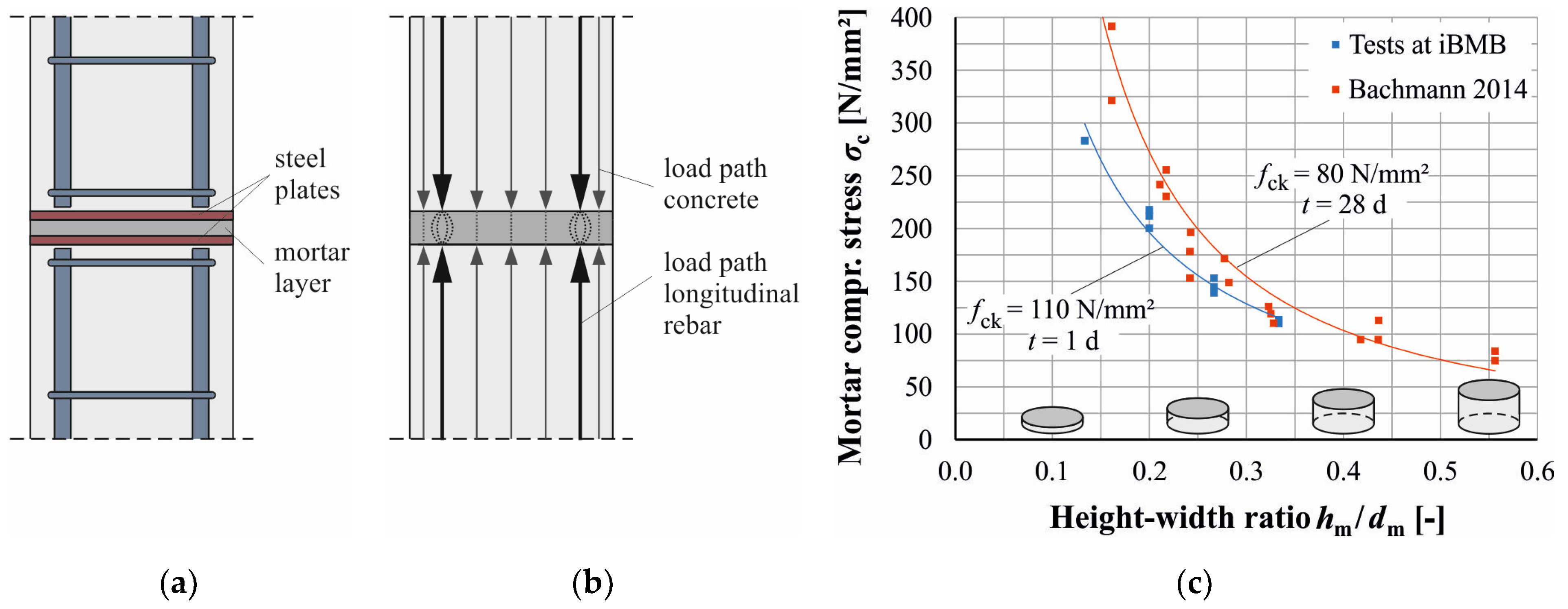
2. State of the Art
- Mortar thickness .
- Steel plate thickness .
- Compressive mortar strength .
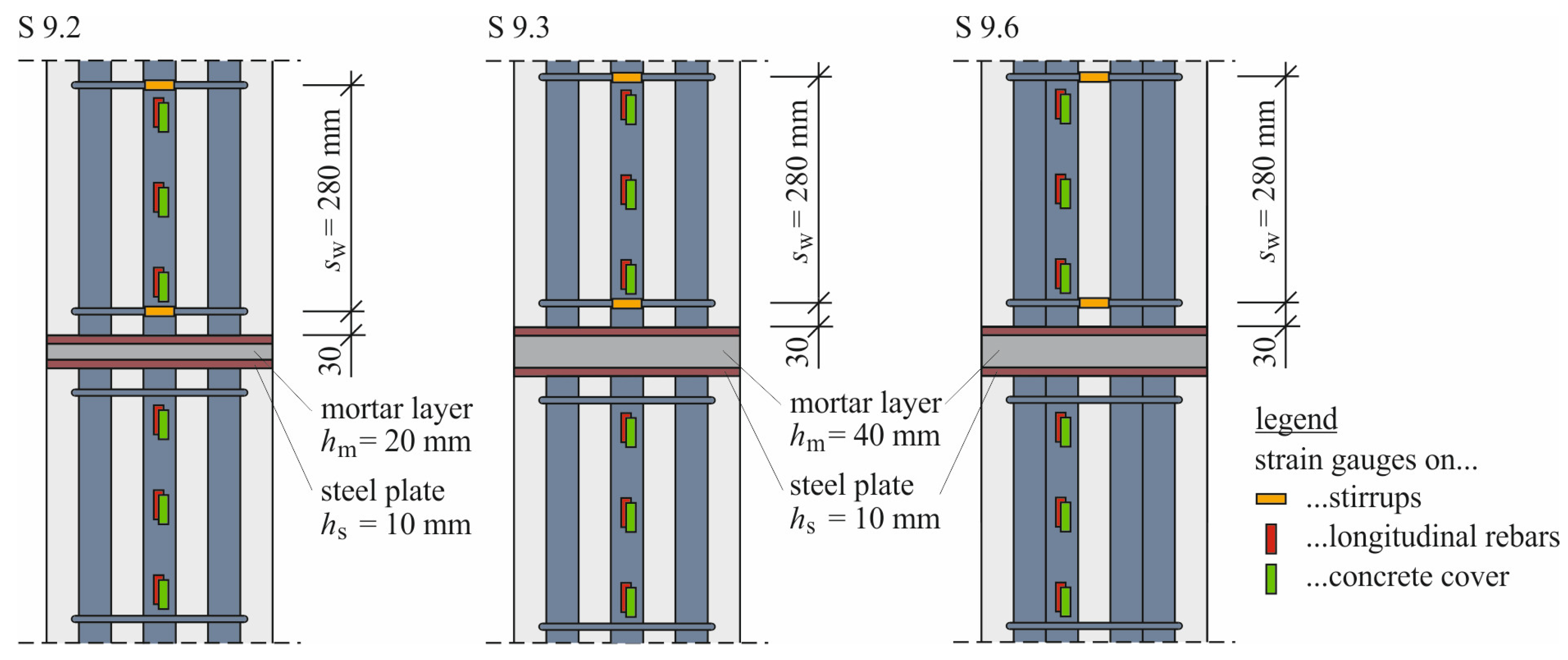
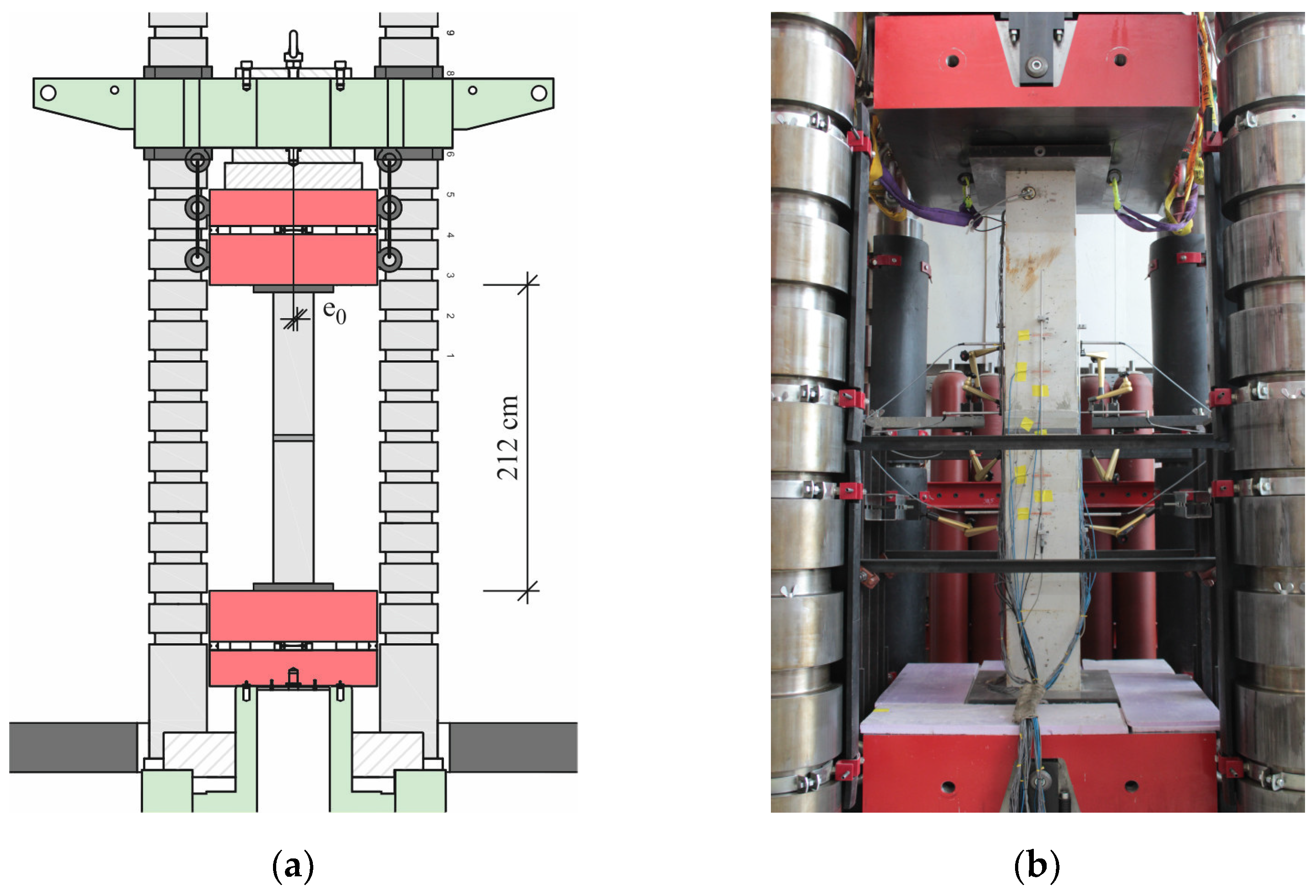
3. Large-Scale Tests
4. Deformation of the Steel Plate
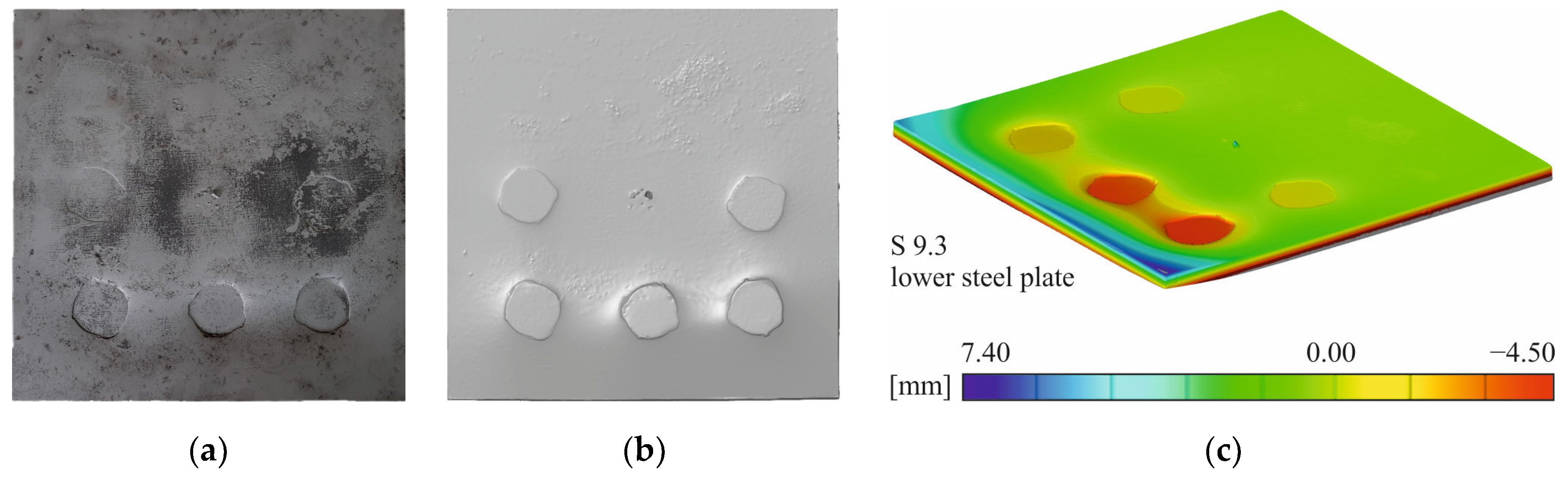
4.1. Experimental Findings
4.2. Numerical Investigations
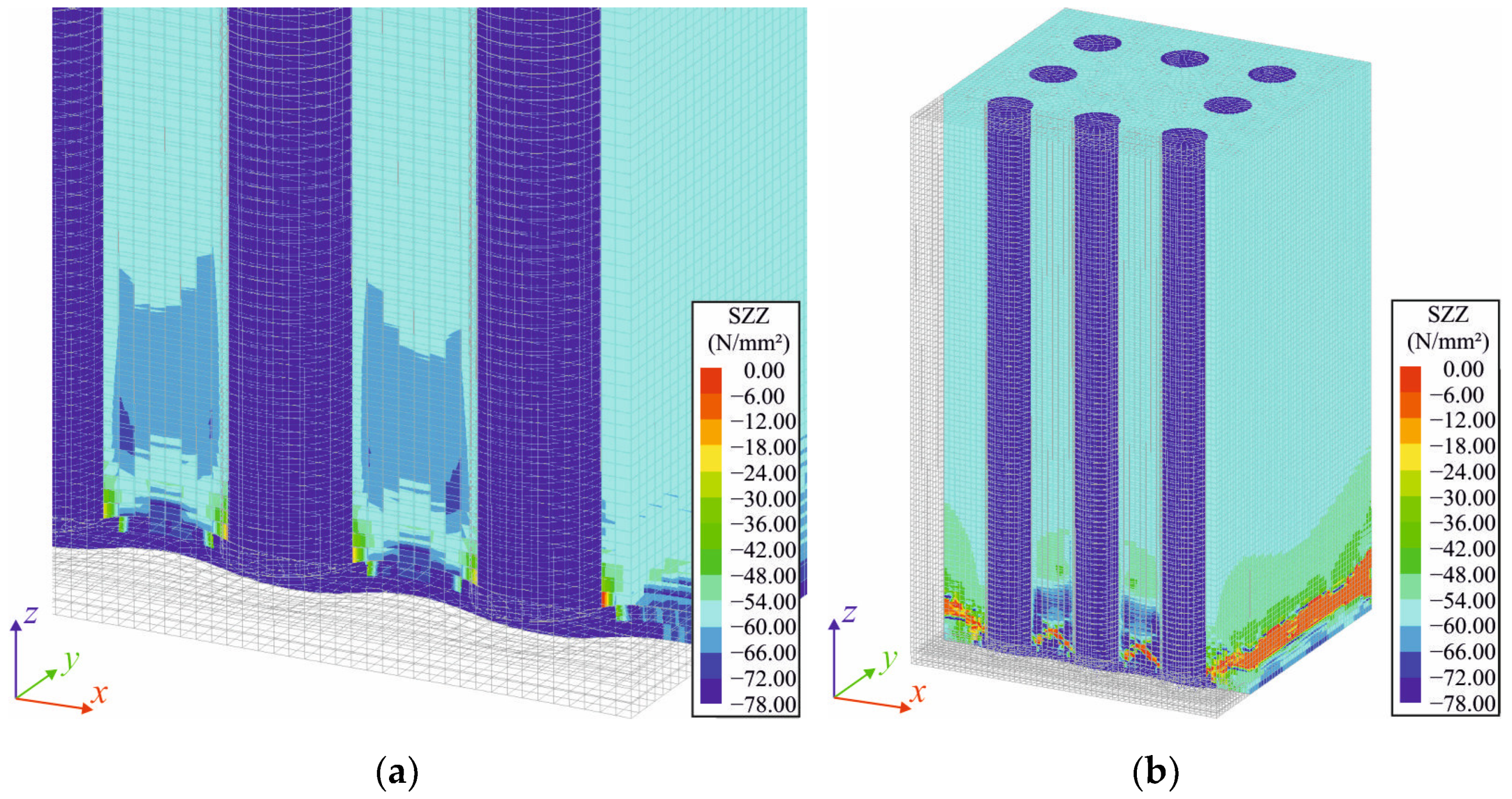
5. Stress Redistribution in Column End Regions
5.1. Experimental Findings
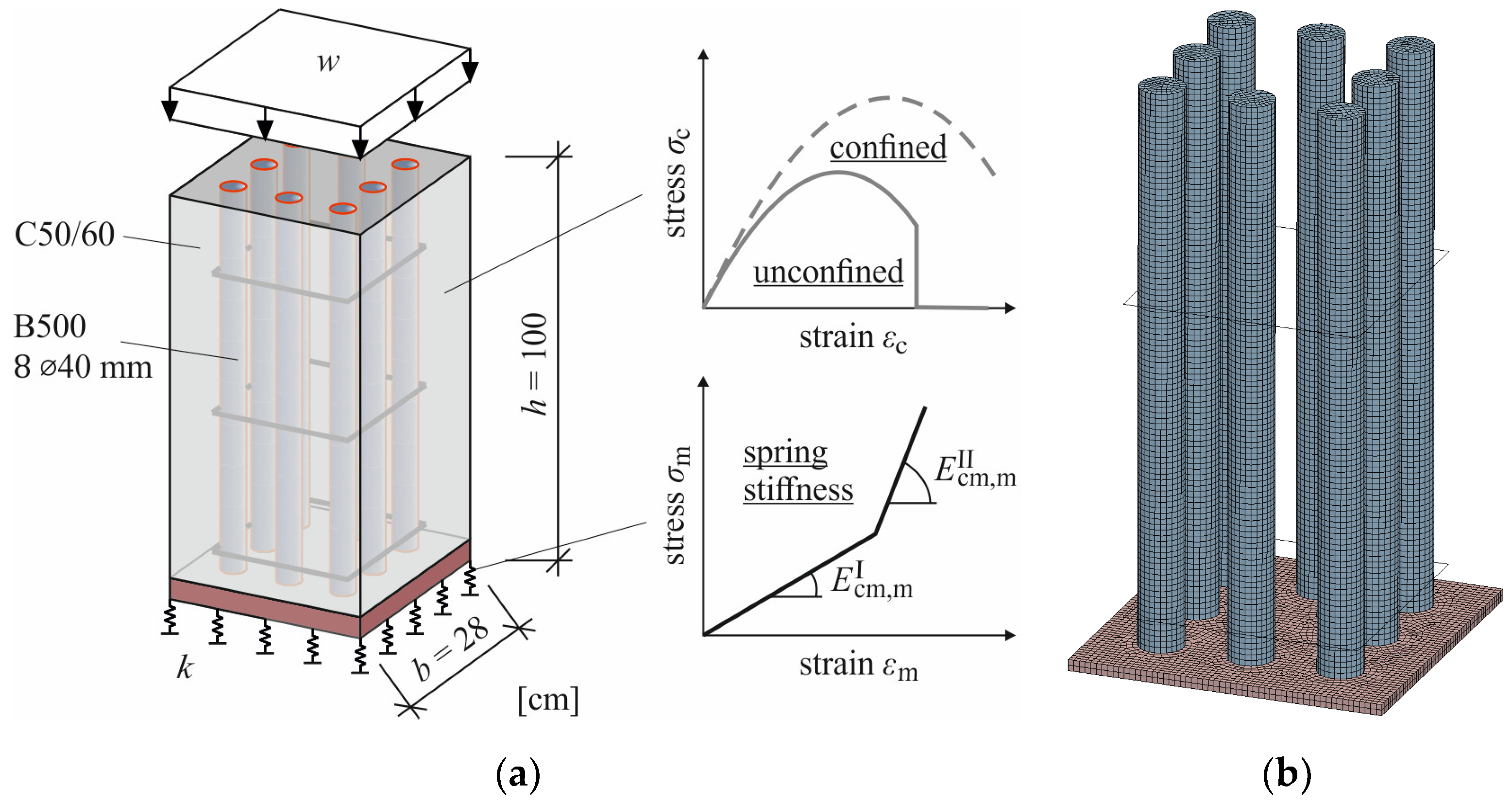
5.2. Confinement
5.3. Numerical Investigations
6. Evaluation of Load-Bearing Behaviour
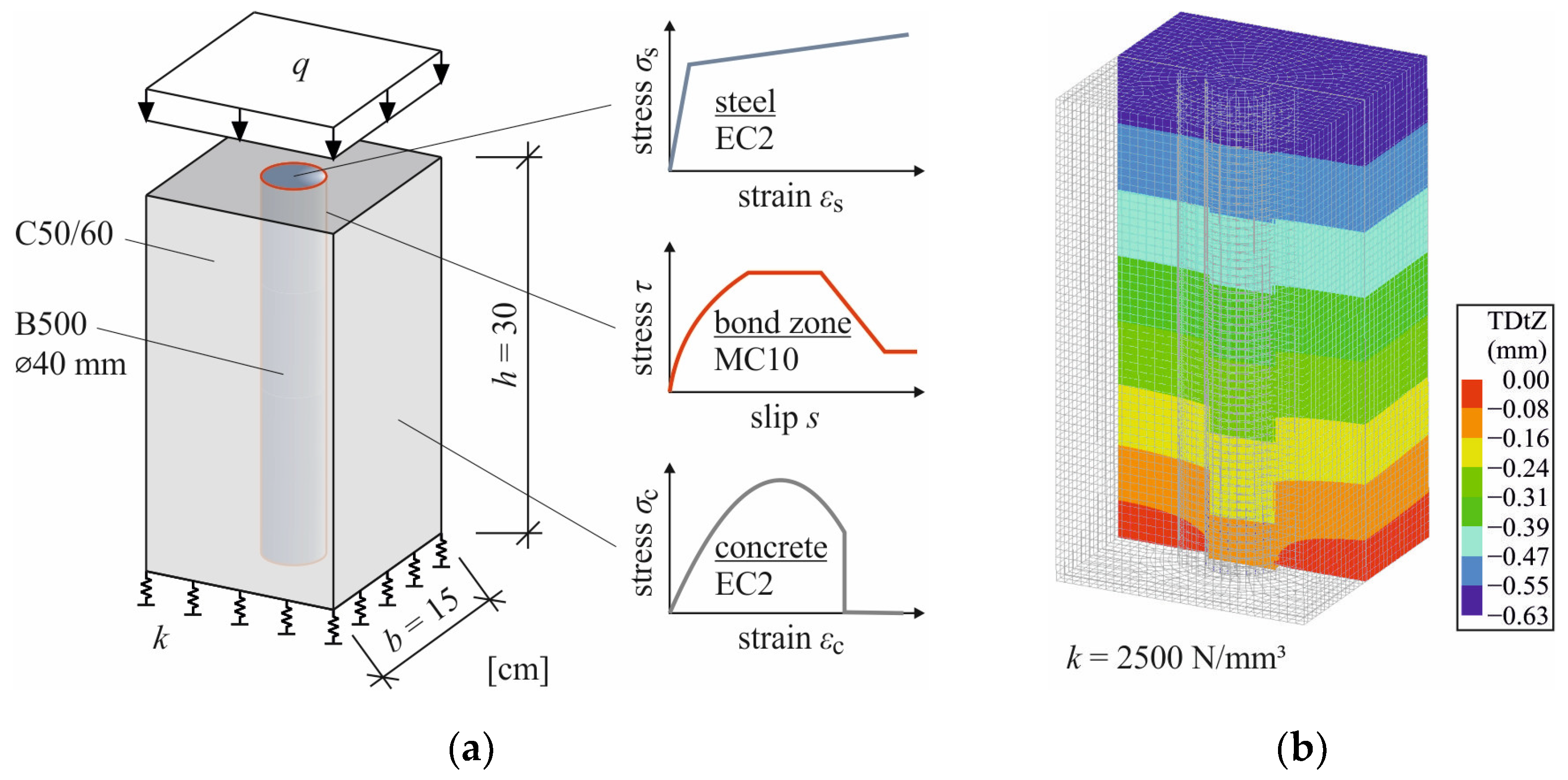
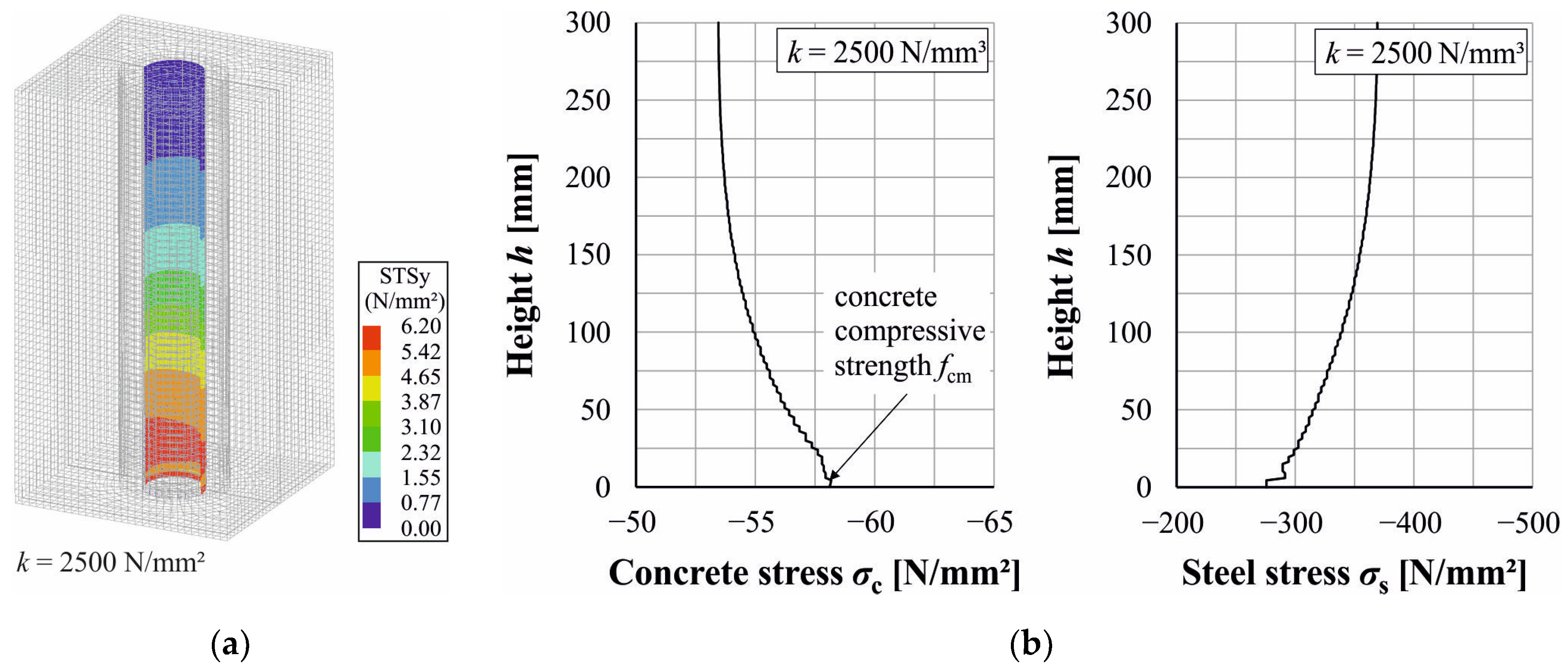
6.1. Large-Scale FE Model
6.2. Influences on the Load-Bearing Behaviour
- Increasing the thickness and grade of the steel plates.
- Increasing the Young’s modulus of the mortar.
- Reducing the thickness of the mortar layer.
- High planarity of the end faces of the columns.
- Minimum gap between longitudinal reinforcement and the steel plate.
7. Conclusions and Outlook
- The ultimate load of the monolithically manufactured columns could no longer be achieved with the addition of butt joints.
- The reduction of the ultimate load increases with greater mortar thickness.
- The reduction of the ultimate load increases with higher longitudinal reinforcement ratio.
- Failure is initiated by spalling off the concrete cover immediately above or below the butt joint.
- There are considerable indentations of the longitudinal rebars into the steel plates.
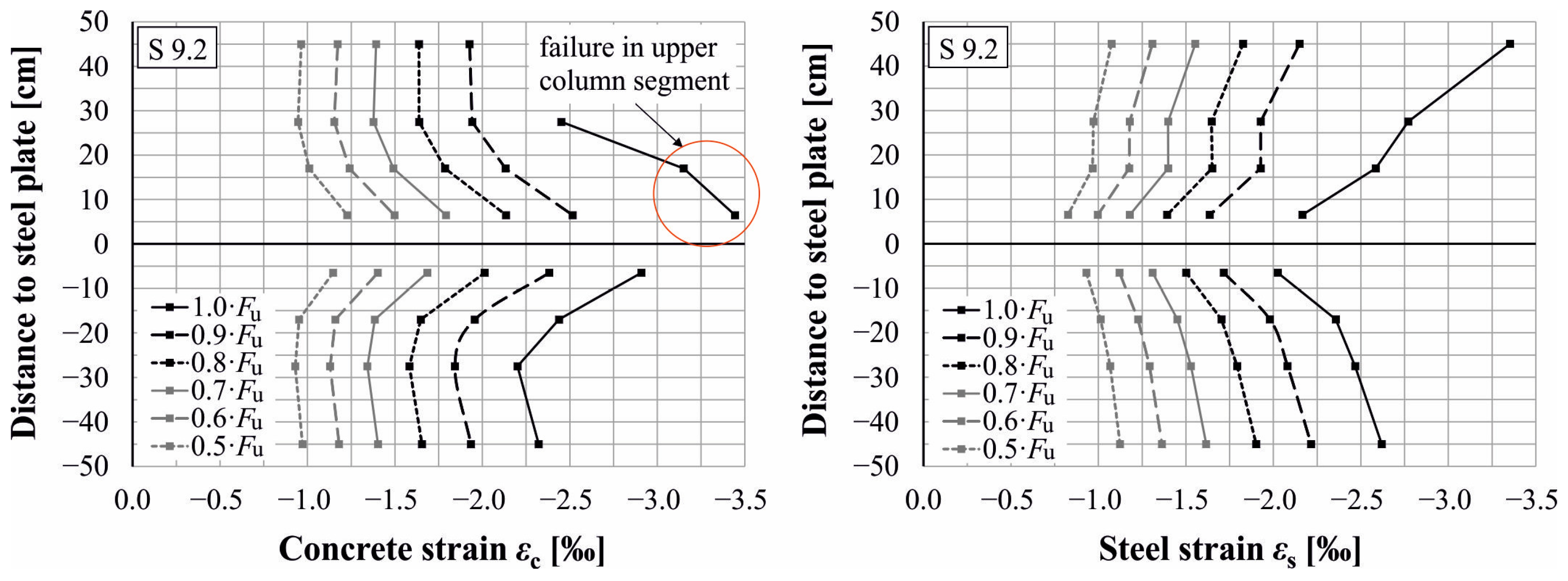
- The strain of the longitudinal rebars decreases in the direction of the butt joint and that the strain in the concrete cover simultaneously increases.
- Premature failure occurs due to overloading of the concrete cover when the concrete compressive strength is reached.
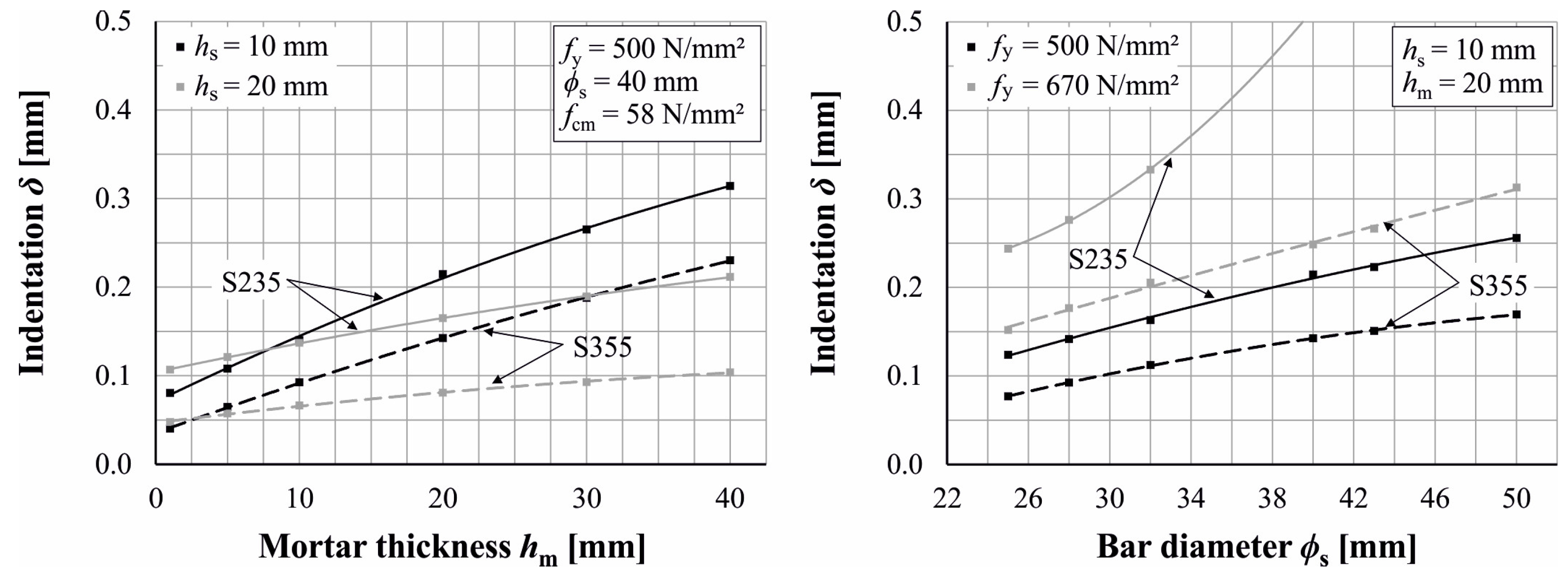
- The indentations of the longitudinal bars into the steel plate increase with enlarging bar diameter as well as thinner steel plates.
- Due to slip between reinforcement and concrete, bond stresses are activated right above the joint.
- Deep indentations lead to significant ultimate load reductions.
- The application of thick mortar layers, thin steel plates, large bar diameters and high reinforcement ratios, respectively, leads to considerable reductions in the ultimate load of the jointed column.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, J.-Y.; Hong, W.-K.; Park, S.-C. Experimental investigation of precast concrete based dry mechanical column-column joints for precast concrete frames. Struct. Des. Tall Spec. Build. 2017, 26, e1337. [Google Scholar] [CrossRef]
- Nzabonimpa, J.D.; Hong, W.-K. Structural performance of detachable precast composite column joints with mechanical metal plates. Eng. Struct. 2018, 160, 366–382. [Google Scholar] [CrossRef]
- Rave-Arango, J.F.; Blandón, C.A.; Restrepo, J.I.; Carmona, F. Seismic performance of precast concrete column-to-column lap-splice connections. Eng. Struct. 2018, 172, 687–699. [Google Scholar] [CrossRef]
- Tullini, N.; Minghini, F. Grouted sleeve connections used in precast reinforced concrete construction—Experimental investigation of a column-to-column joint. Eng. Struct. 2016, 127, 784–803. [Google Scholar] [CrossRef]
- Yu, Z.; Lv, X.; Yu, Y.; Ding, F.; Peng, X. Seismic Performance of Precast Concrete Columns with Improved U-type Reinforcement Ferrule Connections. Int. J. Concr. Struct. Mater. 2019, 13, 54. [Google Scholar] [CrossRef]
- Bachmann, H. Stützen mit hochfestem Betonstahl sind im Hochhausbau eine gute Alternative zu Stahl- und Stahlverbundstützen: Versuche und Erfahrungen bei den Tanzenden Türmen in Hamburg und beim Bau des Taunusturms in Frankfurt. Der Prüfingenieur 2014, 23, 12–27. [Google Scholar]
- Pfeifer, M. A skyscraper with hip-swing: The Omniturm in Frankfurt am Main. Bautechnik 2021, 98, 446–456. [Google Scholar] [CrossRef]
- Oettel, V.; Empelmann, M. Large bar diameters and high reinforcement ratios—Part 3: Columns. Beton Und Stahlbetonbau 2018, 113, 789–798. [Google Scholar] [CrossRef]
- Empelmann, M. Bewertung des Stumpfstoßes mit Mörtelfuge der Hochhausstützen beim Bauvorhaben FOUR in Frankfurt am Main; Expert report; Technische Universität Braunschweig: Braunschweig, Germany, 2021. [Google Scholar]
- Müller, F.; Sasse, H.R.; Thormählen, U. Stützenstöße im Stahlbeton-Fertigteilbau mit unbewehrten Elastomerlagern, DAfStb-Heft 339, 1st ed.; Beuth Verlag: Berlin, Germany, 1982. [Google Scholar]
- Mühlbauer, C. Fügen von Bauteilen aus ultrahochfestem Beton (UHPC) durch Verkleben. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2012. [Google Scholar]
- Stroband, J.; Poot, S.; Walraven, J. The effect of mortar joints between precast HSC columns loaded in compression. In Proceedings of the 4th International Symposium on Utilization of High-Strength/High-Performance Concrete, Paris, France, 29–31 May 1996; Volume 4, pp. 817–825. [Google Scholar]
- Somerville, G. The Behaviour of Mortar Joints in Compression; Technical report 42.476; Cement and Concrete Association: London, UK, 1972. [Google Scholar]
- Vambersky, J.N.J.A. Mortar Joints Loaded in Compression; Annual Report; TU Delft: Delft, The Netherlands, 1991. [Google Scholar]
- Barboza, A.d.S.R.; El Debs, M.K. Load-bearing capacity of mortar joints between precast elements. Mag. Concr. Res. 2006, 58, 589–599. [Google Scholar] [CrossRef]
- Empelmann, M.; Wichert, M.; Matz, H. Splitting Failure of Grouted Joints between UHPC Segments. Bauingenieur 2020, 95, 55–63. [Google Scholar] [CrossRef]
- Paschen, H.; Zillich, V.C. Versuche zur Bestimmung der Tragfähigkeit Stumpf Gestoßener Stahlbetonfertigteilstützen. DAfStb-Heft 316, 1st ed.; Ernst & Sohn: Berlin, Germany, 1980. [Google Scholar]
- Minnert, J. Tragverhalten von Stumpf Gestoßenen Fertigteilstützen aus Hochfestem Beton. DAfStb-Heft 499, 1st ed.; Beuth Verlag: Berlin, Germany, 2000. [Google Scholar]
- Saleh, H. Ein Beitrag zur Untersuchung und Bemessung von Stumpf Gestoßenen Fertigteilstützen aus Normalfestem Beton. Ph.D. Thesis, Universität Leipzig, Leipzig, Germany, 2002. [Google Scholar]
- Steinle, A.; Bachmann, H.; Tillmann, M. Bauen mit Betonfertigteilen im Hochbau, 3rd ed.; Ernst & Sohn: Berlin, Germany, 2018. [Google Scholar]
- König, G.; Tue, N.V.; Saleh, H.; Kliver, J. Herstellung und Bemessung stumpf gestoßener Fertigteilstützen. Beton Fertigteil Jahrbuch 2003, 198–206. [Google Scholar]
- Schoening, J.; Della Pietra, R.; Hegger, J.; Tue, N.V. Connections of precast UHPC elements. Bautechnik 2013, 90, 304–313. [Google Scholar] [CrossRef]
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization CEN: Brussels, Belgium, 2004.
- Fingerloos, F.; Hegger, J.; Zilch, K. EUROCODE 2 für Deutschland: Kommentierte und konsolidierte Fassung; Ernst & Sohn: Berlin, Germany, 2016. [Google Scholar]
- Martinez, S. Spirally-Reinforced High-Strength Concrete Columns. Ph.D. Thesis, Cornell University, New York, NY, USA, 1982. [Google Scholar]
- Sheikh, S.A.; Uzumeri, S.M. Analytical Model for Concrete Confinement in Tied Columns. J. Struct. Div. 1982, 108, 2703–2722. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical Stress-Strain Model for Confined Concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Euro-International Committee for Concrete; Fédération Internationale de la Précontrainte. CEB-FIP Model Code 1990: Design Code; Telford: London, UK, 1993. [Google Scholar]
- Razvi, S.; Saatcioglu, M. Confinement Model for High-Strength Concrete. J. Struct. Eng. 1999, 125, 281–289. [Google Scholar] [CrossRef]
- Kim, S.; Hong, H.; Han, T. Behavior of an Internally Confined Hollow Reinforced Concrete Column with a Polygonal Cross-Section. Appl. Sci. 2021, 11, 4302. [Google Scholar] [CrossRef]
- Sadrossadat, E.; Ghorbani, B.; Hamooni, M.; Moradpoor Sheikhkanloo, M.H. Numerical formulation of confined compressive strength and strain of circular reinforced concrete columns using gene expression programming approach. Struct. Concr. 2018, 19, 783–794. [Google Scholar] [CrossRef]
- Amirkhani, S.; Lezgy-Nazargah, M. Nonlinear finite element analysis of reinforced concrete columns: Evaluation of different modeling approaches for considering stirrup confinement effects. Struct. Concr. 2022, 23, 2820–2836. [Google Scholar] [CrossRef]
- Li, J.; Deng, Z.; Yao, J. Research on uniaxial compressive behavior of high-strength spiral stirrups confined circular ultra-high performance concrete columns. Struct. Concr. 2020, 21, 2584–2600. [Google Scholar] [CrossRef]
- Chang, W.; Hao, M.; Zheng, W. Strength and ductility of laterally confined concrete. Struct. Concr. 2021, 22, 2967–2991. [Google Scholar] [CrossRef]
- Matz, H.; Empelmann, M. Butt Joints in Prefabricated Columns with High Reinforcement Ratios. In Proceedings of the 6th fib Congress, Oslo, Norway, 12–16 June 2022; Volume 6, pp. 1966–1975. [Google Scholar]
- Matz, H.; Empelmann, M. Butt joints in precast columns using high reinforcement ratios and large bar diameters. Beton Und Stahlbetonbau 2021, 116, 701–711. [Google Scholar] [CrossRef]
- Wolfger, H.; Kollegger, J. Butt jointed precast columns with high-strength reinforcement and large bar diameters. Beton Und Stahlbetonbau 2021, 116, 689–700. [Google Scholar] [CrossRef]
- Wolfger, H.; Kollegger, J. Early failure of high-strength concrete columns with large bar diameters. Beton Und Stahlbetonbau 2022, 117, 397–409. [Google Scholar] [CrossRef]
- Matz, H.; Empelmann, M. Component-specific compressive strength of reinforced concrete columns made of normal- and high-strength concrete. Beton Und Stahlbetonbau 2021, 117, 12–23. [Google Scholar] [CrossRef]
- Empelmann, M.; Javidmehr, S. Sustained load behaviour of normal-strength concrete. Beton Und Stahlbetonbau 2020, 115, 260–269. [Google Scholar] [CrossRef]
- Moccia, F.; Yu, Q.; Fernández Ruiz, M.; Muttoni, A. Concrete compressive strength: From material characterization to a structural value. Struct. Concr. 2021, 22, 634–654. [Google Scholar] [CrossRef]
- DIANA Finite Element Analysis, B.V. User’s Manual—Release 10.6; DIANA FEA BV: Delft, Netherlands, 2022. [Google Scholar]
- Empelmann, M.; Matz, H. Robustness of reinforced concrete columns. Beton Und Stahlbetonbau 2019, 114, 837–846. [Google Scholar] [CrossRef]
- Fédéracion Internationale du Béton Fib. Model Code for Concrete Structures 2010; Ernst & Sohn: Berlin, Germany, 2013. [Google Scholar]
- Selby, R.G.; Vecchio, F.J. A constitutive model for analysis of reinforced concrete solids. Can. J. Civ. Eng. 1997, 24, 460–470. [Google Scholar] [CrossRef]


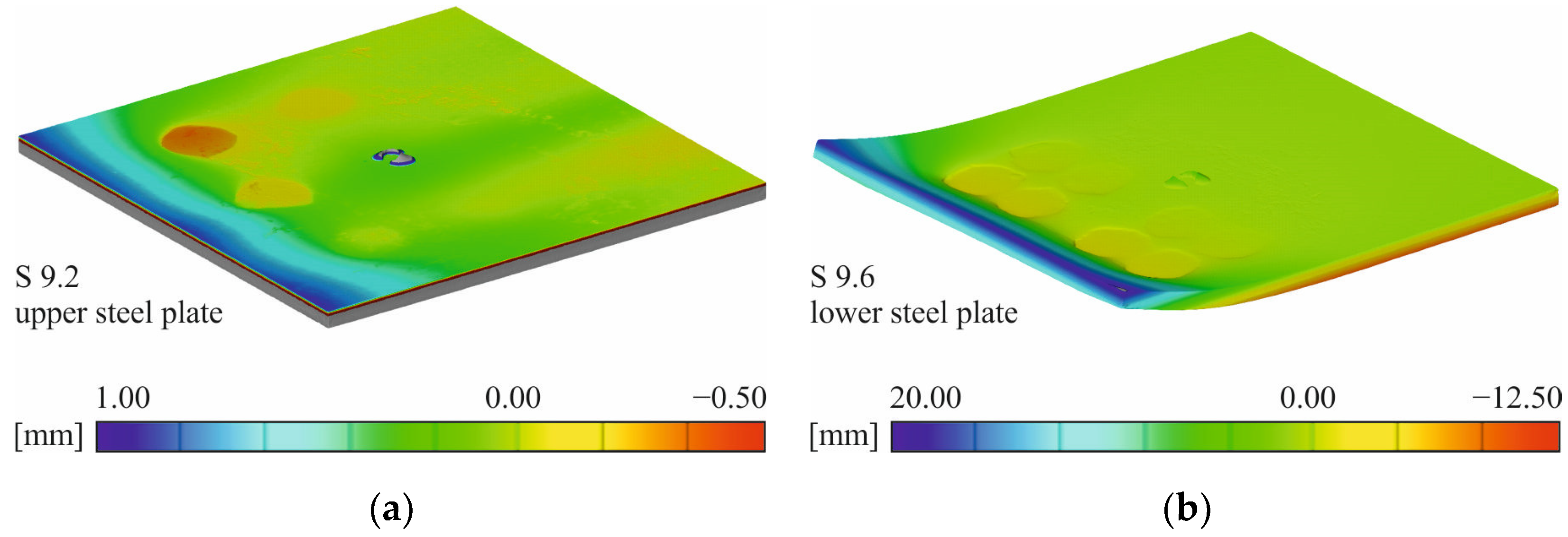
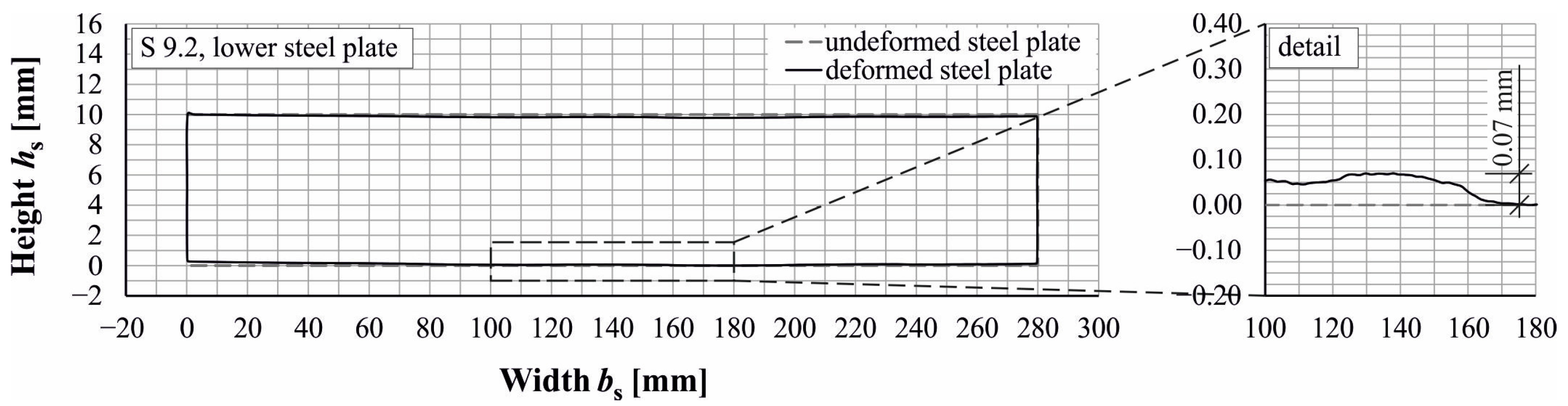
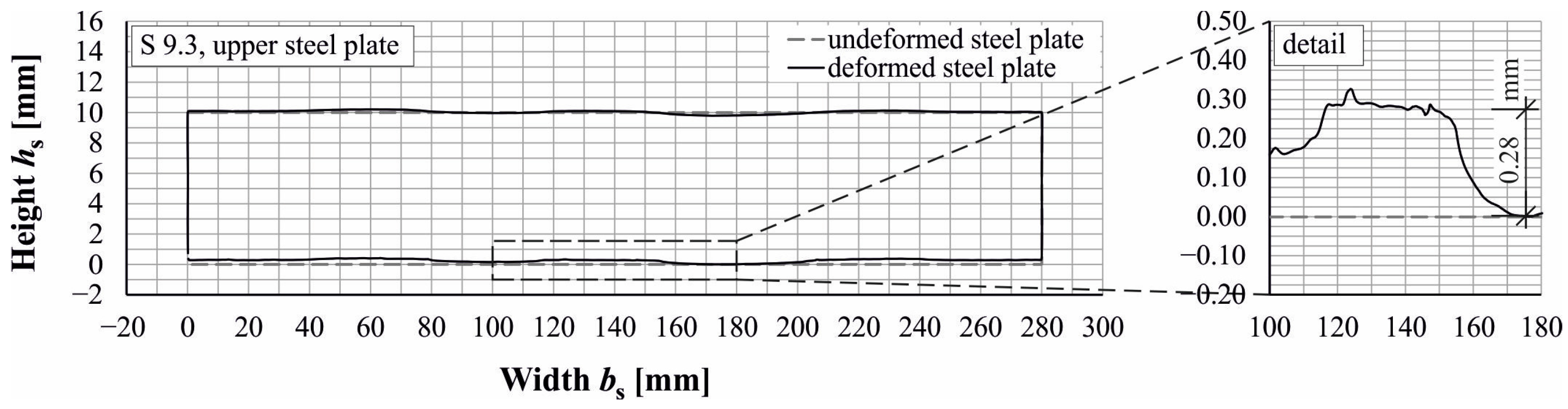
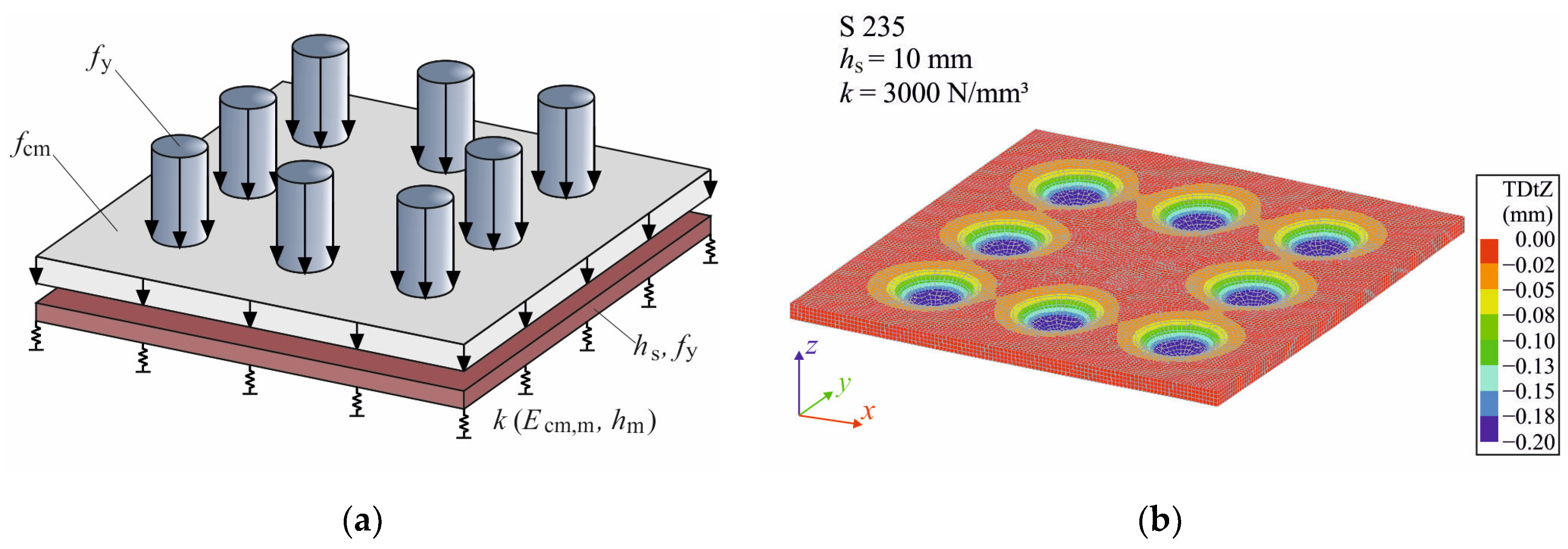



| References | Butt-Jointed Columns | ||||||
|---|---|---|---|---|---|---|---|
| S 9.1 | S 7.7 | S 9.2 | S 9.3 | S 9.6 | |||
| Longitudinal bar diameter | (mm) | 40 | 40 | 40 | 40 | 40 | |
| Number of longitudinal bars | (-) | 8 | 16 | 8 | 8 | 16 | |
| Reinforcement ratio | (%) | 12.8 | 25.6 | 12.8 | 12.8 | 25.6 | |
| Stirrup diameter | (mm) | 10 | 10 | 10 | 10 | 10 | |
| Distance between stirrups | (mm) | 280 | 280 | 280 | 280 | 280 | |
| Mortar thickness | (mm) | - | - | 20 | 40 | 40 | |
| Concrete | Compressive strength | (N/mm²) | 49.0 | 46.9 | 62.5 | 55.2 | 61.0 |
| Young’s modulus | (N/mm²) | 38,000 | - | 40,700 | 39,200 | 37,800 | |
| Mortar | Compressive strength | (N/mm²) | - | - | 80.3 | 81.8 | 74.4 |
| Young’s modulus | (N/mm²) | - | - | 29,900 | 29,400 | 29,100 | |
| Steel | Compressive yield strength | (N/mm²) | 592 | 592 | 592 | 592 | 592 |
| Compressive strength | (N/mm²) | 637 | 437 | 637 | 637 | 637 | |
| References | Butt-Jointed Columns | |||||
|---|---|---|---|---|---|---|
| S 9.1 | S 7.7 | S 9.2 | S 9.3 | S 9.6 | ||
| Experimental ultimate load | (kN) | 6499 | 9811 | 6568 | 6063 | 7725 |
| Calculated ultimate load | (kN) | 6445 | 9860 | 7295 | 6845 | 10,232 |
| Reduction factor | (-) | 1.01 | 0.99 | 0.90 | 0.88 | 0.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matz, H.; Empelmann, M. Butt Jointing of Prefabricated Concrete Columns. CivilEng 2022, 3, 1108-1125. https://doi.org/10.3390/civileng3040063
Matz H, Empelmann M. Butt Jointing of Prefabricated Concrete Columns. CivilEng. 2022; 3(4):1108-1125. https://doi.org/10.3390/civileng3040063
Chicago/Turabian StyleMatz, Henrik, and Martin Empelmann. 2022. "Butt Jointing of Prefabricated Concrete Columns" CivilEng 3, no. 4: 1108-1125. https://doi.org/10.3390/civileng3040063
APA StyleMatz, H., & Empelmann, M. (2022). Butt Jointing of Prefabricated Concrete Columns. CivilEng, 3(4), 1108-1125. https://doi.org/10.3390/civileng3040063








