Simplified Method of Determining Torsional Stability of the Multi-Storey Reinforced Concrete Buildings
Abstract
:1. Introduction
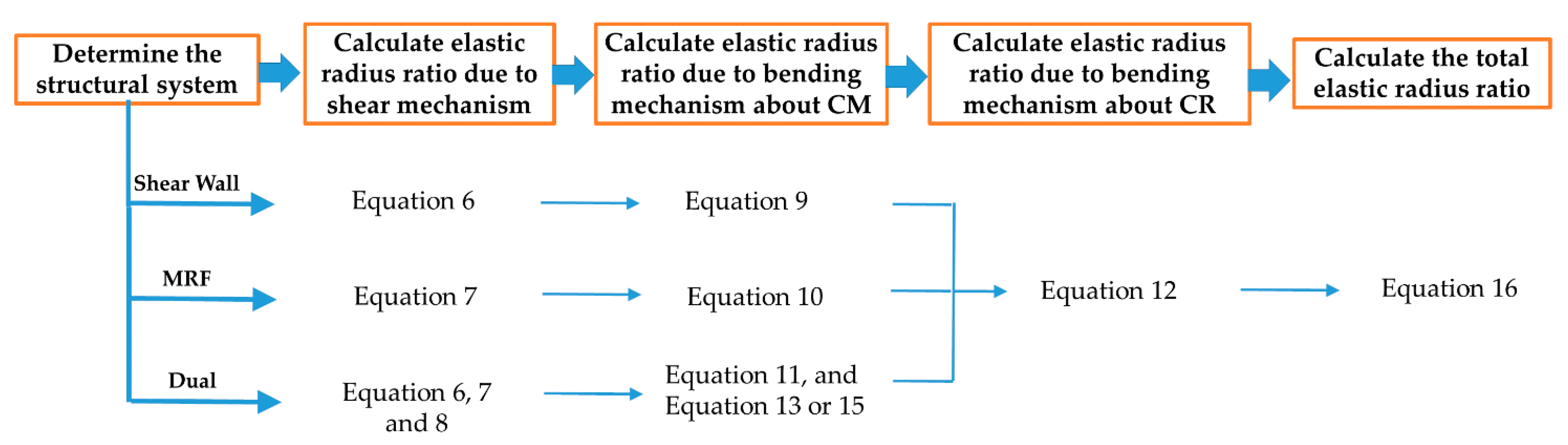
2. Methods and Procedures of Determining Elastic Radius Ratio (br)
2.1. Shear and Bending Combination Method (SBCM)
2.2. Static Analysis Method (SAM)
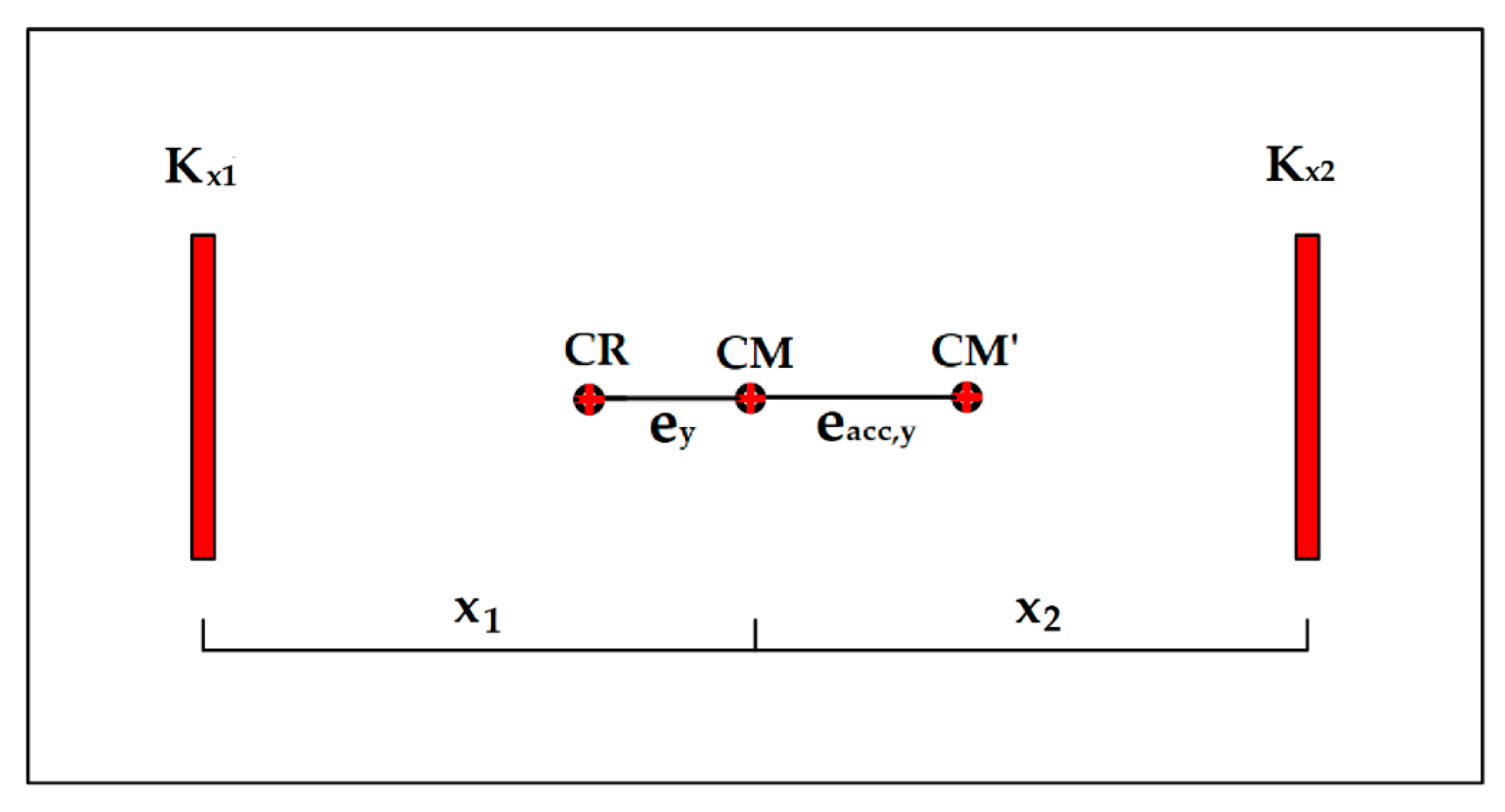
- Determining the effective value of pure translational displacement (Δ2D) by applying a lateral load at an arbitrary location to the building that is restrained for torsional rotation,
- Determining the effective edge displacements: flexible edge displacement (Δmax), and stiff edge displacements (Δmin) for the same lateral load and location without the torsional restraints,
- Determining the position of the center of rigidity (CR). CR from a stiff edge is equal to ,
- Determining the distance between the applied load and the CR. The distance is equal to the sum of eccentricity (e) and accidental eccentricity (eacc). The accidental eccentricity such as 0.05 L or 0.1 L is adopted from the relevant seismic codes.
- The elastic radius ratio (br) is finally determined by substituting the above parameters in Equation (17).
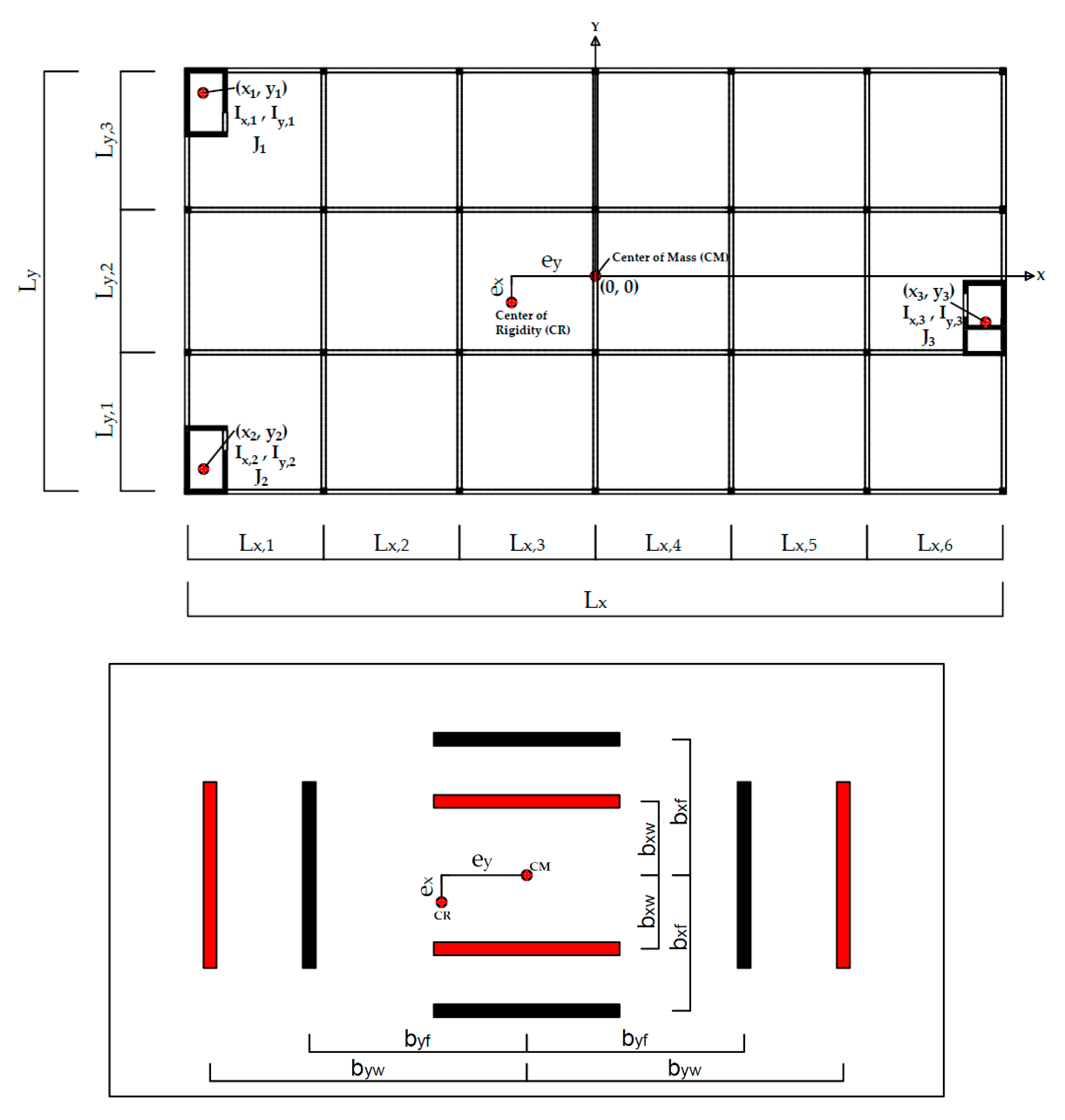
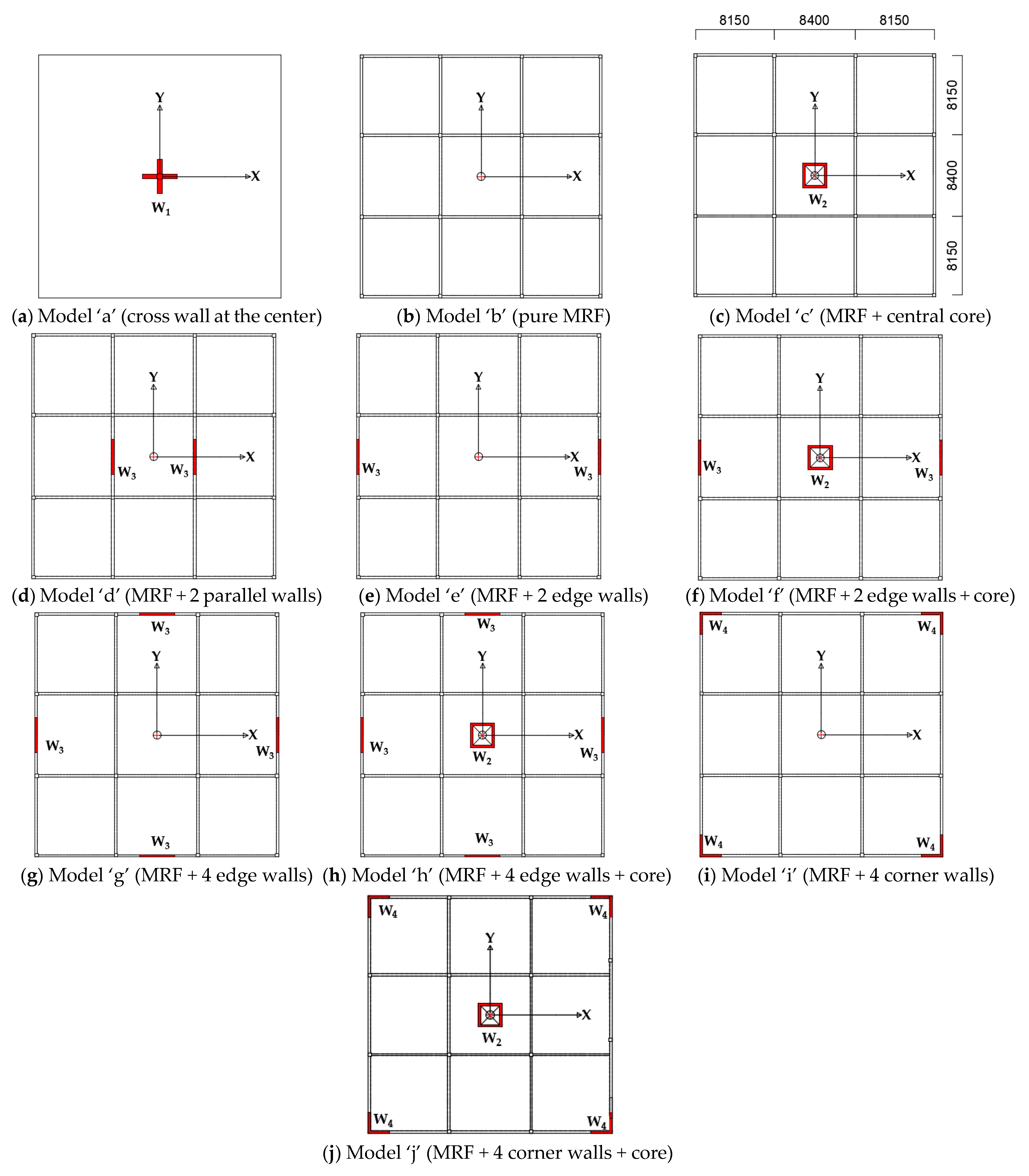
2.3. Parametric Study
3. Results and Discussion
- Model ‘a’ building (pure SW system):
- Model ‘b’ building (pure MRF system):
3.1. Effect of the Disposition of the Lateral Load Resisting Elements in the Building Plan
3.2. Effect of Magnitude of Translational Stiffness (K)
3.2.1. Effect of Shape of the Wall
3.2.2. Effect of Flexural to Shear Stiffness Ratio (P) in Dual System
3.3. Effect of Building Height (H)
3.4. Effect of the Aspect Ratio of the Floor Plan of the Building
3.5. Effect of Eccentricity (e) and Accidental Eccentricity (eacc)
4. Conclusions
- The disposition of the lateral load resisting elements in the building plan was found to be the major determiner of the torsional stiffness of the building. The torsional stiffness is found to be higher for buildings with walls or frames that are located away from the center of rigidity. The highest elastic radius ratio was obtained for buildings with all walls at the building edges or corners. Moreover, a building with wall elements aligned about both principle directions was found to be more torsionally stiffer compared to a building with walls aligned in one direction only.
- The effect of the magnitude of translational stiffness on torsional stiffness was only found in pure shear wall (SW) building consisting of multiple walls, and in building with a dual structural system. In the pure SW system consisting central core wall along with other perimeter walls, the torsional stiffness significantly reduced when the translational stiffness of the central core wall was increased.
- In the dual system, the flexural to shear stiffness ratio was found to influence the torsional stiffness. The higher value of the stiffness ratio is beneficial in building having walls along the edges. On the contrary, a lower stiffness ratio was found to be beneficial for buildings with core walls positioned near the center of the building.
- Shear torsional stiffness was found to be dependent on the shape of the walls. For closed shaped or semi-closed core walls, the torsional stiffness was found to be higher compared to open and rectangular walls. The contribution of these walls were found to increase with the increase in building height.
- A rectangular building with central core walls were found to be more torsionally unstable compared to a square building having the same floor area.
- Reduction in torsional stiffness was found with the increase of both strength eccentricity and accidental eccentricity. However, their effects were found to reduce with the increase of building height.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Appendix A. Derivation of Equation (12)
Appendix B. Example Calculation of the Elastic Radius Ratio for Building Models ‘g’ and ‘k’
| Height | Calculation of the Elastic Radius Ratio |
|---|---|
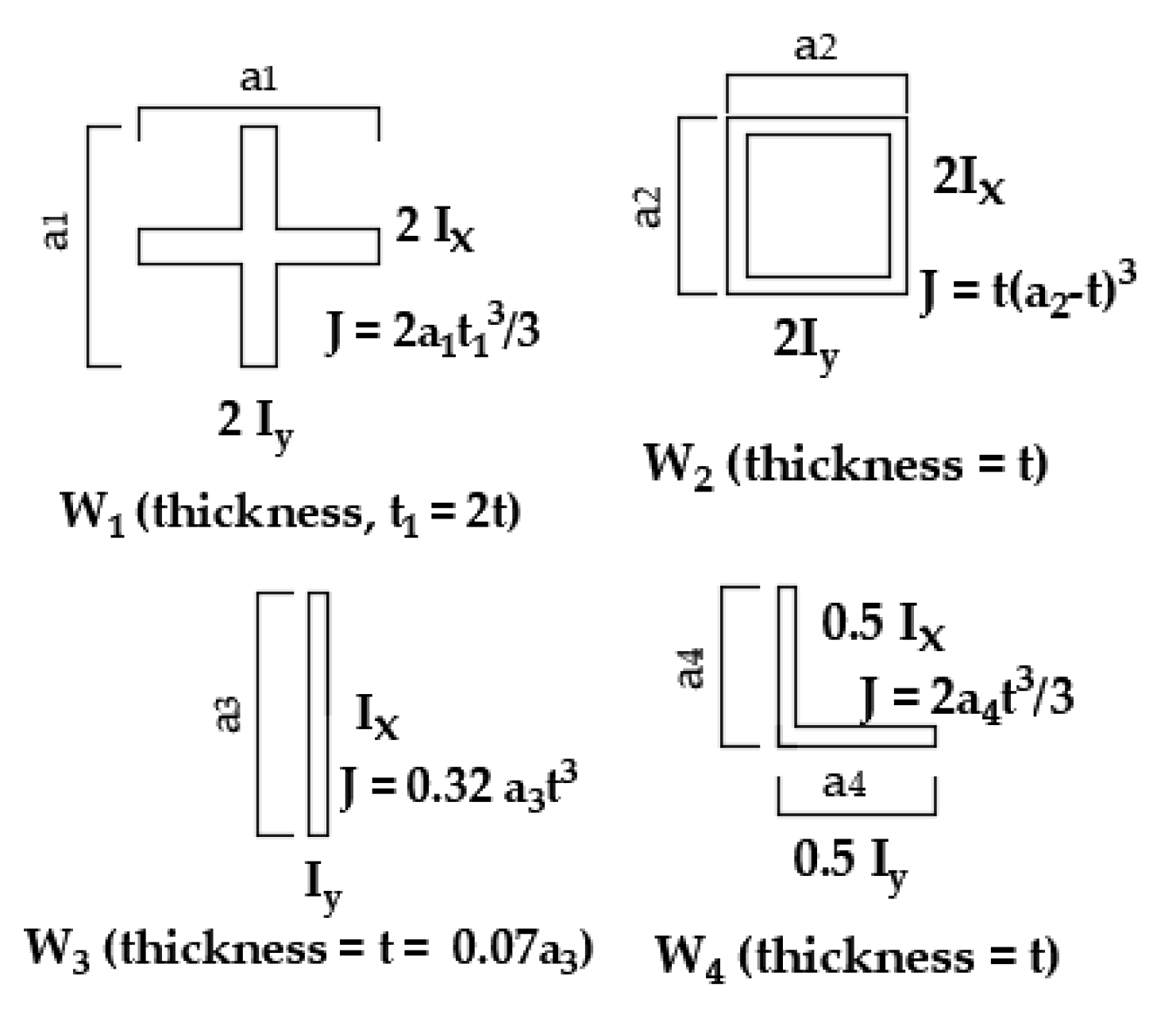
| H = 13.1 m | Size of all columns are 350 mm × 350 mm and size of all beams are 500 mm × 250 mm. Therefore, Icx = 0.00125 m4, Ibx = 0.0026 m4, and J = 0.141bd3 = 0.00212 m3. Size of wall is a3 = 3586.3 mm and t1 = 250 mm. Therefore, Ix = Iy = 0.961 m3 and J = 0.018 m3. From Equations (6) and (7), From Equation (15), For equivalent pure SW system, from Equation (9), For equivalent pure MRF system, from Equation (10), From Equation (11), Now, from Equation (16), = As from SAM is 1.7, the absolute percentage difference is 1.8%. The building is torsionally stable/stiff. |
| H = 31.7 m | , , and = As from SAM is 1.65, the absolute percentage difference is 1.2%. |
| H = 115.4 m | , , and = As from SAM is 1.63, the absolute percentage difference is 0.61%. |
| Height | Calculation of the Elastic Radius Ratio |
|---|---|
| H = 13.1 m | Size of all columns are 350 mm × 350 mm and size of all beams are 250 mm × 500 mm. Therefore, Icx = 0.00125 m4, Ibx = 0.0026 m4, and J = 0.141bd3 = 0.00212 m3. Walls: Iwx,1 = 9.8 m3, Iwx,2 = 7.7 m3, J1 = 0.06 m3, and J2 = 0.07 m3. Eccentricities: ery = 0.17, and eacc,ry = 0.1 L/r = 2.47/10.08 = 0.24. From Equation (6) and Table 1, From Equation (15), For equivalent pure SW system, from Equation (9), For equivalent pure MRF system, from Equation (10), From Equation (11), From Equation (12), Now, from Equation (16), = As from SAM is 1.14, the absolute percentage difference is 0.9%. The building is torsionally stable/stiff. |
References
- Lam, N.T.; Wilson, J.L.; Hutchinson, G.L. Review of the torsional coupling of asymmetrical wall-frame buildings. Eng. Struct. 1997, 19, 233–246. [Google Scholar]
- Chitty, L. On the cantilever composed of a number of parallel beams interconnected by cross bars. Philos. Mag. Lond. Ser. 1947, 7, 685–699. [Google Scholar] [CrossRef]
- Csonka, P. Procedure for rectangular sway frames (in Hungarian). In Mérnöki Továbbképz Intézet. Építészet; Tudományos Könyvkiadó Vállalat: Budapest, Hungary, 1950. [Google Scholar]
- Beck, H. Ein neues Berechnungsverfahren für gegliederte Scheiben, dargestellt am Beispiel des Vierendelträgers. Der Bauing. 1956, 31, 436–443. [Google Scholar]
- Miranda, E. Approximate lateral deformation demands in multistory buildings. J. Struct. Eng. 1999, 125, 417–425. [Google Scholar] [CrossRef]
- Blume, J.A. Dynamic characteristics of multi-story buildings. J. Struct. Div. 1968, 94, 337–402. [Google Scholar] [CrossRef]
- Tso, W.K.; Zhu, T.J. Design of torsionally unbalanced structural systems based on code provisions I: Ductility demand. Earthq. Eng. Struct. Dyn. 1992, 21, 609–627. [Google Scholar] [CrossRef]
- Chandler, A.M.; Duan, X.N. Performance of asymmetric code-designed buildings for serviceability and ultimate limit states. Earthq. Eng. Struct. Dyn. 1997, 26, 717–735. [Google Scholar] [CrossRef]
- Gasparini, G.; Silvestri, S.; Trombetti, T. A simple code-like formula for estimating the torsional effects on structures subjected to earthquake ground motion excitation. In Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, 12–17 October 2008. [Google Scholar]
- Trombetti, T.; Palermo, M.; Silvestri, S.; Gasparini, G. Period shifting effect on the corner displacement magnification of one-storey asymmetric systems. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Lumantarna, E.; Lam, N.; Wilson, J. Displacement-Controlled Behavior of Asymmetrical Single-Story Building Models. J. Earthq. Eng. 2013, 17, 902–917. [Google Scholar] [CrossRef]
- Kan, C.L.; Chopra, A.K. Elastic earthquake analysis of a class of torsionally coupled buildings. J. Struct. Div. 1977, 103, 821–838. [Google Scholar] [CrossRef]
- Rutenberg, A.; Hsu, T.I.; Tso, W.K. Response spectrum techniques for asymmetric buildings. Earthq. Eng. Struct. Dyn. 1978, 6, 427–435. [Google Scholar] [CrossRef]
- Harasimowicz, A.P.; Goel, R.K. Seismic code analysis of multi-storey asymmetric buildings. Earthq. Eng. Struct. Dyn. 1998, 27, 173–185. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.L.; Tsai, K.C. Simplified seismic analysis of asymmetric building systems. Earthq. Eng. Struct. Dyn. 2007, 36, 459–479. [Google Scholar] [CrossRef]
- Khatiwada, P.; Lumantarna, E.; Lam, N.; Looi, D. Fast Checking of Drift Demand in Multi-Storey Buildings with Asymmetry. Buildings 2021, 11, 13. [Google Scholar] [CrossRef]
- Lam, N.; Wilson, J.; Lumantarna, E. Effects of Building Asymmetry in Areas of Low-to-Moderate Seismicity. In Proceedings of the 2015 World Congress on Advances in Structural Engineering and Mechanics, Incheon, Korea, 25–29 August 2015; pp. 25–29. [Google Scholar]
- Dimova, S.L.; Alashki, I. Seismic design of symmetric structures for accidental torsion. Bull. Earthq. Eng. 2003, 1, 303–320. [Google Scholar] [CrossRef]
- De la Llera, J.C.; Chopra, A.K. Estimation of Accidental Torsion Effects for Seismic Design of Buildings. J. Struct. Eng. 1995, 121, 102–114. [Google Scholar] [CrossRef]
- Wang, Y.; Arnaouti, C.; Guo, S. A simple approximate formulation for the first two frequencies of asymmetric wall–frame multi-storey building structures. J. Sound Vib. 2000, 236, 141–160. [Google Scholar]
- Mohamed, O.A.; Mehana, M.S. Assessment of Accidental Torsion in Building Structures Using Static and Dynamic Analysis Procedures. Appl. Sci. 2020, 10, 5509. [Google Scholar] [CrossRef]
- Lumantarna, E.; Menegon, S.J.; Lam, N.; Wilson, J. Simplified approach for multi-storey asymmetrical buildings in regions of low to moderate seismicity. In Proceedings of the Australasian Structural Engineering Conference, Melbourne, Australia, 11–13 November 2020. accepted. [Google Scholar]
- Tso, W.K.; Moghadam, A.S. Application of Eurocode 8 torsional provisions to multi-storey buildings. In Proceedings of the 11th European Conference on Earthquake Engineering, Paris, France, 6–11 September 1998. [Google Scholar]
- Anastassiadis, K.; Athanatopoulou, A.; Makarios, T. Equivalent static eccentricities in the simplified methods of seismic analysis of buildings. Earthq. Spectra 1998, 14, 1–34. [Google Scholar] [CrossRef]
- Makarios, T. Practical calculation of the torsional stiffness radius of multistorey tall buildings. Struct. Des. Tall Spec. Build. 2008, 17, 39–65. [Google Scholar] [CrossRef]
- Khatiwada, P. Determination of center of mass and radius of gyration of irregular buildings and its application in torsional analysis. Int. Res. J. Eng. Technol. 2020, 7, 1–7. [Google Scholar]
- Menegon, S.J.; Tsang, H.H.; Lumantarna, E.; Lam, N.T.K.; Wilson, J.L.; Gad, E.F. Framework for seismic vulnerability assessment of reinforced concrete buildings in Australia. Aust. J. Struct. Eng. 2019, 20, 143–158. [Google Scholar] [CrossRef]
- Gass, S. SPACE GASS 12.85; ITS: Victoria, Australia, 2020. [Google Scholar]
- Standards Australia. AS 1170.4-2007. In Structural Design Actions, Part 4: Earthquake Actions in Australia; Standards Australia: Sydney, Australia, 2007. [Google Scholar]
- Botis, M.F.; Cerbu, C. A Method for Reducing of the Overall Torsion for Reinforced Concrete Multi-Storey Irregular Structures. Appl. Sci. 2020, 10, 5555. [Google Scholar] [CrossRef]



| Conditions | Heff |
|---|---|
| Walls in pure SW system | 1 + 0.77 H |
| Walls in dual system | 3.1 H0.5/ log(H) |
| Columns | h |
| Models 1 | bry,s | bry,w | bry,f | Px | bry,B | bry (SBCM) | bry (SAM) | % Difference |
|---|---|---|---|---|---|---|---|---|
| c13.1 | 0.45 | 0.00 | 1.29 | 5.53 | 0.51 | 0.68 | 0.70 | 3.43 |
| d13.1 | 0.31 | 0.42 | 0.73 | 5.38 | 0.48 | 0.57 | 0.60 | 4.64 |
| e13.1 | 0.07 | 1.23 | 1.25 | 5.38 | 1.23 | 1.23 | 1.24 | 0.35 |
| f13.1 | 0.54 | 0.87 | 1.25 | 10.77 | 0.91 | 1.06 | 1.06 | 0.72 |
| g13.1 | 0.31 | 1.73 | 1.57 | 4.30 | 1.70 | 1.73 | 1.70 | 1.8 |
| h13.1 | 0.55 | 1.23 | 1.57 | 9.01 | 1.26 | 1.38 | 1.41 | 2.47 |
| i13.1 | 0.37 | 1.68 | 1.40 | 4.94 | 1.63 | 1.68 | 1.65 | 1.25 |
| j13.1 | 0.58 | 1.23 | 1.40 | 9.85 | 1.24 | 1.37 | 1.39 | 1.49 |
| c31.7 | 0.53 | 0.00 | 1.29 | 1.06 | 0.90 | 1.04 | 1.08 | 2.97 |
| d31.7 | 0.31 | 0.42 | 0.73 | 1.03 | 0.59 | 0.67 | 0.66 | 0.38 |
| e31.7 | 0.08 | 1.23 | 1.25 | 1.03 | 1.24 | 1.24 | 1.24 | 0.13 |
| f31.7 | 0.61 | 0.87 | 1.25 | 2.06 | 1.01 | 1.18 | 1.21 | 2.74 |
| g31.7 | 0.32 | 1.73 | 1.57 | 0.8 | 1.64 | 1.67 | 1.65 | 1.2 |
| h31.7 | 0.62 | 1.23 | 1.57 | 1.73 | 1.36 | 1.50 | 1.56 | 4.06 |
| i31.7 | 0.40 | 1.68 | 1.40 | 0.95 | 1.54 | 1.59 | 1.56 | 2.07 |
| j31.7 | 0.66 | 1.23 | 1.40 | 1.89 | 1.29 | 1.45 | 1.52 | 4.63 |
| c115.4 | 0.73 | 0.00 | 1.29 | 0.09 | 1.24 | 1.44 | 1.52 | 5.23 |
| d115.4 | 0.32 | 0.42 | 0.73 | 0.08 | 0.71 | 0.78 | 0.74 | 4.84 |
| e115.4 | 0.12 | 1.23 | 1.25 | 0.08 | 1.25 | 1.26 | 1.24 | 1.00 |
| f115.4 | 0.79 | 0.87 | 1.25 | 0.17 | 1.21 | 1.44 | 1.38 | 0.61 |
| g115.4 | 0.34 | 1.73 | 1.57 | 0.06 | 1.58 | 1.62 | 1.63 | 1.8 |
| h115.4 | 0.80 | 1.23 | 1.57 | 0.14 | 1.53 | 1.73 | 1.68 | 3.10 |
| i115.4 | 0.47 | 1.68 | 1.40 | 0.08 | 1.42 | 1.50 | 1.49 | 0.58 |
| j115.4 | 0.86 | 1.23 | 1.40 | 0.15 | 1.38 | 1.63 | 1.64 | 0.96 |
| Models | bry,s | bry,w | bry (SBCM) | bry (SAM) | % Difference |
|---|---|---|---|---|---|
| c13.1 | 0.50 | 0.00 | 0.50 | 0.50 | 0.79 |
| d13.1 | 0.07 | 0.42 | 0.42 | 0.42 | 0.00 |
| e13.1 | 0.07 | 1.23 | 1.23 | 1.23 | 0.09 |
| f13.1 | 0.45 | 0.87 | 0.97 | 0.97 | 0.17 |
| g13.1 | 0.10 | 1.73 | 1.74 | 1.73 | 0.28 |
| h13.1 | 0.45 | 1.23 | 1.31 | 1.30 | 0.19 |
| i13.1 | 0.15 | 1.73 | 1.74 | 1.74 | 0.14 |
| j13.1 | 0.46 | 1.23 | 1.31 | 1.33 | 1.72 |
| c31.7 | 1.14 | 0.00 | 1.14 | 1.14 | 0.34 |
| d31.7 | 0.16 | 0.42 | 0.45 | 0.44 | 0.37 |
| e31.7 | 0.16 | 1.23 | 1.24 | 1.24 | 0.09 |
| f31.7 | 1.01 | 0.87 | 1.33 | 1.36 | 1.69 |
| g31.7 | 0.22 | 1.73 | 1.75 | 1.74 | 0.14 |
| h31.7 | 1.03 | 1.23 | 1.60 | 1.62 | 1.55 |
| i31.7 | 0.35 | 1.73 | 1.77 | 1.78 | 0.59 |
| j31.7 | 1.06 | 1.23 | 1.62 | 1.63 | 0.58 |
| c115.4 | 4.04 | 0.00 | 4.04 | 4.07 | 0.54 |
| d115.4 | 0.56 | 0.42 | 0.70 | 0.70 | 0.36 |
| e115.4 | 0.56 | 1.23 | 1.35 | 1.35 | 0.08 |
| f115.4 | 3.57 | 0.87 | 3.67 | 3.50 | 4.92 |
| g115.4 | 0.79 | 1.73 | 1.90 | 1.93 | 1.47 |
| h115.4 | 3.61 | 1.23 | 3.81 | 3.70 | 3.08 |
| i115.4 | 1.23 | 1.73 | 2.13 | 2.18 | 2.59 |
| j115.4 | 3.72 | 1.23 | 3.92 | 3.85 | 1.82 |
| Models | bry,s | ery | eacc,ry | bry,w | bry,f | Px | bry,B,CM | bry,B | bry (SBCM) | bry (SAM) | % Diff. |
|---|---|---|---|---|---|---|---|---|---|---|---|
| k13.1 | 0.3 | 0.17 | 0.24 | 1.13 | 1.25 | 4.3 | 1.15 | 1.11 | 1.15 | 1.14 | 0.9 |
| l32.8 | 0.1 | 0.01 | 0.31 | 1.53 | 1.60 | 13 | 1.54 | 1.47 | 1.47 | 1.47 | 0 |
| m96.8 | 0.15 | 0.28 | 0.32 | 1.55 | 1.28 | 0.1 | 1.31 | 1.22 | 1.23 | 1.25 | 1.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khatiwada, P.; Lumantarna, E. Simplified Method of Determining Torsional Stability of the Multi-Storey Reinforced Concrete Buildings. CivilEng 2021, 2, 290-308. https://doi.org/10.3390/civileng2020016
Khatiwada P, Lumantarna E. Simplified Method of Determining Torsional Stability of the Multi-Storey Reinforced Concrete Buildings. CivilEng. 2021; 2(2):290-308. https://doi.org/10.3390/civileng2020016
Chicago/Turabian StyleKhatiwada, Prashidha, and Elisa Lumantarna. 2021. "Simplified Method of Determining Torsional Stability of the Multi-Storey Reinforced Concrete Buildings" CivilEng 2, no. 2: 290-308. https://doi.org/10.3390/civileng2020016
APA StyleKhatiwada, P., & Lumantarna, E. (2021). Simplified Method of Determining Torsional Stability of the Multi-Storey Reinforced Concrete Buildings. CivilEng, 2(2), 290-308. https://doi.org/10.3390/civileng2020016






