Mathematical Modeling and Stability Analysis of Agri-Food Tomato Supply Chains via Compartmental Analysis
Abstract
1. Introduction
2. Agri-Food Tomato Supply Chains: Literature Review
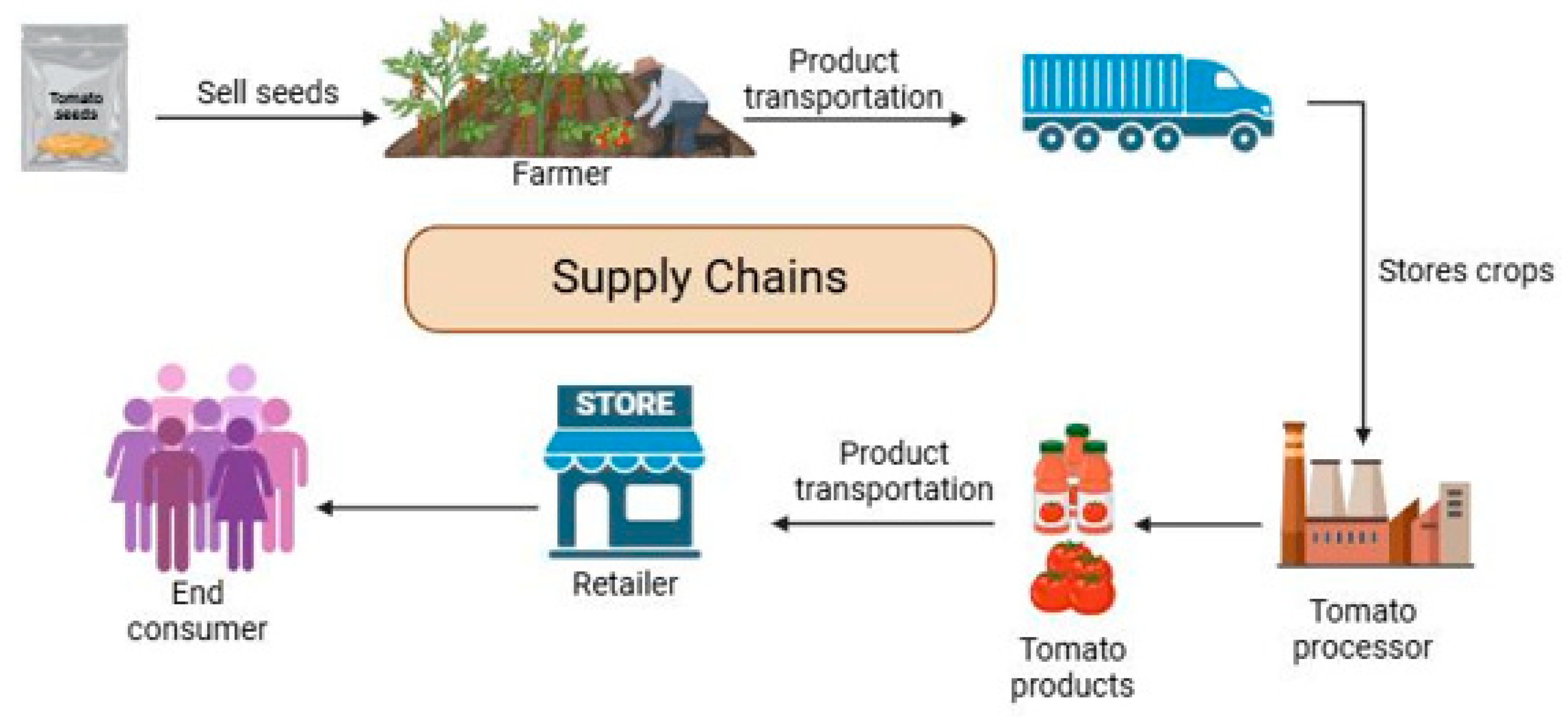
2.1. Agri-Food Tomato Supply Chains (AFTSCs)
2.2. Mathematical Modeling of Agri-Food Tomato Supply Chains
- Systematically classifying the mathematical techniques (e.g., MILP, MINLP, stochastic programming, and simulation [49]) specifically deployed for tomato supply chain optimization;
- Identifying and analyzing the primary objectives, including economic viability, environmental sustainability [50], social aspects, loss minimization, and resilience enhancement;
3. Mathematical Modeling
3.1. The Role of Compartmental Analysis in Agri-Food Tomato Supply Chains (AFTSCs)
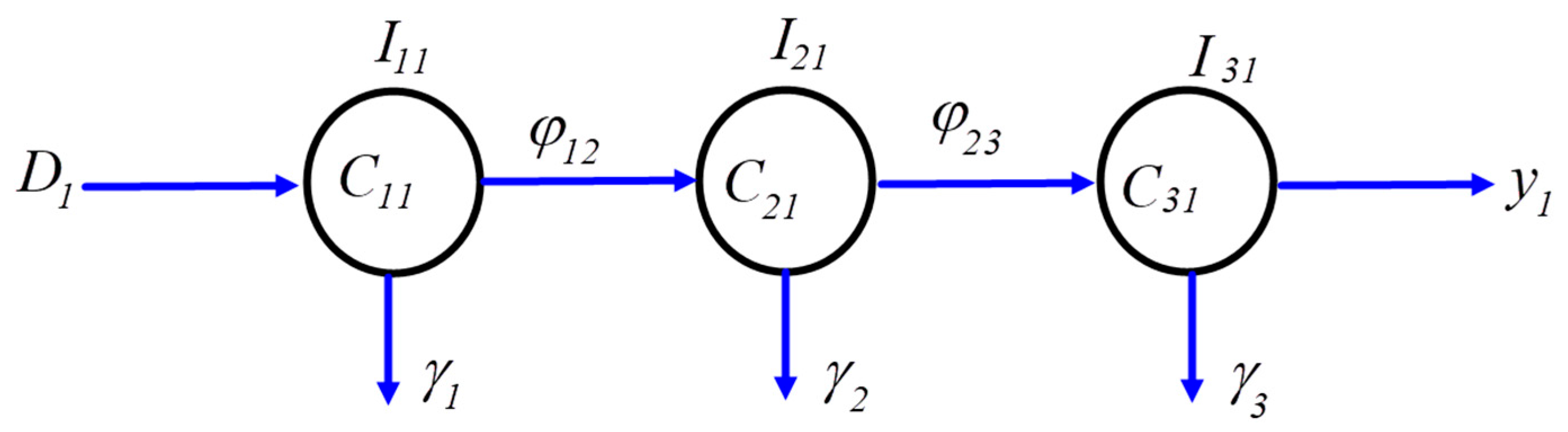
3.2. Mathematical Modeling of an AFTSC with Decrease: System 1
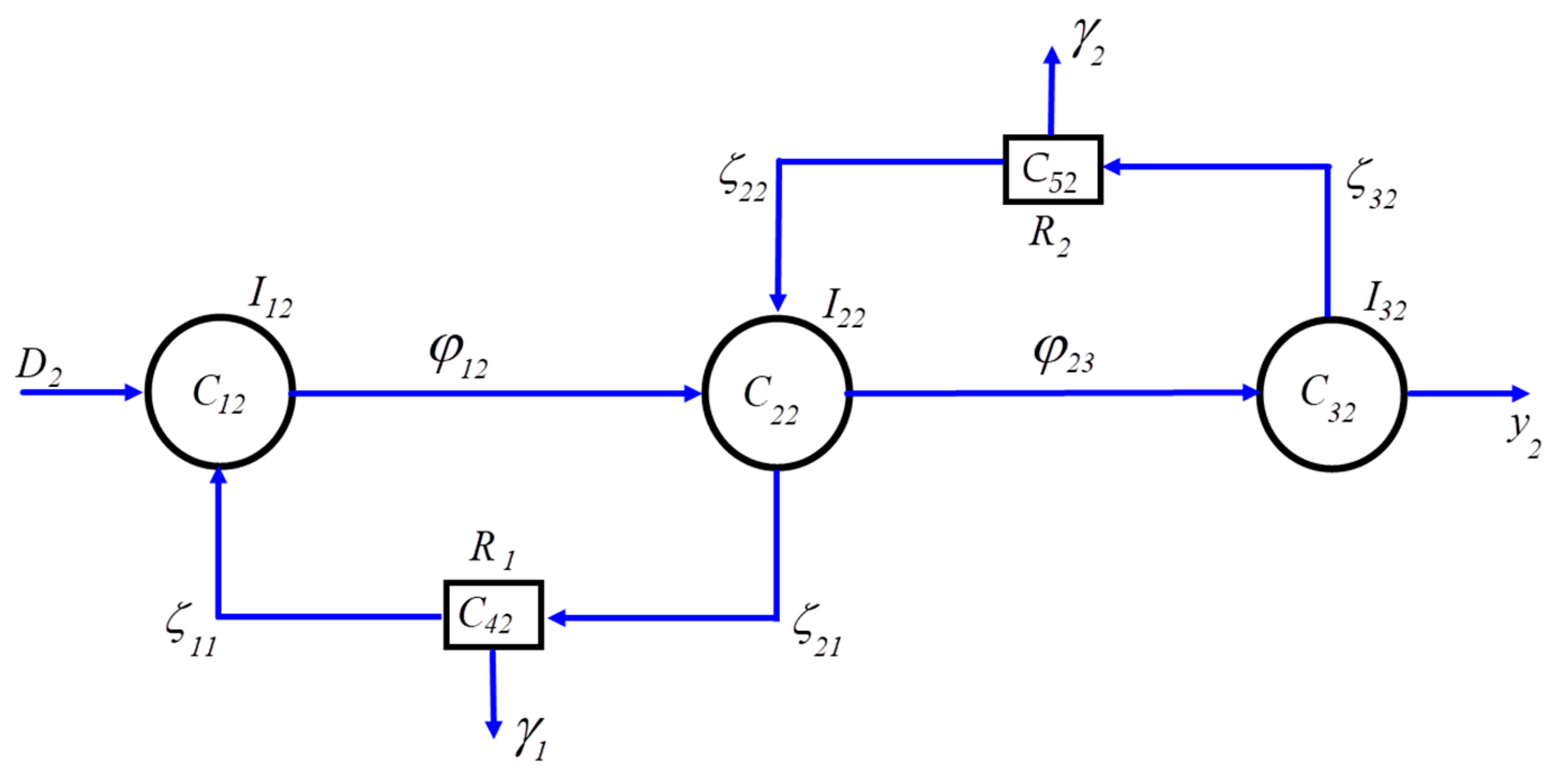
3.3. Mathematical Modeling of an AFTSC with a Decrease and Reprocessing: System 2
- 1.
- Sustainability index: the waste diversion rate, which is approximated by the system 1 and system 2 ratios, expresses that, in system 2, better waste management is performed with sustainability approaches, as compared with system 1 in which the sustainability index presents lower value .
- 2.
- Steady state production: from the simulation parameters in Section 6, in system 2, which is a lower WIP, indicating efficient and agile work, as compared to the WIP in system 1, , which present tasks that are in progress and not fully accomplished.
4. Stability Analysis
4.1. Stability Analysis: System 1
4.2. Stability Analysis: System 2
5. Sensitivity Analysis
5.1. Sensitivity Analysis: System 1
5.2. Sensitivity Analysis: System 2
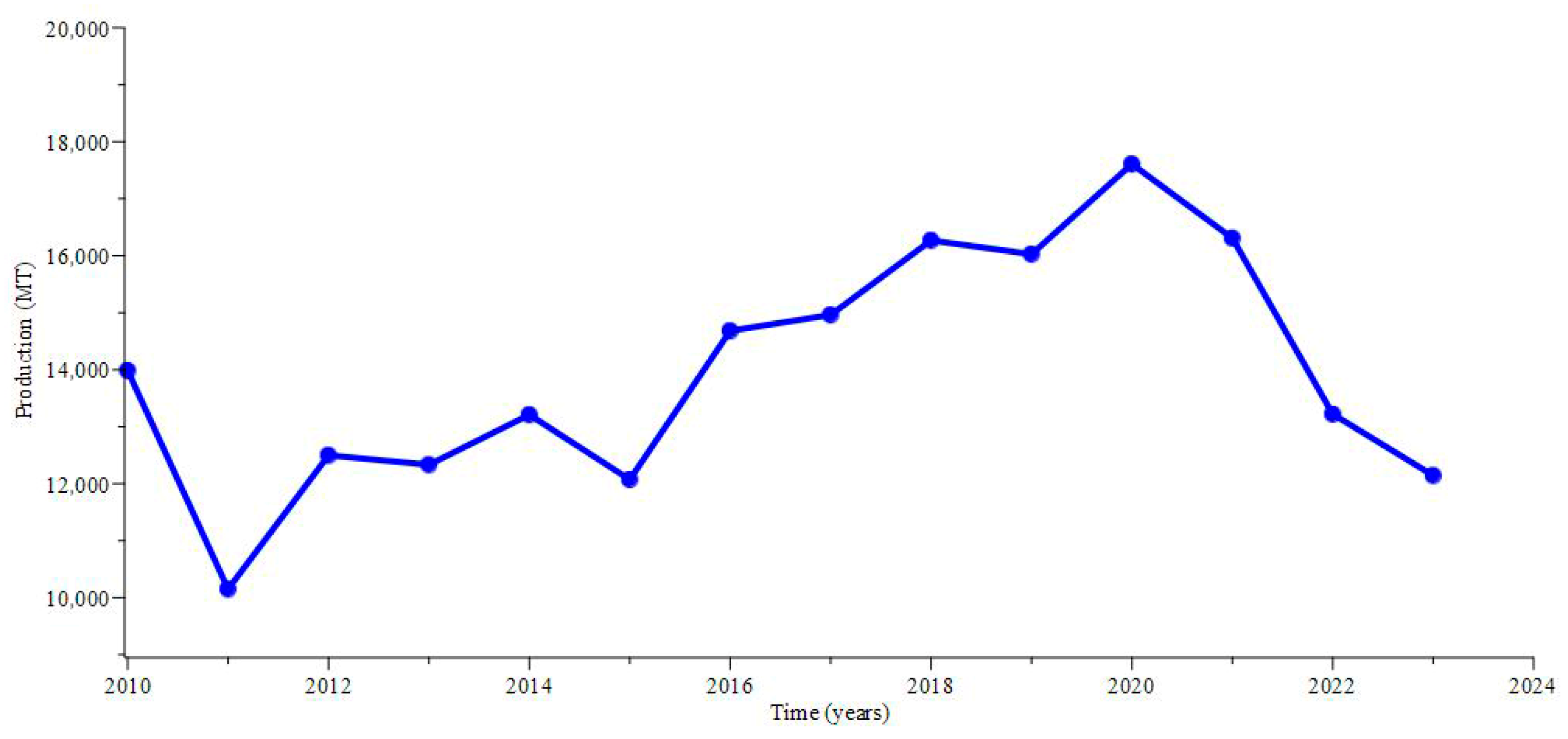
6. Results
6.1. Simulations: System 1
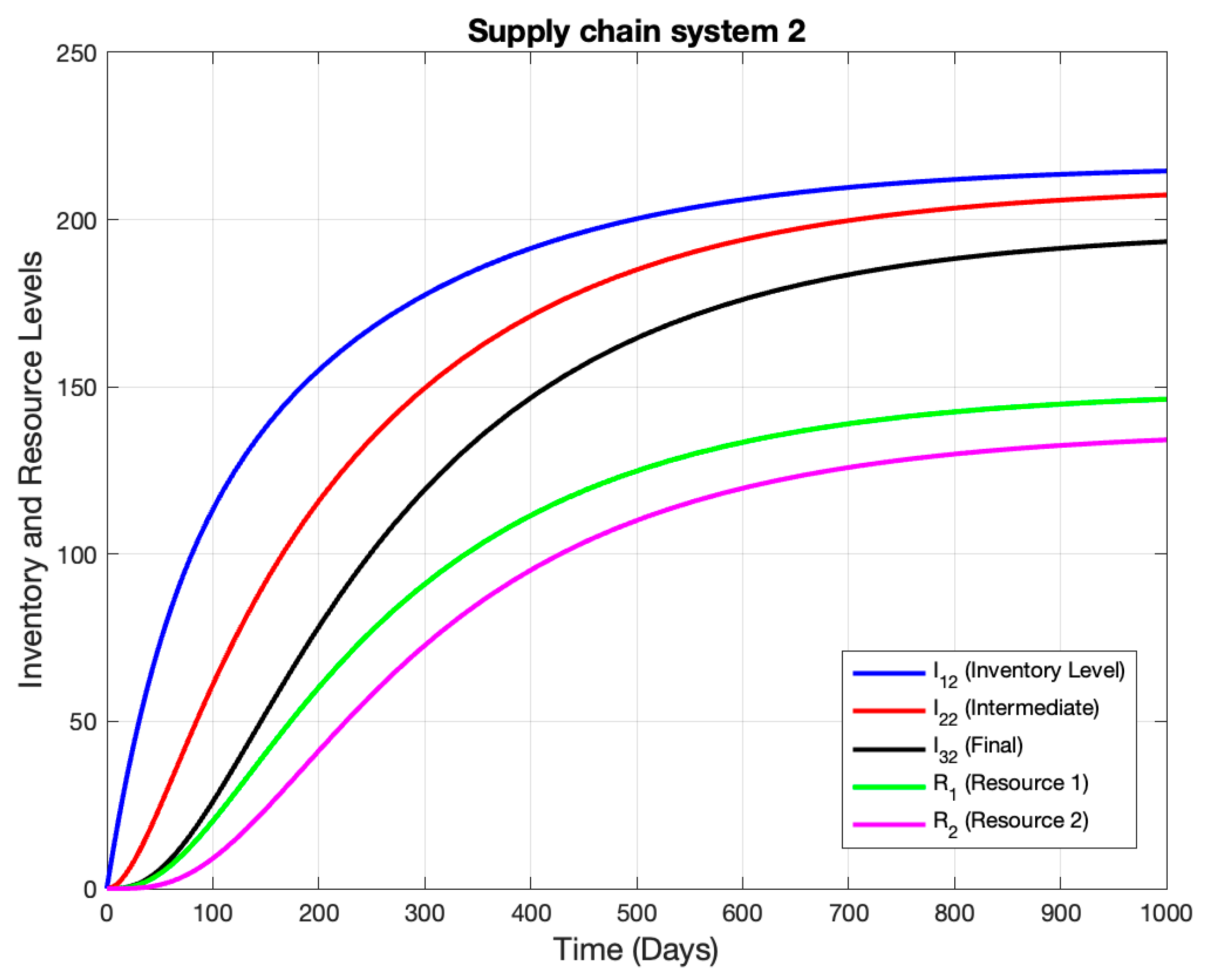
6.2. Simulations: System 2
6.3. Compartmental Analysis in Low-Variability Supply Chains
6.3.1. Variance Propagation
6.3.2. System Stability
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
Appendix C
Appendix D
| Performance | System 1 | System 2 |
| SISO linear systems | Two dissipation stages | Reprocessing and dissipation |
| Lyapunov stability | Asymptotically stable | Asymptotically stable |
| Sustainability index | Less sustainable | More sustainable |
| Sensitivity analysis | Steady state for inventories | Steady state for inventories |
| Stochastic modeling | Not apply (NA) | Not apply (NA) |
| Nonlinear system | Linear system (NA) | Linear system (NA) |
| Empirical data validation | Dynamical system (NA) | Dynamical systems (NA) |
References
- Anastasiadis, F.; Apostolidou, I.; Michailidis, A. Mapping sustainable tomato supply chain in Greece: A framework for research. Foods 2020, 9, 539. [Google Scholar] [CrossRef]
- Granillo-Macías, R.; Rivera-Gómez, H.; González-Hernández, I.J.; Santana-Robles, F. Reconfiguration of Agrifood Supply Chain Management in Latin America during COVID-19: A Brief Literature Review. Sustainability 2024, 16, 3743. [Google Scholar] [CrossRef]
- Sudha, V.; Aswini, D.; Akiladevi, R. Blockchain based tomato supply chain management. In Proceedings of the 2023 2nd International Conference on Advancements in Electrical, Electronics, Communication, Computing and Automation (ICAECA), Coimbatore, India, 16–17 June 2023. [Google Scholar] [CrossRef]
- Akiladevi, R. A Literary Survey for Blockchain Application for Supply Chain Management of Farm Produces. In Proceedings of the 2024 Second International Conference on Emerging Trends in Information Technology and Engineering (ICETITE), Vellore, India, 22–23 February 2024. [Google Scholar] [CrossRef]
- Tian, F. An agri-food supply chain traceability system for China based on RFID & blockchain technology. In Proceedings of the 2016 13th International Conference on Service Systems and Service Management (ICSSSM), Kunming, China, 24–26 June 2016. [Google Scholar] [CrossRef]
- MacCarthy, B.L.; Ahmed, W.A.; Demirel, G. Mapping the supply chain: Why, what and how? Int. J. Prod. Econ. 2022, 250, 108688. [Google Scholar] [CrossRef]
- Canton, H. Food and agriculture organization of the United Nations—FAO. In The Europa Directory of International Organizations 2021; Routledge: London, UK, 2021; pp. 297–305. [Google Scholar]
- Albalate-Ramírez, A.; Padilla-Rivera, A.; Rueda-Avellaneda, J.F.; López-Hernández, B.N.; Cano-Gómez, J.J.; Rivas-García, P. Mapping the Sustainability of Waste-to-Energy Processes for Food Loss and Waste in Mexico—Part 1: Energy Feasibility Study. Sustainability 2024, 16, 6111. [Google Scholar] [CrossRef]
- Mehrbanfar, M.; Bozorgi-Amiri, A.; Nasiri, M.M. A mathematical programming model for sustainable agricultural supply chain network design under uncertainty. J. Qual. Eng. Prod. Optim. 2020, 5, 189–220. [Google Scholar] [CrossRef]
- Safeer, S.; Pulvento, C. Blockchain-Backed Sustainable Management of Italian Tomato Processing Industry. Agriculture 2024, 14, 1120. [Google Scholar] [CrossRef]
- Wang, G.; Wang, Y.; Li, S.; Yi, Y.; Li, C.; Shin, C. Sustainability in Global Agri-Food Supply Chains: Insights from a Comprehensive Literature Review and the ABCDE Framework. Foods 2024, 13, 2914. [Google Scholar] [CrossRef]
- Khan, M.; Papadas, D.; Arnold, L.; Behrendt, K. Sustainability challenges in the multi-tier crop agri-food sector: A systematic review. Agric. Food Econ. 2024, 12, 25. [Google Scholar] [CrossRef]
- FAO. World Food and Agriculture Statistical Yearbook 2024; FAO: Italy, Rome, 2024. [Google Scholar]
- USDA FAS. Mexico: Tomato Annual. In Livestock and Poultry: World Market and Trade; United States Department of Agriculture, Foreign Agricultural Service (USDA FAS): Washington, DC, USA, 2022. [Google Scholar]
- Cui, X.; Guan, Z.; Morgan, K.L.; Huang, K.-M.; Hammami, A.M. Multitiered fresh produce supply chain: The case of tomatoes. Horticulturae 2022, 8, 1204. [Google Scholar] [CrossRef]
- Cahyadi, E.R.; Hidayati, N.; Zahra, N.; Arif, C. Integrating Circular Economy Principles into Agri-Food Supply Chain Management: A Systematic Literature Review. Sustainability 2024, 16, 7165. [Google Scholar] [CrossRef]
- Nguyen, T.-D.; Nguyen-Quang, T.; Venkatadri, U.; Diallo, C.; Adams, M. Mathematical programming models for fresh fruit supply chain optimization: A review of the literature and emerging trends. AgriEngineering 2021, 3, 519–541. [Google Scholar] [CrossRef]
- Alemany, M.; Esteso, A.; Ortiz, Á.; del Pino, M. Centralized and distributed optimization models for the multi-farmer crop planning problem under uncertainty: Application to a fresh tomato Argentinean supply chain case study. Comput. Ind. Eng. 2021, 153, 107048. [Google Scholar] [CrossRef]
- Rahbari, M.; Khamseh, A.A.; Mohammadi, M. Robust optimization and strategic analysis for agri-food supply chain under pandemic crisis: Case study from an emerging economy. Expert Syst. Appl. 2023, 225, 120081. [Google Scholar] [CrossRef] [PubMed]
- Younis, H.; Alsharairi, M.; Younes, H.; Sundarakani, B. The impact of COVID-19 on supply chains: Systematic review and future research directions. Oper. Res. 2023, 23, 48. [Google Scholar] [CrossRef]
- Fang, S.-L.; Kuo, Y.-H.; Kang, L.; Chen, C.-C.; Hsieh, C.-Y.; Yao, M.-H.; Kuo, B.-J. Using sigmoid growth models to simulate greenhouse tomato growth and development. Horticulturae 2022, 8, 1021. [Google Scholar] [CrossRef]
- Garrido, A.; Gil-González, A.B.; García, I.; Calderón, M.; Baños, R. Using LEL and Scenarios to Derive Mathematical Programming Models: Application in a Fresh Tomato Packing Problem. Comput. Electron. Agric. 2020, 170, 105242. [Google Scholar] [CrossRef]
- Aramyan, L. Measuring Supply Chain Performance in the Agri-Food Sector. Ph.D. Dissertation, Wageningen University, Wageningen, The Netherlands, 2006. [Google Scholar]
- Medina-Ruiz, C.A.; Mercado-Luna, I.A.; Soto-Zarazúa, G.M.; Torres-Pacheco, I.; Rico-García, E. Mathematical Modeling on Tomato Plants: A Review. Afr. J. Agric. Res. 2011, 6, 6114–6124. [Google Scholar] [CrossRef]
- Samuel, M.V.; Shah, M.; Sahay, B.S. An Insight into Agri-Food Supply Chains: A Review. Int. J. Value Chain Manag. 2012, 6, 115–140. [Google Scholar] [CrossRef]
- Paam, P.; Berretta, R.; Heydar, M.; Middleton, R.H.; García-Flores, R.; Juliano, P. Planning Models to Optimize the Agri-Fresh Food Supply Chain for Loss Minimization: A Review. In Reference Module in Food Science; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Lau, C.; Kanchanasuwan, S. Fruit Supply Chain Simulation: A Literature Review. Int. J. Logist. Syst. Manag. 2014, 19, 322–342. [Google Scholar]
- Lin, Q.-P.; Li, Y.-H. Status and Problems Analysis of Tomato Supply Chain. Logist. Technol. 2014, 33, 350–352. [Google Scholar] [CrossRef]
- Ghezavati, V.; Hooshyar, S.; Tavakkoli-Moghaddam, R. A Benders’ Decomposition Algorithm for Optimizing Distribution of Perishable Products Considering Postharvest Biological Behavior in Agri-Food Supply Chain: A Case Study of Tomato. Cent. Eur. J. Oper. Res. 2017, 25, 413–433. [Google Scholar] [CrossRef]
- Ganeshkumar, C.; Pachayappan, M.; Madanmohan, G. Agri-Food Supply Chain Management: Literature Review. Intell. Inf. Manag. 2017, 9, 68–96. [Google Scholar] [CrossRef]
- Esteso, A.; Alemany, M.M.E.; Ortiz, A. Métodos y Modelos Deterministas e Inciertos para la Gestión de Cadenas de Suministro Agroalimentarias. Dyna 2017, 62, 41–46. [Google Scholar] [CrossRef]
- Fatemi, M.; Azadi, H.; Rafiaani, P.; Taheri, F.; Dubois, T.; Van Passel, S.; Witlox, F. Effects of Supply Chain Management on Tomato Export in Iran: Application of Structural Equation Modeling. J. Food Prod. Mark. 2018, 24, 127–149. [Google Scholar] [CrossRef]
- Behzadi, G.; O’Sullivan, M.; Olsen, T.L.; Zhang, A. Agribusiness Supply Chain Risk Management: A Review of Quantitative Decision Models. Omega 2018, 79, 21–42. [Google Scholar] [CrossRef]
- Esteso, A.; Alemany, M.M.E.; Ortiz, A. Conceptual Framework for Designing Agri-Food Supply Chains under Uncertainty by Mathematical Programming Models. Int. J. Prod. Res. 2018, 56, 4418–4436. [Google Scholar] [CrossRef]
- Fuchigami, H.Y.; Severino, M.R.; Yamanaka, L.; de Oliveira, M.R. A Literature Review of Mathematical Programming Applications in the Fresh Agri-Food Supply Chain. In Operations Management; Springer: Cham, Switzerland, 2018; pp. 67–88. [Google Scholar] [CrossRef]
- Orjuela-Castro, J.A.; Adarme-Jaimes, W. Evaluating the Supply Chain Design of Fresh Food on Food Security and Logistics. In Logistics Management; Springer: Cham, Switzerland, 2018; pp. 295–307. [Google Scholar] [CrossRef]
- Ahumada, O.; Villalobos, J.R. Decision Support Models for Fresh Fruits and Vegetables Supply Chain Management. In Sustainable Food Supply Chains; Elsevier: Amsterdam, The Netherlands, 2019; pp. 317–337. [Google Scholar] [CrossRef]
- Cruz, L.; Pires-Ribeiro, J.; Barbosa-Póvoa, A.P. Design and Planning of Agri-Food Supply Chains. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2019; Volume 46, pp. 55–60. [Google Scholar] [CrossRef]
- Nguyen, C.; Goff, Z.; Accorsi, R. Mathematical modeling of food and agriculture distribution. In Sustainable Food Supply Chains; Elsevier: Amsterdam, The Netherlands, 2019; pp. 145–158. [Google Scholar] [CrossRef]
- Hasuike, T.; Kashima, T.; Matsumoto, S. Mathematical Modelling for Sustainable Agricultural Supply Chain Management Considering Preferences Between Farmers and Retailers. In Proceedings of the Advances in Production Management Systems. Production Management for Data-Driven, Intelligent, Collaborative, and Sustainable Manufacturing (APMS 2018), Seoul, Republic of Korea, 26–30 August 2018; Springer: Cham, Switzerland, 2018; Volume 535, pp. 43–49. [Google Scholar] [CrossRef]
- Behncke, F.G.H.; Ehrhardt, J.; Lindemann, U. Models for the Optimization of Supply Chains: A Literature Review. In Proceedings of the IEEE International Conference on Industrial Engineering and Engineering Management, Bangkok, Thailand, 10–13 December 2013; pp. 917–921. [Google Scholar] [CrossRef]
- Santoso, I.; Purnomo, M.; Sulianto, A.; Choirun, A. Machine Learning Application for Sustainable Agri-Food Supply Chain Performance: A Review. IOP Conf. Ser. Earth Environ. Sci. 2021, 924, 012059. [Google Scholar] [CrossRef]
- Tebaldi, L.; Vignali, G.; Bottani, E. Digital Twin in the Agri-Food Supply Chain: A Literature Review. In IFIP International Conference on Advances in Production Management Systems; Springer: Cham, Switzerland, 2021; pp. 356–363. [Google Scholar] [CrossRef]
- Novak Pintarič, Z. Multi-Objective Optimization of the Food Chain as a Support for the Development of Agricultural Sector. In Computer Aided Chemical Engineering; Elsevier: Amsterdam, The Netherlands, 2021; Volume 50, pp. 451–456. [Google Scholar] [CrossRef]
- Gurrala, K.R.; Hariga, M. Key Food Supply Chain Challenges: A Review of the Literature and Research Gaps. Oper. Supply Chain Manag. 2022, 15, 518–530. [Google Scholar] [CrossRef]
- Tümenbatur, A.; Tanyaş, M.; Çakmak, E. Agri-Food Supply Chain Holistic Design: Tomato Product Application. Beykoz Akad. Derg. 2022, 10, 250–264. [Google Scholar] [CrossRef]
- Stüve, D.; Van Der Meer, R.; Agha, M.S.; Entrup, M.L. A Systematic Literature Review of Modelling Approaches and Implementation of Enabling Software for Supply Chain Planning in the Food Industry. Prod. Manuf. Res. 2022, 10, 550–578. [Google Scholar] [CrossRef]
- Bando, K. Impact of Optimizing Vegetable Freshness on Agri-Food Supply Chain Design. In Agricultural Economics and Food Policy; Springer: Cham, Switzerland, 2022; pp. 123–140. [Google Scholar] [CrossRef]
- Ali, N.A.; Shuib, A.; Rakibe, I. The Current Trends of Research on Mathematical Programming Models for Perishable Fresh Produce Supply Chain: A Thematic Review. Int. J. Acad. Res. Bus. Soc. Sci. 2023, 13, 2141–2153. [Google Scholar] [CrossRef]
- Esteso, A.R.J.; Alemany, M.; Ortiz, A. Sustainable Agri-Food Supply Chain Planning through Multi-Objective Optimisation. J. Decis. Syst. 2023, 33, 808–832. [Google Scholar] [CrossRef]
- Azab, R.; Mahmoud, R.S.; Elbehery, R.; Gheith, M. A Bi-Objective Mixed-Integer Linear Programming Model for a Sustainable Agro-Food Supply Chain with Product Perishability and Environmental Considerations. Logistics 2023, 7, 46. [Google Scholar] [CrossRef]
- Martella, A.; Franco, S. Ecological Balance of Agri-Food Supply Chains—The Case of the Industrial Tomato. Sustainability 2023, 15, 7846. [Google Scholar] [CrossRef]
- Saralegui-Diez, P.; Aguilera, E.; González de Molina, M.; Guzmán, G.I. From Field to Table through the Long Way. Analyzing the Global Supply Chain of Spanish Tomato. Sustain. Prod. Consum. 2023, 43, 308–320. [Google Scholar] [CrossRef]
- Eslami, E.; Abdurrahman, E.; Ferrari, G.; Pataro, G. Enhancing Resource Efficiency and Sustainability in Tomato Processing: A Comprehensive Review. J. Clean. Prod. 2023, 418, 138996. [Google Scholar] [CrossRef]
- Belamkar, P.; Biswas, S.; Baidya, A.; Majumder, P.; Bera, U.K. Multi-Objective Optimization of Agro-Food Supply Chain Networking Problem Integrating Economic Viability and Environmental Sustainability through Type-2 Fuzzy-Based Decision Making. J. Clean. Prod. 2023, 417, 138294. [Google Scholar] [CrossRef]
- Taboada, H.; Davizón, Y.A.; Espíritu, J.F.; Sánchez-Leal, J. Mathematical Modeling and Optimal Control for a Dynamic Supply Chain Class: A Systems-Theoretic Approach. Appl. Sci. 2022, 12, 5347. [Google Scholar] [CrossRef]
- Martínez-Luaces, V. Square Matrices Associated to Parameter ODE Systems; IntechOpen: London, UK, 2018. [Google Scholar]

| System Dynamics | Sustainability Index | Production (MT) |
|---|---|---|
| System 1 | ||
| System 2 |
| Description | Parameters | Units |
| Capacity for producers 1 | 500 MT | |
| Capacity for distributors 1 | 400 MT | |
| Capacity for customers 1 | 3000 MT/day | |
| Dissipation rate echelon 1 | 3 MT/day | |
| Dissipation rate echelon 2 | 2.5 MT/day | |
| Dissipation rate echelon 3 | 2 MT/day | |
| Production rate echelon 1–2 | 25 MT/day | |
| Production rate echelon 2–3 | 22 MT/day | |
| Throughput | 1.5 MT/day | |
| Demand rate | 5000 MT/day |
| Description | Parameters | Units |
| Capacity for producers 2 | 1500 MT | |
| Capacity for distributors 2 | 1200 MT | |
| Capacity for customers 2 | 1000 MT | |
| Capacity for reprocessing 1 | 800 MT | |
| Capacity for reprocessing 2 | 600 MT | |
| Dissipation rate echelon 1 | 4.5 MT/day | |
| Dissipation rate echelon 2 | 3.8 MT/day | |
| Dissipation rate echelon 3 | 20 MT/day | |
| Production rate echelon 1-2 | 15 MT/day | |
| Production rate echelon 2-3 | 8.9 MT/day | |
| Reprocessing rate echelon 1-1 | 6 MT/day | |
| Reprocessing rate echelon 1-2 | 9.5 MT/day | |
| Reprocessing rate echelon 2-2 | 12 MT/day | |
| Reprocessing rate echelon 3-3 | 11 MT/day | |
| Throughput system 2 | 5 MT/day | |
| Demand rate system 2 | 3000 MT/day |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Benítez-García, I.; Davizón, Y.A.; Hernandez-Santos, C.; de la Cruz, N.; Hernandez, A.; Quiñonez-Ruiz, A.; Smith, E.D.; Sánchez-Leal, J.; Smith, N.R. Mathematical Modeling and Stability Analysis of Agri-Food Tomato Supply Chains via Compartmental Analysis. World 2025, 6, 129. https://doi.org/10.3390/world6030129
Benítez-García I, Davizón YA, Hernandez-Santos C, de la Cruz N, Hernandez A, Quiñonez-Ruiz A, Smith ED, Sánchez-Leal J, Smith NR. Mathematical Modeling and Stability Analysis of Agri-Food Tomato Supply Chains via Compartmental Analysis. World. 2025; 6(3):129. https://doi.org/10.3390/world6030129
Chicago/Turabian StyleBenítez-García, Israel, Yasser A. Davizón, Carlos Hernandez-Santos, Nain de la Cruz, Amadeo Hernandez, Aureliano Quiñonez-Ruiz, Eric D. Smith, Jaime Sánchez-Leal, and Neale R. Smith. 2025. "Mathematical Modeling and Stability Analysis of Agri-Food Tomato Supply Chains via Compartmental Analysis" World 6, no. 3: 129. https://doi.org/10.3390/world6030129
APA StyleBenítez-García, I., Davizón, Y. A., Hernandez-Santos, C., de la Cruz, N., Hernandez, A., Quiñonez-Ruiz, A., Smith, E. D., Sánchez-Leal, J., & Smith, N. R. (2025). Mathematical Modeling and Stability Analysis of Agri-Food Tomato Supply Chains via Compartmental Analysis. World, 6(3), 129. https://doi.org/10.3390/world6030129






