New Approach of Blind Adaptive Equalizer Based on Genetic Algorithms
Abstract
1. Introduction
- The BLE-GA combines a stochastic linear programming cost function with genetic algorithm optimization to address challenges in equalization under stochastic conditions.
- BLE-GA demonstrates adaptability across various QAM modulation schemes, including 64-QAM, with improved scalability and efficiency compared to traditional algorithms.
- A block-based architecture is introduced, reducing computational requirements while maintaining effective convergence.
- Simulations under different noise and inter-symbol interference conditions evaluate and demonstrate the performance of BLE-GA.
2. Related Works
3. Methods
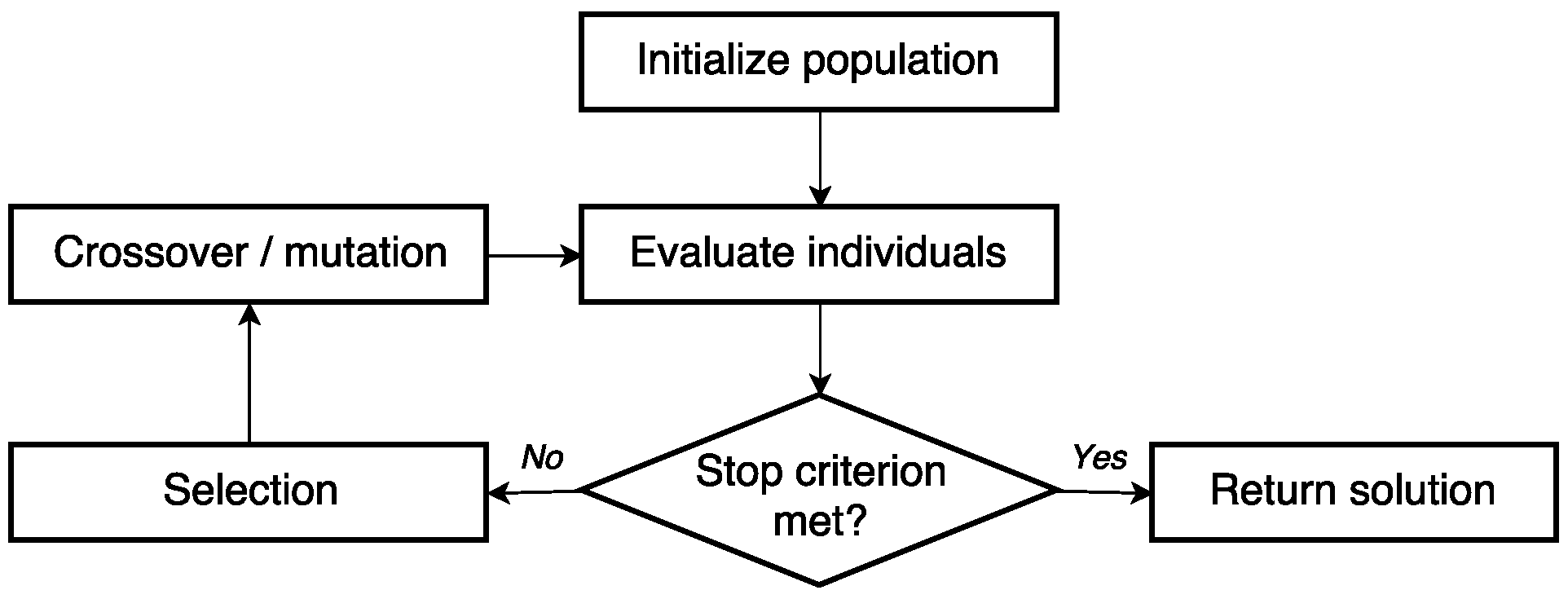
3.1. Background on Genetic Algorithms
3.2. Concepts of Linear Programming Under Uncertainty
- Proportionality assumption: The contribution of each activity to the value of the objective function z is proportional to the level of the activity , as represented by the term in the objective function;
- Additivity assumption: Every function in a linear programming model is the sum of the individual contributions of the respective activities;
- Divisibility assumption: Decision variables in a linear programming model are allowed to have any values, including non-integer values, that satisfy the functional and non-negativity constraints;
- Certainty assumption: The value assigned to each parameter of a linear programming model is assumed to be a known constant.
3.3. Adaptive Blind Equalization
3.3.1. Channel Model
3.3.2. The Constant Modulus Algorithm
3.3.3. Adaptive Blind Equalization Using Linear Programming
3.4. Blind Linear Equalizer Based on Genetic Algorithms
3.4.1. Architecture
3.4.2. Cost Function
3.5. Genetic Algorithm Setting
3.5.1. Objective Function
3.5.2. Encoding
3.5.3. Initial Population
3.5.4. Selection and Reproduction Operators
4. Methodology
5. Results and Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnson, R.J.; Schniter, P.; Endres, T.; Behm, J.; Brown, D.; Casas, R. Blind equalization using the constant modulus criterion: A review. Proc. IEEE 1998, 86, 1927–1950. [Google Scholar] [CrossRef]
- Haykin, S. Communication Systems, 4th ed.; Wiley Publishing: Hoboken, NJ, USA, 2001. [Google Scholar]
- Haykin, S. Adaptive Filter Theory, 4th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- Proakis, J.G. Digital Communications; Mcgraw-Hill College: Upper Saddle River, NJ, USA, 2000. [Google Scholar]
- Haykin, S. (Ed.) Blind Deconvolution; Prentice Hall: Upper Saddle River, NJ, USA, 1994. [Google Scholar]
- Godard, D. Self-Recovering Equalization and Carrier Tracking in Two-Dimensional Data Communication Systems. Commun. IEEE Trans. 1980, 28, 1867–1875. [Google Scholar] [CrossRef]
- Benveniste, A.; Goursat, M. Blind Equalizers. Commun. IEEE Trans. 1984, 32, 871–883. [Google Scholar] [CrossRef]
- Kennedy, R.A.; Ding, Z. Blind adaptive equalizers for quadrature amplitude modulated communication systems based on convex cost functions. Opt. Eng. 1992, 31, 1189–1199. [Google Scholar] [CrossRef]
- Ding, Z.; Luo, Z.Q. A fast linear programming algorithm for blind equalization. Commun. IEEE Trans. 2000, 48, 1432–1436. [Google Scholar] [CrossRef]
- Luo, Z.Q.; Meng, M.; Wong, K.M.; Zhang, J.K. A fractionally spaced blind equalizer based on linear programming. Signal Process. IEEE Trans. 2002, 50, 1650–1660. [Google Scholar] [CrossRef]
- Fernandes, M.A. Linear programming applied to blind signal equalization. AEU-Int. J. Electron. Commun. 2015, 69, 408–417. [Google Scholar] [CrossRef]
- Muhammad, M.; Ding, Z. A Linear Programming Receiver for Blind Detection of Full Rate Space-Time Block Codes. IEEE Trans. Signal Process. 2010, 58, 5819–5834. [Google Scholar] [CrossRef]
- Jacklin, N.; Ding, Z.; Li, Y. On efficient use of pilot symbols for multi-path channel equalization of QAM signals. In Proceedings of the 2013 IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 5553–5558. [Google Scholar]
- Sen, S.; Higle, J.L. An Introductory Tutorial on Stochastic Linear Programming Models. Interfaces 1999, 29, 33–61. [Google Scholar] [CrossRef]
- Mohammed, J.R. A Study on the Suitability of Genetic Algorithm for Adaptive Channel Equalization. Int. J. Electr. Comput. Eng. (IJECE) 2012, 2, 285–292. [Google Scholar] [CrossRef]
- Surajudeen-Bakinde, N.; Zhu, X.; Gao, J.; Nandi, A.; Lin, H. Genetic Algorithm Based Frequency Domain Equalization for DS-UWB Systems without Guard Interval. In Proceedings of the 2011 IEEE International Conference on Communications (ICC), Kyoto, Japan, 5–9 June 2011; pp. 1–5. [Google Scholar]
- Merabti, H.; Massicotte, D. Nonlinear adaptive channel equalization using genetic algorithms. In Proceedings of the 2014 IEEE 12th International New Circuits and Systems Conference (NEWCAS), Trois-Rivieres, QC, Canada, 22–25 June 2014; pp. 209–212. [Google Scholar]
- Gang, X.; Yourong, L. Blind Equalization Based on a Class of Genetic Algorithms for Wireless Communication. In Proceedings of the 2009 International Forum on Information Technology and Applications, Chengdu, China, 15–17 May 2009; Volume 1, pp. 239–244. [Google Scholar]
- Han, S.; Pedrycz, W.; Han, C. Nonlinear channel blind equalization using hybrid genetic algorithm with simulated annealing. Math. Comput. Model. 2005, 41, 697–709. [Google Scholar] [CrossRef]
- Zaouche, A.; Dayoub, I.; Rouvaen, J. Baud-spaced constant modulus blind equalization via hybrid genetic algorithm and generalized pattern search optimization. AEU-Int. J. Electron. Commun. 2008, 62, 122–131. [Google Scholar] [CrossRef]
- Liu, F.; Ge, L.D.; Wu, Y.J.; Li, J.M. Blind equalization based on immune optimized genetic algorithm. In Proceedings of the 2008 9th International Conference on Signal Processing, Beijing, China, 26–29 October 2008; pp. 1719–1721. [Google Scholar]
- Lin, H.; Yamashita, K. Hybrid simplex genetic algorithm for blind equalization using {RBF} networks. Math. Comput. Simul. 2002, 59, 293–304. [Google Scholar] [CrossRef]
- Khafaji, M.J.; Krasicki, M. Uni-Cycle Genetic Algorithm to Improve the Adaptive Equalizer Performance. IEEE Commun. Lett. 2021, 25, 3609–3613. [Google Scholar] [CrossRef]
- Resende, D.F.; Silva, L.R.M.; Nepomuceno, E.G.; Duque, C.A. Optimizing Instrument Transformer Performance through Adaptive Blind Equalization and Genetic Algorithms. Energies 2023, 16, 7354. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhang, F.; Yang, C. AdaNN: Adaptive Neural Network-Based Equalizer via Online Semi-Supervised Learning. J. Light. Technol. 2020, 38, 4315–4324. [Google Scholar] [CrossRef]
- Lauinger, V.; Buchali, F.; Schmalen, L. Blind Equalization and Channel Estimation in Coherent Optical Communications Using Variational Autoencoders. IEEE J. Sel. Areas Commun. 2022, 40, 2529–2539. [Google Scholar] [CrossRef]
- Murphy, S.L.; Townsend, P.D.; Antony, C. SkipNet: An adaptive neural network equalization algorithm for future passive optical networking. J. Opt. Commun. Netw. 2024, 16, 1082–1092. [Google Scholar] [CrossRef]
- Wang, Y.; Chang, W.; Li, J.; Yang, C. Signal processing for enhancing railway communication by integrating deep learning and adaptive equalization techniques. PLoS ONE 2024, 19, e0311897. [Google Scholar] [CrossRef] [PubMed]
- Devrari, A.; Kumar, A.; Kuchhal, P. Global aspects and overview of 5G multimedia communication. Multimed. Tools Appl. 2024, 83, 26439–26484. [Google Scholar] [CrossRef]
- Hassan, A.Y. A new approach for designing and implementing ADF equalization for 5G frequency selective channel based on two operating phases of LS and RLS algorithms. Telecommun. Syst. 2021, 77, 543–562. [Google Scholar] [CrossRef]
- Pinchas, M.; Noy, E. A New Blind Adaptive Equalization Method. In Proceedings of the 2022 International Conference on Frontiers of Communications, Information System and Data Science (CISDS), Guangzhou, China, 25–27 November 2022; pp. 128–132. [Google Scholar] [CrossRef]
- Zhang, L.; Wang, Z.; Zheng, G. OF-FSE: An Efficient Adaptive Equalization for QAM-Based UAV Modulation Systems. Drones 2023, 7, 525. [Google Scholar] [CrossRef]
- Hu, W.; Wang, Z.; Mei, R.; Lin, M. A Simple and Robust Equalization Algorithm for Variable Modulation Systems. Electronics 2021, 10, 2496. [Google Scholar] [CrossRef]
- Kumar Mohapatra, P.; Kumar Rout, S.; Kishoro Bisoy, S.; Kautish, S.; Hamzah, M.; Jasser, M.B.; Mohamed, A.W. Application of Bat Algorithm and Its Modified Form Trained with ANN in Channel Equalization. Symmetry 2022, 14, 2078. [Google Scholar] [CrossRef]
- Chen, Y.; Weng, G.; Luan, S.; Shang, Y.; Liu, C.; Bao, J. Parallel Blind Adaptive Equalization of Improved Block Constant Modulus Algorithm with Decision-Directed Mode. IEEE Access 2023, 11, 85268–85283. [Google Scholar] [CrossRef]
- Li, J.; Zheng, W.X.; Liu, M.; Chen, Y.; Zhao, N. Robust Blind Equalization for NB-IoT Driven by QAM Signals. IEEE Internet Things J. 2024, 11, 21499–21512. [Google Scholar] [CrossRef]
- Holland, J.H. Outline for a Logical Theory of Adaptive Systems. J. ACM 1962, 9, 297–314. [Google Scholar] [CrossRef]
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning, 1st ed.; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1989. [Google Scholar]
- Hillier, F. Introduction to Operations Research; McGraw-Hill: New York, NY, USA, 2014. [Google Scholar]
- Matlab. Create Genetic Algorithm Options Structure. 2016. Available online: http://www.mathworks.com/help/gads/gaoptimset.html (accessed on 22 January 2016).
- Branch, M.; Grace, A. MATLAB Optimization Toolbox: User’s Guide; Computation, Visualization, Programming, MathWorks, Inc.: Natick, MA, USA, 2013. [Google Scholar]















| Ref. | Method | Method Description | Summary |
|---|---|---|---|
| 2022 [31] | Meta-heuristic | Blind adaptive equalization based on a third-order polynomial cost function. | Introduces MSE POLY3 to reduce ISI in QAM systems, outperforming MMA in 16QAM. |
| 2020 [25] | Deep Learning | Adaptive neural network equalizer using semi-supervised learning and Aug-VAT loss. | Proposes AdaNN, improving BER and noise resilience without requiring labeled data online. |
| 2022 [26] | Deep Learning | Blind equalization and channel estimation using variational autoencoders (VAEs). | Utilizes VAEs to address variable channels and advanced modulation, achieving near-MMSE performance. |
| 2023 [32] | Meta-heuristic | Fractionally spaced equalizer with a feedback loop and MDD algorithm for phase correction. | Focuses on CFO correction in UAV QAM systems, reducing ISI with a feedback architecture. |
| 2022 [33] | Algo. Heuristic | Variable Modulation-Decision-Directed LMS using QPSK-like pilot signals. | Optimizes equalization for variable modulations, reducing BER and achieving high operational frequencies. |
| 2023 [24] | Meta-heuristic | Blind equalization for harmonic measurements using LPE filters and GAs for stability. | Improves transformer frequency response under colored noise, meeting IEC standards. |
| 2024 [27] | Deep Learning | Neural network equalizer with pre-trained kernels and adaptive LMS output layers. | SkipNet rapidly reconfigures PAM4 PON systems, outperforming fixed equalizers in dispersion and range. |
| 2024 [28] | Deep Learning | Combines a CNN for feature extraction with WDM and DCO-OFDM modulation for VLC. | Proposes DL-AEA to reduce ISI in railway VLC, achieving BER of 0.0001 with unsupervised learning. |
| 2023 [35] | Algo. Heuristic | Parallel blind equalization using IBCMA-DD for nonlinear satellite channels. | Improves spectral efficiency and reduces ISI in satellite systems without training sequences. |
| 2024 [36] | Algo. Heuristic | Modified CMA and GMCMA with MNM for NB-IoT systems with high-order QAM. | Optimizes blind equalization in NB-IoT, reducing BER and increasing convergence speed. |
| 2022 [34] | Meta-heuristic | Modified bat algorithm with an ANN for nonlinear channel equalization. | Integrates optimization inspired by ecology to improve equalization in noisy nonlinear channels. |
| 2021 [23] | Meta-heuristic | Uni-Cycle GA for adaptive equalizer coefficient optimization during each interval. | Reduces computational costs while maintaining robustness in time-variant channels. |
| Parameter | 4-QAM | 16-QAM | 64-QAM |
|---|---|---|---|
| Equalizer length (N) | 33 | 33 | 33 |
| Equalization delay () | 6 | 6 | 6 |
| BLE-GA Block length (K) | 400 | 400 | 1000 |
| CMA Adaptation step () | |||
| Adjustment period () in symbols |
| GA Parameter | Value |
|---|---|
| Chromosome length | |
| Crossover fraction | 0.9 |
| Elite count | 10 |
| Number of Generations | 100 |
| Population size | 200 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silva, C.A.D.; Fernandes, M.A.C. New Approach of Blind Adaptive Equalizer Based on Genetic Algorithms. Telecom 2025, 6, 6. https://doi.org/10.3390/telecom6010006
Silva CAD, Fernandes MAC. New Approach of Blind Adaptive Equalizer Based on Genetic Algorithms. Telecom. 2025; 6(1):6. https://doi.org/10.3390/telecom6010006
Chicago/Turabian StyleSilva, Caroline A. D., and Marcelo A. C. Fernandes. 2025. "New Approach of Blind Adaptive Equalizer Based on Genetic Algorithms" Telecom 6, no. 1: 6. https://doi.org/10.3390/telecom6010006
APA StyleSilva, C. A. D., & Fernandes, M. A. C. (2025). New Approach of Blind Adaptive Equalizer Based on Genetic Algorithms. Telecom, 6(1), 6. https://doi.org/10.3390/telecom6010006







