Probabilistic Kolmogorov–Arnold Network: An Approach for Stochastic Modelling Using Divisive Data Re-Sorting

Abstract

The Kolmogorov–Arnold network (KAN) is a regression model that is based on a representation of an arbitrary continuous multivariate function by a composition of functions of a single variable. Experimentally obtained datasets for regression models typically include uncertainties, which in some cases, cannot be neglected. The conventional way to account for the latter is to model confidence intervals of the systems’ outputs in addition to the expected values of the outputs. However, such information may be insufficient, and in some cases, researchers aim to obtain probability distributions of the outputs. The present paper proposes a method for estimating probability distributions of the outputs by constructing an ensemble of models. The suggested approach covers input-dependent probability distributions of the outputs and is capable of capturing the multi-modality, as well as the variation of the distribution type with the inputs. Although the method is applicable to any regression model, the present paper combines it with KANs, since their specific structure leads to the construction of computationally efficient models. The source codes are available online.

1. Introduction

The popularity of using the Kolmogorov–Arnold representation [1,2] as a regression model has significantly grown over the last year, largely due to the publication of preprint [3], which promotes term network (leading to abbreviation ‘KAN’). However, the idea of using the Kolmogorov–Arnold representation as a machine-learning model has been out for decades [4,5], and successful implementations of this model and its training method have been available for years [6,7,8,9,10,11,12,13], including the developments by the authors of the present paper [14,15]. The pioneering work of Igelnik and Parikh [9] should be especially emphasised, as it is the first proposed KAN with the spline basis functions. A more detailed literature review on KANs can be found in the recent publication by the authors of the present paper [15].

Most recent preprints focus on deterministic modelling, and only few authors tried using this model for estimating probabilistic properties. For example, in [16], a method for propagating statistical moments through the model is suggested, and in [17], KANs are combined with Bayesian inference for estimating posterior distributions. The present paper proposes an ensemble training method for uncertainty quantification and combines it with KANs.

The prior research on probabilistic modelling can be divided into Bayesian neural networks (BNNs) [18,19,20] and a large group of ensemble methods [21,22,23,24,25,26,27,28]. There are also methods tailored to specific models, such as the Monte Carlo dropout [29]. One particular ensemble method can be highlighted—quantile regression forests (QRFs) [30]. It is a customisation of Random Forests by using a specific classifier, which is designed to perform quantile regression. The original publication did not report quantile values for the benchmark tests, only pinball loss metrics [31]; however, the experiments can be reproduced using freely available libraries (Python package scikit-garden).

Most ensemble methods do not require making choices regarding the expected probability types, as opposed to some probabilistic models, such as BNNs. Practical utilisation of BNNs is facilitated by the publicly available Keras (https://keras.io/examples/keras_recipes/bayesian_neural_networks, accessed on 17 August 2025) library. The users should define and configure the type of the expected distribution. In cases when it is more complex than a single bell-shaped curve, the users need to specify its form, for example a mixture of Gaussian distributions. Assigning the type of the expected distribution can be an additional uncertainty—choosing a uni-modal type leaves no chances for the library to determine multi-modality, while assigning a mixture of Gaussians can reduce the accuracy by forcing to estimate unnecessary extra parameters when the actual distribution is much simpler.

Another popular family of algorithms, natural gradient boosting (NGBoost) [32], also requires the users to choose the distribution type. It aims at improving the probabilistic predictions of gradient boosting models by replacing the standard gradient with the natural gradient, which accounts for the geometry of the output distribution. The accuracy metric, natural log-likelihood, requires parameters of the assumed distribution to be estimated from the modelled sample. When samples are short and the distribution type is a mixture, it brings uncertainty to a quantification method in addition to those that are already in the data.

The aim of the approach proposed in the present paper is to ‘pass’ the burden of the identification of the distribution type from the user to the code. It is an ensemble method and has a capability of making samples large enough for the estimation of the probability distributions, including the capturing of the multi-modality. The method is combined with the KANs’ architecture, resulting in shallow probabilistic models. The reason for building the approach on KANs is the descriptive capabilities of the latter, enabling it to identify hidden properties of the modelled systems via deep-learning steps. The approach was also designed to have a low computational cost.

2. Divisive Data Re-Sorting (DDR)

A dataset is considered to contain independent data records $\left\{{\mathit{x}}_i,y_i\right\}$, $i\in \left\{1,\dots ,N\right\}$, where ${\mathit{x}}_i\in {\mathbb{R}}^m$ is the input of the i-th record, $y_i\in \mathbb{R}$ is the output of the i-th record, and N is the number of records. The records are observations of a system with uncertainty—the output of such system is a random variable with input-dependent probability distribution.

Suppose some deterministic regression model $M_0:{\mathbb{R}}^m\to \mathbb{R}$ can be built using a particular error minimisation process,

$$M_0=\underset{M\in \mathcal{A}}{argmin}\sum _i{\left(y_i-M\left({\mathit{x}}_i\right)\right)}^2,$$

where $\mathcal{A}$ is the space of possible models. Such models will be called expectation models.

The method starts by building one expectation model for the entire dataset $M_{1,1}$, where the first subscript is the step number and the second subscript is the index of the model within the step. Then, the data records are re-sorted according to residuals

$$r_i=y_i-M_{1,1}\left({\mathit{x}}_i\right)$$

and subdivided into two even clusters over the median residual in the sorted list. At the second step, new expectation models are built for each cluster, resulting in $M_{2,1}$ and $M_{2,2}$. Then, within each cluster, the records are again re-sorted according to the residuals. Each cluster is then subdivided into two clusters each over the median residual, resulting in four clusters in total, for which new expectation models $M_{3,1}$, $M_{3,2}$, $M_{3,3}$, and $M_{3,4}$ are built. The process is continued in a similar way.

The user must ensure that the average error for each cluster declines in the subdividing process. Declining errors indicate that the selected model type is good enough for the entire dataset to be represented by a collection of models—the larger the number of models in the collection, the better the fit to all data points. Non-declining errors, in turn, mean that the dataset cannot be represented by a collection of models of the selected type. The latter may be due to model inadequacy.

When the models become sufficiently accurate, the process stops. It is up to the user to decide when the residuals are sufficiently small, i.e. the ‘depth’ of the process (the number of models constituting the final ensemble) becomes a hyperparameter. The ensemble of models obtained at the last subdividing step can now be used for approximating the distribution of the output for each individual record—the outputs of the ensemble can be handled as a sample from the probability distribution of the real output.

If for a given expectation model, the computational complexity is known and is given by dependency $C\left(N\right)$, where N is the number of records on which the model is trained, then, knowing that at the n-th step of the DDR algorithm, exactly $2^{n-1}$ models are built, each on $N/2^{n-1}$ records, the complexity of just building the models of this step is $2^{n-1}C\left(2^{1-n}N\right)$. DDR is of course ideal for parallelisation: each expectation model is independent of the other; hence, at the n-th step of the DDR algorithm, the entire process of constructing the ensemble can be executed within exactly $2^{n-1}$ threads.

The proposed approach falls into the boosting category, since a series of models is built sequentially were the next group of models depends on the previous. It has similarities to some known methods, but in the form proposed here, it is novel to the best knowledge of the authors. A possibly close concept is called anti-clustering [33,34,35], where the data is clustered such that the clusters have maximum similarity, with maximum diversity of the elements within them. Although similar to the established boosting frameworks, such as AdaBoost, the difference to the latter is the building of ‘weak’ models such that each is trained on its own subset of records, without the introduction of weights; the main mechanism of DDR is the formation of the subsets of records (re-sorting), rather than fitting of the weights.

2.1. Interpretation of DDR and Uncertainty Type

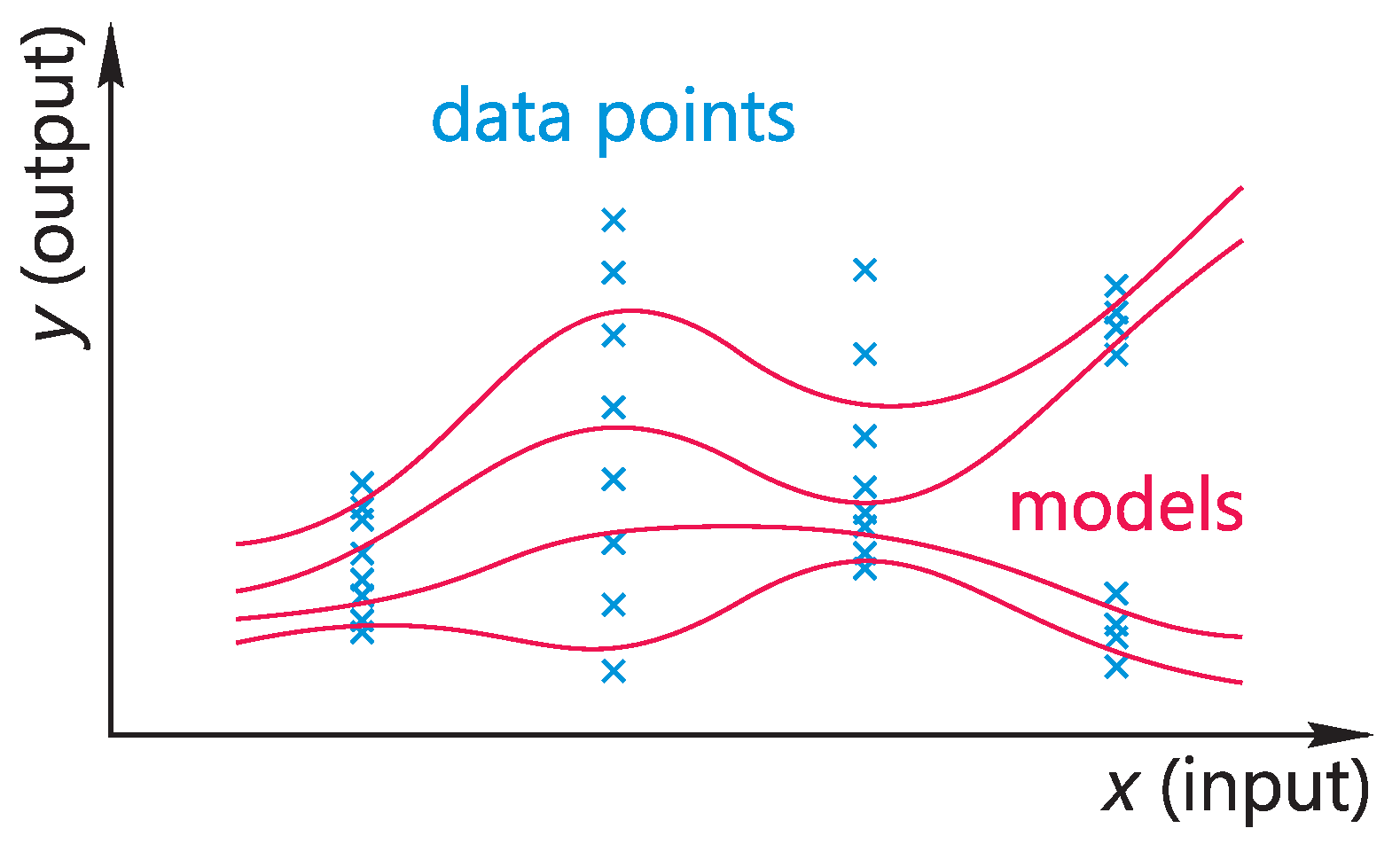
The capability of detecting multi-modality by the proposed algorithm is illustrated schematically in Figure 1. The columns of different output values are multiple outputs corresponding to a single input. The red lines are the expectation models of the ensemble. The line ‘densities’ within each column approximately match the ‘densities’ of the output values, which follows from the construction of the ensemble of the models. Of course, expectation models with the output continuously dependent on the input require the probability distribution of the output of the modelled system to be continuously dependent on the input.

The DDR algorithm does not specifically rely on the type of data uncertainty. Sometimes, it is not easy to identify the uncertainty type even in the case of known underlying physical properties of the system. For example, the uncertainly type of a dataset with self-reported incomes depending on demographic parameters (e.g., age, education level, etc.) can be interpreted in various ways: it can be said that this data has aleatoric uncertainty because multiple records with identical inputs are likely to have different outputs; on the other hand, by expanding the list of inputs and obtaining more demographic details, the uncertainties can be reduced, which may classify them as epistemic. Not in all, but in many cases, the boundary between epistemic and aleatoric uncertainties is arbitrary and is defined by the users as they understand it.

2.2. Relation to k-Nearest Neighbours (kNN)

In general, kNN is considered to be a competitive method for various types of probabilistic modelling [36]. For example, it can be applied to the scenario illustrated in Figure 1. If a given input matches any of the inputs associated with the columns of data points, the application of the kNN algorithm with the proper choice of the number of nearest neighbours will directly give the set of the points from the column. The latter is close to the set of outputs of the models comprising the DDR ensemble. However, the figure shows an ideal scenario only for the explanation of the concept. For non-deal data, the points will be spread along the input axes and there will also be gaps in the data. Furthermore, the applicability of kNN cannot always be determined from the data—even for a deterministic system, the neighbouring points can be collected and variances can be estimated, which may lead to a wrong conclusion.

Thus, the similarity between DDR and kNN consists in returning a pre-defined number of outputs, which in the ideal case (e.g., Figure 1), are similar or identical. These outputs represent the scatter of points corresponding to one input point, given that the considered system is stochastic. However, the DDR’s outputs are the results of the models, while kNN’s outputs are the values directly picked from the dataset.

DDR allows researchers to avoid difficult choices related to kNN, such as the number of neighbours to pick, the weights to be assigned for the points that are slightly shifted, how to cover the gaps in the data, and the applicability of kNN in the first place (whether the object is deterministic or stochastic). The main advantage of DRR is that it does not require the entire dataset to be retained in the memory for each prediction. The numerical comparison of DDR and kNN is provided below.

2.3. Prediction of Probability Density

When the residuals decline sharply during the DDR steps, the number of obtained clusters can be small, e.g., 8 or 16. The modelling goal, however, is to predict the probability distribution, which requires a relatively large ensemble. Some approximation methods, such as kernel density estimation (KDE) [37], can be applied, but DDR allows for significant enlargement of the size of the ensemble, which can be used to build empirical cumulative distribution functions (ECDFs).

When the re-sorting process is completed, any large enough group of adjacent records in the sorted list can be used for building an additional model for the ensemble. This is possible because each cluster contains records that already have been sorted at the preceding step of the algorithm. Building additional models for the existing ensemble can be one option.

The second option is constructing a different (additional) ensemble of models using a sliding-window technique. It is applied to the sorted dataset obtained at the last step. Exactly k sequential records are selected, starting from the first record, and are used to build the first model for the additional ensemble. Then, k sequential records starting from record $\left(s+1\right)$ are used to build the second model for the additional ensemble. This is repeated in the similar way. Such process can be interpreted as having a window of a selected size that is moved along the sorted dataset, and the records that fall into this window are used for training new models for the additional ensemble. When $s<k$, the window is moved with overlapping. The users must make a choice regarding size k and shift s. The size must be selected such that a reliable estimation of model parameters is possible; it is subject to the choice of the parameter estimation algorithm. The shift defines the desired size of the additional ensemble, i.e. the number of points for the ECDFs.

Within the discussed algorithms, the clusters are always even. One can construct modifications of such algorithms considering uneven clusters (with varying number of records); however, this will create difficulties for the choice of the number of the parameters of the expectation models, especially on small datasets.

3. Kolmogorov–Arnold Model/Network

The two-layer Kolmogorov–Arnold model (or network, KAN) is given by the following expression:

$${\tilde{y}}_i=\sum _{k=1}^d{\Phi }_k\left(\sum _{j=1}^m{f}_{kj}\left(x_{i,j}\right)\right),$$

(1)

where scalar ${\tilde{y}}_i$ is the calculated model output of the i-th record, scalars $x_{i,j}$ denote the j-th component of input vector ${\mathbf{x}}_i$, functions $f_{kj}$ and ${\Phi }_k$ constitute the model. In the original work [1,2], it has been shown that the model with $d=2m+1$ can represent any continuous multivariate function (more recently, the restrictions on continuity have been somewhat relaxed, see e.g., [38] and references therein). Functions $f_{kj}$ and ${\Phi }_k$, which are referred to as the ‘inner’ and the ‘outer’ functions, respectively, are further decomposed into the basis functions and the parameters. There are multiple model training methods and choices for the basis functions. It is assumed that the reader is already familiar with this model; an overview of the model and its training methods can be found in the recent publication by the authors [15]; practical examples of the model application can be found on the authors’ website (http://openkan.org, accessed on 17 August 2025).

3.1. KAN and DDR

The present paper proposes the two-layer KAN to be used as an expectation model for the DDR ensemble; more precisely, a specific modification of it—shallow probabilistic model is proposed in the subsection below. However, the expectation model can of course be arbitrary, and its complexity can be optimised using standard tools, such as e.g., minimum description length (MDL) [39].

First versions of the present paper proposed another expectation model—a multi-layer deep KAN with a specific architecture. It is called a binary Urysohn tree and is characterised by doubling the number of the underlying functions from layer to layer from top to bottom. It is a successful model with descriptive capabilities equivalent to shallow KANs and with some of its own advantages. The main reason for mentioning it is the historical significance—it was a successful implementation of a multi-layer deep KAN back in 2021 by the authors of the present paper. Interested readers can access version 3 of the present paper [40] containing a detailed description of the model and numerical experiences. Subsequent versions of the present paper refocused on the shallow KANs.

3.2. Shallow Probabilistic Model

For relatively large datasets, the entire KAN can of course be used as the expectation model for DDR. In this case, its structure can optimised via a range of techniques; for example, running variational Bayesian inference on KANs can yield a model that is optimal in terms of size (e.g., as is carried out for other models [41]). However, for relatively small datasets, that might not be possible—subdivision of the dataset into clusters may lead to such cluster size that the number of records within a cluster is insufficient for model training without overparametrisation. The latter can be addressed using the idea as follows.

Model (1) can be rewritten as

$$\begin{array}{cc}\hfill & {\tilde{y}}_i=\sum _{k=1}^d{\Phi }_k\left({\theta }_{i,k}\right),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & {\theta }_{i,k}=\sum _{j=1}^m{f}_{kj}\left(x_{i,j}\right),\hfill \end{array}$$

(3)

where intermediate variable ${\mathit{\theta }}_i\in {\mathbb{R}}^d$ has been introduced, with index i indicating the record number; scalars ${\theta }_{i,k}$ denote the k-th component of ${\mathit{\theta }}_i$. A single expectation model (KAN) is fitted for the entire dataset first. Then, the model is used to calculate the values of intermediate variables ${\mathit{\theta }}_i$. These values are then assembled into a new dataset $\left\{{\mathit{\theta }}_i,y_i\right\}$, $i\in \left\{1,\dots ,N\right\}$. Finally, the DDR algorithm is applied to the new dataset with the expectation model having the form given by Equation (2).

Such approach allows for a significant reduction in the number of estimated parameters within a single expectation model in the ensemble, also leading to a faster training (compared to using KANs as expectation models). Model (2) is called a generalised additive model (GAM)—it can be viewed as a constituent part of KAN.

4. Elementary Example—Application of DDR

The aim of the first test is to demonstrate the capabilities of DDR using a simple expectation model (without the combination with KAN). Several computational tests of the present paper use synthetic data, as the reference (true) distributions are required for the validation; in the case of experimentally-obtained datasets of stochastic systems, true distributions are unknown.

4.1. Data and Expectation Model

Synthetic data is generated using the Monte Carlo (MC) algorithm. The data corresponds to a stochastic system, the output of which is the sum of outcomes of q ten-sided dice rolls. There are three inputs: $q_1$, $q_2$, and p, where $1\le q_{1,2}\le 10$. The number of dice is then chosen as $q=q_1$ with probability p, and $q=q_2$ with probability $\left(1-p\right)$. The output of such system is a discrete random variable, the distribution of which is input-dependent and is also bi-modal for a large range of inputs. The training and the validation datasets consist of 1000 and 100 records, respectively; the inputs are drawn independently from a uniform distribution; the validation dataset is generated independently from the training dataset.

Seven steps of the DDR algorithm are performed, resulting in $2^{7-1}=64$ expectation models in the DDR ensemble. Afterwards, the sliding-window technique is applied with the window size of 20 records, which is moved along the sorted records without overlapping, providing the final ensemble of 50 models. The sliding-window method is not necessary for this particular dataset, but its usage is a part of the test.

For this example, the most simple expectation model is chosen—a multilinear (trilinear) model:

$${\tilde{y}}^i=c_0+c_1{x}_{i,1}+c_2{x}_{i,2}+c_3{x}_{i,3}+c_4{x}_{i,1}{x}_{i,2}+c_5{x}_{i,1}{x}_{i,3}+c_6{x}_{i,2}{x}_{i,3}+c_7{x}_{i,1}{x}_{i,2}{x}_{i,3},$$

(4)

where ${\tilde{y}}^i$ is the estimated output of the i-th record, $x_{i,j}$ denote the j-th component of the input vector, and $c_j$ are the model parameters.

4.2. Accuracy Metrics

To assess the performance of the approach, the modelling results are compared to the MC simulations that can be considered to represent true distributions.

The first comparison step considers means and standard deviations obtained from the DDR ensemble (modelling) and from the MC simulations (reference solution). The normalised root mean square error (RMSE) measure is used:

$$E_{\mathrm{RMSE}}={\displaystyle \frac{1}{max\left(Z_{\mathrm{MC}}\right)-min\left(Z_{\mathrm{MC}}\right)}}\sqrt{{\displaystyle \frac{1}{N}}\sum _i{\left(Z_{i,\mathrm{DDR}}-Z_{i,\mathrm{MC}}\right)}^2},$$

(5)

where Z stands for either mean or standard deviation, subscript ‘$\mathrm{DDR}$’ denotes the value obtained from the DDR ensemble, subscript ‘$\mathrm{MC}$’ denotes the value obtained from the MC sampling, N is the number of records used for the comparison, and the sum is over record number i.

Furthermore, goodness-of-fit comparisons are also performed. Both tested sample and MC generated population have large number of ties (equal values), which makes many standard tests, such as Cramér–von Mises and Anderson–Darling, inapplicable. Also, this particular case is not bounded by two tested samples only; independent true samples of any sizes can be generated by MC. This advantage is used for introduction of a customised test similar to the Cramér–von Mises test.

The statistic is the relative distance between the median trees constructed as follows. When two samples are compared, each one is subdivided by the median into two clusters; this median is the first entry in the list; another two medians for each of the obtained clusters are added to the list; the process continues in the same way until the predefined number of the clusters’ or nested medians is obtained. They are sorted, resulting in a vector that can be called the median tree. The vectors corresponding to the two samples (U and V) are compared using the relative distance:

$$S=2\sqrt{2}{\displaystyle \frac{\parallel U-V\parallel }{\parallel U\parallel +\parallel V\parallel }}.$$

(6)

Such metric is, in fact, a set of quantiles, i.e. vectors of multiple quantiles for different samples are compared. It is easy to show that if two samples correspond to the same continuous random variable with probability density function f, then the numerator of S is related to statistic T from the Cramér–von Mises test [42]. In particular, statistic

$$T_{*}={\displaystyle \frac{ab}{c\left(a+b\right)}}\sum _i{\left(\left(U_i-V_i\right)f\left({\displaystyle \frac{U_i+V_i}{2}}\right)\right)}^2,$$

(7)

where a and b are the sizes of two samples, c is the number of medians (elements in U or V), has the same limiting distribution as T when $a\to \infty$, $b\to \infty$, and $a/b\to \lambda$, where $\lambda$ is finite. Statistic S simply omits f and is scaled differently to $T_{*}$. Theoretical limits for S are $0\le S\le 2\sqrt{2}$, but the expected value of S for two random U and V, assuming the uniform distribution with the same limits, is 1; therefore, this value is a convenient measure with conventional range $[0,1]$.

The standard approach for most similar testing procedures is to compare the statistic computed for two samples to tabulated values. Since this is a new test, such tables are not available, but can be created ad hoc. The MC sample can be as large as necessary and represents the population, against which the model sample is tested. Random sub-samples from the MC population are taken, statistic S is calculated for each taken sub-sample and the MC population, the values are sorted and used as an ECDF for the validation. For the examples of this paper, the number of sub-samples is taken to be 100, and when the statistic for the model sample is below the maximum value, the test is considered to be passed at a $1\%$ significance level.

4.3. Test Results

The results are shown in

Table 1. Test results for the dice example.

sequential number	1	2	3	4	5	6	7	8
RMSE for mean	0.04	0.03	0.05	0.03	0.04	0.05	0.04	0.03
RMSE for standard deviation	0.15	0.14	0.14	0.15	0.14	0.14	0.14	0.15
passed goodness-of-fit tests, DDR	79	91	80	92	86	77	89	87
passed goodness-of-fit tests, kNN	62	81	70	62	77	73	83	73

. Each column is obtained by independent execution of the programme, which includes the data generation, the training, and the validation (against MC) as described above. For this example, the normalised RMSEs for the mean and for the standard deviation obtained from the DDR ensemble are approximately $4\%$ and $14\%$, respectively. The samples given by the DDR ensemble pass approximately 85 out of 100 goodness-of-fit tests.

The last row of Table 1 shows the application of kNN to the example above. The number of neighbours is the same as the number of models in the DDR ensemble. It can be seen that kNN samples pass fewer goodness-of-fit tests, approximately 73 out of 100.

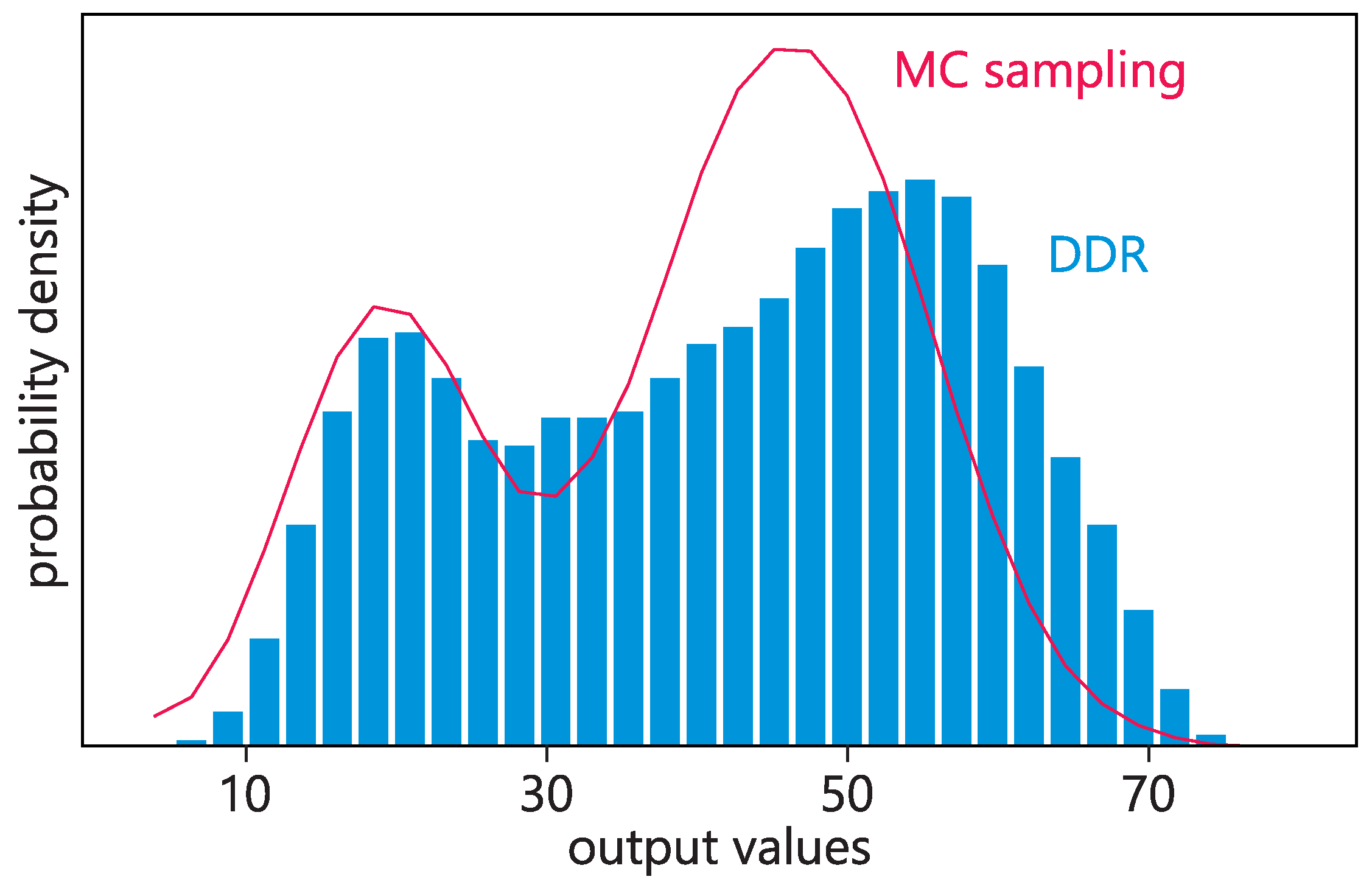
Estimation of the probability density using KDE applied to the DDR ensemble is shown in Figure 2 for $p=0.3$, $q_1=4$, $q_2=9$, where it can be seen that the bi-modal character of the distribution is captured. The method consists in replacing a single value in a sample by a smooth distribution curve (e.g., Gaussian) and obtaining the distribution as a result of superposition. The expected smoothness of the distribution is controlled by a numerical parameter.

Table 2. Decline of the relative error in the DDR algorithm with increase of the number of clusters.

number of clusters	1	2	4	8	16	32	64
RMSE for output	0.153	0.107	0.058	0.032	0.018	0.009	0.004

shows a sharp decline of the relative error in the subdividing process of the DDR algorithm computed during training on the training dataset itself, confirming the aleatoric nature of the uncertainty. The source code is available online (https://github.com/andrewpolar/vdice_bilinear, accessed on 17 August 2025).

4.4. Comparison to Bayesian Neural Networks (BNNs)

The multi-modal input-dependent probability distributions of the outputs of a stochastic system can also be estimated using BNNs [20]. A well-tested and popular code Keras (https://keras.io/examples/keras_recipes/bayesian_neural_networks, accessed on 17 August 2025) is taken for the comparison. Since the reference input-dependent distributions should be known (i.e., needed for the validation), in the provided example (https://archive.ics.uci.edu/ml/datasets/wine+quality, accessed on 17 August 2025), the experimentally obtained dataset has been replaced by the above-described synthetic dataset. The code has been used almost as is, with only one necessary change—to support multi-modality, the posterior (output) distribution type has been changed from a single normal distribution to a mixture of two normal distributions, e.g.,

$$f\left(x\right)=\sum _j{p}_j{f}_{\mathcal{N}}\left(x;{\mu }_j,{\sigma }_j^2\right),$$

(8)

where weights $p_j$, expectations ${\mu }_j$, and standard deviations ${\sigma }_j$ are estimated from the data. The latter is a typical way of incorporating multi-modality in probabilistic neural networks [43].

The results are shown in

Table 3. Test results for the dice example, modelled using BNN.

sequential number	1	2	3	4	5	6	7	8
RMSE for mean	0.19	0.17	0.19	0.14	0.15	0.18	0.15	0.17
RMSE for standard deviation	0.20	0.21	0.30	0.43	0.43	0.26	0.32	0.23
passed goodness-of-fit tests	19	23	18	16	13	25	23	23

. It can be seen that it is less accurate than DDR for this particular dataset. The reason for this is a relatively small dataset size, but it is a part of the test. BNN also captures multi-modality, which can be shown by making the dataset less challenging—by increasing the size, excluding uni-modal records, or narrowing the variation ranges for the inputs, e.g., $3\le q_{1,2}\le 6$. The source code is available online (https://github.com/andrewpolar/vdice-python, accessed on 17 August 2025).

5. Comparison to Quantile Regression Forests (QRFs)

Quantile regressions are commonly used for prediction of the confidence intervals along with the expectations and the medians. The experiment in this section is the comparison of the confidence intervals estimated for the Boston housing dataset by DDR and QRF. The latter was installed as Python package scikit-garden. In both tests, 5-fold cross validation was used. The dataset is short (506 records) and significantly imbalanced.

The generalised additive model (GAM) was chosen as an expectation model for DDR:

$${\tilde{y}}_i=\sum _{j=1}^m{f}_j\left(x_{i,j}\right),$$

(9)

with 6 nodes and piecewise linear basis functions. For DDR, the sliding-window size of 20 and the shift of 14 were taken. In the test, the number of points falling into the interval defined by two quantile values was counted and divided by the number of test records in the validation set.

For confidence interval $[0.05,0.95]$, the ideal prediction result is of course $0.90$. The comparison is shown in

Table 4. Quantile regression test for estimation of confidence interval $[0.05,0.95]$ for QRF and DDR.

sequential number	1	2	3	4	5	6	7	8
QRF	0.8735	0.8597	0.8775	0.8656	0.8794	0.8557	0.8773	0.8745
DDR	0.9051	0.8794	0.8577	0.8597	0.8695	0.9012	0.8834	0.8932

, where the sequential numbers denote different code executions. The difference is insignificant; both methods give good results for this dataset.

Table 5. Quantile regression test for estimation of confidence interval $[0.20,0.80]$ for QRF and DDR.

sequential number	1	2	3	4	5	6	7	8
QRF	0.6047	0.5929	0.6166	0.6107	0.6304	0.6107	0.6067	0.6146
DDR	0.6067	0.6086	0.6107	0.6166	0.5790	0.5770	0.6126	0.5810

shows the same test for narrower limits $[0.20,0.80]$, for which the ideal prediction value is $0.60$. It can be seen that the results again are very close and, considering the given data quality, can be judged to be very accurate.

The hyperparameters, such as the sliding-window size and the shift in DDR, can be conveniently calibrated by dividing the dataset into three subsets: training, selection, and testing. The selection subset is used for the comparison of quantile values for different hyperparameters and is not directly used in the training.

6. Probabilistic KAN Test

This example introduces a more complex and closer to reality dataset that cannot be modelled by simple models, requiring a complex network-type model with multiple layers. The data is computed using the following formula:

$$\begin{array}{cc}\hfill & y={\displaystyle \frac{2+2x_3^{*}}{3\pi }}\left(arctan\left(20\left(x_1^{*}-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{x_2^{*}}{6}}\right)exp\left(x_5^{*}\right)\right)+{\displaystyle \frac{\pi }{2}}\right)+\hfill \\ \hfill & \phantom{y}+{\displaystyle \frac{2+2x_4^{*}}{3\pi }}\left(arctan\left(20\left(x_1^{*}-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{x_2^{*}}{6}}\right)exp\left(x_5^{*}\right)\right)+{\displaystyle \frac{\pi }{2}}\right),\hfill \\ \hfill & x_j^{*}=x_j+\delta \left(c_j-0.5\right),j\in \left\{1,\dots ,5\right\},\hfill \end{array}$$

(10)

where y is the system output, $x_j$ are the system inputs, $c_j\sim unif\left(0,1\right)$ are uniformly distributed random variables (noise), multiplier $\delta =0.4$ is the aleatoric uncertainty level (the system becomes deterministic for $\delta =0$). For data generation, inputs $x_j\sim unif\left(0,1\right)$ are taken.

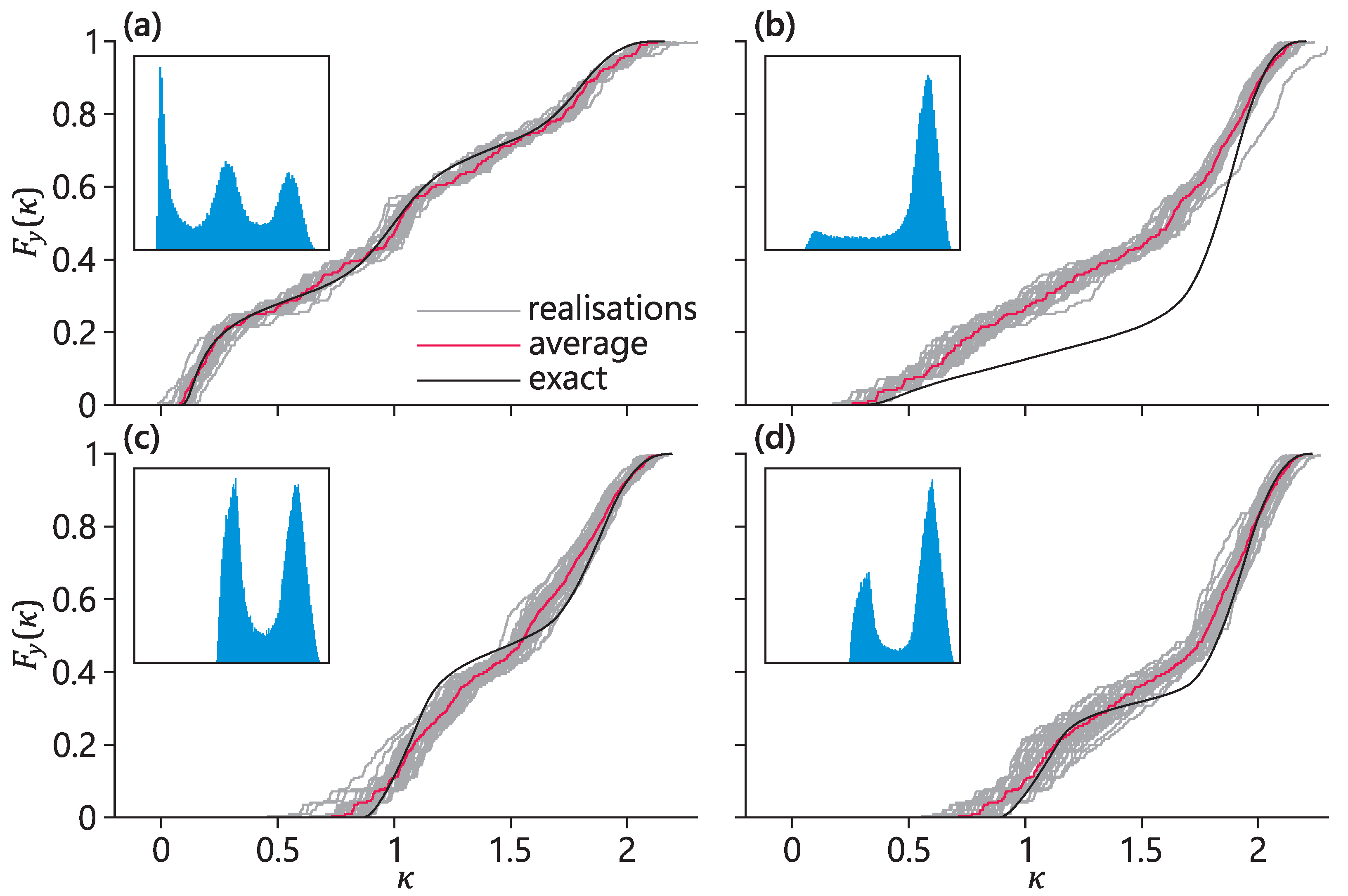
The probability density of the output significantly changes depending on the inputs. In Figure 3, in the insets (blue figures), four examples of probability densities of y are shown for four different inputs:

$$\begin{array}{cc}\hfill & {\mathit{x}}_{\mathrm{a}}=\left[\begin{array}{ccccc}0.5& 0.5& 0.5& 0.5& 0.5\end{array}\right],\hfill \\ \hfill & {\mathit{x}}_{\mathrm{b}}=\left[\begin{array}{ccccc}0.65& 0& 0.5& 0.5& 0.5\end{array}\right],\hfill \\ \hfill & {\mathit{x}}_{\mathrm{c}}=\left[\begin{array}{ccccc}0.68& 1& 0.5& 0.5& 0.5\end{array}\right],\hfill \\ \hfill & {\mathit{x}}_{\mathrm{d}}=\left[\begin{array}{ccccc}0.74& 1& 0.5& 0.5& 1\end{array}\right],\hfill \end{array}$$

corresponding to Figure 3a–d, respectively. The probability density functions (PDFs) are built using the MC sampling of ${10}^5$ points.

To benchmark the DDR procedure, a total of 40 runs of the programme have been performed. During each run, a dataset of ${10}^6$ records has been generated, the ensemble of models has been constructed using the DDR algorithm, and the ECDFs for the four points given above have been calculated using the sliding-window technique. The number of the outer functions of the Kolmogorov–Arnold model has been selected to be 11; the inner and the outer functions have been taken to be piecewise linear with 5 and 7 equidistant nodes, respectively.

In Figure 3, the four inputs given above are considered, the ECDFs of the output built using the MC sampling are shown in black, and the ECDFs obtained using the DDR procedure (with the sliding-window technique) are shown in grey (the output of the system, denoted as y in Equation (10), is a random variable; hence, the ECDF of y is denoted as $F_y$, and its argument is denoted as $\kappa$, which stands for a value that y may take). Furthermore, an average ECDF across all realisations (i.e., average of grey curves) is shown in red. For the purposes of this discussion, the MC-sampling ECDFs are referred to as the exact. It can be seen that the ensemble of models reproduces qualitatively the major features of the exact CDFs and predicts quantitatively the range of the output. The subfigures show different representative scenarios: for input ${\mathit{x}}_{\mathrm{a}}$, the ensemble ECDF is very close to the exact CDF; for input ${\mathit{x}}_{\mathrm{b}}$, the ensemble ECDF is somewhat far from the exact CDF quantitatively, although it reproduces qualitatively the change in the slope; for inputs ${\mathit{x}}_{\mathrm{c}}$ and ${\mathit{x}}_{\mathrm{d}}$, the ensemble ECDF is rather close to the exact CDF, although somewhat smoothed.

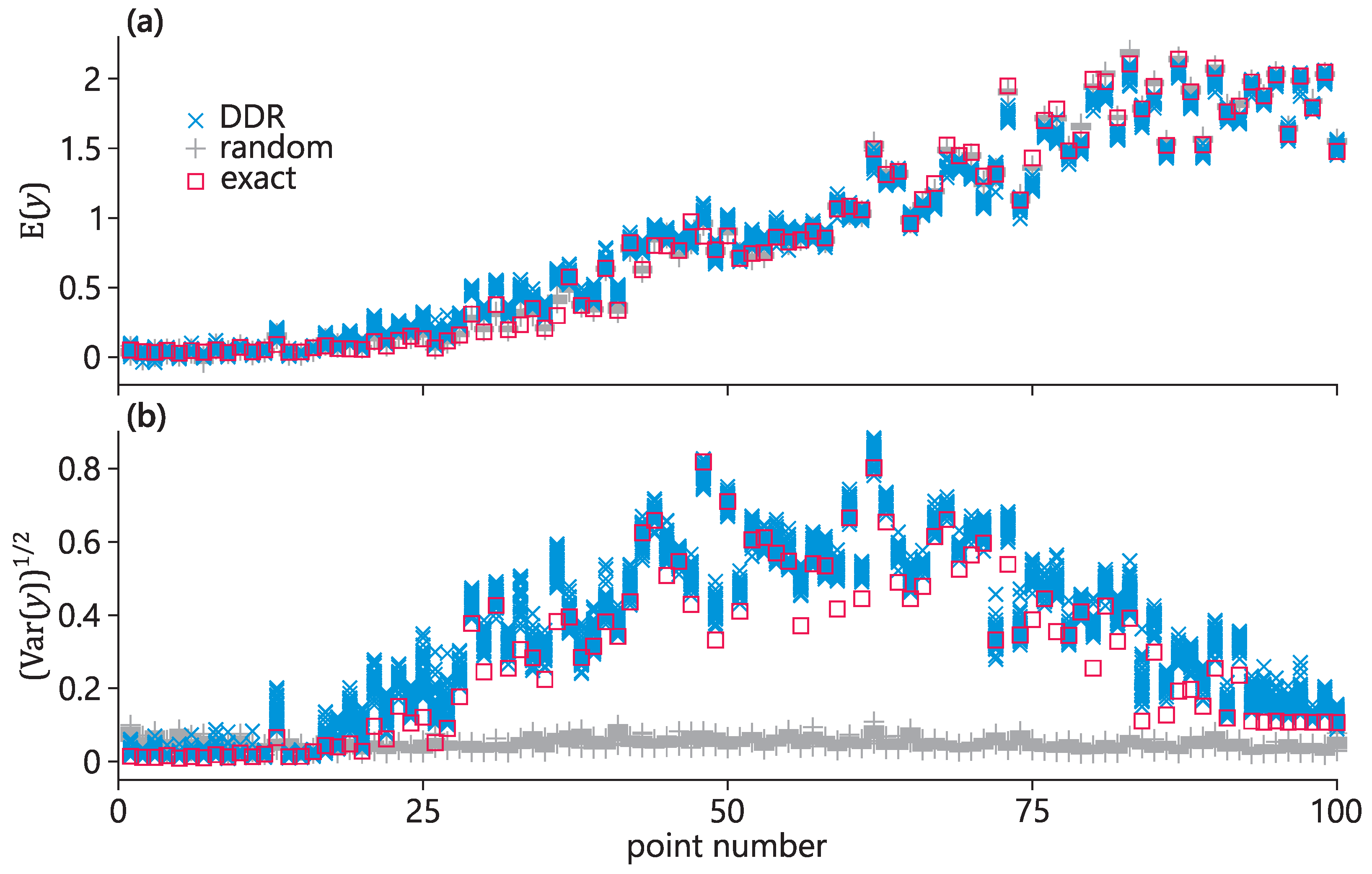
The DDR algorithm builds the ensemble of models using the specifically created set of data clusters. Therefore, it is crucial to emphasise its advantage over an ensemble built using clusters containing random records. To show this, a set of 100 input points have been randomly generated. For each input point, the true mean and the true standard deviation have been calculated using the MC sampling. Next, for each input point, the mean and the standard deviation have been calculated using the DDR ensembles and the random ensembles (the entire dataset is shuffled randomly, split into the same number of clusters as the DDR ensemble contains, and the ensemble of models is created such that each model is trained on its cluster). In Figure 4, the results are compared and it can be seen that the random ensembles can model the means well, which is a known fact, but cannot model the standard deviations at all. Meanwhile, the DDR ensembles predict the standard deviations both qualitatively and quantitatively.

Shallow Probabilistic KAN

Following Section 3.2, a shallow model is constructed for the example above. The number of records is decreased to ${10}^4$. The structure of the Kolmogorov–Arnold model is changed to 6 and 12 equidistant nodes for the inner and the outer functions, respectively (as above, piecewise linear functions are used). Five steps of the DDR algorithm are performed, resulting in $2^{5-1}=16$ clusters. For the training of the DDR ensemble models, the number of equidistant nodes for the outer functions is decreased to 7. The sliding window of 500 records with the shift of 300 records is used, providing the final ensemble of 32 models. Thus, each individual model of the final ensemble containing 77 parameters (since there are 11 outer functions with 7 nodes per function) is trained on 500 records (the sliding window size).

The same accuracy metrics as in the dice example are used, and the results are shown in

Table 6. Test results for shallow probabilistic KAN.

sequential number	1	2	3	4	5	6	7	8
RMSE for mean	0.04	0.03	0.04	0.03	0.04	0.03	0.04	0.03
RMSE for standard deviation	0.10	0.13	0.12	0.16	0.10	0.14	0.12	0.13
passed goodness-of-fit tests	58	58	62	60	64	63	63	64

. The errors for the mean and for the standard deviation are even lower than for the dice example; the number of passed goodness-of-fit tests is lower, but accounting for the complexity of the input-dependent distributions (shown in the insets of Figure 3), the authors consider this result to be acceptable. The source code is available online (https://github.com/andrewpolar/pkan, accessed on 17 August).

One common problem for probabilistic models is a relatively long training time (e.g., several minutes even for relatively small datasets). The construction of the shallow probabilistic KAN using DDR in this example took approximately $0.25$ s on Intel(R) Core(TM) i7-8550U 1.80 GHz CPU, which can be considered to be a relatively good result. This can be crucial for cases focusing on unsupervised learning using large datasets typically requiring hours and days for training.

7. Detecting Public Bias in Bookmakers’ Odds for the English Premier League

The sports betting market is a tightly-regulated social system involving multiple large groups with opposing interests but common rules. Bookmakers’ odds can be regarded as a probabilistic model, crafted by highly-skilled and motivated professionals to secure a long-term profit. Football match outcomes, however, exhibit substantial aleatoric uncertainty, making them an attractive testing ground for probabilistic modelling.

In this experiment, the objective is not to maximise the percentage of correct predictions, but to design a betting strategy that maximises the net profit using the approach proposed above. In this scenario, the match outcome prediction accuracy as a performance metric is misleading: for example, consistently betting on favourites in the British Premier League yields roughly $50\%$ correct outcomes but no monetary gain. Purely random betting results in small but consistent losses, typically around $5\%$. Thus, the approach focuses on detecting patterns of public bias embedded in bookmakers’ odds and exploiting it for profitable betting decisions.

7.1. What Is Public Bias?

Bookmakers operate in a competitive market, which limits their commission rates—typically around $3\%$ to $7\%$ as reported on their websites. This commission, embedded in the offered odds, is often referred to as a Dutch booking. In a perfectly balanced market, a Dutch book guarantees profit regardless of the match result.

In practice, bettors’ preferences are often biased and mismatched with presumed probabilities. To manage this, bookmakers adjust their odds to influence betting behaviour and restore the balance—sometimes visible in last-minute odds changes [44]. Most bookmakers also prohibit AI-assisted betting and may suspend accounts of suspected violators, though their detection methods are not disclosed.

7.2. Modelling Concept

The model produces probabilistic predictions for each possible match outcome: home win, draw, or away win, based on historical records. For each match, it selects the single outcome with the highest expected profit given the offered odds. A fixed virtual stake of £100 is placed on a single selected outcome for each match. Profit or loss is accumulated over the full Premier League season of 380 matches (each of the 20 teams playing every other team twice, once at home and once away).

Performance is reported as return on total stake (ROS) R:

$$R={\displaystyle \frac{M}{nB}},$$

(11)

where n is the number of bets, B is the virtual stake in the given currency ($B=\pounds 100$), and M is the total profit in the given currency. For example, $R=0.1$ corresponds to a $10\%$ return, which is $\pounds 3800$ profit over $\pounds 38000$ in total wagers. The denominator is used only for the reference; an actual bankroll of $\pounds 38\mathrm{K}$ is not required. For comparison, purely random betting produces $R\approx -0.05$.

7.3. Modelling Details

The model is the probabilistic KAN as described above. It predicts the goal difference (home minus away) as a real-valued output. Predictions are then converted into the categorical outcomes (home win, away win, draw) using a simple threshold (above $0.5$, below $-0.5$, and between these values, respectively).

Two seasons were modeled with different feature sets:

• 2019–2020 season:

  ‑

  Features: current standings positions for each team (integers 0–19).

  ‑

  Standings at the season start are taken from the previous season; updated after each match.

  ‑

  Training data: the preceding 15 seasons.

  ‑

  Newly promoted teams are assigned the initial standings positions.

  ‑

  Results:

  Table 7. Sports betting results for 2019–2020 season of the English Premier League.

  sequential number	1	2	3	4	5	6	7	8
  ROS	0.13	0.21	0.14	0.14	0.15	0.12	0.15	0.09

  (code/data publicly available (http://openkan.org/bpl1.html, accessed on 17 August 2025)).

• 2020–2021 season:

  ‑

  Features: recent match performance—the total goal differences in the lost matches, the total goal differences in won matches, and the number of draws—for both home and away teams (6 features per match).

  ‑

  Features are updated after each match.

  ‑

  Features at the season start are taken from the previous season; updated after each match.

  ‑

  Training data: the preceding 16 seasons.

  ‑

  Newly promoted teams are excluded; only 17 teams from the prior season are modelled.

  ‑

  Results:

  Table 8. Sports betting results for 2020–2021 season of the English Premier League.

  sequential number	1	2	3	4	5	6	7	8
  ROS	0.15	0.13	0.20	0.23	0.21	0.14	0.15	0.13

  (code/data publicly available (http://openkan.org/bpl2.html, accessed on 17 August 2025)).

7.4. Discussion

Across both seasons, the model’s recommended wagers fell predominantly on underdogs. Only about $30\%$ of these bets were correct, yet the overall ROS was strongly positive—evidence that the model identified instances where potential payouts justified the risk. This behaviour is consistent with the principle of value betting, in which profit arises from exploiting the market odds that underestimate an outcome’s true probability.

Considering the deliberately elementary feature sets used, the performance is notable. By comparison, studies focused on maximizing predictive accuracy for sports outcomes, e.g., [45], often employ extensive feature sets, sometimes exceeding 100 variables, and report higher outcome prediction accuracy. The objective of the present experiment, however, was to detect systematic mismatches between bookmakers’ publicly-offered odds, shaped by bettors’ biases, and the actual probabilities inferred from the historical records, rather than to maximise raw prediction accuracy.

8. Conclusions

The present paper has introduced a new approach to modelling of stochastic systems—the divisive data re-sorting (DDR) method. It consists in recursive steps of training of an ensemble of models, each on an individual cluster of data records, sorting of the records, and increasing of the ensemble size. The method can be combined with any expectation model, but the model should have adequate descriptive capabilities for the considered data. The suggested method can capture the multi-modality of the input-dependent probability distribution of the system’s output, as numerical experiments have shown. The method can also be used when users do not need a distribution and are satisfied with first two statistical moments for the computed outputs. The method is related to kNN but is free from many of its hard choices, as well as from retaining the entire dataset for each prediction.

The DDR method has been then combined together with the Kolmogorov–Arnold model (or network, KAN) resulting in the shallow probabilistic KAN. It has been found to be an efficient combination of a regression model with high descriptive capabilities and a simple model (the generalised additive model, or GAM) as a component of the DDR ensemble for producing the probabilistic output. Its relatively quick training time may be crucial for some applications.