Investigation of Mixing of Solid Particles in a Plowshare Mixer Using Discrete Element Method (DEM)
Abstract
1. Introduction
2. Method Description
2.1. Particle Shape
2.2. Discrete Element Method Theory
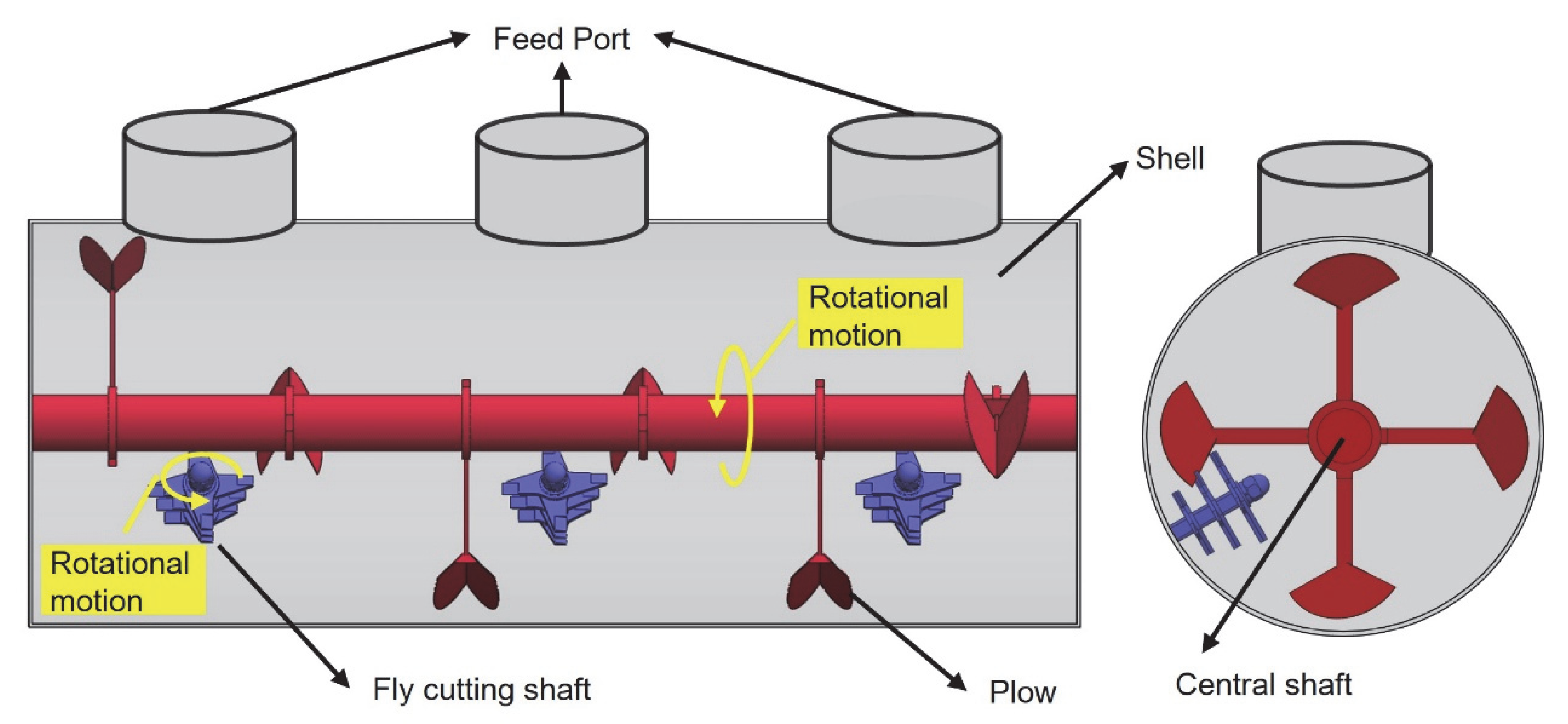
2.3. Geometry of Plowshare Mixer with Fly Cutting
3. Simulation Conditions
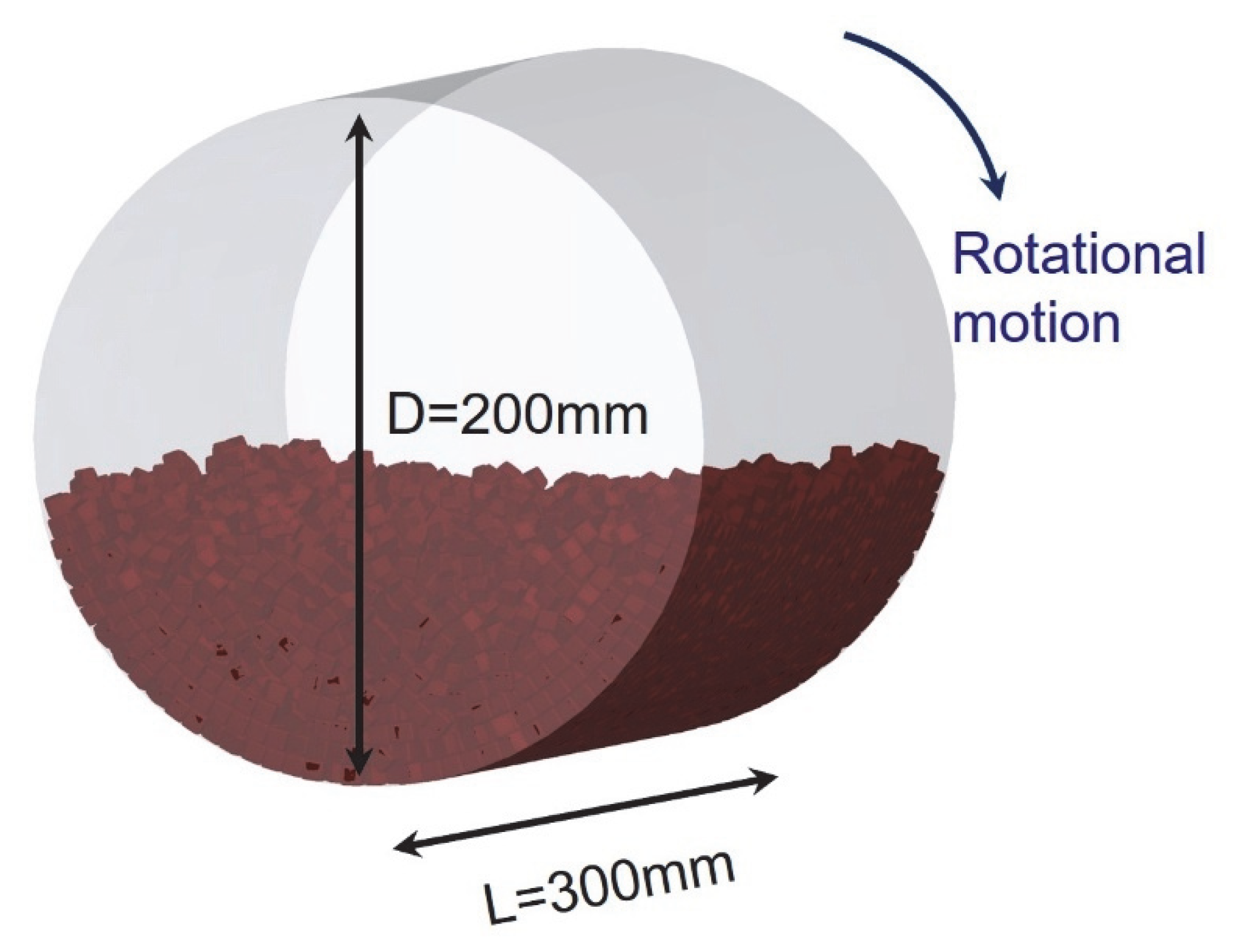
3.1. Model for Calibration
3.2. Simulation Experiments
4. Results and Discussions
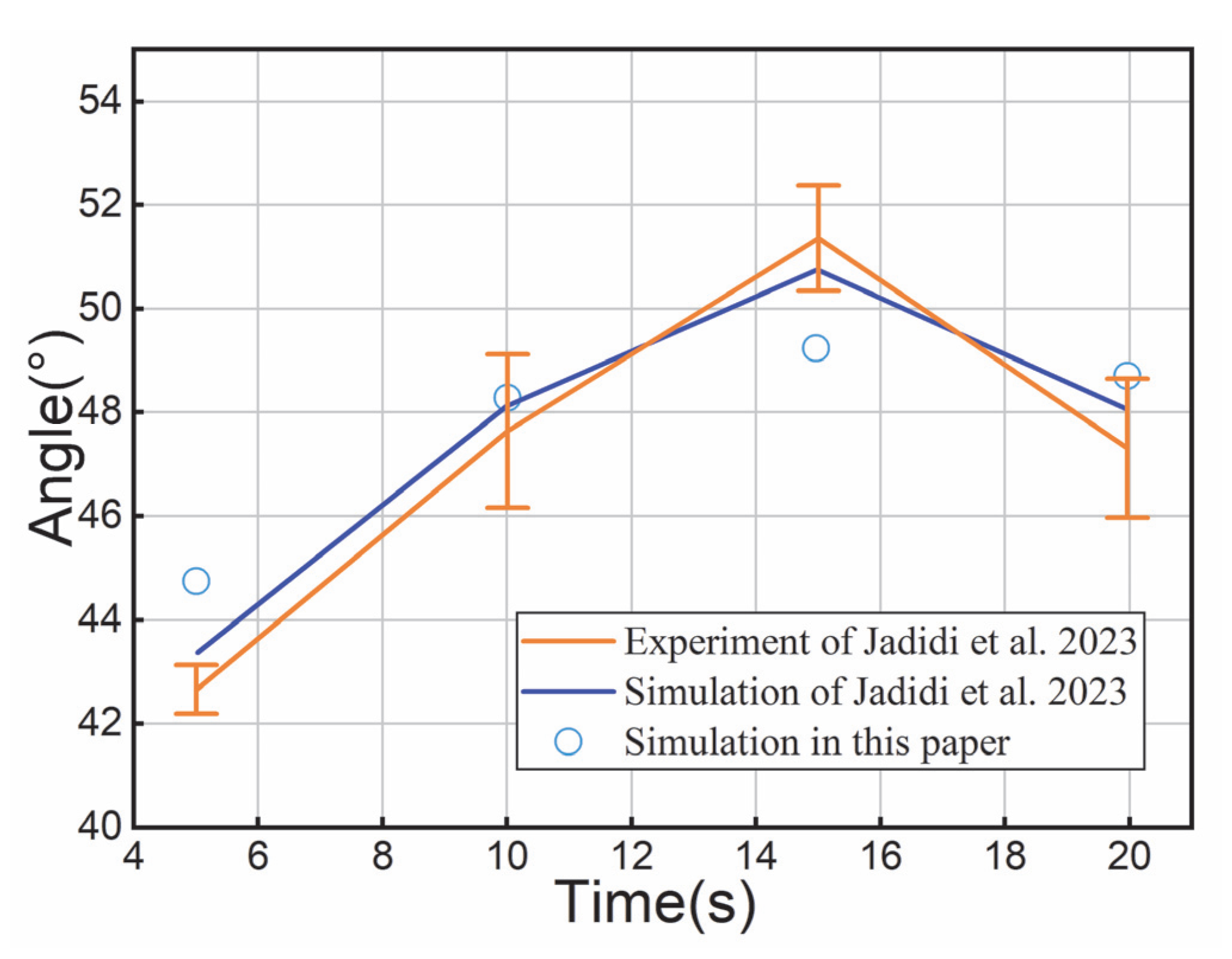
4.1. Model Calibration
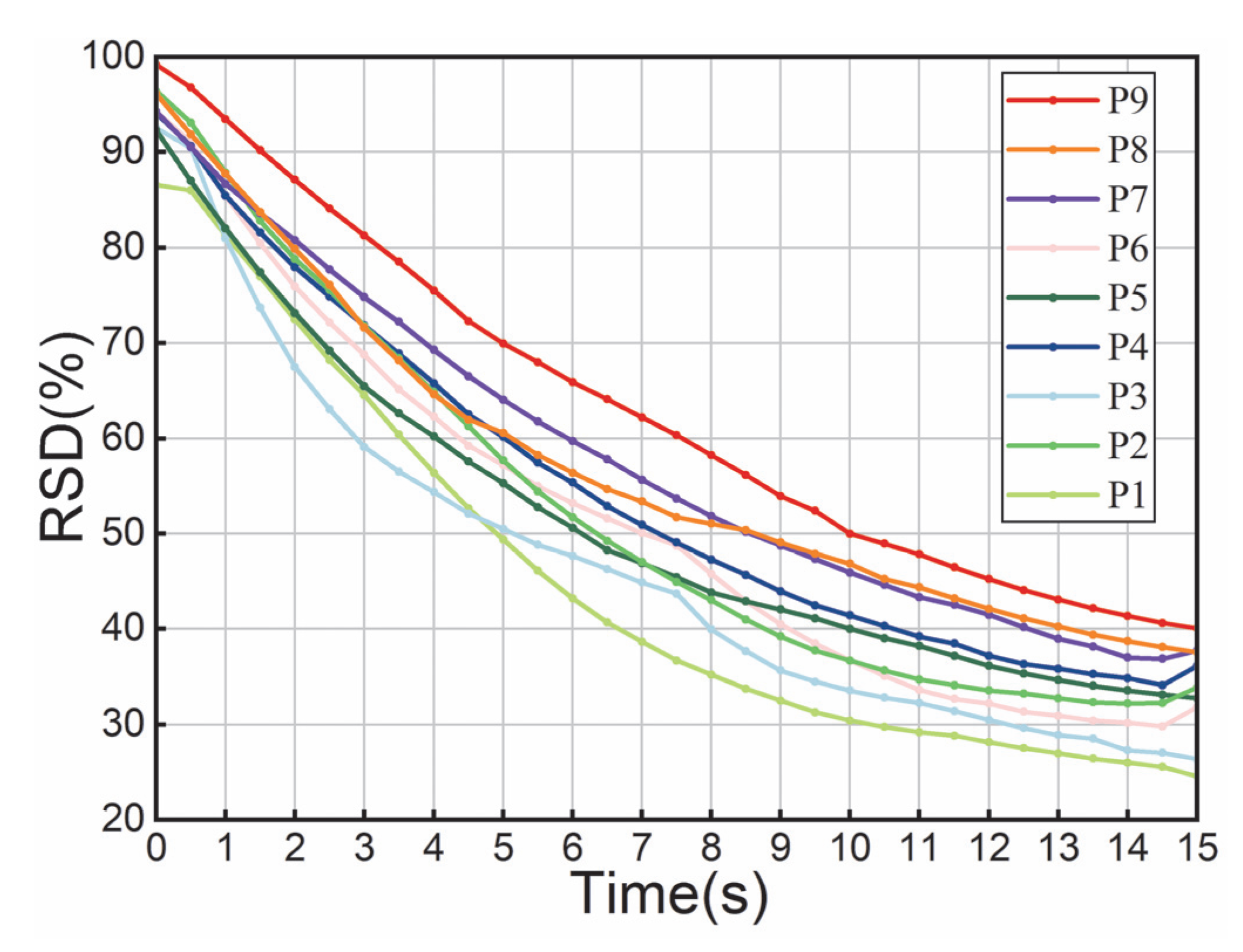
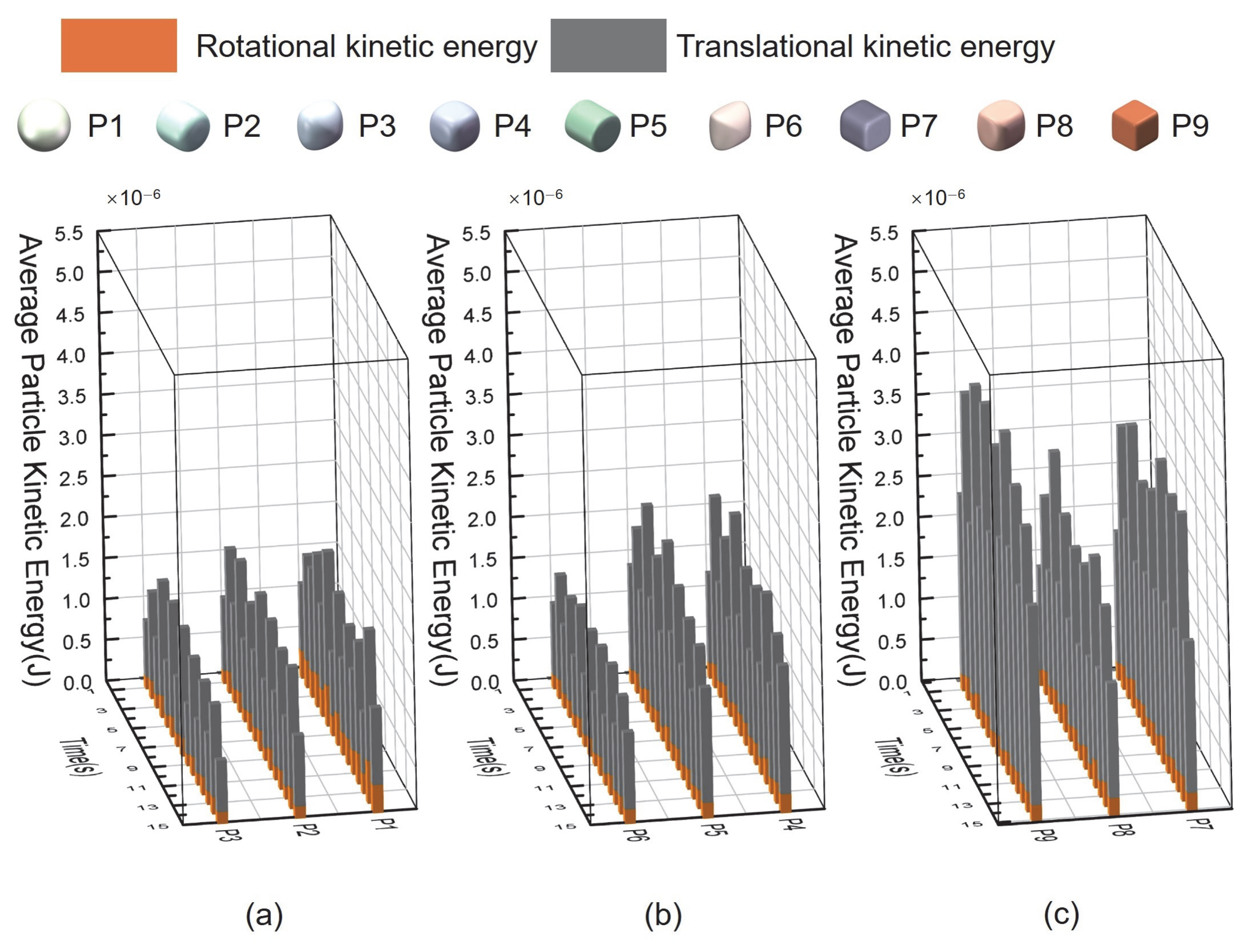
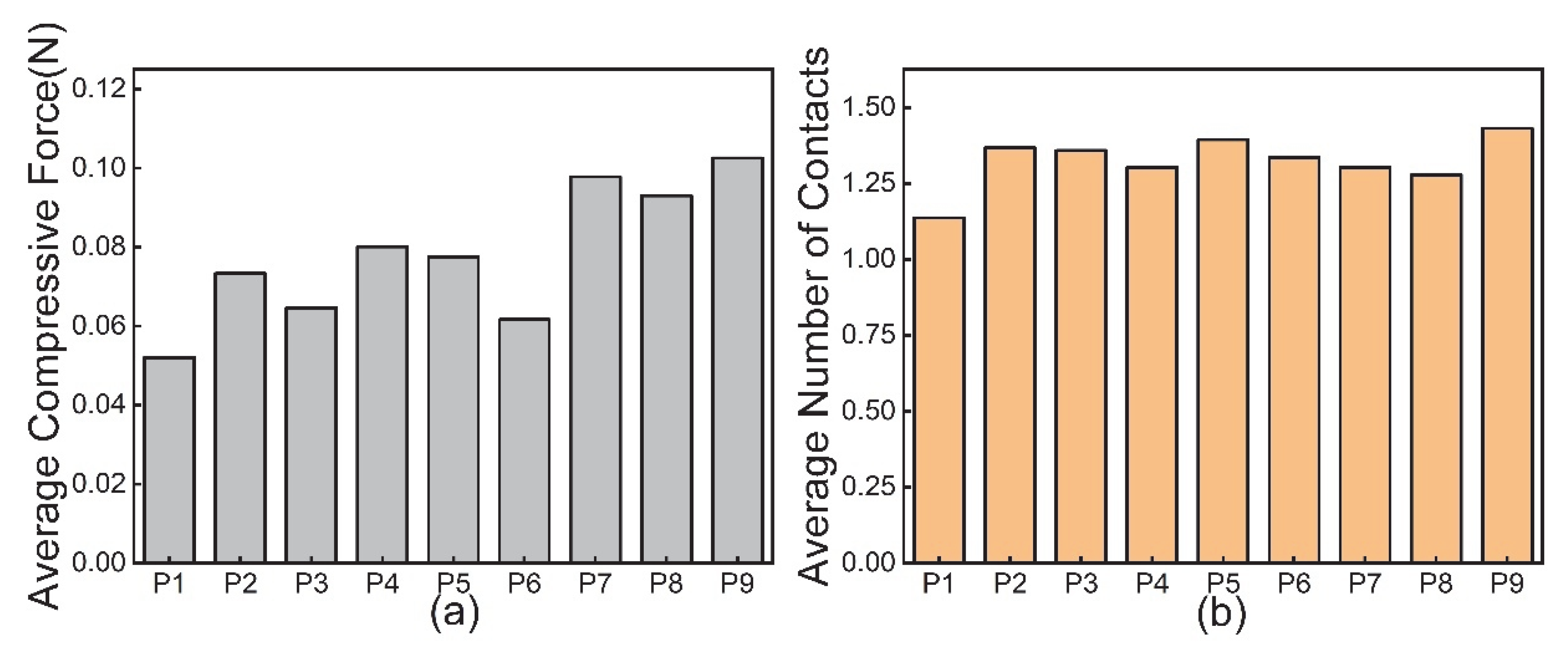
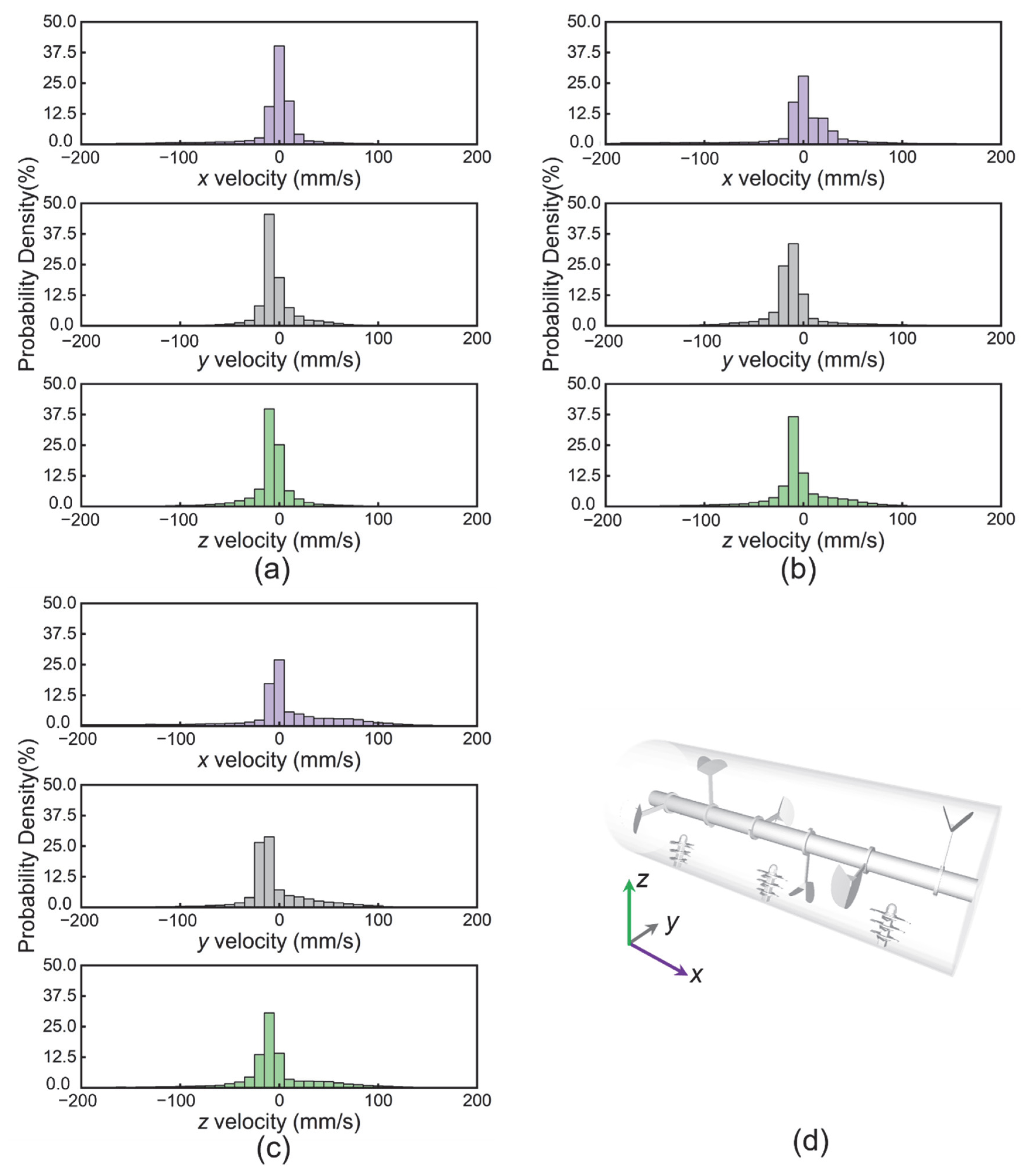
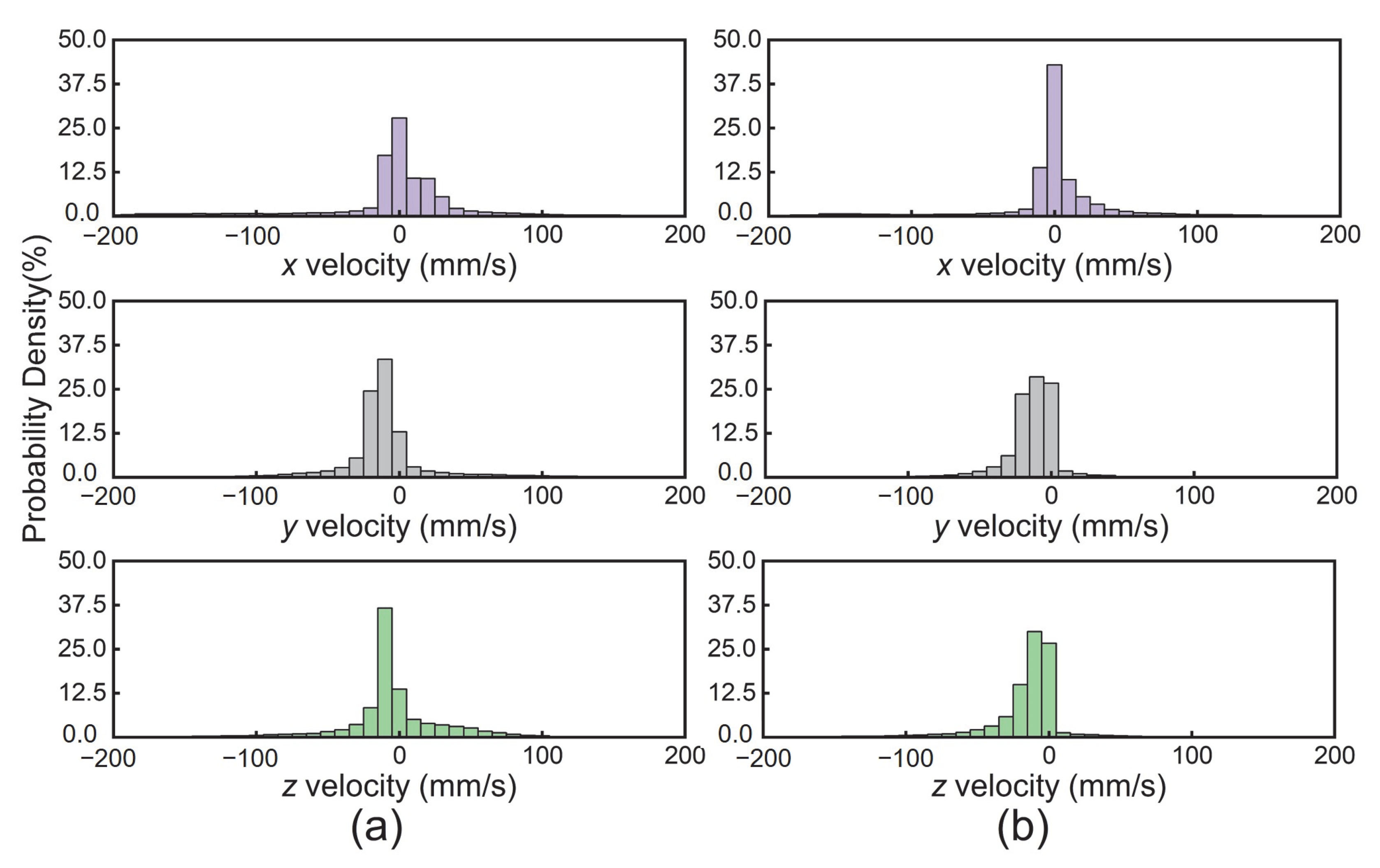
4.2. Effects of Particles’ Shape
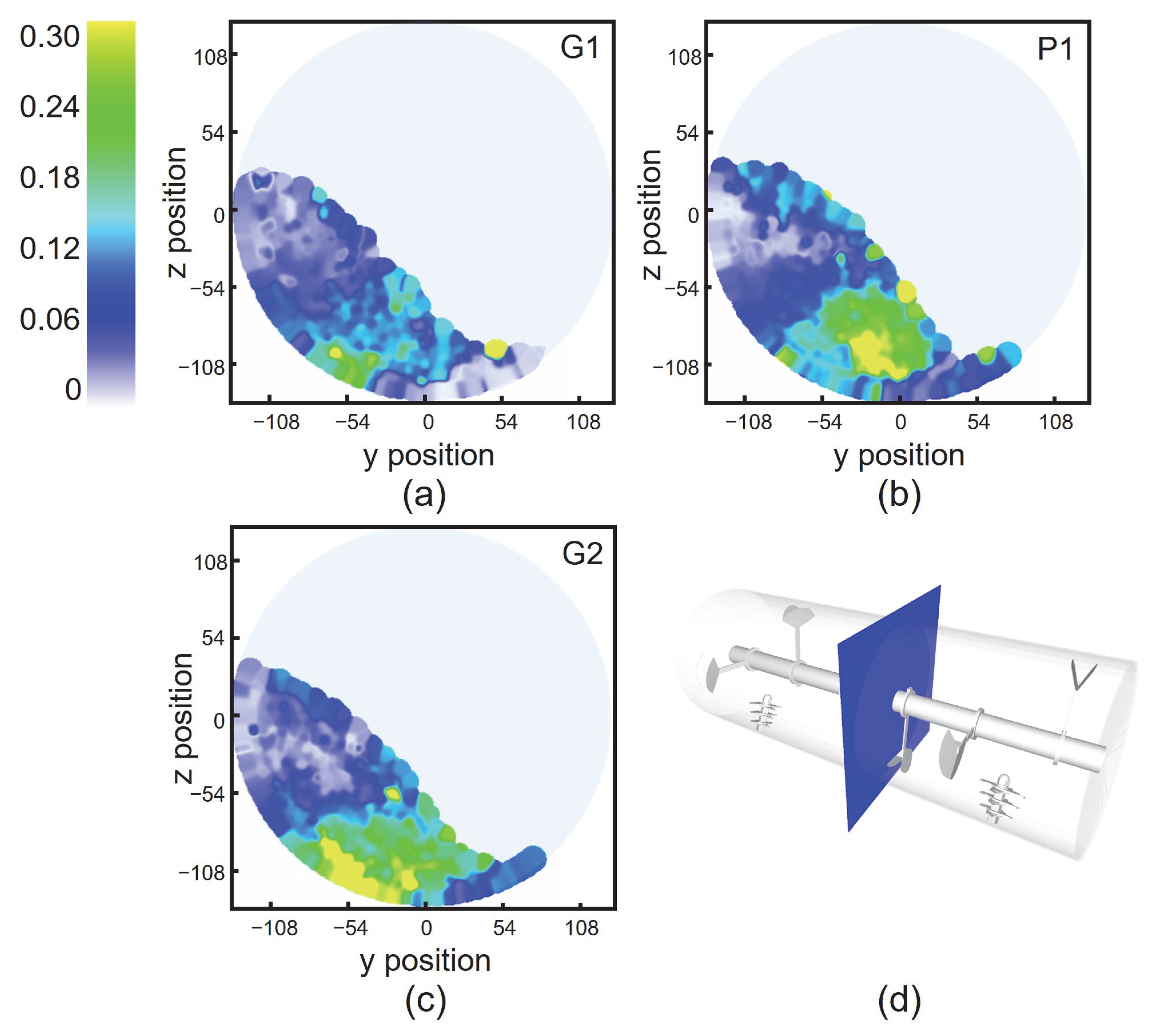
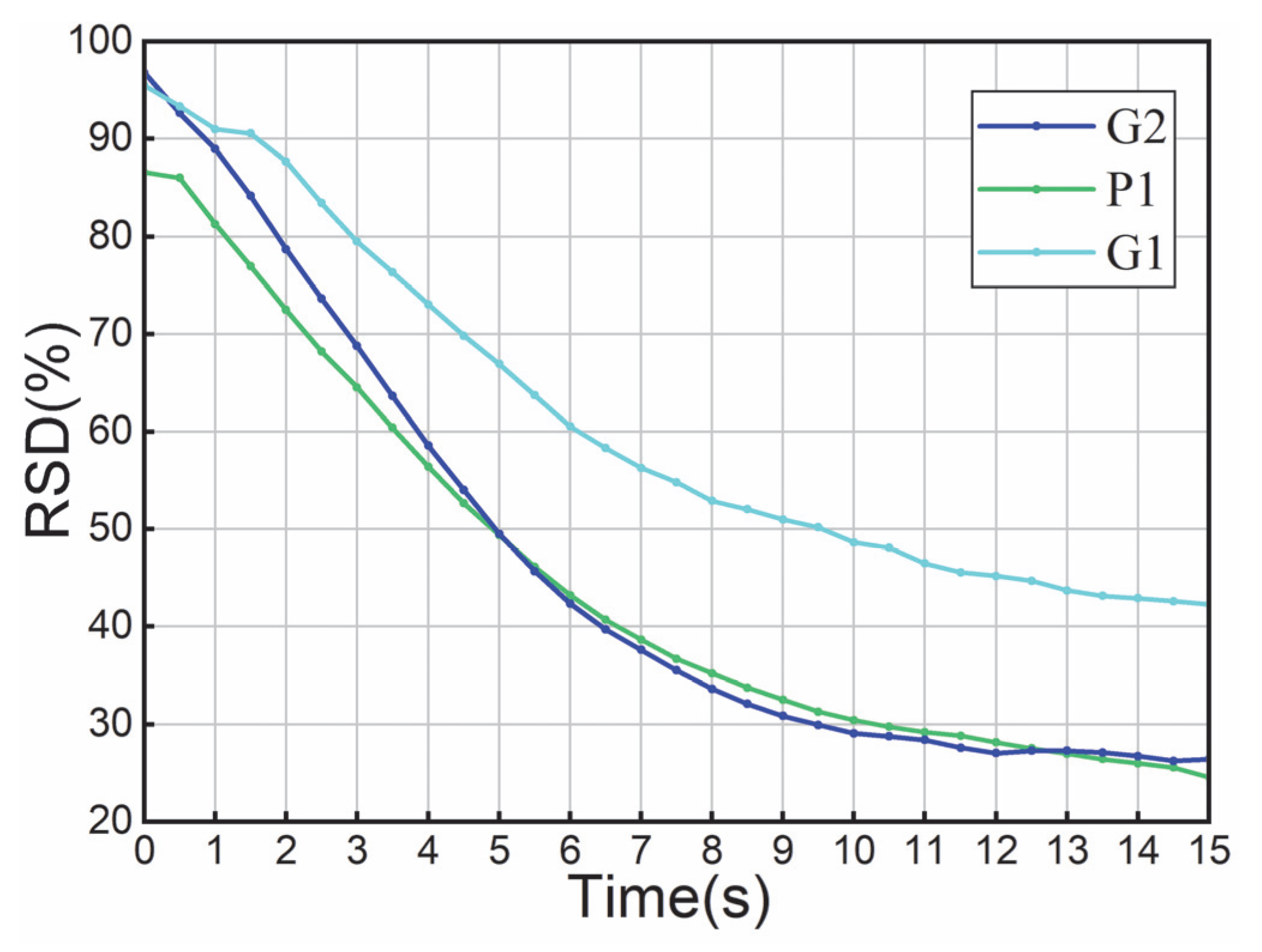
4.3. Effects of Geometry
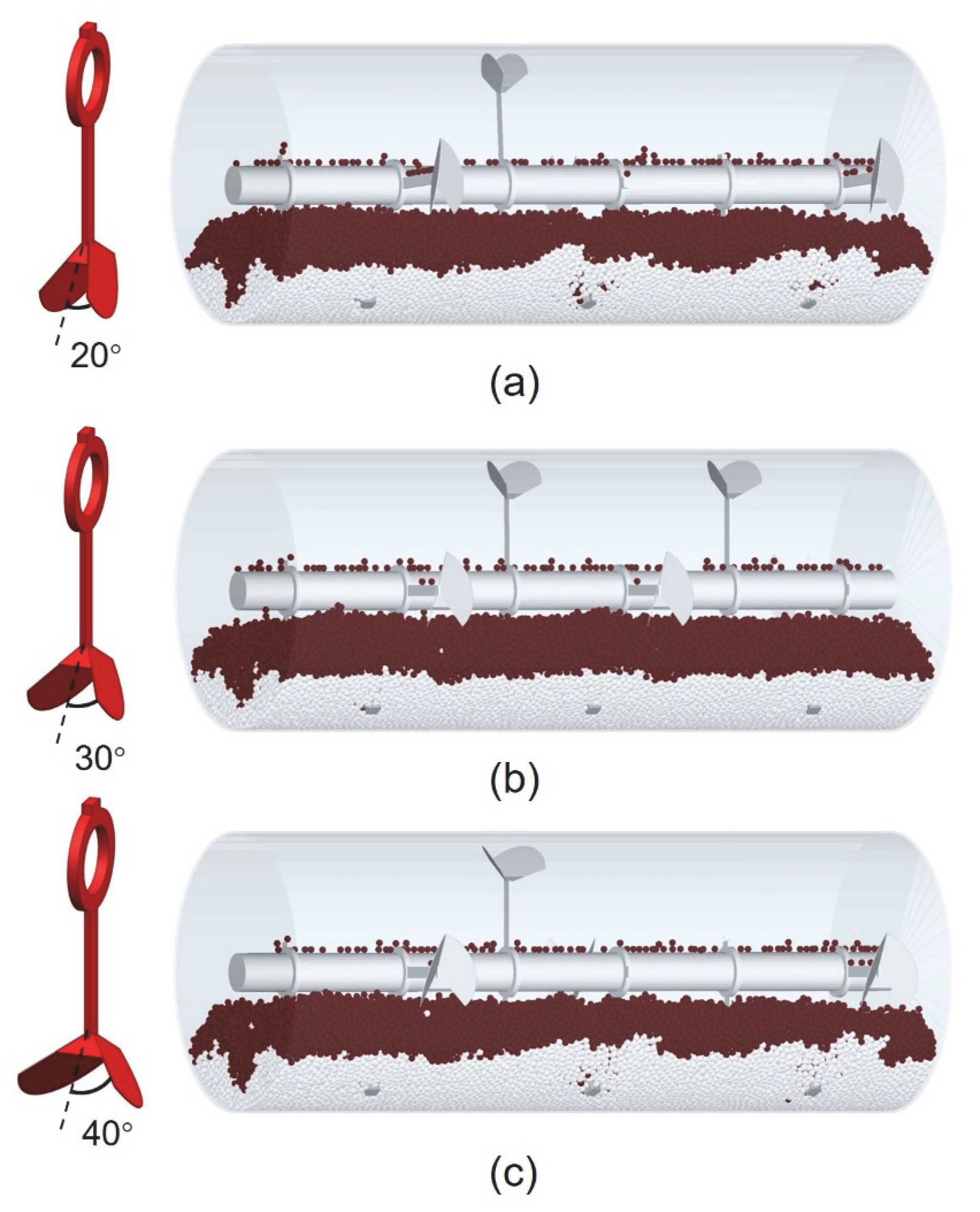
4.3.1. Effects of Plow Angle
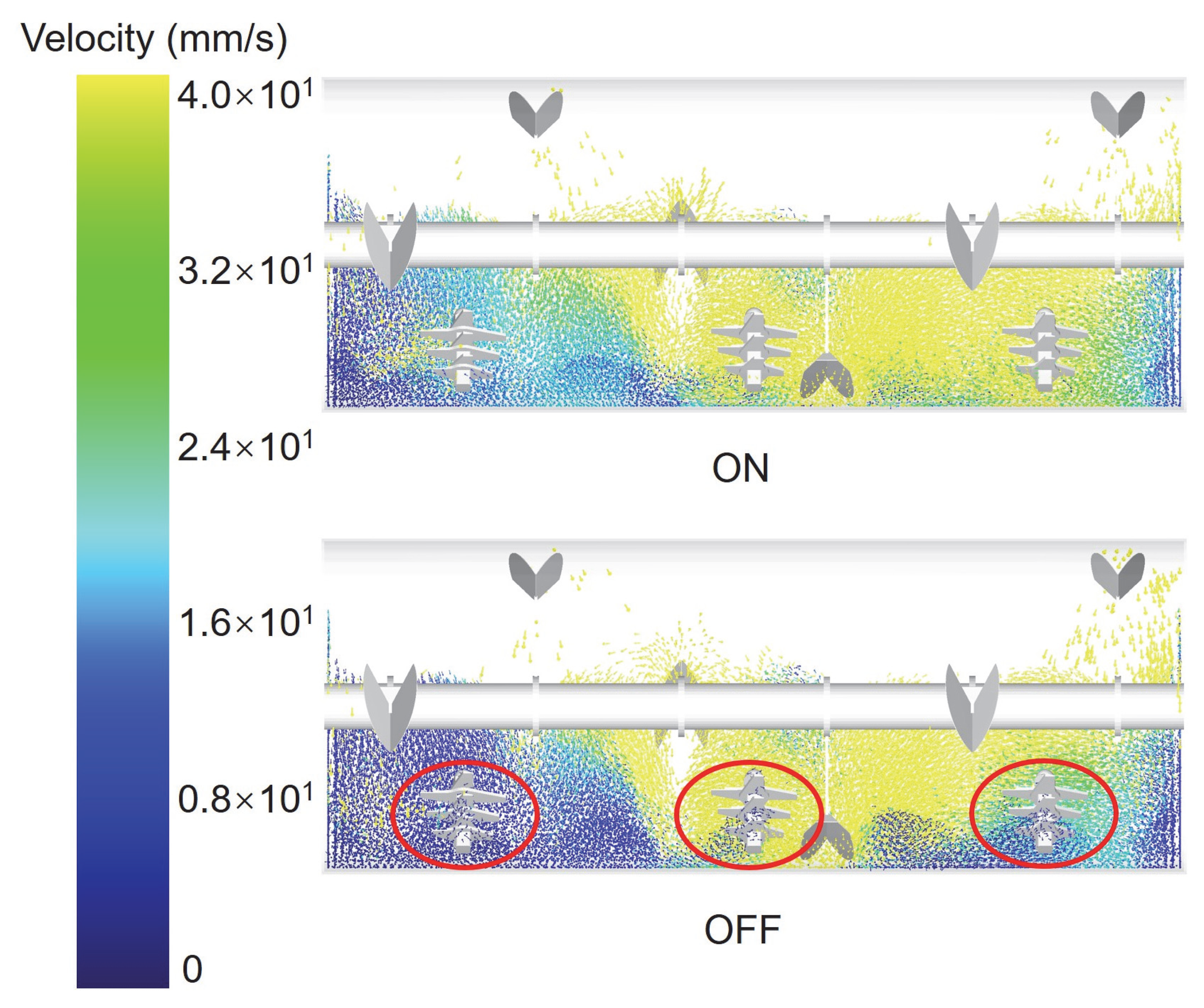
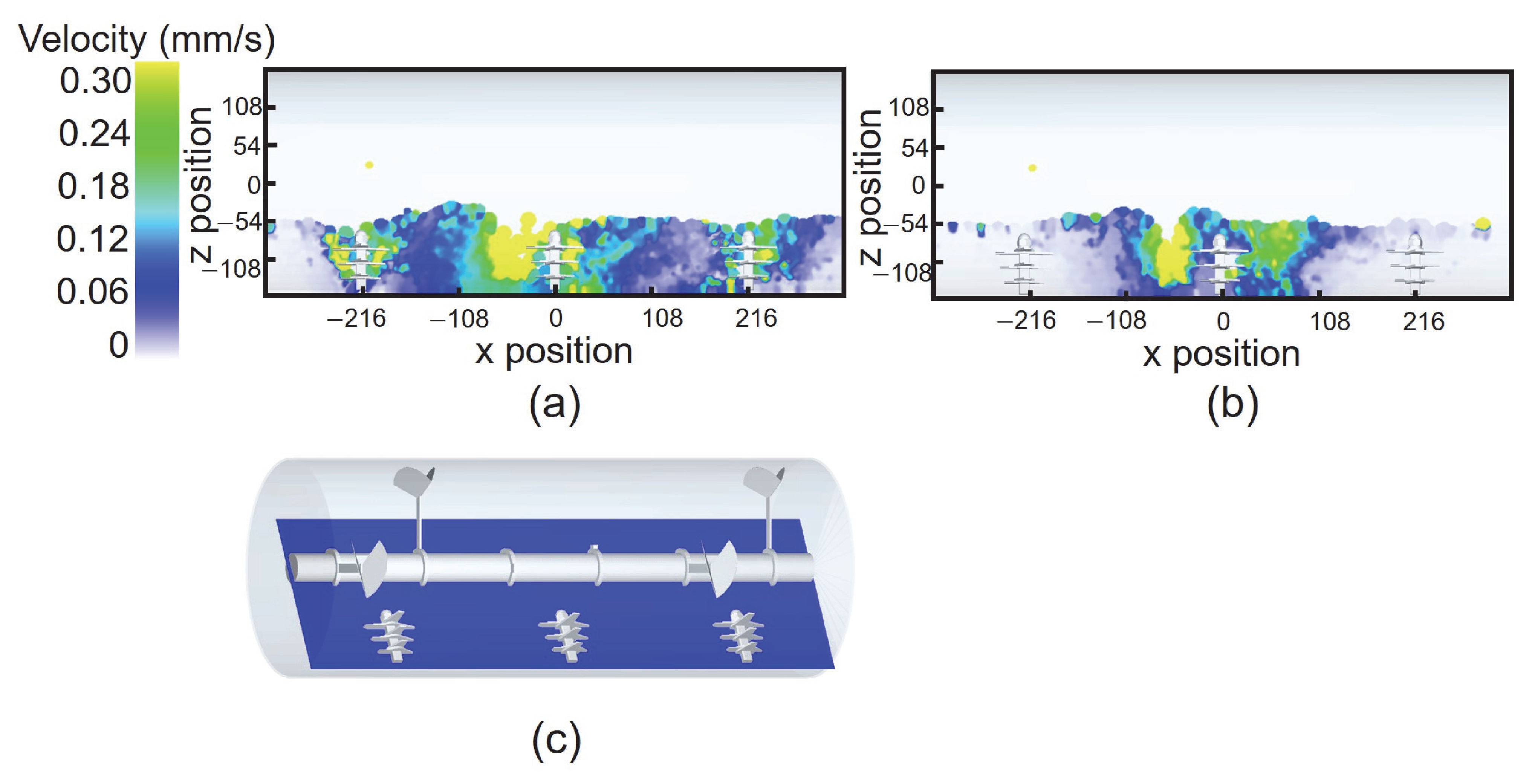
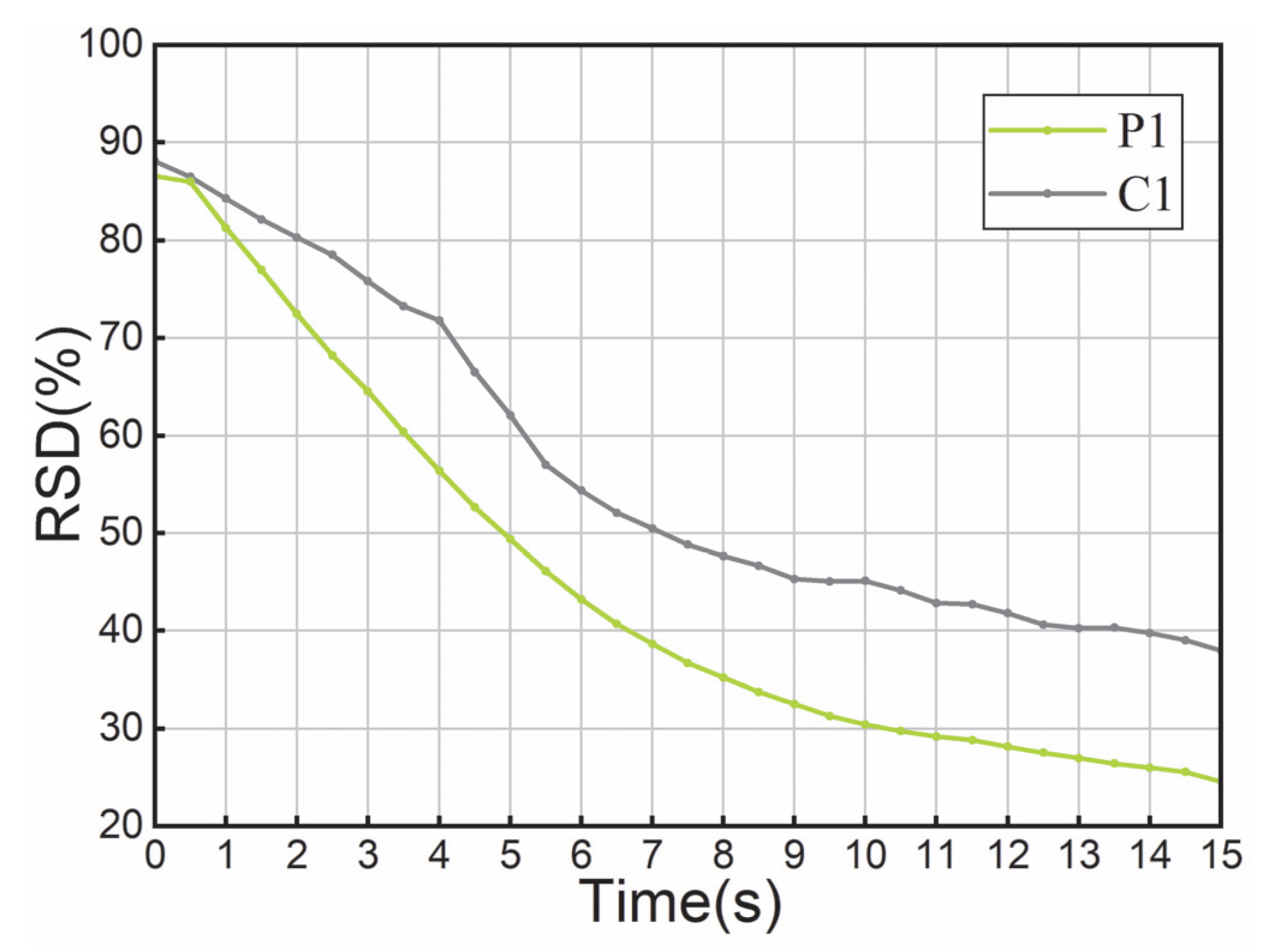
4.3.2. Effects of Chopper
5. Conclusions
- (1)
- To validate the feasibility of the superquadratic equation, a classic rotating drum model is used for parameter calibration. Comparisons with previous studies, both qualitatively and quantitatively, showed good agreement in the dynamic angle of repose.
- (2)
- The simulation results indicate that sharper particle shapes (rounded cubes and sharp-edged cubes) exhibit poorer mixing performance, while disc-shaped particles demonstrate better mixing than cylindrical ones. This is attributed to shape-induced differences in system resistance. Additionally, sharper shapes lead to a higher number of interparticle contacts and greater compressive forces, resulting in increased energy dissipation. Combined with stable mechanical interlocking, ultimately leads to inferior mixing performance. In actual mixing, sharper particles require more operating parameters, such as rotational speed, to enhance the mixing quality.
- (3)
- Increasing the plowshare angle enhances interlayer convection and axial diffusion of particles, further improving mixing efficiency. Excessively small plowshare angles may fail to achieve homogeneous mixing. The results show that optimizing the plow Angle can improve the mixing efficiency.
- (4)
- The auxiliary shearing effect of fly knives enables high-speed flow of particles in dead zones, strengthening convection and diffusion, which overcomes mixing dead zones between plowshares. The installation of the flying knife mechanism can effectively overcome the mixing dead zone.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jin, X.; Chandratilleke, G.R.; Wang, S.; Shen, Y.S. DEM investigation of mixing indices in a ribbon mixer. Particuology 2022, 60, 37–47. [Google Scholar] [CrossRef]
- Yang, W.J.; Neoh, K.G.; Kang, E.T.; Teo, S.L.M.; Rittschof, D. Polymer brush coatings for combating marine biofouling. Prog. Polym. Sci. 2014, 39, 1017–1042. [Google Scholar] [CrossRef]
- Chandratilleke, G.R.; Yu, A.B.; Bridgwater, J.; Shinohara, K. A particle-scale index in the quantification of mixing of particles. AIChE J. 2012, 58, 1099–1118. [Google Scholar] [CrossRef]
- Rhodes, M.J.; Wang, X.S.; Nguyen, M.; Stewart, P.; Liffman, K. Study of mixing in gas-fluidized beds using a DEM model. Chem. Eng. Sci. 2001, 56, 2859–2866. [Google Scholar] [CrossRef]
- Nadeem, H.; Subramaniam, S.; Nere, N.K.; Heindel, T.J. A particle scale mixing measurement method using a generalized nearest neighbor mixing index. Adv. Powder Technol. 2023, 34, 103933. [Google Scholar] [CrossRef]
- Fry, A.M.; Umbanhowar, P.B.; Ottino, J.M.; Lueptow, R.M. Diffusion, mixing, and segregation in confined granular flows. AIChE J. 2019, 65, 875–881. [Google Scholar] [CrossRef]
- Deng, X.L.; Zheng, K.; Davé, R.N. Discrete element method based analysis of mixing and collision dynamics in adhesive mixing process. Chem. Eng. Sci. 2018, 190, 220–231. [Google Scholar] [CrossRef]
- Fan, H.J.; Guo, D.C.; Dong, J.C.; Cui, X.; Zhang, M.C.; Zhang, Z.X. Discrete element method simulation of the mixing process of particles with and without cohesive interparticle forces in a fluidized bed. Powder Technol. 2018, 327, 223–231. [Google Scholar] [CrossRef]
- Escotet-Espinoza, M.S.; Foster, C.J.; Ierapetritou, M. Discrete Element Modeling (DEM) for mixing of cohesive solids in rotating cylinders. Powder Technol. 2018, 335, 124–136. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Wang, S.Q.; Liang, D.F.; Ji, S.Y. DEM study on mixing behaviors of concave-shaped particles in rotating drum based on level-set method. Powder Technol. 2023, 430, 118961. [Google Scholar] [CrossRef]
- You, Y.; Zhao, Y.Z. Discrete element modelling of ellipsoidal particles using super-ellipsoids and multi-spheres: A comparative study. Powder Technol. 2018, 331, 179–191. [Google Scholar] [CrossRef]
- Bao, Y.Y.; Li, T.C.; Wang, D.F.; Cai, Z.Q.; Gao, Z.M. Discrete element method study of effects of the impeller configuration and operating conditions on particle mixing in a cylindrical mixer. Particuology 2020, 49, 146–158. [Google Scholar] [CrossRef]
- Basinskas, G.; Sakai, M. Numerical study of the mixing efficiency of a ribbon mixer using the discrete element method. Powder Technol. 2016, 287, 380–394. [Google Scholar] [CrossRef]
- Hu, Z.; Liu, X.Y. A novel Markov chain method for predicting granular mixing process in rotary drums under different rotation speeds. Powder Technol. 2021, 386, 40–50. [Google Scholar] [CrossRef]
- Gui, N.; Yan, J.; Xu, W.K.; Ge, L.; Wu, D.L.; Ji, Z.L.; Gao, J.S.; Jiang, S.Y.; Yang, X.T. DEM simulation and analysis of particle mixing and heat conduction in a rotating drum. Chem. Eng. Sci. 2013, 97, 225–234. [Google Scholar] [CrossRef]
- Ma, H.Q.; Zhao, Y.Z. Modelling of the flow of ellipsoidal particles in a horizontal rotating drum based on DEM simulation. Chem. Eng. Sci. 2017, 172, 636–651. [Google Scholar] [CrossRef]
- Cleary, P.W. Large scale industrial DEM modelling. Eng. Comput. 2004, 21, 169–204. [Google Scholar] [CrossRef]
- Lin, J.M.; Bao, M.; Zhang, F.; Yang, J.H.; Li, H.Z. Mixing simulation of cohesive particles in a soil mixer. Powder Technol. 2022, 399, 117218. [Google Scholar] [CrossRef]
- Hoorijani, H.; Esgandari, B.; Zarghami, R.; Sotudeh-Gharebagh, R.; Mostoufi, N. Predictive modeling of mixing time for super-ellipsoid particles in a four-bladed mixer: A DEM-based approach. Powder Technol. 2023, 430, 119009. [Google Scholar] [CrossRef]
- Alian, M.; Ein-Mozaffari, F.; Upreti, S.R. Analysis of the mixing of solid particles in a plowshare mixer via discrete element method (DEM). Powder Technol. 2015, 274, 77–87. [Google Scholar] [CrossRef]
- Emmerink, J.; Hadi, A.; Jovanova, J.; Cleven, C.; Schott, D.L. Parametric Analysis of a Double Shaft, Batch-Type Paddle Mixer Using the Discrete Element Method (DEM). Processes 2023, 11, 738. [Google Scholar] [CrossRef]
- Jin, X.; Wang, S.; Shen, Y.S. DEM study of the effect of impeller design on mixing performance in a U-shape ribbon mixer. Adv. Powder Technol. 2022, 33, 103334. [Google Scholar] [CrossRef]
- Zhao, S.W.; Zhao, J.D. A poly-superquadratic-based approach on particle morphology for DEM modeling of granular media. Int. J. Numer. Anal. Met. 2019, 43, 2147–2169. [Google Scholar] [CrossRef]
- Wu, K.; Sun, W.C.; Liu, S.Y.; Cai, G.J. Influence of particle shape on the shear behavior of superquadratics by discrete element method in 3D. Adv. Powder Technol. 2021, 32, 4017–4029. [Google Scholar] [CrossRef]
- Laurent, B.F.C.; Bridgwater, J. Performance of single and six-bladed powder mixers. Chem. Eng. Sci. 2002, 57, 1695–1709. [Google Scholar] [CrossRef]
- Jones, J.R.; Parker, D.J.; Bridgwater, J. Axial mixing in a ploughshare mixer. Powder Technol. 2007, 178, 73–86. [Google Scholar] [CrossRef]
- Cleary, P.W. Particulate mixing in a plough share mixer using DEM with realistic shaped particles. Powder Technol. 2013, 248, 103–120. [Google Scholar] [CrossRef]
- Domian, E.; Cenkier, J. Flowability and Homogeneity of Food Powders with Plated Oil Ingredient. J. Food Process Eng. 2013, 36, 626–633. [Google Scholar] [CrossRef]
- Laurent, B.F.C. Scaling factors in granular flow—Analysis of experimental and simulations results. Chem. Eng. Sci. 2006, 61, 4138–4146. [Google Scholar] [CrossRef]
- Forrest, S.; Bridgwater, J.; Mort, P.R.; Litster, J.; Parker, D.J. Flow patterns in granulating systems. Powder Technol. 2003, 130, 91–96. [Google Scholar] [CrossRef]
- Fang, Z.Q.; Peng, S.L.; Yi, J.G.; Du, J. Structure optimization of plough blades in a ploughshare mixer using the DEM simulations. Eng. Comput. 2020, 37, 3455–3475. [Google Scholar] [CrossRef]
- Patil, A.V.; Hofsteenge, J.; Bujalski, J.M.; Johansen, S.T. DPM model segregation validation and scaling effect in a rotary drum. Comput. Part. Mech. 2022, 9, 693–707. [Google Scholar] [CrossRef]
- Wu, W.C.; Chen, K.C.; Tsotsas, E. Prediction of particle mixing in rotary drums by a DEM data-driven PSO-SVR model. Powder Technol. 2024, 434, 119365. [Google Scholar] [CrossRef]
- Lange, A.; Meitzner, C.; Specht, E.; Kruggel-Emden, H. Exploring transverse particle motion in rotary drums: DEM analysis of the influence of cross-shaped internals on material transport. Powder Technol. 2024, 443, 119907. [Google Scholar] [CrossRef]
- Jadidi, B.; Ebrahimi, M.; Ein-Mozaffari, F.; Lohi, A. Investigation of impacts of particle shape on mixing in a twin paddle blender using GPU-based DEM and experiments. Powder Technol. 2023, 417, 118259. [Google Scholar] [CrossRef]
- Jadidi, B.; Ebrahimi, M.; Ein-Mozaffari, F.; Lohi, A. A comprehensive review of the application of DEM in the investigation of batch solid mixers. Rev. Chem. Eng. 2023, 39, 729–764. [Google Scholar] [CrossRef]
- Jadidi, B.; Ebrahimi, M.; Ein-Mozaffari, F.; Lohi, A. Mixing performance analysis of non-cohesive particles in a double paddle blender using DEM and experiments. Powder Technol. 2022, 397, 117122. [Google Scholar] [CrossRef]
- Shi, Q.; Sakai, M. Recent progress on the discrete element method simulations for powder transport systems: A review. Adv. Powder Technol. 2022, 33, 103664. [Google Scholar] [CrossRef]
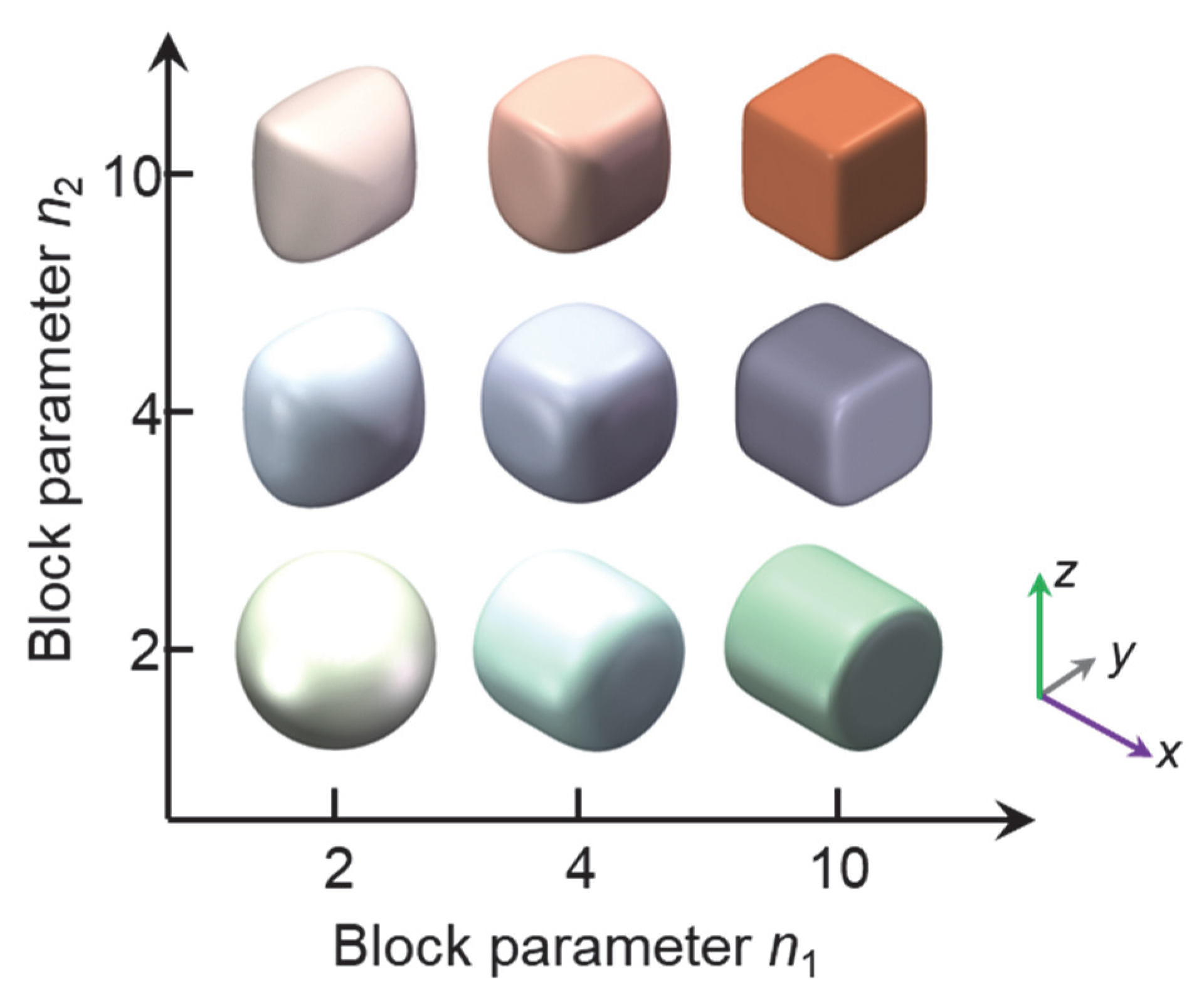



| Simulation | Particle | Geometry | |||||
|---|---|---|---|---|---|---|---|
| Shape | n1 | n2 | a/c | b/c | Plow Angle (°) | Chopper Motion | |
| P1 |  | 2 | 2 | 1 | 1 | 30 | ON |
| P2 |  | 4 | 2 | 1 | 1 | 30 | ON |
| P3 |  | 2 | 4 | 1 | 1 | 30 | ON |
| P4 |  | 4 | 4 | 1 | 1 | 30 | ON |
| P5 |  | 10 | 2 | 1 | 1 | 30 | ON |
| P6 |  | 2 | 10 | 1 | 1 | 30 | ON |
| P7 |  | 10 | 4 | 1 | 1 | 30 | ON |
| P8 |  | 4 | 10 | 1 | 1 | 30 | ON |
| P9 |  | 10 | 10 | 1 | 1 | 30 | ON |
| G1 |  | 2 | 2 | 1 | 1 | 20 | ON |
| G2 |  | 2 | 2 | 1 | 1 | 40 | ON |
| C1 |  | 2 | 2 | 1 | 1 | 30 | OFF |
| Time (s) | 5 | 10 | 15 | 20 |
|---|---|---|---|---|
| Results in Ref. [36] |  |  |  |  |
| Simulation in this paper |  |  |  |  |
| 40 RPM | Dynamic Angle of Repose (°) | 70 RPM | Dynamic Angle of Repose (°) | |
|---|---|---|---|---|
| Results in Ref. [36] |  | 47 |  | 50 |
| 48 | 51 | |||
| Simulation in this paper |  | 48.54 |  | 52.53 |
| Shape | Shape Index n1 | Shape Index n2 | Diffusion Coefficient | ||
|---|---|---|---|---|---|
| Dxx | Dyy | Dzz | |||
 | 2 | 2 | 2.35 × 10−4 | 2.83 × 10−4 | 5.45 × 10−5 |
 | 4 | 2 | 1.69 × 10−4 | 1.86 × 10−4 | 3.92 × 10−5 |
 | 2 | 4 | 1.79 × 10−4 | 1.89 × 10−4 | 4.20 × 10−5 |
 | 4 | 4 | 1.48 × 10−4 | 1.50 × 10−4 | 2.81 × 10−5 |
 | 10 | 2 | 1.59 × 10−4 | 1.49 × 10−4 | 2.80 × 10−5 |
 | 2 | 10 | 1.80 × 10−4 | 1.92 × 10−4 | 4.45 × 10−5 |
 | 10 | 4 | 1.45 × 10−4 | 1.03 × 10−4 | 1.27 × 10−5 |
 | 4 | 10 | 1.45 × 10−4 | 1.37 × 10−4 | 2.43 × 10−5 |
 | 10 | 10 | 1.54 × 10−4 | 8.38 × 10−5 | 5.06 × 10−6 |
| Particle Types | Particle Voidage Φ |
|---|---|
| P1 | 49.05% |
| P2 | 39.12% |
| P3 | 38.36% |
| P4 | 37.07% |
| P5 | 38.32% |
| P6 | 39.12% |
| P7 | 36.68% |
| P8 | 37.08% |
| P9 | 39.56% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luan, X.; Li, W.; Li, Y.; Zou, J. Investigation of Mixing of Solid Particles in a Plowshare Mixer Using Discrete Element Method (DEM). Modelling 2025, 6, 111. https://doi.org/10.3390/modelling6030111
Luan X, Li W, Li Y, Zou J. Investigation of Mixing of Solid Particles in a Plowshare Mixer Using Discrete Element Method (DEM). Modelling. 2025; 6(3):111. https://doi.org/10.3390/modelling6030111
Chicago/Turabian StyleLuan, Xi, Wenzhao Li, Yibo Li, and Junwei Zou. 2025. "Investigation of Mixing of Solid Particles in a Plowshare Mixer Using Discrete Element Method (DEM)" Modelling 6, no. 3: 111. https://doi.org/10.3390/modelling6030111
APA StyleLuan, X., Li, W., Li, Y., & Zou, J. (2025). Investigation of Mixing of Solid Particles in a Plowshare Mixer Using Discrete Element Method (DEM). Modelling, 6(3), 111. https://doi.org/10.3390/modelling6030111






