Abstract
In a carsharing organization, vehicle availability is considered as a measure of the quality of service. This paper presents a discrete event simulation model to evaluate the performance of round-trip (return to the same station) vs. one-way (return to any station) fleet management strategies used by carsharing organizations. The proposed model evaluates the customer rejection rate for each fleet management strategy and recommends the one with the least number of rejections. A customer request is deemed to be rejected when a vehicle cannot be made available to the user at the requested time and location. A case study for the carsharing organization Communauto in Montreal is conducted. The simulation results show that the one-way model has a greater request rejection rate of 13%, compared to 8% for the round-trip model. Therefore, a round-trip strategy is recommended to Communauto for managing its current fleet operations.
1. Introduction and Related Literature
The use of carsharing has been growing over the years. A carsharing organization (CSO) provides its members with shared-use vehicles for a short period of time, from a few hours to almost a day or a week. Once the member finishes their trip, the car is returned to the carsharing organization. If the vehicle is returned to the same station as it was picked up from, it is called a round trip. If it is returned to a different station than the one it was picked up from, then it is called a one-way trip. The member is billed at the end of each month for a specific fixed fee plus a mileage-based charge according to their individual usage or the distance traveled [1].
Despite the growing interest in carsharing systems, there remains a lack of comparative studies that evaluate round-trip and one-way models using simulation techniques. Most existing research focuses on optimization or analytical modeling, often overlooking the dynamic and stochastic nature of real-world operations. This study addresses this gap by applying discrete event simulation (DES), a method well-suited to modeling complex, time-dependent systems, to assess the operational performance of both models. Furthermore, this study is one of the few to focus on the Quebec context, providing localized insights that can inform policy and operational decisions for carsharing providers in similar urban environments.
Carsharing organizations are often faced with the problem of dynamic fleet management [2]. There are times when the demand from customers is not known until the last minute. Often customers do not return the vehicles on time, causing a vehicle availability problem for the next customer. The major dilemma for most CSOs is to decide which type of model to implement as part of their business model. The advantage of having a round-trip model is that there is no requirement for a vehicle relocation mechanism or an operator to make sure that the car returns to its original station. The disadvantage, however, is that the user does not have the flexibility to return the car to any station. In a one-way model, the customer has the flexibility of picking up and dropping off the car at different stations; however a vehicle relocation mechanism implemented by operators is required to bring the vehicle back to its original station, which adds to the fleet management costs. Studies show that the one-way model allows for more trips compared to the round-trip model, which is minimally used for trips with purposes such as shopping or leisure [3].Ferrero et al. [4] provide an annotated review of carsharing services.
Several researchers have addressed fleet management issues in the one-way model in recent years. The first category of models developed focus on operation planning in carsharing. Several studies have utilized discrete event simulation (DES) to model carsharing systems and analyze different operational strategies. These models typically assess the vehicle demand, service reliability, customer satisfaction, and fleet utilization, making them useful for understanding operational trade-offs and improving system design. D’Orso and Migliore [5] propose a methodology for designing one-way station-based carsharing services in a GIS environment for the city of Palermo. Wang et al. [6] simulate one-way electric carsharing systems using a multi-agent model. Huang et al. [7] perform a comparative study of operator-based and user-based methods for vehicle relocation in one-way station-based electric carsharing systems. Deng and Cardin [8] integrate operational decisions into the planning of one-way vehicle sharing systems under uncertainty. Barth and Todd [9] and Barth et al. [10] evaluate shared vehicle systems, particularly focusing on multiple-station systems and user behavior evaluation for intelligent shared electric vehicle (EV) systems. These studies consider factors like the vehicle distribution, user preferences, and operational constraints in optimizing fleet management. A significant portion of the literature on carsharing focuses on the simulation of operations and performance analysis.
The second category of models address vehicle relocation and fleet management. Vehicle relocation is a common challenge in carsharing systems, especially one-way systems. Effective strategies are crucial for ensuring vehicle availability in high-demand areas without incurring excessive operational costs. Illgen & Höck [11] and Eliyan and Kerbache [12] conducted literature reviews of the vehicle relocation problem in one-way carsharing networks. Iacobucci et al. [13] propose a multi-stage optimization approach to design relocation strategies in one-way carsharing systems with stackable cars. Wagner et al. [14] conduct data analytics for enabling user-based relocation of carsharing vehicles. Bruglieri et al. [15] and Carlier et al. [16] address relocation strategies for one-way electric vehicle sharing systems. They propose mathematical models and optimization frameworks to minimize the costs associated with vehicle relocation while ensuring service coverage. Nourinejad et al. [17] compare vehicle relocation and staff rebalancing strategies in one-way systems. Their findings suggest that a combination of vehicle relocation policies and staff management can significantly enhance operational efficiency. In this context, dynamic fleet management, including the use of feedback dynamic pricing [18], is considered an effective solution for balancing the fleet distribution in real time.
The third category of models are decision support and optimization models. Several studies in the literature focus on decision-making models to optimize the location of carsharing stations, vehicle assignment, and fleet sizing. Li et al. [19] perform optimization of the fleet, staff configuration, and operational strategies in one-way mixed-fleet carsharing systems using a Lagrangian relaxation-based approach. Liu et al. [20] study stochastic one-way carsharing systems with dynamic relocation incentives using preference learning. Giorgione et al. [21] propose an agent-based simulation approach for assessing two-way and one-way carsharing. Yang et al. [22] perform double-balanced relocation optimization of a one-way carsharing system with real-time requests. Boyaci et al. [23] present an optimization framework to develop efficient one-way carsharing systems, accounting for vehicle allocation, the station location, and the user demand. These decision support systems help to improve the effectiveness of carsharing services by ensuring that the location of stations and the size of the fleet are aligned with actual demand patterns. Alfian et al. [24] perform a comparison of reservation-based and instant-access one-way carsharing services through discrete event simulation. Nourinejad and Roorda [25] compared one-way vs. two-way operational policies for carsharing operations using integer programming. Bruglieri et al. [15] propose a mixed-integer programming approach for addressing the electric vehicle relocation problem in one-way carsharing systems. Barrios and Rodier [26] propose a simulation for fleet sizing of flexible carsharing systems. Clemente et al. [27] address the vehicle relocation problem in carsharing systems using petrinets. The development of a dynamic discrete stochastic simulation model for evaluation of one-way versus round-trip carsharing systems has been reported by Yoon and Lee [28]. Di Febbraro et al. [29] developed a discrete event simulation model for a user-based vehicle relocation policy for a one-way carsharing system. Awasthi et al. [30] propose a multi-criteria decision-making approach to select locations for carsharing stations, considering factors like accessibility, the demand, and the environmental impact. Awasthi and Chauhan [31] apply an Analytical Hierarchy Process (AHP) to the selection of locations for carsharing stations in medium-sized cities, providing a systematic method to weigh various criteria for optimal station placement. Nakayama et al. [32] propose a genetic algorithm-based approach for optimal management of carsharing vehicles in a one-way system. It can be seen that optimization and simulation techniques are popularly used techniques to address the vehicle relocation problem.
The fourth category of models are dedicated to assessment of the environmental and financial impacts of carsharing services. Carsharing systems are often promoted as a sustainable alternative to traditional car ownership, with the potential to reduce traffic congestion and CO2 emissions. Several studies focus on evaluating the environmental and financial impacts of these systems. Vasconcelos et al. [33] investigate the environmental and financial impacts of adopting alternative vehicle technologies and relocation strategies in station-based one-way carsharing for the city of Lisbon, Portugal. El Fassi et al. [34] evaluate growth strategies for carsharing networks using discrete event simulation, considering the financial and environmental implications of network expansion. Their study suggests that the integration of electric vehicles in carsharing networks can further reduce their environmental footprints. While the environmental benefits of carsharing are generally well-recognized, there is a need for deeper studies to quantify these impacts more accurately and evaluate the cost-effectiveness of different models. Shaheen et al. [35] discuss the environmental benefits of carsharing, including reduced vehicle ownership and a corresponding decrease in urban traffic congestion and pollution.
The fifth category of models is dedicated to investigating user behavior and system adoption. Understanding user behavior and system adoption is critical for designing carsharing systems that meet customers’ needs while ensuring high system efficiency. Guo and Hou [36] investigate rebalancing of one-way carsharing systems, considering the elastic demand and waiting time. Wang and Liao [37] perform analysis of first-come-first-served mechanisms in one-way carsharing services. Huang et al. [38] solve the station-based one-way carsharing network planning problem using relocations and non-linear demand. Yoon and Lee [28] explore an operation model for carsharing services using simulation, focusing on user behavior and the demand for vehicles. The study investigates factors that influence customer preferences, including the vehicle availability, service time, and pricing. de Lorimier and El-Geneidy [39] study factors affecting vehicle usage and availability in round-trip systems using regression analysis. Morency et al. [40] study a typology of carsharing users in round-trip systems using cluster analysis. Ciari et al. [41] perform estimation of the carsharing demand using activity-based simulation for round-trip systems. Zheng et al. [42] conduct regression analysis to estimate the size of the carsharing market. Catalano et al. [43] perform estimation of the demand for carsharing using a random utility model. Barth et al. [44] examine user-based vehicle relocation techniques, analyzing the impact of user behavior on the effectiveness of vehicle relocation strategies in shared-use vehicle systems. The adoption of carsharing systems can be influenced by various factors, including pricing, availability, user experiences, and social attitudes towards shared mobility. Further research into user incentives, trust-building strategies, and behavioral economics could provide valuable insights into the system adoption rates and overall user satisfaction.
The sixth category of models address fleet sizing and pricing strategies. The issue of fleet sizing is central to carsharing systems’ performance. The literature suggests that the fleet size needs to be optimized to balance the demand with the operational costs. Fantola et al. [45] perform a profitability comparison between a “one-way” carsharing service and a “modified one-way” carsharing service. Repoux et al. [46] investigate fleet sizing and optimization using simulation and optimization models. They focus on one-way systems and investigate how different fleet sizes can affect the service quality and operational costs. Bianchessi et al. [18] propose a feedback dynamic pricing approach to optimize fleet balancing, which is particularly useful for managing demand fluctuations and reducing operational inefficiencies. The integration of dynamic pricing models and feedback systems in fleet management can enhance flexibility and scalability, improving the overall system performance.
The objective of this paper to evaluate one-way vs. round-trip business models for carsharing fleet management operations using discrete event simulation. In the literature, although vehicle relocation operations in one-way or round-trip systems have been investigated by several researchers, studies on comparative evaluation of one-way vs. round-trip systems are very few. In addition, studies conducted in the context of Quebec are limited. These are the challenges we are addressing in this paper.
The rest of this paper is organized as follows. Section 2 presents the discrete event simulation approach. Section 3 presents the case study of Communauto, Montreal, followed by a discussion of the results, findings, and recommendations in Section 4. Section 5 provides the conclusions and suggestions for future work.
2. Discrete Event Simulation Approach
The objective of this study is to develop a simulation model to evaluate one-way vs. round-trip (or two-way) business models of carsharing to facilitate fleet management operations. A discrete event simulation model is proposed and modeled using Arena™ (www.arenasimulation.com). Arena is a discrete event simulation and automation software platform developed by Systems Modeling and acquired by Rockwell Automation in 2000. It uses the SIMAN processor and simulation language. The user builds an experiment model through the placement of modules (boxes of different shapes) that represent processes or logic. Connector lines join these modules and specify the flow of entities. Statistical data, such as the entities in, entities out, system utilization, cycle time, and WIP (work-in-process) levels, can be recorded and generated as output reports. Arena is widely used in academia and industry for modeling various complex, real-life discrete event simulation problems.
The following assumptions are made in our simulation model.
2.1. Assumptions
- The requests arrive at a constant rate of 400 requests per hour (based on Communauto data) up to a total of 4263 requests.
- The station allocation for the requests is randomly generated.
- The customer does not wait more than 15 min at a station for a car. If the customer does not get the car within 15 min, the request is canceled and that order counts as a rejection at that particular station.
- All the cars are available and free at the start and the end of the simulation.
- Trip extensions and car breakdowns have not been taken into consideration. The actual percentage of trips during which breakdowns occurred, which was confirmed with Communauto, was very minimal.
- The parking space in the one-way model is assumed to be flexible. In other words, users have no trouble finding a parking place near their destination.
- The trip duration is assumed to be normally distributed with a mean reservation length of 7.86 h. The minimum and maximum durations of a reservation for the year 2024 were 6.436 h (November) and 10.86 h (July), respectively.
- All the vehicles are assumed to be of same size and automatic and carry the same number of passengers (or have the same capacity).
- At the start of the simulation, all the vehicles are available and parked at various stations. This is ensured in order to set the same initial conditions for the one-way and round-trip policies when testing the return of vehicles.
The assumptions used in this simulation model are grounded in real operational data obtained from Communauto for the year 2011, combined with standard practices in discrete event simulation. Specifically, the original request arrival rate of 48.55 requests per hour was calculated from the 2011 dataset comprising 419,507 annual reservations. To improve the relevance of the model to the current operational conditions, this baseline was proportionally scaled using Communauto’s projected figures for 2024. Based on a projected annual reservation volume of 3,500,000, the updated arrival rate was estimated at approximately 400 requests per hour. This 2024-adjusted rate was used as the arrival parameter in the simulation to reflect the expected future demand and evaluate the system performance under modern usage conditions.
The 15 min maximum wait time reflects a realistic customer tolerance threshold, as confirmed by Communauto experts. The assumption of flexible parking in the one-way model was made to isolate the impact of vehicle relocation without introducing parking constraints. While these assumptions help streamline the model and focus on key operational variables, they may limit the generalizability of the results to other settings with different demand levels, vehicle types, or urban layouts.
To address this, we extended the original dataset by applying a projection formula to the 2011 data and incorporating publicly available insights from Communauto’s website. This approach allowed us to simulate more contemporary operational conditions while preserving consistency in the overall model structure.
In this study, the same average trip duration of 7.86 h was applied to both the round-trip and one-way models. While we acknowledge that the real-world demand fluctuates throughout the day and across seasons, incorporating time-dependent arrival rates was beyond the scope of this study. Future work could integrate peak and off-peak demand patterns to better reflect the temporal variability in customer behavior.
2.2. Discrete Event Simulation (DES) Model
2.2.1. Process Map
Figure 1 presents the conceptual model (process map) used for developing the DES model. It explains how carsharing works. A customer can book cars by making online or phone requests. The system checks for the nearest available car upon receiving the request. If there is a car available at a nearby station, then the booking is confirmed for the requested time period and the vehicle pickup details are sent to the customer. Upon completion of the trip, the vehicle is returned to the same station (round trip) or any of the carsharing operator’s stations (one-way).
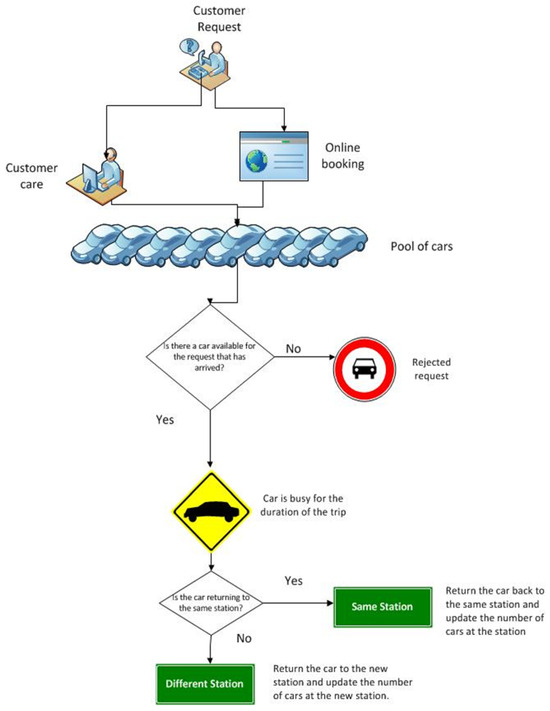
Figure 1.
Process map.
2.2.2. DES Algorithm
Figure 2 presents the DES algorithm based on the process map for the system (Figure 1). It defines the various entities and events in the DES model. The car entities are first generated all together. They read their pickup station or origin from an input table. Once the car entities are assigned their specific origin, they go to the respective station and wait for an incoming request entity. The request entity is generated and is assigned the origin and destination attributes which are provided as inputs to the DES model. The input file for the round-trip model would be different from the one that is used for the one-way model. However, the file with the origin data for the car entity would remain the same in both the models. The generated request entities are recorded. Once the request entity is matched with a car entity, they are batched together. The batched entities are then delayed for the duration of the trip. Upon trip completion, the entities are split based on their original entity types, which separates the request entity and the car entity. The destination of the request entity is saved into a variable. The car entity is delayed for some time; this is performed so that the destination of the request entity is first saved into the variable and then is assigned as the new origin for the car entity. The new origin of the car entity is recorded. The car entity is then sent back to the set of stations, where it waits to be matched with a request entity.
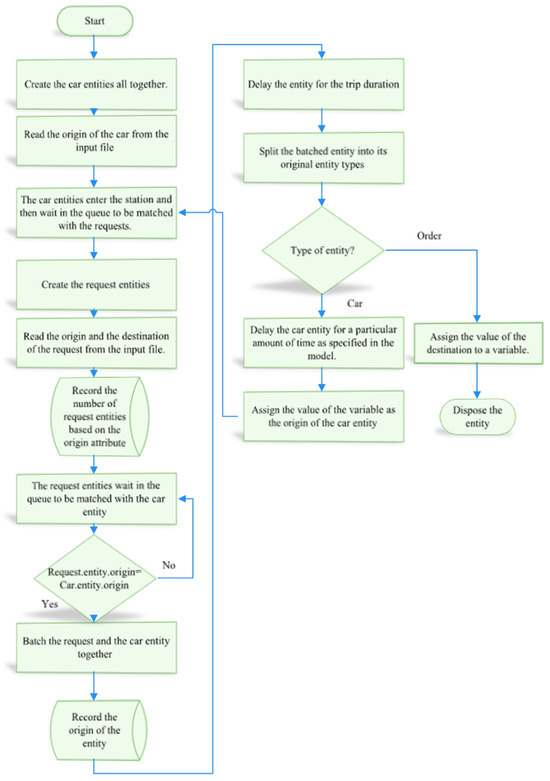
Figure 2.
Flowchart for the DES algorithm.
2.3. Model Development in Arena
Using the process map and the DES algorithm, the discrete event simulation model was developed in Arena. It consists of four modules: the request generation module (Figure 3a), the car generation module (Figure 3b), the request rejection module (Figure 3c), and the main module (Figure 3d). The request generation module generates request entities. The car generation module creates the car entity. The main module block matches the car entities and the request entities. The request rejection module checks and records the number of requests that are being rejected at the various stations.
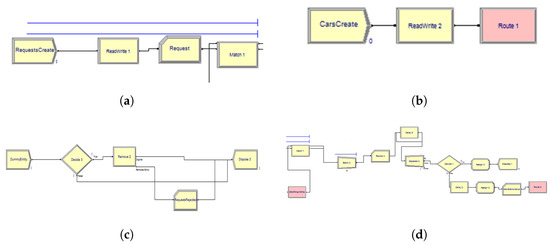
Figure 3.
Overview of simulation modules. (a) Request generation. (b) Car creation. (c) Request rejection. (d) Main module.
In the simulation, the trip duration is modeled as a normally distributed variable with a mean of 7.86 h and a standard deviation of 1.2 h, based on synthetic reservation data generated for the year 2024. To ensure realism and avoid negative or implausibly short trip durations, a lower-bound constraint was implemented in the simulation. Specifically, any generated value below a minimum threshold (e.g., 1 h) was either truncated or resampled. This method preserved the intended variability in the trip durations while guaranteeing that all the simulated values remained meaningful within the operational context.
2.4. Model Verification and Validation
Model verification is performed in order to ensure that the model is producing the right results, while model validation is performed to ensure that the right method is used. For verification, the expected and observed results (number of request arrivals, number of cars at the stations) were matched to determine their closeness. The closer the values, the better the model. Two types of validation were used in our study—a parameter variability sensitivity analysis and face validity analysis. The parameter variability sensitivity analysis investigated the impact of a change in the modeling parameters on the stability of the final results, whereas the face validity analysis involved the use of experts. Three experts from Communauto were involved in the face validity analysis, namely the Operations Manager, Business Development Manager, and a Finance representative. These experts looked at the simulation model results and assessed whether they matched data obtained in practice, thereby validating the theoretical (simulation) results.
3. Case Study of Communauto, Montreal (QC), Canada
Communauto is a privately owned carsharing organization founded in the city of Quebec in 1994 which merged with its competitor, Auto-com, in 2000. Since then, Communauto has expanded its activities across a large portion of the Quebec province by servicing four different agglomerations: Quebec, Montreal, Gatineau, and Sherbrooke. By May 2012, Communauto had a total of 36000 members, 883 vehicles, and 330 stations. A network map of the 330 Communauto stations across the city of Montreal is shown in Figure 4 below.
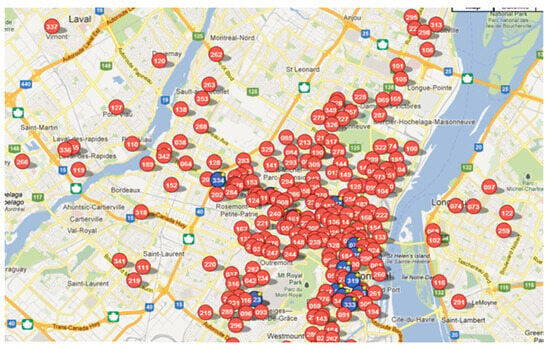
Figure 4.
Network map of Communauto stations across city of Montreal.
Communauto uses a round-trip policy for the return of its vehicles. This solves the problem of vehicle relocations for them. Recently, Communauto has also started providing a free-floating service where users can leave cars at any of the designated stations in their service area. In this paper, Communauto is interested in evaluating the impact of a one-way carsharing system on user request fulfillment.
3.1. Data Collection
This study primarily utilized real operational data from Communauto for the year 2011. However, to evaluate fleet management strategies under more current conditions, we also generated a synthetic dataset representing the year 2024. This dataset was created using a projection formula based on historical trends and supplemented with publicly available information from Communauto’s official website ([47]). This approach allowed us to simulate contemporary demand patterns while maintaining consistency within the model framework. The data obtained from Communauto included the total number of requests per month and the average number of hours per reservation per month (i.e., the duration or length of the reservation). Figure 5 compares key operational indicators between the years 2011 and 2024, including the number of cars in the fleet, total annual reservations, and average request rate per minute.
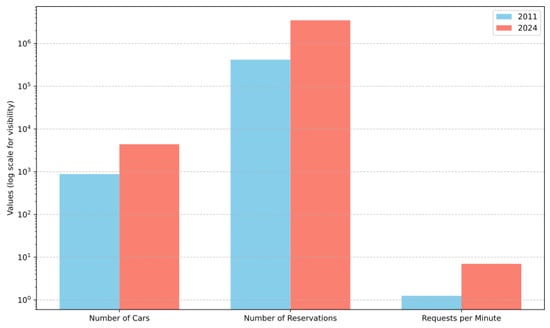
Figure 5.
Comparison of core operational indicators for Communauto carsharing system in 2011 and projected values for 2024.
The average trip duration of 7.86 h was derived from synthetic reservation data generated for 2024 to reflect the expected user behavior and operational patterns. Notably, this average aligns closely with historical reservation data from 2011, reinforcing the plausibility of our synthetic assumptions. While we recognize that the trip durations may vary by the station location, time of day (e.g., morning vs. evening), user profile, and even season (e.g., summer tourism peaks), we opted to use a single average value in the simulation model. This simplification was necessary due to data limitations and was used to maintain the model clarity and ensure consistency in the evaluation of fleet management strategies. Using a uniform trip duration allowed for a controlled comparison of key performance indicators such as the rejection rates and vehicle utilization, without introducing additional variability that could obscure the strategic differences between the one-way and round-trip systems. We acknowledge that incorporating location-specific, time-dependent, or seasonal variation would improve the realism, and we propose this as a direction for future research, particularly if real-time or historical demand data becomes available.
Figure 6 indicates that the demand is distributed throughout the year, with notable peaks in May, October, and December, each exceeding 315,000 reservations. These peak months align with expected increases in mobility needs during the spring and year-end periods. Other important data in the DES model include the total number of vehicles, which was 4400 (calculated as the sum of the cars present at each station), and the average number of rental hours per reservation, which was 7.86 h.
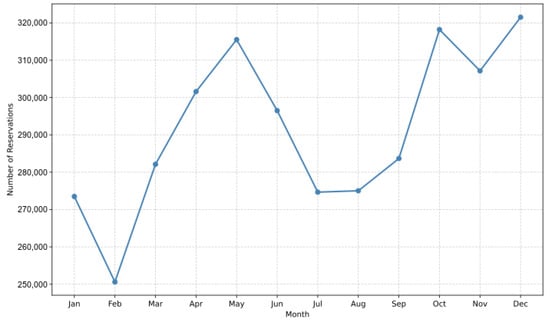
Figure 6.
Forecasted monthly reservations for Communauto in 2024.
3.2. Synthetic Data Projection Using Exponential and Poisson Models
While recent carsharing data specific to Communauto was unavailable, prior studies (e.g., that by Alencar et al. [48]) have demonstrated the use of systematic demand forecasting and simulation modeling in carsharing contexts. These methods supported the use of CAGR-based exponential projections and Poisson-based arrival rate scaling to generate defensible synthetic 2024 data. The current study employed Poisson-process-based modeling for simulating customer arrival events, a well-established method in carsharing simulation frameworks. For instance, Deng and Pantuso [49] model the customer arrival times as a Poisson-distributed variable in a round-trip carsharing context to identify optimal pricing strategies under uncertainty. Similarly, in a Q1 journal, Zhong et al. [50] apply stochastic modeling techniques to estimate the spatiotemporal demand rates in free-floating carsharing systems, demonstrating methodological rigor and forecasting accuracy. These studies provide strong support for the use of Poisson-based arrival scaling in forecasting and simulation modeling of the shared mobility demand.
To evaluate the proposed system under realistic future conditions, this study adopted exponential growth modeling and Poisson-based arrival rate scaling to project synthetic data for the year 2024, using 2011 Communauto operational data as a baseline. The exponential growth formula, , where is the future value, is the base value, r is the annual growth rate, and t is the number of years, enabled scalable estimation of key indicators such as the reservations and fleet size. This formulation was selected because it reflects the compounding nature of adoption and growth in shared mobility systems, as supported by the Q1 literature on sustainable transportation. The annual growth rate r was derived using the compound annual growth rate (CAGR) formula, , which is widely used to back-calculate consistent annual trends from known historical and projected values.
Based on the projected growth in the annual reservations—from 419,507 in 2011 to 3.5 million in 2024—the estimated CAGR was approximately 17.18%. This rate was applied to scale the reservation demand and related input variables. Additionally, customer arrivals were modeled in the simulation using a Poisson process, commonly employed in discrete event simulation to represent stochastic arrival patterns. To reflect the increased system usage in 2024, the Poisson rate parameter , representing the average number of requests per minute, was scaled using the ratio of the total reservations across the years:
Using the base rate of 1.25 requests/minute in 2011 and the known reservation growth factor of approximately 8.34, the projected request rate for 2024 was calculated to be 10.43 requests/minute. A conservative value of seven requests/minute was ultimately selected to account for operational variability and to avoid oversaturation while still maintaining a realistic high-demand simulation scenario.
Assuming a consistent compound annual growth rate (CAGR) of 17.18%—the same rate of growth as that observed in the reservation volume—the number of carsharing stations was projected to have increased from 273 in 2011 to approximately 2104 by 2024. This projection was made using the formula
which supported scalability analysis in terms of the infrastructure and operational coverage.
3.3. Identifying Probability Distribution
The arrival rate was approximated as being constant over a period of time. The steps used in approximation involved modeling the arrivals over a time period, say, [0, T], dividing the period [0, T] into k equal intervals of the length , and determining the estimated arrival rate during the time period, , to be the average number of arrivals over the length of the time interval (Banks et al. [51]), , where n represents the period of observations and the number of arrivals that occurred during the time interval in the period of observation. Based on the projected annual reservation volume of 3,500,000 requests in 2024, the average number of reservations per month was approximately 291,667. When further divided, this corresponded to an estimated 9589 requests per day, 399.5 requests per hour, or 6.66 requests per minute. Hence, a constant arrival rate of approximately seven requests per minute was used in the simulation model to reflect realistic future demand conditions. The data on the total number of requests at each station was generated at random using the RANDBETWEEN function in Excel. Since we used a simple random sampling technique, the Cochran technique [52] was used for determining the sample size. To determine the sample size, we used the formula , where n = 4263, assuming a 95% confidence interval (critical z value = 1.96), p = q = 0.5 is an estimate of the variance, the population size was N = 3.5 million for the year 2024, and d = 0.015 is the acceptable margin of error. The data on the total number of cars present at each station in the model was provided by Communauto.
3.4. Output Results
The DES model was run for a total of 200 h. The output data consisted of the number of requests per station, the number of accepted requests, the number of rejections per station, the total number of cars present at each station at the start of the simulation, the number of cars present at each station at the end of the simulation, the total acceptance ratio, the utilization ratio of each station, and finally the rejection ratio of each station. A sample output table for a one-way model is shown in Table 1 below.

Table 1.
Sample output report table for one-way model (TVs: Total Vehicles; TRs: Total Requests; ARs: accepted requests; RRs: rejected requests; FVS: Final Number of Vehicles at Station; TUR: total utilization rate; RRate: rejection rate).
The simulation was run for 200 h to generate a statistically meaningful sample of customer requests under the projected 2024 conditions. A total of 4263 customer requests were simulated, derived from the projected request arrival rate of 7 requests per minute. This value was based on the results generated by a compound annual growth model applied to the 2011 operational data from Communauto. The 200 h duration included both weekday and weekend timeframes, allowing the simulation to indirectly capture temporal demand variability. Although a constant arrival rate was assumed, the model reflected the updated system scale and usage intensity. Future work could incorporate time-of-day and seasonal variations to more explicitly model the peak and off-peak dynamics under real-time conditions.
3.5. Result Verification
Table 2 shows the input request data (expected) for randomly selected stations, which was fed to the simulation model along with the observed results. It can be seen that the two sets of values matched, and therefore the results were verified.

Table 2.
Sample data verification.
Table 3 shows the results for the total number of cars present at each station (expected) and the results from the simulation (observed). It can be seen that the two sets of values matched, and therefore the results were verified.

Table 3.
Sample data verification for number of cars.
Please note that in this paper, we have shown model verification through a few test cases. For generalization of the model results, all the results should be verified.
3.6. Result Validation
Table 4 shows the results of the parameter variability sensitivity analysis. It can be seen that the average request acceptance rates were higher and the rejection rates were lower in the round-trip model.

Table 4.
Tests and the corresponding results.
Table 5 presents the results of a face validation procedure applied to simulation outputs generated from synthetic data. Since real-world expert input was not used in this version of the model, the validation was conducted by examining whether the results exhibited plausible patterns. For example, stations showing high rejection rates in the simulation typically had fewer vehicles or a higher demand, which aligns with expected system behavior. This helped ensure that the model behaves logically and reflects reasonable assumptions about urban carsharing dynamics, even though no external data or expert panel was available to perform a direct comparison.

Table 5.
Face validity results.
3.7. Comparing Alternative Configurations
Table 6 presents a sample simulation output file containing information on the number of stations and their individual numbers of requests, the number of cars present at each station, the total number of rejections, and so on. To model an alternative configuration, cars were moved from a station with a lower rejection rate to stations with more rejections or less cars. It can be seen that station 119 had 117 rejections out of 192 requests, while stations 251 and 061 had 0 rejections. To model an alternative configuration, 10 cars from station 251 and 15 cars from station 061, or a total number of 25 cars, were moved to station 119.

Table 6.
Sample output for one-way model.
Table 7 shows the results for the alternative configuration. It can be seen that the number of rejections at station 119 decreased from 117 to 67, and at the same time we can also see that even after removing 15 cars from station 061, the number of requests accepted was still the same. This indicates that station 061 had cars which were unutilized and moving them to station 119 helped reduce the number of rejected requests.

Table 7.
Sample output for one-way model with alternative configuration.
Similarly, based on the output generated we listed the stations with high rejection rates (Table 8) and stations with more than 60 cars and zero rejections (Table 9). Then we moved cars from the stations with a lower rejection rate to stations with a higher rejection rate.

Table 8.
List of stations with high rejection rates.

Table 9.
List of stations with zero rejections.
Table 10 shows the new results for the stations with the higher rejection rates. It can be seen that station 171, 75e Avenue et Parent, had just 5 vehicles present; we moved 50 cars from station 2, St-Sacrement, to station 171, and the rejection rate went from an average of 45% to 0%. Also the total number of rejections at station 2 still remained the same. Based on the results, we could see the optimum number of cars that needed to be present at each station in order to avoid higher rejection rates. Similarly, we moved cars from station 124 to station 316, from station 148 to station 235, and finally from station 04 to station 65. All of these changes showed a tremendous decrease in the total number of rejections. In addition, the results were found to be better for the round-trip model, i.e., it had a lower request rejection rate.

Table 10.
New values for stations with alternative configuration.
Based on the above results, we can say that the round-trip model showed better performance than the one-way model for the test stations. By analyzing the output file, CSOs can make more conscious decisions regarding relocating cars from not-so-busy stations to stations with a lot of requests and fewer cars and thereby reduce the number of request rejections. Analysis of the output can also help in deciding on an adequate number of cars to be kept at each station.
It is important to clarify that no formal optimization algorithm was used in this study. The term ’optimum number of cars’ refers to the number of cars in empirically improved configurations derived from simulation output analysis. Specifically, vehicle transfers between stations were performed in an ad hoc manner by manually identifying stations with high rejection rates and reallocating vehicles from stations with low utilization or zero rejections. This heuristic approach allowed us to explore the potential benefits of rebalancing the fleet, but it does not guarantee a mathematically optimal solution. Future work could incorporate formal optimization models, such as mixed-integer programming or metaheuristic algorithms, to systematically determine optimal vehicle allocations.
4. Discussion of Results, Findings, and Recommendations for Communauto
Based on the simulation tests performed for the one-way model and the round-trip model, we observed that the round-trip model performs better than the one-way model in terms of having a lower request rejection rate. The vehicle relocation costs are also lower. It was also found that in the round-trip model, there are cars at some stations which are unutilized, and in the one-way model there is an imbalance in the number of cars at each station; some stations have excess cars and some have no cars at all. Using the alternative configuration method, we can decide on the optimum number of cars to be stationed at each individual station in order to avoid rejections. In order to move the unutilized cars to stations with a greater demand in the round-trip model and distribute the cars evenly among the stations in the one-way model, various vehicle return/relocation strategies need to be implemented. Vehicle return strategies can be one of two types: an operator-based relocation strategy or a customer-based relocation strategy.
In a customer-based relocation strategy, the customer is persuaded to relocate the vehicle to a specific station using an incentive technique; the incentives could range from a lower rate to free rides. Another way of influencing the customer for relocation purposes can be achieved by combining carsharing and carpooling techniques, such as sharing a ride with a fellow customer traveling to a similar location to receive discounted rates, as well as offering free rides to customers via social media platforms for relocating a vehicle to its destination station. The advantage of using a customer-based relocation technique is that it helps in reducing the costs of hiring transporters to manually transfer the vehicles; also it is environmentally sustainable. The disadvantage of a customer-based relocation technique is that the customer can only be persuaded/influenced up to a certain degree; the decision whether to accept an incentive solely depends on the customer.
On the other hand, an operator-based relocation strategy is initiated by the carsharing organization and involves a station manager and a transporter. The station manager would calculate the total number of cars that need to be kept at each station at regular intervals, and the transporter would relocate the vehicles to those specific stations. The advantage of an operator-based relocation technique is that there is no dependency on the customer to relocate the vehicle, and any maintenance work needed on the car can be reported to the station manager in a timely manner. However, the disadvantages include additional staff costs, the time consumed when moving the car, etc.
CSOs provide flexibility to their users by using a one-way carsharing model with the option to return the car to a parking zone within a given region; this type of system is known as a free-floating system. In the future, Communauto can provide its customers with the flexibility of a one-way carsharing model and use a customer-based relocation technique by providing lucrative incentives, and in order to avoid excess costs for renting parking spaces within the city it should opt for a free-floating system.
The proposed results are also in agreement with those of Nourinejad & Roorda (2015), who compared one-way vs. two-way operational policies for carsharing operations and found that one-way systems require the lowest fleet size but the highest number of vehicle relocation hours.
For confidentiality reasons, the proposed strategies were tested on a limited amount of data provided by Communauto. For generalization of the results, large datasets should be used and tested under different uncertainty scenarios, including different system starting states (burn-ins required), a long-tailed distribution for the average rental times per reservation, different vehicle types and geographical contexts, etc.
Model verification ensures that a simulation produces the correct outcomes, while model validation evaluates whether appropriate modeling techniques have been applied. For verification, we compared the expected and observed values—such as the request arrivals and vehicle availability at the stations—to assess their consistency and accuracy.
Two validation strategies were employed: parameter variability sensitivity analysis and face validity analysis. In the sensitivity analysis, key parameters—particularly the number of vehicles at each station (TVs)—were varied to observe their impact on performance indicators like the rejection rate (RR) and vehicle utilization rate (TUR). The results showed that modifying the vehicle count at specific stations led to significant changes in the rejection and acceptance rates, confirming that the model behaves as expected under varying conditions.
While this analysis focused on the fleet size, other parameters such as the customer request rate or trip duration were held constant. Expanding this investigation to include a wider range of variables is recommended in future work to further assess the model robustness.
Additionally, face validity analysis was conducted through expert consultation with three professionals from Communauto. These included the Operations Manager, the Business Development Manager, and a Finance representative. Their feedback confirmed that the simulation outputs aligned well with real-world operational behaviors and expectations.
5. Conclusions, Limitations, and Future Work
In this paper, we address the problem of fleet management for carsharing operations and evaluate two business models, namely one-way and round-trip vehicle return strategies, using discrete event simulation. A practical application of the proposed model for a carsharing organization called Communauto based in Montreal is provided. The inputs for the simulation model were randomly generated based on the data provided by Communauto. The simulation model was run for a total of 200 h/replication and 10 replications for both the round-trip and one-way models with three different sets of data. The average acceptance rate for the round-trip model was found to be 92%, which is higher than that for the one-way model, 87%, and is therefore recommended to Communauto for implementation. Based on the output analysis, it can be suggested that even though the round-trip model has a lower rejection rate compared to the one-way model, in order to utilize unused cars the one-way model should be implemented along with a customer-based vehicle relocation technique to ensure a balanced distribution of the cars at various stations. The alternative configuration analyses for both the models showed that the optimum number of cars should be kept at the stations to reduce the rejection rate. The tests indicate that using an alternative configuration, the rejection rate can be reduced from an average of 50% to a mere 12%. While the customer request rejection rate is a key indicator of the service quality and vehicle availability, it does not fully capture the overall fleet management performance. Additional metrics—such as the vehicle utilization rate, seasonal demand variations (e.g., during festivals), and the vehicle relocation frequency—can provide a more comprehensive evaluation of the operational efficiency.
Limitations of the study: One limitation of the current simulation model is the assumption of a constant request arrival rate throughout the simulation period. While this simplifies the modeling process and aligns with the average hourly request rate derived from historical data, it does not capture temporal variations such as peak and off-peak demand periods. As a result, the model may underestimate the rejection rates during high-demand intervals and overestimate them during low-demand periods.
Another key limitation of this study is the use of simulated data for the year 2024. Although the synthetic dataset was carefully constructed to reflect realistic carsharing trends based on historical patterns and publicly available information from Communauto, it does not fully capture the complexity of real-world operations. Consequently, the simulation results—particularly those related to rejection rates and vehicle utilization—may differ from the outcomes based on actual 2024 operational data. These findings should therefore be interpreted as indicative rather than definitive. Future work should aim to validate the model using updated real-world datasets as they become available.
Although the simulation was based on synthetic reservation data generated to reflect the projected operational patterns in 2024, the modeling framework itself was inspired by the structure and dynamics of real-world systems like that of Communauto in Montreal. The framework and insights are applicable to other urban carsharing systems that share similar characteristics, such as vehicle pooling, station-based reservations, and user behavior influenced by urban mobility patterns.
Future work required to improve the existing model includes the following:
- The actual number of requests per station could be used to develop a more precise output.
- Various relocation techniques to move excess cars from busy stations to stations with no cars or less cars can be incorporated.
- The possibility of using customer-driven vehicle relocation techniques could be explored.
- Cost parameters could be incorporated.
- Use of a hybrid model which is a combination of a one-way model and a round-trip model can be tested.
- Models incorporating cluster region classification could be used in order to promote the use of a one-way model within a small community, while the use of a round-trip model could be continued across the city.
- Innovative vehicle return strategies based on pricing incentives for users, trip splitting, trip joining, and predictive vehicle relocation can also be investigated.
Author Contributions
Conceptualization, A.C.; methodology, A.C.; software, A.C.; validation, A.C., M.K.; formal analysis, A.C., M.K.; investigation, A.C., M.K.; data curation, A.C., M.K.; writing—original draft preparation, A.C.; writing—review and editing, M.K., A.A.; supervision, A.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data will be provided upon request to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Correction Statement
This article has been republished with a minor correction to the Data Availability Statement. This change does not affect the scientific content of the article.
References
- Shaheen, S.A.; Bansal, A.; Chan, N.; Cohen, A. Mobility and the sharing economy: Industry developments and early understanding of impacts. In Low Carbon Mobility for Future Cities: Principles and Applications; California Digital Library: Oakland, CA, USA, 2017; Volume 213. [Google Scholar]
- Awasthi, A.; Chauhan, S.S.; Breuil, D. Sustainable mobility solutions: A pre-implementation questionnaire study for carsharing, International Journal of Services Sciences, Special Issue on Methods. Tools Appl. Transp. Logist. Serv. 2009, 2, 242–264. [Google Scholar]
- Degirmenci, K.; Breitner, M.H. Carsharing: A literature review and a perspective for information systems research. In Proceedings of the Multikonferenz Wirtschaftsinformatik (MKWI 2014), Paderborn, Germany, 26–28 February 2014. [Google Scholar]
- Ferrero, F.; Perboli, G.; Rosano, M.; Vesco, A. Car-sharing services: An annotated review. Sustain. Cities Soc. 2018, 37, 501–518. [Google Scholar] [CrossRef]
- D’Orso, G.; Migliore, M. A Methodology for Designing One-Way Station-Based Carsharing Services in a GIS Environment: A Case Study in Palermo. ISPRS Int. J. Geo-Inf. 2024, 13, 148. [Google Scholar] [CrossRef]
- Wang, D.; Ye, J.; Yu, B.; Jing, P.; Gao, L. Simulating one-way electric carsharing systems with a multi-agent model. Transportation 2024, 51, 2277–2300. [Google Scholar] [CrossRef]
- Huang, K.; An, K.; Rich, J.; Ma, W. Vehicle relocation in one-way station-based electric carsharing systems: A comparative study of operator-based and user-based methods. Transp. Res. Part E Logist. Transp. Rev. 2020, 142, 102081. [Google Scholar] [CrossRef]
- Deng, Y.; Cardin, M.A. Integrating operational decisions into the planning of one-way vehicle-sharing systems under uncertainty. Transp. Res. Part C Emerg. Technol. 2018, 86, 407–424. [Google Scholar] [CrossRef]
- Barth, M.; Todd, M. Simulation model performance analysis of a multiple station shared vehicle system. Transp. Res. C 1999, 7, 237–259. [Google Scholar] [CrossRef]
- Barth, M.; Todd, M. User behaviour evaluation of an intelligent shared electric vehicle system. Transp. Res. Rec. 2001, 1760, 145–152. [Google Scholar] [CrossRef]
- Illgen, S.; Höck, M. Literature review of the vehicle relocation problem in one-way car sharing networks. Transp. Res. Part B Methodol. 2019, 120, 193–204. [Google Scholar] [CrossRef]
- Eliyan, A.F.; Kerbache, L. Vehicle Relocation in One-Way Carsharing: A Review. Sustainability 2024, 16, 1014. [Google Scholar] [CrossRef]
- Iacobucci, R.; Bruno, R.; Boldrini, C. A multi-stage optimisation approach to design relocation strategies in one-way car-sharing systems with stackable cars. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17048–17061. [Google Scholar] [CrossRef]
- Wagner, S.; Willing, C.; Brandt, T.; Neumann, D. Data analytics for location-based services: Enabling user-based relocation of carsharing vehicles. In Proceedings of the Thirty Sixth International Conference on Information Systems, Fort Worth, TX, USA, 13–16 December 2015; pp. 279–287. [Google Scholar]
- Bruglieri, M.; Colorni, A.; Luè, A. The relocation problem for the one-way electric vehicle sharing. Networks 2014, 64, 292–305. [Google Scholar] [CrossRef]
- Carlier, A.; Munier-Kordon, A.; Klaudel, W. Mathematical model for the study of relocation strategies in one-way carsharing systems. Transp. Res. Procedia 2015, 10, 374–383. [Google Scholar] [CrossRef]
- Nourinejad, M.; Zhu, S.; Bahrami, S.; Roorda, M.J. Vehicle relocation and staff rebalancing in one-way carsharing systems. Transp. Res. E 2015, 81, 98–113. [Google Scholar] [CrossRef]
- Bianchessi, A.G.; Formentin, S.; Savaresi, S.M. Active fleet balancing in vehicle sharing systems via feedback dynamic pricing. In Proceedings of the 16th International IEEE Conference on Intelligent Transportation Systems-(ITSC), The Hague, The Netherlands, 6–9 October 2013; pp. 1619–1624. [Google Scholar]
- Li, H.; Wang, Z.; Chen, S.; Xu, W.; Li, Y.; Wang, J. Optimizing fleet, staff configuration and operational strategies in one-way mixed fleet carsharing systems: A Lagrangian relaxation-based approach. Transp. Lett. 2024, 17, 1030–1052. [Google Scholar] [CrossRef]
- Liu, Y.; Xie, J.; Chen, N. Stochastic one-way carsharing systems with dynamic relocation incentives through preference learning. Transp. Res. Part E Logist. Transp. Rev. 2022, 166, 102884. [Google Scholar] [CrossRef]
- Giorgione, G.; Bolzani, L.; Viti, F. Assessing two-way and one-way carsharing: An agent-based simulation approach. Transp. Res. Procedia 2021, 52, 541–548. [Google Scholar] [CrossRef]
- Yang, S.; Wu, J.; Sun, H.; Qu, Y.; Li, T. Double-balanced relocation optimization of one-way car-sharing system with real-time requests. Transp. Res. Part C Emerg. Technol. 2021, 125, 103071. [Google Scholar] [CrossRef]
- Boyaci, B.; Zografos, K.G.; Geroliminis, N. An optimization framework for the development of efficient one-way car-sharing systems. Eur. J. Oper. Res. 2015, 240, 718–733. [Google Scholar] [CrossRef]
- Alfian, G.; Rhee, J.; Kang, Y.S.; Yoon, B. Performance comparison of reservation based and instant access one-way car sharing service through discrete event simulation. Sustainability 2015, 7, 12465–12489. [Google Scholar] [CrossRef]
- Nourinejad, M.; Roorda, M.J. Carsharing operations policies: A comparison between one-way and two-way systems. Transportation 2015, 42, 497–518. [Google Scholar] [CrossRef]
- Barrios, J.; Godier, J. Fleet sizing for flexible carsharing systems: Simulation-based approach. Transp. Res. Rec. 2014, 2416, 1–9. [Google Scholar] [CrossRef]
- Clemente, M.; Fanti, M.P.; Mangini, A.M.; Ukovich, W. The vehicle relocation problem in car sharing systems: Modeling and simulation in a petri net framework. In International Conference on Applications and Theory of Petri Nets and Concurrency; Springer: Berlin/Heidelberg, Germany, 2013; pp. 250–269. [Google Scholar]
- Yoon, B.; Lee, S. An operation model of carsharing service: Application of simulation method. J. Traffic Logist. Eng. 2013, 1, 15–19. [Google Scholar] [CrossRef]
- Di Febbraro, A.; Sacco, N.; Saeednia, M. One-way carsharing: Solving the relocation problem. Transp. Res. Rec. 2012, 2319, 113–120. [Google Scholar] [CrossRef]
- Awasthi, A.; Breuil, D.; Chauhan, S.S.; Parent, M.; Reveillere, T. A multicriteria decision making approach for carsharing stations selection. J. Decis. Syst. 2007, 16, 57–78. [Google Scholar] [CrossRef]
- Awasthi, A.; Chauhan, S.S.; Hurteau, X.; Breuil, D. An Analytical Hierarchical Process-based decision-making approach for selecting car-sharing stations in medium size agglomerations. Int. J. Inf. Decis. Sci. 2008, 1, 66–97. [Google Scholar] [CrossRef]
- Nakayama, S.; Yamamoto, T.; Kitamura, R. A Simulation Analysis for the Management of an Electric-Vehicle Sharing System: The Case of the Kyoto Public-Car System, Transportation Research Board, Proceedings. In Proceedings of the 80th Annual Meeting, Washington, DC, USA, 11–15 January 2001. [Google Scholar]
- Vasconcelos, A.S.; Martinez, L.M.; Correia, G.H.; Guimarães, D.C.; Farias, T.L. Environmental and financial impacts of adopting alternative vehicle technologies and relocation strategies in station-based one-way carsharing: An application in the city of Lisbon, Portugal. Transp. Res. Part D Transp. Environ. 2017, 57, 350–362. [Google Scholar] [CrossRef]
- El Fassi, A.; Awasthi, A.; Viviani, M. Evaluation of carsharing network’s growth strategies through discrete event simulation. Expert Syst. Appl. 2012, 39, 6692–6705. [Google Scholar] [CrossRef]
- Shaheen, S.; Sperling, D.; Wagner, C. A short history of carsharing in the 90’s. J. World Transp. Policy Pract. 1999, 5, 16–37. [Google Scholar]
- Guo, G.; Hou, Y. Rebalancing of one-way car-sharing systems considering elastic demand and waiting time. IEEE Trans. Intell. Transp. Syst. 2022, 23, 23295–23310. [Google Scholar] [CrossRef]
- Wang, D.; Liao, F. Analysis of first-come-first-served mechanisms in one-way car-sharing services. Transp. Res. Part B Methodol. 2021, 147, 22–41. [Google Scholar] [CrossRef]
- Huang, K.; de Almeida Correia, G.H.; An, K. Solving the station-based one-way carsharing network planning problem with relocations and non-linear demand. Transp. Res. Part C Emerg. Technol. 2018, 90, 1–17. [Google Scholar] [CrossRef]
- de Lorimier, A.; El-Geneidy, A. Understanding the factors affecting vehicle usage and availability in carsharing networks: A case study of Communauto carsharing system from Montréal, Canada. Proceedings of 90th Transportation Research Board Annual Meeting, Washington, DC, USA, 23–27 January 2011; Available online: https://tram.mcgill.ca/Research/Publications/carsharing_IJST.pdf (accessed on 15 January 2024).
- Morency, C.; Trépanier, M.; Agard, B. ‘Typology of Carsharing Members’, in 90th Transportation Research Board. 2011. Available online: https://brunoagard.mgi.polymtl.ca/fr/publications/doc/2011/2011_TRB-CM-MT-BA.pdf (accessed on 15 January 2024).
- Ciari, F.; Schuessler, N.; Axhausen K., W. Estimation of car-sharing demand using an activity-based microsimulation approach: Model discussion and preliminary results [Communication écrite]. In Proceedings of the 90th Annual Meeting of the Transportation Research Board, Washington, DC, USA, 23–27 January 2011; Available online: https://strc.ch/2010/Ciari.pdf (accessed on 15 January 2024).
- Zheng, J.; Scott, M.; Rodriguez, M.; Sierzchula, D.; Guo, J.; Adams, T. Carsharing in a University Community–Assessing Potential Demand and Distinct Market Characteristics. Transp. Res. Rec. J. Transp. Res. Board 2009, 2110, 18–26. [Google Scholar] [CrossRef]
- Catalano, M.; Lo Casto, B.; Migliore, M. Car sharing demand estimation and urban transport demand modelling using stated preference techniques. Eur. Transp. 2008, 40, 33–50. [Google Scholar]
- Barth, M.; Todd, M.; Xue, L. User-based vehicle relocation techniques for multiple-station shared-use vehicle systems. In Proceedings of the Transportation Research Board 83rd Annual Meeting, Washington, DC, USA, 11–15 January 2004. [Google Scholar]
- Fantola, M.; Olivo, A.; Devoto, R.; Dìaz Maroto Llorente, N. A profitability comparison between a “one-way” car sharing service and a “modified one-way” car sharing service. IJTTE 2017, 7, 19–36. [Google Scholar] [CrossRef]
- Repoux, M.; Boyaci, B.; Geroliminis, N. Simulation and optimization of one-way car-sharing systems with variant relocation policies. In Proceedings of the Transportation Research Board 94th Annual Meeting (No. 15-1907), Washington, DC, USA, 11–15 January 2015. [Google Scholar]
- Communauto. Another Season of Expansion for Communauto in Montreal and Longueuil. 2025. Available online: https://communauto.com/2025-another-season-of-expansion-for-communauto-in-montreal-and-longueuil/?lang=en (accessed on 15 January 2024).
- Alencar, V.A.; Pessamilio, L.R.; Rooke, F.; Bernardino, H.S.; Borges Vieira, A. Forecasting the carsharing service demand using uni and multivariable models. J. Internet Serv. Appl. 2021, 12, 4. [Google Scholar] [CrossRef]
- Deng, J.; Pantuso, G. Pricing carsharing services under decision-dependent demand uncertainty: A two-stage stochastic programming approach. In Proceedings of the 12th Triennial Symposium on Transportation Analysis conference (TRISTAN XII), Okinawa, Japan, 22–27 June 2025. [Google Scholar]
- Zhong, Y.; Luo, Q.; Gao, T.; Long, Y.; Liu, L. Carsharing operation optimization with the comprehensive consideration of economic and social benefits. PLoS ONE 2025, 20, e0315323. [Google Scholar] [CrossRef] [PubMed]
- Banks, J.; Carson, J.S.; Nelson, B.L.; Nicol, D.M. Discrete-Event System Simulation, 5th ed.; Prentice Hall: Hoboken, NJ, USA, 2010. [Google Scholar]
- Cochran, W.G. Sampling Techniques, 3rd ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1977. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).