Analysis of Short-Range Ordering Effect on Tensile Deformation Behavior of Equiatomic High-Entropy Alloys TiNbZrV, TiNbZrTa and TiNbZrHf Based on Atomistic Simulations

Abstract

In the study, the combined molecular dynamics and Monte Carlo (MD/MC) simulation was used to investigate the short-range ordering effect on tensile deformation of bicrystals with grain boundaries (GBs) Σ3(1$\overline{1}$2)[110]. Three different equiatomic high-entropy alloys, namely, ZrTiNbV, ZrTiNbTa and ZrTiNbHf, were considered. The tensile loading at 300K was applied in the direction perpendicular to the GBs’ planes. The stress–strain response as well as the structure evolution of the alloys with initial random distribution of atoms were compared with results obtained for the corresponding materials relaxed during the MD/MC procedure. It was revealed that the distribution of atoms in the alloys significantly affects the deformation process. Ordered clusters of Nb atoms are able to suppress the dislocation sliding and twin formation increasing the yield strength of ZrTiNbV. On the contrary, in ZrTiNbTa, the twinning mechanism is dominant in the case of the ordered structure due to the absence of Nb clusters and the presence of areas enriched with Zr atoms, which ease nucleation of dislocations and twins. Since Hf decreases the stability of the body-centered cubic lattice, the main deformation mechanism of ZrTiNbHf is the stress-induced phase transition; however, Nb clusters inside grains of the relaxed alloy slightly delay this process.

1. Introduction

High-entropy alloys (HEAs) are a relatively new class of materials obtained by mixing equal or relatively large fractions of typically four or more elements. These materials attract considerable research attention due to their exceptional properties that exceed those of conventional alloys. Normally, such alloys have high strength and demonstrate good resistance to cracking and corrosion [1,2]. They have a vast compositional space that has not yet been explored, which opens up opportunities to develop alloys with unique properties.

Unlike traditional face-centered cubic (fcc) alloys, which become more brittle at low temperatures and show insufficient yield strength, body-centered cubic (bcc) HEAs often retain high strength, stiffness, and fracture resistance even at cryogenic temperature. Among bcc HEAs, ZrTiNb-based alloys are of increasing interest. Such materials are found to have excellent mechanical properties and often exhibit a balance between strength and ductility [3,4,5], surpassing the characteristics of most existing HEAs. Such alloys demonstrate very good corrosion resistance and biocompatibility, which is important for their use as biomedical materials [6,7]. Moreover, it was experimentally demonstrated that the bcc HEAs TiZrVHfNb [8], TiVCrNb [9], and TiZrCrMnFeNi [10] exhibit excellent characteristics in hydrogen storage. These properties make the ZrTiNb-based alloys good candidates for structural applications, use in the aerospace and automotive industries, as well as in the energy sector.

Studies of bcc HEAs show that deformation of such materials is controlled predominantly by the slip of screw dislocations overcoming the Peierls stress [11,12]. The high yield strength of the alloys is often attributed to the interaction of dislocations with constituent atoms, while the high strain hardening is explained by the high density of dislocations and the formation of shear bands [12,13]. It was found also that the short-range ordering (SRO) with formation of various clusters and particles can inhibit the movement of dislocations in HEAs [14,15]. The decrease in the stacking fault energy due to such chemical ordering can trigger twinning and phase transformation leading to additional hardening [16]. That is why it is believed that the presence of structural inhomogeneities in bcc HEAs can be an effective way to improve strain hardening. For example, it was found that the addition of a small amount of O to the bcc HEA TiZrHfNb leads to the formation of complexes (O, Ti, Zr). Dislocations are pinned by these clusters leading to strain hardening and, as a result, the increased strength [17].

Metastable alloys demonstrating transformation-induced and/or twinning-induced plasticity (TRIP/TWIP) during deformation often exhibit a balance of high strength and ductility. In several works, so-called “metastable engineering” was applied to the bcc HEAs to achieve improved ductility by triggering TRIP/TWIP. For example, Huang et al. [18] showed that the ductility can be significantly improved by reducing the Ta content in TaHfZrTi alloy when the bcc to hexagonal close-packed (hcp) TRIP is activated, and the strain hardening rate increases. In another work, it was found that the presence of TiZr-rich regions formed during deformation of NbZrTiTa alloy decreases the stability of bcc structure and leads to structure transformation [19]. A number of works [20,21] on the bcc HEAs containing Ti propose an alloy design strategy to control metastability, which involves modification of the composition to promote the martensitic transformation.

Nowadays, atomistic simulation methods are widely used to study the influence of SRO on the deformation behavior of HEAs. The combined molecular dynamics (MD) and Monte-Carlo (MC) approach is often used to establish the correlation between chemical composition and the atomic ordering, as well as to evaluate the influence of the latter on the deformation process [14,22,23,24,25]. Using this method, it was shown that in nanocrystalline alloys, the short-range ordering can suppress the inverse Hall–Petch dependence [26], change the stacking fault energy [27], and provide an explanation for the synergy of high strength and ductility [28]. Recently, it was analyzed how the addition of an extra component, in particular Al, exceeding the average atomic size of matrix atoms, and the presence of grain boundaries (GBs), can influence the SRO process and mechanical properties of the HEA with fcc structure [22]. Due to stabilization of GBs by segregation of Al, formed during material relaxation, the GB migration and GB sliding are inhibited, which leads to an increased yield strength. The similar effect of GB segregations on the deformation of the CoCrCuFeNi HEAs was also revealed in [29]. It was concluded in [22] that the improved strength of the HEA with Al addition is explained by the increase in the stacking fault energy caused by the formation of Al-Fe clusters. Wu et al. [30] summarized both experimental and theoretical findings on the SRO effect on mechanical properties of HEAs. The authors highlighted that controlling SRO could be an effective way for improving mechanical properties of HEAs.

However, there are not many works on SRO in TiNbZr-based HEAs to unambiguously interpret their cold deformation behavior. Therefore, the aim of this work is to analyze the effect of possible atomic ordering on the tensile deformation of three different HEAs, namely, ZrTiNbV, ZrTiNbTa and ZrTiNbHf, at room temperature. The results of the study will be compared with those obtained for the corresponding alloys with atoms distributed randomly within the structures.

2. Modelling

2.1. Materials and MD Model

HEAs with three different equiatomic compositions are considered, namely, ZrTiNbV, ZrTiNbTa and ZrTiNbHf. The simulations are performed for a MD model in the form of bicrystal (Figure 1) randomly filled with about 50,000 atoms of the corresponding alloy elements forming the bcc structure. Furthermore, the HEAs with the random distribution of atoms can also be denoted as M1r, M2r and M3r, respectively. The dimensions of the bicrystal considered are about 18.0 nm × 20.0 nm × 2.8 nm along the x-, y- and z-axes, respectively.

To form the bicrystal, the standard method for constructing the coincidence site lattice GBs is adopted [31,32]. Two low-energy symmetric tilt GBs Σ3(1$\overline{1}$2)[110] are introduced into the initial defect-free bcc sample with crystallographic directions [$\overline{1}$11], [1$\overline{1}$2] and [110] oriented along the x-, y- and z-axes, respectively. To obtain the GBs, the upper part of the defect-free sample is rotated by about 70.53^o around the [110] axis against the lower part. One of the GBs is located right in the middle of the constructed bicrystal, while the second is formed by its top and bottom edges perpendicular to the y-direction, when the periodic boundary conditions are applied along this direction (Figure 1).

2.2. MD/MC Relaxation Procedure

To obtain the steady-state condition of the considered HEAs, the hybrid MD/MC modeling is performed for the alloys M1r, M2r and M3r. This procedure of material relaxation includes simultaneous atomic swapping according to the MC approach described below, and the MD thermalization by integrating the classical equations of motion.

Before the MD/MC simulation, the bicrystals of M1r, M2r and M3r are subjected to energy minimization by the conjugate gradient method and further equilibrated within 40 ps, keeping all the pressure components at 0 Pa and the temperature at 300K (the NPT ensemble). Just as in the subsequent MC atomic swapping, the timestep here is set to 1 fs, and the periodic boundary conditions are applied along the x-, y- and z-axes.

Swapping of one atom type with an atom of another type is realized with the use of the widely used MC procedure that follows the Metropolis acceptance criterion [33] which determines swap probability at a chosen temperature. According to this approach, the MC swap takes place if the alloy energy E after the (i + 1) atom exchange is lower than the energy at previous attempt i. In the opposite situation, the swap is accepted with a probability defined as follows:

P = exp(−(E(i + 1) − E(i))/kT),

(1)

where T is a certain temperature and k is the Boltzmann constant. Within one timestep, only one swap is realized. Before and after such atom exchange, the kinetic energy is kept unchanged. A total of 100,000 swaps are performed for each atomic pair of the considered materials within 50 MD/MC cycles. After each cycle of the MC swapping, the MD relaxation procedure is performed for 20 ps in the NPT ensemble. Note, hereinafter, the alloys ZrTiNbV, ZrTiNbTa and ZrTiNbHf after such MD/MC relaxation procedure can also be denoted as M1o, M2o and M3o, respectively.

2.3. Tensile Deformation

The subsequent tensile deformation is conducted for the bicrystals M1r, M2r, M3r, M1o, M2o and M3o at the room temperature (300K) and the strain rate of 1.0 × 10⁸ s⁻¹. Similar to the MC/MD simulation, the tensile loading is performed in the NPT ensemble. All the stress components except σ_yy are controlled to be zero during the deformation. The loading is performed up to ε_yy = 0.20.

Both the MD/MC relaxation and the MD modelling of tensile deformation are conducted with the large-scale atomic/molecular massively parallel simulator (LAMMPS) [34], which is widely used to study various molecular and atomic systems and related problems such as, for example, mass transfer and atomic vibrations in solids [35,36,37], or the permeability of water molecules through membranes for water desalination [38,39,40,41], and many others. In this work, the interatomic forces in the HEAs ZrTiNbV and ZrTiNbTa are described by the many-body modified embedded-atom method (MEAM) potential recently developed by Nitol et al. [42], while for the HEA ZrTiNbHf, the forces are determined by the MEAM potential of Huang et al. [43]. Interatomic potentials for many-component alloys are believed to be less accurate than for single element metals due to their complexity, however new approaches are being developed to obtain reliable potentials [44,45,46]. For visualization of the atomic structure and the dislocation analysis, the Open Visualization Tool (OVITO) [47,48,49] is utilized.

3. Results

3.1. SRO

Figure 2 demonstrates how fast the average total energies per one atom, E_atom, for the initial structures (M1r, M2r and M3r) decrease with the MC/MD relaxation cycles, N. As can be seen, the HEAs ZrTiNbV and ZrTiNbTa with the initial random distribution of atoms have higher energies than that for ZrTiNbHf (−6.010 eV and −6.325 eV over −6.374 eV, respectively). This is especially evident for M1r. Upon the MC/MD relaxation; the energies for the materials M1r, and especially M2r, drop significantly within the first 10 cycles. After the final MC/MD cycle, the energies for the relaxed alloys M1o, M2o and M3o are about −6.125 eV, −6.562 eV and −6.396 eV, respectively. Unlike the other two materials, the energy reduction for ZrTiNbHf is very insignificant.

SRO in the HEAs and the chemical affinity between their elements can be assessed by calculating the Warren–Cowley parameter (WCP) for a pair of constituent atoms at the first nearest neighbor shell after the MC/MD relaxation of the alloys using the following equation:

WCP = 1 − Z_mn/(χ_nZ_m)

(2)

Here, χ_n is the atomic fraction of n-atoms in the alloy, Z_mn is the number of n-atoms at the first neighbor shell of m-atoms, and Z_m is the total number of atoms at the first neighbor shell of m-atoms [50]. When the calculated WCP is 0, the m-n atomic pairs are distributed randomly, while if this value is positive, they are observed in the structure less often. In the case when WCP is negative, the formation of clusters of m-n atoms with chemical bonds between them is more likely.

In Figure 3, the diagrams show WCPs calculated using Equation (2) for the possible atomic pairs of the relaxed HEAs M1o, M2o and M3o. It is seen that in M1o (Figure 3a), the MD/MC relaxation leads to the formation of Nb, Zr and V-Ti clusters. At the same time, the V atoms do not tend to form chemical bonds with each other, and the same can be said for the Nb-Ti and Nb-Zr atomic pairs. The other atomic combinations in this alloy are distributed almost randomly in the structure. As for the HEA M2o (Figure 3b), strong chemical ordering can be observed for the Ta and Zr atoms; however, the clusters of Ta and Zr are separated from each other, since the WCP for the Ta-Zr pair is positive. A similar trend can be seen for the atomic pairs Ta-Ti and Nb-Zr, while the other atomic combinations are distributed randomly within the structure. Despite a very small decrease in energy of M3r during the MD/MC relaxation (Figure 2), SRO of Zr, and especially Nb atoms, takes place, and, according to the calculated WCPs, separate conglomerates of these elements tend to be far from each other (Figure 3c). In addition, some clustering of the Hf atoms can be detected here.

Figure 4 shows the distribution of atoms in the HEAs after the MD/MC relaxation cycles. The atomic structures presented here are in good agreement with the calculated values of WCPs (Figure 3). For all the materials, the formation of ordered clusters can be observed. Both the bicrystals, M1o and M3o, contain randomly distributed clusters of the Nb and Zr atoms colored blue and pink, respectively; however, the size of the clusters in M3o are smaller. At the same time, the ordered clusters of Nb cannot be observed in M2o, but here, the separate conglomerates of Ta and Zr atoms easily can be found. They are noticeably bigger than the clusters in the other two alloys. In addition, in M1o, areas with the V-Ti ordered structure can be seen. Due to the low chemical affinity of Ti and Nb to Ta and Zr, respectively (see Figure 3), such atoms are located preferably on the border of the Ta and Zr clusters forming in M2o interphase segregations. Here, the lines of Ti atoms are contiguous with the Zr clusters, while the lines of the Nb atoms are adjacent to the Ta clusters. It should be noted that there is a sign of GB segregation formation in M3o. The horizontal lines of Ti and Zr atoms colored in yellow and pink, respectively, occupy atomic positions at the GBs, while relatively small Nb clusters are located preferably inside the grains. In the other two materials, GB segregations are absent.

3.2. Stress–Strain Curves

To reveal the effect of SRO in the considered systems on the tensile deformation behavior, the tensile test simulation is performed for the relaxed HEAs (M1o, M2o and M3o) and for the corresponding alloys before the MC/MD relaxation (M1r, M2r and M3r).

Figure 5 shows the stress–strain curves obtained during the tensile deformation of bicrystals M1r, M2r, M3r, M1o, M2o and M3o at 300K, while in

Table 1. Yield strength, σ_y, and yield strain, ε_y, of the HEAs.

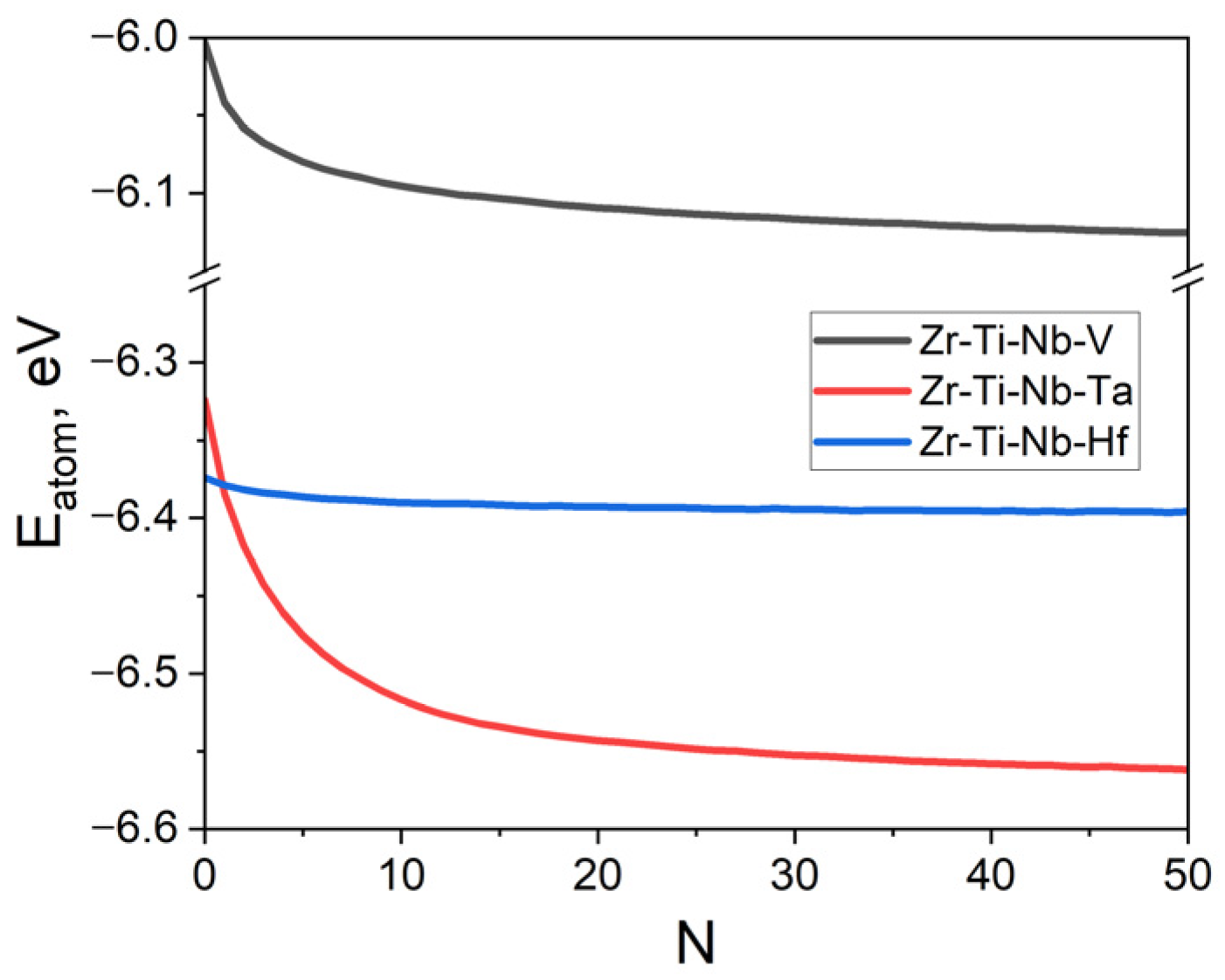
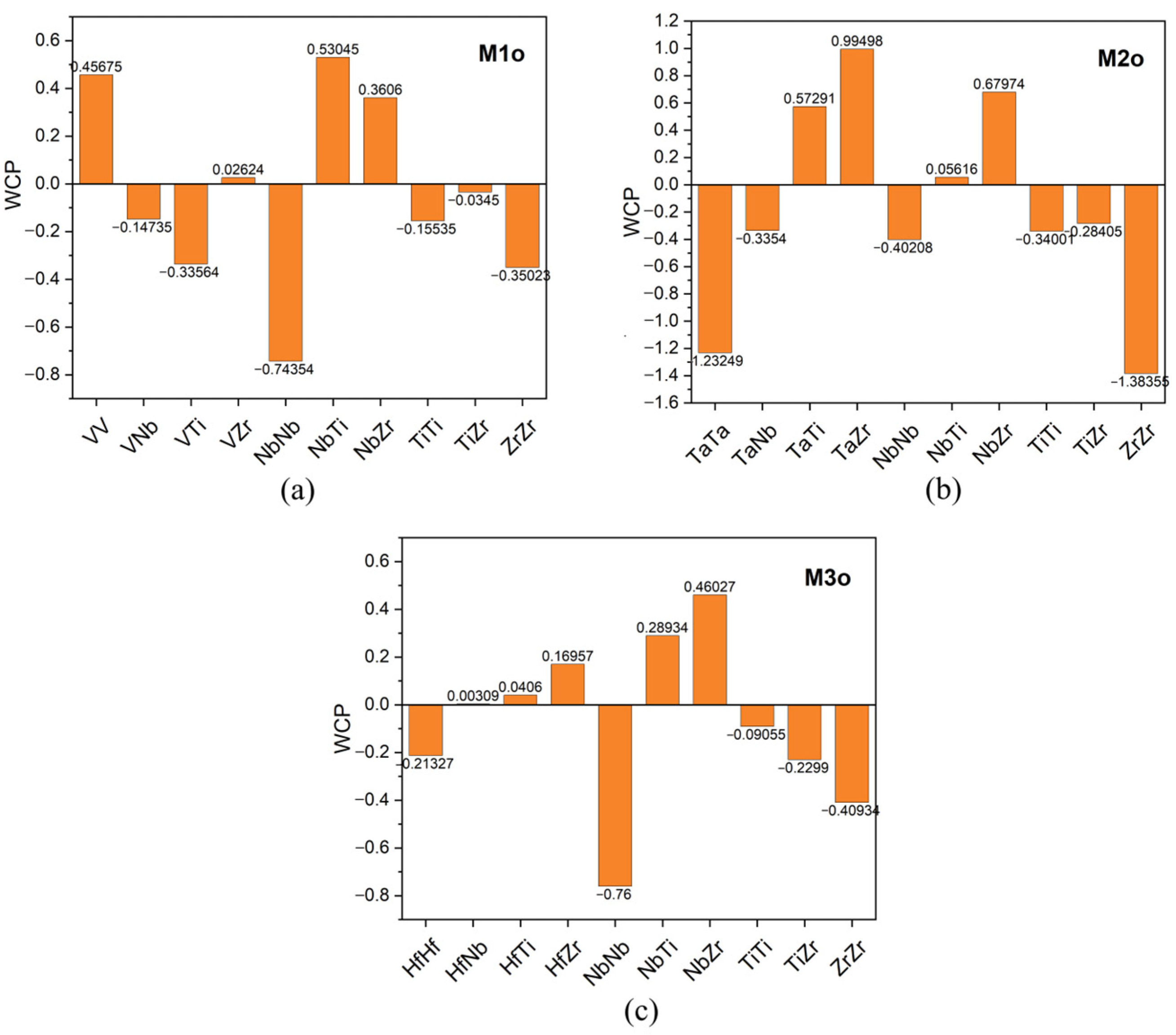
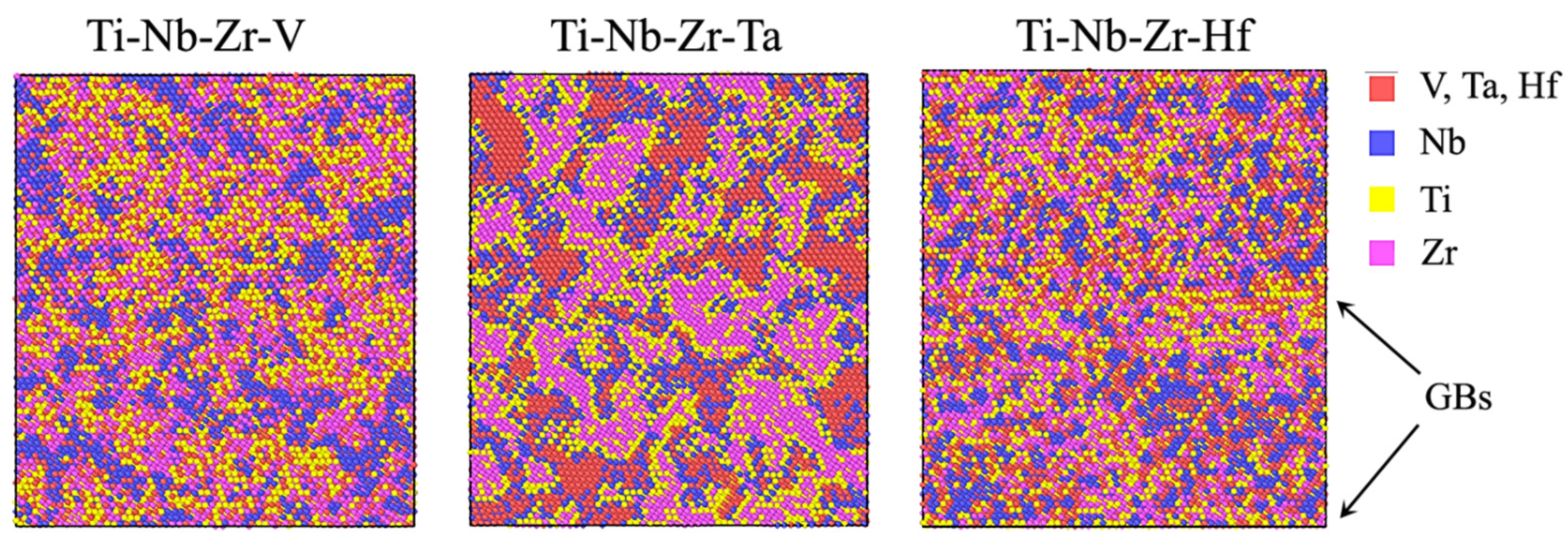
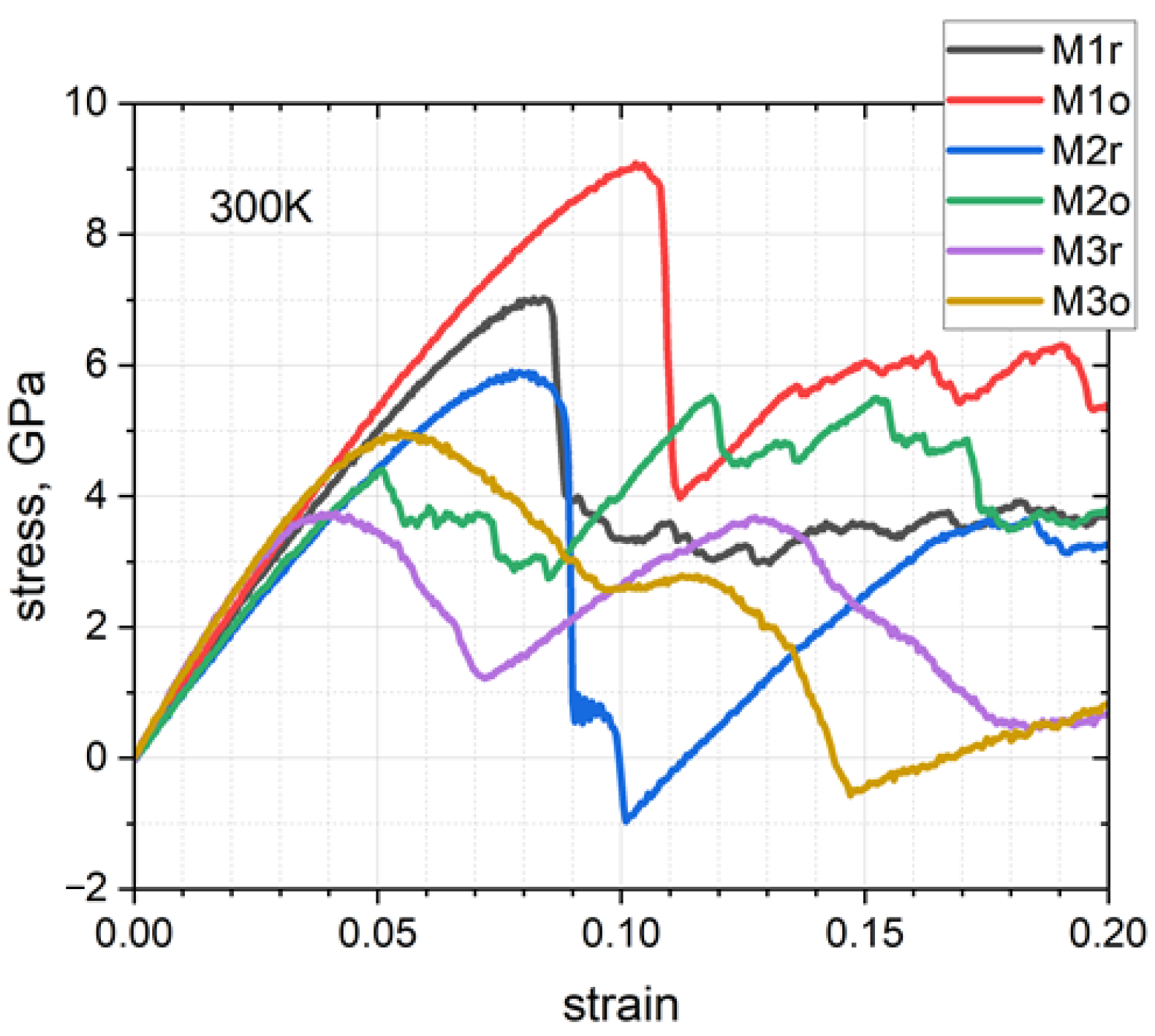
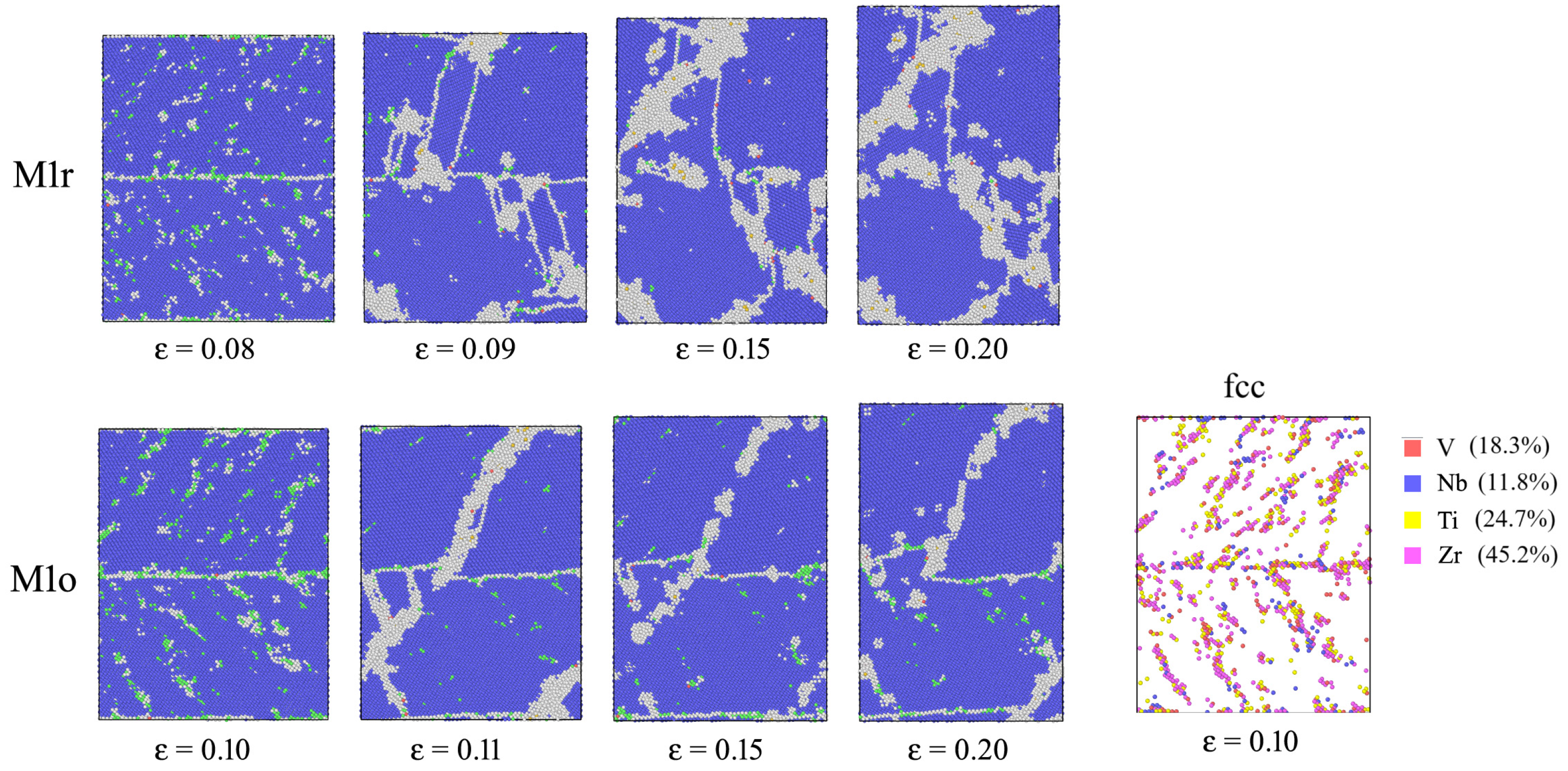
HEA	M1r	M1o	M2r	M2o	M3r	M3o
εy	0.084	0.103	0.078	0.051	0.033	0.051
σy, GPa	7.019	9.081	5.902	4.399	3.561	4.927

, the corresponding values of the yield strength, σ_y, and yield strain, ε_y, of the HEAs are listed. It can be seen that both the chemical composition and the distribution of atoms in the materials significantly affect the deformation behavior of the alloys. When we deal with a random distribution of atoms, the yield strength of alloys decreases in the sequence M1r→M2r→M3r, but for ordered structures it changes to M1o→M3o→M2o. The strength of M1o and M3o is higher than those of M1r and M3r, respectively, while the situation is opposite for the ZrTiNbTa alloy: SRO leads to a weakening of the material.

4. Discussion

To understand the difference in deformation behavior of the HEAs, their structure evolution upon tensile loading is analyzed. The following Figure 6, Figure 7, Figure 8 and Figure 9 demonstrate the structure evolution in the bicrystals of the HEAs ZrTiNbV, ZrTiNbTa and ZrTiNbHf before and after the MD/MC relaxation. Here, the constituent atoms are colored according to the common neighbor analysis: the bcc, fcc, hcp and disordered structures are given in blue, green, red and grey colors, respectively.

Upon tensile loading of both M1r and M1o (Figure 6), first, the randomly distributed areas with the fcc structure appear in the matrix having the bcc structure. It should be noted that in the ordered material, this fcc phase is formed preferably in areas enriched with the Zr. As can be seen from the image in the bottom left corner of Figure 6, the fraction of Zr atoms in the fcc phase is 45.2%. With further deformation, however, the regions with the fcc structure in both the alloys disappear, indicating an unstable feature of the new phase. The latter is accompanied with the abrupt release of stresses caused by the change in deformation mechanisms. At this point, the structure relaxation of M1r occurs through the deformation twinning mechanism. However, in M1o, the formation of twins does not take place, instead, at higher stresses, a shear band emits from one GB and runs through whole the bicrystal crossing the second GB, which results in the material relaxation (Figure 5). Normally, the twinning process in bcc metals starts with the emission of partial dislocations from GBs followed by their propagation inside grains. Such partial dislocations can be produced from the 1/2〈111〉 perfect dislocations lying on {112} planes [51]. It should be noted that in the current work, the number of 1/2〈111〉 perfect dislocations are also observed in M1r at the GB areas. Deformation twins were experimentally found earlier in some refractory bcc HEAs [52,53]. It is believed that the twinning process can improve ductility. Apparently, the absence of twins in the ordered structure of M1o can be explained by the fact that the ordered clusters of Nb and V-Ti (Figure 3a) inhibit the dislocation activity thereby increasing the yield strength (Table 1). Indeed, as has been reported by Fisher [54], when dislocation moves, it destroys atomic order and creates an interface of positive energy; therefore, additional stress is needed to keep the dislocation moving.

When we deal with ZrTiNbTa, the situation looks different (Figure 7). Unlike the previous case, here, the twinning mechanism is dominant in the HEA with ordered structure. This situation shows that the chemical heterogeneity can also promote twin formation. Like in ZrTiNbV, at the beginning of deformation, the clusters of Zr atoms in M2o undergo the bcc to fcc phase transition, and the first twins nucleate from such regions, mostly located at the GB areas. With deformation, the twins become broader and then propagate to the adjacent grain. This process is accompanied with the vanishing of the GBs and transformation of the initial bicrystal to the structure with strips of broad twins oriented perpendicular to the xz plane. At later stages of tensile deformation, amorphization of regions with an excess of Zr atoms can be observed, while hard Ta clusters do not display such behavior (Figure 8b). When the constituent elements of the alloy are distributed randomly (M2r), the tensile loading at the first steps leads to significant lattice distortion. Further strain accumulation leads to the activization of dislocations. The latter results in lattice rotation and fragmentation of initial grains. Borders of such fragments are formed preferably by the <100> sessile edge and 1/2<111> perfect screw dislocations (Figure 8a). Similar deformation behavior was earlier reported for nanocrystalline bcc Fe in [55].

In ZrTiNbHf, regardless of the atom distribution type, the stress-induced phase transition is the main deformation mechanism (Figure 9). It was reported earlier that the addition of Hf decreases the stability of the bcc structure in HEAs [16]. In the current work, deformation of the alloy with Hf starts with the generation of stacking faults. In the ordered alloy M3o, the first stacking faults start propagating from the GBs enriched with the Ti and Zr atoms, as mentioned earlier, while in M3r, they are formed preferably inside grains. The dislocation analysis shows the presence of multiple 1/6<112> Shockley partial dislocations and some 1/3<100> Hirth sessile dislocations separating domains with faulted structures. Apparently, the Nb clusters distributed randomly inside grains of the M3o bicrystal inhibit the dislocation nucleation leading to the higher yield strength and yield strain values compared to those of M3r (Figure 5 and Table 1). That is why the first stacking faults nucleate in M3o at the GB regions. Further tensile loading results in transition of the fragmented faulted areas back to the bcc structure with different crystallographic orientations. Later, such areas can undergo phase transformation with formation of the hcp structure. However, this phase is not stable, especially in the ordered structure, and the reverse transition from hcp to bcc is observed.

5. Conclusions

In this work, the effect of SRO on room temperature tensile deformation of equiatomic HEAs ZrTiNbV, ZrTiNbTa and ZrTiNbHf is analyzed with the help of MD and MC simulation. It was concluded that the chemical ordering during relaxation of the alloys can severely affect their stress–strain response.

It was revealed that the ordered clusters of Nb and V-Ti in ZrTiNbV can suppress the dislocation sliding and twin formation, thereby increasing the yield strength, while in the same alloy without preliminary relaxation, the twinning mechanism prevails. Among the considered HEAs, M1o has the highest yield strength and yield strain.

The opposite situation was revealed for ZrTiNbTa. Here, the twinning mechanism is dominant in the HEA ZrTiNbTa having the ordered structure. This was explained by the absence of Nb clusters and the fact that relatively big areas of the structure enriched with Zr atoms ease nucleation of dislocations and twins. In the non-relaxed material with atoms distributed randomly, the plastic deformation occurs preferably through grain fragmentation which is observed at higher stresses.

The stacking fault formation followed by the stress-induced phase transition are the main deformation mechanisms of ZrTiNbHf regardless of the distribution of constituent atoms. However, the Nb clusters of the relaxed alloy are able to slightly delay the stacking fault formation inside grains. The first dislocations and stacking faults in such alloys nucleate at the GB areas depleted with Nb atoms.