Modeling of a Fluid with Pressure-Dependent Viscosity in Hele-Shaw Flow
Abstract
1. Introduction
2. Mathematical Background
3. Solution near the Corner Edge: General Case
- For antisymmetric flows,
- For symmetric flows,and we require that for , the solution is bounded, i.e., . Therefore, the solution is
- For antisymmetric flows,
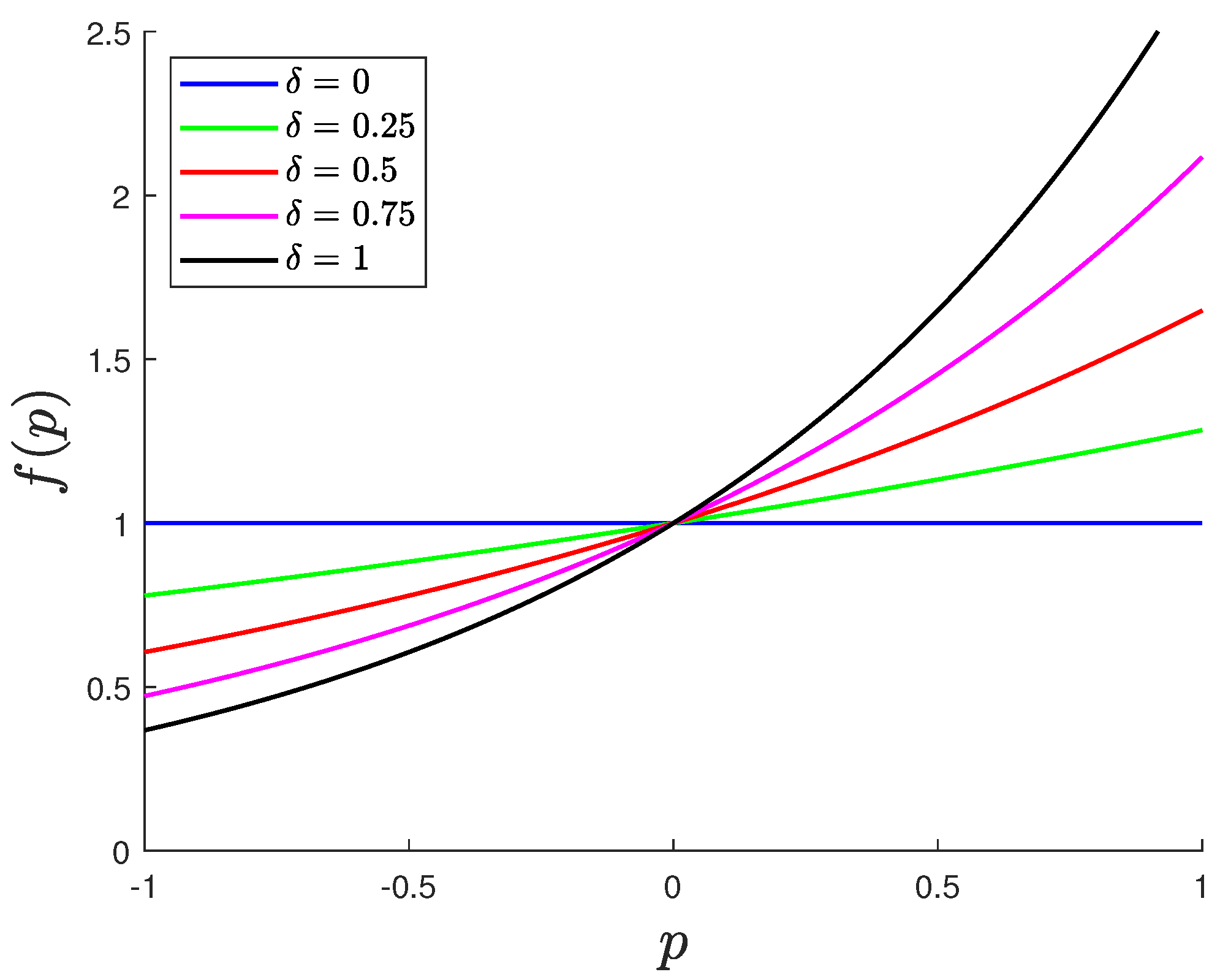
- For symmetric flows,where the smallest eigenvalues and are obtained for , and we set the constants of integration () equal to (1, 0, 1) for antisymmetric flows and () equal to (1, 1, 0) for symmetric flows. As the expression of the dependence of viscosity on pressure is given, we can obtain the pressure field through (28), i.e., by solving with respect to , as follows:
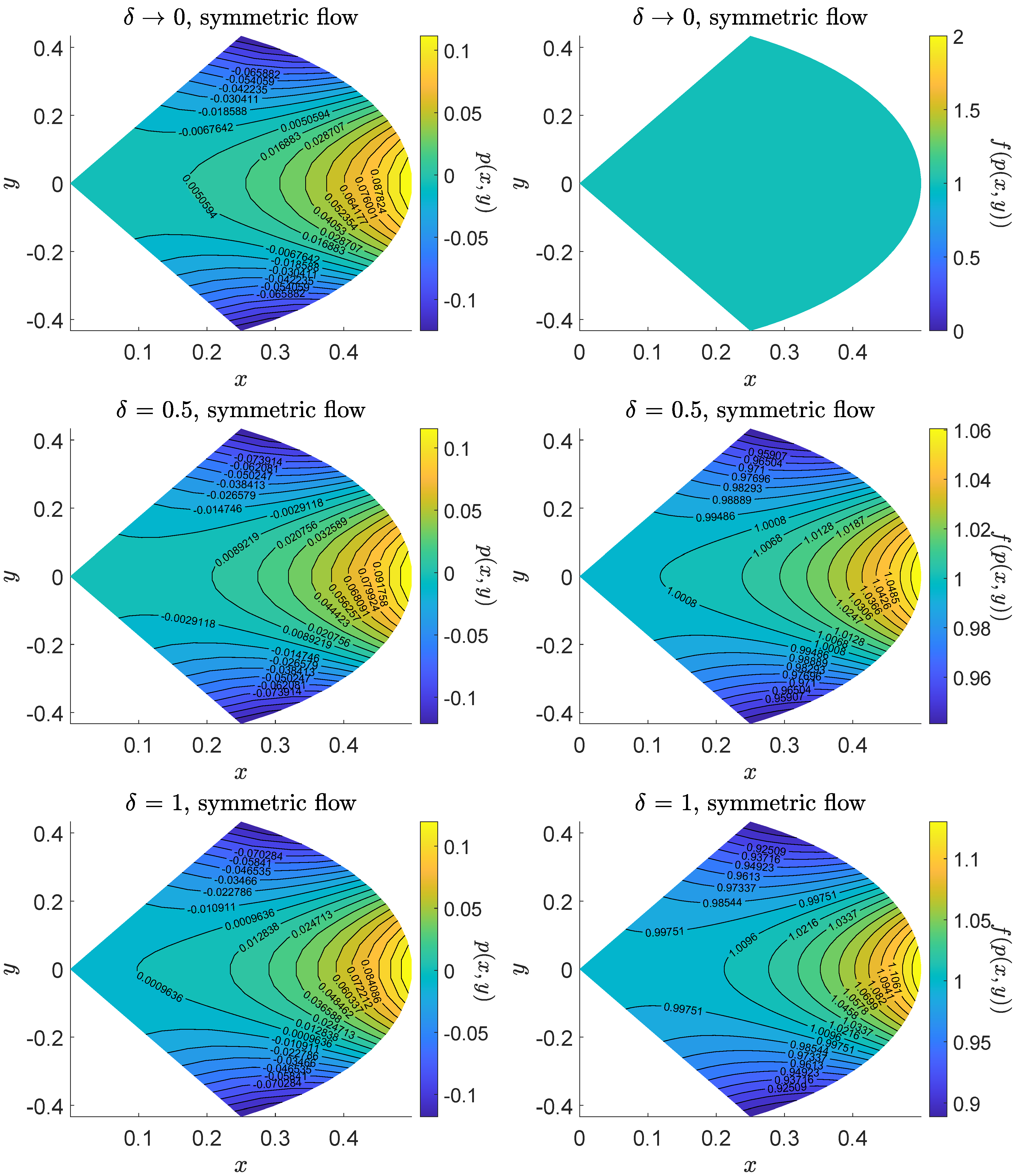
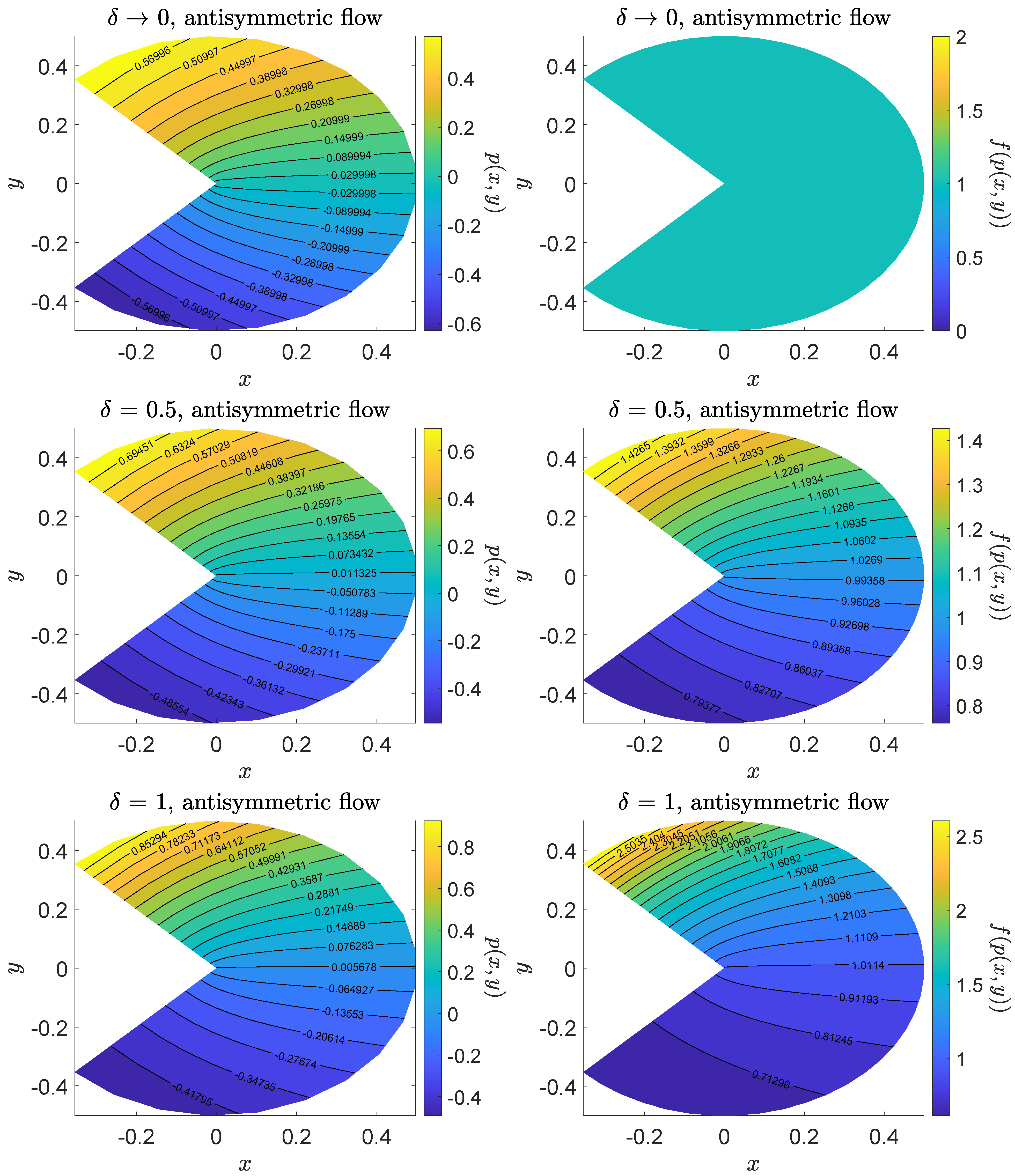
Application to the Case of Viscosity Given by (14)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aronsson, G.; Janfalk, U. On Hele–Shaw flow of power-law fluids. Eur. J. Appl. Math. 1992, 3, 343–366. [Google Scholar] [CrossRef]
- Chupin, L.; Palade, L.I. Generalized Newtonian and Herschel–Bulkley yield stress fluids pressure behavior near the tip of a sharp edge in thin film flows. Phys. Lett. A 2008, 372, 6404–6411. [Google Scholar] [CrossRef]
- Allouche, M.H.; Millet, S.; Botton, V.; Henry, D.; Hadid, H.B.; Rousset, F. Stability of a flow down an incline with respect to two-dimensional and three-dimensional disturbances for Newtonian and non-Newtonian fluids. Phys. Rev. E 2015, 92, 063010. [Google Scholar] [CrossRef] [PubMed]
- Allouche, M.H.; Botton, V.; Millet, S.; Henry, D.; Dagois-Bohy, S.; Güzel, B.; Hadid, H.B. Primary instability of a shear-thinning film flow down an incline: Experimental study. J. Fluid Mech. 2017, 821, R1. [Google Scholar] [CrossRef]
- Balmforth, N.J.; Liu, J.J. Roll waves in mud. J. Fluid Mech. 2004, 519, 33–54. [Google Scholar] [CrossRef]
- Benjamin, T.B. Wave formation in laminar flow down an inclined plane. J. Fluid Mech. 1957, 2, 554. [Google Scholar] [CrossRef]
- Borsi, I.; Farina, A.; Fasano, A.; Rajagopal, K.R. Modelling the combined chemical and mechanical action for blood clotting. Nonlinear Phenom. Energy Dissipation Gakuto Int. Ser. Math. Sci. Appl. Gakkotosho Tokyo 2008, 29, 53–72. [Google Scholar]
- Calusi, B.; Fusi, L.; Farina, A. On a free boundary problem arising in snow avalanche dynamics. ZAMM J. Appl. Math. Mech. Z. Angew. Math. Mech. 2015, 96, 453–465. [Google Scholar] [CrossRef]
- Calusi, B.; Farina, A.; Fusi, L.; Palade, L.I. Stability of a Regularized Casson Flow down an Incline: Comparison with the Bingham Case. Fluids 2022, 7, 380. [Google Scholar] [CrossRef]
- Calusi, B.; Fusi, L.; Farina, A. Linear stability of a Couette flow for non-monotone stress-power law models. Eur. Phys. J. Plus 2023, 138, 933. [Google Scholar] [CrossRef]
- Calusi, B.; Farina, A.; Fusi, L.; Rosso, F. Thermo-mechanical modeling of pancakelike domes on Venus. Phys. Fluids 2024, 36, 056607. [Google Scholar] [CrossRef]
- Chakraborty, S.; Sheu, T.W.H.; Ghosh, S. Dynamics and stability of a power-law film flowing down a slippery slope. Phys. Fluids 2019, 31, 013102. [Google Scholar] [CrossRef]
- Farina, A.; Fusi, L. Viscoplastic Fluids: Mathematical Modeling and Applications. In Non-Newtonian Fluid Mechanics and Complex Flows: Levico Terme, Italy 2016; Farina, A., Mikelić, A., Rosso, F., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 229–298. [Google Scholar] [CrossRef]
- Gholinezhad, S.; Kantzas, A.; Bryant, S.L. Control of interfacial instabilities through variable injection rate in a radial Hele-Shaw cell: A nonlinear approach for late-time analysis. Phys. Rev. E 2023, 107, 065108. [Google Scholar] [CrossRef] [PubMed]
- Hintermüller, M.; Keil, T. Optimal control of geometric partial differential equations. In Geometric Partial Differential Equations—Part II; Elsevier: Amsterdam, The Netherlands, 2021; pp. 213–270. [Google Scholar] [CrossRef]
- Li, P.; Huang, X.; Zhao, Y.P. Active control of electro-visco-fingering in Hele-Shaw cells using Maxwell stress. iScience 2022, 25, 105204. [Google Scholar] [CrossRef] [PubMed]
- Pascal, J.P. Linear stability of fluid flow down a porous inclined plane. J. Phys. D Appl. Phys. 1999, 32, 417–422. [Google Scholar] [CrossRef]
- Petit, N. Optimal control of viscous fingering. J. Process Control 2024, 135, 103150. [Google Scholar] [CrossRef]
- Rajagopal, K.R.; Saccomandi, G.; Vergori, L. Flow of fluids with pressure- and shear-dependent viscosity down an inclined plane. J. Fluid Mech. 2012, 706, 173–189. [Google Scholar] [CrossRef]
- Falsaperla, P.; Giacobbe, A.; Mulone, G. Stability of the Plane Bingham–Poiseuille Flow in an Inclined Channel. Fluids 2020, 5, 141. [Google Scholar] [CrossRef]
- Fernández-Nieto, E.D.; Noble, P.; Vila, J.P. Shallow Water equations for Non-Newtonian fluids. J. Non-Newton. Fluid Mech. 2010, 165, 712–732. [Google Scholar] [CrossRef]
- Fusi, L. Channel flow of viscoplastic fluids with pressure-dependent rheological parameters. Phys. Fluids 2018, 30, 073102. [Google Scholar] [CrossRef]
- Hele-Shaw, H.S. The Flow of Water. Nature 1898, 58, 34–36. [Google Scholar] [CrossRef]
- Hassager, O.; Lauridsen, T.L. Singular behavior of power–law fluids in Hele–Shaw flow. J. Non-Newton. Fluid Mech. 1988, 29, 337–346. [Google Scholar] [CrossRef]
- Hieber, C.; Shen, S. A finite-element/finite-difference simulation of the injection-molding filling process. J.-Non-Newton. Fluid Mech. 1980, 7, 1–32. [Google Scholar] [CrossRef]
- Huilgol, R. On the derivation of the symmetric and asymmetric Hele–Shaw flow equations for viscous and viscoplastic fluids using the viscometric fluidity function. J. Non-Newton. Fluid Mech. 2006, 138, 209–213. [Google Scholar] [CrossRef]
- Ouyang, Y.; Md Basir, M.F.; Naganthran, K.; Pop, I. Unsteady magnetohydrodynamic tri-hybrid nanofluid flow past a moving wedge with viscous dissipation and Joule heating. Phys. Fluids 2024, 36, 062009. [Google Scholar] [CrossRef]
- Barus, C. Isothermals, isopiestics and isometrics relative to viscosity. Am. J. Sci. 1893, s3–45, 87–96. [Google Scholar] [CrossRef]
- Bridgman, P. The Physics of High Pressure; The Macmillan Compan: New York, NY, USA, 1931. [Google Scholar]
- Fusi, L.; Tozzi, R. Falkner–Skan boundary layer flow of a fluid with pressure-dependent viscosity past a stretching wedge with suction or injection. Int. J. Non-Linear Mech. 2024, 163, 104746. [Google Scholar] [CrossRef]
- Klettner, C.; Dang, T.; Smith, F. On the flow past ellipses in a Hele-Shaw cell. J. Fluid Mech. 2023, 971, A12. [Google Scholar] [CrossRef]
- Kondic, L.; Palffy-Muhoray, P.; Shelley, M.J. Models of non-Newtonian Hele-Shaw flow. Phys. Rev. E 1996, 54, R4536–R4539. [Google Scholar] [CrossRef]
- Nassehi, V. Generalized Hele-Shaw models for non-Newtonian, nonisothermal flow in thin curved layers. IMA J. Manag. Math. 1996, 7, 71–88. [Google Scholar] [CrossRef]
- Rajagopal, K.R. On Implicit Constitutive Theories. Appl. Math. 2003, 48, 279–319. [Google Scholar] [CrossRef]
- Rajagopal, K.R.; Saccomandi, G.; Vergori, L. Stability analysis of the Rayleigh–Bénard convection for a fluid with temperature and pressure dependent viscosity. Z. Angew. Math. Phys. 2009, 60, 739–755. [Google Scholar] [CrossRef]
- Rajagopal, K.; Saccomandi, G.; Vergori, L. On the Oberbeck–Boussinesq approximation for fluids with pressure dependent viscosities. Nonlinear Anal. Real World Appl. 2009, 10, 1139–1150. [Google Scholar] [CrossRef]
- Saccomandi, G.; Vergori, L. Piezo-viscous flows over an inclined surface. Q. Appl. Math. 2010, 68, 747–763. [Google Scholar] [CrossRef][Green Version]
- Hron, J.; Málek, J.; Rajagopal, K.R. Simple flows of fluids with pressure–dependent viscosities. Proc. R. Soc. Lond. Ser. A. Math. Phys. Eng. Sci. 2001, 457, 1603–1622. [Google Scholar] [CrossRef]
- Rajagopal, K.; Saccomandi, G.; Vergori, L. Unsteady flows of fluids with pressure dependent viscosity. J. Math. Anal. Appl. 2013, 404, 362–372. [Google Scholar] [CrossRef]
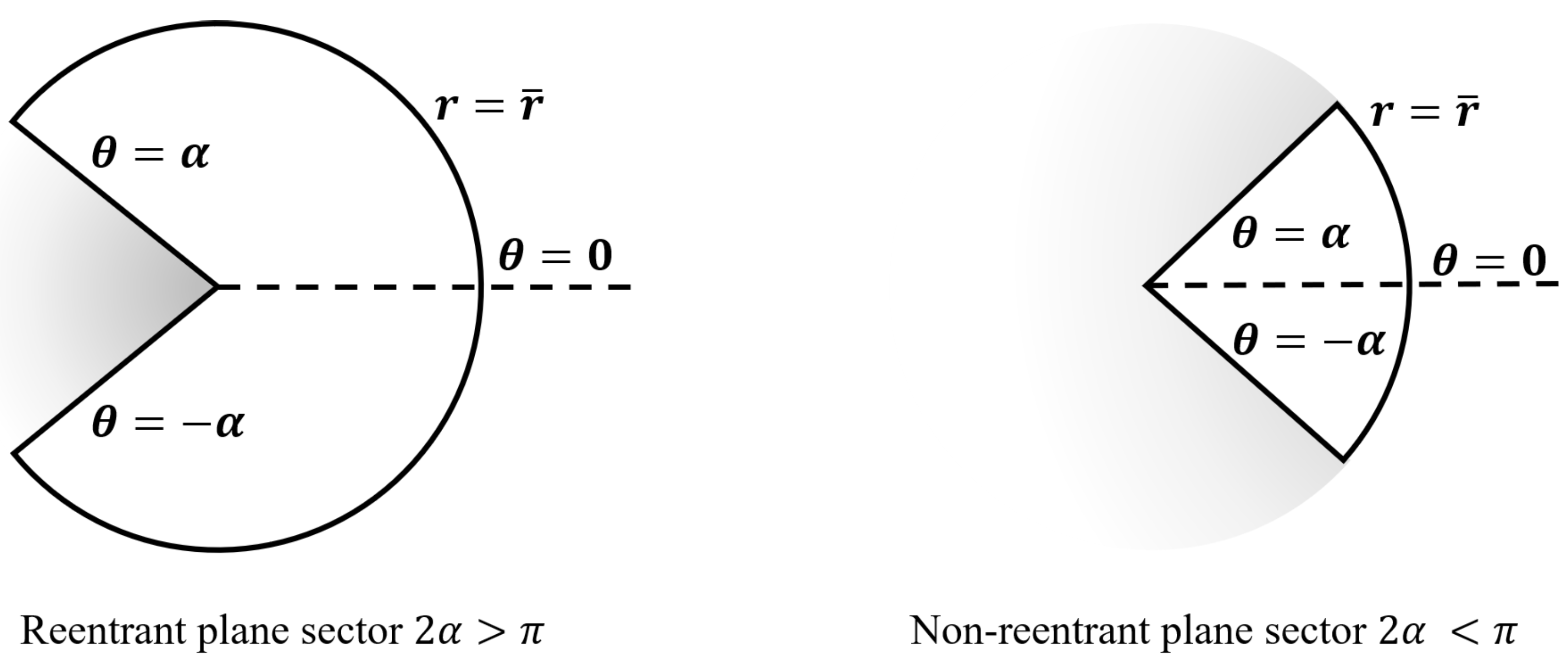





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Calusi, B.; Palade, L.I. Modeling of a Fluid with Pressure-Dependent Viscosity in Hele-Shaw Flow. Modelling 2024, 5, 1490-1504. https://doi.org/10.3390/modelling5040077
Calusi B, Palade LI. Modeling of a Fluid with Pressure-Dependent Viscosity in Hele-Shaw Flow. Modelling. 2024; 5(4):1490-1504. https://doi.org/10.3390/modelling5040077
Chicago/Turabian StyleCalusi, Benedetta, and Liviu Iulian Palade. 2024. "Modeling of a Fluid with Pressure-Dependent Viscosity in Hele-Shaw Flow" Modelling 5, no. 4: 1490-1504. https://doi.org/10.3390/modelling5040077
APA StyleCalusi, B., & Palade, L. I. (2024). Modeling of a Fluid with Pressure-Dependent Viscosity in Hele-Shaw Flow. Modelling, 5(4), 1490-1504. https://doi.org/10.3390/modelling5040077






