Path Planning Method for Wire-Based Additive Manufacturing Processes
Abstract
1. Introduction
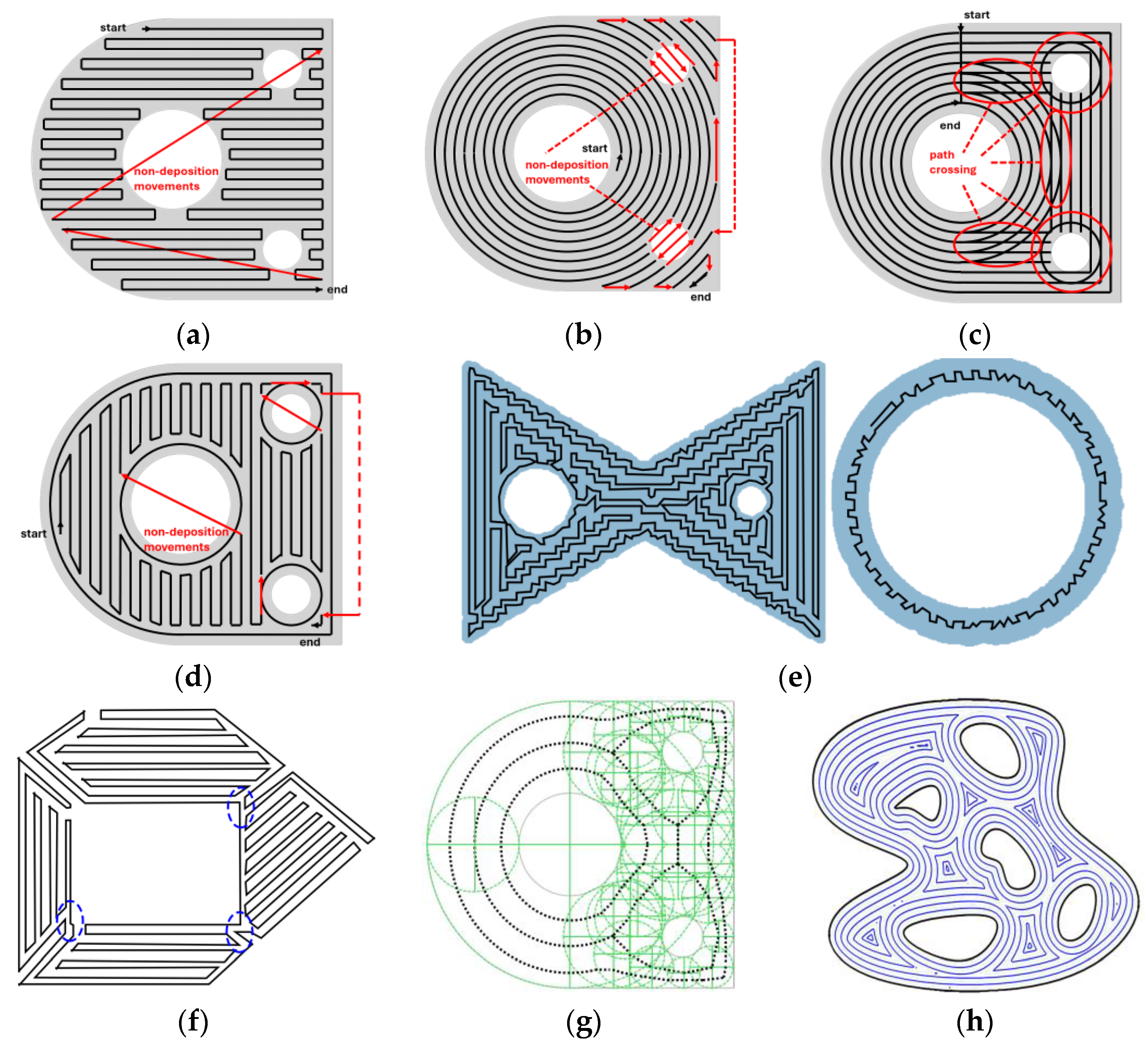
2. Methods
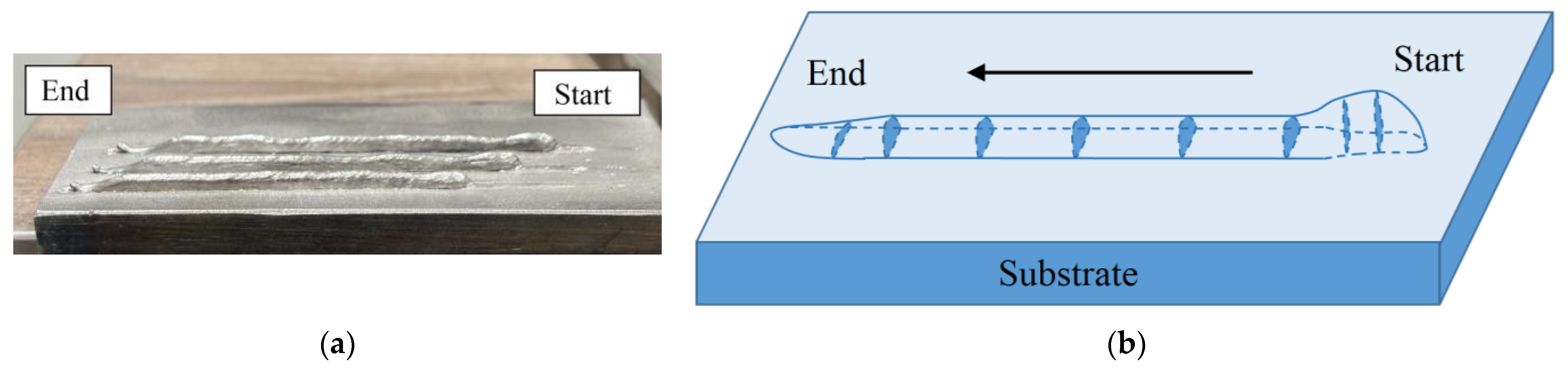
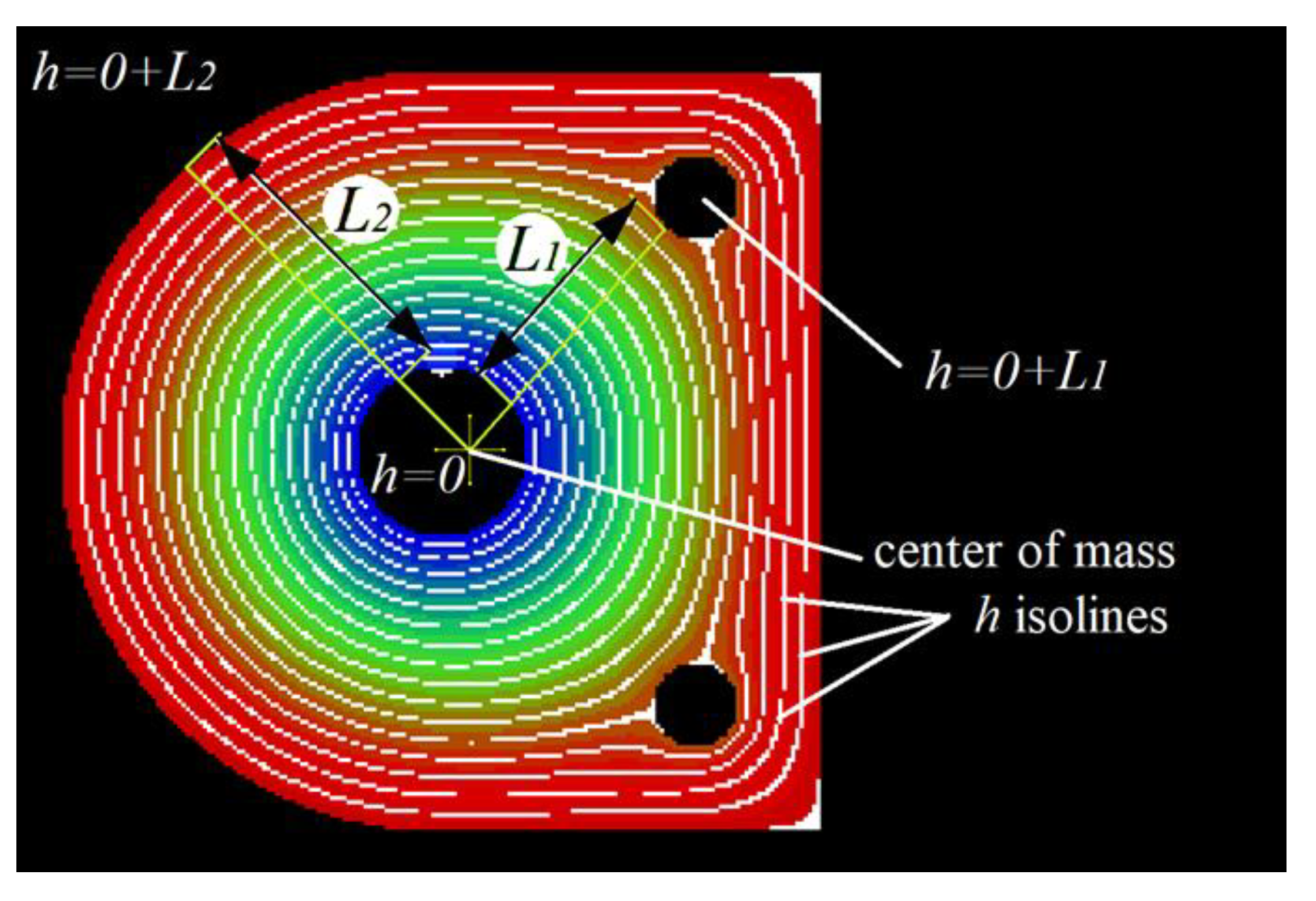
2.1. Layer Cross-Section Analysis
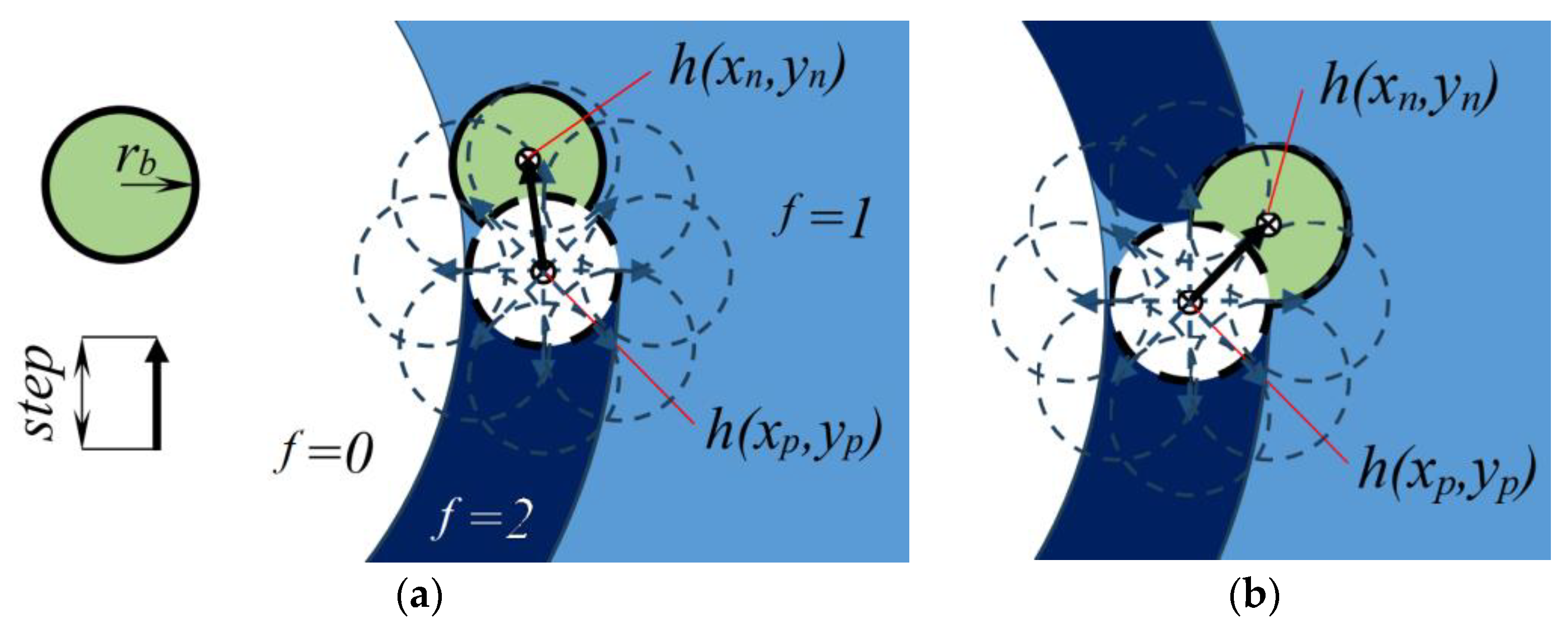
2.2. Path Planning
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Pant, H.; Arora, A.; Gopakumar, G.S.; Chadha, U.; Saeidi, A.; Patterson, A.E. Applications of wire arc additive manufacturing (WAAM) for aerospace component manufacturing. Int. J. Adv. Manuf. Technol. 2023, 127, 4995–5011. [Google Scholar] [CrossRef]
- Stavropoulos, P.; Panagiotopoulou, V.C. Developing a Framework for Using Molecular Dynamics in Additive Manufacturing Process Modelling. Modelling 2022, 3, 189–200. [Google Scholar] [CrossRef]
- Li, Y.; Su, C.; Zhu, J. Comprehensive review of wire arc additive manufacturing: Hardware system, physical process, monitoring, property characterization, application and future prospects. Results Eng. 2022, 13, 100330. [Google Scholar] [CrossRef]
- Shaikh, M.O.; Chen, C.C.; Chiang, H.C.; Chen, J.R.; Chou, Y.C.; Kuo, T.Y.; Ameyama, K.; Chuang, C.H. Additive manufacturing using fine wire-based laser metal deposition. Rapid Prototyp. J. 2020, 26, 473–483. [Google Scholar] [CrossRef]
- Fuchs, J.; Schneider, C.; Enzinger, N. Wire-based additive manufacturing using an electron beam as heat source. Weld World 2018, 62, 267–275. [Google Scholar] [CrossRef]
- Jafari, D.; Vaneker, T.H.J.; Gibson, I. Wire and arc additive manufacturing: Opportunities and challenges to control the quality and accuracy of manufactured parts. Mater. Des. 2021, 202, 109471. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, Y. Path Planning Strategies to Optimize Accuracy, Quality, Build Time and Material Use in Additive Manufacturing: A Review. Micromachines 2020, 11, 633. [Google Scholar] [CrossRef] [PubMed]
- Schmitz, M.; Wiartalla, J.; Gelfgren, M.; Mann, S.; Corves, B.; Hüsing, M. A Robot-Centered Path-Planning Algorithm for Multidirectional Additive Manufacturing for WAAM Processes and Pure Object Manipulation. Appl. Sci. 2021, 11, 5759. [Google Scholar] [CrossRef]
- Martina, F.; Mehnen, J.; Williams, S.W.; Colegrove, P.; Wang, F. Investigation of the benefits of plasma deposition for the additive layer manufacture of Ti–6Al–4V. J. Mater. Process. Technol. 2012, 212, 1377–1386. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Li, P.; Male, A.T. Weld deposition-based rapid prototyping: A preliminary study. J. Mater. Process. Technol. 2003, 135, 347–357. [Google Scholar] [CrossRef]
- Nguyen, Q.L. Tool Path Planning for Wire-Arc Additive Manufacturing Processes. Ph.D. Dissertation, Faculty of Mechanical Engineering, Electrical and Energy Systems of the Brandenburg University of Technology Cottbus, Cottbus, Germany, 2022. [Google Scholar]
- Ferreira, R.P.; Vilarinho, L.O.; Scotti, A. Enhanced-pixel strategy for wire arc additive manufacturing trajectory planning: Operational efficiency and effectiveness analyses. Rapid Prototyp. J. 2024, 30, 1–15. [Google Scholar] [CrossRef]
- Ferreira, R.P.; Scotti, A. The Concept of a Novel Path Planning Strategy for Wire + Arc Additive Manufacturing of Bulky Parts: Pixel. Metals 2021, 11, 498. [Google Scholar] [CrossRef]
- Ferreira, R.P.; Vilarinho, L.O.; Scotti, A. Development and implementation of a software for wire arc additive manufacturing preprocessing planning: Trajectory planning and machine code generation. Weld. World 2022, 66, 455–470. [Google Scholar] [CrossRef]
- Sohrabi, S.; Ziarati, K.; Keshtkaran, M.A. Greedy randomized adaptive search procedure for the orienteering problem with hotel selection. Eur. J. Oper. Res. 2020, 283, 426–440. [Google Scholar] [CrossRef]
- Ding, D.; Pan, Z.; Cuiuri, D.; Li, H. A tool-path generation strategy for wire and arc additive manufacturing. Int. J. Adv. Manuf. Technol. 2014, 73, 173–183. [Google Scholar] [CrossRef]
- Ding, D.; Pan, Z.; Cuiuri, D.; Li, H.; Larkin, N. Adaptive path planning for wire-feed additive manufacturing using medial axis transformation. J. Clean. Prod. 2016, 133, 942–952. [Google Scholar] [CrossRef]
- Hong, X.; Xiao, G.; Zhang, Y.; Zhou, J. A new path planning strategy based on level set function for layered fabrication processes. Int. J. Adv. Manuf. Technol. 2022, 119, 517–529. [Google Scholar] [CrossRef]
- Le Dret, H.; Lucquin, B. The Finite Difference Method for Elliptic Problems. In Partial Differential Equations: Modeling, Analysis and Numerical Approximation; International Series of Numerical Mathematics; Birkhäuser: Cham, Switzerland, 2016; Volume 168. [Google Scholar] [CrossRef]
- Herman, E.; Strang, G. Calculus. Volume 3; OpenStax: Houston, TX, USA, 2016. [Google Scholar]
- Zhang, C.; Sun, P. Heuristic Methods for Solving the Traveling Salesman Problem (TSP): A Comparative Study. In Proceedings of the 2023 IEEE 34th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC), Toronto, ON, Canada, 5–8 September 2023; pp. 1–6. [Google Scholar] [CrossRef]
- Kadyrova, G.R. Intelligent Systems; Ul’anovsk State Technical University: Ul’anovsk, Russia, 2017. [Google Scholar]
- Fuchs, C.; Baier, D.; Semm, T.; Zaeh, M.F. Determining the machining allowance for WAAM parts. Prod. Eng. Res. Devel. 2020, 14, 629–637. [Google Scholar] [CrossRef]
- Soh, G.S.; Oh, X.Y. Wire Arc Additive Manufacturing Stepover Optimization based on Varying-Ratio Flat-Top Overlapping Model. In Proceedings of the 9th International Conference of Asian Society for Precision Engineering, Nanotechnology (ASPEN 2022), Singapore, 15–18 November 2022; Sharon, N.M.L., Kumar, A.S., Eds.; [Google Scholar] [CrossRef]
- Yanenko, N.N. The Method of Fractional Steps: The Solution of Problems of Mathematical Physics in Several Variables; Springer: Berlin/Heidelberg, Germany, 1971. [Google Scholar]


| Parameter | Description | Value | Unit |
|---|---|---|---|
| X | layer size along x-axis | 0.2 | m |
| Y | layer size along y-axis | 0.2 | m |
| h | coordinate step | 0.001 | m |
| Δt | time step | 0.5 | s |
| rb | surfacing spot radius | 0.004 | m |
| step | path planning step | 0.0068 | m |
| λ | heat conductivity | 30 | W/(m·K) |
| c | specific heat | 450 | J/(kg·K) |
| ρ | density | 7800 | kg/m3 |
| p | heat source power | 800 | W |
| reff | heat source effective radius | 0.003 | m |
| soverlap | overlap area fraction | 0.35 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shcherbakov, A.; Gudenko, A.; Sliva, A.; Gaponova, D.; Marchenkov, A.; Goncharov, A. Path Planning Method for Wire-Based Additive Manufacturing Processes. Modelling 2024, 5, 2040-2050. https://doi.org/10.3390/modelling5040105
Shcherbakov A, Gudenko A, Sliva A, Gaponova D, Marchenkov A, Goncharov A. Path Planning Method for Wire-Based Additive Manufacturing Processes. Modelling. 2024; 5(4):2040-2050. https://doi.org/10.3390/modelling5040105
Chicago/Turabian StyleShcherbakov, Alexey, Alexander Gudenko, Andrey Sliva, Daria Gaponova, Artem Marchenkov, and Alexey Goncharov. 2024. "Path Planning Method for Wire-Based Additive Manufacturing Processes" Modelling 5, no. 4: 2040-2050. https://doi.org/10.3390/modelling5040105
APA StyleShcherbakov, A., Gudenko, A., Sliva, A., Gaponova, D., Marchenkov, A., & Goncharov, A. (2024). Path Planning Method for Wire-Based Additive Manufacturing Processes. Modelling, 5(4), 2040-2050. https://doi.org/10.3390/modelling5040105






