AutoRL-Sim: Automated Reinforcement Learning Simulator for Combinatorial Optimization Problems

Abstract

Reinforcement learning is a crucial area of machine learning, with a wide range of applications. To conduct experiments in this research field, it is necessary to define the algorithms and parameters to be applied. However, this task can be complex because of the variety of possible configurations. In this sense, the adoption of AutoRL systems can automate the selection of these configurations, simplifying the experimental process. In this context, this work aims to propose a simulation environment for combinatorial optimization problems using AutoRL. The AutoRL-Sim includes several experimentation modules that cover studies on the symmetric traveling salesman problem, the asymmetric traveling salesman problem, and the sequential ordering problem. Furthermore, parameter optimization is performed using response surface models. The AutoRL-Sim simulator allows users to conduct experiments in a more practical way, without the need to worry about implementation. Additionally, they have the ability to analyze post-experiment data or save them for future analysis.

1. Introduction

One of the most critical points of machine learning (ML) is selecting the appropriate algorithm and parameter tuning for the process [1,2,3,4,5]. In this sense, for each dataset and application, there may be an ideal combination of algorithm and parameters, which can make manual evaluation a costly task [6,7,8,9,10]. In the literature, there are several approaches that can be employed to optimize these ML parameters, such as response surface methodology (RSM) [11], variable neighborhood search (VNS) [12], reactive search [13], projective simulation [7], empirical methods [14], random search [15], grid search [16], Bayesian optimization [17], and Hyperband [18].

It should also be noted that defining the initial conditions of the experiment may involve multiple steps and verifications, requiring considerable time from the experimenter. However, even with all this effort, there is still the possibility that the chosen configuration is not the most appropriate for the problem at hand. Therefore, one way to reduce the time spent starting the experiment and help the artificial intelligence user is to automate the ML process. In this context, automated machine learning (AutoML) emerges, which can be used to optimize [2,19,20] and recommend [1,9,21] parameters and algorithms. In AutoML, the objective is to minimize human work by automatically determining the optimal algorithms and/or parameters for the tasks under analysis [1,2,3,6,22].

When AutoML is applied to reinforcement learning (RL), it is called AutoRL (automated reinforcement learning) [23,24]. RL is a field of artificial intelligence and machine learning that covers areas such as statistics and computer science. In this type of learning, an agent is immersed in a dynamic environment without previously knowing which actions should be selected [25,26]. Thus, the agent must learn about the environment through its interactions, using trial and error to determine which actions yield better results [13,25,26]. In AutoRL, in the same way as in conventional RL, the agent has no prior knowledge and learns from the reinforcements received while interacting with the environment. It is worth mentioning that, while in conventional RL, the learning conditions are defined by the experimenter, in AutoRL, the experimental process is automated [7,27,28]. However, the literature still lacks dedicated AutoRL frameworks for combinatorial optimization problems.

Reinforcement learning has relevant applications in combinatorial optimization, such as the vehicle routing problem (VRP) [29], the symmetric traveling salesman problem (TSP) [30,31], the asymmetric traveling salesman problem (ATSP) [30], minimum vertex cover (MVC) [31,32], maximum cut (Max-Cut) [31,32], and the bin-packing problem (BPP) [32]. On the other hand, it can be challenging for users, especially beginners, to develop algorithms and configure initial RL experiment settings for combinatorial optimization. In this sense, several studies in the literature have already addressed the challenge of tuning RL parameters for combinatorial optimization problems. The paper by [11] proposed the application of response surface methodology to model the behavior of learning rate and discount factor parameters in RL performance to solve the TSP. Following this line, the study by [33] investigated the influence of RL parameters in resolving instances of the sequential ordering problem. In another work [34], the effects of RL parameters on a variation of TSP with refueling on routes were evaluated. Faced with this challenge, one way to overcome this problem would be to develop AutoRL simulation environments.

The development of simulation environments and frameworks in order to facilitate experiments for users is a frequent topic in several studies [35,36,37,38,39,40,41]. In the context of reinforcement learning, some work has already been proposed in this area, including applications in combinatorial optimization [39], mobile robotics [42], environmental modeling [43], scheduling problems [44], and automation in test selection for continuous integration [45]. The literature also already has some proposals for AutoRL simulators. For example, the authors of [38] develop a simulator for pH control. In [41], the authors present a framework for automated circuit sizing. In another paper, the authors of [24] develop a framework to automate the creation of pipelines for AutoRL. However, there is still a lack of studies that address the development of simulation environments aimed at tuning RL parameters for combinatorial optimization problems using AutoRL.

In this context, the objective of this paper is to propose an AutoRL simulation environment for carrying out experiments in combinatorial optimization. The proposed framework has applications in three types of problems: the symmetric traveling salesman problem, the asymmetric traveling salesman problem, and the sequential ordering problem (SOP). Furthermore, the developed simulator is free and was developed in the R language, widely covered in research in the ML field. Therefore, in summary, the main contributions of this paper are:

• New AutoRL simulator for combinatorial optimization problems.
• Modules for simulations with three traditional problems from the literature: TSP, ATSP, and SOP.
• Modules for simulations with AutoML for automated parameter tuning.
• Free environment developed using the R language and available in a GitHub repository.
• Case studies with three combinatorial optimization problems using AutoRL.
• Optimization of RL parameters using response surface models for the three applications: TSP, ATSP, and SOP.

This paper is divided into six sections. In Section 2, the theoretical foundation is presented. In Section 3, the automated reinforcement learning simulator (AutoRL-Sim) for combinatorial optimization problems is described in detail. In Section 4, case studies that were carried out are presented. Finally, Section 5 presents a comparison with other literature studies, and Section 6 presents conclusions.

2. Background

2.1. Reinforcement Learning

Reinforcement learning is an artificial intelligence method that is based on the trial-and-error process [25]. This technique is based on Markov decision processes, which are characterized by states (S), actions (A), rewards (R), and a transition function (T). In summary, the probabilistic function T describes state transitions, and R is the reward function that provides rewards for actions performed in specific states [25,46,47].

In RL, an agent makes decisions by taking actions on states based on its perceptions. Subsequently, the agent receives rewards for successes or penalties for failures [25,48]. Through interactions with the environment, the agent acquires knowledge about the learning task. Thus, the learning agent seeks to make decisions that result in optimized rewards [25,26,49].

2.1.1. Q-Learning

Q-learning is a reinforcement learning algorithm based on the temporal difference method proposed by Watkins [50] and is suitable for model-free learning situations [26,51]. Through this method, the agent seeks to learn a value function called Q(s,a), where a represents the action performed in the state s [49].

The update of the learning matrix Q in the Q-learning algorithm is expressed by Equation (1) [26,51]:

$$Q_{t+1}(s_t,a_t)=Q_t(s_t,a_t)+\alpha [r(s_t,a_t)+\gamma ma{x}_{a^{\prime }}Q(s^{\prime },a^{\prime })-Q_t(s_t,a_t)],$$

(1)

in which Q is the learning matrix with dimensions n_s × n_a, where n_s is the number of states and n_a is the number of actions permitted to the agent; α is the learning rate; γ is the discount factor; s_t is the current state; a_t is the action performed in the current state; r(s,a) is the reinforcement received for performing the action a_t in state s_t; s′ is the future state; and a′ is the action that will be performed in the future state.

Algorithm 1 presents the Q-learning [26] procedural form:

Algorithm 1: Q-learning Algorithm

1  Set the parameters: $\alpha , \gamma \mathrm{e} ϵ$ 2  In each s,a do Q(s,a) = 0 3  Observe the state s 4  do 5    Select action a using policy ϵ-greedy 6    Run the action a 7    Receive the immediate reward r(s,a) 8    Observe the new state s’ 9    $Q(s_t,a_t)=Q(s_t,a_t)+\alpha [r(s_t,a_t)+\gamma Q(s^{\prime },a^{\prime })-Q(s_t,a_t)]$ 10    s = s’ 11  while the stop criterion is satisfied;

2.1.2. SARSA

The SARSA algorithm is a variation of Q-learning. This method was named by [52] and is based on the sequence State → Action → Reward→ State → Action [26,49]. The update of the SARSA algorithm is expressed according to Equation (2):

$$Q_{t+1}(s_t,a_t)=Q_t(s_t,a_t)+\alpha [r(s_t,a_t)+\gamma Q(s^{\prime },a^{\prime })-Q_t(s_t,a_t)],$$

(2)

in which Q is the learning matrix; s_t is the current state; a_t is the action performed in the current state; r(s,a) is the reinforcement received for performing the action a_t in the state s_t; α is the learning rate; γ is the discount factor; s′ is the future state; and a′ is the action that will be performed in the future state.

Algorithm 2 shows SARSA [26]:

Algorithm 2: SARSA Algorithm

1  Set the parameters: $\alpha , \gamma \mathrm{e} ϵ$ 2  In each s,a do Q(s,a) = 0 3  Observe the state s 4  Select action a using policy $ϵ$-greedy 5  do 6    Run the action a 7    Receive the immediate reward r(s,a) 8    Observe the new state s′ 9    Select action a′ using policy ϵ-greedy 10    $Q(s_t,a_t)=Q(s_t,a_t)+\alpha [r(s_t,a_t)+\gamma Q(s^{\prime },a^{\prime })-Q(s_t,a_t)]$ 11    s = s′ 12    a = a′ 13  while the stop criterion is satisfied;

2.2. Automated Reinforcement Learning

RL is a constantly evolving research area with applications across a wide range of domains, including games [53,54,55] and robotics [56,57,58]. However, conducting studies in RL can be a challenging task, as experimenters need to define a variety of settings, such as parameters and algorithms [23].

Adjusting the optimal configurations for machine learning methods is crucial, as these can have a significant impact on the results obtained [10,59]. Defining these characteristics can be costly and susceptible to error given the vast number of combinations of possible parameter values, which increases the probability of not finding the best configuration for the problem in question [23].

RL methods present several characteristics that can be optimized, such as algorithms, parameters, and reward functions. One approach to automating these learning decisions is the use of AutoML. Thus, when applied to RL, AutoML is called AutoRL [23,59].

In the literature, there are several studies that address the use of AutoRL. For example, the authors of [60] use AutoRL to optimize the reward function applied to the locomotion of quadruped robots. In [61], the authors apply AutoRL for optimizations during processes carried out with microgrids. In the work of [62], the authors propose a system that uses AutoRL to train an agent capable of controlling traffic lights. The authors of [63] present an automated approach to defining network architectures. Finally, in the work presented by [64], the authors present an automated system for determining appropriate configurations in dynamic pricing problems.

2.3. Combinatorial Optimization Problems

Optimization problem applications seek to minimize or maximize an objective function. Thus, the goal is to find an optimal solution for a specific situation. In summary, an optimization problem can be characterized by the following properties [32,65]:

• Objective function: Contains the criteria that can be adjusted during the search for the optimal solution. All combinatorial optimization problems have at least one objective function.
• Restrictions: Applied to ensure the viability of the solution found. An optimization problem can contain several constraints or none.
• Decision variables: Represent the criteria that will be adjusted during the search process for the optimal solution.

Some examples of combinatorial optimization problems can be found in the literature, such as [32,33,66,67,68]: the symmetric traveling salesman problem (TSP), the asymmetric traveling salesman problem (ATSP), the sequential ordering problem (SOP), and the jobshop scheduling problem (JSP).

3. AutoRL-Sim

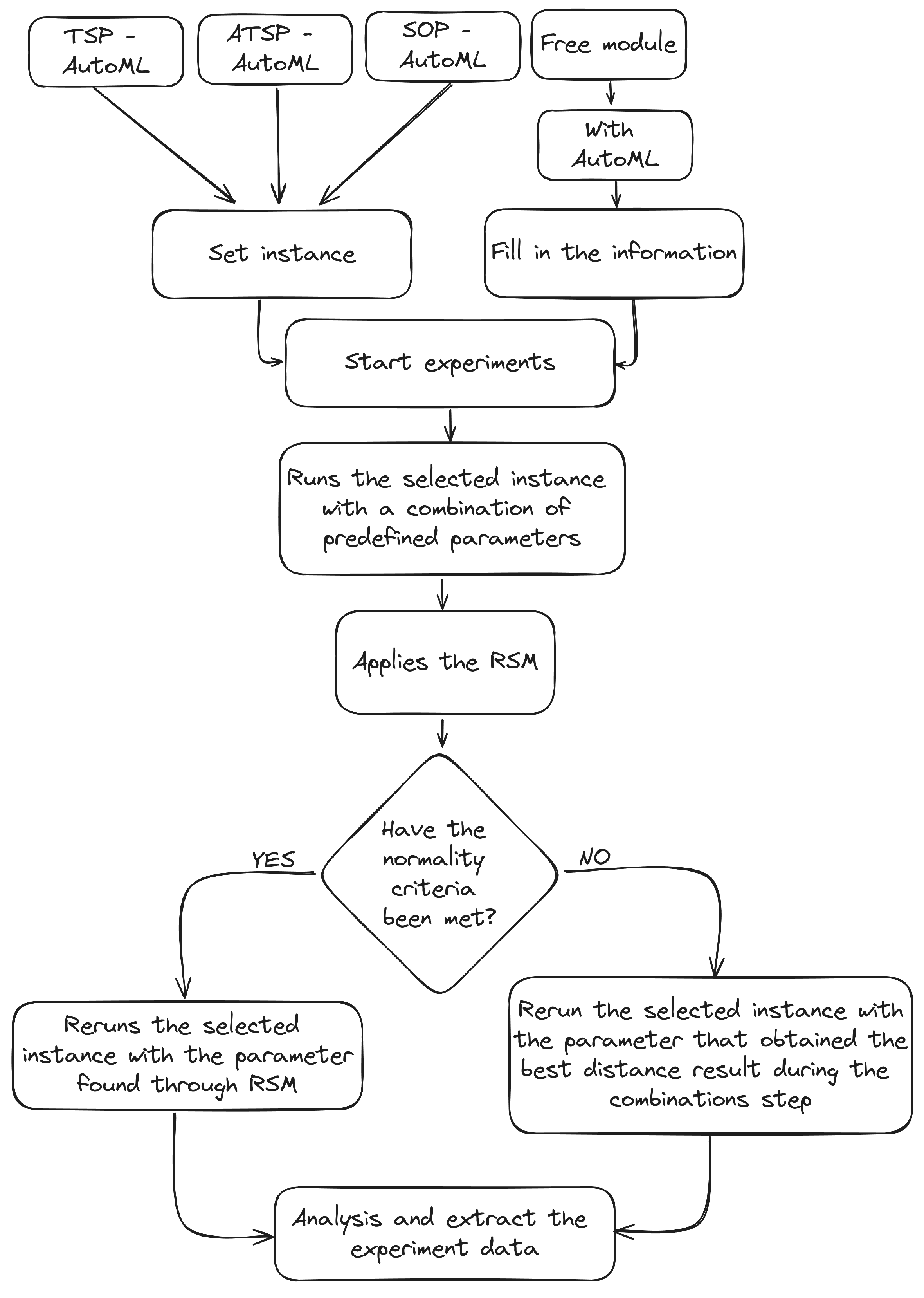
In this section, an automated reinforcement learning simulator for combinatorial optimization problems (AutoRL-Sim) is proposed. The primary objective of this tool is to facilitate the execution of experiments, providing users with a simplified approach and allowing them to focus their efforts on analyzing the results. Figure 1 illustrates an overview of how AutoRL-Sim works.

Algorithms 3 and 4 show how the tool works using procedural algorithms. Algorithm 3 shows how the modules that do not use AutoML work. Algorithm 4 shows how the modules that use AutoML work. It should be noted that the entire description presented in Algorithms 3 and 4 also applies to the free modules, differing only in the way the data are entered before the experiment begins.

Algorithm 3: Workflow of Modules without AutoML

Step 1 (on the interface)

1  Select the TSP/ATSP/SOP instance to be executed 2  Enter the value of the learning rate, the discount factor, the e-greedy policy, and the number of episodes, or choose the option to generate these values randomly 3  Click on the start experiment button

Step 2 (on the server)

4  The values for $\alpha$, $\gamma$, and $ϵ$ and number of episodes used are those defined by the user 5  The number of epochs is set to 1 6  Run SARSA or Q-learning 7  Returns the distance result obtained and the other necessary data

Step 3 (on the interface)

8  Displays the graphs and the report to the user

In Algorithm 3, which represents how the modules work without AutoML, the user must initially enter the information needed to carry out the experiment via the interface. Then, on the server, the selected instance will be executed with the parameters (learning rate, discount factor, e-greedy policy, and number of episodes) defined by the user. Finally, the results obtained are presented to the user on the interface via graphs and a report.

Algorithm 4: AutoML Module Workflow

Step 1 (on the interface)

1  Select the TSP/ATSP/SOP instance to be executed 2  Click on the start experiment button

Step 2 (on the server)

3  The $\alpha$ and $\gamma$ parameters are defined 4  The $ϵ$ parameter is set to 0.01 5  The number of epochs is set to 5 6  The number of episodes is set to 1000 7  foreach ${\alpha }_t$∈α do 8   foreach ${\gamma }_t$∈γ do 9    for epoch to numberEpochs do 10     Run SARSA or Q-learning 11     Stores the distance obtained and the parameters used in the current run 12    end 13   end 14  end 15  Fits a regression model to the data 16  Generates the model’s statistical data 17  Generates the response surface using RSM 18  Extracts the stationary points from the RSM model 19  The new $\alpha$ and $\gamma$ values are defined from the model’s stationary points 20  if (normality > 0.05 & significance < 0.05 & ($0.01<\alpha <1$) & ($0<\gamma <1$)) then 21   $\alpha$ and $\gamma$ values are maintained 22  else 23   The $\alpha$ and $\gamma$ values are updated to the values that gave the best distance result    when running the combinations 24  end 25  The number of episodes is set to 10,000 26  for epoch to numberEpochs do 27   Run SARSA or Q-learning 28  end 29  Returns the best distance result obtained from the 5 epochs and the other necessary data

Step 3 (on the interface)

30  Displays the graphs and the report to the user

Algorithm 4 shows how modules with AutoML work. Here, the user only has to select the instance to be executed (and the other necessary data, if it is an experiment in the free module). On the server, the selected problem will initially be run with various combinations of parameters (the α and γ parameters are initialized with the values [0.01, 0.15, 0.30, 0.45, 0.60, 0.75, 0.90, 0.99], while ϵ is constantly kept at 0.01), and the results will be stored. After that, RSM will be applied to generate the regression model of the problem, and some validations will be carried out. If the model meets the requirements, the learning rate and discount factor parameters are set as the model’s stationary points. Otherwise, the parameters (learning rate and discount factor) are set to the values of alpha and gamma that gave the best result during the combination stage. Next, the problem is run again, this time with only the new parameters and over 5 epochs. Finally, the best result from these 5 epochs and the rest of the information from the experiment are shown to the user in the form of graphs and a report.

AutoRL-Sim is available for download from the GitHub repository (https://github.com/KellyBarbosa/autorl_sim, accessed on 21 August 2024). In the following subsections, details about the operation and structure of AutoRL-Sim are presented.

3.1. Methodology of AutoRL-Sim Development

The methodology proposed for the development of AutoRL-Sim is structured in the following steps:

• Definition of software resources and tools.
• Proposal of graphical interface prototypes.
• Selection of combinatorial optimization problems.
• Definition of a dataset for combinatorial optimization problem experiments.
• Development of reinforcement learning framework with model, algorithms, and parameters.
• Proposal of AutoRL algorithms.
• Simulation of experiments and analysis of results with case studies.

The six initial stages of the proposed methodology are described in the following subsections. Subsequently, in Section 4, the results of the simulations for the proposed case studies are presented.

3.2. Software Tools

AutoRL-Sim uses several software tools. Initially, it is worth highlighting that the R programming language was selected for this project. The R language was chosen based on the following factors: (i) extensively used in machine learning research; (ii) includes various functions and libraries for the use of statistical methods, such as ANOVA and RSM; (iii) development platforms with public access; and (iv) an environment for developing graphical interfaces. Other programming languages were considered, such as Python and MATLAB; however, the R environment is the one that most accurately covers all the aspects analyzed in the selection.

Table 1. Software, libraries, and functions used.

Technology	Version	Type of Technology	Function
R	4.3.3	Programming Language	-
Shiny	1.8.0	Framework	-
HTML	HTML5	Markup Language	-
CSS	CSS3	Style Sheet Language	-
JavaScript	ES2023	Programming Language	-
LaTeX	LaTeX2e	Typesetting System	-
stats	4.3.3	R package	lm()
			anova()
			ks.test()
			summary()
rsm	2.10.4	R package	canonical()
			rsm()

lists the software resources and libraries used, as well as their respective versions and the type of technology they belong to. Furthermore, it presents some of the main R language functions used, specifying which library they belong to.

The Shiny software package was used to develop the interface, together with HTML, CSS, and JavaScript. Furthermore, LaTeX was used to create the reports. The R software with the stats and rsm packages were adopted to develop the system, analyze the model, and adjust the parameters, respectively.

3.3. Interface

The basis for the development of the AutoRL-Sim environment was the Shiny library [69] together with the R language [70]. In addition, resources from HTML, CSS, JavaScript, and LaTeX were also used. Using this set of tools, eight modules were developed, covering the TSP, ATSP, and SOP problems.

For each problem covered by the interface, there is a module without AutoML and another with AutoML. It is also possible to use the “Free module”, which has options with AutoML/without AutoML and accepts problems such as TSP, ATSP, and SOP. The “Free module” adds flexibility to the use of AutoRL-Sim because, while in the other modules the problems are already pre-defined, in the “Free module”, the user is responsible for entering all the data for the problem they wish to analyze.

Figure 2 shows the AutoRL-Sim home page, where the tool logo is displayed. On this same screen, there is a navigation menu containing the options: Home, TSP, ATSP, SOP, TSP-AutoML, ATSP-AutoML, SOP-AutoML, Free module, and More. Below is a brief description of each interface tab.

• Home: Shows the AutoRL-Sim home page.
• TSP: In this module, users can perform TSP experiments using pre-defined instances in the tool.
• ATSP: In this module, users can perform ATSP experiments using pre-defined instances in the tool.
• SOP: In this module, users can perform SOP experiments using pre-defined instances in the tool.
• TSP-AutoML: In this module, users can perform TSP experiments using pre-defined instances in the tool using AutoML.
• ATSP-AutoML: In this module, users can perform ATSP experiments using pre-defined instances in the tool using AutoML.
• SOP-AutoML: In this module, users can perform SOP experiments using pre-defined instances in the tool using AutoML.
• Free module: In this module, the user is responsible for providing all information about the instance, making the tool more flexible in relation to the variety of experiments that can be performed. The user will have access to the “Without AutoML” and “With AutoML” options.
• More: By clicking on this option, the user will have access to the “Additional Information” and “About” options.

  –

  Additional Information: There is an explanation of some of the main topics covered in the tool.

  –

  About: The user will find a brief description of AutoRL-Sim and information about its developers.

In Figure 3, an example of an experiment that can be carried out in AutoRL-Sim is shown. In this case, the experiment was conducted with the “ft70.2” instance of the SOP type. Therefore, to carry out the experiment, the user must select one of the instances already registered in the tool and define the learning rate, the discount factor, the ϵ-greedy policy, and the number of episodes. After completing this information, the user must click on the “START EXPERIMENTS” button. At the end of the experiment, the user will have access to the distance graph and a summary of the results. The user can choose to download the results for later analysis.

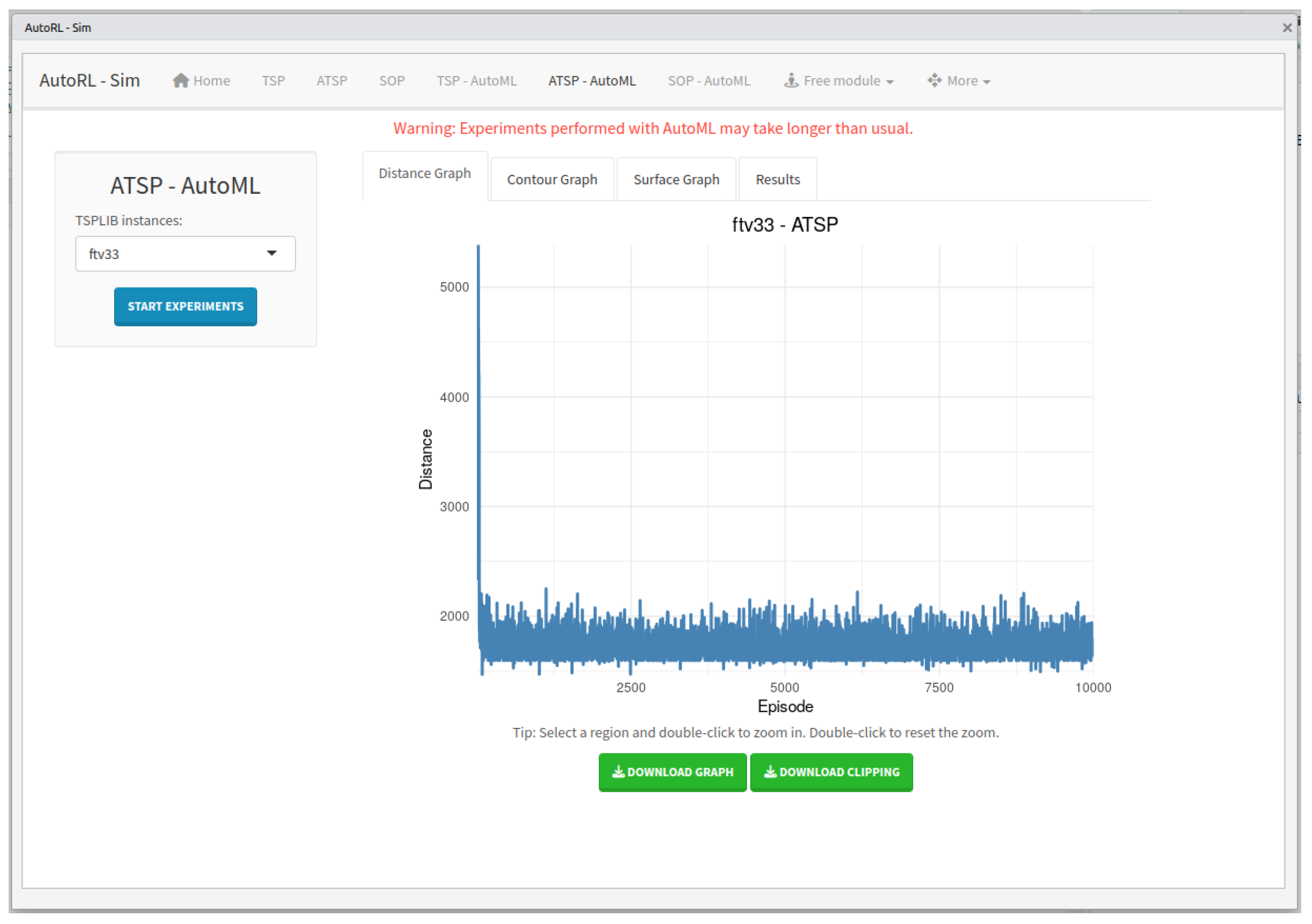
Figure 4 shows a simulation example with AutoML. In the image, the experiment was carried out with the “ftv33” instance of the ATSP type. Initially, the user must select one of the instances already registered in the tool and click on the “START EXPERIMENTS” button. After the simulation, the distance graph, contour graph, surface graph, and experiment results are available. This information is displayed in separate windows with their respective names. It should be noted that the user has the possibility of downloading the results from the corresponding tab for future analysis.

In Figure 5, an example of an experiment using the Free module (with AutoML) is shown. In the image, the simulation was carried out with the “swiss42” instance of the TSP type. To do this, the user must fill in the name of the instance, its type (TSP, ATSP, or SOP), the data format (2D Euclidean or matrix), the dimension of the instance, and whether there is already a known optimal value (if so, the user must enter it). Additionally, the user must upload a “.txt” file containing the instance data. After adding this information, the user must click on the “START EXPERIMENTS” button. After the simulation, the user will have access to the distance graph, the contour graph, the surface graph, and the experiment results. These results are displayed in separate windows with their respective names, and the user can download them for later analysis.

3.4. Combinatorial Optimization Problems

AutoRL-Sim provides simulations with three types of combinatorial optimization problems based on the traveling salesman problem. The traveling salesman problem is one of the classic problems of NP-complete combinatorial optimization, where the objective is to determine a Hamiltonian cycle of minimum cost. In this problem, given a set of cities (nodes), the salesman must visit each city exactly once, returning to the starting node at the end of the route [71,72,73,74].

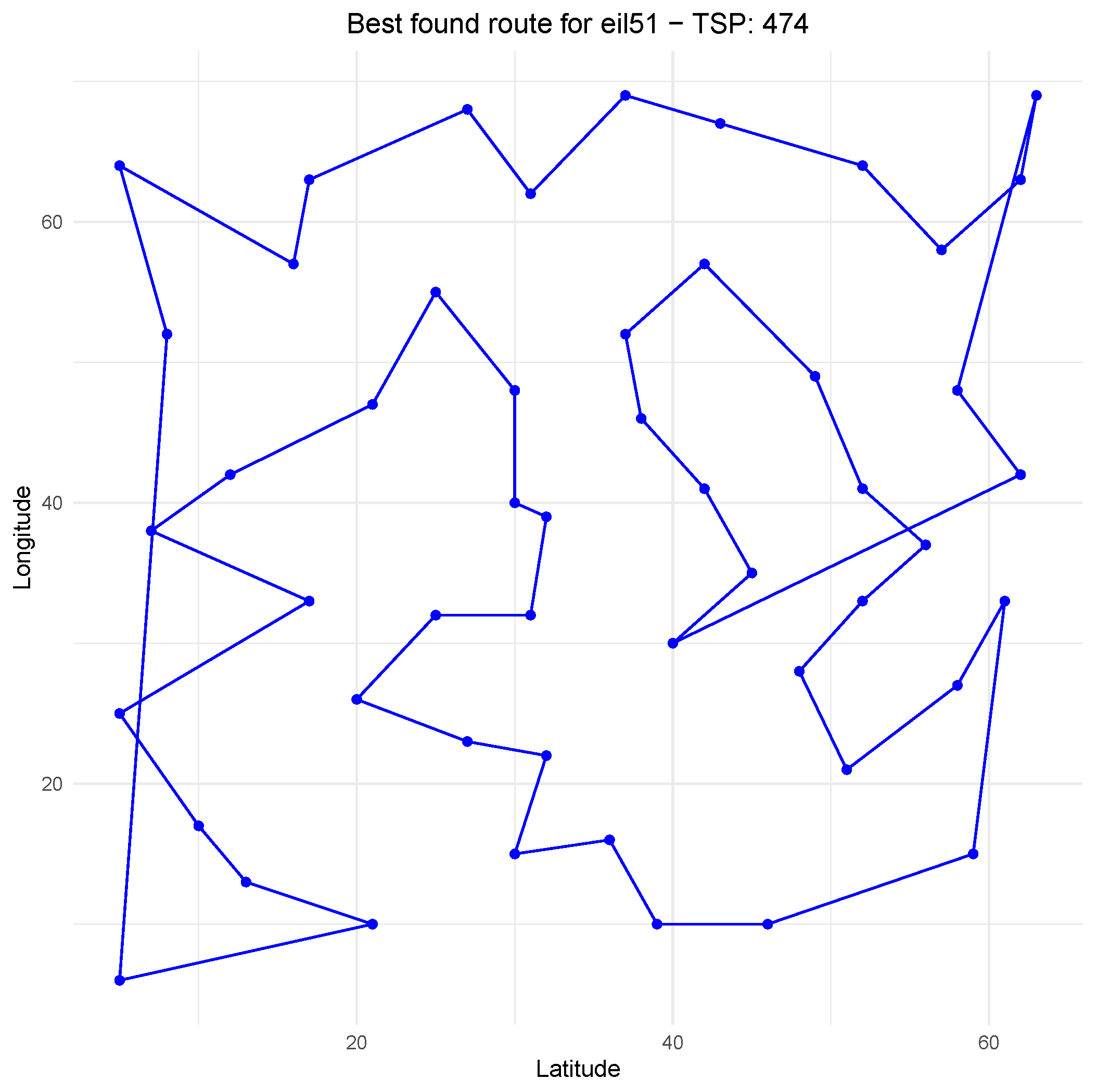
Figure 6 illustrates an example of the route taken by the traveling salesman. This is a problem with 51 cities (represented by nodes) generated during an experiment conducted in AutoRL-Sim.

In the literature, there are several variations of the traveling salesman problem [66,73,75], and three of them are addressed by AutoRL-Sim:

• TSP: In TSP (symmetric), which is the simplest and most general case of the problem, the distance between nodes does not depend on the direction of displacement [71,74].
• ATSP: In ATSP (or asymmetric TSP), the distance between nodes can vary according to the direction of displacement adopted [66,75].
• SOP: This is one of the variations of ATSP. In SOP, as in ATSP, distances between cities may vary depending on the direction of travel adopted. Furthermore, this problem includes the additional order of precedence constraint [73,75].

3.5. Dataset

AutoRL-Sim uses a dataset from the TSPLIB library (http://comopt.ifi.uni-heidelberg.de/software/TSPLIB95/, accessed on 7 July 2023) [76,77]. TSPLIB is an open repository that provides data and known optimal values for combinatorial optimization problems and is widely addressed in the literature. Instances of the TSP, ATSP, and SOP types were selected to create the AutoRL-Sim dataset, according to

Table 2. TSP instances from the TSPLIB dataset.

Problem	Nodes	Best Known Solution
eil51	51	426
berlin52	52	7542
st70	70	675
eil76	76	538
pr76	76	108,159
rat99	99	1211
kroA100	100	21,282
eil101	101	629
bier127	127	118,282
ch130	130	6110
ch150	150	6528
a280	280	2579
lin318	318	42,029
d1655	1655	62,128

,

Table 3. ATSP instances from the TSPLIB dataset.

Problem	Nodes	Best Known Solution
ftv33	34	1286
p43	43	5620
ftv44	45	1613
ftv47	48	1776
ry48p	48	14,422
ft53	53	6905
ftv64	65	1839
ft70	70	38,673

, and

Table 4. SOP instances from the TSPLIB dataset.

Problem	Nodes	Best Known Solution
br17.10	18	55
br17.12	18	55
p43.1	44	28,140
p43.2	44	28,480
p43.3	44	28,835
p43.4	44	83,005
ry48p.1	49	15,805
ry48p.2	49	16,074
ry48p.3	49	19,490
ry48p.4	49	31,446
ft53.1	54	7531
ft53.2	54	8026
ft53.3	54	10,262
ft53.4	54	14,425
ft70.1	71	39,313
ft70.2	71	40,101
ft70.3	71	42,535
ft70.4	71	53,530

, respectively.

In Figure 7, it is possible to check how TSPLIB instances can be accessed. For this, the user must select one of the problems available in “TSPLIB instances”.

In modules where problems are not predefined (Free module), the user must provide the necessary information about the problem data. An example of this situation can be seen in Figure 8.

3.6. Reinforcement Learning

In this section, some reinforcement learning features adopted in the AutoRL-Sim framework are presented. Initially, it is highlighted that the Q-learning and SARSA algorithms were used, as discussed in Section 2. In the following subsections, the RL modeling adopted and the parameters adjusted by AutoRL-Sim are described.

3.6.1. Reinforcement Learning Model

The modeling adopted for RL was based on works available in the literature and involves states, actions, and reinforcements [11,78,79]. Therefore, the RL structure adopted in AutoRL-Sim was defined as follows:

• States: All the cities (nodes) in the studied problem.
• Actions: Possible actions are the cities that have not yet been visited by the agent, that is, the nodes available on the route.
• Reinforcements: The reinforcement received is equivalent to the distance between the cities (nodes i and j) multiplied by $-1$, according to Equation (3):

$$R_{ij}=-D_{ij}.$$

(3)

3.6.2. Parameters

ML algorithms have parameters (or hyperparameters) that directly influence the learning process. When analyzing other types of ML algorithms, it is common to differentiate between the terms “parameters” and “hyperparameters”. For example, in artificial neural networks, the parameters are weights adjusted by the optimization method (e.g., gradient descent), whereas hyperparameters are values defined by the user, such as the number of layers or neurons [80]. In this paper, based on recent studies on RL for combinatorial optimization problems [11,33], the convention that the term “RL parameters” is synonymous with “RL hyperparameters” will be adopted.

The RL algorithms presented in Section 2 have three parameters:

• Learning Rate: The learning rate is represented by the symbol α, and its value can vary between 0 and 1 [81]. The α parameter controls the impact of updates on the learning matrix [82]. When α = 0, no learning occurs, as the learning matrix update equation reduces to $Q_{t+1}(s_t,a_t)=Q_t(s_t,a_t)$.
• Discount Factor: The discount factor is represented by the symbol γ and can be defined between 0 and 1. The value attributed to γ reflects the degree of importance of future rewards for the learning agent. As γ approaches 0, future rewards are considered more insignificant. On the other hand, future rewards gain high relevance when γ approaches 1 [49,83,84,85].
• $\mathit{ϵ}$-greedy: The ϵ-greedy policy has the ϵ parameter, whose value can vary between 0 and 1. This policy is adopted in the selection of actions, and this parameter value determines the degree of randomness in a decision. Through the ϵ-greedy policy, the learning agent can alternate between exploration, which involves searching for new experiences in the environment, and exploitation, which is based on previous experience and accumulated knowledge. The ϵ-greedy policy follows the update rule shown in Equation (4) [13,83,84]:

  $$\pi \left(s\right)=\left\{\begin{array}{c}{a}^{\ast }, \mathrm{with} \mathrm{probability} 1-ϵ\hfill \\ a_a, \mathrm{with} \mathrm{probability} ϵ\hfill \end{array}\right.,$$

  (4)

  where π(s) is the policy for the current state, a* is the highest scoring action in the learning matrix, and a_a is a random action among those available.

3.7. AutoRL Using RSM

In this study, automated tuning of RL parameters was performed using response surface models. To achieve this, the AutoRL structure was based on recent research [11,86], where the RSM approach for parameter recommendation applied to combinatorial optimization problems was proposed and validated.

RSM is a widely recognized mathematical and statistical technique for analyzing and modeling the relationship between input and output variables. In RSM, modeling occurs by fitting a multiple linear regression. This allows you to model equations for problems with one or more independent variables [87,88,89]. During the RSM application process, the values of the independent variables are manipulated and analyzed to find the mathematical equation that best describes the problem along with its respective response (dependent variable). This method makes it possible to optimize the response variable, identifying the ideal values to maximize or minimize the desired output [88,89].

Generally, the most common RSM models are first- or second-order [90]. First-order models can be represented by Equation (5) [87]:

$$y={\beta }_0+\sum _{i=1}^k{\beta }_i{x}_i+\epsilon .$$

(5)

Second-order models can be represented by Equation (6) [87]:

$$y={\beta }_0+\sum _{i=1}^k{\beta }_i{x}_i+\sum _{i=1}^k{\beta }_{ii}{x}_i^2+\sum _{1\le i\le j}^k{\beta }_{ij}{x}_i{x}_j+\epsilon .$$

(6)

In this work, the AutoRL-Sim framework uses second-order RSM models to adjust two RL parameters: α and γ. For this, the model variables were adopted as $x_1$ = α and $x_2$ = γ, and the dependent variable (y) was the adjustment of the final distance covered by the traveling salesman. Thus, the final RSM equation used to automate this reinforcement learning process is defined according to Equation (7) [11,86]:

$$y={\beta }_0+{\beta }_1\alpha +{\beta }_2\gamma +{\beta }_3{\alpha }^2+{\beta }_4{\gamma }^2+{\beta }_5\alpha \gamma +\epsilon .$$

(7)

Figure 9 represents how RSM is used in the proposed simulator. Initially, the selected instance is executed with different combinations of values for the parameters α and γ. Then, RSM is applied. Information about the fitted model is extracted using functions available in the R software. Some of the functions used are:

• rsm: response surface model fitting [91];
• lm: fitting of linear models [70];
• anova: extracts information about analysis of variance models [70];
• canonical: determines the stationary points of the RSM model [91];
• ks.test: performs the Kolmogorov–Smirnov residual normality test [70];
• summary: shows a summary of the adjusted model results [70].

After applying the RSM, some criteria were implemented to determine whether the parameters (α and γ) generated were adequate:

• Is the value of α between 0 and 1?
• Is the value of γ between 0 and 1?
• Are the residuals normal (significance criterion of 5%)?
• Is there statistical significance (significance criterion of 5%)?

If all four criteria are satisfied, the parameters (α and γ) generated by the RSM are considered the most appropriate for the problem studied. Otherwise, the AutoRL-Sim system considers the combination of parameters that resulted in the best final route distance as the most appropriate for the analyzed instance. Finally, the selected instance is executed again, this time with the best values found for α and γ.

4. Case Studies

In this section, four case studies of simulations with AutoRL-Sim are presented:

• Case study 1: module without AutoML.
• Case study 2: module with AutoML.
• Case study 3: Free module.
• Case study 4: comparison between modules with and without AutoML.

4.1. Case Study 1: Module without AutoML

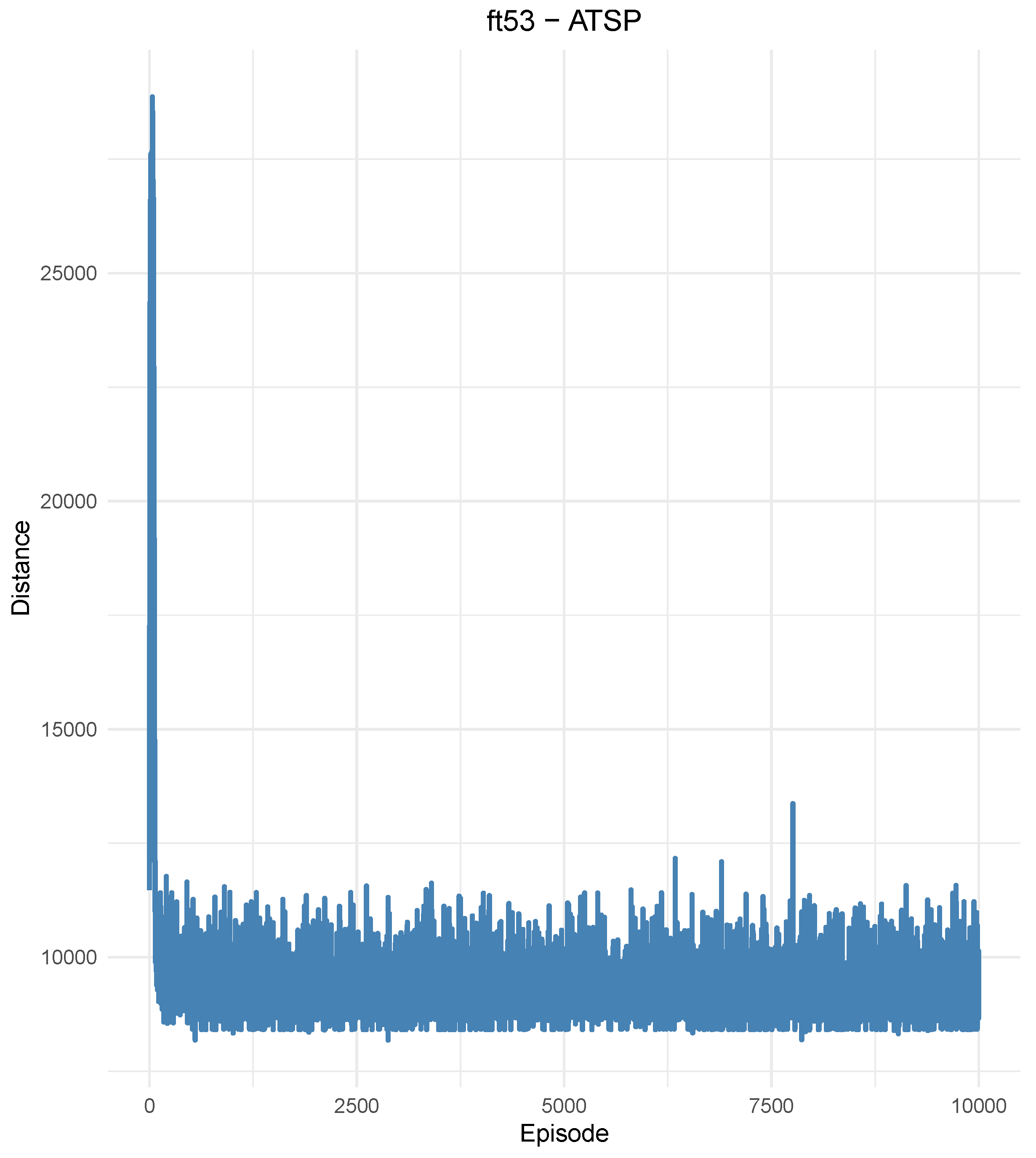
In the first case study, the experiment was carried out with the “ft53” instance (ATSP). For this, the learning rate and discount factor values presented by [86] were used, in which the authors present these parameters as the best combination found for the “ft53” problem. After the simulation, the user has the generated distance graph available (Figure 10). It is observed that, as the episodes are executed, the distance values gradually decrease until they reach a relatively constant stabilization point.

Table 5. Case study 1: Summary and results of experiment with the “ft53” instance.

Problem type	ATSP
Problem	ft53
Average distance	9326.63
Minimum distance	8182
Episode of minimum distance	2877
Optimal distance presented by TSPLIB	6905
Percentage relative error	18.49%
Discount factor	0.4
Learning rate	0.707
E-greedy policy	0.01
Number of episodes	10,000
Runtime	25.4 s

presents the report containing a summary of the settings used and the results obtained. In this aspect, it is noted that the minimum distance value obtained (8182) presented a percentage error of only 18.49% in relation to the optimal value provided by TSPLIB (6905). Furthermore, it is worth highlighting the fact that the minimum distance value obtained coincides with the value presented by [86], which reinforces the effectiveness of AutoRL-Sim.

4.2. Case Study 2: Module with AutoML

In this second case study, the “eil51” instance with the AutoML module was used. To carry out the experiment in this module, it is only necessary to define which instance will be evaluated. After the experiment, the user will be able to analyze the four graphs: route, distance, response surface, and contour lines. Furthermore, the AutoRL-Sim user will also be able to view the report containing a summary of results.

Figure 11 and Figure 12 present the surface and contour graphs, respectively. These graphs allow you to check the value ranges of the learning rate and discount factor parameters that tend to minimize the distance to the final route. In this aspect, the regions corresponding to these ranges of values are represented by the reddest tones in both graphs. It can be seen in Figure 11 and Figure 12 that the parameters that tend to minimize the final distance are approximately $0.15 \le$γ $\le 0.55$ and $0.55 \le$ α $\le 0.85$.

The other graphs generated in the second case study are presented in Figure 13 and Figure 14. Furthermore, the simulation report is shown in

Table 6. Case study 2: Summary and results of experiment with the “eil51” instance.

Problem type	TSP
Problem	eil51
Average distance	562.4
Minimum distance	475
Episode of minimum distance	4670
Epoch of minimum distance	4
Optimal distance presented by TSPLIB	426
Percentage relative error	11.5%
Discount factor	0.34
Learning rate	0.69
E-greedy policy	0.01
Number of episodes	10,000
Number of epochs	5
Runtime	7.28 min

. When analyzing the results of this case study, it is important to highlight the similarity between the results achieved and those presented by [86]. In [86], the adjusted parameters were γ = 0.352 and α = 0.693, with a final route distance of 475. In this work, the parameters obtained in the experiment were γ = 0.34 and α = 0.69, also generating a final route distance of 475. Thus, the results obtained in the second case study reinforce the adequate functioning of AutoRL-Sim.

4.3. Case Study 3: Free Module

In the third case study, the Free module and the “ESC78” instance (SOP) were adopted, with a known optimal value of 18,230 (TSPLIB). In this simulation, the parameter values (learning rate, discount factor, and e-greedy policy) and the number of episodes were randomly defined using the functionality available in the AutoRL-Sim interface called “GENERATE RANDOM VALUES”.

The results of this experiment can be seen in Figure 15 and

Table 7. Case study 3: Summary and results of experiment with the “ESC78” instance.

Problem type	SOP
Problem	ESC78
Average distance	23,097.72
Minimum distance	19,910
Episode of minimum distance	7486
Optimal distance	18,230
Percentage relative error	9.22%
Discount factor	0.415
Learning rate	0.68
E-greedy policy	0.13
Number of episodes	8275
Runtime	33.88 min

. From the simulation, it is possible to observe the learning process of the “ESC78” instance, in which the distance decreases throughout the episodes. Furthermore, it is noteworthy that the minimum distance (19,910) achieved was considerably closer to the optimal value provided by TSPLIB (18,230).

4.4. Case Study 4: Comparison between Modules with and without AutoML

For the fourth case study, some instances of TSP, ATSP, and SOP were selected. This study aims to compare the results obtained when using modules without AutoML and modules with AutoML. It also aims to compare the results obtained with those provided by TSPLIB and other works presented in the literature. The data are shown in

Table 8. Comparison between the results obtained with AutoML, without AutoML, with TSPLIB, and other results in the literature.

Problem	Type	TSPLIB	Without AutoML	With AutoML	Other Authors
berlin52	TSP	7542	9044	7871	7871 [86]
eil76	TSP	538	603	565	545.39 [92]
p43	ATSP	5620	5731	5627	5621.40 [93]
ftv64	ATSP	1839	3010	2100	2140 [94]
br17.10	SOP	55	57	55	55 [33]
ft70.1	SOP	39,313	64,225	56,642	39,313 [95]

. Finally, a comparison will also be made between the execution time of the experiments in the modules with and without AutoML, the results of which are shown in

Table 9. Comparison of experiment time between modules with AutoML and without AutoML.

Problem	Without AutoML (s)	With AutoML (s)
berlin52	5.2	472.2
eil76	17.3	813.6
p43	12.31	644.4
ftv64	20.18	1150.8
br17.10	12.17	2073.6
ft70.1	34.63	35,004.0

.

Table 8 shows the route values for some selected cases. It can be seen that the results obtained with the application of AutoML are, in general, close to the results presented in the literature by other authors and to the value considered optimal by TSPLIB. An important point to note is that the experiments without the application of AutoML were carried out with parameterizations defined at random (using the “GENERATE ALEATORY VALUES” feature available in the tool) in order to simulate an inexperienced experimenter.

Table 9 shows the computational time required to run the experiments described in Table 8. It shows that, as the complexity and size of the problem increase, the time required for the experiment also increases.

Only a few sample cases were selected, not all the problems presented in Table 2, Table 3 and Table 4, due to the high computational cost required to carry out all the experiments. This is evidenced by the case of instance “ft70.1” in Table 9.

It is also important to note that, unlike the other instances, instance “ft70.1” showed a result with a noticeably greater difference compared to the other cases tested. This discrepancy can be explained by the complexity of the problem. As this is a more complex problem, this instance would benefit from more epochs and episodes in addition to those already programmed internally in AutoRL-Sim. However, the computational cost would tend to be much higher.

5. Comparison with Other Studies

This section presents a comparison between AutoRL-Sim and other frameworks present in the literature that simulate reinforcement learning. In this sense, three papers were selected: I [39], II [42], and III [36]. These studies were considered to have relevant similarities with definitions in the present paper. The main factor is that the three papers present new graphical interfaces for reinforcement learning. Furthermore, the papers also adopt the SARSA and Q-learning methods as learning algorithms. It is also important to highlight that these simulators considered for comparison allow adjustments and visualization of graphs/reports, proving to be tools with relevant features for the RL user.

For this, we compared the development environment used, the RL algorithms used, the advanced techniques used, the problems addressed, and the features available.

Table 10. Comparison between AutoRL-Sim and other reinforcement learning frameworks: I [39], II [42], and III [36].

		AutoRL-Sim	I	II	III
Environment	R	✓	-	-	-
	MATLAB	-	✓	✓	-
	Visual Studio	-	-	-	✓
Algorithms	SARSA	✓	✓	✓	✓
	Q-learning	✓	✓	✓	✓
Advanced techniques	AutoML	✓	-	-	-
Problems addressed	TSP	✓	✓	-	-
	ATSP	✓	-	-	-
	SOP	✓	-	-	-
	MKP	-	✓	-	-
	Navigation	-	✓	✓	-
	Reservoir system	-	-	-	✓
Features	Parameter optimization	✓	-	-	-
	Selecting instances	✓	✓	-	-
	Free module	✓	-	-	-
	Graphics	✓	✓	✓	✓
	Reports	✓	✓	✓	✓

presents a summary of the analysis performed.

Table 10 shows that the proposed system (AutoRL-Sim) presents important advances in relation to previous studies. First, the proposed environment was developed with the R language, while the other works used MATLAB ([39,42]) and Visual Studio ([36]). Furthermore, AutoRL-Sim stands out as a dedicated tool for experiments with automated machine learning. In AutoRL-Sim, this technique is implemented with RSM for the purpose of parameter optimization. Furthermore, the Free module allows the user to enter new data and also perform simulations with AutoML.

Regarding the problems addressed, AutoRL-Sim is focused on three classic combinatorial optimization problems: TSP, ATSP, and SOP. In general, the other studies analyzed developed tools for other applications, such as agent navigation [39,42], MKP [39], and reservoir systems [36].

As for the functionalities available, all proposed systems offer the option of generating graphs and reports, but only AutoRL-Sim offers parameter optimization with AutoML. Furthermore, only AutoRL-Sim and the Ottoni et al. [39] proposal allow the selection of the instance to be studied. Another point to highlight is that only AutoRL-Sim offers an additional module in which the user can insert the data of the problem to be analyzed, providing greater freedom and flexibility in creating their own datasets for experimentation. A similarity between the studies is the use of classic RL algorithms (Q-learning and SARSA) in all works.

6. Conclusions

This paper proposed a simulation environment aimed at combinatorial optimization problems using automated reinforcement learning. Thus, AutoRL-Sim addresses three classic combinatorial optimization problems: TSP, ATSP, and SOP. It is noteworthy that, when using AutoRL-Sim, users can carry out various experiments and can also choose whether or not they wish to use AutoRL to optimize parameters. Two other modules allow the user to add data to the problems. Furthermore, AutoRL-Sim makes it possible to analyze simulation results using graphs and reports.

In future work, advancements are expected in two specific research areas using AutoRL-Sim. The first source of future developments comprises the adoption of the proposed simulator as a teaching tool in teaching reinforcement learning in undergraduate and postgraduate courses. In this sense, exploring the simulator in the proposal in practical evaluation activities in artificial intelligence training courses is suggested. The second research direction refers to expanding the scope of the simulator by implementing more modules and incorporating new features. In this regard, it is expected to implement other traditional advanced techniques, such as transfer learning [68], and more methods for hyperparameter optimization [2].