Numerical Evaluation of Hydroformed Tubular Adhesive Joints under Tensile Loads
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Joint Geometries
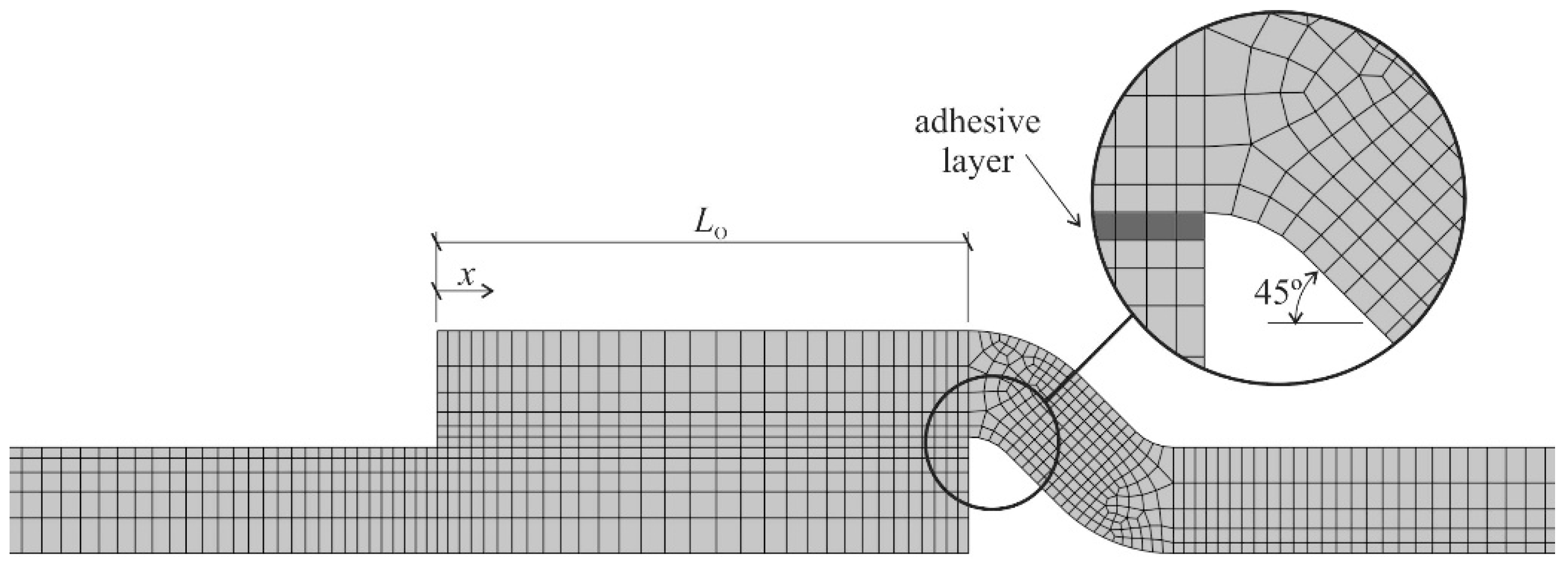
2.3. Numerical Modelling
3. Results and Discussion
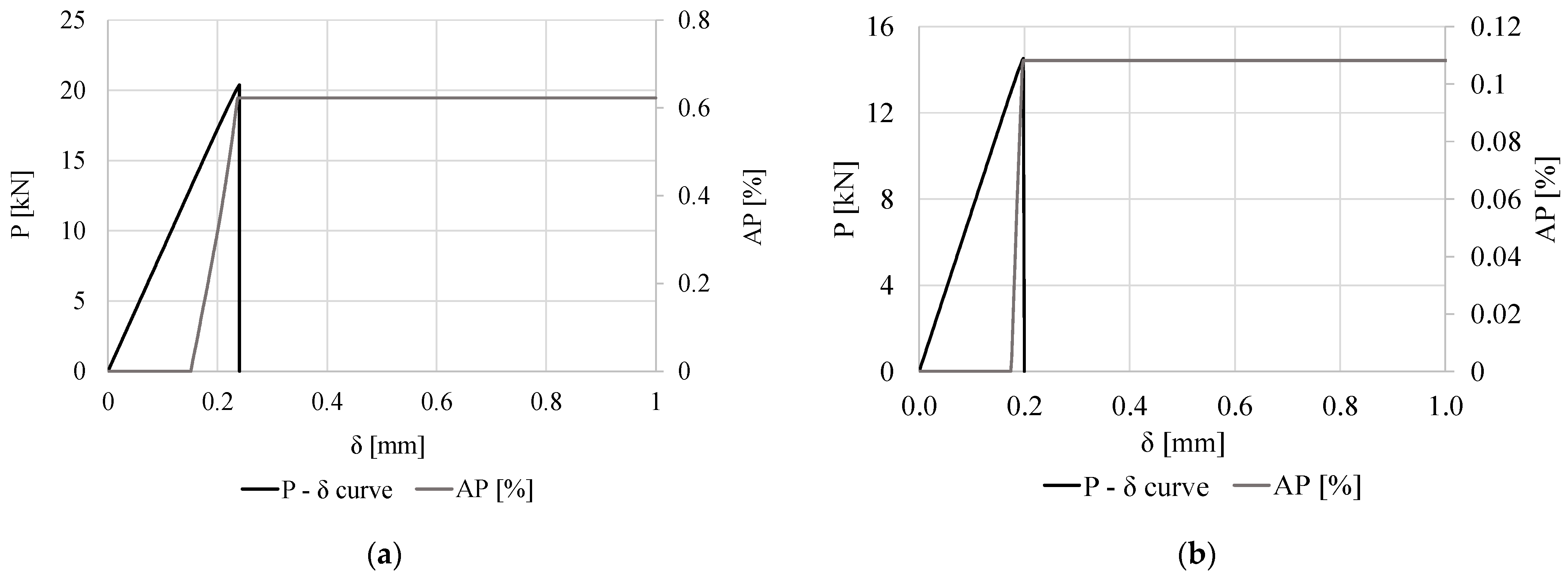
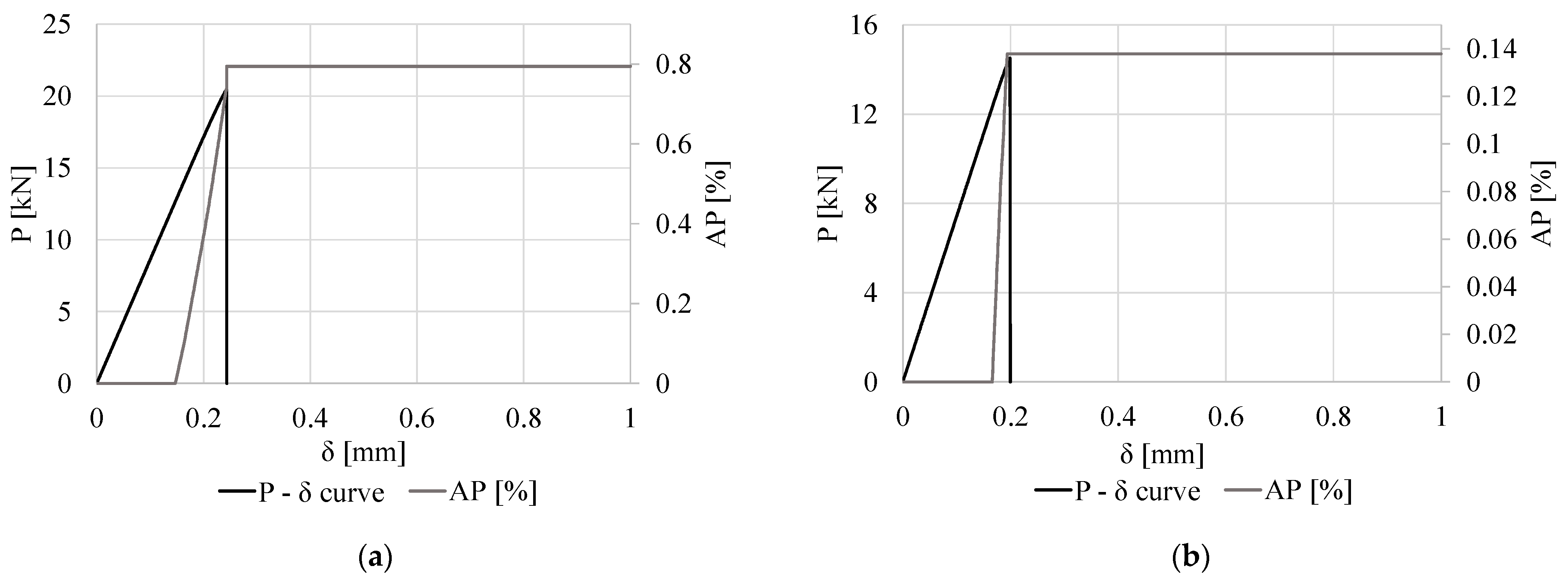
3.1. Validation with Experiments
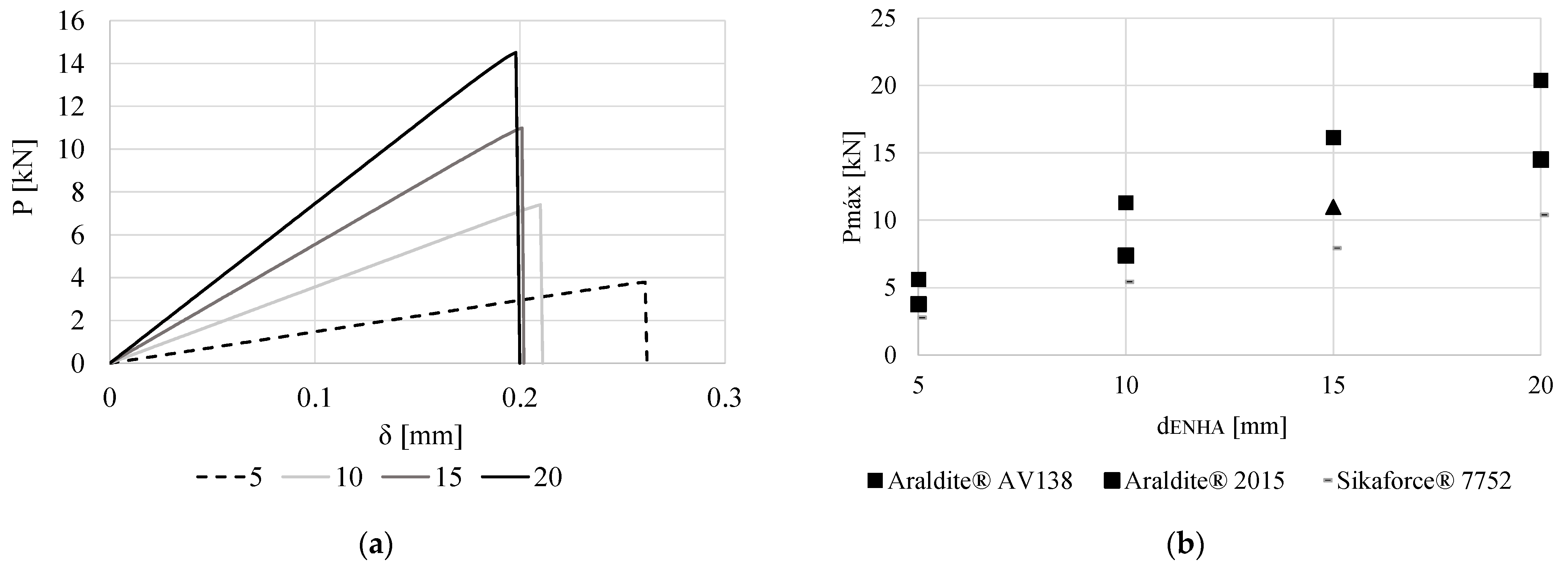
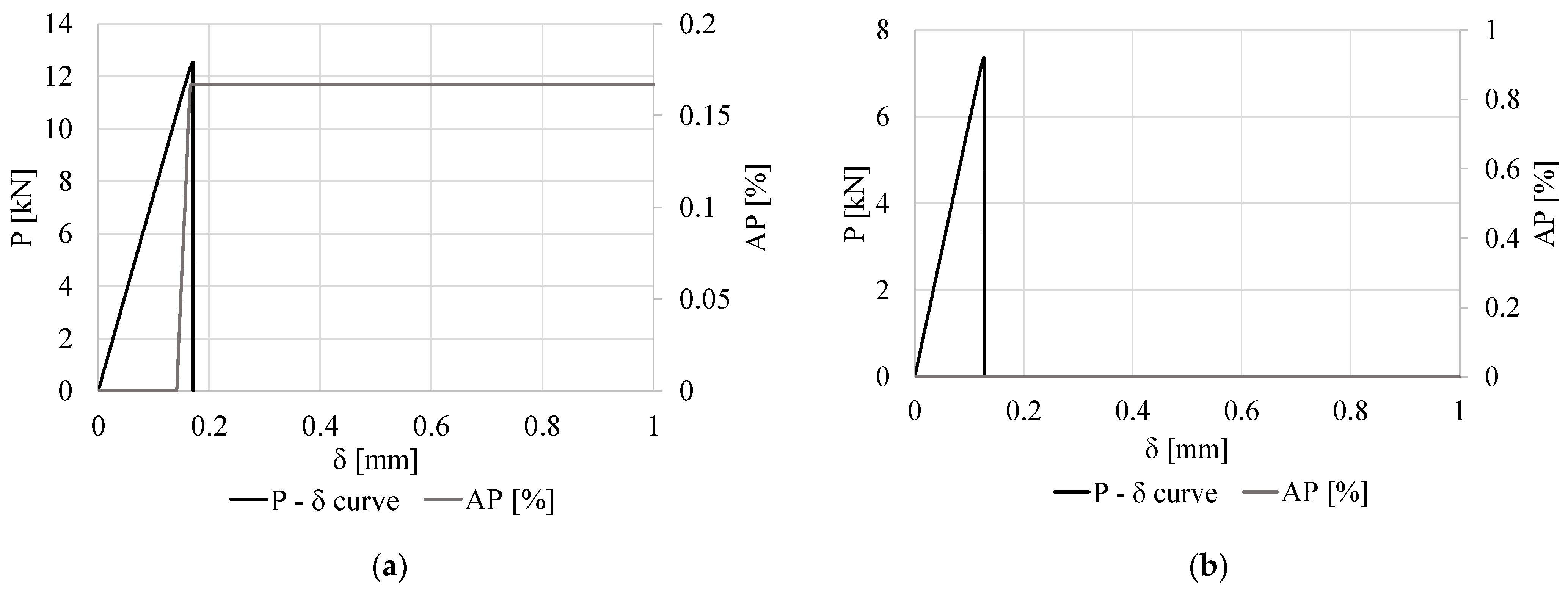
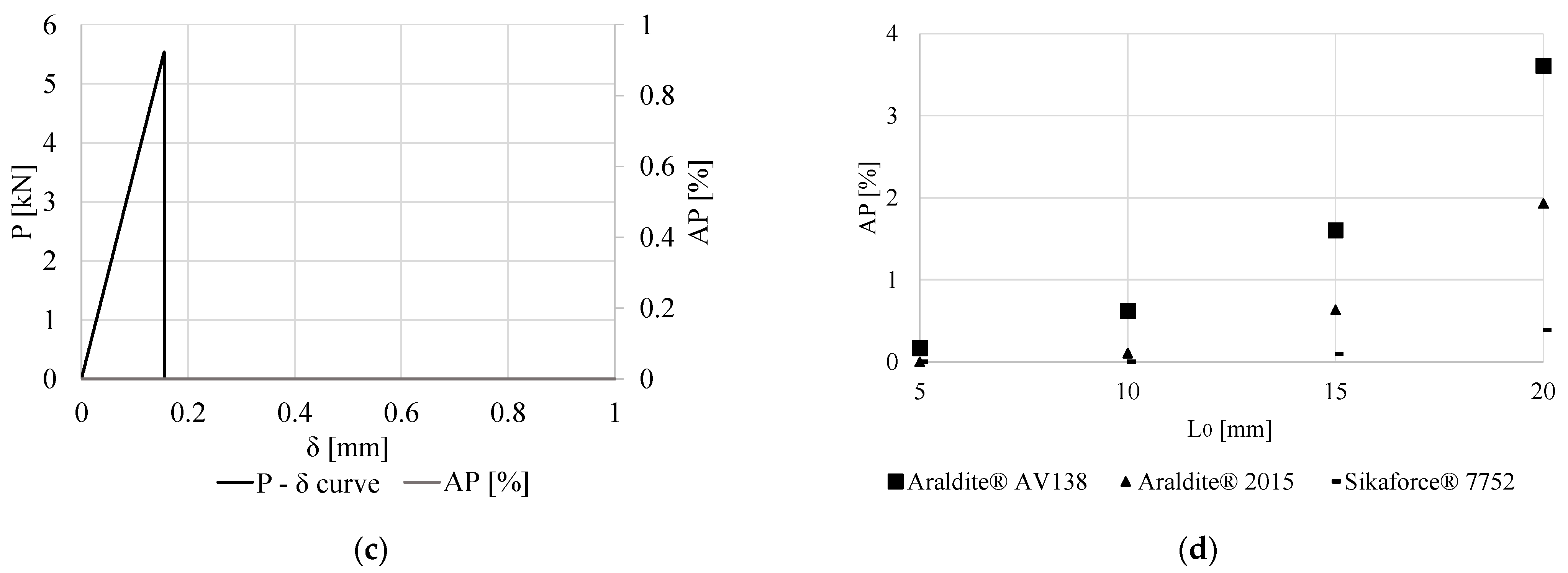
3.2. Effect of the Outer Diameter
- AV138: Joint failure was cohesive in the adhesive for all geometries using the AV138. For the AV138, there was a relative decrease in P at AP onset (PSAP) in relation to the corresponding Pm value as dENHA values increased. There was a proportional increase in δ at AP onset (δSAP) in relation to δ at failure (δf) for the two lowest dENHA values analyzed and a decrease in this parameter for the others.
- 2015: Joint failure was cohesive in the adhesive for all joints analyzed. For the 2015, null PSAP and δSAP values were recorded for dENHA ≤ 10 mm. For dENHA = 10 mm, AP occurred, although both geometries showed PSAP and δSAP values very close to Pm and δf, respectively.
- 7752: For all analyzed joint geometries, there was no AP in any case, and the joint failure was always cohesive in the adhesive.
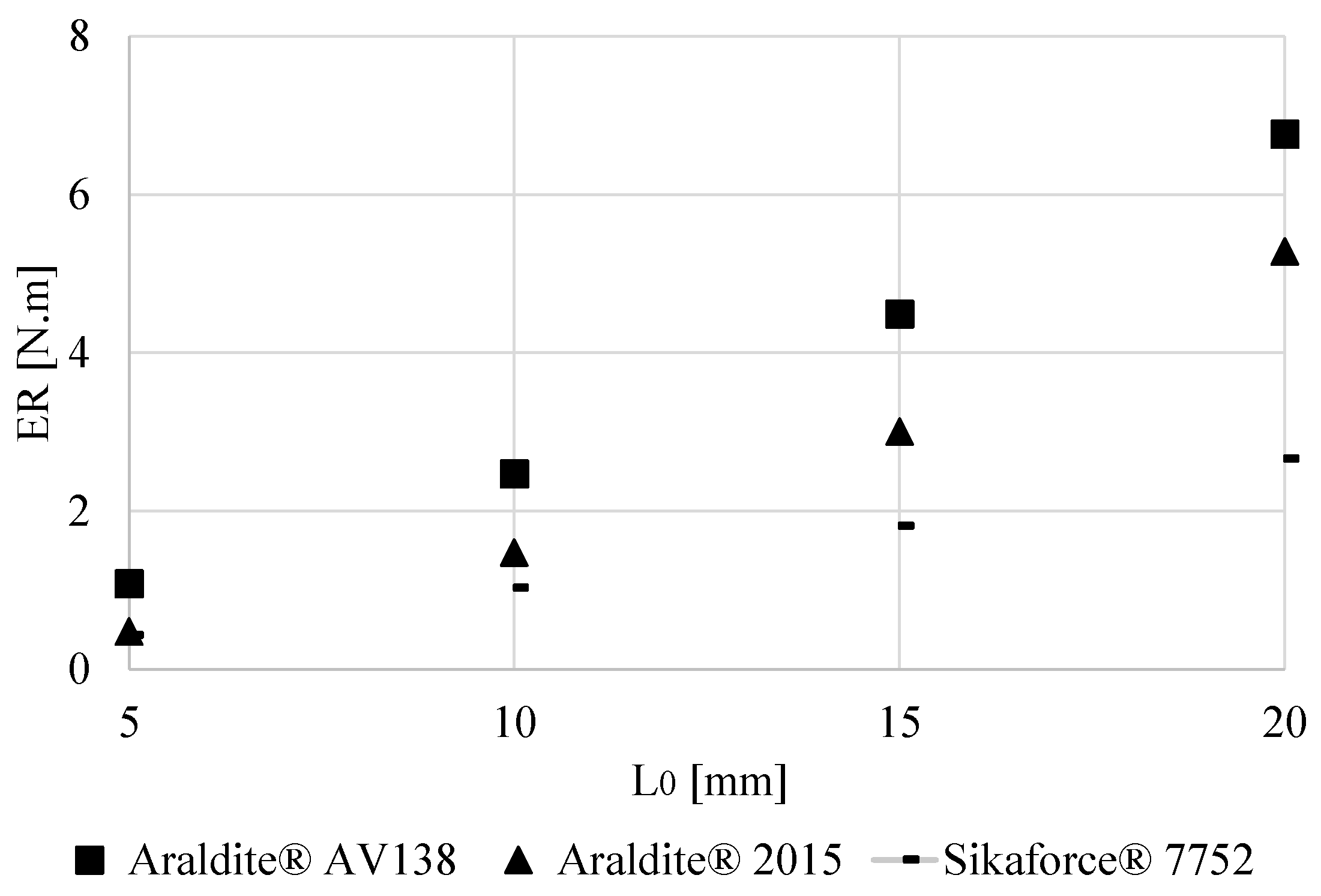
3.3. Effect of the Overlap Length
- AV138: Joint failure was cohesive in the adhesive for all geometry of joints. For higher LO values, the δSAP value tends to decrease in relation to δf. The percentile increase in δSAP maximizes the strength of the adhesive layer elements.
- 2015: Joint failure was cohesive in the adhesive for all geometries using the 2015. For LO = 5 mm, no AP occurred. For higher LO values, the δSAP value tends to decrease in relation to δf.
- 7752: Joint failure was cohesive in the adhesive for all geometries analyzed. The δSAP value tends to decrease in relation to the δf for higher LO values.
3.4. Effect of the Tube Thickness
- AV138: Joint failure was cohesive in the adhesive, for all geometries. For lower tAd values, δSAP tends to decrease in relation to δf. When varying tAd and the adhesive under study, the joint bonded with the AV138 registered the highest AP, with tAd = 1 mm.
- 2015: Joint failure was cohesive in the adhesive for all geometries using the 2015, and for higher tAd values, δSAP tends to approach δf.
- 7752: For tAd = 2, 3, and 4 mm, there was no AP, and joint failure was cohesive in the adhesive.
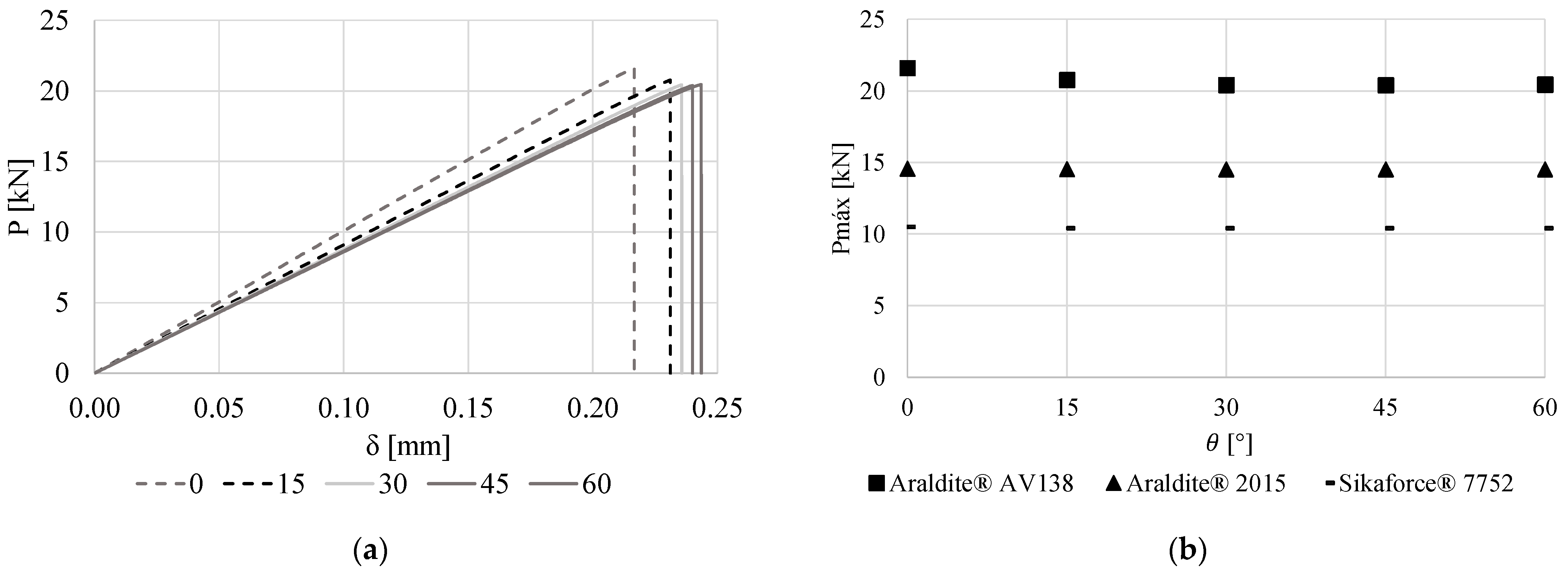
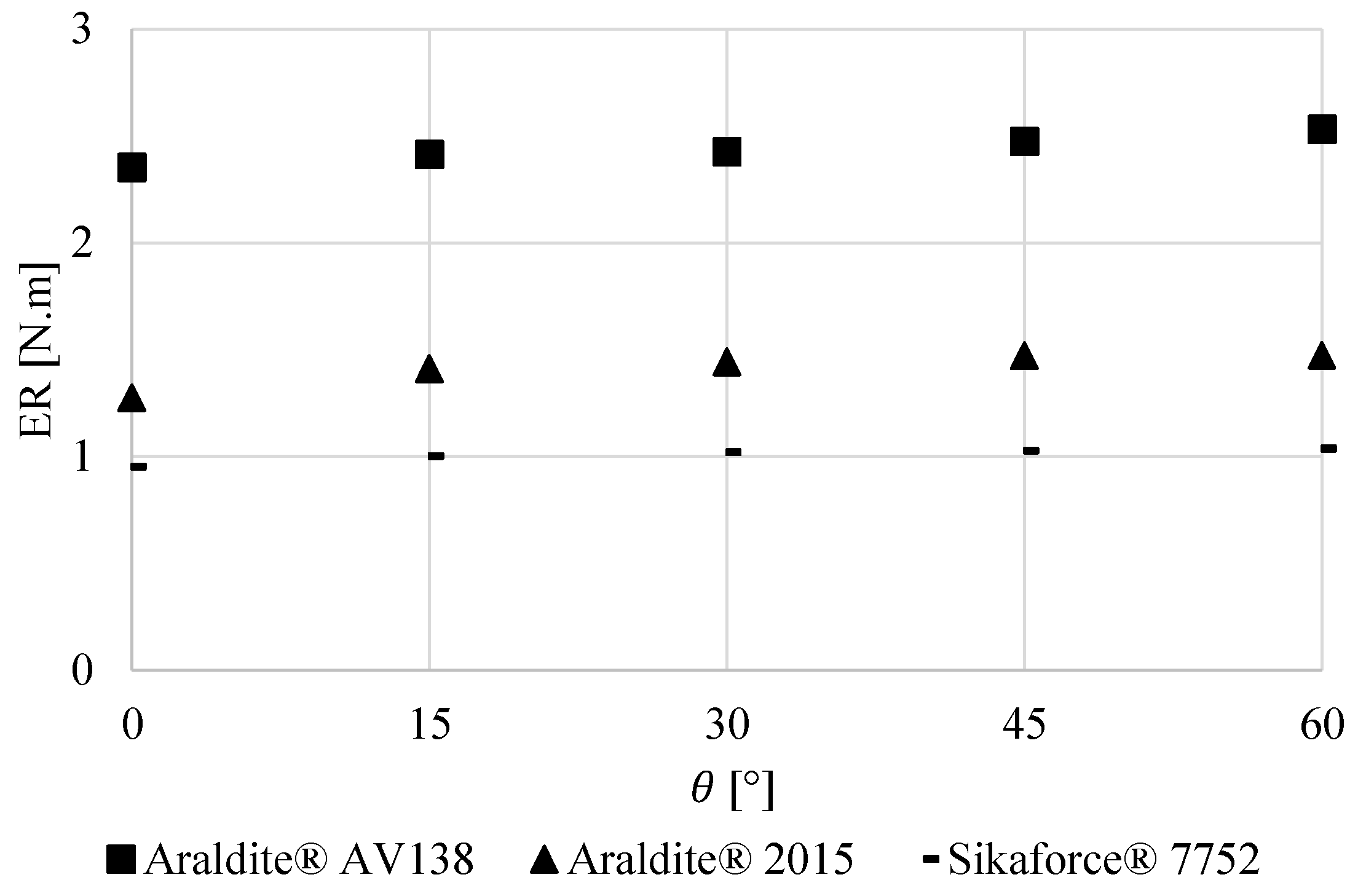
3.5. Effect of the Joggle Angle
- AV138: Joint failure was cohesive in the adhesive for all geometries of joint, and for higher θ values, δSAP decreases in relation to the corresponding δf. When varying θ and the adhesive under study, the adhesive joint with the highest AP value uses the AV138, with θ = 60°.
- 2015: Joint failure was cohesive in the adhesive for all the geometries using the 2015. For θ ≥ 30°, the value of δSAP decreases in relation to the corresponding δf.
- 7752: No AP occurred for any of the geometries analyzed, and joint failure was always cohesive in the adhesive.
4. Conclusions
- dENHA: Led to an increase of Pm for all adhesives. The AV138 provided the best Pm results, followed by the 2015 and 7752. The highest Pm increase was found for the 2015, and was smallest for the AV138 due to its brittleness. ER increased with dENHA for all adhesives, with the same qualitative difference between adhesives as for Pm. AP was highest for the AV138, but with low absolute values, which did not prevent a cohesive failure of the adhesive layer for all joint conditions.
- LO: Pm increased nearly proportionally with LO for all adhesives within the tested LO range. From best to worse Pm, the order of adhesives was AV138, 2015, 7752. ER showed the same tendency and adhesive ranking, although with higher percentile improvements over the smallest LO of 5 mm. AP showed an exponential increase with LO, reaching almost 4% for the AV138 and LO = 20 mm, but nonetheless failure took place in the adhesive layer for all tested conditions.
- tAd: Higher tAd provide a Pm improvement, mostly between 1 and 2 mm, while between 2 and 4 mm the differences were minimal. The best results relate to the AV138 and the worst to the 7752. The improvements are moderate compared to the previously mentioned variables. ER decreased with tAd for all adhesives, mostly due to the smaller df. AP reached shortly below 6% for the AV138 and tAd = 1 mm, and highly reduced for bigger tAd. AP was negligible for the remaining adhesives.
- θ provided the smallest variation in Pm between all variables, and the best results were found for q = 0°. In the observed Pm order of adhesives (highest for the AV138 and lowest for the 7752), the AV138 was affected the most by θ, showing an approximate 5% improvement. ER showed negligible variations with θ. The joint failure was cohesive in the adhesive for all the geometries analyzed, regardless of the adhesive employed. In the case of the 7752, no AP occurred.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kallitsis, N.; Anyfantis, K.N. On the design of composite patch repair for strengthening of marine plates subjected to compressive loads. Modelling 2022, 3, 127–139. [Google Scholar] [CrossRef]
- Correia, S.; Anes, V.; Reis, L. Effect of surface treatment on adhesively bonded aluminium-aluminium joints regarding aeronautical structures. Eng. Fail. Anal. 2018, 84, 34–45. [Google Scholar] [CrossRef]
- Petrie, E.M. Handbook of Adhesives and Sealants, 2nd ed.; McGraw Hill: New York, NY, USA, 2002. [Google Scholar]
- Da Silva, L.F.M.; de Magalhaes, A.G.; de Moura, M.F.S. Juntas Adesivas Estruturais; Publindústria Portugal: Porto, Portugal, 2007. [Google Scholar]
- Deng, P.; Guo, J.; Liu, Y.; Yang, B. Damaged tubular t-joints retrofitted with carbon fiber reinforced polymer subjected to monotonic and cyclic loadings. Int. J. Steel Struct. 2021, 21, 299–314. [Google Scholar] [CrossRef]
- Sonsino, C.M.; Łagoda, T.; Demofonti, G. Damage accumulation under variable amplitude loading of welded medium- and high-strength steels. Int. J. Fatigue 2004, 26, 487–495. [Google Scholar] [CrossRef]
- Lieurade, H.P.; Huther, I.; Lefebvre, F. Effect of weld quality and postweld improvement techniques on the fatigue resistance of extra high strength steels. Weld. World 2008, 52, 106–115. [Google Scholar] [CrossRef]
- Ahola, A.; Savolainen, J.; Brask, L.; Björk, T. Fatigue enhancement of welded thin-walled tubular joints made of lean duplex steel. J. Constr. Steel Res. 2024, 218, 108738. [Google Scholar] [CrossRef]
- Sorrentino, L.; Parodo, G.; Giuliano, G. Lightweight structures: An innovative method to uniform the thickness of metal sheets by patchwork blanks. Int. J. Lightweight Mater. Manuf. 2022, 5, 20–28. [Google Scholar] [CrossRef]
- Lee, D.G.; Kim, J.K.; Cho, D.H. Effects of adhesive fillers on the strength of tubular single lap adhesive joints. J. Adhes. Sci. Technol. 1999, 13, 1343–1360. [Google Scholar]
- Lavalette, N.P.; Bergsma, O.K.; Zarouchas, D.; Benedictus, R. Influence of geometrical parameters on the strength of Hybrid CFRP-aluminium tubular adhesive joints. Compos. Struct. 2020, 240, 112077. [Google Scholar] [CrossRef]
- Wang, J.; Kang, Y.L.; Qin, Q.H.; Fu, D.H.; Li, X.Q. Identification of time-dependent interfacial mechanical properties of adhesive by hybrid/inverse method. Comput. Mater. Sci. 2008, 43, 1160–1164. [Google Scholar] [CrossRef]
- Volkersen, O. Die Nietkraftverteilung in zugbeanspruchten Nietverbindungen mit konstanten Laschenquerschnitten. Luftfahrtfor Schung 1938, 15, 41–47. [Google Scholar]
- Adams, R.; Peppiatt, N. Stress analysis of adhesive-bonded lap joints. J. Strain Anal. 1974, 9, 185–196. [Google Scholar] [CrossRef]
- Harris, J.A.; Adams, R.A. Strength prediction of bonded single lap joints by non-linear finite element methods. Int. J. Adhes. Adhes. 1984, 4, 65–78. [Google Scholar] [CrossRef]
- Sosa, J.C.; Karapurath, N. Delamination modelling of GLARE using the extended finite element method. Compos. Sci. Technol. 2012, 72, 788–791. [Google Scholar] [CrossRef]
- Gribanov, I.; Taylor, R.; Thijssen, J.; Fuglem, M. Investigating Ice Loads on Subsea Pipelines with Cohesive Zone Model in Abaqus. Modelling 2023, 4, 394–407. [Google Scholar] [CrossRef]
- Stein, N.; Felger, J.; Becker, W. Analytical models for functionally graded adhesive single lap joints: A comparative study. Int. J. Adhes. Adhes. 2017, 76, 70–82. [Google Scholar] [CrossRef]
- Razavi, S.M.J.; Ayatollahi, M.R.; Majidi, H.R.; Berto, F. A strain-based criterion for failure load prediction of steel/CFRP double strap joints. Compos. Struct. 2018, 206, 116–123. [Google Scholar] [CrossRef]
- Dionísio, J.; Ramalho, L.; Sánchez-Arce, I.; Campilho, R.; Belinha, J. Fracture mechanics approach to stress singularities in composite adhesive joints. Compos. Struct. 2021, 276, 114507. [Google Scholar] [CrossRef]
- Zhang, Q.; Cheng, X.; Cheng, Y.; Li, W.; Hu, R. Investigation of tensile behavior and influence factors of composite-to-metal 2D-scarf bonded joint. Eng. Struct. 2019, 180, 284–294. [Google Scholar] [CrossRef]
- Huang, J.; Zeng, J.; Bai, Y.; Cheng, Z.; Wang, Y.; Zhao, Q.; Liang, D. Effect of adhesive layer properties on the shear strength of single-lap structures of dissimilar materials based on the cohesive zone model. J. Mech. Sci. Technol. 2021, 35, 133–143. [Google Scholar] [CrossRef]
- Sun, L.; Tie, Y.; Hou, Y.; Lu, X.; Li, C. Prediction of failure behavior of adhesively bonded CFRP scarf joints using a cohesive zone model. Eng. Fract. Mech. 2020, 228, 106897. [Google Scholar] [CrossRef]
- Ahmad, H.; Crocombe, A.D.; Smith, P.A. Strength prediction in CFRP woven laminate bolted double-lap joints under quasi-static loading using XFEM. Compos. Part. A Appl. Sci. Manuf. 2014, 56, 192–202. [Google Scholar] [CrossRef]
- Ma, X.; Bian, K.; Liu, H.; Wang, Y.; Xiong, K. Numerical and experimental investigation of the interface properties and failure strength of CFRP T-Stiffeners subjected to pull-off load. Mater. Des. 2020, 185, 108231. [Google Scholar] [CrossRef]
- Kwon, J.W.; Lee, D.G. The effects of surface roughness and bond thickness on the fatigue life of adhesively bonded tubular single lap joints. J. Adhes. Sci. Technol. 2000, 14, 1085–1102. [Google Scholar] [CrossRef]
- Albiez, M.; Vallée, T.; Fricke, H.; Ummenhofer, T. Adhesively bonded steel tubes—Part I: Experimental investigations. Int. J. Adhes. Adhes. 2019, 90, 199–210. [Google Scholar] [CrossRef]
- Nguyen, V.; Kedward, K.T. Non-linear modeling of tubular adhesive scarf joints loaded in tension. J. Adhes. 2001, 76, 265–292. [Google Scholar] [CrossRef]
- Esmaeel, R.A.; Taheri, F. Influence of adherend’s delamination on the response of single lap and socket tubular adhesively bonded joints subjected to torsion. Compos. Struct. 2011, 93, 1765–1774. [Google Scholar] [CrossRef]
- Hosseinzadeh, R.; Shahin, K.; Taheri, F. A simple approach for characterizing the performance of metallic tubular adhesively-bonded joints under torsion loading. J. Adhes. Sci. Technol. 2007, 21, 1613–1631. [Google Scholar] [CrossRef]
- Oh, J.H. Strength prediction of tubular composite adhesive joints under torsion. Compos. Sci. Technol. 2007, 67, 1340–1347. [Google Scholar] [CrossRef]
- Choi, J.K.; Lee, D.G. Torque transmission capabilities of bonded polygonal lap joints for carbon fiber epoxy composites. J. Adhes. 1995, 48, 235–250. [Google Scholar] [CrossRef]
- Breckner, M. Hydraulic systems for hydroforming. In Proceedings of the International Conference on Hydroforming, Stuttgart, Germany, 12–13 October 1999; pp. 12–13. [Google Scholar]
- Andelfinger, U.; Ramm, E. EAS-elements for two-dimensional, three-dimensional, plate and shell structures and their equivalence to HR-elements. Int. J. Numer. Methods Eng. 1993, 36, 1311–1337. [Google Scholar] [CrossRef]
- Simo, J.C.; Rifai, M. A class of mixed assumed strain methods and the method of incompatible modes. Int. J. Numer. Methods Eng. 1990, 29, 1595–1638. [Google Scholar] [CrossRef]
- Hughes, T.J. The Finite Element Method Prentice-Hall; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1987. [Google Scholar]
- Faria, A.L.; Campilho, R.D.S.G. Parametric analysis of composite tubular joints bonded by the bi-adhesive technique. Acad. Mat. Sci. 2024, 1, 1–10. [Google Scholar]
- Nunes, S.L.S.; Campilho, R.D.S.G.; da Silva, F.J.G.; de Sousa, C.C.R.G.; Fernandes, T.A.B.; Banea, M.D.; da Silva, L.F.M. Comparative failure assessment of single and double-lap joints with varying adhesive systems. J. Adhes. 2016, 92, 610–634. [Google Scholar] [CrossRef]
- Campilho, R.D.S.G.; Banea, M.D.; Pinto, A.M.G.; da Silva, L.F.M.; de Jesus, A.M.P. Strength prediction of single- and double-lap joints by standard and extended finite element modelling. Int. J. Adhes. Adhes. 2011, 31, 363–372. [Google Scholar] [CrossRef]
- Campilho, R.D.S.G.; Banea, M.D.; Neto, J.A.B.P.; da Silva, L.F.M. Modelling adhesive joints with cohesive zone models: Effect of the cohesive law shape of the adhesive layer. Int. J. Adhes. Adhes. 2013, 44, 48–56. [Google Scholar] [CrossRef]
- Faneco, T.M.S.; Campilho, R.D.S.G.; Silva, F.J.G.; Lopes, R.M. Strength and fracture characterization of a novel polyurethane adhesive for the automotive industry. J. Test. Eval. 2017, 45, 398–407. [Google Scholar] [CrossRef]
- Sugiman, S.; Ahmad, H. Comparison of cohesive zone and continuum damage approach in predicting the static failure of adhesively bonded single lap joints. J. Adhes. Sci. Technol. 2017, 31, 552–570. [Google Scholar] [CrossRef]
- Carneiro Neto, R.M.; Sampaio, E.M.; Assis, J.T. Numerical and experimental analysis of bonded joints with combined loading. Int. J. Adhes. Adhes. 2019, 90, 61–70. [Google Scholar] [CrossRef]
- Álvarez, D.; Blackman, B.; Guild, F.; Kinloch, A. Mode I fracture in adhesively-bonded joints: A mesh-size independent modelling approach using cohesive elements. Eng. Fract. Mech. 2014, 115, 73–95. [Google Scholar] [CrossRef]
- Tserpes, K.; Barroso-Caro, A.; Carraro, P.A.; Beber, V.C.; Floros, I.; Gamon, W.; Kozłowski, M.; Santandrea, F.; Shahverdi, M.; Skejić, D.; et al. A review on failure theories and simulation models for adhesive joints. J. Adhes. 2022, 98, 1855–1915. [Google Scholar] [CrossRef]
- Rocha, R.; Campilho, R. Evaluation of different modelling conditions in the cohesive zone analysis of single-lap bonded joints. J. Adhes. 2018, 94, 562–582. [Google Scholar] [CrossRef]
- Dragoni, E.; Goglio, L. Adhesive stresses in axially-loaded tubular bonded joints—Part I: Critical review and finite element assessment of published models. Int. J. Adhes. Adhes. 2013, 47, 35–45. [Google Scholar] [CrossRef]








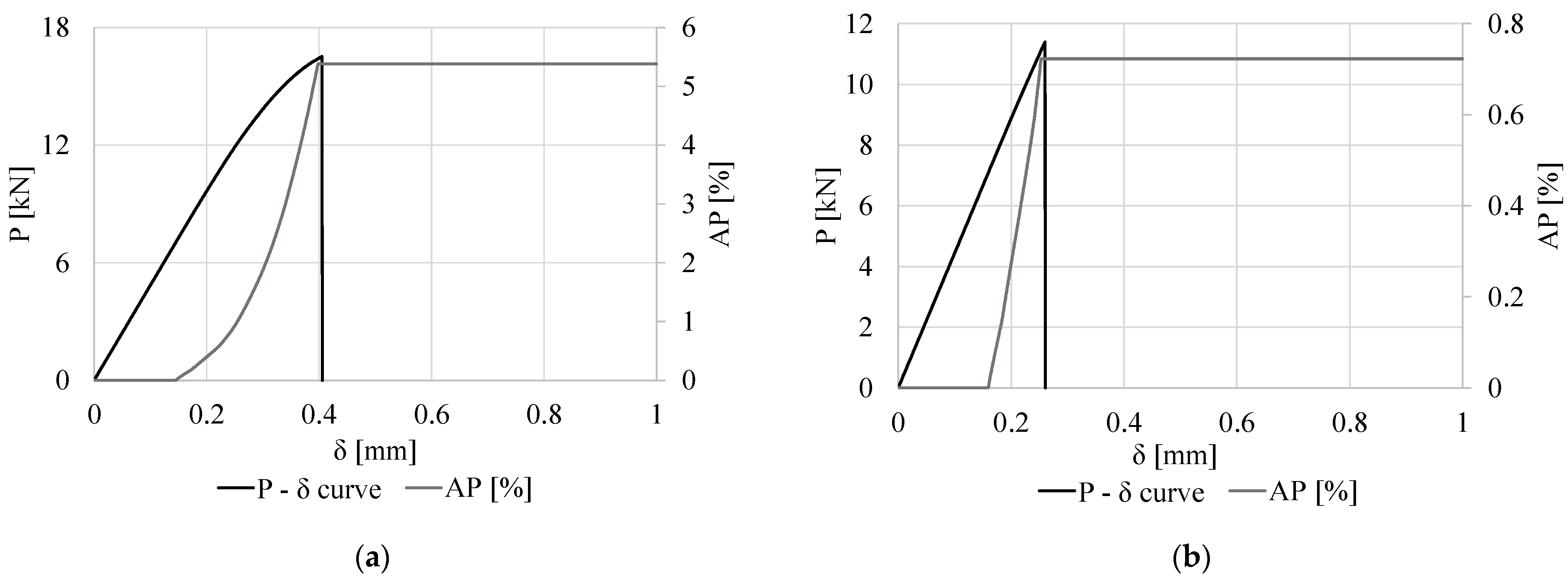


| Adherend Material | AW6082-T651 Aluminum Alloy |
|---|---|
| Young’s modulus, E [GPa] | 70.07 ± 0.83 |
| Tensile yield stress, σe [MPa] | 261.67 ± 7.65 |
| Tensile strength, σf [MPa] | 324.00 ± 0.16 |
| Tensile failure strain, εf [%] | 21.70 ± 4.24 |
| Property | AV138 | 2015 | 7752 |
|---|---|---|---|
| Young’s modulus, E [GPa] | 4.89 ± 0.81 | 1.85 ± 0.21 | 0.49 ± 0.09 |
| Poisson’s ratio, ν | 0.35 a | 0.33 a | 0.30 a |
| Tensile yield stress, σe [MPa] | 36.49 ± 2.47 | 12.63 ± 0.61 | 3.24 ± 0.48 |
| Tensile strength, σf [MPa] | 39.45 ± 3.18 | 21.63 ± 1.61 | 11.48 ± 0.25 |
| Tensile failure strain, εf [%] | 1.21 ± 0.10 | 4.77 ± 0.15 | 19.18 ± 1.40 |
| Shear modulus, G [GPa] | 1.81 b | 0.70 b | 0.19 b |
| Shear yield stress, τe [MPa] | 25.1 ± 0.33 | 14.6 ± 1.3 | 5.16 ± 1.14 |
| Shear strength, τf [MPa] | 30.2 ± 0.40 | 17.9 ± 1.8 | 10.17 ± 0.64 |
| Shear failure strain, γf [%] | 7.8 ± 0.7 | 43.9 ± 3.4 | 54.82 ± 6.38 |
| Toughness in tension, GIC [N/mm] | 0.20 c | 0.43 ± 0.02 | 2.36 ± 0.17 |
| Toughness in shear, GIIC [N/mm] | 0.38 c | 4.70 ± 0.34 | 5.41 ± 0.47 |
| AV138 | 2015 | 7752 | ||||
|---|---|---|---|---|---|---|
| LO [mm] | 20 | 40 | 20 | 40 | 20 | 40 |
| Experimental avg. [N] | 32,797 | 37,857 | 27,238 | 39,067 | 23,856 | 35,930 |
| Numerical [N] | 33,568 | 39,631 | 28,897 | 40,210 | 19,455 | 30,779 |
| Relative deviation [%] | 2.4 | 4.7 | 6.1 | 2.9 | −18.4 | −14.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Faria, A.L.; Campilho, R.D.S.G. Numerical Evaluation of Hydroformed Tubular Adhesive Joints under Tensile Loads. Modelling 2024, 5, 990-1008. https://doi.org/10.3390/modelling5030052
Faria AL, Campilho RDSG. Numerical Evaluation of Hydroformed Tubular Adhesive Joints under Tensile Loads. Modelling. 2024; 5(3):990-1008. https://doi.org/10.3390/modelling5030052
Chicago/Turabian StyleFaria, André Lima, and Raul Duarte Salgueiral Gomes Campilho. 2024. "Numerical Evaluation of Hydroformed Tubular Adhesive Joints under Tensile Loads" Modelling 5, no. 3: 990-1008. https://doi.org/10.3390/modelling5030052
APA StyleFaria, A. L., & Campilho, R. D. S. G. (2024). Numerical Evaluation of Hydroformed Tubular Adhesive Joints under Tensile Loads. Modelling, 5(3), 990-1008. https://doi.org/10.3390/modelling5030052







