Abstract
The pseudocontinuum models of reactions in packed beds are complicated, and an assessment of the reliability of the predictability of their numerical solution is difficult. The predictability reliability depends on validity and verifiability, whereas the numerical solutions of models of reactions in packed beds cannot be validated or verified. Scientific acceptability cannot commence by metaphysics alone, and the truth of the speculative justifications of the results of the numerical models without robust empirical confirmation is a matter of chance occurrence. Adherence to the principles of noncontradiction and mathematical consistency seems to be the minimal criterion if a pseudocontinuum model is to demonstrate a degree of reliability in prediction, simulation, and design. This article is an exposition of the verifiability, validity, and confirmability characteristics of multiphase multidimensional models of reactions in packed beds. It addresses the difficulties of validation and the complexities of construction of models of reactions in packed beds by modeling kinetic data directly to show that often the claims of validity, verifiability, or confirmability of the results of multidimensional or even one-dimensional models of chemical reactions in packed beds, in spite of robust statistical tools, should be viewed with some degree of skepticism.
| Secondly, ChE has changed our accepted concepts and our ways of thinking in science and technology. Here, modeling stands out as the primary development. | |
| Levenspiel [1] |
1. Introduction
Engineers in several disciplines often use the continuum model to make inferences about the velocity, concentration, and temperature for reactions in packed beds. Since the partial differential equations of the continuum model cannot be integrated across the bed, in almost all cases, such inferences from numerical simulations are made based on a number of assumptions. Commonly, assumptions consist of empirically correlated velocity and transport parameters. However, a reliable profile of velocity in a packed bed is hard to obtain, and the insufficiency of an empirical choice velocity and the ensuing approach in analyzing reactions in packed beds carries with it inherently a fundamental implication: Unless the extrinsically superimposed velocity is the true velocity, the trend of the computed variables internal to the system will be partially predetermined. The disparity between the true and select profile of velocity renders a model inconsistent and compromises the reliability of the results. This discrepancy is amplified in two or multidimensional models since the semiempirical parameters also contribute to the inconsistency of a model.
The validity of the numerical models of physics and engineering is germane to the meaningfulness, reality, and relevance of the inferences made from the numerical simulation of models of fluid dynamics, and several authors have written extensively on the notions of verifiability and validity. Konikow and Bredehoeft [2] write: “Validation in science is a question of great interest to philosophers of science, and central to how we, as scientists, view what we do”. Nevertheless, the possibility of the validation of inferences made from numerical simulations is very much in question, as according to Carnap [3] “no complete verification is possible but only a process of gradually increasing confirmation”. The opening sentence in a paper by Oreskes et al. [4] reads: “Verification and validation of numerical models of natural systems is impossible”.
Often, graphical or informal comparison with experimental data is used as a method of validation of numerical models [5]. Oberkampf and Trucano [6] write that the view that the computer model is validated is not defensible in any meaningful way for complex physical processes and that “it is our view that the present method of qualitative ’graphical validation’, i.e., comparison of computational results and experimental data on a graph, is inadequate. This inadequacy especially affects complex engineered systems that heavily rely on computational simulation for understanding their predicted performance, reliability, and safety”.
Even statistical comparison with experimental data is not sufficient to establish validity, for it is possible that, despite conceptual errors and flawed assumptions, the data corroborate the simulated results. To this, Oreskes et al. [4] write: “If the predicted distribution of dependent data in a numerical model matches observational data, either in the field or laboratory, then the modeler may be tempted to claim that the model was verified. To do so would be to commit a logical fallacy, the fallacy of ’affirming the consequent”’.
There are plenty of recommendations and warnings in the literature from leading scientists and philosophers concerning the importance of the empirical confirmation or verification of theories or scientific models. In his address in 1921 to the Prussian Academy of Sciences, Einstein [7] said: “As far as the laws of mathematics refer to reality, they are not certain; and as far as they are certain, they do not refer to reality”. If uncertainty lurks in the correspondence between the laws of mathematics and reality, the certainty of the correspondence of the numerical simulations of complicated models of porous media, which are a system of differential equations with poorly understood boundary conditions [8] without rigorous empirical confirmation, with regard to the reality of the flow inside a porous bed is very much in doubt. Inspired by Einstein, Popper [9] wrote: “In so far as a scientific statement speaks about reality, it must be falsifiable; and in so far as it is not falsifiable, it does not speak about reality”. In Conjectures and Refutations, he writes: “A theory which is not refutable by any conceivable event is not scientific. Irrefutability is not a virtue of a theory (as people often think) but a vice”.
As scientists, we cannot avoid adhering to a school of thought as a reflection of what it is that we are doing. Konikow and Bredehoeft [2] write that “many, if not most, present day scientists who have considered these issues find themselves in Popper’s camp”. Popper’s criterion of demarcation is a pillar on which scientific truth stands.
Drawing on the falsifiability doctrine of Popper, Babuska and Oden [10] write that “Philosophically, absolute V&V [validity and verifiability] may be impossible, but V&V relative to a specific series of tests and preset tolerances may be perfectly legitimate as a basis for making decisions”. Concerning the philosophical implications of the terminologies of validity and verifiability, they explain that the proper language is to use corroboration, but the use of validity and verifiability is so pervasive in the literature that it is preferable to continue using validity and verifiability, but “place on it the burden of many qualifications”. In this regard, Oberkampf et al. [11] also write that statistical comparison is sufficient for “adequacy of the computational result for the intended uses of the model”. In Chapter 5, the National Research Council (NRC) of 2012 [12] on model validity reports that “A simple declaration that a model is “validated” cannot be justified. Rather, a validation statement should specify the QOIs [Quantity of Interest], accuracy and domain of applicability for which it applies”. Babuska and Oden [10] note that validity can only be made relevant to some tolerance and that for credibility that tolerance has to be statistical, thus defining some level of significance.
A criticism which is often leveled against the pseudocontinuum models, in particular at low Reynolds numbers and aspect ratios, is that they fail to adequately describe the state of reactions inside the bed. Citing the works of Küfner and Hofmann [13], Bey and Eigenberger [14], Giese et al. [15], and Winterberg et al. [16], in an article considering the complete three-dimensional (3D) structure of the packing, Freund et al. [17] write that “even these sophisticated models, which take into account axial and radial variations of the porosity, velocity and the transport parameters can hardly describe local phenomena in detail”. They predicate this on the average information which is part of pseudocontinuum models. While their criticism is proper on analytical grounds, they do not make the case for the superiority of their model or to confirm it, but they rather maintain that “in general, a good agreement of simulated and experimental data can be observed”. Grace and Taghipour [18] reported that, comparatively, the CFD codes for fluidized beds did not perform better than the mechanistic ones under similar conditions. Concerning descriptive attestation to the credibility of comparative analyses of sophisticated models, Oreskes et al. [4] write: “A neutral language is needed for the evaluation of model performance. Judgmental terms such as excellent, good, fair, and poor are useful because they invite, rather than discourage, contextual definition. Legitimately, all we can talk about is the relative performance of a model with respect to observational data, other models of the same site, and our own expectations based on theoretical preconceptions and experience of modeling other sites. None of these things can be discussed in absolute terms”. Freund et al. [17] continue to explain the deviations in velocity, which are between their simulation and experiment by writing that “At this point it should be noted that even though simulations and experiments were carried out for the same geometrical and fluid dynamical conditions, the local structures of the packing were not exactly the same. As the complete 3D structure of the random packing used in the experiments was not available, the packing for the flow field simulations were synthetically generated. While the ordering effect of the wall on the packing yields almost identical local structures near the wall, differences occur with increasing wall distance. This is a probable explanation for the increased deviations of the simulation results and the experimental data in the inner domain of the packing”. With this passage, Freund et al. [17] have laid down the likely prospect of simulating the flow in packed beds and that is that the structure of the packed bed determines the flow field, and without access to the structure of the bed, the results of simulations cannot be ascertained to be the true reflection of the local behavior of the flow. That they have observed relatively more favorable agreement near the wall is because the flow in that region is almost homogeneous, and, as they themselves have reported, within the region near the wall porosity reaches 100%. Acknowledging the promise of the CFD in modeling fluidized beds, Grace and Taghipour [18] caution that “great care is required to verify computational aspects of the model and to plan and execute proper experimental validation tests, covering a wide range of conditions, and where deviations are compared with computational and experimental errors”.
There exists a logical flaw in the structure of multidimensional pseudocontinuum models: inconsistency. A system of differential equations whose dependent variables and parameters belong to noncongruent domains is an inconsistent mathematical system. While validity is not immediately within reach, establishing consistency is readily possible. It is essential that a proposed model be minimally consistent internally. Consistency precedes verification. By internal consistency, we mean that a model should be free of conceptual errors, and having all variables and parameters identically belong to the same domain of the mathematical construct or the model is flawed to start. Once internal consistency is established, a model can be subjected to the process of partial and gradual confirmation. Consistency is an essential requirement for a model to be credible. An inconsistent model is never credible, even if the data occasionally corroborate its outcomes.
“The models developed in the engineering sciences should be distinguished from the models produced in engineering. Whereas the latter usually represent the design of a device or its mechanical workings, models in the engineering sciences aim for scientific understanding of the behaviour of different devices or the properties of diverse materials”, Boon and Knuuttila [19]. The inferences from engineering science models, by virtue of their claim, cannot be authenticated without the strict critical scrutiny of empirical confirmation and verification.
The verification and validation of the outcomes of multidimensional models could prove vital in aerospace, aeronautics, and nuclear engineering. It is not a coincidence that a large number of publications on validity is coming from these disciplines [20]. The IAEA [21] Nuclear Safety and Security Glossary defines validation of the system code “as the assessment of the accuracy of values predicted by the system code against relevant experimental data for the important phenomena expected to occur”. In regard to the process of verification of a computer model, Choudhary and Roy [22] write that “An important first step in solution verification is to check the input data for correctness of input files (e.g., model/geometry in the form of CAD files), grids, and completeness and clarity of supplied initial and boundary conditions. The next step in solution verification is numerical error estimation which involves quantifying known error that occurs in every computational simulation due to numerical approximations (e.g., discretization, insufficient iterations, etc.)”. As complicated as the geometry of an aircraft, a spaceship, or nuclear reactor core is, it is still not as disordered as the geometry of a packing. Furthermore, their geometry is available in its entirety. If not impossible, it is extremely difficult to reproduce the geometry of a packing by cutting it into an infinite number of slices and to also identify an infinite number of boundary conditions for the entire packing inside the bed point by point. But, if local is not every point P at , then local determination is a qualified determination. Now, if an approximate instead of the real geometry of the bed is chosen to avoid this unavoidable infinitude that would also be counter to the purpose of determining the local profile of the flow inside the bed.
Choudhary and Roy [22] discuss a stochastic-based metric as the area between the cumulative distribution of a variable from the model and the experiment. It is shown in Equation (1).
where is the cumulative distribution function (CDF) from the simulation, is the (CDF) from the experiment, and x is the measure of the global discretization error norm or the integrated quantities. This is a very useful metric for an overall evaluation of a multiphase multidimensional model for a well-known geometry such as the geometry of an aircraft or a space probe. Since, for them, is a realistic distribution of the flow, Equation (1) is a reasonable criterion for assessing the reliability of the results. For a poorly defined geometry such as a reactor bed packing however, it is hard to affirm from this relation alone the reality of the 2D or 3D distribution of the flow if the intent of the model is the identification of the 2D or 3D profile of the intrinsic variables.
If only for its aesthetic value alone, longing for the knowledge of the local profile of the intrinsic variables of reactions in a packed bed is a worthwhile pursuit. Nevertheless, until the foundation of such a pursuit is firmly in place, the task of unraveling the inner workings of reactions in packed beds remains a goal and not an end. For chemical reaction engineering applications, average models are the most economical. Average models can be verified easily and, if verified, are least likely to be inconsistent. The usefulness of the average models is in the algebraic form of the differential equations. Their differential equations are ordinary or temporal partial differential, and, in almost all cases, the finite difference suffices for numerical integration. Collecting experimental data to confirm average models is rudimentary and can be done with minimal cost and effort. All things considered (utility, cost, time, risk, safety, confirmability, etc.), average models are advantageous for the design, control, and optimization of chemical reactors.
This article is not concerned with the epistemological ramifications of validity and verifiability in chemical reaction modeling. Original arguments concerning the characteristic complexity of the validation of models of reactions in porous beds are currently available from several sources. Although reflective on the language to some extent, this presentation is not to be mistaken as a philosophical abstraction but an astute exposition of a problem in the rendition of conservation equations of porous media in need of an academicwide discussion. It concerns the utility, consistency, and confirmability characteristics of the pseudocontinuum models of reaction engineering. Much of what is to follow focuses on the degree of credibility of the inferences that can be made from a model of reactions in porous beds. It is intended as a practical example and is fashioned in an engineering context aimed at addressing these difficulties by the direct modeling of the data and statistical analysis of the results. The order of presentation of this article is as follows. Velocity is perhaps the most impactful operative in the resolution of the multidimensional systems of reactions in porous beds [23]. Section 2 presents a discussion of the profile of velocity from the solution of the steady state continuity and the equation of motion. Section 3.1 concerns the indispensability of validation (corroboration) of model outcomes with experimental data. And, Section 3.2 presents a comparative study of methanation reactions and addresses the necessity of the compatibility of input data and parameters in comparative analyses before verification can be claimed.
2. Velocity
Choudhary and Roy [22] wrote that an important first step in solution verification is the correctness of the input data and the initial and boundary conditions. Perhaps the most important input to a model of reactions in packed beds is the velocity. Prophetically, Bischoff and Levenspiel [24] cautioned that the “velocity profile data for packed beds will probably never be accurate enough to use …as a predictive equation for precise values of the effective overall axial dispersion coefficient”. This is not a claim but a mathematical truth.
In the simplest possible case, if we ignore dissipation, rotation, and potential forces, the steady state equations of continuity and motion for axial flow in cylindrical coordinates in a packed bed is given by Equations (2) and (3).
All of the variables are defined in the space of . If we assume that is known and that its radial component is insignificant, these equations can be solved in principle to obtain an expression for and as follows:
for some functions and , which satisfy the boundary conditions stipulated by Equation (6).
The unavailability of and has necessitated the simplification of conservation equations to formulate expressions that help solve the packed bed differential equations.
2.1. Plug Flow: Radially Independent Variables
Plug flow is often assumed to solve packed bed equations. Plug flow implies total radial mixing, which implies the radial constancy of all intrinsic variables. Under this assumption, the solution of the equation of continuity from part one of Equation (4) will be as in Equation (7).
This assumption leads to the bizarre conclusion that porosity is a separable function of z and r, as in . A remedy to avoid this absurdity has been to assume a constant value for porosity with the implication that is also a constant. But, these assumptions do not change the nature of the bed porosity, and this conception of the flow does not alter multiphase flow into single phase flow.
The assumption of plug flow with constant porosity seems to be plausible for isothermal differential reactors. But, it does not seem adequate for the resolution of processes in industrial reactors. Stegehake et al. [25] write that, in packed beds, the velocity deviates from the plug flow due to the porosity distribution and the friction near the wall. Highly exothermic and endothermic reactions both induce a radial temperature gradient that could undermine the assumption of perfect radial mixing. Lerou and Froment [26] studied the longitudinal temperature in a packed bed and recommended the inclusion of the radial profiles of porosity and velocity for the accurate design of highly exothermic processes. They also showed that the model that included the local properties of velocity and porosity was more sensitive to the local inlet and wall temperature variations. Vortmeyer and Haidegger [27] compared three models to show the inappropriateness of the assumption of constant velocity. They wrote: “It was found by comparison that the solutions of the classical WHT model failed gravely due to the inherent assumptions of constant porosity, plug flow, and near-wall temperature jump”. Although this fact has been known for several decades, the plug flow still is assumed in the simulation and analysis of industrial reactors [28].
2.2. Velocity and Ideal Gas State Equation
The 1D packed bed model with the plug flow equation of , in conjunction with the ideal gas law, is defined as in Equation (8):
which has been often employed to find a relation for superficial velocity in place of the solution of the continuity and the equation. This, subject to the provisions of Section 2.1, minimally satisfies the consistency requirement under the working hypothesis of plug flow for computing the axial profile of temperature and concentration.
Equation (8) violates the continuity equation in a 2-D spatial model if the intent is to probe the local profile of temperature or concentration. For example, to study the local transport of an endothermic and an exothermic reaction, Dixon [5,29] used Equation (9) in terms of cross-sectional averages of temperature and molecular weight to compute as input to a 2-D model to simulate the radial variations of temperature and mole fractions in a fixed bed tubular reactor.
From a 2-D model (base, Dixon [5,29]), he obtained the radial variations in the profiles of temperature and mole fraction (Figs. 19 and 20, page 175, [5]; and Figs 15 and 16, pp. 20–21, [29]) for both systems. But, based on Dixon [5]’s reported radial variations of temperature and mole fraction in the conclusion of the work, the computed density will be , and Equation (9) rewritten for ideal gas will be as Equation (10).
What is truly important and not transparent as a consequence of injecting Equation (9) in the rendition of the 2-D model is that during the integration process the Equation (10) keeps lurking within the confines of the packed bed unnoticeably in violation of the law of conservation of mass from the beginning to the end of the bed. As described [22], an important first step in solution verification is the correctness of the input data and the initial and boundary conditions, because once in motion the software will produce numbers which might have no basis in the reality of the process of interest. The grand error which is remarkable from assuming Equation (9) that inevitably leads to Equation (10) is the unwritten or perhaps unintended assertion that the point mass flux is equal to the total mass flux, a claim that can hardly withstand the scrutiny of reason.
The conservation of mass applied to the ideal gas law is given by Equation (11).
From the law of conservation of mass, one can only infer a relation among cross-sectional averages, which is derived according to Equation (15).
where , , and .
In terms of the initial feed data, Equation (15) might be expressed as Equation (16).
And, in terms of the superficial velocity, this equation appears as follows:
It does not seem plausible that Equation (9) might be applied to determine the local profiles of temperature or the concentration in a packed bed.
2.3. Mass Conservation
What is true for porous beds is the conservation of mass, which is obtained from Equation (5) as in Equation (18).
is the cross-sectionally averaged flux from which Equation (19) may be inferred.
where is the cross-sectionally averaged density, and is the interstitial velocity.
Recently, we [30] showed that, for irrotational flow in tubular reactors, the interstitial and superficial velocity are related according to Equation (20).
where is the characteristic of the bed porosity and can be considered to be constant throughout the length of the reactor. Also, is the area open to flow and is given by Equation (21).
Thus, one may come up with a simple relation as in Equation (22), which ties the cross-sectional density to the superficial velocity.
where is the mass flux in an empty tube.
Experimental measurements of the velocity in packed beds under many flow regimes and in particular for low Reynolds numbers and low aspect ratios [31,32] reject the idea of the existence of a simplified profile for velocity. The velocity in packed beds remains unknown. It is not possible to make a priori approximating assumptions about functions whose properties are unknown. Simplifying assumptions without a firm mathematical and physical foundation to merely facilitate the resolution of the conservation equations is untenable, and as Rajagopal [33] writes, “[s]uch assumptions, while leading to models within the framework that is proposed, are quite useless as such higher gradients generally lead to theories that require boundary conditions in addition to the usual boundary conditions in classical theories”. Ensuring consistency and presenting convincing confirming evidence are critical to the meaningfulness of inferences made from a model.
3. Indispensability of Corroboration with Experimental Data
Two sets of data correlation results will be presented in this section to examine the extent to which claims to the truth of a model stand to reason. Section 3.1 tests a model versus data from isotope transient tracing of methanation in a differential reactor. This will show that the claim of validity, even in spite of apparent statistical confirmation, needs to be viewed with a degree of skepticism. Section 3.2 considers data correlation for methanation reaction in an integral reactor. This section concerns the appropriateness of the input data and flow parameters for comparative analyses and model verification or validation.
3.1. The Fit, Insufficient Statistics, and Validation
Methanation on Ni/Al2O3 proceeds according to the following overall chemical equations:
In a differential reactor, the yield of carbon dioxide is minimal, and the water–gas shift and methanation of carbon dioxide can be ignored. Thus, the focus of isotope tracing of methanation will be only on the hydrogenation of carbon monoxide. The comprehensive methanation reaction is described by all three reactions, and they will be used in the discussion of the integral reaction in Section 3.2.
By and large, the following elementary chemical equations are hypothesized as a methane pathway on Ni catalysts.
The average model for tracing experiments in a differential reactor is described in an earlier paper [34]. The material balance equation for the average fractional concentration of labeled carbon monoxide, , is as in Equation (26).
The rate of consumption of CO is given by Equation (27).
is the ratio of the backward to the forward rates of the desorption/adsorption of carbon monoxide. Under steady state 13CO tracing, . If we add Equation (26) to its equivalent for , we will obtain the following equation:
With this constraint, we will have Equation (28) for the fractional marking in carbon monoxide.
The initial and boundary conditions for for pure compounds are as follows:
The material balance equations for the adsorbed intermediates are as follows:
For the fractional concentration of methane, we have Equation (34):
Since , and by using the constraint that for the reaction running at steady state is , Equation (34) will simplify as Equation (35).
The initial and boundary conditions for for pure compounds are given by Equation (36).
13CO tracing cannot distinguish between , and . Hence, the concentrations of these are lumped together as one parameter. It is shown as in the results.
We call the system of Equations (26)–(33) and Equation (35) Model A. The results for Model A are reported in Table 1.

Table 1.
Results from tracing of methanation on Ni-Al2O3 with Model A.
Figure 1 shows the fit of the data to the model.
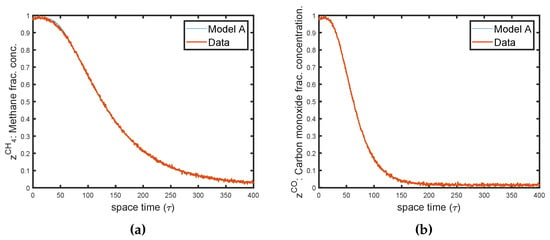
Figure 1.
Model A: (a) Fractional tracer marking in CH4. (b) Fractional tracer marking in CO.
The relatively small SEMs are due to the large number of data points (>800). Our estimate of CO uptake is 174 mol/g. Vannice [35] reported an uptake of 110 mol/g at room temperature for an alumina-supported nickel. Underwood and Bennett [36] reported a total of 181 mol/g of carbon for methanation on a alumina-supported nickel catalyst within a temperature range of 180–240 °C.
We considered another model (Model B) for which parameters and were taken to be different for carbon monoxide and methane. The results are reported in Table 2.

Table 2.
Results from tracing of methanation on Ni-Al2O3 with Model B.
The graphs of this fit are shown in Figure 2.
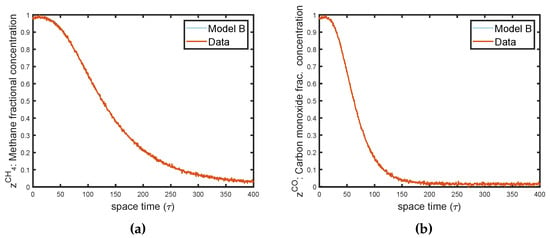
Figure 2.
Model B: (a) Fractional tracer marking in CH4. (b) Fractional tracer marking in CO.
The fits in Figure 1 and Figure 2 can be figuratively considered “perfect”. While these fits are virtually indistinguishable, only the comparative analysis of the results with the literature indicates that, of the two models, Model B is not supported by the experimental data. Even then, validity cannot be claimed for the Model A outcomes. All that can be said is that the results generated by Model A are consistent with the experimental data. But, while the results of Model A are consistent with the literature, still there could be many other possible sets of parameters, which give as good or a better fit and provide improved statistical diagnostic information about data correlation of which we may perhaps have no knowledge of yet. We are cognizant of the identifiability characteristics of models, which may potentially provide several more sets of parameters [37,38]. Unfortunately, the mathematics of identifiability is complicated, and, except for simple models, it cannot be usefully implemented to determine all the possible sets of parameters [39].
As demonstrated, even a statistical analysis is not sufficient to validate a numerical model but only to invalidate it, as our analysis invalidated Model B. It takes more than one methodical comparison before the claim to the truth of a model of packed beds can be made with a degree of reliability.
3.2. Incompatible Flow Parameters and Verification
Taylor and Rumsey [40] write that detailed attention must be paid to all aspects of CFD verification (from code verification through to solution verification) to ensure that computational models are being solved correctly (i.e., without coding errors) and to a quantified numerical accuracy. Without this, there is an increased risk of misinterpreting and incorrectly attributing or quantifying the reasons for, or magnitude of, any residual disparity in the computed and measured data. Forcellini [41] lists four source of errors in numerical modeling: (1) modeling error, (2) input errors, (3) numerical errors, and (4) human mistakes. Under human mistakes, he includes mistakes in data input or wrong guesses of the initial values. Human mistakes or the misrepresentation of data could indeed result in unsubstantiated claims.
Chein et al. [42] applied the Maxwell–Stefan method to simulate the isothermal methanation process by solving the multidimensional Navier–Stokes energy transport equations to also obtain the radial profiles of velocity, temperature, and concentration inside a short integral reactor. They used the experimental data for the fixed-bed reactor reported in the study of Hu et al. [43] and Liu et al. [44] to validate their numerical model.
In an earlier work [45], the same isothermal methanation process discussed by Chein et al. [42] was analyzed by an average model in an integral reactor by fitting the Equations (37) and (38) to the experimental data reported by Hu et al. [43] and Liu et al. [44].
This is a two-phase flow system, and Equations (37) and (38) were solved in conjunction with the diffusion equation in the solid phase. The details of the model and the data correlation are given by Otarod and Supkowski [45].
Table 3 contains the experimental data, the results from our model, and Chein et al. [42]’s simulation. Figure 3a and Figure 3b each consists of three response curves and two sets of experimental data. The solid line curve identified by the legend “—Chein et al.” is the result Chein et al. [42] reported by simulating the methanation reaction with a flow rate of 60 mL/min. The physical data are under Alternative parameters in Table 3. This curve was scanned from their work and reproduced here. The dashed curve identified by the legend “- - -Eq. 37 & 38†” is the result of fitting Equations (37) and (38) to Hu et al. [43] data with the actual flow rate of 250 mL/min ( m3/s). This corresponds to data identified with the symbol in Table 3. The dash–dotted curve identified by the legend “-.-.-. Eqs. 37 & 38‡” is the solution of Equations (37) and (38) using the physical data used by Chein et al. [42] but at the actual flow rate of 250 mL/min.

Table 3.
Catalyst, reactor, and transport data.
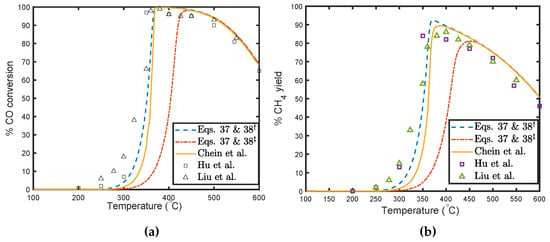
Figure 3.
Comparison of the responses of three models with experimental data under different assumptions, formulation, and physical parameters: (a) percentage conversion of CO; (b) percentage yield of CH4 [42,43,44].
The parameters that Chein et al. [42] used for the verification and perhaps the validation of their model with data reported by Hu et al. [43] and Liu et al. [44] are very different. The flow rate, particle size, and tube diameter were part of the experimental design for the verifiability and perhaps the validity of the model. These cannot be selected differently to simulate a process for comparative purposes. Although the curves reported by Chein et al. [42] compare quite well with the data and the profile we reported by fitting the model to the data, i.e., the curve identified by the legend “- - - Eqs. (37) and (38)†”, the claim of the verifiability and validity of their model is not justified by any acceptable logical and mathematical criterion. Obviously, lowering the flow rate is tantamount to a smaller space time and, therefore, a longer contact time with the catalyst and subsequently a higher conversion. But, those results need to be compared with data generated from another experiment at a lower flow rate and different physical parameters. Moreover, their conclusion that “a typical plug flow velocity distribution is resulted for the fixed-bed flow field” is not supported by the literature for an aspect ratio of eight and a Reynolds numbers less than one. This example is an affirmation of [40]’s statement that coding errors increase the risk of misinterpreting and incorrectly attributing or quantifying the reasons for, or magnitude of, any residual disparity in the computed and measured data.
The review article by Stegehake et al. [25] concludes with the following paragraphs:
At present, the experimental measurement of the mechanisms within and between the catalyst phase and within the catalyst particles is only partially possible. Thus, a higher degree of detail is not inherently associated with a higher accuracy of a model approach.
Particle-resolved modelling has a great potential to describe the complex physical and chemical interactions in mathematical detail, so that a deeper understanding can be achieved. However, with the currently available computing power it is only possible to map sub-processes and small geometries. On the other hand, model validation with the currently available measurement methods can only be carried out to a limited extent.
In contrast, the average model described by Equations (37) and (38) is an example of a simple model that satisfies the criteria for validity (corroboration) and verifiability. The estimated parameters were the tortuosity and the methanation activation energy. They were obtained by fitting the model to the data. The statistics are reported in Table 3. The measured parameters are comparable to the data reported by other investigators. In another article [30], we presented an average model consisting of the averages of all intrinsic variables of velocity, concentration and temperature while incorporating into the model the variations of the porosity of the bed. The outcomes of the model were statistically compared to the existing available data.
4. Concluding Remarks
Assumptions made to make a model amenable to numerical analysis introduce subjectivity into the results. The subjective perception of a process need not coincide with the objective reality inside the bed. For a model that is intensively modified mathematically to be computable numerically to project a semblance of reliability, it has to be critically and rigorously confirmed empirically. Citing visual or graphical comparison to support a projected claim comes short of scientific standards.
A complex model is not always more telling of the reaction details in a porous bed because if not impossible it is not easy to mathematically trace the path of the flow inside the packing while in the interest of relevancy every statement in a model needs to be accounted for. A simple but approximate model which within the boundaries of its claims is rigorously confirmed by experimental data is far more superior scientifically than a complex model which appeals to visual judgement to conjure the patrons of knowledge for acceptance. Considering that the more complicated a model the less likely is the possibility of acquiring confirming experimental data, the utility of average models is evident.
There are parameters that can be reasonably selected as inputs to a model, and there are variables that might not be altered or assumed a priori. Empirically correlated parameters such as the dispersion coefficients, activation energies, average particle diameter, tortuosity, binary diffusion coefficients, thermal conductivity, etc., belong to the former category, and their approximate nature is a given. As long as they are carefully correlated, they belong to the category of the working hypotheses and the results are evaluated relative to them and their approximating impact can be tolerated. But, the intrinsically computable variables of a model such as velocity can never be assumed antecedently unless there is indisputable evidence to their authenticity. It is never logically befitting to foreordain the consequence of a process and refer to it as evidence of validity, verifiability, or confirmability.
The numerical solution of a system of partial differential equations is always the set of points obtained along the mesh lines. Regardless of the case, meshing predetermines the results. The difference between the numerical solution of the partial differential equations of porous media and the partial differential equations of homogeneous systems is in the mathematics of the numerical method. The mathematical rendition of homogeneous media is well established. This is not true of the case of multidimensional spatial meshing within the cryptic geometry of a packed bed. There does not exist a mathematical basis for establishing that the meshing of porous beds produces results that converge to the reality of the flow inside the bed, no matter the type of software, hardware, numerical method, or the size or the geometry of the meshing. The primal cause of the inscrutability of the profile of reaction variables in porous beds is neither the incapacity of the digital machines, nor is it because of the method of numerical analysis. The principal cause is the indefinability of the geometry of the porous beds, and the prospect of resolving the bed geometry does not seem to be imminent any time soon. Meshing for a porous bed analysis is a far cry from meshing for a homogeneous medium. It is because the former is not substantiated by any conceivable mathematical logic, but the latter is. Furthermore, since the local values of intrinsic variables are in effect immeasurable, it would be counterintuitive to presume that a particular software, together with a particular meshing, under the algorithm of a particular numerical method would produce the solution that would converge to an indiscernible local profile, even approximately.
To be scientifically sound, a novel approach for dissecting a porous bed needs to be based on a solid mathematical foundation such as Simpson’s rule and the potentiality of statistical empirical confirmation. Such a method is yet to be conceived for porous media. Adherence to the principles of scientific inquiry demands that the claims of research findings be supported by evidence. Ironically, while the criteria of scientific falsifiability are universally acknowledged by scientists and engineers alike, when it comes to the porous media literature is teeming with articles with very little to present as evidence of consistency or confirmability. The consideration of mathematical and physicochemical restrictions in the application of conservation equations to the porous media is essential. Making approximating assumptions is not the same as softly violating the principles of logic and mathematics. Once mathematical and physicochemical restrictions are relaxed or brushed aside, unsubstantiated conclusions are easy to follow. The proper application of mathematical principles, the observance of the rules of correspondence in comparative analyses, and the careful use of scientific language are indispensable in scholarship. Today’s research findings find their way into tomorrow’s curricula. Such a practice in scholarship shall benefit the students of the physical sciences, since an apprentice of knowledge often believes without questioning what is in print.
Funding
This research received no external funding.
Data Availability Statement
The simulation data from Chein et al. [42] were scanned from their work and reproduced here for the isothermal integral reactor simulation and are reported here in Figure 3: https://www.sciencedirect.com/science/article/abs/pii/S0016236116307268 (accessed on 30 April 2024). The experimental data from Hu et al. [43] were scanned and reported in Figure 3. https://pubs.acs.org/doi/10.1021/ie300049f (accessed on 30 April 2024). The experimental data from Liu et al. [44] were scanned and reported in Figure 3. https://pubs.rsc.org/en/content/articlelanding/2015/ra/c4ra13634a#! (accessed on 30 April 2024).
Conflicts of Interest
The author declares no conflicts of interest.
Nomenclature
| mole fraction | |
| cup mixing fractional concentration of reactant A | |
| cup mixing fractional concentration of product B | |
| particle diameter (m) | |
| initial velocity (m/s) | |
| r | radial coordinate |
| z | axial coordinate |
| v | interstitial velocity (m/s) |
| superficial velocity (m/s) | |
| ℓ | adsorption site |
| axial thermal conductivity (W/m/K) | |
| radial thermal conductivity (W/m/K) | |
| heat of reaction (J/m/kg) | |
| interfacial heat (J/m/kg) | |
| CV | specific heat (J/kg/K) |
| Cj | surface concentration, (mol/kg) |
| W | total catalyst weight (g) |
| Q0 | inlet volumetric flow rate () |
| reaction rate of a gas phase compound (kg/m3/s) | |
| mass flow rate (kg/s) | |
| cumulative distribution function | |
| empirical distribution function | |
| L | reactor length (m) |
| radially averaged concentration (mol/m3) | |
| DL | axial dispersion coefficient |
| DT | radial dispersion coefficient |
| T | temperature (K) |
| Tc | center temperature (K) |
| Tw | wall temperature (K) |
| F | flow rate (m3/s) |
| VCO | steady state rate of CO conversion (mol/s/kg) |
| Vb | steady state backward rate (mol/s/kg) |
| Vf | steady state forward rate (mol/s/kg) |
| A0 | empty reactor cross sectional area (m2) |
| P | pressure (Pa) |
| M | average molecular weight (kg/mol) |
| mean axial Péclet number | |
| mass flux () | |
| fluid density () | |
| bed void fraction | |
| fractional conversion | |
| dimensionless axial coordinate | |
| dimensionless time | |
| measure of axial dispersion coefficient cofactor | |
| measure of coefficient of convective term | |
| measure of reciprocal average concentration fluctuation | |
| measure of radial concentration fluctuation factor | |
| tortuosity |
References
- Levenspiel, O. Modeling in chemical engineering. Chem. Eng. Sci. 2002, 57, 4691–4696. [Google Scholar] [CrossRef]
- Konikow, L.F.; Bredehoeft, J.D. Ground-water models cannot be validated. Adv. Water Res. 1992, 15, 75–83. [Google Scholar] [CrossRef]
- Carnap, R. Testability and Meaning. Philos. Sci. 1936, 3, 419–471. [Google Scholar] [CrossRef]
- Oreskes, N.; Shrader-Frechette, K.; Belitz, K. Verification, Validation, and Confirmation of Numerical Models in the Earth Sciences. Science 1994, 263, 641–646. [Google Scholar] [CrossRef] [PubMed]
- Dixon, A.G. Local transport and reaction rates in a fixed bed reactor tube: Exothermic partial oxidation of ethylene. Chem. Eng. Sci. 2021, 231, 116305. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Trucano, T.G. Verification and validation in computational fluid dynamics. Prog. Aerosp. Sci. 2002, 38, 209–272. [Google Scholar] [CrossRef]
- Einstein, A. Sidelights on Relativity; Dover Publications: New York, NY, USA, 1983; p. 28. [Google Scholar]
- Gelhar, L.W. Stochastic subsurface hydrology from theory to applications. Water Resour. Res. 1986, 22, 135S–145S. [Google Scholar] [CrossRef]
- Popper, K.R. The Logic of Scientific Discovery; Martino Publishing: Eastford, CT, USA, 2014. [Google Scholar]
- Babuska, I.; Oden, J. Verification and validation in computational engineering and science: Basic concepts. Comput. Methods Appl. Mech. Eng. 2004, 193, 4057–4066. [Google Scholar] [CrossRef]
- Oberkampf, W.L.; Trucano, T.G.; Hirsch, C. Verification, validation, and predictive capability in computational engineering and physics. Appl. Mech. Rev. 2004, 57, 345–384. [Google Scholar] [CrossRef]
- National Research Council. Assessing the Reliability of Complex Models: Mathematical and Statistical Foundations of Verification, Validation, and Uncertainty Quantification; The National Academies Press: Washington, DC, USA, 2012. [Google Scholar] [CrossRef]
- Küfner, R.; Hofmann, H. Implementation of radial porosity and velocity distribution in a reactor model for heterogeneous catalytic gasphase reactions (TORUS-Model). Chem. Eng. Sci. 1990, 45, 2141–2146. [Google Scholar] [CrossRef]
- Bey, O.; Eigenberger, G. Fluid flow through catalyst filled tubes. Chem. Eng. Sci. 1997, 52, 1356–1376. [Google Scholar] [CrossRef]
- Giese, M.; Rottschäfer, K.; Vortmeyer, D. Measured and modeled superficial flow profiles in packed beds with liquid flow. AIChE J. 1998, 44, 484–490. [Google Scholar] [CrossRef]
- Winterberg, M.; Tsotsas, E.; Krischke, A.; Vortmeyer, D. A simple and coherent set of coefficients for modelling of heat and mass transport with and without chemical reaction in tubes filled with spheres. Chem. Eng. Sci. 2000, 55, 967–979. [Google Scholar] [CrossRef]
- Freund, H.; Zeiser, T.; Huber, F.; Klemm, E.; Brenner, G.; Durst, F.; Emig, G. Numerical simulations of single phase reacting flows in randomly packed fixed-bed reactors and experimental validation. Chem. Eng. Sci. 2003, 58, 903–910. [Google Scholar] [CrossRef]
- Grace, J.R.; Taghipour, F. Verification and validation of CFD models and dynamic similarity for fluidized beds. Powder Technol. 2004, 139, 99–110. [Google Scholar] [CrossRef]
- Boon, M.; Knuuttila, T. Models as Epistemic Tools in Engineering Sciences. In Philosophy of Technology and Engineering Sciences; Meijers, A., Ed.; Handbook of the Philosophy of Science; North-Holland: Amsterdam, The Netherlands, 2009; pp. 693–726. [Google Scholar]
- Luckring, J.M.; Shaw, S.; Oberkampf, W.L.; Graves, R.E. Model validation hierarchies for connecting system design to modeling and simulation capabilities. Prog. Aerosp. Sci. 2023, 142, 100950. [Google Scholar] [CrossRef]
- IAEA. IAEA Nuclear Safety and Security Glossary; Non-Serial Publications; International Atomic Energy Agency: Vienna, Austria, 2022; p. 218. [Google Scholar]
- Choudhary, A.; Roy, C.J. Verification and Validation for Multiphase Flows. In Handbook of Multiphase Flow Science and Technology; Yeoh, G.H., Joshi, J.B., Eds.; Springer Nature Singapore: Singapore, 2023; pp. 467–503. [Google Scholar] [CrossRef]
- Schertz, W.W.; Bischoff, K.B. Thermal and material transport in nonisothermal packed beds. AIChE J. 1969, 15, 597–604. [Google Scholar] [CrossRef]
- Bischoff, K.B.; Levenspiel, O. Fluid dispersion-generalization and comparison of mathematical models-II. Comparison of models. Chem. Eng. Sci. 1962, 17, 257–264. [Google Scholar] [CrossRef]
- Stegehake, C.; Riese, J.; Grünewald, M. Modeling and Validating Fixed-Bed Reactors: A State-of-the-Art Review. ChemBioEng Rev. 2019, 6, 28–44. [Google Scholar] [CrossRef]
- Lerou, J.J.; Froment, G.F. Velocity, temperature and conversion profiles in fixed bed catalytic reactors. Chem. Eng. Sci. 1977, 32, 853–861. [Google Scholar] [CrossRef]
- Vortmeyer, D.; Haidegger, E. Discrimination of three approaches to evaluate heat fluxes for wall-cooled fixed bed chemical reactors. Chem. Eng. Sci. 1991, 46, 2651–2660. [Google Scholar] [CrossRef]
- Pantoleontos, G.; Kikkinides, E.S.; Georgiadis, M.C. A heterogeneous dynamic model for the simulation and optimisation of the steam methane reforming reactor. Int. J. Hydrogen Energy 2012, 37, 16346–16358. [Google Scholar] [CrossRef]
- Dixon, A.G. Local transport and reaction rates in a fixed bed reactor tube: Endothermic steam methane reforming. Chem. Eng. Sci. 2017, 168, 156–177. [Google Scholar] [CrossRef]
- Otarod, M. Area averaging of packed bed in continua conservation equations in axial flow. Can. J. Chem. Eng. 2024, 102, 2527–2547. [Google Scholar] [CrossRef]
- Götz, J.; Zick, K.; Heinen, C.; König, T. Visualisation of flow processes in packed beds with {NMR} imaging: Determination of the local porosity, velocity vector and local dispersion coefficients. Chem. Eng. Process. 2002, 41, 611–629. [Google Scholar] [CrossRef]
- Rexwinkel, G.; Heesink, A.B.M.; Swaaij, W.P.M.V. Mass transfer in packed beds at low Péclet numbers–wrong experiments or wrong interpretations? Chem. Eng. Sci. 1997, 52, 3995–4003. [Google Scholar] [CrossRef]
- Rajagopal, K.R. On Implicit Constitutive Theories. Appl. Math. 2003, 48, 279–319. [Google Scholar] [CrossRef]
- Otarod, M.; Supkowski, R.M. Low Reynolds number isotope transient kinetic modeling in isothermal differential tubular catalytic reactors. AIChE J. 2018, 64, 1317–1329. [Google Scholar] [CrossRef]
- Vannice, M. The catalytic synthesis of hydrocarbons from H2/CO mixtures over the group VIII metals: II. The kinetics of the methanation reaction over supported metals. J. Catal. 1975, 37, 462–473. [Google Scholar] [CrossRef]
- Underwood, R.; Bennett, C. The CO/H2 reaction over nickel-alumina studied by the transient method. J. Catal. 1984, 86, 245–253. [Google Scholar] [CrossRef]
- Casas-Orozco, D.; Villa, A.L.; Guerra, O.J.; Reklaitis, G.V. Dynamic parameter estimation and identifiability analysis for heterogeneously-catalyzed reactions: Catalytic synthesis of nopol. Chem. Eng. Res. Des. 2018, 134, 226–237. [Google Scholar] [CrossRef]
- Happel, J. Identifiability and Distinguishability; Academic Press: Cambridge, MA, USA, 1986; Chapter 6; pp. 123–137. [Google Scholar]
- Villaverde, A.F.; Barreiro, A.; Papachristodoulou, A. Structural Identifiability Analysis via Extended Observability and Decomposition. IFAC-PapersOnLine 2016, 49, 171–177. [Google Scholar] [CrossRef]
- Taylor, N.J.; Rumsey, C.L. CFD Validation Experiments: Toward a Broader Perspective. In Proceedings of the AIAA Scitech 2021 Forum, Virtual, 11–15 and 19–21 January 2021. [Google Scholar] [CrossRef]
- Forcellini, D. The role of falsification in the validation of numerical models. Civ. Eng. Environ. Syst. 2023, 40, 50–59. [Google Scholar] [CrossRef]
- Chein, R.Y.; Yu, C.T.; Wang, C.C. Numerical simulation on the effect of operating conditions and syngas compositions for synthetic natural gas production via methanation reaction. Fuel 2016, 185, 394–409. [Google Scholar] [CrossRef]
- Hu, D.; Gao, J.; Ping, Y.; Jia, L.; Gunawan, P.; Zhong, Z.; Xu, G.; Gu, F.; Su, F. Enhanced Investigation of CO Methanation over Ni/Al2O3 Catalysts for Synthetic Natural Gas Production. Ind. Eng. Chem. Res. 2012, 51, 4875–4886. [Google Scholar] [CrossRef]
- Liu, Y.; Gao, J.; Liu, Q.; Gu, F.; Lu, X.; Jia, L.; Xu, G.; Zhong, Z.; Su, F. Preparation of high-surface-area Ni/α-Al2O3 catalysts for improved CO methanation. RSC Adv. 2015, 5, 7539–7546. [Google Scholar] [CrossRef]
- Otarod, M.; Supkowski, R. A new outlook and a model of reactions in porous media. Can. J. Chem. Eng. 2021, 100, 1569–1583. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).