Theoretical Study of Some Angle Parameter Trigonometric Copulas

Abstract

Copulas are important probabilistic tools to model and interpret the correlations of measures involved in real or experimental phenomena. The versatility of these phenomena implies the need for diverse copulas. In this article, we describe and investigate theoretically new two-dimensional copulas based on trigonometric functions modulated by a tuning angle parameter. The independence copula is, thus, extended in an original manner. Conceptually, the proposed trigonometric copulas are ideal for modeling correlations into periodic, circular, or seasonal phenomena. We examine their qualities, such as various symmetry properties, quadrant dependence properties, possible Archimedean nature, copula ordering, tail dependences, diverse correlations (medial, Spearman, and Kendall), and two-dimensional distribution generation. The proposed copulas are fleshed out in terms of data generation and inference. The theoretical findings are supplemented by some graphical and numerical work. The main results are proved using two-dimensional inequality techniques that can be used for other copula purposes.

1. Introduction

Multidimensional functions called copulas are important in modeling multivariate random variables and understanding their dependence structures. They find their origin and prime property in the Sklar theorem (see [1]). Mathematically, for any integer n, a n-dimensional copula can be defined as a cumulative distribution function defined on ${[0,1]}^n$ with standard uniform marginal distributions. For the purposes of this article, the definition of a two-dimensional copula in the absolutely continuous case is given below.

Definition 1.

In the absolutely two-dimensional continuous case, the function$C:{[0,1]}^2\to [0,1]$is a two-dimensional copula if and only if

• $C(x,0)=C(0,y)=0$for any$(x,y)\in {[0,1]}^2$;
• $C(x,1)=x$and$C(1,y)=y$for any$(x,y)\in {[0,1]}^2$;
• the two-increasing property holds:${\partial }^{2}C(x,y)/\left(\partial x\partial y\right)\ge 0$for any$(x,y)\in {[0,1]}^2$.

This definition has a certain flexibility, but the main critical point remains the validity of the two-increasing property. On the practical side, copulas are crucial for estimating and interpreting the correlations of measures involved in real or experimental phenomena. Due to the plurality of possible phenomena of interest, a large number of copulas with various attributes are necessary. This has motivated researchers over the years to introduce valuable copulas, and apply them in concrete, real-life scenarios. The Frank, Gumbel–Hougaard, Ali–Mikhail–Haq, Joe, Farlie–Gumbel–Morgenstern, Clayton, Plackett, Raftery, elliptical, Fréchet, Galambos, and Marshall–Olkin are some of the classical copulas. Their definitions are based on motivated transformations of power-polynomial–exponential–logarithmic functions. They have specific qualities that make them of great interest in the context of random dependence modeling. Further details on these copulas can be found in the books of [1,2,3,4].

Recently, a lot of attention has been paid to copulas defined (partially or not) with trigonometric functions. The inclusion of trigonometric functions in this context confers on the copula some oscillating features that are appropriate to model the correlations into phenomena of periodic, circular, or seasonal nature. In particular, they are ideal for analyzing correlations involved in movement data, circular data, and environmental data. The theory of the classical trigonometric copulas can be found in [5,6,7,8,9,10,11]. For practice, we refer to [12,13,14,15,16]. Furthermore, the R package named Cylcop, recently developed by [17], gives the trigonometric (and circular) copulas a new dimension of applicability.

In this article, we present and study trigonometric copulas depending on a tuning angle parameter. They are derived from the very general family of copulas (not especially trigonometric) introduced in [18], but with the importance of the angle parameter in mind. To be more specific, the proposed copulas are defined by the following form:

$$C(x,y)=xyf\left(\theta \right(1-x\left)\right(1-y\left)\right),$$

where $f\left(x\right)$ is a simple one-dimensional function involving a trigonometric function, and $\theta$ is the angle parameter that only modulates this trigonometric function. Despite the potential for modeling correlations into periodic, circular, or seasonal phenomena, this area of research appears to have received little attention; none of the references [5,6,7,8,9,10,11] consider such an angle parameter approach. Thus, we describe the most intuitive of such angle parameter copulas, and study them on the theoretical side with a maximum of details. In particular, we emphasize the optimal set of values for $\theta$ such that the corresponding copula remains valid. We determine the expressions of the corresponding copula density, survival copula, and survival copula density. Some mixed trigonometric copulas are also given. Then, we examine a maximum of theoretical properties of the proposed angle parameter copulas, including symmetry properties, quadrant dependence properties, copula ordering, various expansions, tail dependences, medial correlation, Spearman correlation, Kendall correlation, and two-dimensional distribution generation. Data generation and inference from the proposed copulas are sketched. The theory is illustrated by means of graphics. The proofs of the main results are based on some two-dimensional inequality techniques that can be of independent interest.

The following is the outline for the rest of the article: A cosine angle parameter copula is presented in Section 2, along with its main theoretical properties. In Section 3, an analogue sine copula is introduced and studied. Section 4 contains the conclusions and perspectives.

2. Cosine Angle Parameter Copula

This section is devoted to a simple cosine copula with an angle parameter.

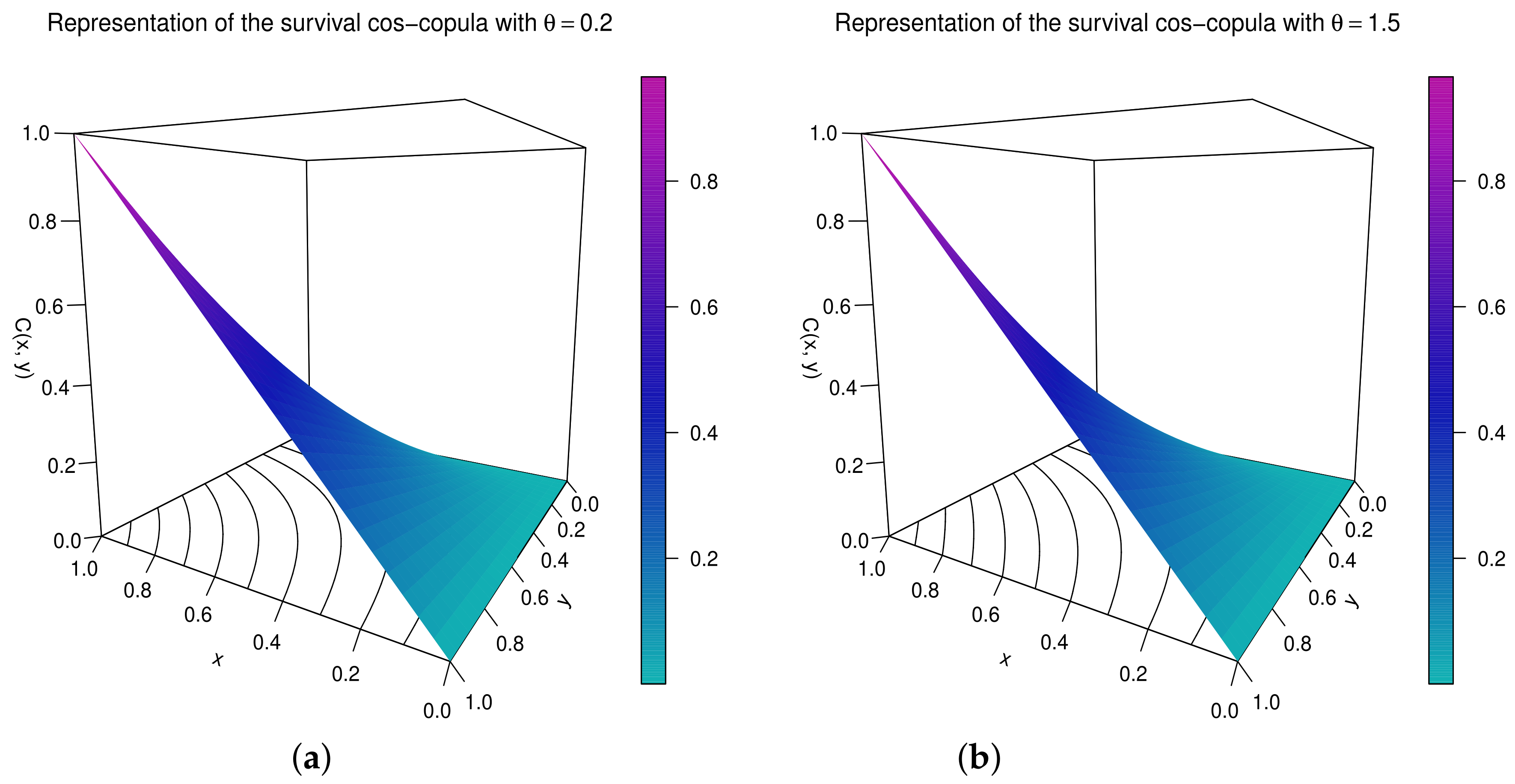
2.1. Definition and Graphics

The following proposition presents the considered cosine copula.

Proposition 1. 

The function$C_{\ast }:{[0,1]}^2\to [0,1]$defined by

$$\begin{array}{c}\hfill C_{\ast }(x,y)=xycos\left[\theta (1-x)(1-y)\right],\end{array}$$

(1)

with$\theta \in [0,\pi /2]$is a valid copula.

Proof. 

Let us prove the main points defining an absolutely continuous two-dimensional copula, as recalled in Definition 1.

• For any $x\in [0,1]$, we have $C_{\ast }(x,0)=x\times 0\times cos\left[\theta (1-x)(1-0)\right]=0$, and, for any $y\in [0,1]$, $C_{\ast }(0,y)=0\times ycos\left[\theta (1-0)(1-y)\right]=0$.
• For any $x\in [0,1]$, we have $C_{\ast }(x,1)=x\times 1\times cos\left[\theta (1-x)\times 0\right]=x$ and, similarly, for any $y\in [0,1]$, $C_{\ast }(1,y)=1\times y\times cos\left[\theta \times 0\times (1-y)\right]=y$.
• For any $(x,y)\in {[0,1]}^2$, using standard derivation techniques, simplifications and factorizations, we have

  $$\begin{array}{ll}\frac{{\partial }^2}{\partial x\partial y}{C}_{\ast }(x,y)& =\left[1-{\theta }^{2}xy(1-x)(1-y)\right]cos\left[\theta (1-x)(1-y)\right]\\ & -3\theta xysin\left[\theta (1-x)(1-y)\right]+\theta (x+y)sin\left[\theta (1-x)(1-y)\right].\end{array}$$

Let us prove the two-increasing property: ${\partial }^2{C}_{\ast }(x,y)/(\partial x\partial y)\ge 0$.

Since $\theta \in [0,\pi /2]$, we have $\theta (1-x)(1-y)\in [0,\pi /2]$. It follows from the inequality $sin\left(a\right)\ge acos\left(a\right)$, $a\in [0,\pi /2]$ applied with $a=\theta (1-x)(1-y)$ that

$$\begin{array}{cc}\hfill & \frac{{\partial }^2}{\partial x\partial y}{C}_{\ast }(x,y)\ge \left[1-{\theta }^{2}xy(1-x)(1-y)\right]cos\left[\theta (1-x)(1-y)\right]\hfill \\ \hfill & -3\theta xysin\left[\theta (1-x)(1-y)\right]+{\theta }^2(x+y)(1-x)(1-y)cos\left[\theta (1-x)(1-y)\right]\hfill \\ \hfill & =\left[1+{\theta }^2(x+y-xy)(1-x)(1-y)\right]cos\left[\theta (1-x)(1-y)\right]\hfill \\ \hfill & -3\theta xysin\left[\theta (1-x)(1-y)\right]\hfill \\ \hfill & \ge A_1+A_2,\hfill \end{array}$$

where

$$A_1={\theta }^2(x+y-xy)(1-x)(1-y)cos\left[\theta (1-x)(1-y)\right]$$

and

$$A_2=cos\left[\theta (1-x)(1-y)\right]-3\theta xysin\left[\theta (1-x)(1-y)\right].$$

Let us prove that $A_1\ge 0$ and $A_2\ge 0$.

For $A_1$, we can remark that $x+y-xy=1-(1-x)(1-y)\in [0,1]$. So $A_1\ge 0$ as a product of positive terms.

For $A_2$, it follows from the inequality $sin\left(a\right)\le a$, $a\in [0,\pi /2]$ applied with $a=\theta (1-x)(1-y)$ that

$$\begin{array}{c}\hfill A_2\ge \psi (x,y;\theta ),\end{array}$$

(2)

where

$$\psi (x,y;\theta )=cos\left[\theta (1-x)(1-y)\right]-3{\theta }^{2}xy(1-x)(1-y).$$

We have

$$\frac{\partial }{\partial \theta }\psi (x,y;\theta )=-(1-x)(1-y)\left\{6\theta xy+sin\left[\theta (1-x)(1-y)\right]\right\}\le 0,$$

implying that $\psi (x,y;\theta )$ is a decreasing function with respect to $\theta$. Therefore, for any $\theta \in [0,\pi /2]$, we have

$$\begin{array}{c}\hfill \psi (x,y;\theta )\ge \psi (x,y;\pi /2),\end{array}$$

(3)

with

$$\begin{array}{cc}\hfill \psi (x,y;\pi /2)& =cos\left[\frac{\pi }{2}(1-x)(1-y)\right]-\frac{3{\pi }^2}{4}xy(1-x)(1-y).\hfill \end{array}$$

By applying the Kober inequality: $cos\left(a\right)\ge 1-(2/\pi )a$ for $a\in [0,\pi /2]$ (see [19,20]), with $a=(\pi /2)(1-x)(1-y)\in [0,\pi /2]$, we get

$$\begin{array}{cc}\hfill \psi (x,y;\pi /2)& \ge \varphi (x,y),\hfill \end{array}$$

(4)

where

$$\varphi (x,y)=x+y-xy-\frac{3{\pi }^2}{4}xy(1-x)(1-y).$$

Let us prove that $\varphi (x,y)\ge 0$ for any $(x,y)\in {[0,1]}^2$. First, $\varphi (x,y)$ is a continuous function for $(x,y)\in {[0,1]}^2$, and ${[0,1]}^2$ is a compact set, so the maximum and minimum of $\varphi (x,y)$ on this set are attained. Let us now perform a critical points analysis. We have

$$\begin{array}{c}\hfill {\displaystyle \left\{\begin{array}{c}{\displaystyle \frac{\partial }{\partial x}\varphi (x,y)=\frac{1}{4}(1-y)(3{\pi }^2(2x-1)y+4)}\hfill \\ {\displaystyle \frac{\partial }{\partial y}\varphi (x,y)=\frac{1}{4}(1-x)(3{\pi }^2(2y-1)x+4)}\hfill \end{array}\right..}\end{array}$$

Therefore, we have $\partial \varphi (x,y)/(\partial x)=0$ and $\partial \varphi (x,y)/(\partial y)=0$ if and only if

• $y=1$ and $x=1$; or
• $y=1$ and $3{\pi }^2(2y-1)x+4=0$ which implies that $x=-4/\left(3{\pi }^2\right)\notin [0,1]$, so this case is excluded; or
• $x=1$ and $3{\pi }^2(2x-1)y+4=0$ which implies that $y=-4/\left(3{\pi }^2\right)\notin [0,1]$, so this case is excluded; or
• $3{\pi }^2(2x-1)y+4=0$ and $3{\pi }^2(2x-1)y+4=0$, which implies that $x=y$ and $3{\pi }^2(2x-1)x+4=0$, which is a polynomial of degree 2 with the discriminant equal to $\Delta =1-32/\left(3{\pi }^2\right)<0$. Therefore, there is no (real) solution.

As a result, there is only one critical point for $\varphi (x,y)$, and it is $(1,1)$. This point clearly gives a maximum value for $\varphi (x,y)$ since $\varphi (1,1)=1\ge x+y-xy\ge \varphi (x,y)$. Since there is no other critical point, $\varphi (x,y)$ has a “two-dimensional decreasing pattern”, and the minimum value of $\varphi (x,y)$ is attained on point(s) on the borders of ${[0,1]}^2$. Therefore, for any $(x,y)\in {[0,1]}^2$, we have

$$\begin{array}{cc}\hfill & \varphi (x,y)\ge \hfill \\ \hfill & \underset{(x,y)\in {[0,1]}^2}{inf}\varphi (x,y)=min[\underset{x\in [0,1]}{inf}\varphi (x,0),\underset{y\in [0,1]}{inf}\varphi (0,y),\underset{x\in [0,1]}{inf}\varphi (x,1),\underset{y\in [0,1]}{inf}\varphi (1,y)]\hfill \\ \hfill & =min(\underset{x\in [0,1]}{inf}x,\underset{y\in [0,1]}{inf}y,\underset{x\in [0,1]}{inf}1,\underset{y\in [0,1]}{inf}1)=0.\hfill \end{array}$$

(5)

It follows from Equations (2)–(5) that $A_2\ge 0$. The two-increasing property is proved.

As a result, $C_{\ast }(x,y)$ is a valid two-dimensional copula. This ends the proof of Proposition 1. □

Remark 1.

For the more restrictive case$\theta \in [0,\pi /4]$, we can prove the two-increasing property in a more simple and direct manner. We have

$$\begin{array}{cc}\hfill & \frac{{\partial }^2}{\partial x\partial y}{C}_{\ast }(x,y)\hfill \\ \hfill & =\left[1-{\theta }^{2}xy(1-x)(1-y)\right]cos\left[\theta (1-x)(1-y)\right]-\theta (3xy-x-y)sin\left[\theta (1-x)(1-y)\right].\hfill \end{array}$$

Since $\theta \in [0,\pi /4]\subseteq [0,1]$, we have ${\theta }^{2}xy(1-x)(1-y)\le 1$, and by applying the inequality $cos\left(a\right)\ge sin\left(a\right)$ for any $a\in [0,\pi /4]$ with $a=\theta (1-x)(1-y)\in [0,\pi /4]$, we get

$$\begin{array}{cc}\hfill \frac{{\partial }^2}{\partial x\partial y}{C}_{\ast }(x,y)& \ge \left[1-{\theta }^{2}xy(1-x)(1-y)\right]sin\left[\theta (1-x)(1-y)\right]\hfill \\ \hfill & -\theta (3xy-x-y)sin\left[\theta (1-x)(1-y)\right].\hfill \end{array}$$

Since $\theta \in [0,1]$, we have ${\theta }^{2}xy(1-x)(1-y)\le (1-x)(1-y)$ and $\theta (3xy-x-y)=\theta [xy+x(y-1)+y(x-1\left)\right]\le xy$. Thus

$$\begin{array}{cc}\hfill \frac{{\partial }^2}{\partial x\partial y}{C}_{\ast }(x,y)& \ge \left[1-(1-x)(1-y)\right]sin\left[\theta (1-x)(1-y)\right]-xysin\left[\theta (1-x)(1-y)\right]\hfill \\ \hfill & =[x(1-y)+y(1-x)]sin\left[\theta (1-x)(1-y)\right]\ge 0.\hfill \end{array}$$

The two-increasing property is proved. This ends this alternative proof for $\theta \in [0,\pi /4]$.

For the purposes of this study, we call the copula $C_{\ast }(x,y)$ in Equation (1) as the cos-copula. It has the feature of having a tuning angle parameter $\theta$ that modulates its correlation features. For $\theta =0$, we clearly have $C_{\ast }(x,y)=xy$; the cos-copula is reduced to the independence copula. Furthermore, we can remark that the cos-copula is still valid for $\theta \in [-\pi /2,0]$ because of the evenness of the cosine function. We can, thus, define the cos-copula with $\theta \in [-\pi /2,\pi /2]$ without loss of generality.

To end the presentation, Figure 1 represents the two-dimensional plot of the cos-copula for selected values of $\theta$.

From Figure 1, we see that the parameter $\theta$ skews the triangular shape of the cos-copula.

The next parts are devoted to the functions related to the cos-copula, as well as its main properties.

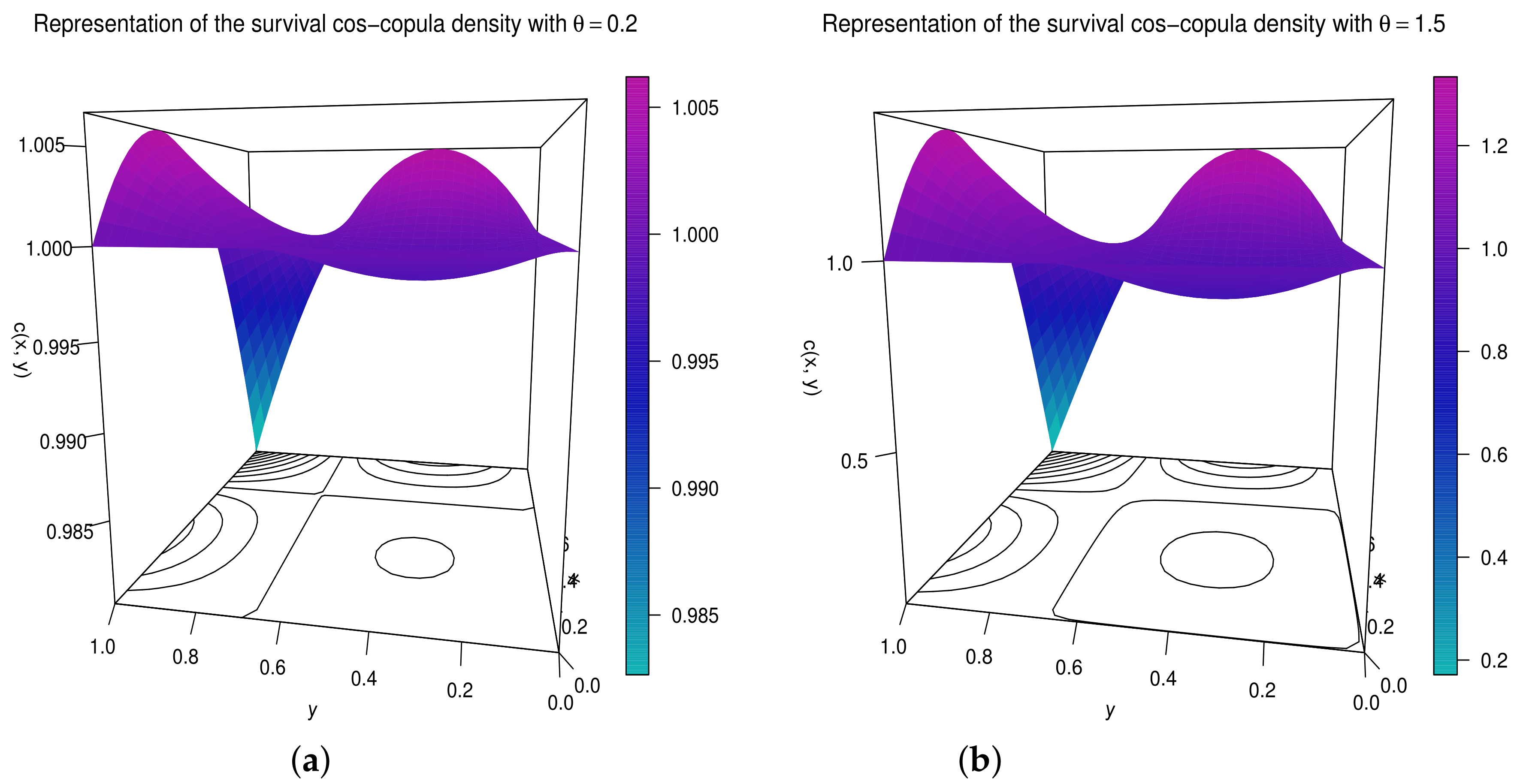
2.2. Related Functions

The density associated with the cos-copula is the function $c_{\ast }:{[0,1]}^2\to [0,+\infty )$ given by

$$\begin{array}{cc}\hfill & c_{\ast }(x,y)=\frac{{\partial }^2}{\partial x\partial y}{C}_{\ast }(x,y)\hfill \\ \hfill & =\left[1-{\theta }^{2}xy(1-x)(1-y)\right]cos\left[\theta (1-x)(1-y)\right]-\theta (3xy-x-y)sin\left[\theta (1-x)(1-y)\right].\hfill \end{array}$$

It is worth noting that $c_{\ast }(0,0)=cos\left(\theta \right)$ which can be negative for some values of $\theta$. In particular, $C_{\ast }(x,y)$ is not a copula for $\theta \in (\pi /2,\pi ]$. In this sense, if we restrict our attention to the interval $[0,\pi ]$, $[0,\pi /2]$ is the optimal set of values for $\theta$.

As usual, the copula density can be involved in various moment-type measures, and estimation methods (see, for instance, Refs. [13,17]).

Figure 2 represents the two-dimensional plot of the cos-copula density for selected values of $\theta$.

Thus, we see how the parameter $\theta$ affects the overall shape of the cos-copula density.

As a last important function, the survival cos-copula is the function ${\widehat{C}}_{\ast }:{[0,1]}^2\to [0,1]$ defined by

$$\begin{array}{cc}\hfill & {\widehat{C}}_{\ast }(x,y)=x+y-1+C_{\ast }(1-x,1-y)\hfill \\ \hfill & =x+y-1+(1-x)(1-y)cos\left(\theta xy\right)\hfill \\ \hfill & =xy-(1-x)(1-y)\left[1-cos\left(\theta xy\right)\right].\hfill \end{array}$$

It defines a valid copula, which is also a new trigonometric copula with an angle parameter represented by $\theta$.

Figure 3 represents the two-dimensional plot of the survival cos-copula for selected values of $\theta$.

The density associated with the survival cos-copula is given by

$$\begin{array}{cc}\hfill {\widehat{c}}_{\ast }(x,y)& =\frac{{\partial }^2}{\partial x\partial y}{\widehat{C}}_{\ast }(x,y)\hfill \\ \hfill & =\left[1-{\theta }^{2}xy(1-x)(1-y)\right]cos\left(\theta xy\right)-\theta (3xy-2x-2y+1)sin\left(\theta xy\right).\hfill \end{array}$$

To have an idea of its shapes, Figure 4 shows the two-dimensional plot of the survival cos-copula density for selected values of $\theta$.

Because any convex linear combination of copulas is a copula (see [1]), the cos-copula can be used in a variety of new mixed copulas. For instance, we can consider the following mixed cos-copulas:

• Mixed copula 1: For any angle parameters ${\theta }_1\in [0,\pi /2]$ and ${\theta }_2\in [0,\pi /2]$ and $\lambda \in [0,1]$, by setting $C_{\ast }(x,y)=C_{\ast }(x,y;\theta )$, a possible mixed copula is given as

  $$\begin{array}{cc}\hfill C_{▹}(x,y)& =\lambda C_{\ast }(x,y;{\theta }_1)+(1-\lambda )C_{\ast }(x,y;{\theta }_2)\hfill \\ \hfill & =\lambda xycos\left[{\theta }_1(1-x)(1-y)\right]+(1-\lambda )xycos\left[{\theta }_2(1-x)(1-y)\right].\hfill \end{array}$$
• Mixed copula 2: A second example is

  $$\begin{array}{cc}\hfill C_{▵}(x,y)& =\frac{1}{2}\left[C_{\ast }(x,y)+y-C_{\ast }(1-x,y)\right]\hfill \\ \hfill & =\frac{1}{2}\left\{xycos\left[\theta (1-x)(1-y)\right]+y-(1-x)ycos\left[\theta x(1-y)\right]\right\}.\hfill \end{array}$$

They are also new angle parameter trigonometric copulas by construction.

2.3. Properties

We now list the important properties of the cos-copula $C_{\ast }(x,y)$ as specified in Equation (1).

• As already mentioned before:

  –

  For $\theta =0$, it is clear that $C_{\ast }(x,y)=xy$. Therefore, the cos-copula is reduced to the independence copula.

  –

  If we restrict our attention to the interval $[0,\pi ]$, the set $[0,\pi /2]$ is the optimal set of values for $\theta$ for validating $C_{\ast }(x,y)$ as a copula.

• For any $\theta \in [0,\pi /2]$, we have $C_{\ast }(x,y)\le xy$. Hence, the cos-copula satisfies the negative quadrant dependence property (see [21]).
• The cos-copula is symmetric since $C_{\ast }(x,y)=C_{\ast }(y,x)$ for any $(x,y)\in {[0,1]}^2$.
• The cos-copula can be expressed under various analytical forms. Two of them are given below:

  –

  In terms of simple cosine-sine functions, we can write

  $$\begin{array}{cc}\hfill C_{\ast }(x,y)& =xy[sin(\theta )sin(\theta x)sin(\theta y)sin(\theta xy)+cos(\theta )cos(\theta x)cos(\theta y)cos(\theta xy)\hfill \\ \hfill & +sin\left(\theta \right)sin\left(\theta x\right)cos\left(\theta y\right)cos\left(\theta xy\right)+sin\left(\theta \right)cos\left(\theta x\right)sin\left(\theta y\right)cos\left(\theta xy\right)\hfill \\ \hfill & -cos\left(\theta \right)sin\left(\theta x\right)sin\left(\theta y\right)cos\left(\theta xy\right)-sin\left(\theta \right)cos\left(\theta x\right)cos\left(\theta y\right)sin\left(\theta xy\right)\hfill \\ \hfill & +cos\left(\theta \right)sin\left(\theta x\right)cos\left(\theta y\right)sin\left(\theta xy\right)+cos\left(\theta \right)cos\left(\theta x\right)sin\left(\theta y\right)sin\left(\theta xy\right)]\hfill \end{array}$$

  We thus see the intrinsic analytical complexity into the cos-copula.

  –

  In terms of power series, by using the cosine series expansion and binomial formula, we get

  $$\begin{array}{cc}\hfill C_{\ast }(x,y)& =xy\sum _{k=0}^{+\infty }\frac{{(-1)}^k}{\left(2k\right)!}{\theta }^{2k}{(1-x)}^{2k}{(1-y)}^{2k}\hfill \\ \hfill & =\sum _{k=0}^{+\infty }\sum _{\ell =0}^{2k}\sum _{m=0}^{2k}\frac{{(-1)}^{k+\ell +m}}{\left(2k\right)!}{\theta }^{2k}\left(\genfrac{}{}{0pt}{}{2k}{\ell }\right)\left(\genfrac{}{}{0pt}{}{2k}{m}\right)x^{\ell +1}{y}^{m+1}.\hfill \end{array}$$

  (6)

  In particular, upon differentiation with respect to x and y on the interior of the domain of convergence, one has

  $$\begin{array}{cc}\hfill c_{\ast }(x,y)& =\sum _{k=0}^{+\infty }\sum _{\ell =0}^{2k}\sum _{m=0}^{2k}\frac{{(-1)}^{k+\ell +m}}{\left(2k\right)!}{\theta }^{2k}\left(\genfrac{}{}{0pt}{}{2k}{\ell }\right)\left(\genfrac{}{}{0pt}{}{2k}{m}\right)(\ell +1)(m+1)x^{\ell }{y}^m.\hfill \end{array}$$

  This expansion can be used in a variety of mathematical applications, such as determining various moment-type measurements.

• By arbitrary taking $\theta =\pi /2$, we notice that

  $$C_{\ast }\left(\frac{1}{4},C_{\ast }\left(\frac{1}{2},\frac{1}{3}\right)\right)=0.01925131\ne 0.02047885=C_{\ast }\left(C_{\ast }\left(\frac{1}{4},\frac{1}{2}\right),\frac{1}{3}\right).$$
  As a result, the cos-copula is not Archimedean (see [1]). In other words, there is no generator function $\psi :[0,1]\to [0,+\infty )$ such that $C(x,y)={\psi }^{[-1]}[\psi \left(x\right)+\psi \left(y\right)]$, where ${\psi }^{[-1]}\left(x\right)$ denotes the pseudo-inverse of $\psi \left(x\right)$.
• The cos-copula is not radially symmetric since there clearly exists $(x,y)$ such that ${\widehat{C}}_{\ast }(x,y)\ne C_{\ast }(x,y)$.
• As any copula, the Fréchet–Hoeffding bounds can be expressed as follows: For any $(x,y)\in {[0,1]}^2$, we have $max(x+y-1,0)\le C_{\ast }(x,y)\le min(x,y)$.
• Thanks to the Kober inequality, the following inequality holds:

  $$C_{\ast }(x,y)\ge C_{†}\left(x,y;-\frac{2}{\pi }\theta \right),$$

  where $C_{†}(x,y;\lambda )=xy+\lambda xy(1-x)(1-y)$ with $\lambda \in [-1,1]$ refers to the Farlie–Gumbel–Morgenstern (FGM) copula (see [1]). Since $-(2/\pi )\theta \in [-1,1]$, the cos-copula and FGM copula are involved in a complete copula ordering.
• For any $\theta \in [0,\pi /2]$, the two following results are obtained:

  $${\lambda }_L=\underset{x\to 0}{lim}\frac{C_{\ast }(x,x)}{x}=\underset{x\to 0}{lim}xcos\left[\theta {(1-x)}^2\right]=0$$

  and

  $$\begin{array}{cc}\hfill {\lambda }_U& =\underset{x\to 1}{lim}\frac{1-2x+C_{\ast }(x,x)}{1-x}=\underset{x\to 1}{lim}\frac{1-2x+x^{2}cos\left[\theta {(1-x)}^2\right]}{1-x}\hfill \\ \hfill & =\underset{x\to 1}{lim}\frac{1-2x+x^2}{1-x}=\underset{x\to 1}{lim}(1-x)=0.\hfill \end{array}$$
  Hence, the cos-copula has no tail dependence (see [1]).
• The medial correlation of the cos-copula is defined by

  $$M=4C_{\ast }\left(\frac{1}{2},\frac{1}{2}\right)-1=cos\left(\frac{\theta }{4}\right)-1.$$
  It is clearly a decreasing and negative function with respect to $\theta$ for $\theta \in [0,\pi /2]$, with $M=0$ for $\theta =0$ and $M=-0.07612047$ for $\theta =\pi /2$. Figure 5 represents the medial correlation for $\theta \in [0,1.5]$.
  Thus, the cos-copula has a weak medial correlation with $M\in [-0.076,0]$.
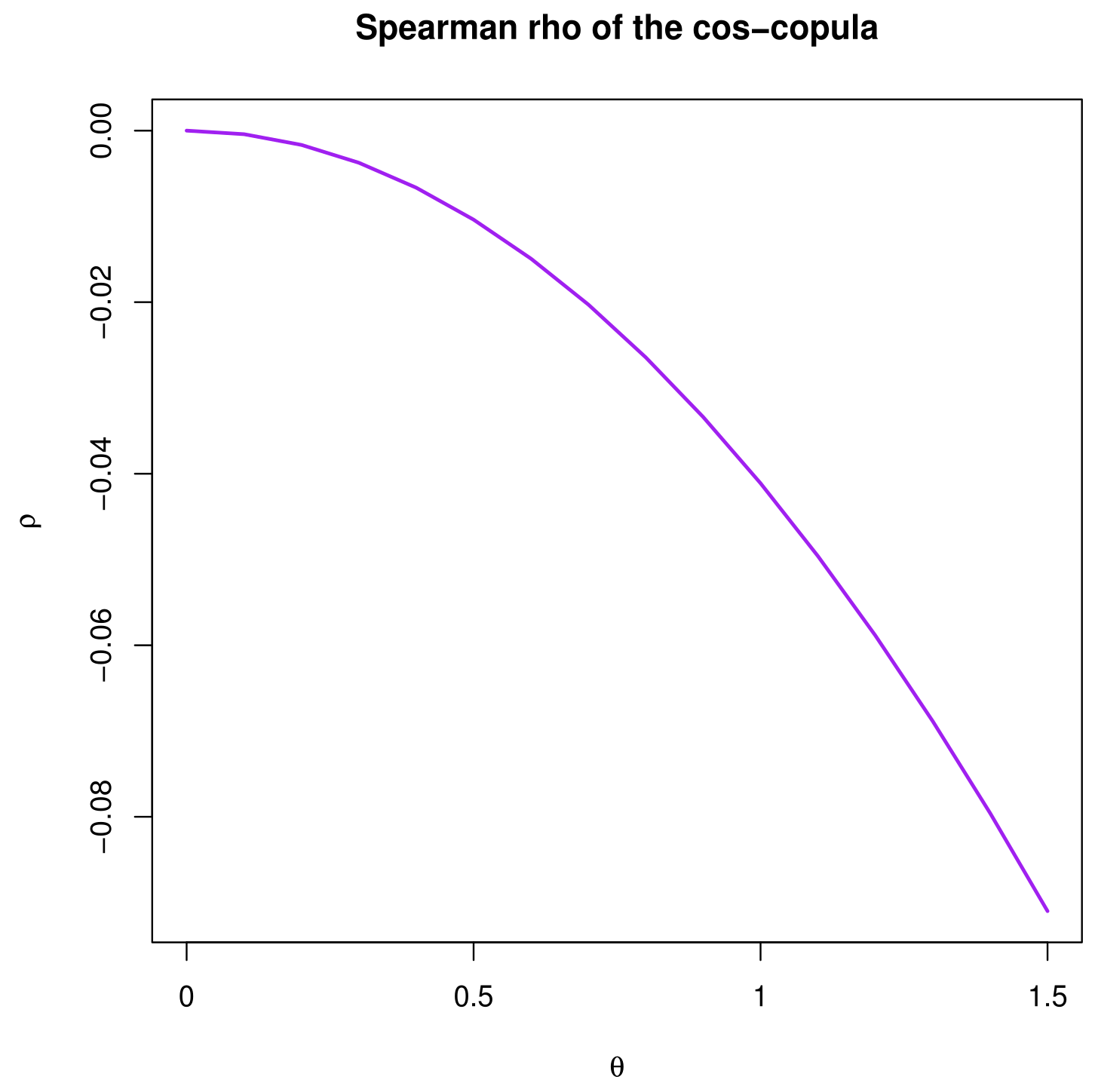
• A useful dependence measure based on copula is the Spearman rho (see [1]). The Spearman rho of the cos-copula, as an example of copula, is defined by

  $$\begin{array}{c}\hfill \rho =12{\int }_0^1{\int }_0^1{C}_{\ast }(x,y)dxdy-3.\end{array}$$

  (7)

Based on well-known mathematical techniques, the following proposition provides a mathematical expression for this measure.

Proposition 2.

The Spearman rho of the cos-copula can be expressed as

$$\begin{array}{c}\hfill \rho =\left\{\begin{array}{cc}{\displaystyle 0,}\hfill & \mathrm{for}\theta =0\hfill \\ \\ {\displaystyle \frac{12}{{\theta }^2}\left[Ci\left(\theta \right)+\theta Si\left(\theta \right)-log\left(\theta \right)+cos\left(\theta \right)-\gamma -1\right]-3,}\hfill & \mathrm{for}\theta \in (0,\pi /2]\hfill \end{array}\right.,\end{array}$$

where $Ci\left(x\right)$ denotes the cosine integral defined by $Ci\left(x\right)=-{\int }_x^{\infty }[cos\left(t\right)/t]dt$, $Si\left(x\right)$ denotes the sine integral referred by $Si\left(x\right)={\int }_0^x[sin\left(t\right)/t]dt$, and $\gamma \approx 0.5772$ is the Euler–Mascheroni constant.

Proof. 

• For $\theta =0$, we have $C_{\ast }(x,y)=xy$ and, by Equation (7), it is immediate that $\rho =0$.
• For $\theta \in (0,\pi /2]$, based on Equation (7), only the integral term requires attention. By using a step-by-step integration and some properties of the special functions $Ci\left(x\right)$ and $Si\left(x\right)$, we obtain

  $$\begin{array}{cc}\hfill & {\int }_0^1{\int }_0^1{C}_{\ast }(x,y)dxdy={\int }_0^1\left\{{\int }_0^{1}xycos\left[\theta (1-x)(1-y)\right]dx\right\}dy\hfill \\ \hfill & =\frac{1}{{\theta }^2}{\int }_0^1{\left.\left\{y\frac{\theta x(y-1)sin\left[\theta (1-x)(1-y)\right]+cos\left[\theta (1-x)(1-y)\right]}{{(1-y)}^2}\right\}\right|}_{x=0}^{x=1}dy\hfill \\ \hfill & =\frac{1}{{\theta }^2}{\int }_0^{1}y\frac{1-cos\left[\theta (1-y)\right]}{{(1-y)}^2}dy\hfill \\ \hfill & =\frac{1}{{\theta }^2}{\left.\left\{log(1-y)-Ci\left[\theta (1-y)\right]-\theta Si\left[\theta (1-y)\right]+\frac{1-cos\left[\theta \right(1-y\left)\right]}{1-y}\right\}\right|}_{y=0}^{y=1}\hfill \\ \hfill & =\frac{1}{{\theta }^2}\left[Ci\left(\theta \right)+\theta Si\left(\theta \right)-log\left(\theta \right)+cos\left(\theta \right)-\gamma -1\right].\hfill \end{array}$$

  (8)

The desired result follows immediately.

The proof of Proposition 2 ends. □

Thus, $\rho$ is a decreasing function with respect to $\theta$ for $\theta \in [0,\pi /2]$, with $\rho =0$ for $\theta =0$ and $\rho =-0.1$ for $\theta =\pi /2$. Figure 6 represents the Spearman rho for $\theta \in [0,1.5]$.

In light of the above results, the cos-copula is adapted to model weak negative correlations.

Remark 2.

Based on Equations (6) and (8), upon integration over ${[0,1]}^2$ and some arrangements, the following series formula holds:

$$\begin{array}{cc}\hfill & \sum _{k=0}^{+\infty }\sum _{\ell =0}^{2k}\sum _{m=0}^{2k}\frac{{(-1)}^{k+\ell +m}}{\left(2k\right)!}{\theta }^{2(k+1)}\left(\genfrac{}{}{0pt}{}{2k}{\ell }\right)\left(\genfrac{}{}{0pt}{}{2k}{m}\right)\frac{1}{(\ell +2)(m+2)}\hfill \\ \hfill & =Ci\left(\theta \right)+\theta Si\left(\theta \right)-log\left(\theta \right)+cos\left(\theta \right)-\gamma -1.\hfill \end{array}$$

Of course, this result is of independent interest to our copula study. It is, however, fascinating to see the versatility in the nature of the functions involved, i.e., logarithmic, special integral function, cosine function, and Euler–Mascheroni constant.

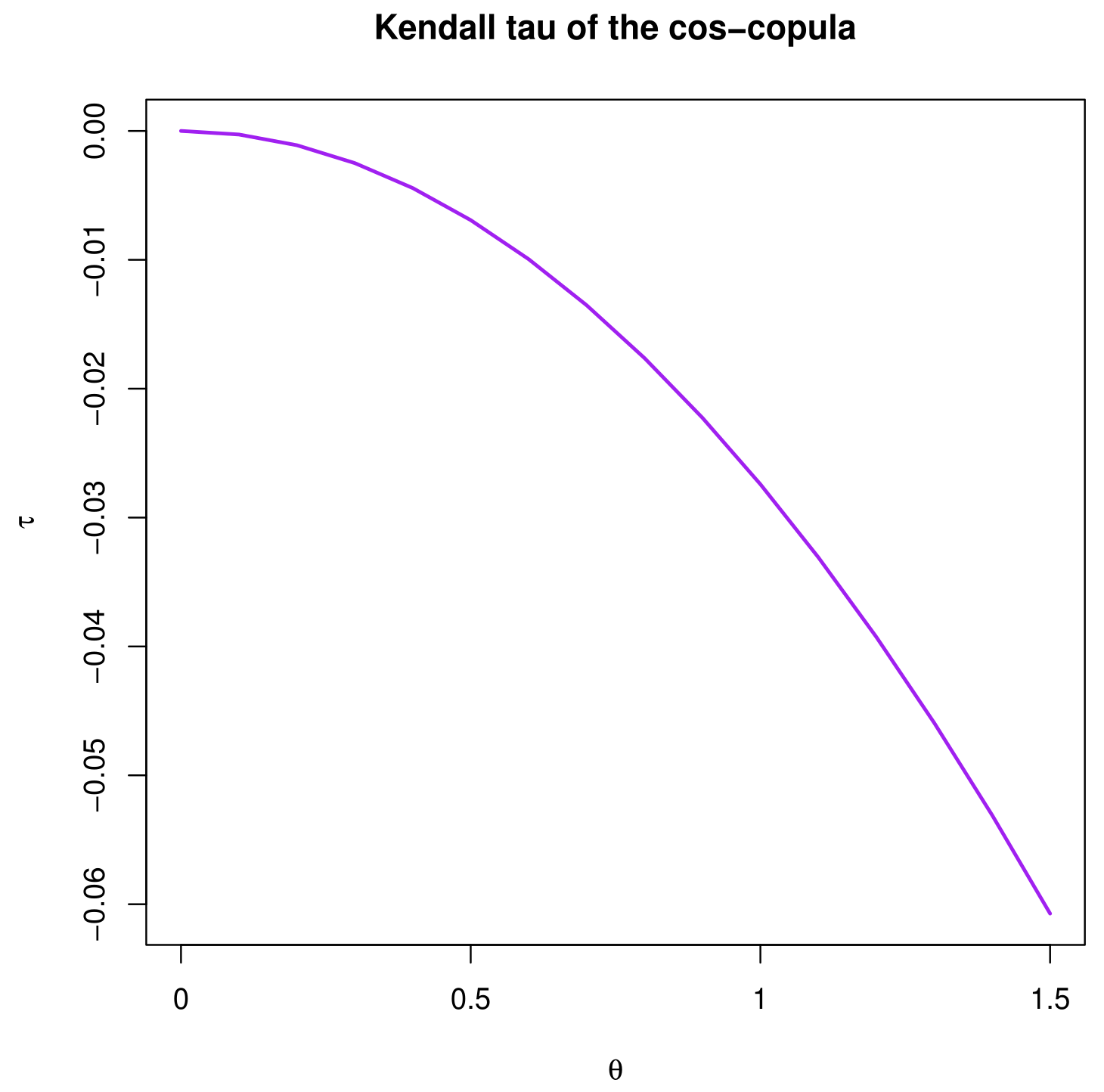
• In complement of the Spearman rho, we can present the Kendall tau of the cos-copula. It is defined by

  $$\tau =4{\int }_0^1{\int }_0^1{C}_{\ast }(x,y)c_{\ast }(x,y)dxdy-1.$$

The closed form expression for $\tau$ is unmanageable due to the complexity of the product function $C_{\ast }(x,y)c_{\ast }(x,y)$. We can, however, state that it is a decreasing function with respect to $\theta$ for $\theta \in [0,\pi /2]$, with $\tau =0$ for $\theta =0$ and $\tau =-0.06641903$ for $\theta =\pi /2$. Figure 7 represents the Kendall tau for $\theta \in [0,1.5]$.

The small values of $\tau$ confirm the fact that the cos-copula is ideal to model weak negative correlations.

• The cos-copula opens some interesting perspectives in distribution theory and modeling. The most immediate of these perspectives is the creation of simple and new two-dimensional distributions with cumulative distribution functions of the following form: $H(x,y)=C_{\ast }(F\left(x\right),G\left(y\right))$, so

  $$H(x,y)=F\left(x\right)G\left(y\right)cos\left[\theta (1-F(x\left)\right)(1-G(y\left)\right)\right],$$

  where $F\left(x\right)$ and $G\left(x\right)$ denote two cumulative distribution functions. This gives two-dimensional trigonometric distributions, which seem slightly underexplored in the literature. By considering the exponential distribution as the parent, we may define the cos-two-exponential distribution by the following cumulative distribution:

  $$H(x,y;\alpha ,\beta )=(1-e^{-\alpha x})(1-e^{-\beta y})cos\left[\theta e^{-(\alpha x+\beta y)}\right],(x,y)\in {[0,+\infty )}^2,$$

  and $H(x,y;\alpha ,\beta )=0$ for $(x,y)\notin {[0,+\infty )}^2$. To understand the importance of the trigonometric distributions in theory and practice for the uni-dimensional case, we may refer to [22,23].

2.4. Data Generation and Inference

The most straightforward method of generating random data (or values) from a distribution defined by a copula is what might be termed the inverse conditional method. For any positive integer n, with the aim of generating n data from the cos-copula, this method may be described as follows:

• Generate n data $(s_1,t_1),\dots ,(s_n,t_n)$ from a random vector $(S,T)$, where S and T are independent random variables with the uniform distribution over $(0,1)$.
• Choose a value of $\theta \in [0,\pi /2]$.
• Consider the following “conditional function”:

  $${\mathfrak{C}}_{\ast }(x,y)=\frac{\partial }{\partial x}{C}_{\ast }(x,y)=y\left\{cos\left[\theta (1-x)(1-y)\right]+\theta x(1-y)sin\left[\theta (1-x)(1-y)\right]\right\}.$$
• For any $i=1,\dots ,n$, compute $u_i$ such that ${\mathfrak{C}}_{\ast }(s_i,u_i)=t_i$.
• Then $(s_1,u_1),\dots ,(s_n,u_n)$ are n data generated from the cos-copula defined with the chosen $\theta$.

Other methods exist (see [24]). Such simulated data can be used for computational tests, or estimation purposes.

On the other hand, in a data analysis scenario, the angle parameter $\theta$ is generally unknown. Its evaluation is, thus, of interest for precise data fitting, or at least to know if $\theta$ is close to 0 corresponding to the independent case, or close to $\pi /2$, corresponding to the most highly correlated case. For this evaluation, it can be estimated from n data $(x_1,y_1),\dots ,(x_n,y_n)$, that are susceptible to coming from the cos-copula distribution, by the maximum likelihood method; $\theta$ is thus estimated by

$$\tilde{\theta }={argmax}_{\theta \in [0,\pi /2]}\prod _{i=1}^n{c}_{\ast }(x_i,y_i)={argmax}_{\theta \in [0,\pi /2]}\sum _{i=1}^{n}log\left[c_{\ast }(x_i,y_i)\right],$$

provided that it is unique. This estimation method ensures satisfying qualities to $\tilde{\theta }$, such as underlying consistency and asymptotic normality, which are the basis for the construction of confidence intervals and statistical tests (see, for instance, Refs. [13,17]). At this point, concrete applications of the aforementioned techniques to real-world datasets remain a possibility.

3. Sine Angle Parameter Copula

This section completes the findings of the previous section; it is devoted to a simple sine copula with an angle parameter. This copula can be viewed as a parametric generalization of one copula introduced in [18]. Indeed, in ([18], Example 9), it is proved that the function $C_{▿}:{[0,1]}^2\to [0,1]$ defined by

$$C_{▿}(x,y)=xy\left\{1+sin\left[\frac{\pi }{4}(1-x)(1-y)\right]\right\},$$

is a valid copula. Among the questions that arise are:

• Can we replace the angle-value $\pi /4$ with a tuning parameter and, if so, what is its “optimal values set”?
• What are the related functions of such a copula?
• What are its theoretical properties?

The answers to these questions are given below.

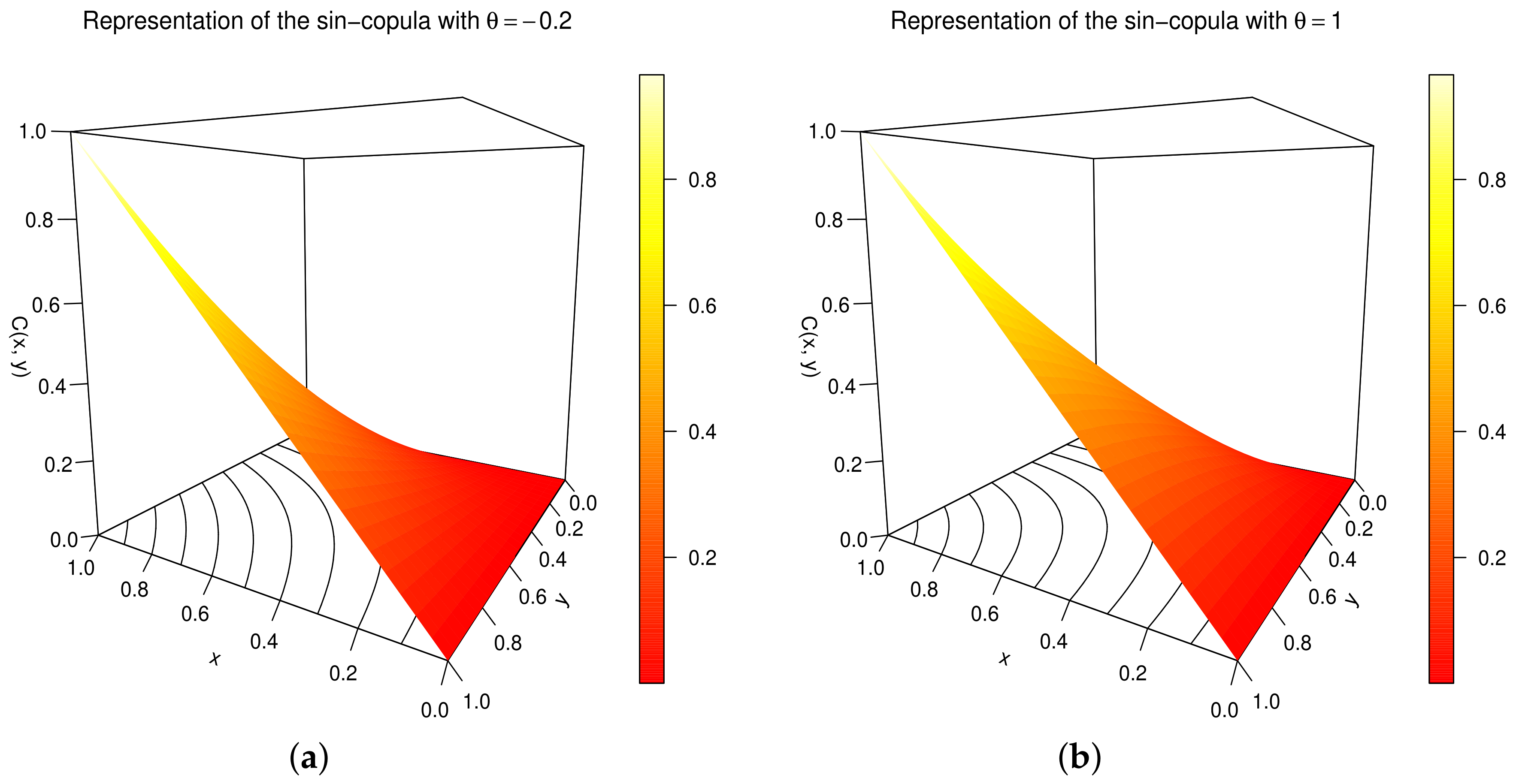
3.1. Definition and Graphics

The following proposition presents the considered angle parameter sine copula.

Proposition 3.

The function $C_{\circ }:{[0,1]}^2\to [0,1]$ defined by

$$\begin{array}{c}\hfill C_{\circ }(x,y)=xy\left\{1+sin\left[\theta (1-x)(1-y)\right]\right\},\end{array}$$

(9)

with $\theta \in [-1,1]$ is a valid copula.

Proof. 

Let us prove the main points defining an absolutely continuous two-dimensional copula, as recalled in Definition 1.

• For any $x\in [0,1]$, we have $C_{\circ }(x,0)=x\times 0\times \left\{1+sin\left[\theta (1-x)(1-0)\right]\right\}=0$, and, for any $y\in [0,1]$, $C_{\circ }(0,y)=0\times y\left\{1+sin\left[\theta (1-0)(1-y)\right]\right\}=0$.
• For any $x\in [0,1]$, we have $C_{\circ }(x,1)=x\times 1\times \left\{1+sin\left[\theta (1-x)\times 0\right]\right\}=x$, similarly, for any $y\in [0,1]$, $C_{\circ }(1,y)=1\times y\left\{1+sin\left[\theta \times 0\times (1-y)\right]\right\}=y$.
• For any $(x,y)\in {[0,1]}^2$, using standard derivation techniques, we have

  $$\begin{array}{cc}\hfill \frac{{\partial }^2}{\partial x\partial y}{C}_{\circ }(x,y)& =1+\left[1-{\theta }^{2}xy(1-x)(1-y)\right]sin\left[\theta (1-x)(1-y)\right]\hfill \\ \hfill & +\theta (3xy-x-y)cos\left[\theta (1-x)(1-y)\right].\hfill \end{array}$$
  Let us now study the sign of the above function by distinguishing the case $\theta \in [0,1]$ and the case $\theta \in [-1,0)$.
  Case $\theta \in [0,1]$: We can write

  $$\begin{array}{cc}\hfill \frac{{\partial }^2}{\partial x\partial y}{C}_{\circ }(x,y)& =A_1+A_2,\hfill \end{array}$$

  where

  $$A_1=1+\theta (3xy-x-y)cos\left[\theta (1-x)(1-y)\right]$$

  and

  $$A_2=\left[1-{\theta }^{2}xy(1-x)(1-y)\right]sin\left[\theta (1-x)(1-y)\right].$$
  Let us prove that $A_1\ge 0$ and $A_2\ge 0$.
  For $A_1$, let us first remark that

  $$\begin{array}{c}\hfill 3xy-x-y=(1-x)(1-y)+2xy-1\ge -1.\end{array}$$

  (10)
  Therefore, since $\theta \in [0,1]$ and $cos\left(a\right)\in [0,1]$ for any $a\in [0,1]$, we have

  $$A_1\ge 1-\theta cos\left[\theta (1-x)(1-y)\right]\ge 1-\theta \ge 0.$$
  For $A_2$, since $\theta \in [0,1]$, we have $\theta (1-x)(1-y)\in [0,1]\subseteq [0,\pi /2]$, implying that $sin\left[\theta (1-x)(1-y)\right]\ge 0$, and $1-{\theta }^{2}xy(1-x)(1-y)\ge 0$. It follows that $A_2\ge 0$. Hence

  $$\begin{array}{cc}\hfill \frac{{\partial }^2}{\partial x\partial y}{C}_{\circ }(x,y)& =A_1+A_2\ge 0.\hfill \end{array}$$
  The two-increasing property is proved.

Case $\theta \in [-1,0)$: For this case, we develop a strategy different to the previous case. We can write

$$\begin{array}{cc}\hfill \frac{{\partial }^2}{\partial x\partial y}{C}_{\circ }(x,y)& =B_1+B_2,\hfill \end{array}$$

where

$$B_1=-{\theta }^{2}xy(1-x)(1-y)sin\left[\theta (1-x)(1-y)\right]$$

and

$$B_2=1+sin\left[\theta (1-x)(1-y)\right]+\theta (3xy-x-y)cos\left[\theta (1-x)(1-y)\right].$$

Let us prove that $B_1\ge 0$ and $B_2\ge 0$.

For $B_1$, since $\theta \in [-1,0)$, we have $-sin\left[\theta (1-x)(1-y)\right]\ge 0$, which implies that $B_1\ge 0$.

For $B_2$, since $\theta \in [-1,0)$, the following inequality holds: $sin\left(a\right)\le a$ for any $a>0$, which implies that $sin\left(\theta a\right)=-sin\left[\right(-\theta \left)a\right]\ge \theta a$ for any $a>0$. It follows from this inequality applied with $a=\theta (1-x)(1-y)$, the inequality

$$\theta (3xy-x-y)=\theta [xy+x(y-1)+y(x-1\left)\right]\ge \theta xy,$$

and the inequality: $cos\left(a\right)\le 1$ for any $a\in \mathbb{R}$, applied with $a=\theta (1-x)(1-y)$, that

$$\begin{array}{cc}\hfill B_2& \ge 1+\theta \left\{(1-x)(1-y)+xycos\left[\theta (1-x)(1-y)\right]\right\}\hfill \\ \hfill & \ge 1-\left\{(1-x)(1-y)+xy\right\}=x+y-2xy=x(1-y)+y(1-x)\ge 0.\hfill \end{array}$$

Hence

$$\begin{array}{cc}\hfill \frac{{\partial }^2}{\partial x\partial y}{C}_{\circ }(x,y)& =B_1+B_2\ge 0.\hfill \end{array}$$

The two-increasing property is proved.

As a result, $C_{\circ }(x,y)$ is a valid two-dimensional copula. This ends the proof of Proposition 3.

□

For the purposes of this paper, we call the copula $C_{\circ }(x,y)$ in Equation (9) as the sin-copula. Like the cos-copula, it has the feature to have a tuning angle parameter $\theta$. Clearly, for $\theta =0$, we have $C_{\circ }(x,y)=xy$; the sin-copula is reduced to the independence copula, and for $\theta =\pi /4$, it is reduced to the copula in ([18], Example 9).

To end the presentation, Figure 8 represents the two-dimensional plot of the sin-copula for selected values of $\theta$.

From Figure 8, we see that the parameter $\theta$ skews the triangular shape of the sin-copula.

The functions of the sin-copula, as well as its key features, are discussed in the following parts.

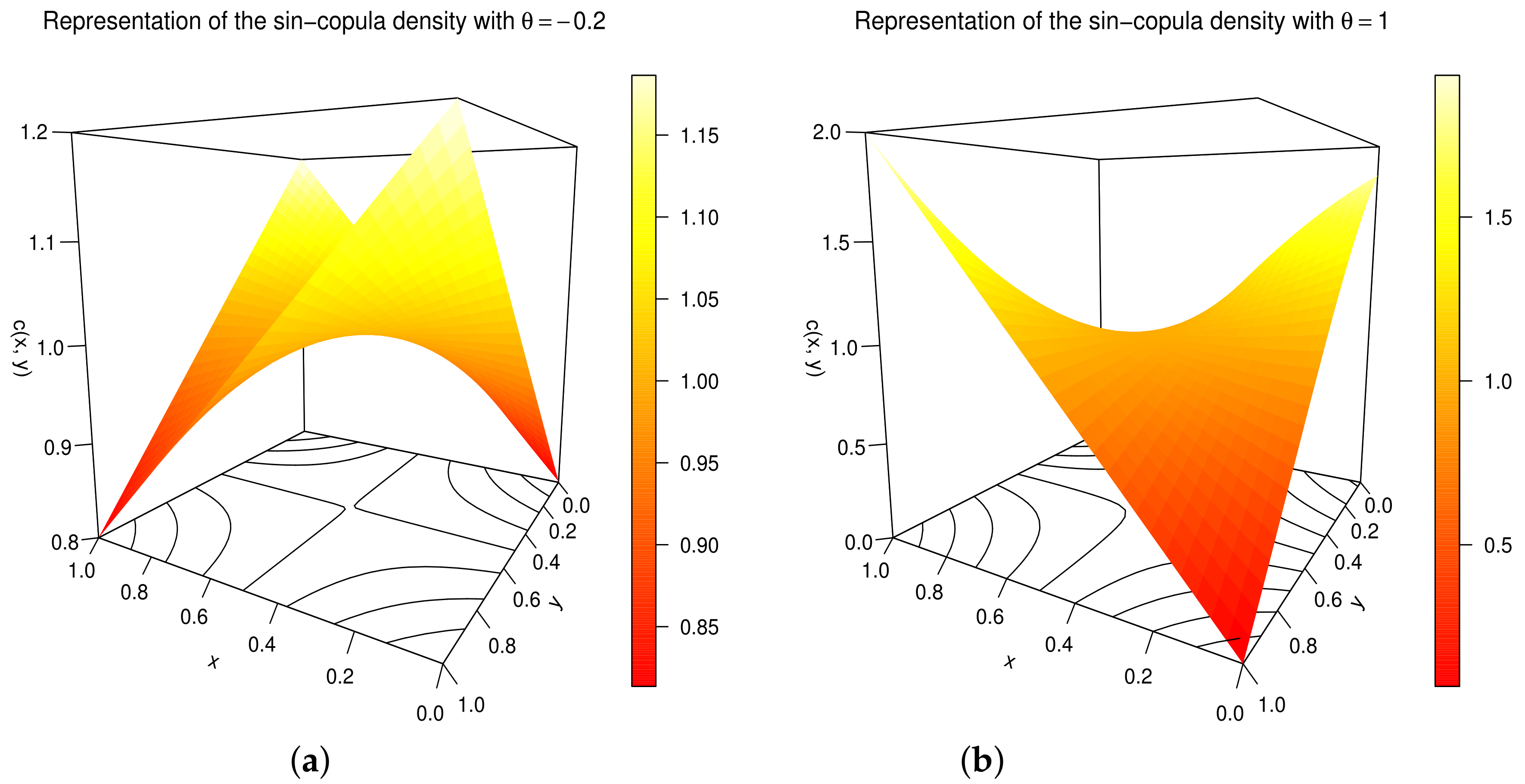
3.2. Related Functions

The density associated with the sin-copula is the function $c_{\circ }:{[0,1]}^2\to [0,+\infty )$ given by

$$\begin{array}{cc}\hfill & c_{\circ }(x,y)=\frac{{\partial }^2}{\partial x\partial y}{C}_{\circ }(x,y)\hfill \\ \hfill & =1+\left[1-{\theta }^{2}xy(1-x)(1-y)\right]sin\left[\theta (1-x)(1-y)\right]\hfill \\ \hfill & +\theta (3xy-x-y)cos\left[\theta (1-x)(1-y)\right].\hfill \end{array}$$

It is worth noting that $c_{\circ }(1,0)=1-\theta$, which is negative for $\theta >1$, and $c_{\circ }(1,1)=1+\theta$, which is negative for $\theta <-1$; $C_{\circ }(x,y)$ is not a copula for $\theta \in \mathbb{R}[-1,1]$. In this sense, $[-1,1]$ is the optimal set of values for $\theta$.

Figure 9 represents the two-dimensional plot of the sin-copula density for selected values of $\theta$.

As a result of Figure 9, we can see how $\theta$ influences the overall form of the sin-copula density.

As a last important function, the survival sin-copula is the function ${\widehat{C}}_{\circ }:{[0,1]}^2\to [0,1]$ defined by

$$\begin{array}{cc}\hfill & {\widehat{C}}_{\circ }(x,y)=x+y-1+C_{\circ }(1-x,1-y)\hfill \\ \hfill & =xy+(1-x)(1-y)sin\left(\theta xy\right).\hfill \end{array}$$

It establishes a valid copula, which is also a new trigonometric copula with $\theta$ as an angle parameter.

Figure 10 represents the two-dimensional plot of the survival sin-copula for selected values of $\theta$.

The copula density associated with the survival sin-copula is given by

$$\begin{array}{cc}\hfill {\widehat{c}}_{\circ }(x,y)& =\frac{{\partial }^2}{\partial x\partial y}{\widehat{C}}_{\circ }(x,y)\hfill \\ \hfill & =1+\left[1-{\theta }^{2}xy(1-x)(1-y)\right]sin\left(\theta xy\right)+\theta (3xy-2x-2y+1)cos\left(\theta xy\right).\hfill \end{array}$$

To have an idea of its shapes, Figure 11 shows its two-dimensional plot for selected values of $\theta$.

On the other hand, the sin-copula can be used in a variety of new mixed copulas. For instance, we can consider the following mixed sin-copulas:

• Mixed copula 1: For any angle parameters ${\theta }_1\in [-1,1]$ and ${\theta }_2\in [-1,1]$, and $\lambda \in [0,1]$, by setting $C_{\circ }(x,y)=C_{\circ }(x,y;\theta )$, we can consider

  $$\begin{array}{cc}\hfill C_{◃}(x,y)& =\lambda C_{\circ }(x,y;{\theta }_1)+(1-\lambda )C_{\circ }(x,y;{\theta }_2)\hfill \\ \hfill & =xy+xy\left\{\lambda sin\left[{\theta }_1(1-x)(1-y)\right]+(1-\lambda )xysin\left[{\theta }_2(1-x)(1-y)\right]\right\}.\hfill \end{array}$$
• Mixed copula 2: Similarly, for any angle parameters ${\theta }_1\in [0,\pi /2]$ and ${\theta }_2\in [-1,1]$, and $\lambda \in [0,1]$, by setting $C_{\ast }(x,y)=C_{\ast }(x,y;\theta )$ and $C_{\circ }(x,y)=C_{\circ }(x,y;\theta )$, we can set

  $$\begin{array}{cc}\hfill C_{⥀}(x,y)& =\lambda C_{\ast }(x,y;{\theta }_1)+(1-\lambda )C_{\circ }(x,y;{\theta }_2)\hfill \\ \hfill & =\lambda xycos\left[{\theta }_1(1-x)(1-y)\right]+(1-\lambda )xy\left\{1+sin\left[{\theta }_2(1-x)(1-y)\right]\right\}.\hfill \end{array}$$
• Mixed copula 3: Another example is

  $$\begin{array}{cc}\hfill C_{\S }(x,y)& =\frac{1}{2}\left[C_{\circ }(x,y)+y-C_{\circ }(1-x,y)\right]\hfill \\ \hfill & =xy+\frac{1}{2}\left\{xysin\left[\theta (1-x)(1-y)\right]+y-(1-x)ysin\left[\theta x(1-y)\right]\right\}.\hfill \end{array}$$

They are also new angle parameter trigonometric copulas by construction.

3.3. Properties

The main features of the sin-copula $C_{\circ }(x,y)$ as described in Equation (9) are now listed.

• As already mentioned before:

  –

  For $\theta =0$, it is clear that $C_{\circ }(x,y)=xy$. Therefore, the sin-copula is reduced to the independence copula.

  –

  The set $[-1,1]$ is the optimal set of values for $\theta$ for validating $C_{\circ }(x,y)$ as a copula.

• For any $\theta \in [-1,0]$, we have $C_{\circ }(x,y)\le xy$, so the negative quadrant dependence property is satisfied. Similarly, for any $\theta \in [0,1]$, we have $C_{\circ }(x,y)\ge xy$, so the positive quadrant dependence property is satisfied (see [21]).
• The sin-copula is symmetric since $C_{\circ }(x,y)=C_{\circ }(y,x)$ for any $(x,y)\in {[0,1]}^2$.
• The sin-copula can be expressed under various analytical forms. Two of them are given below:

  –

  In terms of simple cosine-sine functions, we can write

  $$\begin{array}{cc}\hfill C_{\circ }(x,y)& =xy[1+sin(\theta )cos(\theta x)cos(\theta y)cos(\theta xy)-sin(\theta )sin(\theta x)sin(\theta y)cos(\theta xy)\hfill \\ \hfill & +sin\left(\theta \right)sin\left(\theta x\right)cos\left(\theta y\right)sin\left(\theta xy\right)+sin\left(\theta \right)cos\left(\theta x\right)sin\left(\theta y\right)sin\left(\theta xy\right)\hfill \\ \hfill & -cos\left(\theta \right)sin\left(\theta x\right)cos\left(\theta y\right)cos\left(\theta xy\right)-cos\left(\theta \right)cos\left(\theta x\right)sin\left(\theta y\right)cos\left(\theta xy\right)\hfill \\ \hfill & +cos\left(\theta \right)cos\left(\theta x\right)cos\left(\theta y\right)sin\left(\theta xy\right)-cos\left(\theta \right)sin\left(\theta x\right)sin\left(\theta y\right)sin\left(\theta xy\right)].\hfill \end{array}$$

  As a result, we can observe that the sin-copula has inherent analytical complexity.

  –

  In terms of power series, by using the cosine series expansion and binomial formula, we get

  $$\begin{array}{cc}\hfill C_{\circ }(x,y)& =xy+xy\sum _{k=0}^{+\infty }\frac{{(-1)}^k}{(2k+1)!}{\theta }^{2k+1}{(1-x)}^{2k+1}{(1-y)}^{2k+1}\hfill \\ \hfill & =xy+\sum _{k=0}^{+\infty }\sum _{\ell =0}^{2k+1}\sum _{m=0}^{2k+1}\frac{{(-1)}^{k+\ell +m}}{(2k+1)!}{\theta }^{2k+1}\left(\genfrac{}{}{0pt}{}{2k+1}{\ell }\right)\left(\genfrac{}{}{0pt}{}{2k+1}{m}\right)x^{\ell +1}{y}^{m+1}.\hfill \end{array}$$

  (11)

  In particular, upon differentiation with respect to x and y on the interior of the domain of convergence, one has

  $$\begin{array}{cc}\hfill & c_{\circ }(x,y)=1\hfill \\ \hfill & +\sum _{k=0}^{+\infty }\sum _{\ell =0}^{2k+1}\sum _{m=0}^{2k+1}\frac{{(-1)}^{k+\ell +m}}{(2k+1)!}{\theta }^{2k+1}\left(\genfrac{}{}{0pt}{}{2k+1}{\ell }\right)\left(\genfrac{}{}{0pt}{}{2k+1}{m}\right)(\ell +1)(m+1)x^{\ell }{y}^m.\hfill \end{array}$$

  This expansion can be used to determine various moment-type measurements in a range of mathematical applications.

• By arbitrary taking $\theta =-1$, we notice that

  $$C_{\circ }\left(\frac{1}{4},C_{\circ }\left(\frac{1}{2},\frac{1}{3}\right)\right)=0.01071536\ne 0.01119522=C_{\circ }\left(C_{\circ }\left(\frac{1}{4},\frac{1}{2}\right),\frac{1}{3}\right).$$
  As a result, the sin-copula is not Archimedean (see [1]).
• The sin-copula is not radially symmetric since there exists $(x,y)$ such that ${\widehat{C}}_{\circ }(x,y)\ne C_{\circ }(x,y)$.
• As any copula, the Fréchet-Hoeffding bounds can be expressed as follows: For any $(x,y)\in {[0,1]}^2$, we have $max(x+y-1,0)\le C_{\circ }(x,y)\le min(x,y)$.
• Thanks to the inequality: $sin\left(a\right)\le a$ and the Jordan inequality: $sin\left(a\right)\ge (2/\pi )a$ for $a\in [0,\pi /2]$ (see [20]), we have a copula ordering between the sin-copula and FGM copula:

  –

  For $\theta \in [0,1]$, we have

  $$C_{†}\left(x,y;\frac{2}{\pi }\theta \right)\le C_{\circ }(x,y)\le C_{†}(x,y;\theta ).$$

  –

  For $\theta \in [-1,0]$, the contrary holds:

  $$C_{†}\left(x,y;\frac{2}{\pi }\theta \right)\ge C_{\circ }(x,y)\ge C_{†}(x,y;\theta ).$$

• The following relationship between the cos-copula and sin-copula holds:

  $$\begin{array}{c}\hfill C_{\circ }(x,y)-C_{\ast }(x,y)=2\sqrt{2}xysin\left(\frac{\theta (1-x)(1-y)}{2}\right)sin\left(\frac{\theta (1-x)(1-y)}{2}+\frac{\pi }{4}\right).\end{array}$$

  (12)
  Therefore, the following ordering results are established:

  –

  For $\theta \in [-1,0]$, since the first sine term in Equation (12) is negative, and the second one is positive, we have

  $$C_{\circ }(x,y)\le C_{\ast }(x,y).$$

  –

  For $\theta \in [0,1]$, since the first sine term in Equation (12) is positive, and the second one too, we have

  $$C_{\circ }(x,y)\ge C_{\ast }(x,y).$$

• For any $\theta \in [0,\pi /2]$, the two following results are obtained:

  $${\lambda }_L=\underset{x\to 0}{lim}\frac{C_{\circ }(x,x)}{x}=\underset{x\to 0}{lim}x\left\{1+sin\left[\theta {(1-x)}^2\right]\right\}=0$$

  and

  $$\begin{array}{cc}\hfill {\lambda }_U& =\underset{x\to 1}{lim}\frac{1-2x+C_{\circ }(x,x)}{1-x}=\underset{x\to 1}{lim}\frac{1-2x+x^2\left\{1+sin\left[\theta {(1-x)}^2\right]\right\}}{1-x}\hfill \\ \hfill & =\underset{x\to 1}{lim}(1-x)(1+\theta x^2)=0.\hfill \end{array}$$
  Hence, the sin-copula has no tail dependence.
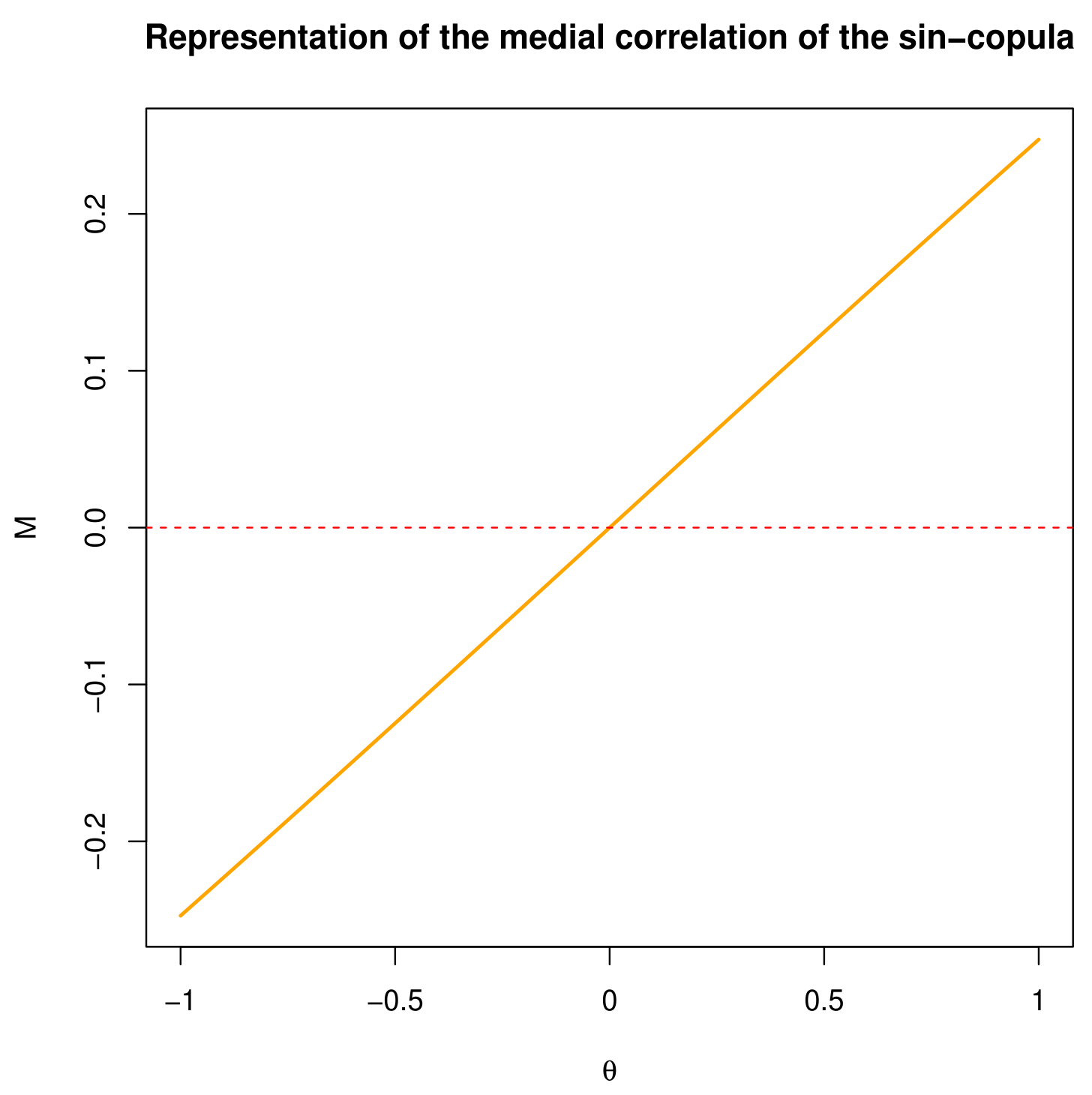
• The medial correlation of the sin-copula is defined by

  $$M=4C_{\circ }\left(\frac{1}{2},\frac{1}{2}\right)-1=sin\left(\frac{\theta }{4}\right).$$
  It is clearly an increasing function with respect to $\theta$ for $\theta \in [-1,1]$, with $M=-0.247404$ for $\theta =-1$ and $M=0.247404$ for $\theta =1$. Figure 12 represents the medial correlation for $\theta \in [-1,1]$.
  The possible values of this medial correlation are not negligible; we have $M\in [-0.25,0.25]$. Hence, the sin-copula has a certain flexibility in this regard.
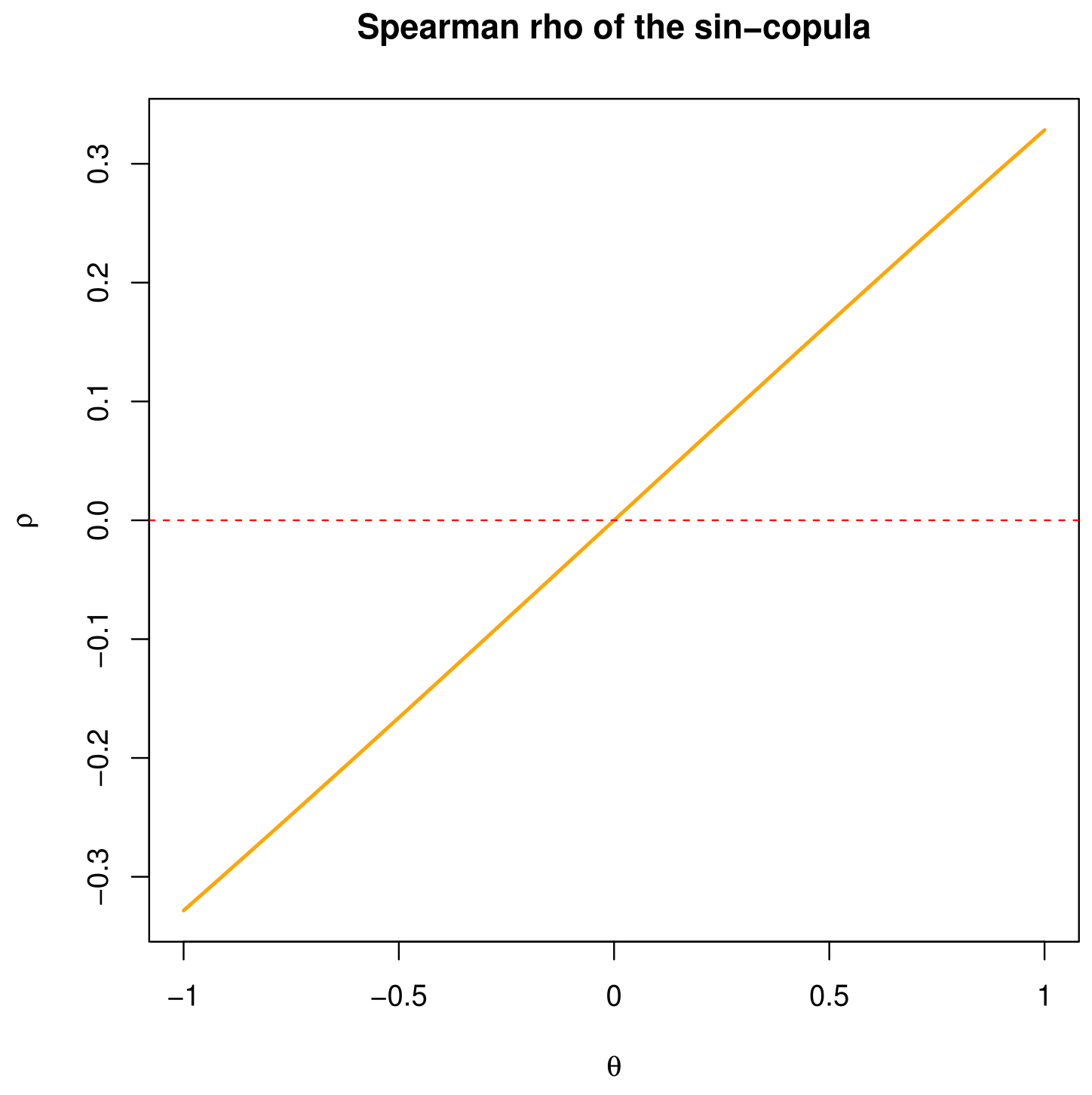
• The Spearman rho of the sin-copula, as an example of copula, is defined by

  $$\begin{array}{c}\hfill \rho =12{\int }_0^1{\int }_0^1{C}_{\circ }(x,y)dxdy-3.\end{array}$$

  (13)
  Using well-known mathematical methods, the following assertion provides a mathematical expression for this measure.

Proposition 4.

The Spearman rho of the sin-copula can be expressed as

$$\begin{array}{c}\hfill \rho =\left\{\begin{array}{cc}{\displaystyle 0,}\hfill & \mathrm{for}\theta =0\hfill \\ \\ {\displaystyle \frac{12}{{\theta }^2}\left[-\theta Ci\left(\theta \right)+Si\left(\theta \right)+\theta (log(\theta )+\gamma -2)+sin\left(\theta \right)\right],}\hfill & \mathrm{for}\theta \in (0,1]\hfill \\ \\ {\displaystyle -\frac{12}{{\theta }^2}\left[\theta Ci(-\theta )+Si(-\theta )-\theta (log(-\theta )+\gamma -2)-sin\left(\theta \right)\right],}\hfill & \mathrm{for}\theta \in [-1,0)\hfill \end{array}\right..\end{array}$$

Proof. 

• For $\theta =0$, we have $C_{\circ }(x,y)=xy$ and, by Equation (13), it is immediate that $\rho =0$.
• For $\theta \in (0,1]$, still based on the definition of $\rho$ in Equation (13), we have

  $$\begin{array}{c}\hfill \rho =12{\int }_0^1{\int }_0^1{C}_{\circ }(x,y)dxdy-3=12{\int }_0^1{\int }_0^{1}xysin\left[\theta (1-x)(1-y)\right]dxdy.\end{array}$$
  By using a step-by-step integration, we obtain

  $$\begin{array}{cc}\hfill & {\int }_0^1{\int }_0^{1}xysin\left[\theta (1-x)(1-y)\right]dxdy={\int }_0^1\left\{{\int }_0^{1}xysin\left[\theta (1-x)(1-y)\right]dx\right\}dy\hfill \\ \hfill & =\frac{1}{{\theta }^2}{\int }_0^1{\left.\left\{y\frac{sin\left[\theta (1-x)(1-y)\right]-\theta x(y-1)cos\left[\theta (1-x)(1-y)\right]}{{(1-y)}^2}\right\}\right|}_{x=0}^{x=1}dy\hfill \\ \hfill & =\frac{1}{{\theta }^2}{\int }_0^{1}y\frac{\theta (1-y)-sin\left[\theta (1-y)\right]}{{(1-y)}^2}dy\hfill \\ \hfill & =\frac{1}{{\theta }^2}{\int }_0^1{\left.\left\{\theta Ci\left[\theta (1-y)\right]-Si\left[\theta (1-y)\right]-\theta y-\theta log(1-y)-\frac{sin\left[\theta (1-y)\right]}{1-y}\right\}\right|}_{y=0}^{y=1}dy\hfill \\ \hfill & =\frac{1}{{\theta }^2}\left[-\theta Ci\left(\theta \right)+Si\left(\theta \right)+\theta (log(\theta )+\gamma -2)+sin\left(\theta \right)\right].\hfill \end{array}$$

  (14)
  Immediately, the intended result occurs.
• For $\theta \in [-1,0)$, thanks to the oddity of the sine function, we can write

  $$\begin{array}{cc}\hfill \rho & =12{\int }_0^1{\int }_0^{1}xysin\left[\theta (1-x)(1-y)\right]dxdy\hfill \\ \hfill & =-12{\int }_0^1{\int }_0^{1}xysin\left[(-\theta )(1-x)(1-y)\right]dxdy.\hfill \end{array}$$
  Since $-\theta \in (0,1]$, the expression of $\rho$ can be transposed with $-\theta$ instead of $\theta$, with the minus in factor of the overall expression.

The stated proposition is proved. □

The measure $\rho$ is an increasing function with respect to $\theta$ for $\theta \in [-1,1]$, with $\rho =0$ for $\theta =0$, $\rho =-0.3283896$ for $\theta =-1$, and $\rho =0.3283896$ for $\theta =1$. Figure 13 represents the Spearman rho for $\theta \in [-1,1]$.

In light of the above results, the sin-copula is adapted to model moderate correlations, which may be negative or positive.

Remark 3.

Similarly to Remark 2, a fascinating series formula, not repertoried to the best of our knowledge, can be proved. Based on Equations (6) and (8), upon integration over ${[0,1]}^2$, the following formula holds:

$$\begin{array}{cc}\hfill & \sum _{k=0}^{+\infty }\sum _{\ell =0}^{2k+1}\sum _{m=0}^{2k+1}\frac{{(-1)}^{k+\ell +m}}{(2k+1)!}{\theta }^{2k+3}\left(\genfrac{}{}{0pt}{}{2k+1}{\ell }\right)\left(\genfrac{}{}{0pt}{}{2k+1}{m}\right)\frac{1}{(\ell +2)(m+2)}\hfill \\ \hfill & =-\theta Ci\left(\theta \right)+Si\left(\theta \right)+\theta (log(\theta )+\gamma -2)+sin\left(\theta \right).\hfill \end{array}$$

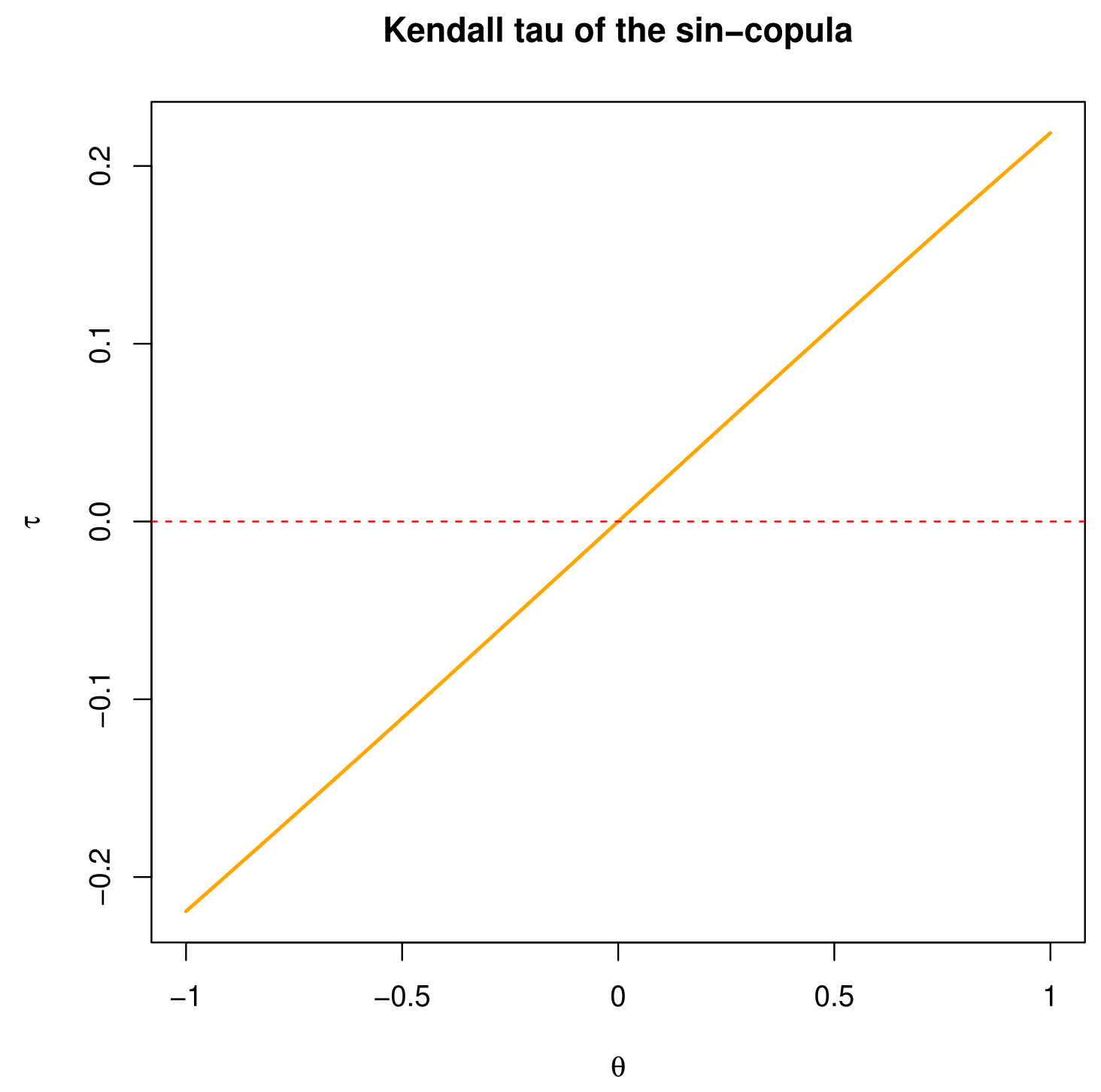
• In complement of the Spearman rho, we can present the Kendall tau of the sin-copula. It is defined by

  $$\tau =4{\int }_0^1{\int }_0^1{C}_{\circ }(x,y)c_{\circ }(x,y)dxdy-1.$$
  The complexity of the product function $C_{\circ }(x,y)c_{\circ }(x,y)$ makes the closed form expression for $\tau$ unmanageable. We can, however, show that it is an increasing function with respect to $\theta$ for $\theta \in [-1,1]$, with $\tau =0$ for $\theta =0$, $\tau =-0.2185653$ for $\theta =-1$ and $\tau =0.2185653$ for $\theta =1$. Figure 14 represents the Kendall tau for $\theta \in [-1,1]$.
  The wide range of values of $\tau$ confirm the fact that the sin-copula is ideal to model moderate correlations.
• Similarly to the cos-copula, the sin-copula opens up several fascinating possibilities, such as the development of simple and new two-dimensional distributions with cumulative distribution functions of the form: $H(x,y)=C_{\circ }(F\left(x\right),G\left(y\right))$, so

  $$H(x,y)=F\left(x\right)G\left(y\right)\left\{1+sin\left[\theta (1-F(x\left)\right)(1-G(y\left)\right)\right]\right\},$$

  where $F\left(x\right)$ and $G\left(x\right)$ denote two cumulative distribution functions. As a result, probabilistic or statistical modeling in this context becomes more feasible.

3.4. Data Generation and Inference

The data generation method described in Section 2.4 can be configured for the sin-copula. For any positive integer n, we can generate n data from the sin-copula by proceeding as follows:

• Generate n data $(s_1,t_1),\dots ,(s_n,t_n)$ from a random vector $(S,T)$, where S and T are independent random variables with the uniform distribution over $(0,1)$.
• Choose a value for $\theta \in [-1,1]$.
• Consider the following “conditional function”:

  $$\begin{array}{cc}\hfill {\mathfrak{C}}_{\circ }(x,y)& =\frac{\partial }{\partial x}{C}_{\circ }(x,y)\hfill \\ \hfill & =y\left\{1+sin\left[\theta (1-x)(1-y)\right]-\theta x(1-y)cos\left[\theta (1-x)(1-y)\right]\right\}.\hfill \end{array}$$
• For any $i=1,\dots ,n$, compute $u_i$ such that ${\mathfrak{C}}_{\circ }(s_i,u_i)=t_i$.
• Then $(s_1,u_1),\dots ,(s_n,u_n)$ are n data generated from the sin-copula defined with the chosen value of $\theta$.

Other techniques are available (see [24]).

In a data analysis scenario, the angle parameter $\theta$ is usually unknown. Its estimation is thus useful for exact data fitting, or at the very least for determining if $\theta$ is close to 0, corresponding to the independent case, or close to $-1$ or 1, corresponding to the most highly negatively or positively correlated situations, respectively. For this evaluation, it can be estimated from n data $(x_1,y_1),\dots ,(x_n,y_n)$, that are susceptible to coming from the sin-copula distribution, by the maximum likelihood method; $\theta$ is thus estimated by

$$\tilde{\theta }={argmax}_{\theta \in [-1,1]}\prod _{i=1}^n{c}_{\circ }(x_i,y_i)={argmax}_{\theta \in [-1,1]}\sum _{i=1}^{n}log\left[c_{\circ }(x_i,y_i)\right].$$

Concrete applications of the aforementioned methodologies to real-world datasets are thus possible.

4. Conclusions and Perspectives

4.1. Conclusions

We have introduced and studied several trigonometric copulas that have the features to depend on a tuning angle parameter. We have shown that they are quite simple from the mathematical point of view, and possess interesting properties.

For the first copula, called cos-copula, we have demonstrated that: (i) it extends the independence copula; (ii) it has the negative quadrant property; (iii) it is symmetric; (iv) it is not Archimedean; (v) it is not radially symmetric; (vi) a special ordering exists between it and the FGM copula; (vii) it has no tail dependence; (viii) the medial correlation belongs to the interval $[-0.0762,0]$; (ix) the Spearman rho belongs to the interval $[-0.1,0]$; (x) the Kendall tau belongs to the interval $[-0.067,0]$; (xi) it can serve to create a plethora of trigonometric two-dimensional distributions. Thus, the cos-copula is adapted to model weak negative correlations. It is thus not adapted to model moderate or large correlations. The corresponding copula density, survival copula, and survival copula density have been expressed, as well as two mixed copula versions.

For the second copula, called the sin-copula, its properties can be listed as follows: (i) it extends the independence copula; (ii) it has the negative and positive quadrant properties; (iii) it is symmetric; (iv) it is not Archimedean; (v) it is not radially symmetric; (vi) comprehensive ordering exists between it and both the FGM copula and cos-copula; (vii) it has no tail dependence; (viii) the medial correlation belongs to the interval $[-0.25,0.25]$; (ix) the Spearman rho belongs to the interval $[-0.33,0.33]$; (x) the Kendall tau belongs to the interval $[-0.22,0.22]$; (xi) it can also serve to create a plethora of trigonometric two-dimensional distributions. Thus, the sin-copula is adapted to model moderate negative or positive correlations. The corresponding copula density, survival copula, and survival copula density have been expressed, as well as three mixed copula versions.

The shapes of the principal functions and their related features have been visually observed using graphics.

4.2. Perspectives

Thus, the first elements for the promotion of the proposed copulas are in this article. Perspectives of further research includes the following points:

• Following the spirit of some power-extended FGM copulas (see [25]), one can think of considering some extensions of the cos-copula and sin-copula of the forms:

  $$C_{\ast \ast }(x,y)=xycos\left[\theta {(1-x^{\alpha })}^c{(1-y^{\beta })}^c\right]$$

  and

  $$C_{\circ \circ }(x,y)=xy\left\{1+sin\left[\theta {(1-x^{\alpha })}^c{(1-y^{\beta })}^c\right]\right\},$$

  respectively, where $\alpha$, $\beta$ and c are newly introduced shape parameters. However, the possible values of $\alpha$, $\beta$ and c such that $C_{\ast \ast }(x,y)$ and $C_{\circ \circ }(x,y)$ are valid copulas remain to discover.
• The n-dimensional versions of the cos-copula and sin-copula, which can be defined as $C_{\ast }:{[0,1]}^n\to [0,1]$ and $C_{\circ }:{[0,1]}^n\to [0,1]$, respectively, where

  $$C_{\ast }(x_1,\dots ,x_n)=\left\{\prod _{i=1}^n{x}_i\right\}cos\left[\theta \prod _{i=1}^n(1-x_i)\right]$$

  and

  $$C_{\circ }(x_1,\dots ,x_n)=\left\{\prod _{i=1}^n{x}_i\right\}\left\{1+sin\left[\theta \prod _{i=1}^n(1-x_i)\right]\right\},$$

  respectively, deserve to be investigated for $n\ge 3$. Especially, the possible values for $\theta$ in this case need to be determined.
• The use of the sin-copula and cos-copula for data analysis, following the methodology in [13,15], is an important perspective. Furthermore, the development of an R package is envisageable, inspired by the research design of Cylcop developed by [17].
• Last but not least, other simple angle parameter copulas can be created on the basis of this study. One could think of $C_{\diamond }:{[0,1]}^2\to [0,1]$ defined by

  $$C_{\diamond }(x,y)=xy\left\{1+tan\left[\theta (1-x)(1-y)\right]\right\},$$

  but the optimal values of $\theta$ such that $C_{\diamond }(x,y)$ is a valid copula remain unknown. It is proven that $\theta \in [0,\pi /4]$ satisfies the required conditions (in an unpublished work), but this set is thought to be less than optimal.