Abstract
Precise environmental modelling of pollutants distributions represents a key factor for addresing the issue of urban air pollution. Nowadays, urban air pollution monitoring is primarily carried out by employing sparse networks of spatially distributed fixed stations. The work in this paper aims at improving the situation by utilizing machine learning models to process the outputs of multi-sensor devices that are small, cheap, albeit less reliable, thus a massive urban deployment of those devices is possible. The main contribution of the paper is the design of a mathematical model providing sensor fusion to extract the information and transform it into the desired pollutant concentrations. Multi-sensor outputs are used as input information for a particular machine learning model trained to produce the CO, NO2, and NOx concentration estimates. Several state-of-the-art machine learning methods, including original algorithms proposed by the authors, are utilized in this study: kernel methods, regularization networks, regularization networks with composite kernels, and deep neural networks. All methods are augmented with a proper hyper-parameter search to achieve the optimal performance for each model. All the methods considered achieved vital results, deep neural networks exhibited the best generalization ability, and regularization networks with product kernels achieved the best fitting of the training set.
1. Introduction
Air pollution monitoring is one of the most important emerging environmental issues in the treatment of urban air pollution. Urban atmospheric pollutants are responsible for the respiratory and other illness of urban citizens. Some of the pollutants (e.g., benzene) are known to induce cancers in case of prolonged exposure. Therefore, the precise modelling of pollutants distribution is needed for traffic management and for the definition of mobility plans designed to face these problems. Nowadays, urban air pollution monitoring is primarily carried out employing networks of spatially distributed fixed stations. A limited number of those stations represent a problem in estimating the real distribution of gases and particles in a complex urban environment.
The work in this paper aims at improving the situation by utilizing machine learning models to process outputs of multi-sensor devices that are small and cheap, thus a massive urban deployment of those devices is possible. The outputs of those sensors are less reliable in comparison to the currently used fixed stations, therefore a mathematical model providing sensor fusion is utilized to extract the information and transform it into desired pollutant concentrations. The main idea is that multi-sensor outputs are used as input information for a particular machine learning model which is trained to produce the CO, NO2, and NOx concentrations in a supervised learning scenario. The desired outputs of the model are provided by reliable but expensive measurements of the pollutants. Our results should provide a proof of concept of this approach, and show that with clever processing of sufficient data, it is possible to model and estimate concentrations of desired pollutants even from cheap and unreliable sensors.
Machine learning models have recently been successfully applied to many challenging problems from image recognition and robotics to language translation and DNA sequencing [1,2]. In the majority of these areas they now provide the best solutions available, surpassing the ”white-box” analytic solutions. While the lack of explanation abilities of these approaches can be seen as a disadvantage, their efficiency of data modelling and their adaptivity to new problems and datasets represent big benefits. In particular, the area of cheap gas sensors, where the exact analytic descriptions are hard to obtain or differ for different sensor technologies, seems to be a suitable domain for machine learning where expert knowledge is augmented by efficient autonomous algorithms.
The application of machine learning models to the processing of sensor data presents several challenges that have already been identified and tackled by previous research. The majority of related work in this area uses regression approaches to model individual sensor outputs, or in more advanced settings, to provide multi-sensor fusion with relevant data (such as pollutant concentrations) as the output of the model.
The authors of [3] have applied several simple machine learning models for classification and regression tasks to utilize multi-sensor data in the indoor environment for the task of occupancy prediction formulated as supervised learning. Their models include decision trees, Bayesian networks and linear regression. The importance of raw data preprocessing and using multiple inputs (including augmenting data collected by humans) was stressed. The similar indoor scenario is used in paper [4] where Bayesian and neural networks are used for predicting and correcting multi-sensor outputs measuring temperature, humidity, pressure, and so forth. Their results with relatively small datasets and simple models imply the possibility of reconstructing relevant information by multi-sensor fusion.
In the last several years, deep neural networks became a very popular machine learning tool and they were also applied in sensor information processing field. The authors of [5] describe a low-cost multi-sensor hardware device measuring CO2 concentrations. The complete system consists of six sensors and a deep neural network model that demonstrated superior performance compared to linear regression, albeit the computing requirements for training (dozens of hours) are large. A recent work [6] presents a successful application of deep (convolutional) network for multi-sensor data fusion solving the problem of steel element defects. Their results seem to be dependent on clever preprocessing and analysis of the sensor output.
In this paper, we work with datasets that have been already used for analysis and modelling by different machine learning models by De Vito et al. [7,8]. The data consists of dozens of thousands of measurements of concentrations of several gas pollutants obtained from multi-sensor devices recording. As mentioned earlier, the measurements are labelled by reliable conventional air pollution monitoring stations. The technical nature of the data is described in detail in Section 4.
Several machine learning models are compared on the task of prediction of CO, NO2 and NOx concentrations based on the multi-sensor fusion of the above obtained data. The tested methods represent state-of-the-art approaches ranging from kernel methods to deep neural networks. It is important to stress that all methods have been extensively tested for their performance not only by the standard statistical measures and approaches as the cross-validation, but also the optimal choice of hyper-parameters (types of a kernel, size of a model, etc.) has been performed by extensive global search. In the case of regularization networks, the hyper-parameter search is performed by a genetic algorithm, and in the case of deep neural networks, it is performed by an evolution strategy [9].
The obtained results show that all machine learning models we have tested were able to perform the task of modelling the pollutant concentrations from multi-sensor data in a satisfiable way. The overall best model in terms of generalization criteria has been a particular architecture of a deep neural network. On the other hand, the best precision on training data has been achieved by our original architecture of kernel networks with product units.
The paper is organized as follows. In the next section, related work concerning machine learning models is discussed. Section 3 describes the used machine learning algorithms in more detail, namely Section 3.1 derives the regularization network, Section 3.2 introduces the extension of regularization network via composite kernels, while Section 3.3 explains how composite kernels are evolved. Then, Section 3.4 briefly introduces deep neural networks and Section 3.5 describes how architecture of deep neural networks is optimized. Finally, Section 4 describes the dataset. Section 5 contains the results of our experiments and our conclusion can be found in Section 6.
2. Related Work
Among machine learning methods, kernel methods became very popular in the 1990s. They have been applied to many real-world problems, and they are still considered to be state-of-the-art methods in various domains [10]. In this work, we study the regularization network (RN), a feed-forward neural network with one hidden layer, designed for supervised learning. RN are based on a good theoretical background and their architecture has been mathematically proven to be the solution to the problem of supervised learning formulated as a minimization problem with regularization (see [11,12,13,14]).
The paper [15] demonstrates how the kernel function choice significantly influences the RN performance. Therefore, the optimal choice of the kernel function always depends on a task given. Kůrková et al. have studied the theoretical properties of kernel units with variable and fixed widths [16,17,18,19].
More complex models, described in detail in Section 3.2, belong to the class of the multi-kernel models. Recently, this field has been studied extensively [10,20,21,22]; however, corresponding algorithms are mostly designed for the support vector machines (SVM).
In addition, the Support Vector Regression (SVR) model is used in this paper. It is an extension of the well-known Support Vector Machine (SVM) for regression problems. Like the SVM model, SVR depends only on a subset of the training data, because the cost function ignores any training data close to the model prediction [23,24].
Finally, the last method considered in this work is the Deep Neural Network (DNN). DNNs have become the state-of-the-art methods in many machine learning application areas, recently. They have been applied to various problems, such as image and speech recognition, natural language processing [1,2].
DNN are neural networks with multiple hidden layers. In this paper, we consider only feed-forward networks. The types of network units typically depend on the particular application. The commonly used units are traditional perceptrons or the rectified linear unit (ReLU).
The weights of DNN are trained by algorithms based on stochastic gradient descent. However, the architecture (i.e., a number and sizes of layers, and a type of activation function) has to be set up manually by an expert. The choice of architecture influences significantly the performance of the DNN, but still, it is typically done by a trial and error method [25].
3. Machine Learning Methods
In this section, we will describe the machine learning models used in our experiments in more details, with the emphasis on our original modifications and extensions. The most important part deals with a hyper-parameter search for (composite) kernel and deep neural networks. We have utilized evolutionary computing optimization to provide a global search procedure for the hyper-parameter sweep. This is done to make sure the optimal model (within some reasonable constraints) is found, and thus the performance comparison is as fair as possible.
First, let us overview the models and hyper-parameter search algorithms:
- regularization networks (RN);
- -
- evolutional algorithm for RN hyper-parameter search;
- RN with composite kernels;
- -
- evolutional algorithm for RN and composite kernel hyper-parameter search;
- deep neural networks (DNN);
- -
- evolution strategies for DNN architecture search.
The models and algorithms in bold are our original extensions.
3.1. Regularization Networks and Kernels
This section introduces the regularization network architecture used for supervised learning. The supervised learning we reformulate in the context of a function approximation. Given a set of data points (where is an input, is a corresponding output, and N is a number of data points) obtained by random sampling of a real function f, the goal of supervised learning is to search for this function. Generally, the problem is ill-posed. Therefore we add a priori knowledge about f. It is usually assumed that f is smooth, that is, each pair of similar inputs corresponds to a pair of similar outputs. The solution to the problem is found by minimization the functional (1) which contains both the data and the regularization term.
where is a regularization term and is the regularization parameter. For a wide class of regularization terms, the solution can be represented by a feed-forward neural network with one hidden layer, and linear output units called a regularization network (RN) [14,26]. The RN obtained as a solution is unique and it has the form:
where I is the identity matrix, K is the matrix , K is an appropriate kernel function, and .
For the given and the type of kernel function K, the algorithm is simple and efficient, since it is, in fact, a problem of solving a linear system. In our approach, the search for suitable hyper-parameters is performed by a genetic algorithm optimization technique. This will be described in detail in Section 3.3.
3.2. Composite Kernels
The kernel function represents our presumption (called bias in machine learning) about a solution to the given approximation problem. Therefore, it is usually assumed to be chosen by a user. However, this choice has a significant impact on the learning performance and therefore should be done for each task independently.
In theory, it is typically assumed that a kernel is a symmetric and positive-definite function. On the other hand, in practice, various other functions are used. In [27], it was shown that conditionally positive definite kernels possibly outperform classical kernels.
Commonly used kernel functions are: linear , polynomial , Gaussian radial basis function , sigmoid . Where, , d and r are the kernel’s parameters.
Recently, several algorithms have been proposed to use composite kernel functions, that is, functions consisting of combinations of basic kernel functions [20]. Data are often multi-modal and then such composite kernels may better reflect the character of data.
In our previous papers [28,29], we have proposed composite kernel functions for RN and, consequently, evolutionary algorithms searching for data-dependent optimal kernel functions have been proposed in [30] for networks with product units, and in [31] for networks with sum units. Based on Aronszajn’s breakthrough results [32], we have shown that it is possible to use composite kernels as activation functions in the RNs (cf. [33]). Such composite kernels also often outperform a simple kernel function.
The product kernel is a function K:
where are kernel functions defined on () respectively, and .
The sum kernel is a function K: , where and are kernel functions.
It is possible to combine various types of kernels or just two functions of same type but with different parameters, that is, two Gaussians of different widths (note that in this case the Gaussians have the same center).
3.3. Genetic Search for Kernels
In order to find the right kernel function in a data-dependent and autonomous way, a suitable search algorithm is needed. A sound and robust global optimization method called genetic algorithms (GA) [34] was used in our approach. Considered to be an efficient stochastic population-based meta-heuristic, the GA allows to search for various types of kernels, including composite kernels. The GAs work with a population of individuals encoding feasible solutions. During the process of search, each individual is evaluated by a fitness function value that reflects the quality of the corresponding solution.
Populations in GA evolve so as to approach better individuals. The algorithm starts with individuals generated randomly, and it creates a new population each iteration of the algorithm (generation). In each iteration, the fitness of all individuals is evaluated. Based on the fitness, the individuals are stochastically selected for reproduction and then altered by genetic operators mutation and crossover.
To find suitable hyper-parameters for RN (described above), our individuals encode the kernel function type, other possible parameters of the kernel function, and the regularization parameter.
For example, a simple kernel function is encoded as where K is the type of kernel function, p is a kernel parameter, and is a regularization parameter, that is,
The product kernel function can be represented by the individual: where are the types of kernel functions, are kernel parameters, and is an index of kernel by which the i-th attribute is processed, i.e
The genetic operators of mutation and crossover are rather simple and based on standard evolutionary approaches for vectors of floating-point and discrete values. Our mutation operator is a standard biased mutation which performs small random perturbation drawn from normal distribution to a small number of randomly selected numerical values of an individual.
The crossover operator differs slightly for different types of regularization networks: for simple kernels of the same type, we use an arithmetic crossover that modifies the kernel parameter and , that is, the new values are generated randomly:
where is a random number, and are parents’ values, and is the offspring value.
In the case of composite kernels, the situation is more complicated, and the standard discrete one-point crossover is used—the sub-kernels are interchanged.
A standard and robust tournament selection is used as a selection operator.
The fitness value must reflect the quality of the corresponding RN. To estimate the real generalization ability of a network we use a cross validation error [35]. Thus, it should be stressed that we are looking for such hyper-parameters that minimize the crossvalidation error.
3.4. Deep Neural Networks
Artificial neural networks (ANNs) are a class of computational models used in machine learning. In general, an ANN is a large collection of simple connected units called artificial neurons. The neurons are typically organized in layers. Networks with more layers between the input and output layer are known as deep neural networks (DNN).
A neuron is a computational unit with n real inputs and one real output y. It realizes a function , where g is an activation function, and are weights. A typical activation function is the sigmoid function but a current popular alternative to sigmoid is the so-called rectified linear unit (ReLU):
DNN realizes a function , where N is the number of input neurons and M is a number of output neurons, W is a matrix of network parameters, the weights. The learning of DNN consists of the optimization of a cost function with respect to weights W. This optimization is typically done by a version of the stochastic gradient descent algorithm. To prevent overfitting, various regularization techniques can be used. The most common method is the so-called dropout, which is a very efficient way of performing model averaging by dropping out individual neurons.
The hyper-parameters of DNN (traditionally referred to as an architecture), that is, the number of hidden layers, the number of neurons in individual layers, and so forth, are typically chosen by a user, often by the time-consuming trial and error method.
3.5. Evolution Strategies for DNN Design
In our work, we use evolution strategies to search for the optimal architecture (hyper-parameters) of DNN, while the weights are learned by a conventional gradient based technique.
Evolution strategies (ES) are a kind of evolutionary algorithm. They were designed for real-valued individuals [36]. Similarly to GA, they work with a population of individuals, evolving them by means of selection, crossover and mutation operators. The key operator in ES is the Gaussian mutation:
where x is a variable under mutation and is the corresponding strategy coefficient, is a mutation coefficient, stands for normal distribution.
There are two traditional forms for evolution strategies. The -ES generates new generation by deterministically choosing n best individuals from the set of parents and offspring. The -ES generates new generation by selecting from m new offspring (typically, ). The latter approach is considered more robust against local optima premature convergence.
Evolution strategies represent a very successful optimization approach used for solving complex and large problems.
The main idea of our approach to applying ES for DNN architecture search is to restrict the space of feasible architectures as much as possible. Therefore, the architecture specification is simplified. It directly follows the implementation of DNN in the popular Keras library [37], where networks are specified as a list of fully connected layers. A layer is then defined by the number of neurons, the type of an activation function, and the type of regularization (such as dropout).
In our algorithm, the -ES is used. Offspring are generated using both mutation and crossover operators. Our individuals represent network topologies and therefore they are not represented by real-valued vectors. So, our operators have to slightly differ from classical ES.
Each individual represents one DNN. It consist of blocks defining the network’s layers.
where H is the number of hidden layers, is the number of neurons in corresponding layer that is dense (fully connected) layer, is the dropout rate (zero value represents no dropout), is an activation function, and and are strategy coefficients corresponding to size and dropout.
The crossover operator is implemented as a one-point crossover exchanging the whole blocks (layers).
There is a variety of mutation operators. Each time mutation is performed, one of them is chosen at random.
- mutateLayer—operates on one randomly selected layer. One of the following actions is performed:
- -
- changeLayerSize—Gaussian mutation is used, adapting strategy parameters , the final number is rounded (since size has to be an integer);
- -
- changeDropOut—the dropout rate is mutated by Gaussian mutation adapting strategy parameters ;
- -
- changeActivation—a new activation function is selected randomly from the list of available activations;
- addLayer—new block is generated at random and inserted at random position;
- delLayer—deletes random block.
Note that the ES-like mutation comes in play only when the size of layer or dropout parameter is changed.
Fitness and selection are similar to the GA used for evolution of kernels. The classical cross validation error is used as fitness, and a tournament selection is utilized.
4. Data Set
We have used a real-world dataset [7,8]. It contains measurements of gas multi-sensor MOX array devices recording several gas pollutants concentrations. Data are labelled by a conventional air pollution monitoring station. The frequency of measurements is 1 hour, but data contain many missing values (due to sensor malfunctions). In this paper, we use data from 10 March 2004 to 4 April 2005. Lines with missing values are neglected. There are five sensor measurements as inputs, and we have chosen three output values, representing concentrations of CO, NO2 and NOx gases, as targets.
In the following text, we describe two experiments with different subsets of the data. The first experiment was rather a simple one, it should identify if our models are able to provide reliable results in a simplified scenario. For the first experiment, we have chosen 4 data samples per day for training, and the rest of the data is used for testing. It means we are predicting relatively small intervals between measurements.
The second experiment presents a more realistic scenario. The data were divided into five uniform intervals. In each of the sub-experiments, one of the intervals is chosen for training, while the remaining of the data were left for testing. We have considered three different strategies for how to choose the training part. This task may thus be more difficult, since the testing may also be performed on distant parts of the data, meaning, for example, a different season of the year. Experts in the application area have suggested that, from their experience, the model build for the winter period will probably not work for summer.
Table 1 lists the size of individual datasets. All sets have five inputs and one target. All numbers are normalized to .

Table 1.
Overview of datasets’ sizes.
5. Results
5.1. Experimental Setup
Models applied to sensor data include the above described RN, support vector regression (SVR), and DNN.
RN were used with Gaussian, product and sum kernels. Kernels were evolved using the GA described in Section 3.3. The set of available sub-kernels contained Gaussian, Multiquadric, Inverse-Multiquadric, and Sigmoid functions. The population size of GA was set up to 20 and a stop criterion to 300 generations. Elite with 2 individuals was used. Ten-fold cross validation was utilized for fitness.
SVR were trained using the Scikit-learn package [23]. We used SVR with linear, RBF, polynomial and sigmoid kernels [24]. Hyper-parameters were tuned by extensive grid search (10,000 different pairs of regularization parameter and kernel parameter).
Finally, the DNN were trained by RMSProp [37] for 500 epochs. The network architecture was found by the ES evolutionary algorithm described in Section 3.5. The ES was run with and for 100 generations. During the fitness evaluation, a five-fold cross validation was used.
Resulting errors are computed on the training and testing sets as mean square error multiplied by the factor of 100. Each experiment was run 10 times, evaluating average errors and their standard deviations.
5.2. Experimental Results
See Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8 and Table 9 and Figure 1 for results of the first and second experiment, respectively.

Table 2.
Task 1: Experiment on sparse measurements with RNs. Average errors and standard deviations are listed for networks with Gaussian, Product and Sum kernel. The lowest errors are highlighted.

Table 3.
Task 1: Comparison of RNs, SVR, and DNN. Average error values are listed. The lowest errors are highlighted.

Table 4.
Task 2: Comparison of training errors for RN trained on single epochs. Average values, standard deviations, minimum and maximum values are listed. The lower average and minimum errors are highlighted.

Table 5.
Task 2: Comparison of testing errors for RN trained on single epochs. Average values, standard deviations, minimum and maximum values are listed. The lower average and minimum errors are highlighted.

Table 6.
Task 2: Comparison of average training errors for different models: Regularization Networks with Gaussian and Product kernels, SVR with RBF, linear, polynomial and sigmoid kernels. Lowest error for each dataset is highlighted.

Table 7.
Task 2: Comparison of average testing errors for different models: Regularization Networks with Gaussian and Product kernels, SVR with RBF, linear, polynomial and sigmoid kernels. Lowest error for each dataset is highlighted.

Table 8.
Task 2: Comparison of average training errors of RN with Product kernels and DNN. Average, standard deviation, minimal and maximal values are listed. The lower average value for each dataset is highlighted.

Table 9.
Task 2: Comparison of average testing errors of RN with Product kernels and DNN. Average, standard deviation, minimal and maximal values are listed. The lower average value for each dataset is highlighted.
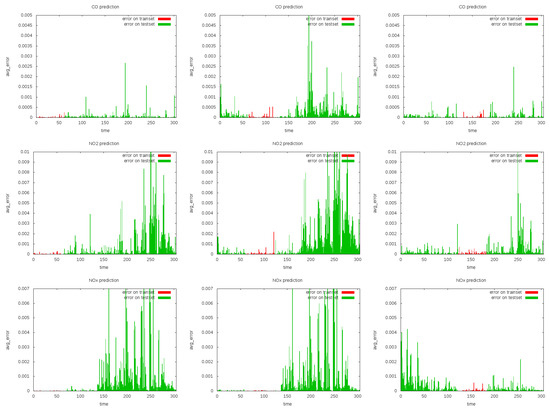
Figure 1.
Task 2: Example of product kernel model performance on five splits on training and testing data. The rows correspond to predictions of , , and concentrations. The three figures in one row correspond to three different training/testing splits.
The first task contains four training values per day, the rest of measurements is left as a test set. Errors for RN with evolved Gaussian kernels, product and sum kernels are listed in Table 2. Note that product kernels perform the best on training data and under cross validation scenario, while they have results on the test data comparable to other kernels.
Table 3 lists training and testing errors on the first task for RN with product kernels, SVR with linear, RBF, polynomial, and sigmoid kernels, and DNN. Product kernels performed best both in terms of training and testing errors.
Figure 1 shows model performance on five splits on training and testing data. It can be seen that some periods are more suitable for training and general prediction than the others.
The second task is the more difficult one. The meassurements are split into five parts. Each time, one part represents a training data, the rest the test set. So, the predictions are made for seasons that were not included in the training data.
Table 4 and Table 5 contain the resulting errors for RN with Gaussian and product kernels, respectively. The situation is the same as in the first experiment. Considering training errors, product kernels achieved lower errors in 10 cases from 15. In case of testing errors, products were winners only in seven cases. However, taking into account minimal values, the product kernels are best in all runs except one in case of training errors and except three in case of test errors. That means it is still possible to improve the search for product kernel. Note that the evolved product kernels are mainly composed of Gaussian and Inverse-Multiquadric functions.
The comparison of RN to SVR on the second task is listed in Table 6 and Table 7. In terms of training errors, the RN with product kernels performed best (in nine cases), in terms of testing errors the RN with Gaussian kernels performed best (in seven cases). In general, RN gives better results than SVR.
Finally, Table 8 and Table 9 show a comparison of RN with product kernels and DNN on the second task. Product kernels performed better in the case of training error (in 12 cases), while DNN are better in the case of testing error (in 10 cases). The DNN showed a better generalization ability, while RN with product kernels are more prone to overfitting.
Since the dataset used is quite small, the evolved DNN had typically only one hidden layer consisting of 70 ReLU units, using dropout rate 0.3.
6. Discussion
The goal of this study was to verify the usability of machine learning models in the area of multi-sensor fusion for air pollution modelling. We have identified several machine learning methods that have performed well in related areas of data mining and included several original improvements of those methods from our previous research. The methods proposed by the authors include:
- regularization networks with product and sum kernels;
- evolution of kernels based on a genetic algorithm;
- evolution of DNN architectures based on evolutionary strategies.
Comparisons to the very popular support vector machine regression models with Gaussian, polynomial and sigmoid kernels were also performed.
The model performance has been tested on real datasets described and used by other researchers before. The problem was formulated as a regression task from sensor measurements of air pollution. To ensure the best behaviour of studied methods, the extensive search for optimal hyper-parameters is performed by evolutionary optimization of cross validation error.
The results described above show that all models we have tested provided sound interpretations of the available data, they were able to perform multi-sensor fusion to predict the pollutant concentrations.
The insight into the temporal nature of the data can be obtained from the second experiment which compared results of models trained on 5 data splits. The first general observation is that short-term temporal dependencies were not a problem for the models that were able to reliably predict pollutant concentrations from sensor values. The cross validation results indicate that a well performing predictive model can be built using only 20 percent of the data. The second observation indicates a seasonal aspect of the data that is in correspondence with expert estimates. This is demonstrated by the generally poorer test performance of models trained on the fourth split of the data containing the winter months only. Thus, for the practical deployment of the models, some ensemble technique combining models trained on different seasons would be recommended.
When comparing the relative performances of the models, we can generalize the following outcomes.
The most difficult pollutant to predict is NO2, for which we get the highest errors.
Product kernels, our original model, can outperform standard classical RN models. In comparison to SVR, product kernels have been able to produce better results in the majority of the cases.
DNN performed comparatively to product kernels, achieving better generalizations in certain cases. Namely, on the first task, where values ’in between’ are approximated, the product kernels are the winners, benefiting from their local character. On the second task, which is more difficult in general, product kernels performed better in terms of training errors, but in terms of testing errors, DNN provided better results in most cases. It suggests that DNN have better generalization capabilities, while product kernels are more prone to overfitting. Both RN and DNN are vital alternatives for the task of air pollution prediction.
Although our work presented in this paper has been performed on one (relatively representative) dataset, it demonstrates several general issues that are probably relevant to the whole application area. There seems to be a relevant problem with missing data which was not addressed in this work. Since simple mean inputting does not seem to be sufficient, we recommend employing some more sophisticated methods, such as clustering or semi-supervised methods. In general, better data preprocessing and cleaning should improve the results. Next, interesting statistical properties of the data that have been identified, such as relevant differences between summer and winter concentrations, should be studied further in accordance with domain experts, which can probably lead to a creation of several specialized models, or even ensemble methods.
Author Contributions
Both authors contributed to the manuscript equally. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Czech Grant Agency grant 18-23827S and institutional support of the Institute of Computer Science RVO 67985807.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this work are also available at UCI ML Repository, see https://archive.ics.uci.edu/ml/datasets/Air+quality (accessed on 1 October 2021).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Moraru, A.; Pesko, M.; Porcius, M.; Fortuna, C.; Mladenic, D. Using machine learning on sensor data. In Proceedings of the ITI 2010, 32nd International Conference on Information Technology Interfaces, Dubrovnik, Croatia, 21–24 June 2010; pp. 573–578. [Google Scholar]
- Smith, M.K.; Castello, C.C.; New, J.R. Machine Learning Techniques Applied to Sensor Data Correction in Building Technologies. In Proceedings of the 2013 12th International Conference on Machine Learning and Applications, Miami, FL, USA, 4–7 December 2013; Volume 1, pp. 305–308. [Google Scholar] [CrossRef]
- Ahn, J.; Shin, D.; Kim, K.; Yang, J. Indoor Air Quality Analysis Using Deep Learning with Sensor Data. Sensors 2017, 17, 2476. [Google Scholar] [CrossRef] [PubMed]
- Psuj, G. Multi-Sensor Data Integration Using Deep Learning for Characterization of Defects in Steel Elements. Sensors 2018, 18, 292. [Google Scholar] [CrossRef] [PubMed]
- Vito, S.D.; Massera, E.; Piga, M.; Martinotto, L.; Francia, G.D. On field calibration of an electronic nose for benzene estimation in an urban pollution monitoring scenario. Sens. Actuators B Chem. 2008, 129, 750–757. [Google Scholar] [CrossRef]
- De Vito, S.; Fattoruso, G.; Pardo, M.; Tortorella, F.; Di Francia, G. Semi-Supervised Learning Techniques in Artificial Olfaction: A Novel Approach to Classification Problems and Drift Counteraction. Sensors 2012, 12, 3215–3224. [Google Scholar] [CrossRef]
- Vidnerová, P.; Neruda, R. Evolution Strategies for Deep Neural Network Models Design. In Proceedings of the ITAT 2017: Information Technologies—Applications and Theory, CEUR Workshop Proceedings, Oravská Lesná, Slovakia, 22–29 September 2017; pp. 159–166. [Google Scholar]
- Vert, J.P.; Tsuda, K.; Scholkopf, B. A primer on kernel methods. InKernel Methods in Computational Biology; MIT Press: Cambridge, MA, USA, 2004; pp. 35–70. [Google Scholar]
- Cucker, F.; Smale, S. On the Mathematical Foundations of Learning. Bull. Am. Math. Soc. 2001, 39, 1–49. [Google Scholar] [CrossRef]
- Girosi, F. An Equivalence between Sparse Approximation and Support Vector Machines; Technical Report; Massachutesetts Institute of Technology: Cambridge, MA, USA, 1997; A.I. Memo No. 1606. [Google Scholar]
- Girosi, F.; Jones, M.; Poggio, T. Regularization Theory and Neural Networks Architectures. Neural Comput. 1995, 2, 219–269. [Google Scholar] [CrossRef]
- Poggio, T.; Smale, S. The Mathematics of Learning: Dealing with Data. Not. AMS 2003, 50, 536–544. [Google Scholar]
- Kudová, P. Learning with Kernel Based Regularization Networks. In Information Technologies—Applications and Theory. Košice; Prírodovedecká fakulta Univerzity Pavla Jozefa Šafárika: Košice, Slovak Republic, 2005; pp. 83–92. [Google Scholar]
- Kainen, P.C.; Kůrková, V.; Sanguineti, M. Complexity of Gaussian radial-basis networks approximating smooth functions. J. Complex. 2009, 25, 63–74. [Google Scholar] [CrossRef][Green Version]
- Kůrková, V.; Kainen, P.C. Kernel networks with fixed and variable widths. In Proceedings of the ICANNGA 2011, Ljubljana, Slovenia, 14–16 April 2011; LNCS 6593. Springer: Berlin/Heidelberg, Geremany, 2011; pp. 12–21. [Google Scholar]
- Kůrková, V. Some comparisons of networks with radial and kernel units. In Neural Networks: Brain-Inspired Computing and Machine Learning Research; Springer: Berlin/Heidelberg, Germany, 2012; LNCS 7553; pp. 17–24. [Google Scholar]
- Kůrková, V.; Kainen, P.C. Comparing fixed and variable-width Gaussian networks. Neural Netw. 2014, 57, 23–28. [Google Scholar] [CrossRef] [PubMed]
- Gönen, M.; Alpaydin, E. Multiple Kernel Learning Algorithms. J. Mach. Learn. Res. 2011, 12, 2211–2268. [Google Scholar]
- Cortes, C. Invited Talk: Can Learning Kernels Help Performance? In Proceedings of the 26th Annual International Conference on Machine Learning, Montreal, QC, Canada, 14–18 June 2009; ACM: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Kloft, M.; Blanchard, G. The Local Rademacher Complexity of Lp-Norm Multiple Kernel Learning. In Advances in Neural Information Processing Systems 24; Shawe-Taylor, J., Zemel, R., Bartlett, P., Pereira, F., Weinberger, K., Eds.; Curran Associates, Inc.: New York, NY, USA, 2011; pp. 2438–2446. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1997, 9, 155–161. [Google Scholar]
- Vidnerova, P.; Neruda, R. Evolving keras architectures for sensor data analysis. In Proceedings of the 2017 Federated Conference on Computer Science and Information Systems (FedCSIS), Sofia, Bulgaria, 6–10 September 2017; pp. 109–112. [Google Scholar] [CrossRef]
- Poggio, T.; Girosi, F. A Theory of Networks for Approximation and Learning; Technical Report; Massachusetts INST of TECH Cambridge Artificial Intelligence LAB: Cambridge, MA, USA, 1989; A.I. Memo No.1140. [Google Scholar]
- Boughorbel, S.; Tarel, J.P.; Boujemaa, N. Conditionally Positive Definite Kernels for SVM Based Image Recognition. In Proceedings of the 2005 IEEE International Conference on Multimedia and Expo, Amsterdam, The Netherlands, 6–8 July 2005; pp. 113–116. [Google Scholar]
- Vidnerová, R.N.P. Product Multi-kernels for Sensor Data Analysis. In Artificial Intelligence and Soft Computing; Rutkowski, L.M., Scherer, R., Tadeusiewicz, R., Zadeh, L., Zurada, J., Eds.; ICAISC 2015; Lecture Notes in Computer Science; Springer: Cham, Switzerland, 2015; Volume 9119. [Google Scholar]
- Vidnerová, P.; Neruda, R. Sensor Data Air Pollution Prediction by Kernel Models. In Proceedings of the 2016 16th IEEE/ACM International Symposium on Cluster, Cloud and Grid Computing (CCGrid), Cartagena, Columbia, 16–19 May 2016; pp. 666–673. [Google Scholar] [CrossRef]
- Vidnerová, P.; Neruda, R. Evolutionary Learning of Regularization Networks with Product Kernel Units; IEEE: Piscataway, NJ, USA, 2011; pp. 638–643. [Google Scholar]
- Vidnerová, P.; Neruda, R. Evolving Sum and Composite Kernel Functions for Regularization Networks; Lecture Notes in Computer Science; ICANNGA (1); Dobnikar, A., Lotric, U., Ster, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6593, pp. 180–189. [Google Scholar]
- Aronszajn, N. Theory of Reproducing Kernels. Trans. AMS 1950, 68, 337–404. [Google Scholar] [CrossRef]
- Kudová, P.; Šámalová, T. Sum and Product Kernel Regularization Networks. Artificial Intelligence and Soft Computing; Rutkowski, L., Tadeusiewicz, R., Zadeh, L., Zurada, J., Eds.; Lecture Notes in Artificial Intelligence; Springer: Berlin/Heidelberg, Germany, 2006; pp. 56–65. [Google Scholar]
- Mitchell, M. An Introduction to Genetic Algorithms; MIT Press: Cambridge, MA, USA, 1996. [Google Scholar]
- Stone, M. Cross-validation: A review. Math. Oper. Stat. 1978, 9, 127–140. [Google Scholar]
- Beyer, H.G.; Schwefel, H.P. Evolutionary Strategies: A Comprehensive Introduction. Nat. Comput. 2002, 1, 3–52. [Google Scholar] [CrossRef]
- Chollet, F. Keras. 2015. Available online: https://github.com/fchollet/keras (accessed on 1 October 2021).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).