Tensile Fracture Mechanism of Masonry Wallettes Parallel to Bed Joints: A Stochastic Discontinuum Analysis

1. Introduction

Masonry is a heterogeneous, nonlinear, and composite construction material consisting of units and mortar. The components within a masonry assemblage may have a considerable difference in terms of stiffness and strength, which makes it challenging to predict the deformation behavior (e.g., stress–displacement curve) of the material at the macro-level. Additionally, the heterogeneous character of mortar, unit, and unit–mortar interface properties inherently leads to large scattering in the experimental results, as noted by several researchers [1,2]. From the computational point of view, most of the numerical models presented in the literature are deterministic and rely on the continuum-based representation of the masonry, described as an equivalent orthotropic continuum associated with either plasticity or damage constitutive laws. In the present research, an alternative approach is employed using the discrete element method (DEM), where the masonry texture is replicated via discrete polyhedral blocks, as shown in Figure 1. Note that generated blocks are grouped to simulate masonry units and unit–mortar interfaces, where each masonry unit in the discrete model is expanded up to the half-thickness of the mortar joints (see Figure 1). Therefore, with the help of the proposed discontinuum-based modeling strategy, cracking in the masonry units and sliding/tension failure modes at the unit–mortar interfaces can be captured. The mechanical interaction among the blocks is represented using nonlinear spring models at the contact points, defined among the adjacent blocks, similarly to work published elsewhere [3,4,5]. Hence, utilizing the discontinuum representation of masonry, this research aimed to better understand the influence of material properties in masonry wallettes on the fracture mechanism and stress–displacement behavior, subjected to tension parallel to bed joints.

In a preceding study by the authors, Pulatsu et al. [6], a deterministic modeling strategy was used to explore the tensile behavior of the masonry wallettes using average contact properties. The contribution of the present study furthers this investigation and explores the effect of statistically varied contact properties. In other words, the emphasis of this work is on the stochastic analysis of masonry wallettes within the discrete element method framework. Therefore, the goals of this research are as follows:

• To investigate the effect of nonlinear contact properties on the macro behavior of the masonry wallettes subjected to tension parallel to bed joints.
• To gain a better understanding of the tensile fracture mechanism in masonry, considering strong masonry unit–weak mortar joint and weak masonry unit–strong mortar joint systems.

In the following sections, a brief overview of the applied computational method and the statistical sampling method are presented.

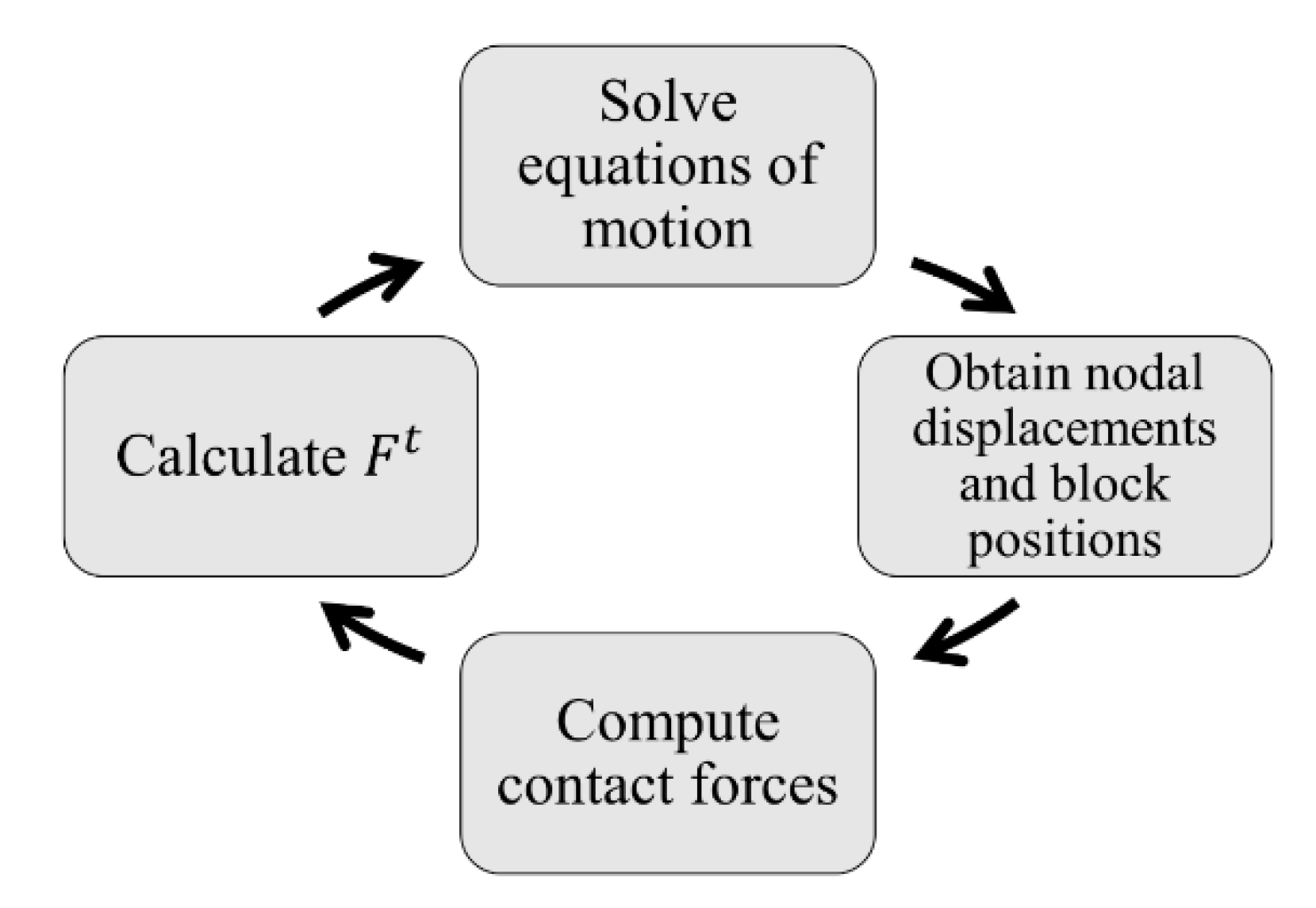
2. Computational Framework

The employed modeling strategy, discrete element method (DEM), is developed by Cundall [7] in the early 1970s to analyze the progressive collapse mechanism of the jointed rock masses. Since then, DEM has been applied to various engineering disciplines ranging from micro- to macro-scale. Fundamentally, DEM was developed to explore the mechanical behavior of the discontinuous systems by considering them as an assembly of rigid and/or deformable blocks, interacting with each other through the contact points. Deformability of the blocks is introduced by constant strain tetrahedral element (CST) discretization of the block, referred to as finite-difference zones, that may be considered as an internal mesh.

In DEM, the mechanical interaction between the adjacent polyhedral blocks is simulated based on the point contact hypothesis [8], as shown in Figure 2. The random generation of the polyhedral blocks is performed using an open-source software package NEPER. The interested readers can access the mathematical background and applications of this software in related sources [9,10,11,12,13]. The elastic response of the contact is controlled by the orthogonal springs both in the normal and shear directions, based on the assigned contact stiffness $k_n$ and $k_s$, respectively; whereas the post-peak behavior is governed by the nonlinear parameters, namely tensile strength ($f_T$) defined in the normal direction and cohesion ($c$) as well as the friction angle ($\varphi$) in the shear direction (see Figure 2). In the present study, semi-rigid blocks are used considering relatively high stiffness at the finite-difference zones (i.e., 10 times macro elastic stiffness) to lump the linear and nonlinear displacements at the joints as performed in relevant studies [3,6,13]. Therefore, deformations develop at the joints (i.e., along the boundaries of adjacent polyhedral blocks) instead of within the block domain and block deformations have negligible influence on the macro stress–displacement behavior of the system.

The computational procedure of DEM relies on the explicit integration scheme of the equations of motion for the nodal points. The governing equations of motion are solved using the central difference method and turn into a compact form (see Equation (1)), evaluated at the mid-time intervals ($t^{+}=t+\Delta t/2$, $t^{-}=t-\Delta t/2;$ $\Delta t:$ time step).

$$\begin{gathered} {\dot{u}}_i^{t+}={\dot{u}}_i^{t-}+\left[\Sigma F_i^t-{\left(F_d\right)}_i\right]\frac{\Delta t}{m} \\ {\left(F_d\right)}_i=\lambda \left|F_i^t\right|sgn({\dot{u}}_i^{t-}) \end{gathered}$$

(1)

where $m$, $\dot{u}$, and $F$ are the nodal mass, nodal velocity vector, and the resultant nodal force vector, respectively. The resultant nodal force vector is calculated as the sum of the external forces, contact forces, gravity forces, and the contribution to the internal stress in the zones adjacent to the nodes. Furthermore, $F_d$ and $\lambda$ denote the damping force and dimensionless damping constant (default value is 0.8). Note that local type of damping is applied during the analyses, which is proportional to the magnitude of the unbalanced force ($\left|F_i^t\right|$) and applied to the opposite direction of the velocity vector [14]. Thus, the damping force varies from one point to another in the model, depending on the magnitude of the unbalanced force. Once the nodal velocities are computed, nodal displacements ($\Delta u_i={\dot{u}}_i^{t+}\Delta t$) are obtained to update the position of the blocks. Accordingly, the contact stresses, developing among the adjacent blocks, are calculated based on the defined contact stress–displacement laws then multiplied with the contact area to be utilized in Equation (1). It is worth noting that small displacement theory is assumed through the computational procedure; thus, only initially established contacts are taken into consideration and updated during the analyses. At each time step, elastic stress increments ($\Delta \sigma , \Delta \tau$) are computed using the relative contact displacements ($\Delta u_n, \Delta u_s$) and added to the previous contact stresses (${\sigma }^{old}, {\tau }^{old}$) to obtain the new ones (${\sigma }^{new}, {\tau }^{new}$) as expressed in Equation (2).

$$\begin{gathered} {\sigma }^{new}={\sigma }^{old}+\Delta \sigma ; \Delta \sigma =k_n\Delta u_n \\ {\tau }^{new}={\tau }^{old}+\Delta \sigma ; \Delta \tau =k_s\Delta u_s \end{gathered}$$

(2)

Moreover, the dilatancy is taken into account upon the shear failure at the contact point, considering the dilation angle (ψ) to modify the normal stress increment as follows; $\Delta {\sigma }_{Total}=\Delta \sigma +k_n\Delta u_{s}tan\psi$. The numerical stability of the explicit integration scheme is ensured by utilizing a sufficiently small time-step during the analysis, calculated as follows.

$$\Delta t=2\sqrt{m/k_{gp}}$$

(3)

where $k_{gp}$ denotes nodal stiffness obtained by adding zone and contact stiffness [15]. Hence, the computational procedure is executed in a cyclic manner, presented in Figure 3, until the quasi-static equilibrium is reached at the discontinuum system.

Throughout this research, a commercial discrete element code 3DEC, developed by Itasca, is used, where the custom contact constitutive models are adopted into the software (3DEC) via a user-defined constitutive model option [16].

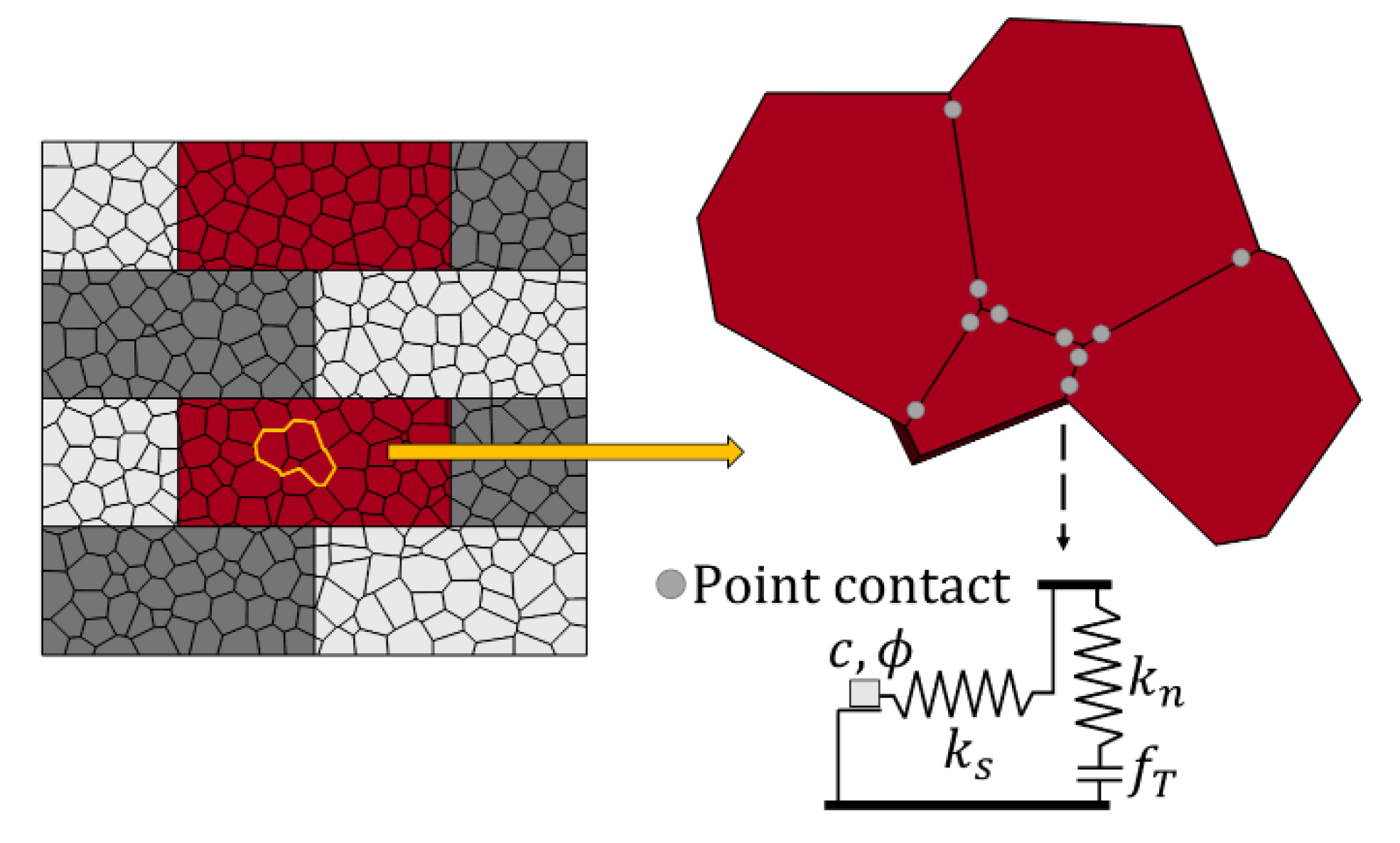
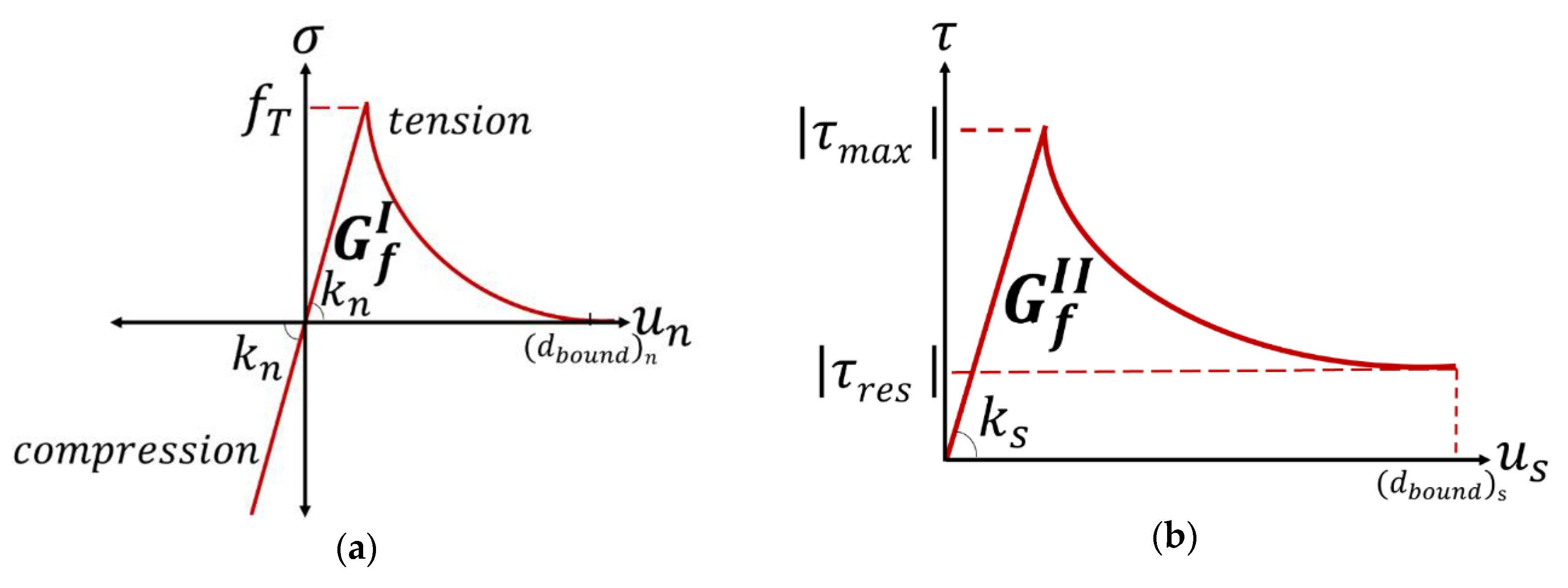
2.1. Contact Constitutive Models

As mentioned earlier in the article, the linear response (elastic deformation) of the discrete models is controlled by the contact stiffnesses (normal and shear springs), which can be computed by Equation (4), given in [17,18].

$$k_n=E/t;k_s=G/t$$

(4)

where $t$ indicates the average thickness of the fracture zone, whereas $E$ and $G$ denote the macro elastic and shear modulus of masonry, respectively. Contact stiffness values have an inverse relationship with the thickness of the fracture zone (or the number of blocks), which means that the contact stiffness increases with a higher number of blocks, as discussed in the literature [13]. In the nonlinear regime, computed contact stresses are updated based on the defined failure criteria. Typically, most discrete element models consider sudden stress drops at the contact points in the normal direction (i.e., zero tensile strength is adopted, or the contact is deleted after the contact stress reaches the ultimate stress) and residual shear strength upon the sliding failure. However, softening behavior (i.e., a gradual decrease of stress with increasing deformation) is a salient feature of the quasi-brittle materials (e.g., concrete, mortar, clay brick, and rock) due to a process of progressive internal crack growth [19,20]. To address this gradual degradation and the corresponding decrease in the load carrying capacity of the material, nonlinear contact constitutive models are implemented in 3DEC to be utilized in tension and shear failure criteria considering exponential softening functions (Figure 4). The mathematical formulations of the exponential functions, given by Lourenço et al. [21], and further details about the contact models can be found in the related study [6]. It is important to note that the Coulomb slip joint model is utilized in the shear direction, where the maximum and residual shear strengths are calculated as written in Equation (5), and the descending branch beyond the peak is defined via softening of the cohesion [22]. Once the contact stress reaches its capacity, the implemented contact models are activated and updated (new) contact stresses are calculated. The contact models (linear and polynomial softening) developed by the authors are available online and free to download for all 3DEC users [23].

$${\tau }_{max}=c_0+tan{\varphi }_0 \sigma ; {\tau }_{res}=c_{res}+tan{\varphi }_{res} \sigma$$

(5)

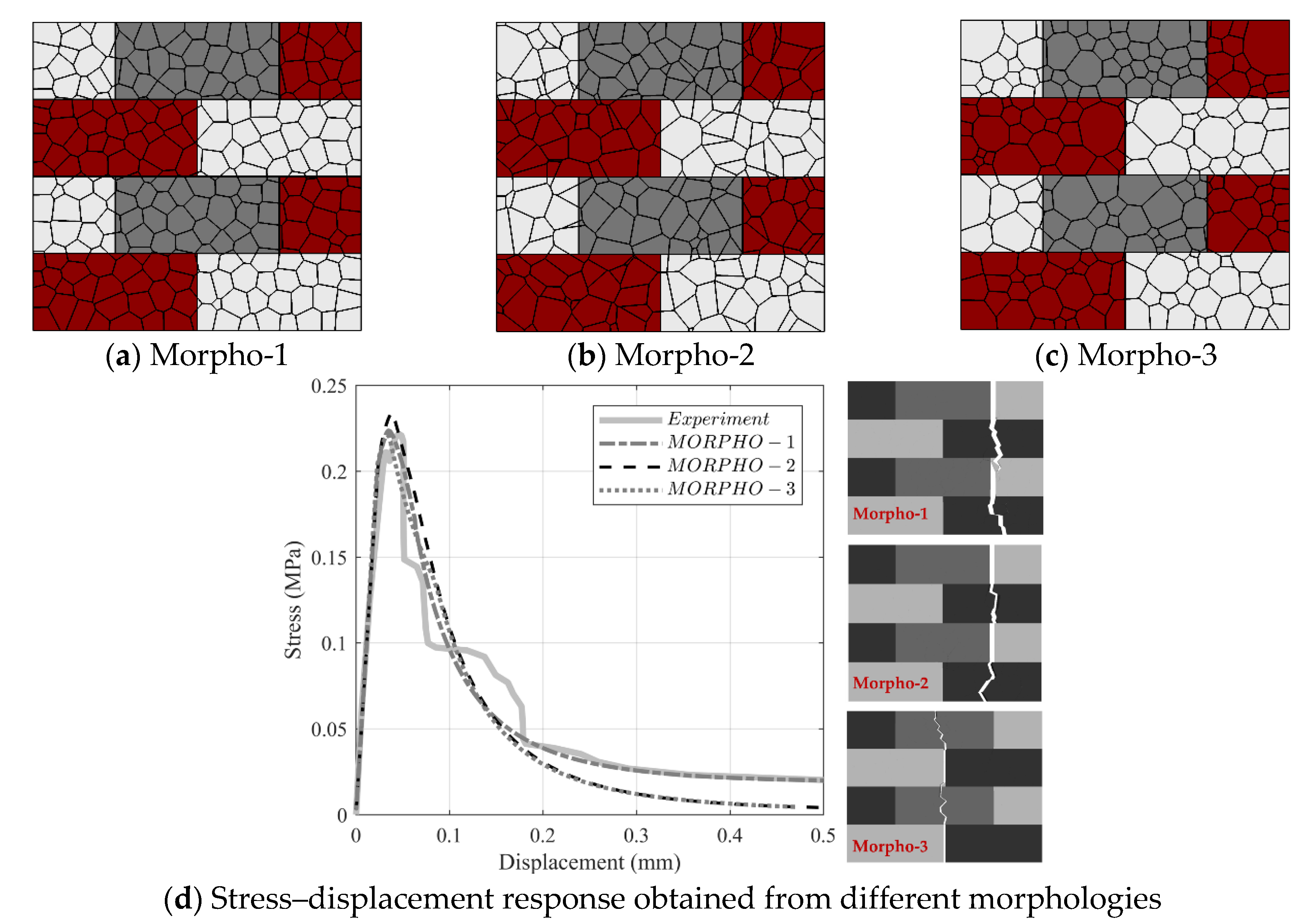
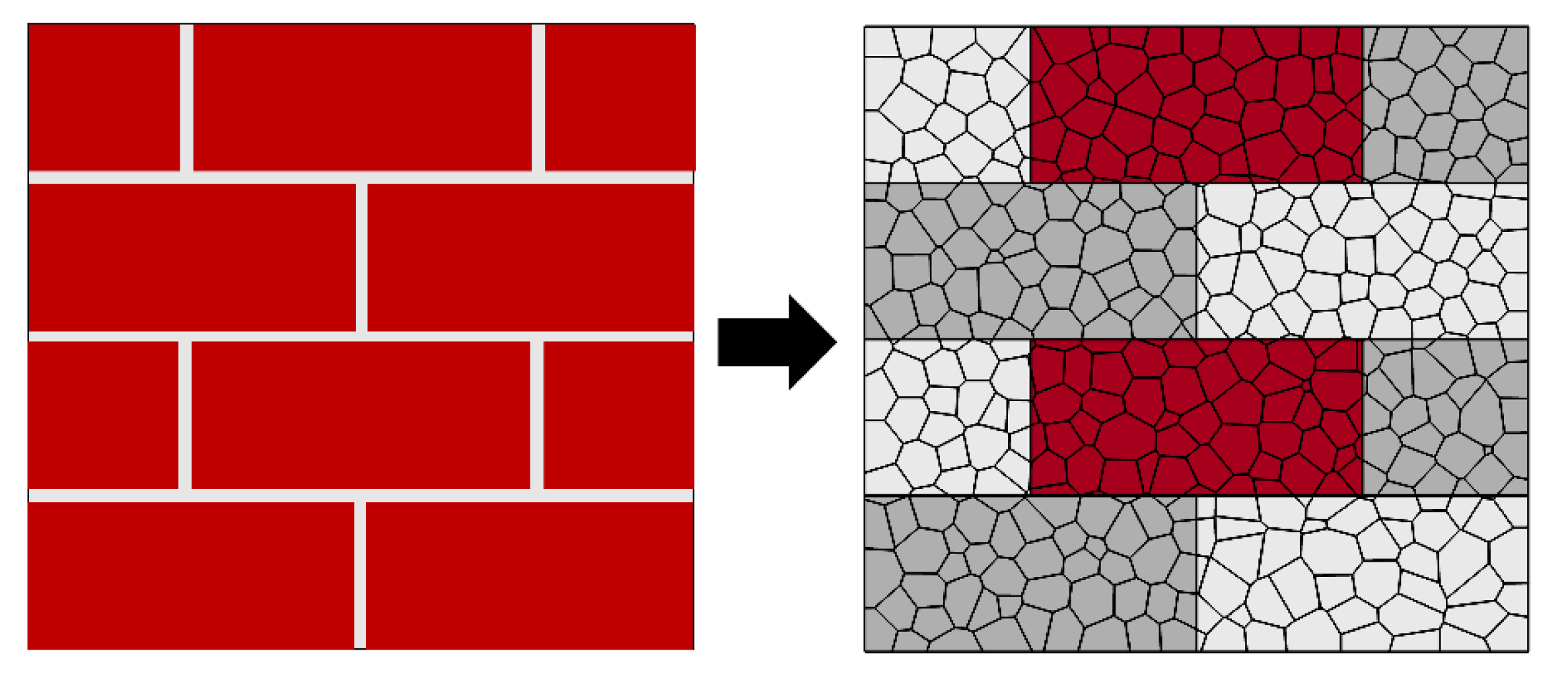
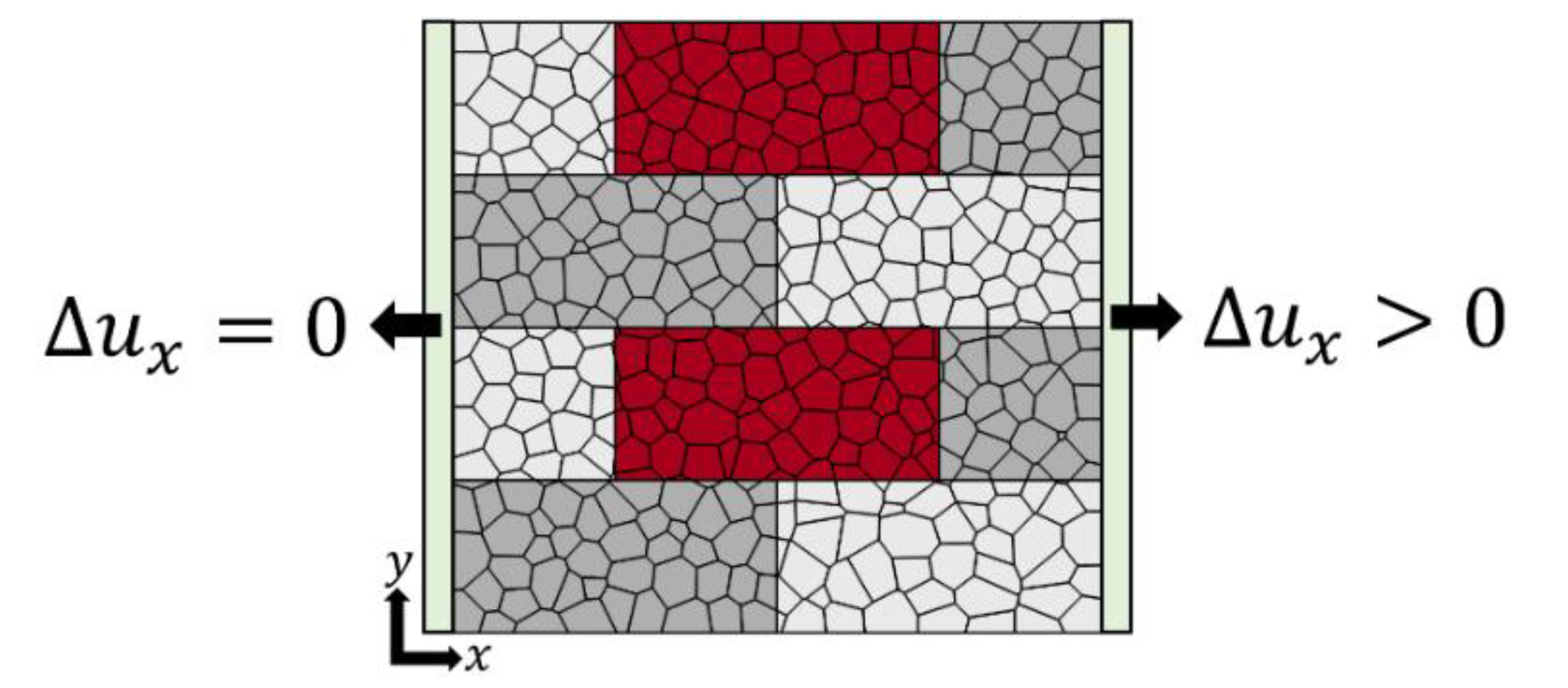
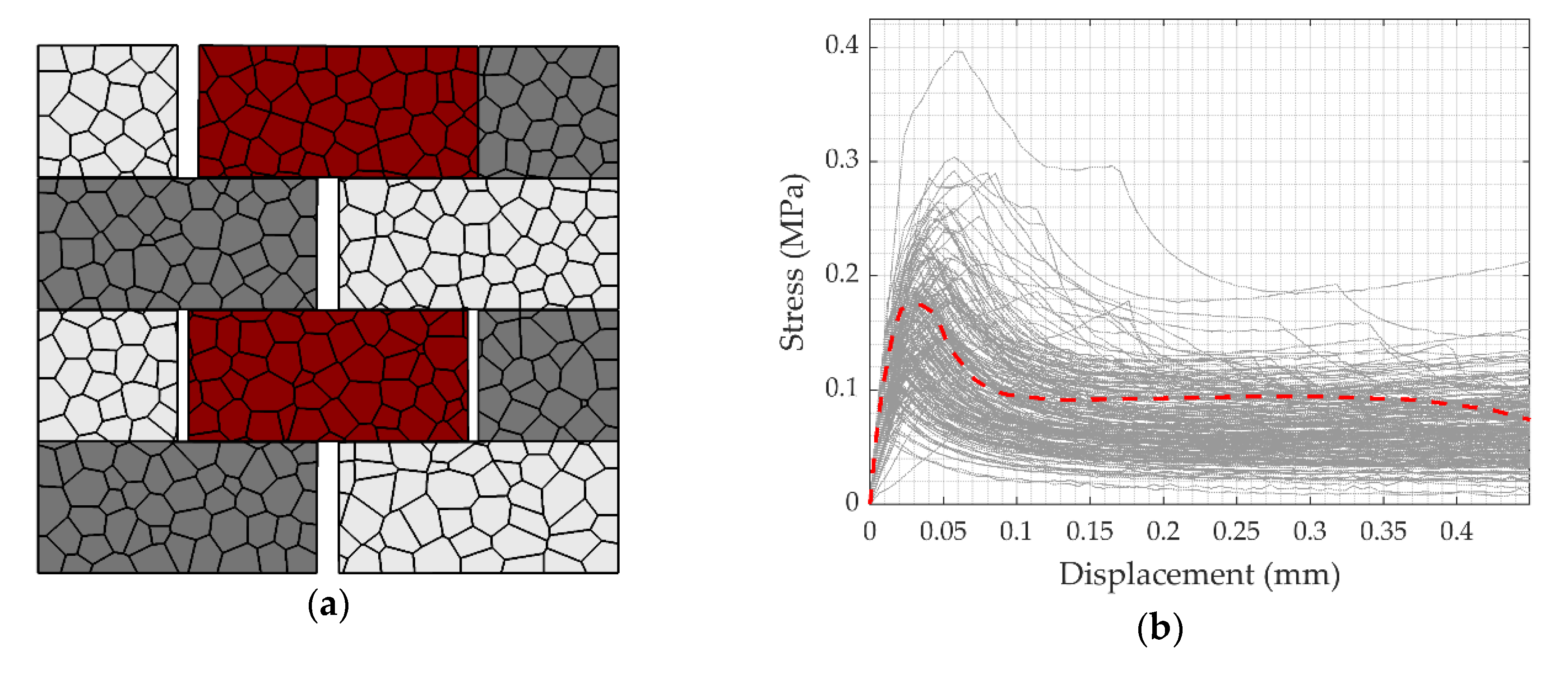
2.2. Benchmark Study and Testing Setup

The cracking mechanism of masonry depends on the mechanical properties of its constituents and their interactions. However, most experimental studies are related to the tensile response of masonry components (i.e., bricks) and tension perpendicular to the unit–mortar interface [24,25]. There are a limited number of works available in the literature related to the tensile response of masonry parallel to bed joints [26].

In this research, the well-known test setup and experimental results, presented by Backes [2], are used as the benchmark study, where different types of masonry units and mortar combinations were tested. Throughout the testing program, masonry wallettes, composed of four courses of units with unit dimensions of 240 mm × 115 mm × 113 mm, were subjected to uniaxial tensile forces applied through steel plates that were glued to both sides of the wallette. In Figure 5, an illustration of the test setup and boundary conditions are demonstrated on the discontinuum model, in which the lateral deflections are imposed to the right-hand side of the specimen while the opposite side is restricted. Specifically, the constant nodal velocities are prescribed for all gridpoints at the right-hand side of the specimen, whereas gridpoints at the opposite side are restricted in the horizontal direction. To ensure the numerical stability during the analysis, a relatively low displacement rate (i.e., 1 mm/s) is defined at the gridpoints, allowing to obtain a smooth response from the numerical solutions as discussed in [27]. Reaction forces are extracted from gridpoints, in which the constant velocity is applied, via the implemented subroutine in the software based on FISH functions (an executable programming language in 3DEC).

The experimental findings show that two failure mechanisms develop depending on the type of masonry constituents: (i) tensile and shear debonding at the unit–mortar interfaces (failure mode I) and (ii) tensile failure in the mortar joint and cracking at the units (failure mode II). The former was obtained when the weak mortar joint with strong masonry units was used, whereas the latter was observed when weaker masonry units and relatively strong mortar joint were utilized. Typical failure patterns obtained from the experiment are shown in Figure 6a. Furthermore, these two failures modes led to different stress–displacement (or stress–strain) curves, where the failure mode I resulted in an approximately constant residual stress after the peak due to interlocking effect of the units and friction, and the failure mode II demonstrated a sharp descending branch after the maximum tensile stress was obtained (see Figure 6b), as typical in quasi-brittle materials such as concrete. For further details about the testing, readers are referred to [2].

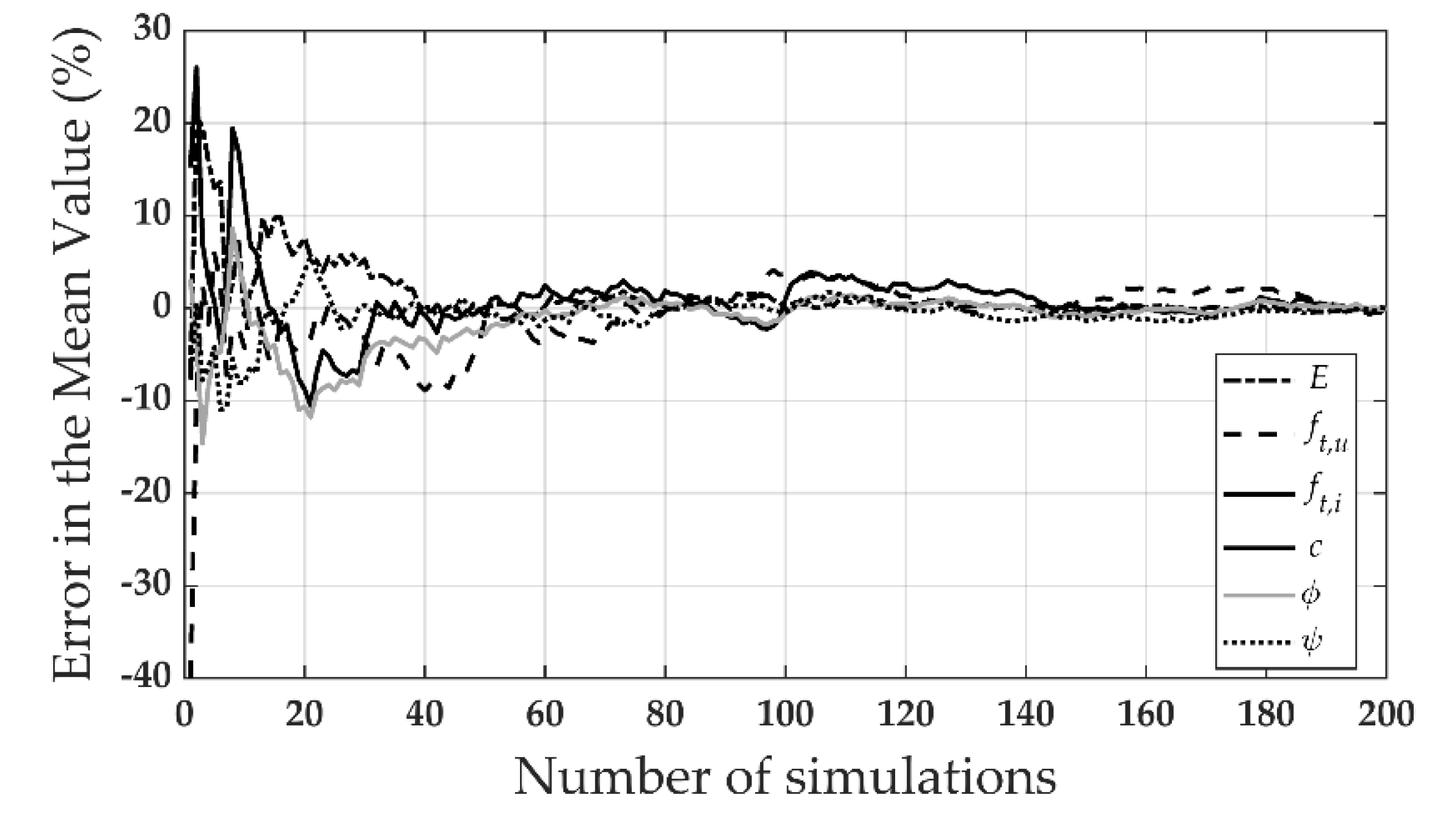
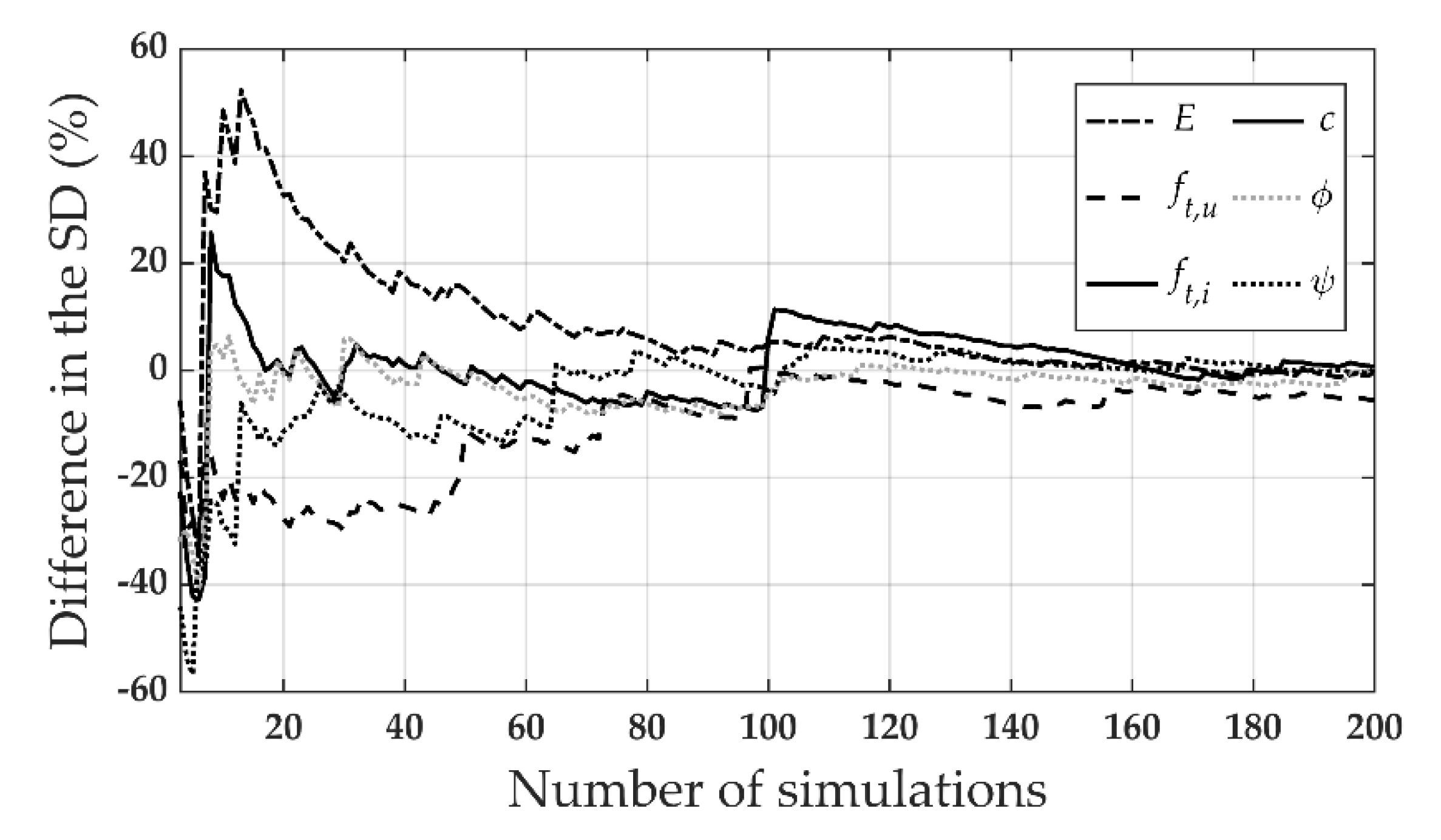
3. Statistical Representation of the Material Properties

The elastic modulus of the masonry assembly ($E$), the tensile strength of the masonry unit ($f_{t,u}$), the bond (unit–mortar interface) tensile strength ($f_{t,i}$), bond cohesion ($c$), the friction angle ($\varphi$), and the dilation angle ($\psi )$ are the random variables considered in the probabilistic analyses. The mean values of variables are either obtained from the experimental data (if applicable) [2] or adopted from similar tests, presented in the literature [22,28,29]. Furthermore, the residual friction angle (${\varphi }_{res}$) is taken as 20% less than initial friction angle ($\varphi$) for all the joints.

The normal distribution is determined for the contact friction angle and the elastic modulus of masonry following the examples in literature [30,31,32,33], while lognormal distribution is assumed for the other parameters. The distributions of the random variables and their parameters are presented in

Table 1. Random variables and their distributions for the strong unit–weak bond (SU-WB).

Random Variable	Prob. Distribution	$\mathbf{Mean} \left(\mathit{\mu }\right)$	Coeff. of Variation	$\mathbf{Lognormal} \mathbf{Mean} \left({\mathit{\mu }}_{\mathit{l}\mathit{n}}\right)$	$\mathbf{Lognormal} \mathbf{Std} \mathbf{Dev} \left({\mathit{\sigma }}_{\mathit{l}\mathit{n}}\right)$
$E$ (GPa)	Normal	4	0.30	N/A	N/A
$f_{t,u} \left(\mathrm{MPa}\right)$	Lognormal	1.0	0.45	−0.0922	0.4294
$f_{t,i} \left(\mathrm{MPa}\right)$	Lognormal	0.10	0.45	−2.3948	0.4294
$\varphi$ (degrees)	Normal	35	0.30	N/A	N/A
$c \left(\mathrm{MPa}\right)$	Lognormal	0.15	0.45	−1.9893	0.4294
$\psi$ (degrees)	Lognormal	2	0.30	0.6501	0.2936

and

Table 2. Random variables and their distributions for weak unit–strong bond (WU-SB).

Random Variable	Prob. Distribution	$\mathbf{Mean} \left(\mathit{\mu }\right)$	Coeff. of Variation	$\mathbf{Lognormal} \mathbf{Mean} \left({\mathit{\mu }}_{\mathit{l}\mathit{n}}\right)$	$\mathbf{Lognormal} \mathbf{Std} \mathbf{Dev} \left({\mathit{\sigma }}_{\mathit{l}\mathit{n}}\right)$
$E$ (GPa)	Normal	4	0.30	N/A	N/A
$f_{t,u} \left(\mathrm{MPa}\right)$	Lognormal	0.25	0.45	−1.4785	0.4294
$f_{t,i} \left(\mathrm{MPa}\right)$	Lognormal	0.20	0.45	−1.7016	0.4294
ϕ (degrees)	Normal	35	0.30	N/A	N/A
$c \left(\mathrm{MPa}\right)$	Lognormal	0.30	0.45	−1.2962	0.4294
$\psi$ (degrees)	Lognormal	2	0.30	0.6501	0.2936

for the strong unit–weak bond (SU-WB) and weak unit–strong bond (WU-SB) systems, respectively. Note that the shear contact parameters for the masonry units (i.e., cohesion ($c_u$) and friction angle (${\varphi }_u$)) are kept constant throughout the analyses, where $c_u=1.5f_{t,u}$ and ${\varphi }_u=45°$, respectively. Moreover, mode-I and -II fracture energies are computed based on the tensile strength and cohesion parameters, as suggested in [34,35].

Dependency between the random variables is considered via the correlation coefficient, which is a linear dependency ratio. A strong relationship among $f_{t,i}$, $c,$ and $\varphi$ is assumed and defined by 85% correlation, whereas a moderate relationship between $E$ and $f_{t,u}$ is represented by a 50% correlation. With the predefined statistical distributions and the correlation between the random variables, the Latin Hypercube Sampling (LHS) method is used to derive sample values for the simulations. The LHS method reduces the variance in the Monte Carlo Simulation and, thus, lowers the number of required simulations [36,37]. For each case (SU-WB and WU-SB), 200 simulations—400 simulations in total—were conducted to derive the random parameters. In Figure 7, the graphical illustration of the input variables for WB-SM, together with the corresponding histograms and probability distributions, is presented.

The number of simulations is determined by monitoring the relative difference between the mean values after a number of simulations with the prescribed mean values in Table 1 and Table 2. The percentage of the error is used to express the relative difference. The magnitude of the difference in the mean and standard deviation values after “j” simulations can be tracked in Figure 8 and Figure 9. As can be seen from these figures, the final values of the errors/or differences are smaller than 0.1% for most of the random variables.

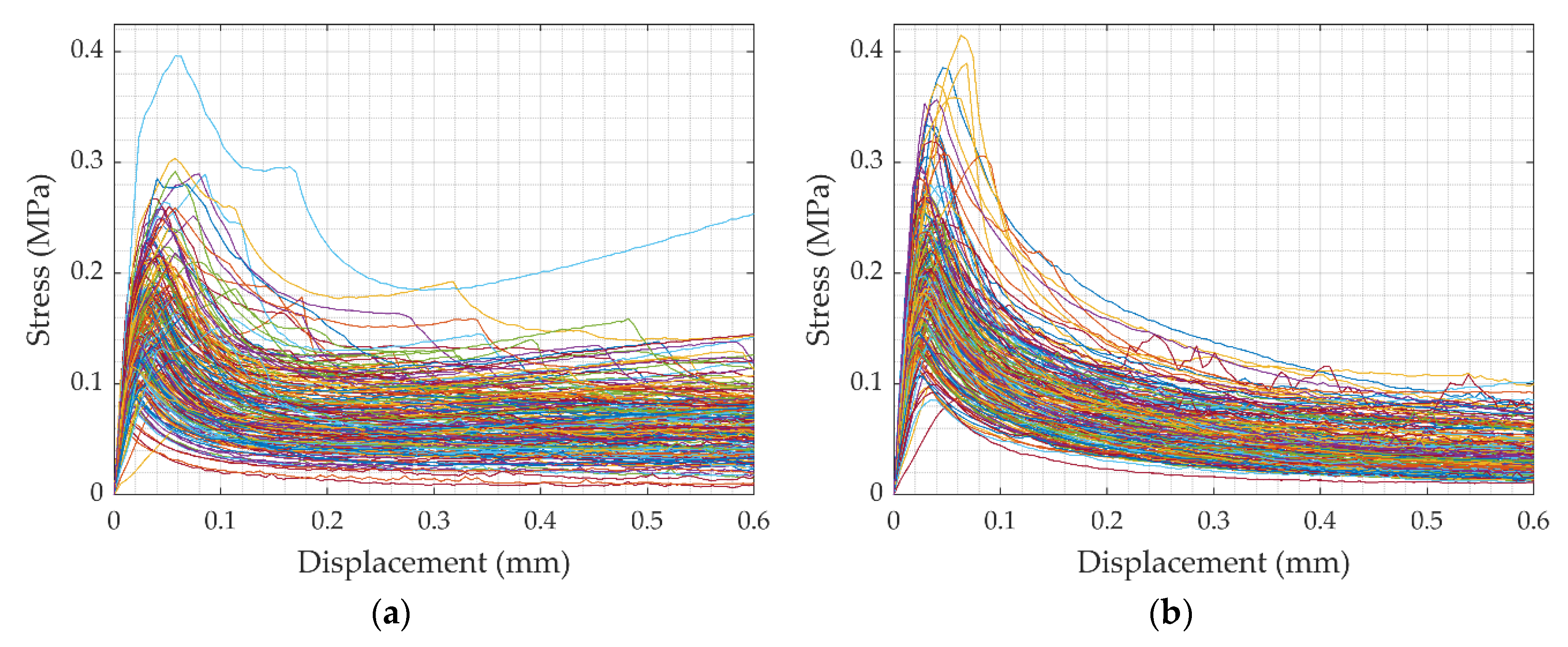
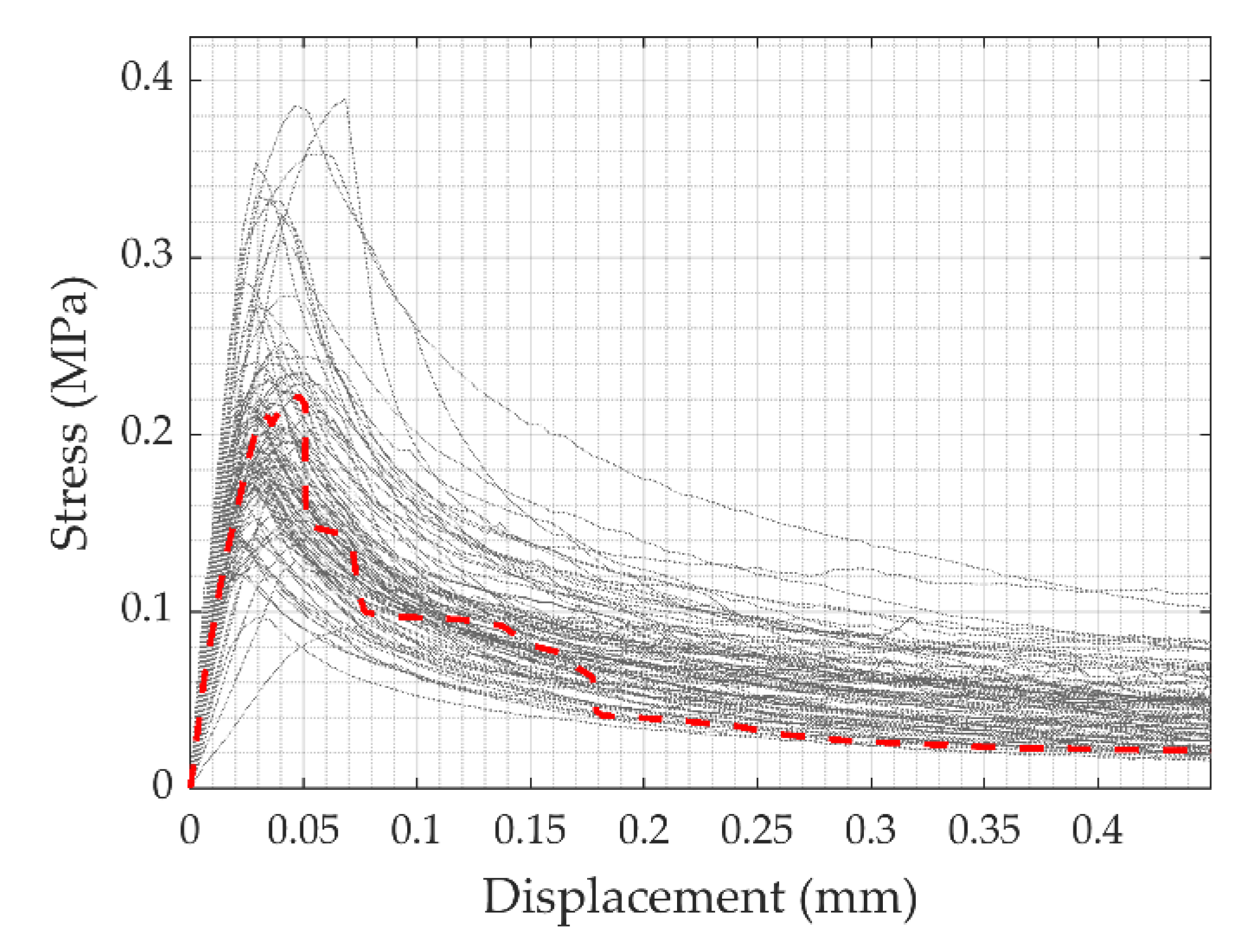
4. Results of the Computational Models

In this section, the results of the computational models are presented. A range of values for input parameters ($E,f_{t,u},f_{t,i},c$, and $\varphi$) are established for each simulation described in the previous section, using statistical methods. The results of the analyses clearly show that the macro behavior of the masonry wallettes reveals two separate stress–displacement trends corresponding to SU-WB and WU-SB combinations, presented in Figure 10. As mentioned earlier in the article, similar stress–displacement behaviors were also noted from the experimental observations. Moreover, readers may find a brief discussion regarding the effect of block size and shape provided in the Appendix A.

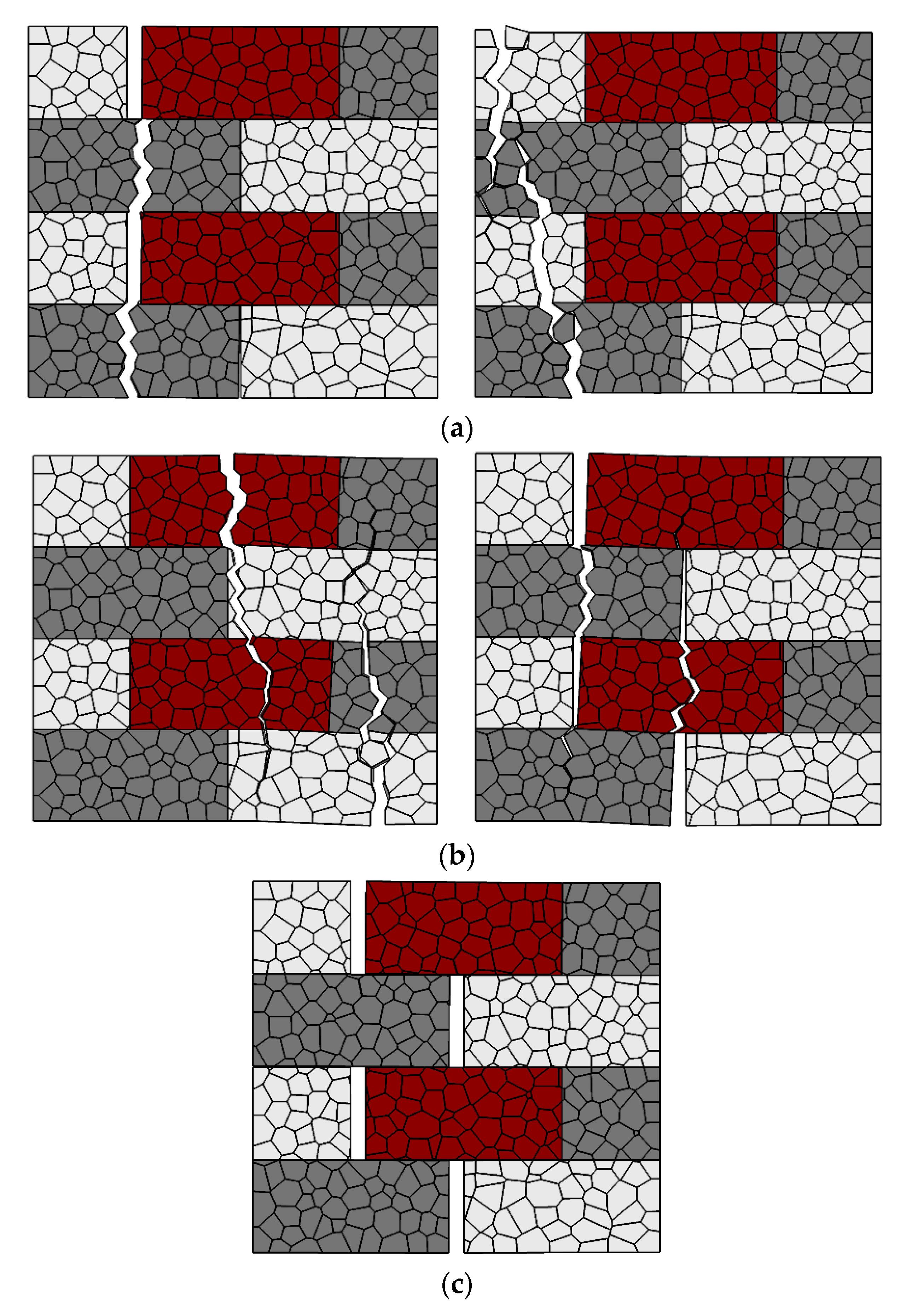
4.1. Failure Mode I: Strong Unit–Weak Bond (SU-WB) Behavior

When the strength of the units is higher than the mortar joints (i.e., strong unit–weak bond system), experimental work demonstrated that the failure mode is governed by the unit–mortar interfaces. A typical failure (denoted as mode I) indicates a zig-zag failure pattern, including shear deformations (sliding) at the bed joints and the cracks at the head joints. A similar failure mechanism is successfully obtained using the proposed modeling strategy, shown in Figure 11a. Furthermore, performed stochastic analyses provide a wide range of stress–displacement results depending on the defined contact properties (see Figure 11b). Regarding the fracture pattern, no significant difference is observed during the analysis for this particular set of material properties. Results of the analyses show that there is a 94.8% correlation between the bond strength ($f_{t,i} \mathrm{and} c$) and the overall capacity, and an 81.4% correlation between unit–mortar interface (bond) friction angle ($\varphi$) and the overall capacity (Figure 12). Since the governing mechanism for mode I is concentrated at the bed and head joints, the capacity is strongly affected by bond tensile strength, cohesion, and friction angle, as expected. The strong linear correlation between the tensile capacity and these two modeling parameters even allows capacity prediction without requiring any simulations.

4.2. Failure Mode II: Weak Unit–Strong Bond (WU-SB) Behavior

The second failure mode of masonry wallettes includes more complex fracture patterns compared to mode I. Specifically, when the tensile strength of the masonry units gets close to the bond strength or even smaller than the bond strength, several distinctive fracture patterns are observed via the proposed modeling strategy, categorized as two subgroups (fracture mechanisms) of failure mode II. In the first subgroup, cracks develop through the head joints and units (FM-1 and FM-4 in Figure 13), which was given as a typical fracture pattern in the benchmark study. On the other hand, in the second subgroup, only the units fail under tension, corresponding to the condition where the bond tensile strength is higher than the tensile strength of the masonry units ($f_{t,i}>f_{t,u}$), denoted as FM-2 and FM-3 in Figure 13. In addition, a typical sliding mechanism (same as the mode I) is obtained from the discontinuum models, reflecting the SU-WB combination (Figure 13c). However, this should be expected depending on the determined data set and statistical distribution, in which there is a chance to assign contact properties, where the masonry units may have relatively higher tensile strength than the bond ($f_{t,i}\ll f_{t,u}$). Fracture simulations of FM-1 and FM-2 are shared as video at the supplementary documents.

In the benchmark study, FM-1 was presented as the typical fracture pattern for strong bond masonry wallettes, mentioned in Section 2.1. Our results also show that FM-1 has the highest probability with 43%. In order to compare the stress–displacement curves obtained for FM-1 from the discontinuum analyses, with the experimental result, they are plotted in the same graph in Figure 14. This comparison demonstrates that the determined response envelope for the range of input material properties in DEM is in good agreement with the experimental findings and can be considered representative of possible dispersion of a larger number of testing series. For instance, in Figure 14, the average trend of the numerical solutions resembles the experimental one, although an exact match is not possible due to assumed statistical distributions of the random parameters.

Furthermore, the influence of contact parameters on the system’s overall capacity is investigated considering each failure mode. The results show that there is a 64% correlation between the unit tensile strength and capacity for WU-SB masonry wallettes, where the dispersion of the relation regarding each specific failure mechanisms can be found in Figure 15a. FM-2 and FM-3 indicate a perfect linear correlation (100%) between the tensile strength of the unit and the capacity, while the scattered distribution of the data is related to the mechanisms involving the bond failure (Figure 15a).

A similar correlation factor, 65%, is obtained for the bond tensile strength ($f_{t,i}$) and the ultimate load-carrying capacity. Note that, for bond tensile strength, FM-1 and FM-5 present 92% and 99% correlation, whereas a more scattered data cloud is noted for FM-2 and FM-3 since these failure modes are directly related to the cracking in masonry units (see Figure 15b). Finally, the lowest correlation factor, 54%, is computed for the contact friction angle at the unit–mortar interfaces. Given the fact that only the FM-5 reveals a sliding mechanism at the bed joints, there should be a low correlation expected for the other fracture mechanisms (Figure 15c). Partitioning of the modeling parameters for each fracture mechanism allows deriving further correlation with the load-carrying capacity and corresponding failure.

5. Conclusions

In this research, a stochastic discontinuum analysis is performed within the discrete element method framework to analyze the diverse fracture mechanism of masonry wallettes subjected to tension parallel to the bed joints. According to the results of the analyses, the following conclusions are derived.

• The proposed modeling strategy allows detailed and realistic (based on comparison with experimental results) fracture patterns of masonry wallettes. This is accomplished by representing the masonry components (masonry units and unit–mortar interfaces) using mechanically interacting discrete polyhedral blocks.
• The inherent uncertainty in the mechanical properties of masonry constituents yields various possible fracture mechanisms. Through this research, all possible fracture patterns of masonry wallettes under tension parallel to bed joints are explored. There is a great economy in performing such a comprehensive study computationally instead of a very broad and costly experimental campaign.
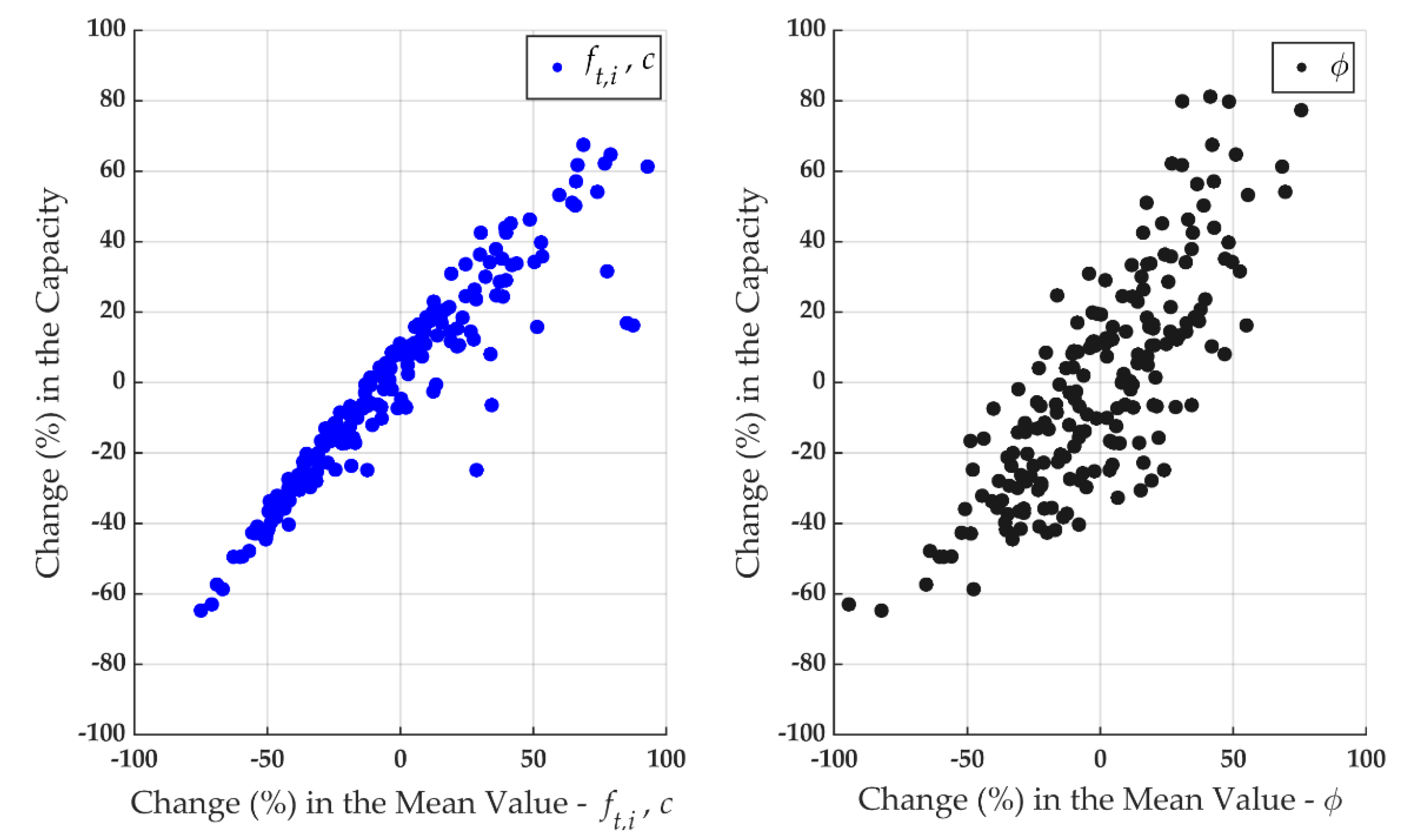
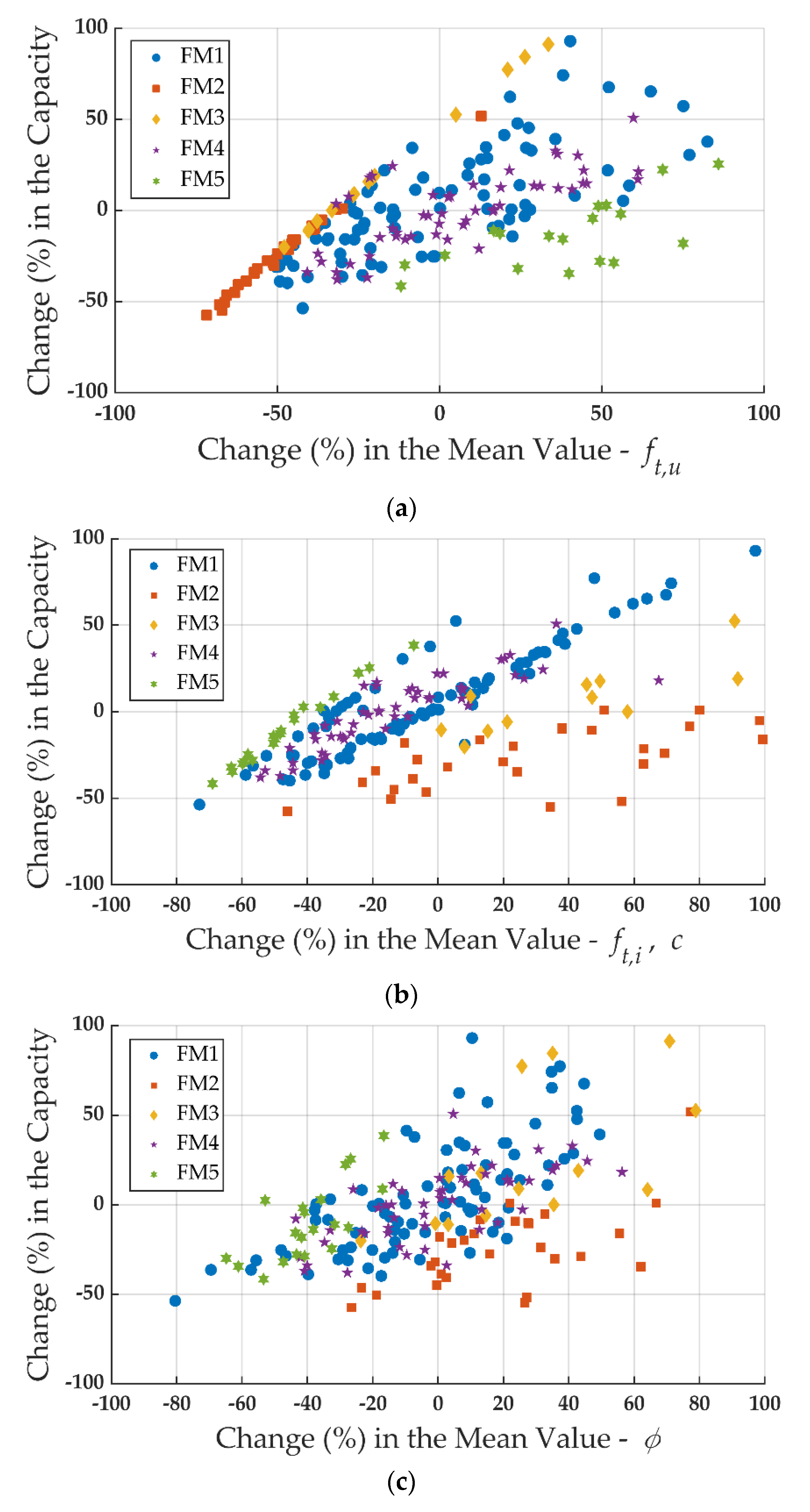
• Stochastic analyses enable us to attain the dispersion of the load-carrying capacity concerning the modeling parameters ($E,f_{t,u},f_{t,i},c$, and $\varphi$). They highlight both the direct and indirect influence of these parameters on the fracture patterns and stress–displacement behavior. Direct correlation of the parameters such as the bond tensile strength, friction angle, or the unit tensile strength with the capacity reflects the physically expected phenomena. In the future, results of these determined correlations can be used to estimate the capacity of different arrangements of masonry materials without using numerical simulations and may lead to the derivation of new empirical formulas to predict the tensile capacity of masonry parallel to bed joints.
• For the given probability distributions of the material parameters, the fracture mechanisms and their likelihood have been found. Moreover, the influence of the modeling parameters on the tensile strength of masonry has been quantified. However, it should be noted that the results presented within this study may be restricted to the statistical distributions and the parameters used.

Currently, the practical applications of this work are restricted to the capacity prediction concerning the change in the modeling parameters for specific fracture mechanisms. Future studies (both experimental testing and stochastic numerical analyses) considering different material properties and masonry unit sizes will help define reference values and empirical equations for tensile strength prediction, which can then be used directly by practitioners. A further step ahead would be using statistical learning methods to predict both the fracture mechanism and the tensile strength in the multi-dimensional parameter space.