1. Introduction
Multilayer composite beams, plates and shells are today widely employed in several fields of engineering, for example in the aerospace, naval, automotive and biomedical sectors, among others [
1]. The reason for their success is largely related to the possibility of achieving excellent stiffness-to-weight and strength-to weight ratios and especially to the possibility of tailoring such properties with respect to the application features, e.g., following the load paths, so as to increase the overall structural efficiency in terms of weight.
The availability of techniques for manufacturing composite laminates employing layers with multi-physics properties has led to the concept of smart laminates, in which different laminae may exhibit couplings between different physical fields, e.g., mechanical, thermal, electric, magnetic or even a combination of more than two of such fields, thus enabling the design of devices with multifunctional capabilities, besides the basic structural employment [
2,
3,
4,
5]. A remarkable example is provided by piezoelectric materials and laminates that, exploiting the coupling between the mechanical and electrical fields, may be employed in several applications of engineering or scientific interest [
6,
7,
8,
9].
The width of the available design space for this kind of multi-physics multilayer materials, deriving from the variety of properties of the individual laminae and from the layup flexibility, induces the need of a preliminary careful assessment of the properties of the assembled laminate: their heterogeneous nature, the mismatch of material features between contiguous layers and the variety of external loading condition may indeed result in complex multi-physics states that, if not carefully designed, may lead to unwanted behaviors or unforeseen damage/failure patterns.
For such a reason, several analytical, numerical and computational methods have been developed for the analysis of multilayer composites. The reconstruction of the fields (mechanical, thermal, electrical, etc.) within the laminate is a fully three-dimensional problem for which analytical solutions are available only for basic configurations: in general engineering applications, the employment of numerical/computational methods is then necessary. Besides fully three-dimensional approaches, which may be employed to capture complex localized field details (see, e.g., [
10]), thin and relatively thick multilayered composite structures have been investigated using suitable plate theories, which are based on specific assumptions about the behavior of some specific field components throughout the laminate thickness and allow reducing the total number of unknowns and thus the computational cost associated with the numerical models: familiar examples are provided by the Kirchhoff and Mindlin kinematic assumptions in the case of purely structural plates, while also the coupling with the electric fields must be considered in piezoelectric plates (see, e.g., [
1,
11]).
The structural theories for laminated plates may be classified into
equivalent-single-layer (ESL) and
layer-wise (LW) models, which have been used for both elastic and multi-physics plates [
12,
13,
14,
15]. ESL models are based on an initial expression of some unknown fields, e.g., displacements in elastic plates or displacements and electric potential in the case of piezoelectric plates, in terms of a sum of individual contributions given by the products of known through-the-thickness functions and unknown in-plane functions, where the through-the-thickness functions span the whole thickness of the laminate. LW models differ from ESL ones for the adoption of through-the-thickness functions restrained to individual layers, which must be then complemented by suitable inter-laminar continuity conditions. While ESL models are suitable for capturing global behaviors of the laminate, LW models provide a more accurate representation of the fields on a layer-by-layer basis.
Once an ESL or LW representation of the multi-physics behavior of the structural element is assumed, the reduced equations, expressed in terms of the unknown in-plane functions, must be numerically solved. A popular strategy for the numerical treatment of the problem is based on the employment of a suitable multi-physics, or
generalized, variational statement, providing the weak formulation of the problem, followed by the application of a suitable solution technique, e.g., the finite element method [
13], the Rayleigh–Ritz method [
16,
17,
18] or other similar approaches.
In FEM-based methods, the unknown fields are approximated over each finite element in terms of shape functions and
nodal values and inter-element continuity is ensured by enforcing that contiguous elements share the same nodal values. Although it appears quite natural, this aspect may represent a limiting constraint when high-order, adaptive or non-conforming meshes are adopted. More advanced FE-based methods, which have been developed also for piezo-electric plates and structures, bypass such issues and allow retrieving discontinuous kinematics by resorting to node-dependent fields expansions, in which the generalized structural theory is a function of the node and may vary within the element itself (see, e.g., [
19,
20,
21,
22]).
An alternative approach to a continuous approximation of the solution, and to the mentioned advanced FE strategies with node-dependent kinematics, is provided by the
discontinuous Galerkin (dG)
method [
23], which admits a discontinuous interpolation of the solution among the mesh elements and naturally handles arbitrary meshes, high-order basis functions and contiguous mesh elements with different order of approximation. When compared to the FEM literature, the adoption of dG-based numerical schemes for multilayered plates appears quite limited and mostly focused on the Classical Laminated Plate Theory [
24,
25,
26,
27] or the First-order Shear Deformation Theory [
28,
29]. Recently, Gulizzi et al. [
30,
31] presented dG formulations for ESL and LW theories for elastic plates, whereas, to the best of the Authors’ knowledge, no discontinuous Galerkin formulation for LW theories of piezoelectric plates is available.
In this work, we thus present an interior penalty discontinuous Galerkin formulation for multilayered piezoelectric plates based on a suitable generalization of the Principle of Virtual Displacements, which allows a high-order resolution of the electro-elastic problem. Throughout the thickness, the plate is represented adopting a LW representation, which naturally allows selecting a high-order expansion of the unknown fields within each layer, whereas, within the plate domain, the discontinuous nature of dG schemes allows employing general high-order mesh elements.
The paper is organized as follows. The basic equations of the problem in hand are first recalled in
Section 2, which reviews the generalized formulation of piezoelectricity, the layer-wise formulation for piezoelectric laminates and the related laminates governing equations. The proposed method is formulated in
Section 3. Numerical results on single and multiple layers piezoelectric plates are provided by
Section 4, which is followed by the
Conclusions.
2. Boundary-Value Problem
In this section, the basic equations describing the mechanics of general piezoelectric laminated plates are recalled.
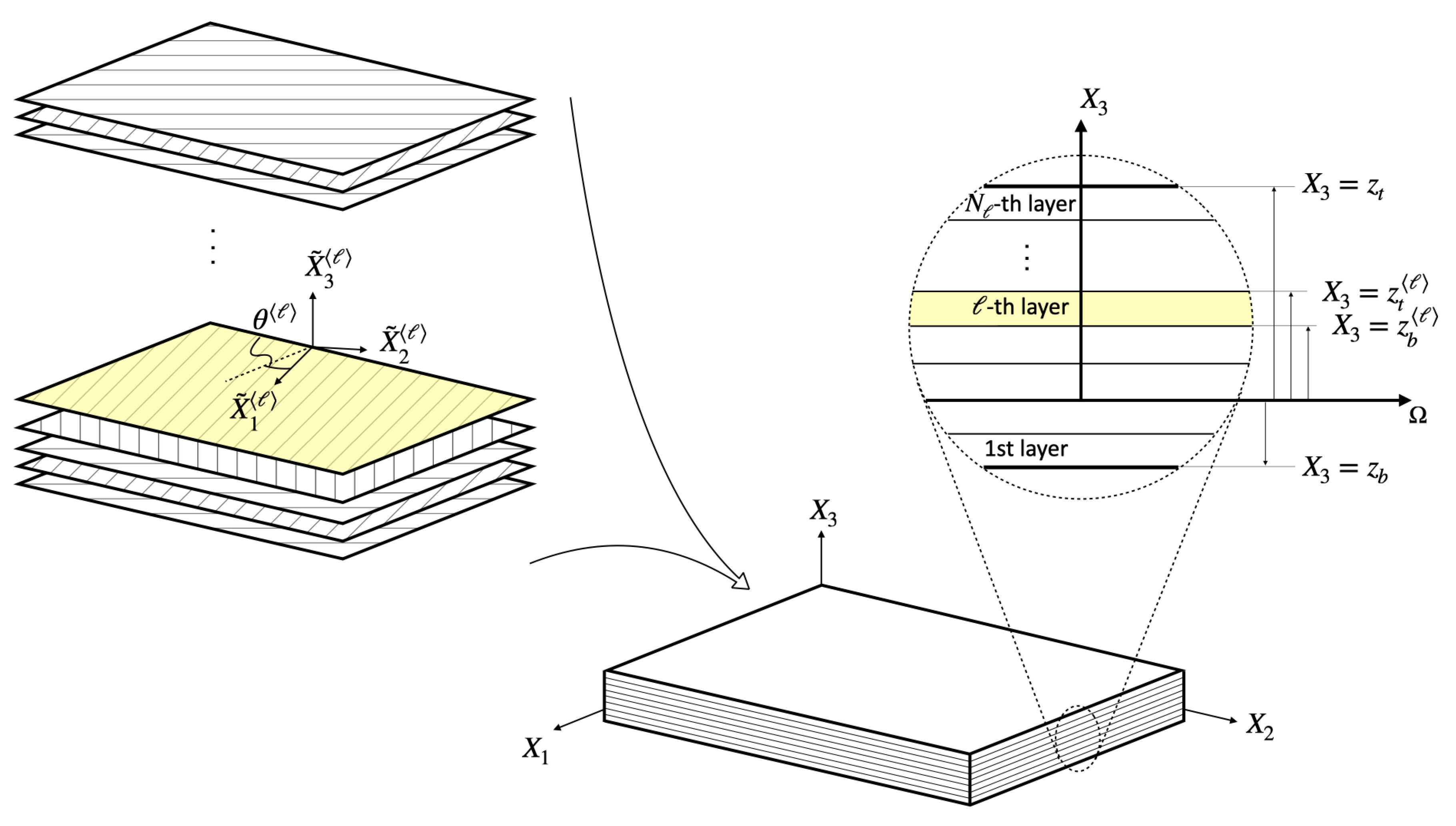
Figure 1 shows a multilayered plate obtained by stacking
suitably oriented piezoelectric layers. In the figure,
denotes the angle between the
ℓth layer’s local reference system
and the plate global reference system
.
The plate lies in the domain , where identifies the height of the plate bottom surface, is the height of its top surface and denotes the modelling domain of the plate spanned by the coordinates . The layers are stacked in such a way that , for , and , being and the coordinates of the ℓth layer’s bottom and top surfaces, respectively. Henceforth, quantities related to the layer ℓ are denoted by the superscript .
The electro-mechanical behavior of the multilayered piezoelectric plates is described in terms of mechanical displacements and electric potential , , which represent the primary variables of the problem.
The gradients of the primary variables, namely the strains
and the electric field
, may be expressed as
where the matrices
,
,
,
,
,
are defined as
and
It is worth noting that, in Equation (
1) and the continuation of the paper, Greek subscripts take value in
and the Einstein’s implicit summation convention over repeated subscripts is assumed.
The problem description is completed by assigning the constitutive relation to its piezoelectric layers, which are assumed to be homogeneous and governed by linear piezoelectricity. Then, the constitutive behavior of the
ℓth layer can be expressed as
where
collects the stress components in the same order as that used for the strain components in
;
collects the components of the electric displacement in the same order as that used for the electric field components in
; and the matrices
,
and
denote, respectively, the elasticity, dielectric and piezoelectric constitutive matrices of the
ℓth layer. Equations (
1) and (
4) can be straightforwardly combined to link the stress
and electric displacement
with the primary variables. It is worth noting that, when the piezoelectric constants are set to zero, decoupled elastic and dielectric behaviors are retrieved.
2.1. Generalized Formulation for Piezoelectricity
The form of Equations (
1)–(
4) suggests the introduction of
generalized quantities (see, e.g., [
32,
33,
34]). More specifically, for the sake of the present formulation, it is convenient to define the
generalized displacement vector
, the
generalized strain vector
and the
generalized stress vector
as
Then, using Equation (
5), Equation (
1) can be rewritten as
while the constitutive relationships given in Equation (
4) become
2.2. Layer-Wise Formulation for Multilayered Plates
Layer-wise formulations for multilayered plates are based on the introduction of suitable assumptions regarding the through-the-thickness behavior of the primary variables [
1,
13]. In this work, the primary variables are collected in the vector
,
, which is assumed to be give by a linear combination of
known thickness functions of the coordinate
and
unknown in-plane functions of the coordinates
. More specifically, the
ith generalized displacement component
of
is written as
where
denotes the order of expansion,
is
kth known thickness function and
is the unknown in-plane function associated to
ith generalized displacement component of the
ℓth layer.
Consistently with the notation introduced in [
30,
31], Equation (
8) can be expressed in matrix form as
where
is a
vector collecting the in-plane functions and
is a
matrix collecting the corresponding thickness functions being
. Further details about the explicit expression of the thickness functions and how the in-plane functions are ordered within the matrix
to satisfy the continuity at the layers’ interfaces can be found in [
31].
Eventually, substituting Equation (
9) into Equations (
6) and (
7) allows expressing the generalized strain vector
and the generalized stress vector
in terms of
.
2.3. Governing Equations
The partial differential equations governing the electro-mechanical behavior of a multilayered piezoelectric plate, modelled according to the LW formulation derived in the previous section, can be obtained from the Principle of Virtual Displacements (PVD) for piezoelectric media (see, e.g., [
35]). For the generic
ℓth layer, the PVD reads
where
is the vector of the mechanical volume forces,
is the body electric charge,
is the vector of the mechanical tractions and
is the surface electric charge. Upon using the generalized notation introduced in Equation (
5), the PVD can be written in a more compact form as
where
denotes the
generalized volume loads and
denotes the
generalized surface tractions.
Substituting Equations (
6), (
7) and (
9) into Equation (
11), one obtains
which represents the PVD for the
ℓth layer of a piezoelectric plate modelled via LW theories. In Equation (
12), the matrices
,
and
are obtained by the following integrals defined over the thickness of the layer
On the other hand,
stems from the generalized volume loads
,
from the generalized surface tractions defined over the bottom surface of the layer and
from the generalized surface tractions defined over the top surface of the layer, i.e.,
Similarly, the generalized surface tractions defined over the lateral surface of the
ℓth layer contribute to the definition of the boundary term
Equation (
12) represents the layer building block allowing to state the generalized PVD for the whole piezoelectric plate. In fact, upon summing over the total number of layers and considering the equilibrium condition
and the zero net surface charge condition
, for
, the PVD for the assembled plate is written as
where the LW assembly technique described in [
31,
36] is employed to define the vectors
,
,
,
and
and the matrices
,
and
. It is worth noting that
collects the
in-plane functions, which are the unknowns of the present LW formulation of piezoelectric plates.
Equation (
16) represents the weak form of the governing equations for the considered problem; eventually, through standard variational calculus, it is possible to obtain the corresponding strong from of the governing equations and the relative boundary conditions as follows
where
is the
th component of the outer unit normal of the boundary
,
are the plate’s volume loads,
are the plate’s prescribed boundary displacements,
are the plate’s prescribed boundary tractions and
and
denote non-overlapping subsets of
over which Dirichlet and Neumann boundary conditions apply.
3. Discontinuous Galerkin Formulation
The equations given in (
17) denote a system of second-order elliptic partial differential equations with suitably defined Dirichlet and Neumann boundary conditions. The derivation of a solution scheme based on the discontinuous Galerkin method generally involves [
23]: (i) the introduction of an auxiliary variable that allows to rewrite the second-order system as a first-order system; and (ii) a weak statement of said first-order system for each element of the mesh discretizing the considered domain. Here, the derivation proposed by Gulizzi et al. [
30,
31] is employed.
The form of Equation (
17) suggests defining as auxiliary variable the quantity
so that the system of equations given in Equation (
17) may be rewritten as
Upon introducing the generic mesh element
and the test functions
, where
is the space of discontinuous vector fields for the considered mesh, the weak statements of the first two equations in (
19) can be written as
and
In Equation (20a,b), denotes the boundary of ; and denote the dG solutions and are in general approximations of the exact solutions and , respectively; and and are the so-called numerical fluxes, which allow recovering the continuity of the solution at the elements’ boundaries.
Different choices of the numerical fluxes lead to different discontinuous Galerkin formulations [
23]. However, prior to giving their explicit expression, it is useful to introduce
and
as the subsets of
where Dirichlet and Neumann boundary conditions, respectively, are to be enforced; furthermore, considering that the mesh discretization introduces a subdivision of the plate domain
, we define
as the part of
that the element
e shares with its neighboring elements. Then, upon employing the interior penalty dG formulation introduced in [
30,
31], the numerical fluxes are chosen as follows
and
where
and
are, respectively, the so-called
average and
jump operators, which are defined at the interface between the element
e and its generic neighbour
. It is noted that the numerical flux
given in (
22) depends on the so-called
penalty parameter
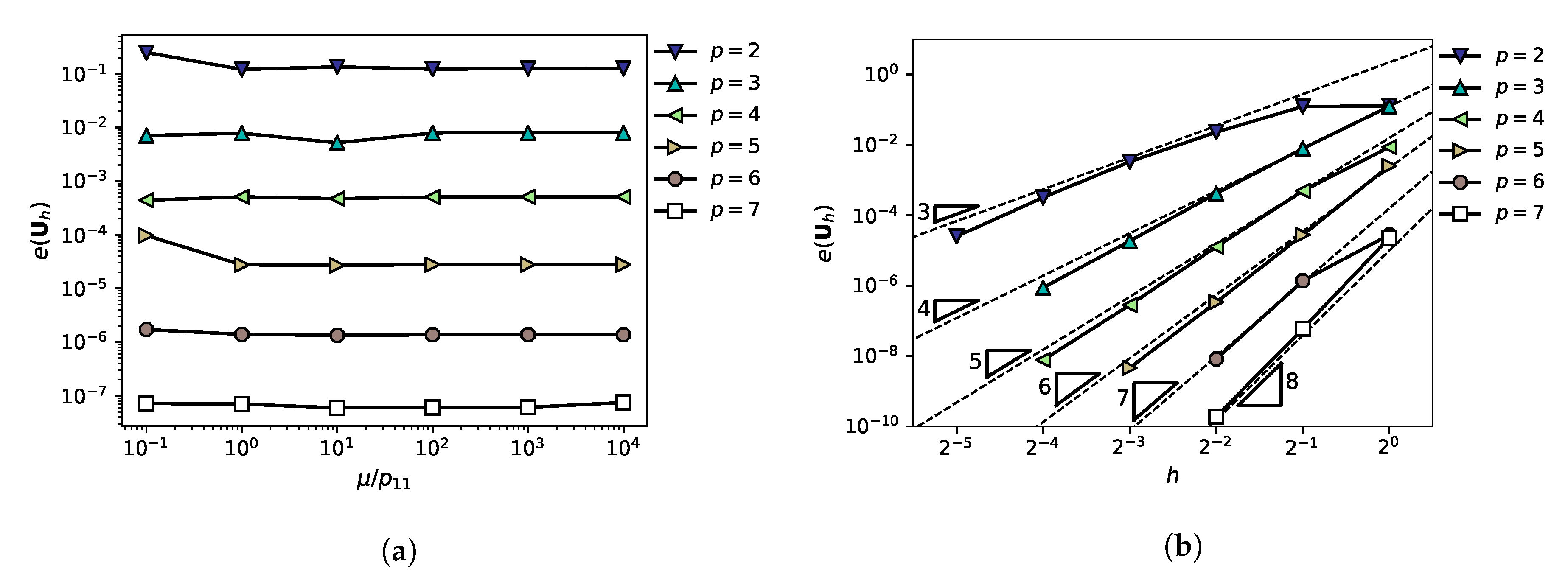
, whose influence on the numerical solution is addressed in
Section 4.
Eventually, upon substituting Equations (
21) and (
22) into Equation (20a,b), respectively, setting
and summing over all the mesh elements, Equation (20a,b) can be combined to obtain the interior penalty dG variational statement for multilayered piezoelectric plates:
where
and
The integrals appearing in Equations (
24) and (
25) are referred to as the
broken integrals and are defined as
and
where
is the total number of mesh elements,
is the total number of inter-element interfaces that have been introduced along with the mesh discretization and
is the generic
ith interface between the neighboring elements
e and
, i.e.,
,
,
,
and
.
It is underlined that the bilinear form given in Equation (
24), stemming from the choice of the numerical fluxes given in Equations (
21) and (
22), is symmetric and verifies the Galerkin orthogonality. As shown in
Section 4, this allows avoiding super-penalization [
23] and obtaining optimal
-convergence with values of the penalty parameter
that have the same order of magnitude of the constants of the differential operators involved in the governing equations.