Foucault–Barker Mask: Nonconventional Schlieren Technique

Abstract

We present a theoretical framework for designing optical masks, which are useful for implementing nonconventional Schlieren techniques. We revisit the use of effective transfer functions, which emphasize the role of symmetries in the design of coded masks. The proposed technique implements an optical autocorrelation of a mask, which is coded with the Barker sequences. For the same purpose, one can also use masks coded with the pseudorandom sequences. For the sake of completeness, we link our deterministic theoretical framework with a simple statistical model. The proposed technique may be useful for the automatic sensing of phase gradients.

1. Introduction

For rendering visible transparent structures, researchers have used several optical techniques. Applications abound in optical microscopy, optical testing and in fluid dynamics [1,2,3,4]. Foucault proposes the use of a knife-edge for visualizing departures of sphericity in mirrors and lenses [5]. Provided that the optical system generates nearly spherical waves, the knife-edge has a high sensitivity when detecting phase gradients.

Toepler employed a knife-edge for visualizing changes in the density in a fluid [6]. Toepler’s contribution initiated the field of Schlieren techniques, which can detect angular deflections of a parallel beam. Schlieren techniques generate irradiance distributions that are proportional to the first partial derivative of fluid density. In reference [7], there is an overview of density-sensitive visualization techniques.

For generating irradiance distributions that are proportional to the fluid’s density, one commonly uses interferometric methods. If the density variations produce weak angular deflections, one can use Zernike’s phase contrast technique [8]. Under the assumption of weak phase delays, this technique generates irradiance distributions that are proportional to the fluid density. Independently of Zernike, Lyot proposed a phase contrast technique for visualizing weak polishing inhomogeneities in a coronagraph [9].

Advanced Schlieren techniques have benefited from improvements in digital photography, as well as from developments in computer algorithms [10,11,12]. Further improvements are associated with the use of bright white-light sources, and the incorporation of suitable spatial filters. In reference [13], the authors describe a method that helps to increase the dynamic range of a detector. For a good description of quantitative Schlieren techniques, readers are referred to reference [14].

Our current discussion does not intend to make comparisons between well-described Schlieren techniques. Here, for visualizing phase gradients, we are proposing to employ the autocorrelation function of a suitably selected coded mask. For our rationale, we describe a simple scalar diffraction treatment, which provides a method for coding the source and for coding the spatial filter. We point out that there are numerical sequences that are useful for obtaining highly peaked autocorrelations. Consequently, there are sets of coded masks that can be applied for visualizing phase gradients. The use of the autocorrelation of a coded mask may help to increase the light gathering power of the Schlieren techniques.

As is common in Fourier optics, transfer functions are often discussed using gratings. As a natural extension, we employ nonconventional transfer functions that can describe the visualization of phase gratings. The discussions based on the use of gratings are regularly associated with deterministic signals. Here, we show that the use of an autocorrelation function (for visualizing phase gradients) is also valid when describing randomly located phase prisms.

In what follows, we unveil the use of a pair of optical masks for implementing a nonconventional Schlieren technique. Our proposal exploits the generation of highly peaked autocorrelation functions. To this end, we employ masks coded with the Barker sequences [15]. Equivalent results can be achieved by using pseudorandom sequences [16]. Our proposal does not include experimental verifications. Schardin used grids of transparent and opaque lines as coded light sources [17], and Jeffree used multiple color-coded slits as a light source with a grid cutoff [18]. However, these 2D methods are not based on an optical autocorrelation.

For developing our proposal, we make the following assumptions: (a) we assume that an extended source plane is under coherent illumination; (b) phase gradients are described in terms of either a weak phase grating, or of a randomly located prism; (c) we use a nonconventional transfer function, as proposed by Menzel et al. [19,20,21,22,23,24,25]. The nonconventional transfer function maps the Fourier components of the phase gradient into the Fourier components of an irradiance distribution.

In Section 2, we revisit the use of an effective transfer function [26,27]. In Section 3, we discuss a simple statistical model of phase gradients. This statistical treatment is in good agreement with a treatment of deterministic signals. In Section 4, we discuss the use of an autocorrelation function between a coded source and a coded spatial filter. This autocorrelation is described by an integral transformation, which is like those used in phase-space representations [28,29,30,31,32,33,34,35]. In Section 4, we make some numerical comparisons between the autocorrelations obtained using pseudorandom sequences or those attained with the Barker sequences. In Section 5, we summarize our contributions.

2. A Nonconventional Transfer Function

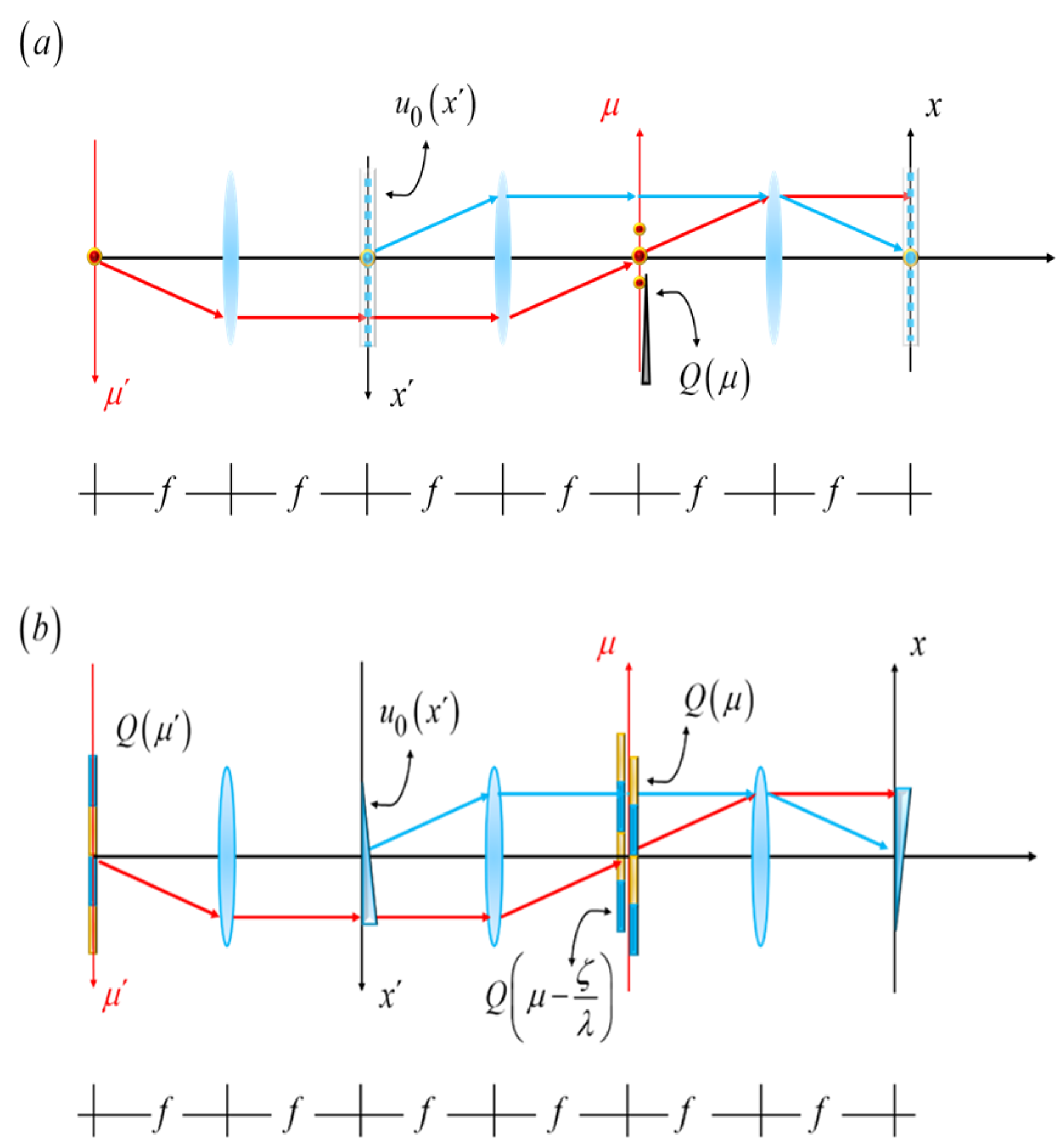
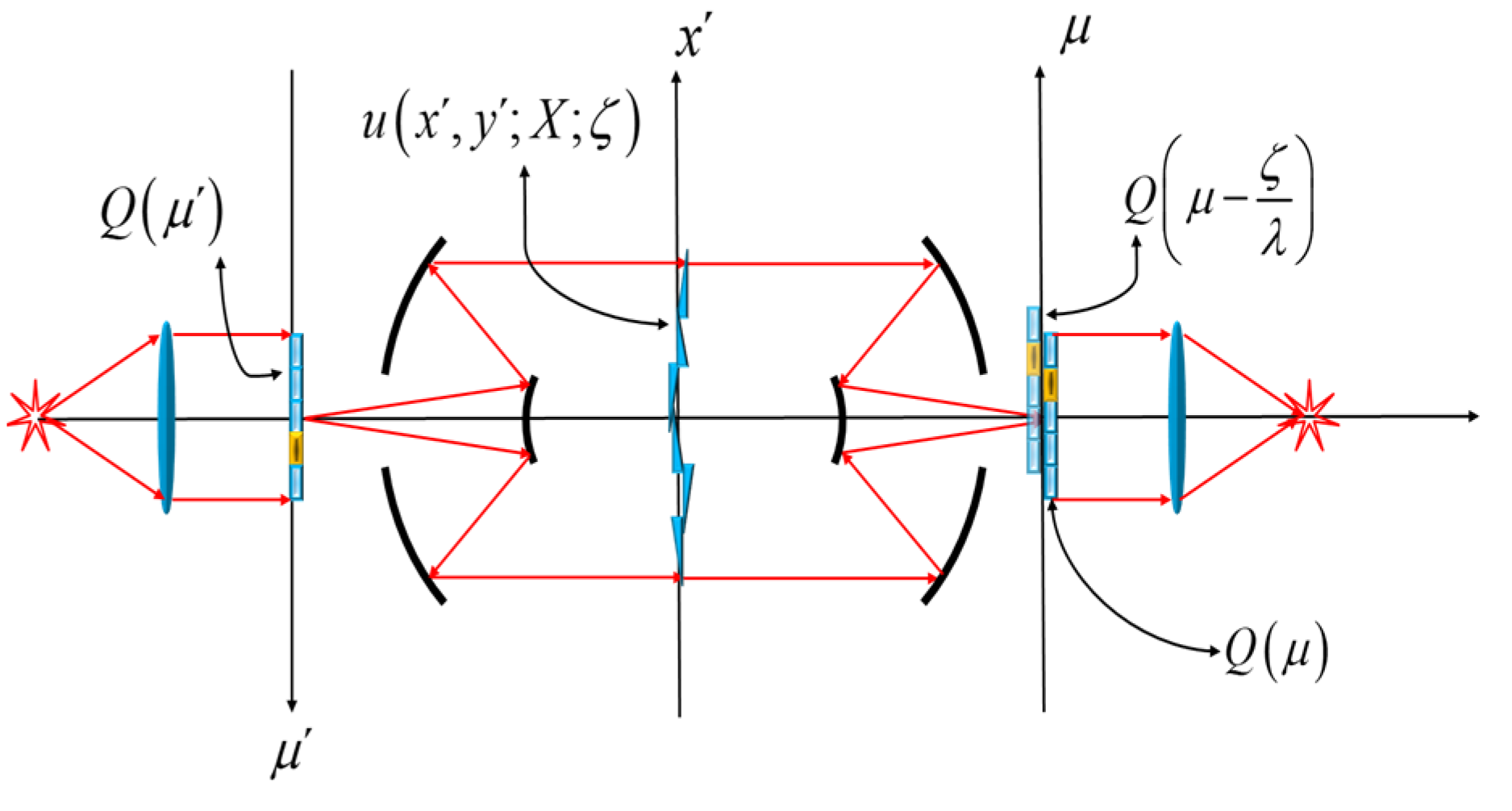
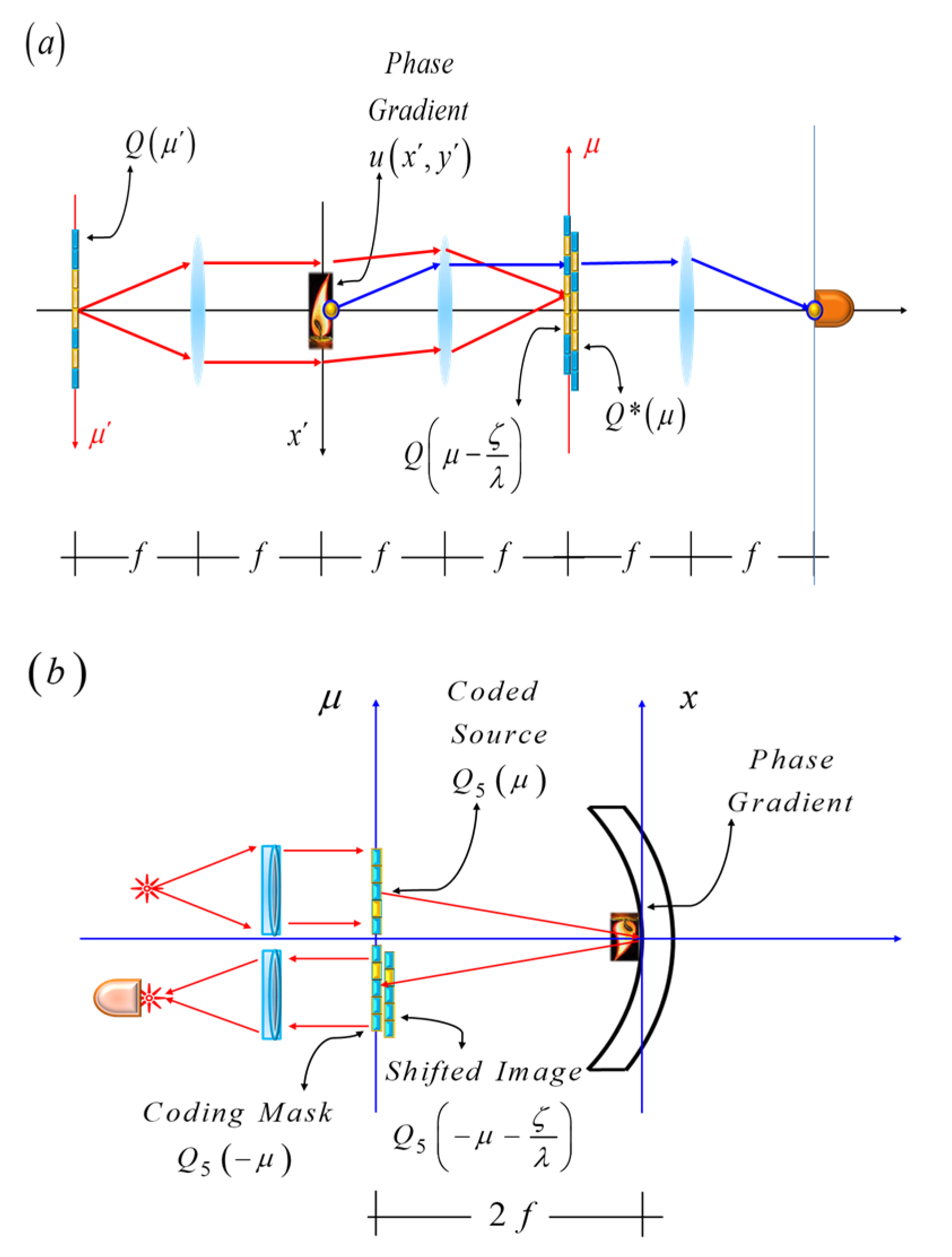
In Figure 1, we show the schematics of an optical processor that depicts our proposal.

In Figure 1b, a phase gradient is placed along the axis x’. Now, as a phase gradient, we consider a sinusoidal phase grating. The sinusoidal phase variations have in amplitude “a”, and a period “d”. The proposed complex amplitude transmittance is

$$t\left(x\prime ,y\prime \right)=\exp \left[i\hspace{0.17em}2\hspace{0.17em}\pi \hspace{0.17em}\left({\displaystyle \frac{a}{\lambda }}\right)\hspace{0.17em}\sin \left(2\hspace{0.17em}\pi {\displaystyle \frac{x\prime }{d}}\right)\right].$$

(1)

In Equation (1), the lower-case Greek letter λ denotes the wavelength. It is convenient to consider that the grating has weak phase variations, which are ${\left({\displaystyle \frac{a}{\lambda }}\right)}^2\ll \left({\displaystyle \frac{a}{\lambda }}\right).$ Under this assumption, Equation (1) can be approximated by two terms of a Taylor expansion. Then, the phase structure has a complex amplitude distribution that reads

$$u_0\left(x\prime ,y\prime \right)=1+i\hspace{0.17em}2\hspace{0.17em}\pi \hspace{0.17em}\left({\displaystyle \frac{a}{\lambda }}\right)\hspace{0.17em}\sin \left(2\hspace{0.17em}\pi {\displaystyle \frac{x\prime }{d}}\right).$$

(2)

The Fourier spectrum of Equation (2) is:

$$U_0\left(\mu ,\nu \right)=\delta \left(\mu \right)\hspace{0.17em}\delta \left(\nu \right)+\hspace{0.17em}\pi \hspace{0.17em}\left({\displaystyle \frac{a}{\lambda }}\right)\left[\hspace{0.17em}\delta \left(\mu -{\displaystyle \frac{1}{d}}\right)-\delta \left(\mu +{\displaystyle \frac{1}{d}}\right)\right]\delta \left(\nu \right).$$

(3)

In Equation (3), the Greek letters, μ and ν, denote the spatial frequencies at the Fourier domain. In Equation (3), the mathematical expression represents the complex amplitude distribution that impinges on the spatial filter. If the amplitude transmittance of the spatial filter is $Q\left(\mu ,\nu \right)$, then after the spatial filter, the amplitude transmittance reads

$$U\left(\mu ,\nu \right)=Q\left(\mu ,\nu \right)\hspace{0.17em}{U}_0\left(\mu ,\nu \right).$$

(4)

By taking an inverse Fourier transformation of Equation (4), we obtain the complex amplitude distribution at the image plane:

$$\begin{array}{c}u\left(x,y\right)=Q\left(0,0\right)+\\ \pi \hspace{0.17em}\left({\displaystyle \frac{a}{\lambda }}\right)\left[\hspace{0.17em}Q\left({\displaystyle \frac{1}{d}},0\right)\exp \left(i\hspace{0.17em}2\hspace{0.17em}\pi {\displaystyle \frac{x}{d}}\right)-Q\left(-{\displaystyle \frac{1}{d}},0\right)\exp \left(-i\hspace{0.17em}2\hspace{0.17em}\pi {\displaystyle \frac{x}{d}}\right)\right].\end{array}$$

(5)

Here, we recognize that in a unique manner $Q\left(\mu ,0\right)\hspace{0.17em}$ can be expressed as the sum of two functions. The function $E\left(\mu \right)=E\left(-\mu \right)$ is an even function. And the function $\Theta \hspace{0.17em}\left(\mu \right)=-\hspace{0.17em}\Theta \hspace{0.17em}\left(-\mu \right)$ is an odd function. For further details, see Appendix A.

$$Q\left(\mu ,0\right)=E\left(\mu \right)+\Theta \hspace{0.17em}\left(\mu \right).$$

(6)

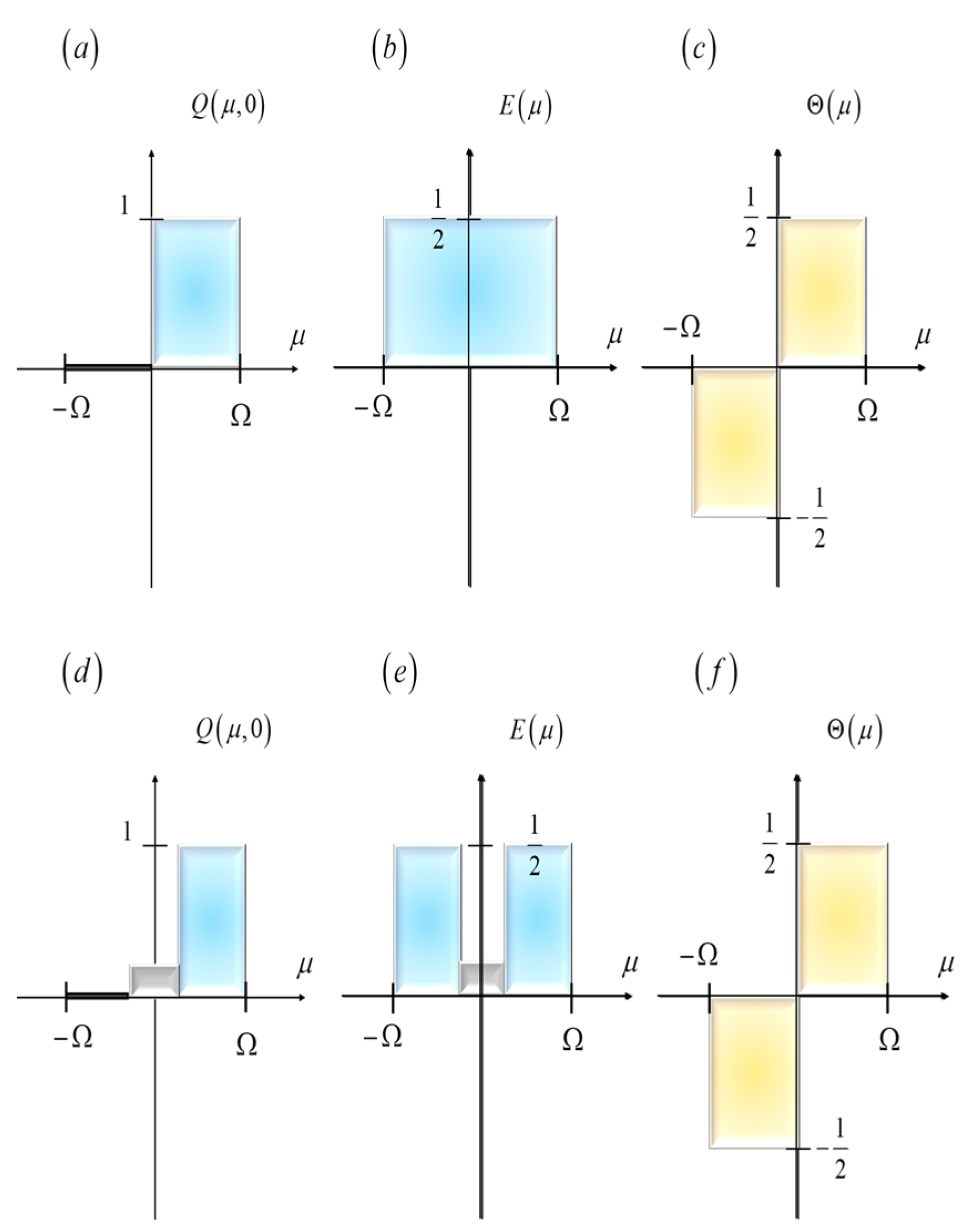
In Figure 2, we depict the even component, $E\left(\mu \right)$, and the odd component, $\Theta \hspace{0.17em}\left(\mu \right)$, associated with the amplitude transmittance of two spatial filters $Q\left(\mu ,0\right).$

If we substitute Equation (6) in Equation (5), we obtain

$$\begin{array}{c}u\left(x,y\right)=Q\left(0,0\right)+\hspace{0.17em}\hspace{0.17em}\\ +\hspace{0.17em}\left(2\hspace{0.17em}\pi {\displaystyle \frac{a}{\lambda }}\right)\hspace{0.17em}\hspace{0.17em}\Theta \left({\displaystyle \frac{1}{d}}\right)\cos \left(2\hspace{0.17em}\pi {\displaystyle \frac{x}{d}}\right)+\hspace{0.17em}\hspace{0.17em}i\hspace{0.17em}\left(2\hspace{0.17em}\pi {\displaystyle \frac{a}{\lambda }}\right)\hspace{0.17em}E\left({\displaystyle \frac{1}{d}}\right)\sin \left(i\hspace{0.17em}2\hspace{0.17em}\pi {\displaystyle \frac{x}{d}}\right).\end{array}$$

(7)

We define the normalized image irradiance as

$$I\left(x,y\right)={\left|{\displaystyle \frac{u\left(x,y\right)}{Q\left(0,0\right)}}\right|}^2.$$

(8)

From Equations (7) and (8), we obtain that the normalized image irradiance distribution is

$$I\left(x,y\right)=1+\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\left({\displaystyle \frac{2\hspace{0.17em}\pi \hspace{0.17em}a\hspace{0.17em}}{\lambda }}\right)\left({\displaystyle \frac{2}{E\left(0\right)}}\Theta \left({\displaystyle \frac{1}{d}}\right)\hspace{0.17em}\right)\hspace{0.17em}\hspace{0.17em}\cos \left(2\hspace{0.17em}\pi {\displaystyle \frac{x}{d}}\right).$$

(9)

Now, it is relevant to make the following comparison between Equations (2) and (9). The complex amplitude distribution, in Equation (2), is mapped as the image irradiance distribution in Equation (9). Equivalently, the initial sinusoidal variation is transferred as a cosinusoidal variation, with a modulation that is equal to

$$H\left({\displaystyle \frac{1}{d}}\right)\hspace{0.17em}={\displaystyle \frac{2}{E\left(0\right)}}\hspace{0.17em}\hspace{0.17em}\Theta \left({\displaystyle \frac{1}{d}}\right).$$

(10)

As depicted in Figure 3, there is a spatial frequency mapping, which can be associated with an effective transfer function.

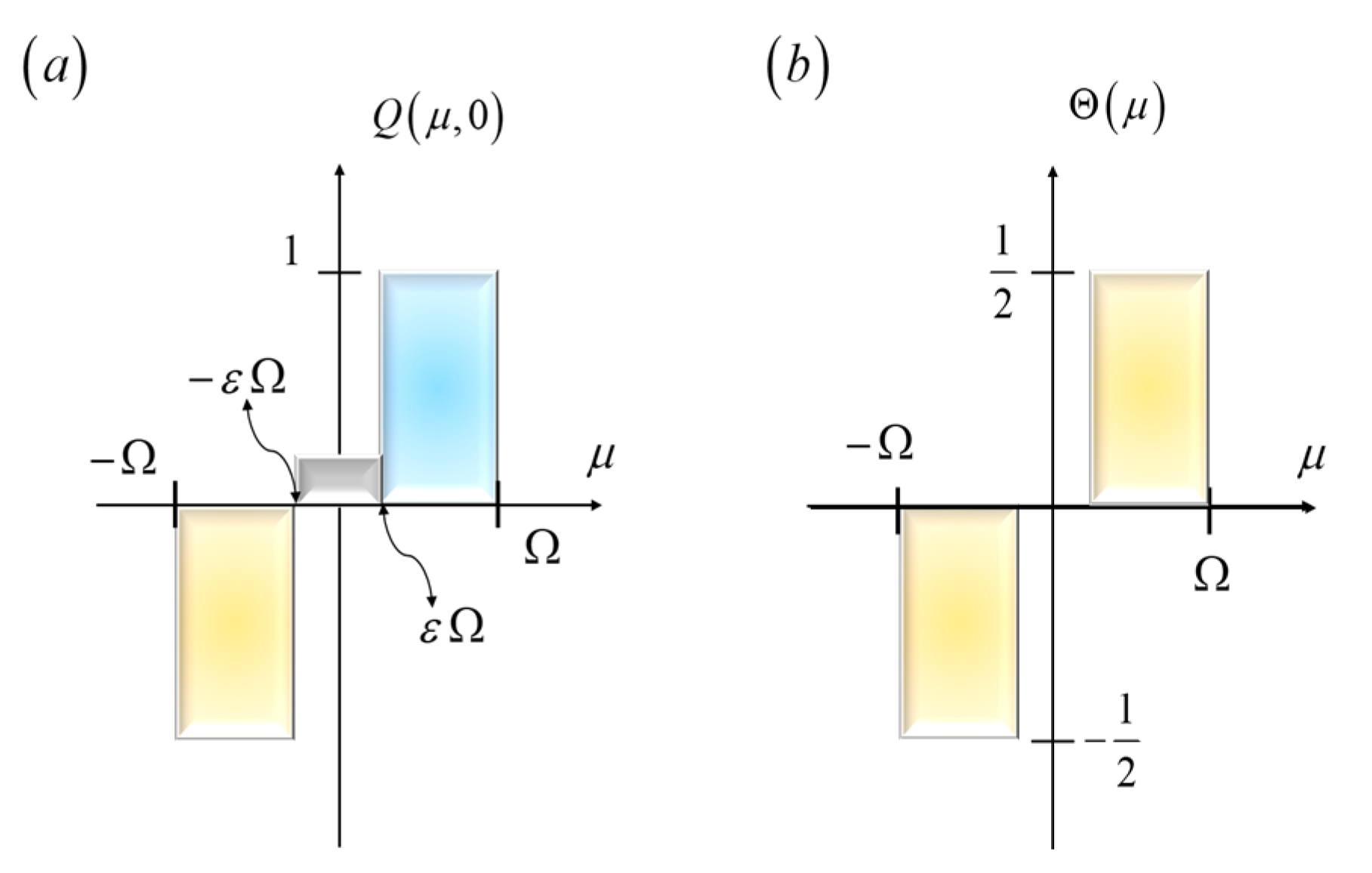
It is apparent from Equation (10) that the action of effective transfer function can be enhanced by reducing the transmittance at the center of the spatial filter. This observation is useful for proposing two nonconventional Schlieren techniques. Next, we consider Wolter’s phase-edge [27]. Its amplitude transmittance is

$$Q\left(\mu ,\nu \right)=\left\{\begin{array}{c}-\hspace{0.17em}1\hspace{1em}if\hspace{1em}-\Omega <\mu <0\\ \hspace{0.17em}\hspace{1em}1\hspace{1em}if\hspace{1em}0<\mu <\Omega \hspace{1em}\end{array}\right\}.$$

(11)

In Equation (11), the Greek letter Ω denotes the cut-off spatial frequency. In Figure 4a, we plot Equation (11). For the modulation contrast technique, the amplitude transmittance is

$$Q\left(\mu ,\nu \right)=\left\{\begin{array}{c}0\hspace{1em}if\hspace{1em}-\Omega <\mu <-\epsilon \hspace{0.17em}\Omega \\ \begin{array}{l}\hspace{0.17em}\alpha \hspace{1em}if\hspace{1em}-\epsilon \hspace{0.17em}\Omega <\mu <\epsilon \hspace{0.17em}\Omega \\ \hspace{0.17em}1\hspace{1em}if\hspace{1em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\epsilon \hspace{0.17em}\Omega <\mu <\hspace{0.17em}\Omega \hspace{1em}\end{array}\end{array}\right\}.$$

(12)

In Equation (12), the Greek letters α and ε denote two real numbers that have values lower than unity. The letter α represents an attenuation coefficient at the center of the mask and the letter ε indicates the fraction of the length associated with the central section. And the letter ε indicates the fraction of the length associated with the central section.

In Figure 4, we plot the amplitude for an improved version, which incorporates a transmission equal to minus unity; as in Wolter’s phase edge [27]. And it also incorporates a central attenuation coefficient, as in the modulation contrast technique. Its amplitude distribution reads

$$Q\left(\mu ,\nu \right)=\left\{\begin{array}{c}-1\hspace{1em}if\hspace{1em}-\Omega <\mu <-\epsilon \hspace{0.17em}\Omega \\ \begin{array}{l}\hspace{0.17em}\hspace{0.33em}\alpha \hspace{1em}if\hspace{1em}-\epsilon \hspace{0.17em}\Omega <\mu <\epsilon \hspace{0.17em}\Omega \\ \hspace{0.17em}\hspace{0.33em}1\hspace{1em}if\hspace{1em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\epsilon \hspace{0.17em}\Omega <\mu <\hspace{0.17em}\Omega \hspace{1em}\end{array}\end{array}\right\}.$$

(13)

For grounding our above description, we simulate a phase gradient as a weak phase grating. Then, it is natural to ask whether the above results are valid for other types of phase gradients. We will answer this question in the next section.

3. Random Phase Gradients

We note the existence of heuristic descriptions for considering a transparent structure as a set of randomly located prisms. Each prism deflects a parallel beam. Then, a knife-edge can block the undeflected beam, allowing the passing of the deflected beam. In this manner, one can visualize the presence of a phase gradient.

This heuristic description ignores any discussions on scalar diffraction. For rectifying this limitation, next we develop a simple statistical model. As depicted in Figure 5, we consider a set of prisms. Each prism has a random deflection angle ζ. Each member of the set is randomly located at the position X. The prism has a length equal to L. Then, its associated optical signal is:

$$u\left(x\prime ,y\prime ;X;\zeta \right)=\exp \left[i\hspace{0.17em}2\hspace{0.17em}\pi \left({\displaystyle \frac{\zeta }{\lambda }}\left(x-X\right)\right)\right]\hspace{0.33em}\left[{\displaystyle \frac{1}{2\hspace{0.17em}L}}rect\left({\displaystyle \frac{x}{2\hspace{0.17em}L}}\right)\right].$$

(14)

Equivalently, Equation (14) can be written as

$$u_0\left(x\prime ,y\prime ;X;\zeta \right)=\left[\exp \left(-\hspace{0.17em}i\hspace{0.17em}2\hspace{0.17em}\pi \hspace{0.17em}{\displaystyle \frac{\zeta }{\lambda }}X\right)\left({\displaystyle \frac{1}{2\hspace{0.17em}L}}rect\left({\displaystyle \frac{x}{2\hspace{0.17em}L}}\right)\right)\right]\hspace{0.33em}\exp \left(i\hspace{0.17em}2\hspace{0.17em}\pi \hspace{0.17em}{\displaystyle \frac{\zeta }{\lambda }}x\right).$$

(15)

The statistical variations in X are described by the probability density function p_X(x). The Fourier transform pair of function p_X(x) is the characteristic function Φ_X(µ), namely

$${\mathsf{\Phi }}_X\left(\mu \right)={\displaystyle \underset{-\hspace{0.33em}\infty }{\overset{\infty }{\int }}}{p}_X\left(x\right)\hspace{0.17em}\hspace{0.17em}\exp \left(-\hspace{0.17em}i\hspace{0.17em}2\hspace{0.17em}\pi \hspace{0.17em}\mu \hspace{0.17em}x\right)\hspace{0.17em}\hspace{0.17em}dx.$$

(16)

Now, the Fourier spectrum of Equation (15) is the amplitude impulse response of the optical system in Figure 5,

$$U_0\left(\mu ,\nu ;X;\zeta \right)=\exp \left(-\hspace{0.17em}i\hspace{0.17em}2\hspace{0.17em}\pi \hspace{0.17em}{\displaystyle \frac{\zeta }{\lambda }}X\right)\hspace{0.33em}\sin \mathrm{c}\left[\left(\mu -{\displaystyle \frac{\zeta }{\lambda }}\right)\hspace{0.17em}2\hspace{0.17em}L\right]\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\delta \left(\nu \right)\hspace{0.17em}.$$

(17)

As the value of L increases, the amplitude impulse response can be approximated as

$$U_0\left(\mu ,\nu ;X;\zeta \right)=\exp \left[-\hspace{0.17em}i\hspace{0.17em}2\hspace{0.17em}\pi \left({\displaystyle \frac{\zeta }{\lambda }}X\right)\right]\hspace{0.33em}\hspace{0.17em}\delta \left(\mu -{\displaystyle \frac{\zeta }{\lambda }}\right)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\delta \left(\nu \right)\hspace{0.17em}.$$

(18)

Along the µ’-axis we place a coded mask. Its amplitude transmittance is Q(µ’). The µ-axis is the geometrical optics conjugate of the µ’-axis. At the image conjugate, one can use Equation (18) for obtaining the following complex amplitude distribution

$$U\left(\mu ,\nu ;X;\zeta \right)={\displaystyle \underset{-\hspace{0.33em}\hspace{0.33em}\infty }{\overset{\infty }{\int }}}Q\left(\mu \prime \right)\hspace{0.33em}\hspace{0.17em}{U}_0\left(\mu -\mu \prime ,\nu -\nu \prime ;X;\zeta \right)\hspace{0.33em}\hspace{0.33em}d \mu \prime \hspace{0.33em}d \nu \prime .$$

(19)

By substituting Equation (18) in Equation (19), we obtain

$$U\left(\mu ,\nu ;X;\zeta \right)=Q\left(\mu -{\displaystyle \frac{\zeta }{\lambda }}\right)\hspace{0.17em}\hspace{0.17em}\exp \left(-\hspace{0.17em}i\hspace{0.17em}2\hspace{0.17em}\pi \hspace{0.17em}{\displaystyle \frac{\zeta }{\lambda }}X\right)\hspace{0.33em}\hspace{0.17em}\delta \left(\nu \right).$$

(20)

Next, it is convenient to evaluate the ensemble average of Equation (20). That is,

$$〈U\left(\mu ,\nu ;\zeta \right)〉={\displaystyle \underset{-\hspace{0.33em}\hspace{0.33em}\infty }{\overset{\infty }{\int }}}{p}_X\left(x\right)\hspace{0.33em}U\left(\mu ,\nu ;x;\zeta \right)\hspace{0.33em}\hspace{0.33em}dX.$$

(21)

By substituting Equation (20) in Equation (21), and using the definition of the characteristic function, we obtain

$$〈U\left(\mu ,\nu ;\zeta \right)〉={\mathsf{\Phi }}_X\left({\displaystyle \frac{\zeta }{\lambda }}\right)\hspace{0.17em}\hspace{0.33em}\delta \left(\mu -{\displaystyle \frac{\zeta }{\lambda }}\right)\hspace{0.33em}\delta \left(\nu \right).$$

(22)

Since the complex amplitude distribution in Equation (22) impinges on the coded mask Q(ζ), just behind this mask the complex amplitude distribution is

$$〈U\left(\mu ,\nu ;\zeta \right)〉\hspace{0.33em}Q\left(\mu \right)={\mathsf{\Phi }}_X\left({\displaystyle \frac{\zeta }{\lambda }}\right)\hspace{0.17em}\hspace{0.33em}Q\left(\mu \right)\hspace{0.33em}Q\left(\mu -{\displaystyle \frac{\zeta }{\lambda }}\right)\hspace{0.33em}\delta \left(\nu \right).$$

(23)

The 2D Fourier transform of Equation (23) reads

$$〈u\left(x,y;\zeta \right)〉\hspace{0.33em}={\mathsf{\Phi }}_X\left({\displaystyle \frac{\zeta }{\lambda }}\right)\hspace{0.17em}\hspace{0.33em}{\displaystyle \underset{-\hspace{0.33em}\hspace{0.33em}\infty }{\overset{\infty }{\int }}}Q\left(\mu \right)\hspace{0.33em}Q\left(\mu -{\displaystyle \frac{\zeta }{\lambda }}\right)\hspace{0.33em}\exp \left(i\hspace{0.17em}2\hspace{0.17em}\pi \hspace{0.17em}x\hspace{0.17em}\mu \right)\hspace{0.33em}d\mu .$$

(24)

In Equation (24), the integrand contains two mathematical operations. As in the autocorrelation function, the integrand contains a product of two laterally shifted signals. The integrand also contains the kernel of a Fourier transformation. This type of integrand appears when evaluating phase-space representations. For signals that evolve in time, a phase-space representation displays simultaneously the variations in time and in the temporal frequency. For signals that evolve in the space domain, a phase-space representation simultaneously displays the position and the spatial frequency. The Wigner distribution and the ambiguity function are two examples of these representations [28,29]. In fact, the Wigner distribution and the ambiguity function are Fourier transform pairs. Phase-space representations are useful in several branches of applied optics [30,31,32,33,34,35]. Any further discussions on this topic are beyond our current scope.

For the sake of completeness of our discussion, in the next section, we describe a deterministic treatment. The deterministic model has good agreement with the above statistical model.

4. Coded Source: A Deterministic Imaging Process

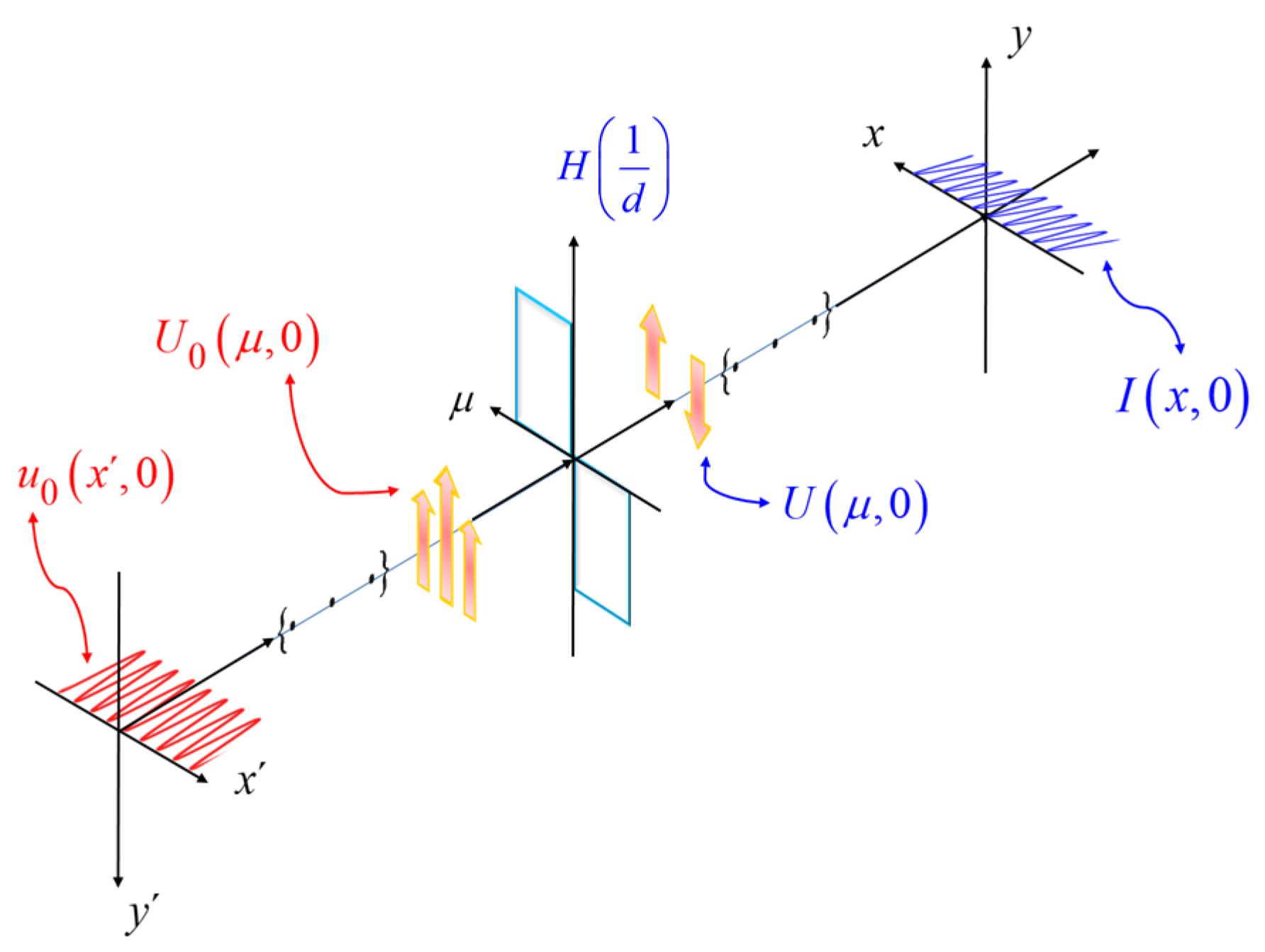
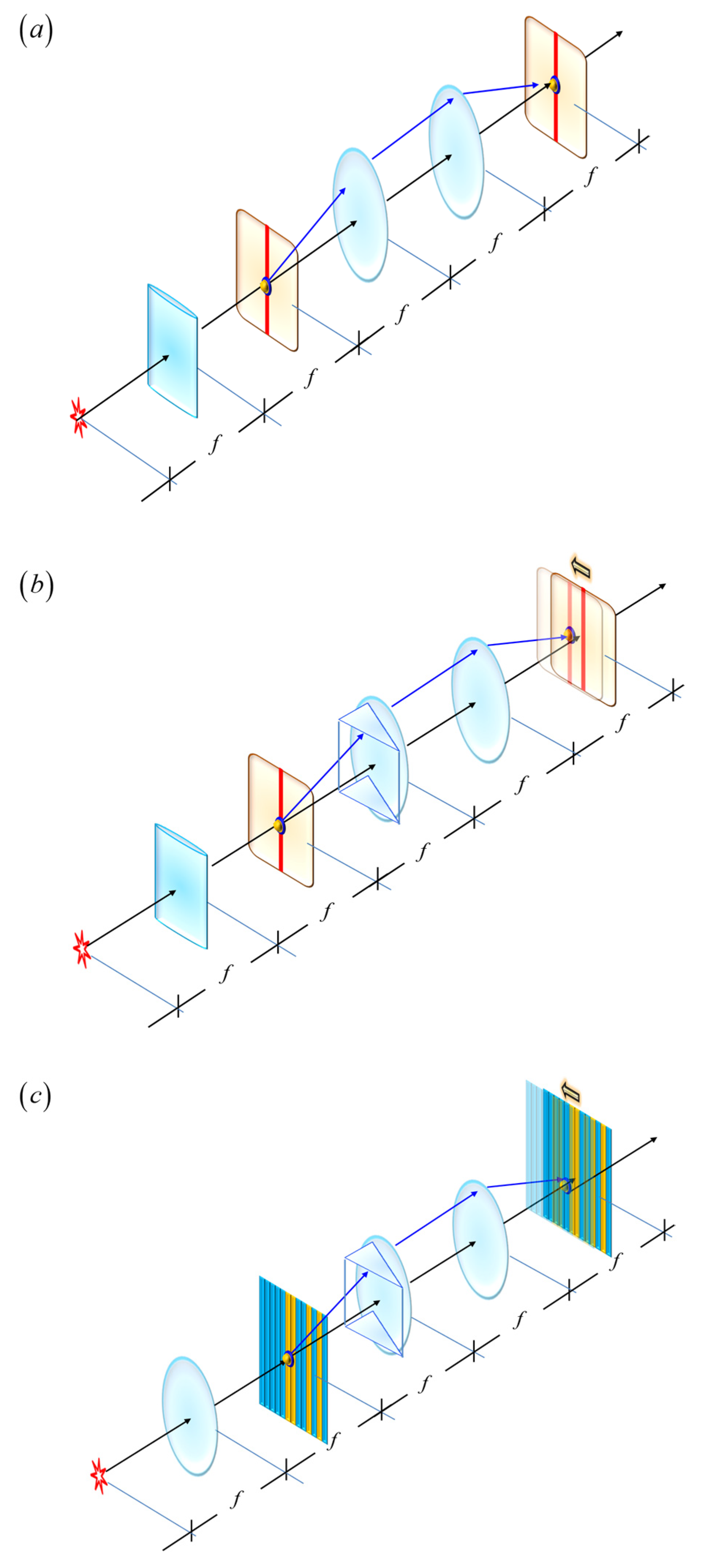
For complementing our previous discussion, on randomly located prisms, next we discuss a fully deterministic treatment. As part of our rationale, first we describe some heuristic arguments. As depicted in Figure 6, we contemplate a coherently illuminated slit. At its conjugated image, (μ, ν), we place a second slit that acts as the spatial filter.

In the absence of phase gradients, the two slits coincide, and the light throughput achieves its maximum value. On the other hand, if a phase gradient is present then the image of the source is laterally shifted (say by the amount ζ/λ). This mismatch generates a drop in light throughput. That is,

$$T={\left|{\displaystyle \underset{-\hspace{0.33em}\infty }{\overset{\infty }{\int }}}rect\left({\displaystyle \frac{\mu }{\Omega }}\right)\hspace{0.17em}\hspace{0.17em}rect\left({\displaystyle \frac{\mu -\frac{\zeta }{\lambda }}{\Omega }}\right)\hspace{0.33em}d \mu \right|}^2\hspace{0.17em}.$$

(25)

In Equation (25), the Greek letter Ω denotes the width of the slit that is used to cover the source. If one evaluates Equation (25), then one obtains:

$$T=\left[1-{\displaystyle \frac{\left|\hspace{0.17em}\zeta \hspace{0.17em}\right|}{2\hspace{0.17em}\Omega \hspace{0.17em}\lambda }}\right]\hspace{0.17em}rect\left({\displaystyle \frac{\zeta }{4\hspace{0.17em}\Omega \hspace{0.17em}\lambda }}\right).$$

(26)

It is apparent from Equation (26) that the light throughput varies slowly with the variable ζ, except for a very narrow slit. However, the light throughput is reduced if one uses narrows slits. Hence, we search next for other options. To conclude, we consider that the source is coded with multiple slits. Then, at the source plane, the amplitude transmittance is:

$$U_0\left(\mu \prime ,\nu \prime \right)=Q\left(\mu \prime \right).$$

(27)

In Equation (27), the Greek letters μ’ and ν’ denote spatial frequency coordinates at the source plane. At the input plane, the coordinates we employ the coordinates x’ and y’. At this plane, the amplitude distribution is the Fourier transform of Equation (30). That is,

$$u_0\left(x\prime ,y\prime \right)=q\left(x\prime \right)\hspace{0.17em}\hspace{0.17em}\delta \left(y\prime \right).$$

(28)

In Equation (28), the function $q\left(x\prime \right)$ is the 1D Fourier transform of the coded source. Next, we consider that a prism alters the amplitude distribution in Equation (28). Then, the new amplitude distribution reads

$$u\left(x\prime ,y\prime \right)=\exp \left(-\hspace{0.17em}i\hspace{0.17em}2\hspace{0.17em}\pi \hspace{0.17em}{\displaystyle \frac{\hspace{0.17em}\zeta }{\lambda }}x\prime \right)\hspace{0.17em}\hspace{0.17em}{u}_0\left(x\prime ,y\prime \right).$$

(29)

In Equation (29) we consider the presence of a phase gradient, with deflection angle ζ. At the pupil aperture, the amplitude distribution is the inverse Fourier transform of Equation (29). That is,

$$U\left(\mu ,\nu \right)=Q\left(\mu -{\displaystyle \frac{\zeta }{\lambda }}\right).$$

(30)

Next, we consider that the amplitude distribution, in Equation (30), impinges on a second coded mask. The second coded mask acts as the spatial filter. Its amplitude transmittance is Q*(μ). Then, just after the mask, the amplitude transmittance is

$$\mathsf{\Psi }\left(\mu ,\nu \right)=Q*\left(\mu \right)\hspace{0.17em}\hspace{0.17em}U\left(\mu ,\nu \right).$$

(31)

It is straightforward to substitute Equation (30) in Equation (31), for obtaining:

$$\mathsf{\Psi }\left(\mu ,\nu \right)=Q*\left(\mu \right)\hspace{0.17em}\hspace{0.17em}Q\left(\mu -{\displaystyle \frac{\hspace{0.17em}\zeta }{\lambda }}\right)\hspace{0.17em}.$$

(32)

As expected, at the pupil aperture, the amplitude distribution is the product of a laterally shifted version of the coded mask times the complex conjugate transmittance of the mask that acts as the spatial filter. Consequently, at the image plane, the amplitude distribution is

$$\psi \left(x,y;\zeta \right)={\displaystyle \underset{-\hspace{0.33em}\infty }{\overset{\infty }{\int }}}Q*\left(\mu \right)\hspace{0.17em}\hspace{0.17em}Q\left(\mu -{\displaystyle \frac{\zeta }{\lambda }}\right)\hspace{0.33em}\hspace{0.33em}\exp \left(i\hspace{0.17em}2\hspace{0.17em}\pi \hspace{0.17em}x\hspace{0.17em}\mu \right)\hspace{0.33em}d\mu \hspace{0.17em}.$$

(33)

As in Equation (24), the mathematical expression in Equation (33) describes an integrand that contains two mathematical operations. It contains the product of two laterally shifted signals. The integrand also contains the kernel of a Fourier transformation. As previously pointed out, the integrand is like those employed when evaluating phase-space representations. Here, we concentrate on the use of Equation (33), if it is evaluated at the origin (x = 0, y = 0). Hence, we are currently interested in the following equation

$${\left|\psi \left(0,0;\zeta \right)\right|}^2={\left|{\displaystyle \underset{-\hspace{0.33em}\infty }{\overset{\infty }{\int }}}Q*\left(\mu \right)\hspace{0.17em}\hspace{0.17em}Q\left(\mu -{\displaystyle \frac{\zeta }{\lambda }}\right)\hspace{0.33em}d \mu \right|}^2\hspace{0.17em}.$$

(34)

Using Equation (34), we advance the following working hypothesis: if the source and the spatial filter are coded with the same sequence, then one can optically implement an autocorrelation operation. This autocorrelation can be usefully applied to the automatic detection of phase gradients. This working hypothesis is discussed in what follows.

5. Optical Visualization and Automatic Detection

The pseudorandom sequences and the Barker sequences can generate highly peaked autocorrelations. Then, they are good candidates for coding masks that employ the autocorrelation function for detecting phase gradients. For elaborating on this working hypothesis, we note that either the pseudorandom sequences, or the Barker sequences have a finite number of elements, say L. This integer number L is denoted as the sequence length. For applications in electronics, the sequences are used as cyclic sequences. However, in optics, due to the finite size of the mask, the coding sequences are noncyclic. We elaborate on this difference.

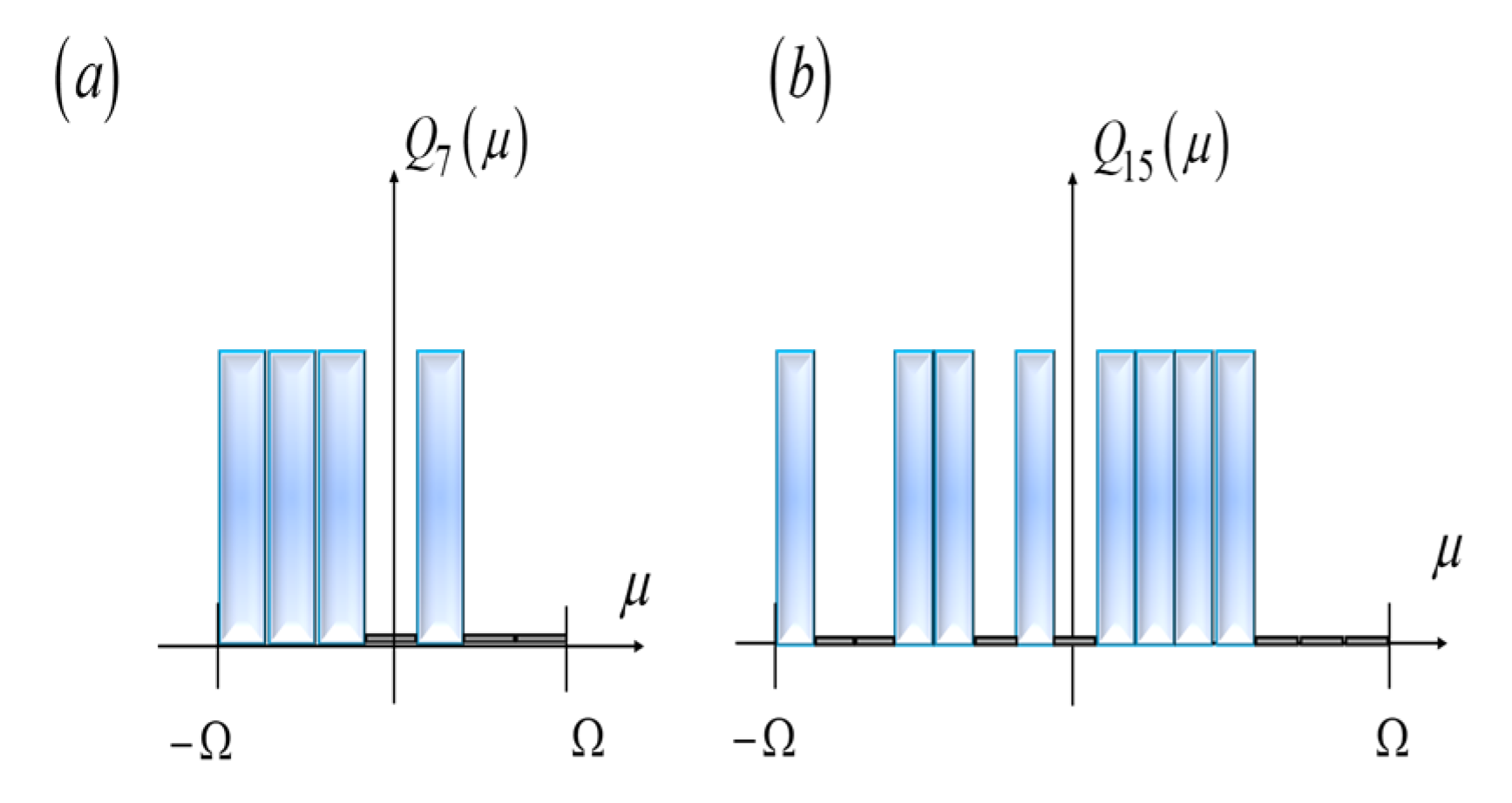
The pseudorandom sequences exhibit a high peak over an otherwise uniform value, as depicted in Figure 7. The selected sequences have amplitude transmittance that are equal to unity, or equal to zero. Then, they are useful for implementing a Schlieren technique with white light. In Figure 7a, the length of the pseudorandom is L = 7. And in Figure 7b, the length is L = 15. These examples are selected for making comparisons with the results in reference [15].

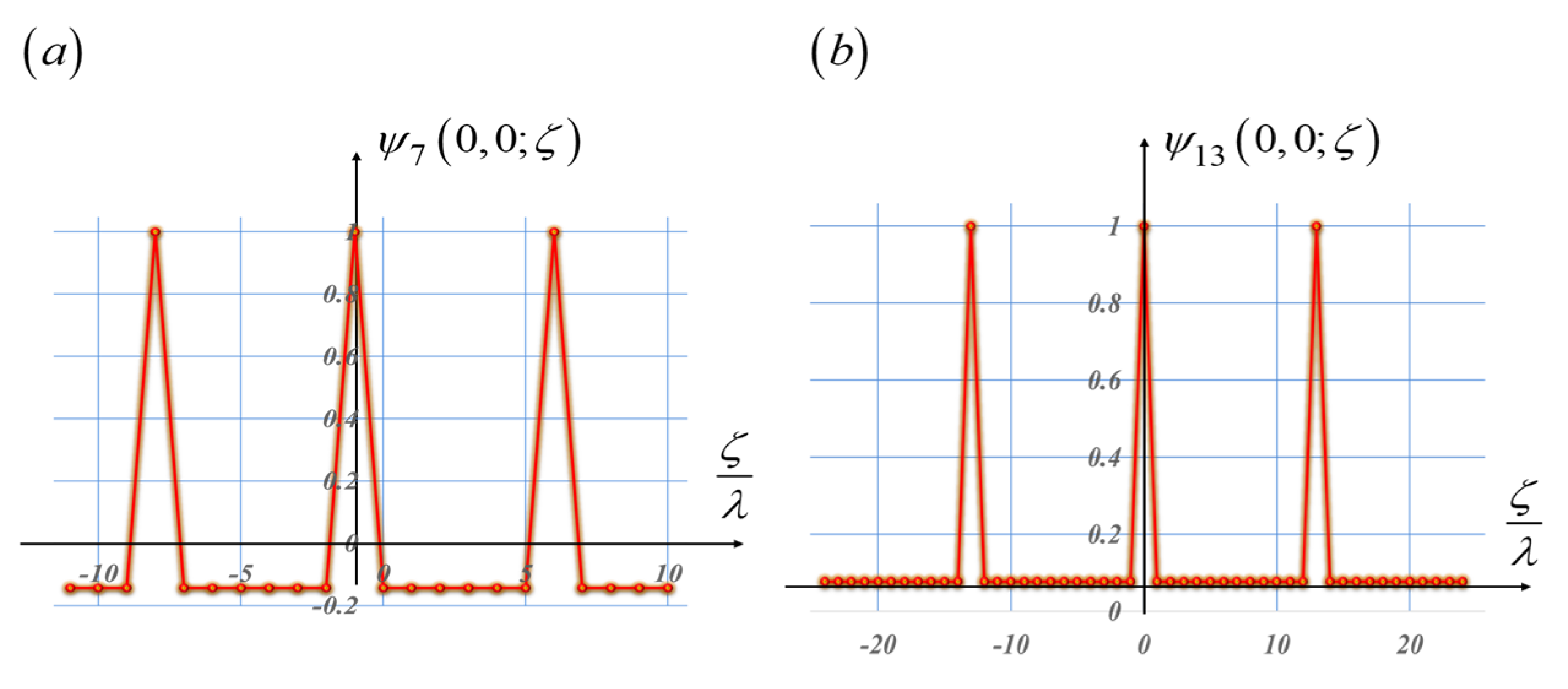
In Figure 8, we show the cyclic autocorrelations associated with the sequences in Figure 7. It is apparent that the autocorrelations exhibit peaks that overshoot a uniform value.

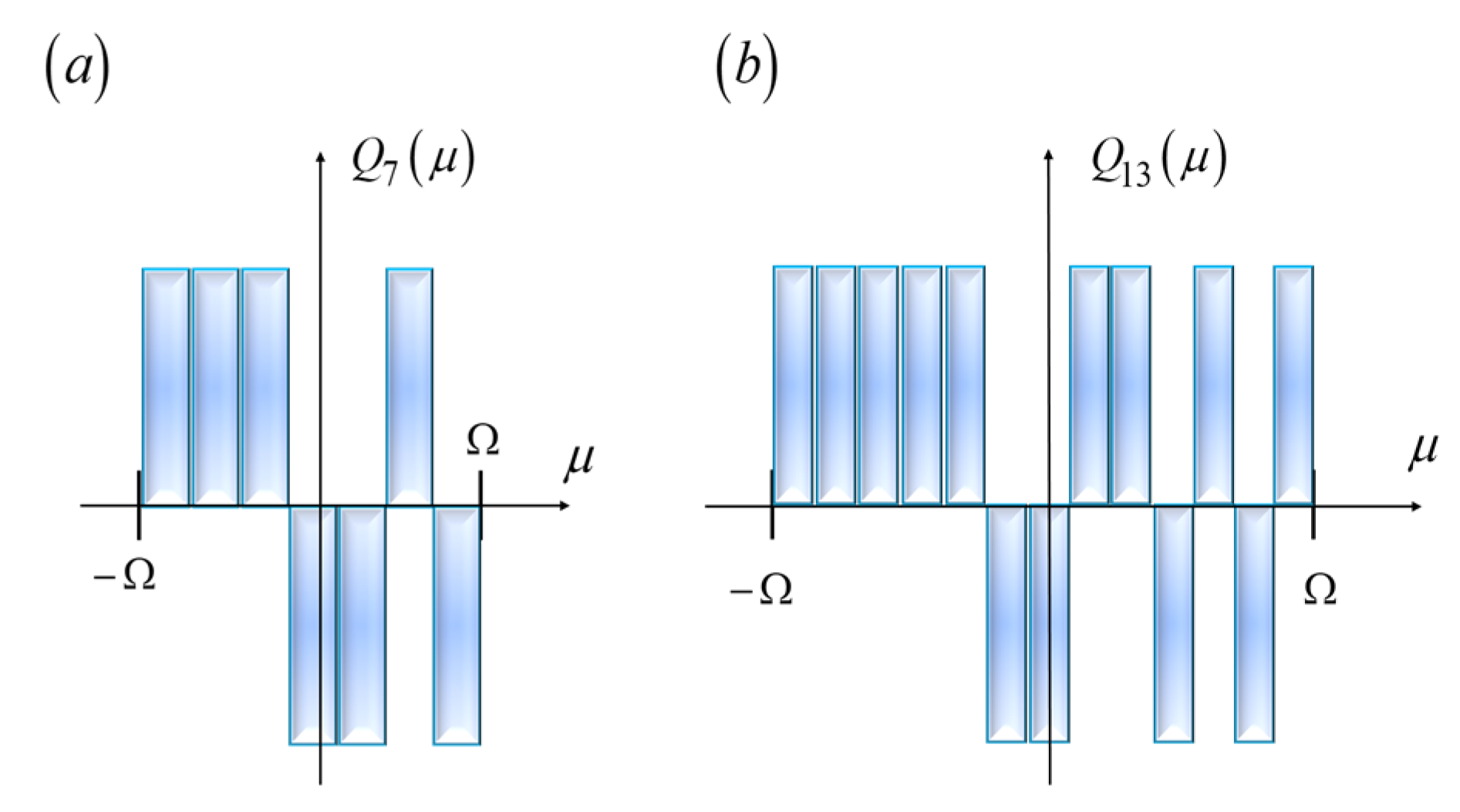
In Figure 9, we show Barker sequences of length L = 7 and L = 13. Now, the amplitude transmittance has values that are either equal to unity, or equal to minus unity.

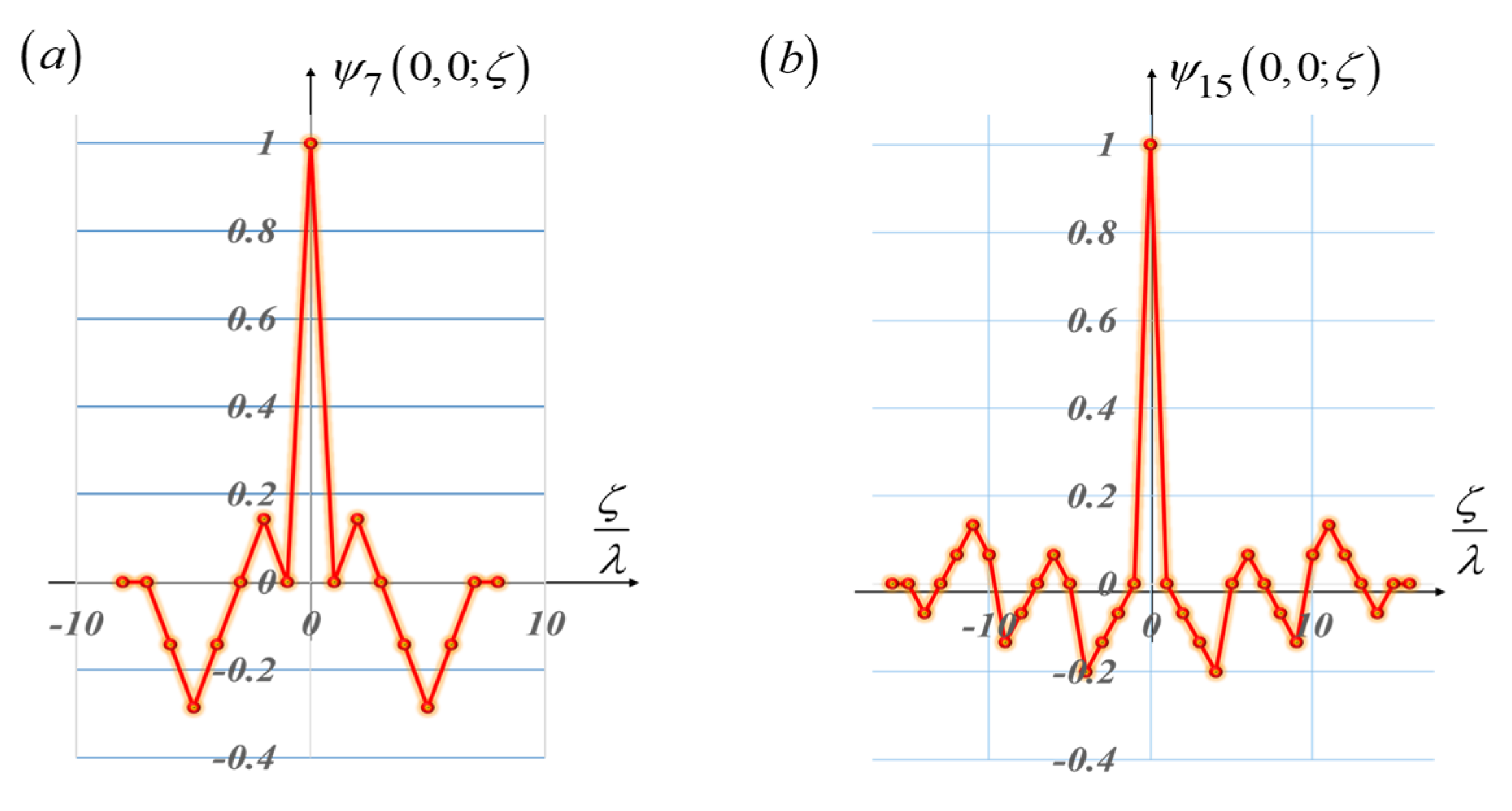
In Figure 10, we plot the cyclic autocorrelation associated with the sequences in Figure 9. It is apparent from Figure 10 that the autocorrelations also have peaks that overrun the values of the adjacent sidelobes. We note that the peaks baselines narrow down, when going from the length L = 7 to the length L = 13.

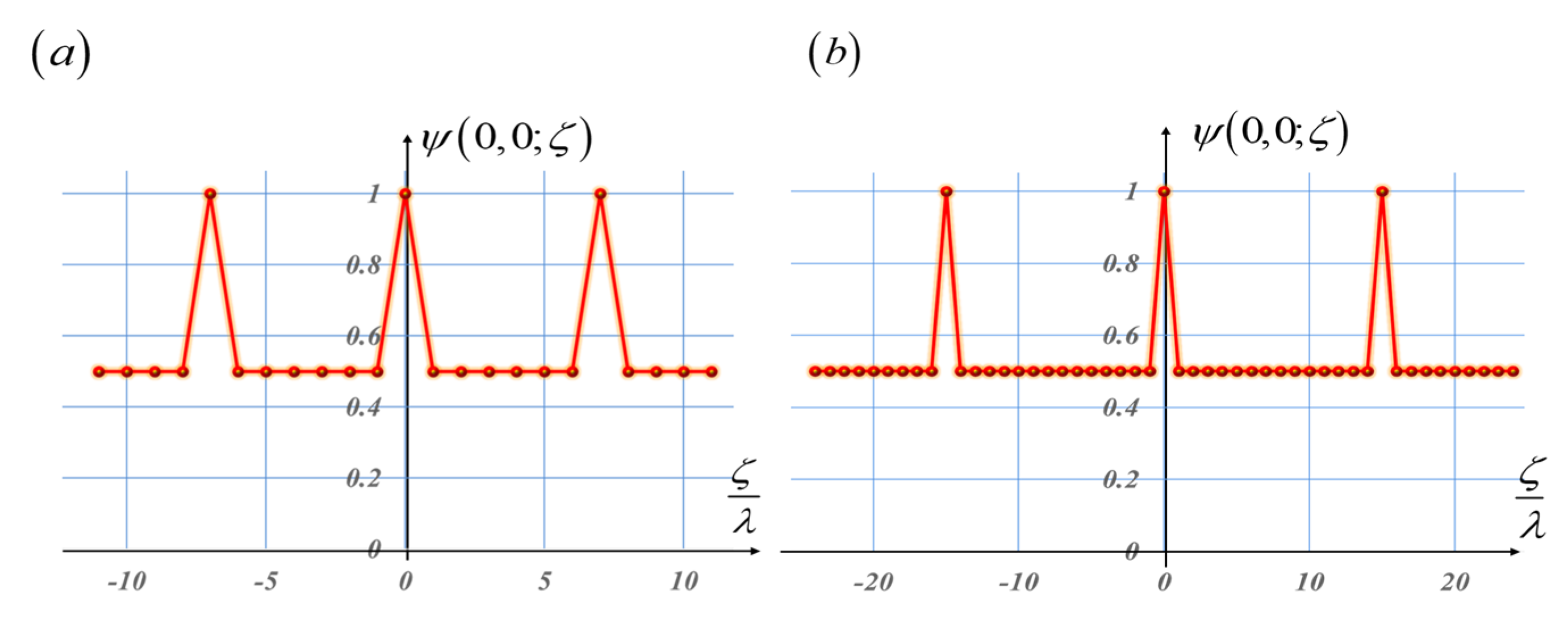
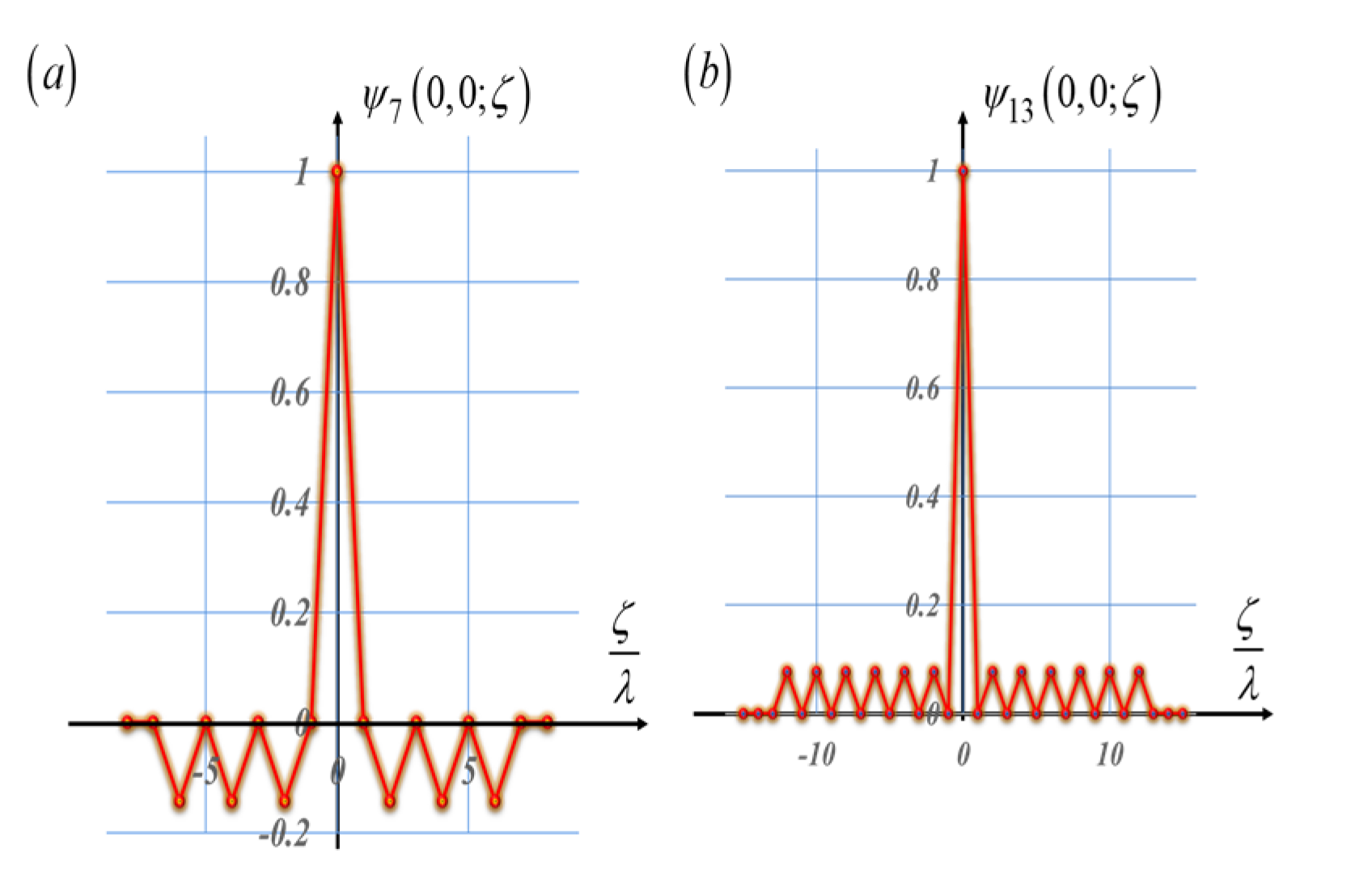
As previously indicated, in optics, one is dealing with noncyclic autocorrelations. This is due to the finite size of the masks. The autocorrelations do not repeat themselves. To visualize the impact of this feature, we present the noncyclic autocorrelations of the pseudo-random sequences, as well as the noncyclic autocorrelations of the Barker sequences. From Figure 11 and Figure 12, we note that the noncyclic autocorrelations do not have replicated peaks. Furthermore, associated with the pseudorandom sequences, the noncyclic autocorrelations exhibit sidelobes having variable values.

From Figure 11 and Figure 12, we note that the noncyclic autocorrelations do not have replicated peaks. Furthermore, associated with the pseudorandom sequences, the noncyclic autocorrelations exhibit sidelobes having variable values.

From Figure 12, we observe that the Barker sequences generate noncyclic autocorrelations that exhibit a distinctive central peak, The sidelobes are replicated with equal values. We observe that in the absence of phase gradients, the noncyclic autocorrelations have a central distinctive peak.

Hence, the Barker codes are a desirable choice for implementing an optical autocorrelation sensor. For this purpose, Figure 13 shows the optical setup, with (a) presenting the unfolded version and (b) depicting the folded version using a spherical mirror.

In Figure 13b, the plane of the phase gradient cannot physically be in contact with the mirror at its center. But it must lie at some small distance in front of the mirror. This then leads to a slight doubling of the phase gradient when a Schlieren image is formed. Finally, we note that the proposed Schlieren technique has not yet been experimentally assessed.

6. Conclusions

We have described a theoretical framework for designing nonconventional Schlieren techniques. To this end, we have revisited the use of an effective transfer function. This discussion clarifies the relevance of employing arguments of symmetry, when designing Schlieren techniques.

We have presented a simple statistical model for describing phase gradients as randomly located prisms. This treatment is in good agreement with a deterministic model, which describes weak phase gradients.

The nonconventional Schlieren techniques employ a pair of coded masks, for implementing an optical autocorrelation. One element of the pair encodes a coherently illuminated plane, which acts as the source. And the second element of the pair acts as the spatial filter. The coded masks are located on geometric–optical conjugate planes.

The described autocorrelator exploits the use of Barker sequences for generating highly peaked, noncyclic irradiance distributions. We have indicated that equivalent results can be achieved by coding the masks with pseudorandom sequences.

The current discussion does not contain experimental verifications of the theoretical framework.