Abstract
The photoelectric effect in a Ge-on-Si single-photon avalanche detector (SPAD) at an ultralow energy in incident pulsed laser radiation is considered in the frame of the classical theory of the electrodynamics of continuous media. It is shown that the energy of incident laser radiation which is shared among a huge number of electrons in a Ge matrix can concentrate on only one of these through the effect of the constructive interference of the fields re-emitted by surrounding electrons. Conservation of energy in this case is upheld because of a substantial narrowing of the effective bandgap in heavily doped p-Ge, which is used in the design of the SPAD considered.
1. Introduction
Metrology of extremely low radiation energies/powers is the subject of vital importance for R&D in the area of quantum technologies, which include quantum communications [1] using quantum key distribution [2,3], secret sharing [4], cryptography [5] protocols, quantum computing [6] and quantum information processing [7]. It also secures progress in more classical technologies [8] such as deep space communications [9], telecommunications [10], sensing [11], rangefinding, light detection and ranging (LiDAR) [12] and depth imaging of objects [13], including imaging through various densities of different obscurants [14] and even covert imaging [15] applications. Single-photon detectors (SPD) are the devices that do the job. Significant advances in both photoelectric and thermal SPDs have been achieved in recent years [16,17,18,19,20,21,22]. As was conventionally happening in the history of science and technologies, the more objects of study and more research involved, the higher probability to find something new and unexpected. In the case of SPDs, such news is that their detection efficiency (DE) can be nonzero when the energy in a pulse of incident laser radiation Wi is less or even much less than the energy of the photon ħω corresponding to the frequency ω of this radiation [19,20,21,22]. Such observations are in clear contradiction with Einstein’s quantum model of the photoelectric effect (PE) [23], which states that a photoelectron appears when the electron absorbs from light the energy of a quantum ħω, i.e., of a photon, which exceeds the work function P or bandgap Eg of a material. This, in essence, a conservation of the energy condition in PE, presumes that the energy of a light pulse Wi, which is transferred to an electron in a medium, has to be not less than P or Eg and ħω. While for the superconductor SPDs [7], in which the energy gap Eg ≡ 2∆ << ħω, the appearance of a photoelectron when Wi << ħω does not contradict the conservation of energy law, in the case of photoelectric SPDs [19,20,21], in which it is presumed that Eg ≤ ħω, such observations look surprising. In this work, a plausible explanation for such observations in Ge-on-Si single-photon avalanche diode (SPAD) detectors is given in the frame of the classical electrodynamics of continuous media. Active R&D interest in such detectors is high [15,20,21,24] because they are sensitive in the near infrared, up to wavelengths of 1600 nm, they operate near room temperature and they are Si CMOS-compatible devices. As a consequence, the amount of data on their characteristics available for their theoretical analysis is high.
2. Device Design and Characteristics
The structure of the SPAD used in [20,21] is presented in Figure 1. The authors presume that an incident light, which enters the detector through a high-concentration boron-doped (∼5 × 1019 cm−3) p++Ge (p-Ge) layer of thickness l = 0.1 µm, is absorbed with the creation of electron–hole pairs in a 1 µm-thick layer of intrinsic Ge (i-Ge). The created PEs are then dragged by an applied voltage of ~40 V toward the intrinsic Si (i-Si) layer of 1 μm thickness. In this layer, these PEs initiate an electron avalanche, which multiplies the number of electrons at the output of this layer to a readily detectable level. The p-doped Si of 0.1 µm thickness forms the charge sheet. It ensures that the electric field in i-Ge layer is well below an avalanche breakdown field, while the field in the Si multiplication layer is 3 times greater than the breakdown field to provide impact ionization. The structure was grown on a highly doped n++Si substrate. The material in i-Ge and i-Si layers is “pure”, i.e., not intentionally doped, that is, with a concentration of uncontrolled admixtures of ~1015 cm−3. The device with a 25 μm entrance aperture diameter operated at temperatures of T = 100–150 K. That SPAD was irradiated by a 10 kHz sequence of 50 ps pulses of laser radiation at wavelengths of λ = 2πc/ω = 1.31 or 1.55 µm. The radiation from a laser was sent to the entrance of the detector through a single mode fiber (core diameter of~10 µm), a calibrated optical attenuator and a two-lens imaging system. This system allowed reducing the energy in each incident pulse Wi up to ~0.01ħω ≅ 10−21 J. The illuminated volume of Ge layers was estimated as V ≈ 1.1 µm × (10 µm)2 ≈ 10−10 cm3. With such a SPAD, DE at Wi ≤ 0.1ħω was measured to be nonzero at both λ (~4% at λ = 1.31 µm and T = 100 K, and ~0.15% at λ = 1.55 µm and T = 150 K) [20]. The measured dependence of DE on Wi at λ = 1.31 µm and T = 125 K, by the authors [21], is presented in Figure 2. As can be seen, DE(Wi) saturates at ~100% when >10ħω and linearly decreases to ~0.1% at ~0.01ħω with ~13% at ~ħω (see Figure 2). In doing so, DE(Wi) does not manifest any peculiarities at Wi ≅ 1ħω, which may be expected according to Einstein’s model [23]. To elucidate the nature of such observations, we first looked more carefully to [23].
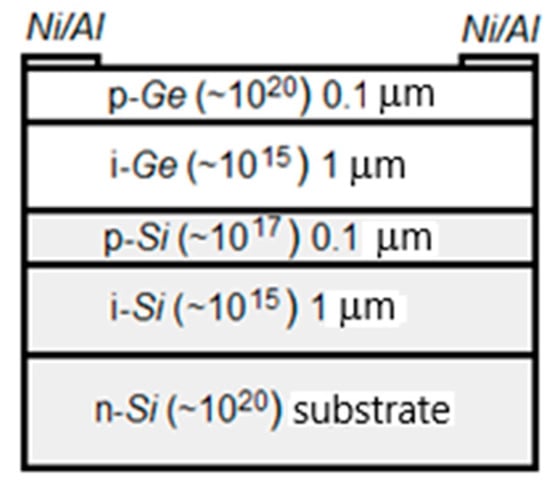
Figure 1.
Ge-on-Si single-photon avalanche diode (SPAD) structure cross-section illustrating two Ge layers, two Si layers, Si substrate, Ni/Al contacts, doping number densities in cm−3 (in brackets) and layer thicknesses.
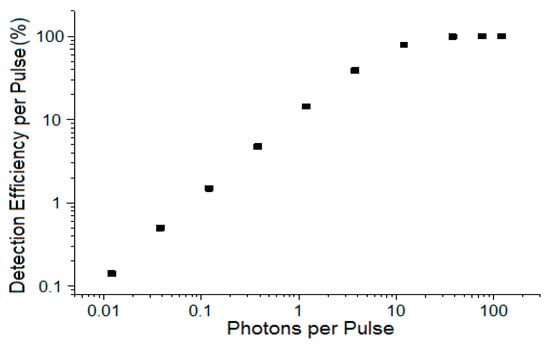
Figure 2.
Detection efficiency (DE) vs. the energy in an incident radiation pulse.
3. Discussion
Analysis of the data presented above has led us to the following questions:
- To what extent is Einstein’s model of PE relevant to the processes in such SPADs and observed results?
- If not Einstein’s model, then how can the observed results and their interpretation be made compatible?
3.1. Einstein’s Model and Its Prerequisites
According to Einstein [23], an electron, which is bound in a medium, becomes a photoelectron when its kinetic energy, acquired from incident radiation, is higher than the energy binding it to the medium. The incident radiation of frequency ω is considered as a flow of quanta with energy ħω. The important prerequisites of his model may be re-formulated as (1) the quanta penetrate to the surface layer of a material, where their energy is converted to the kinetic energy of electrons, and (2) one light quantum gives up all its energy to one electron.
Regarding these prerequisites in relation to detection of a single photon in SPADs, the first one requires that in the region of where a photoelectron is generated, incident radiation, i.e., the energy of a photon, is not attenuated due to its conversion to any other forms of energy, e.g., to heat, radiation of other frequencies. The objective data on the light absorption coefficient (α) in Ge show that this requirement is not met: at λ ≈ 1.3–1.55 µm α = (5 ± 1) × 103 cm−1 in i-Ge [25] and ~(1-2) × 103 cm−1 in heavily doped p-Ge (concentration Np ≥ 5 × 1019 cm−3) [26]. It follows from these data that, while the p-Ge layer is practically transparent (αl ≤ 0.02), the i-Ge layer is half transparent (αl ≅ 0.5). This means, in particular, that if a photoelectron appears in the i-Ge layer, it, most probably, happens in a thin entrance surface part (l < 0.1 µm) of the whole i-Ge layer. This may also happen in the p-Ge layer.
To choose between the two, we must take into account the following circumstances. It is known that conventional i-Ge is a nondegenerate semiconductor with a residual concentration of uncontrolled admixtures and defects of ~1015 cm−3. In such material, the energy gap, Eg, between the valence and conduction bands at T ≈ 100–150 K is of ~0.7 eV, and the Fermi energy level is located in roughly the middle of the forbidden zone, F ≅ Eg/2. Accordingly, the temperature-induced concentration of free electrons Ne(T) in the conduction band of an i-Ge, which is expected to be of <104 cm−3 (at T < 150 K) [27], is negligible compared to Ne ≅ 1015 cm−3 due to uncontrolled admixtures and defects [28]. It then follows that in the volume of i-Ge layer in [20,21], V ≈ 1 µm × (10 µm)2 ≈ 10−11 cm3, the number of free electrons will be of ~105. Obviously, it is problematic to detect the appearance of a single PE on such a background.
The situation is different in a heavily doped p-Ge (Np ≅ (0.5–1) × 1020 cm−3) [27]. The Fermi level in such a case is shifted to the valence band and all free electrons are captured by acceptors. As a result, Ne tends to zero. In this case, the appearance of a single additional free electron is obviously an event. If this is the case, the SPAD we consider operates like a conventional photomultiplier tube (PMT), in which the p-Ge layer plays the role of a photocathode, and the i-Ge layer is equivalent to the vacuum spacing between the photocathode and the multiplying electrons system of dynodes. Such a role of p-Ge and i-Ge layers in SPADs was never discussed before.
It follows from above that the p-Ge layer is transparent for incident light (αl < 0.02) and has a low concentration of free electrons. A material in which such conditions are upheld behaves as an optically transparent dielectric.
3.2. The Electromagnetic Energy in a Dielectric
According to [29], the density of electromagnetic (EM) energy, Ud, in a dielectric medium (µ = 1) is
where Ed and Hd are the amplitudes of electric and magnetic fields, is the permittivity and χ is the susceptibility. The last term in (1) is the part of the EM energy density which is transferred to the movement of the bound electrons (BEs) in a dielectric. It is important to note here that in absence of other losses, this energy returns to the radiation field when it leaves a medium. Dividing this energy by the density of the BEs number, Ne, which are involved in the interaction, one can get the amount of EM energy, which is transferred to one BE, W1. To estimate W1 in the case under consideration, we must take into account that the permittivity of Ge is ε ≅ n2 ≅ 17. This, in particular, means that, to sufficient, accuracy we can suppose that Ud ≅ Uin = Iin/c, where Iin is the intensity of incident laser radiation in vacuum (n = 1), i.e., before it enters the SPAD, in each pulse and c is the velocity of light in vacuum. To estimate Iin and Ud, respectively, we take, for definiteness, the energy in each pulse of 0.1ħω ≅ 1.5 × 10−20 J and the diameter of the irradiated spot at the entrance of the device of 10 μm. Then, for a 50 ps duration of pulses, we get Iin ≅ 0.4 mW/cm2 and Ud ≅ 105 eV/cm3. Therefore, taking into account that the total density of BEs in Ge, defined as Ne, = Na x32 is ≈ 1.3 × 1024 cm−3, where Na is the number of Ge atoms per cm3, which is ~4 × 1022 cm−3, and “32” is the number of electrons in a Ge atom, we get W1 ≅ 10−19 eV. This energy is obviously much, much less than the conventional direct bandgap energy in Ge, e.g., Eg(125K) ≅ 0.7 eV. This is actually true even for radiation pulses with energy of 1sħω, 10sħω, 1000sħω, etc.
Then, the following questions need answers: (1) How can only one of all electrons in the irradiated p-Ge layer get the whole energy from an incident radiation pulse? (2) Why does that electron overcome the bandgap energy barrier presumed to be Eg(125K) ≅ 0.7 eV when the energy it can get from a pulse is much less than Eg?
3.3. The Effect of Interference
To answer the first question, we must account for the fact that an electron driven by an oscillating electric field is the source of a secondary emission. Interference is the only physical phenomenon which is capable of redistributing the averaged energy in a system of many radiation emitters. If we then take into consideration that the incident radiation, which is generated by a laser, is highly coherent throughout the volume of Ge layers, V ≈ 10−10 cm3, the driven oscillations of electrons in this volume and the fields reradiated by each of them will be coherent. As such, re-radiated fields can constructively interfere at some time during irradiation and at some point inside this volume (see, e.g., point C in Figure 3). Taking into account that the total density number of electrons in Ge is Ne ≈ 1.3 × 1024 cm−3, then the number of electrons, involved in such an interaction, is N ≅ Ne × V ≈ 1.4 × 1014, and potentially the factor of radiation intensity, and EM energy density, enhancement may be potentially up to N2 ≈ 2 × 1028. It is much less in reality.
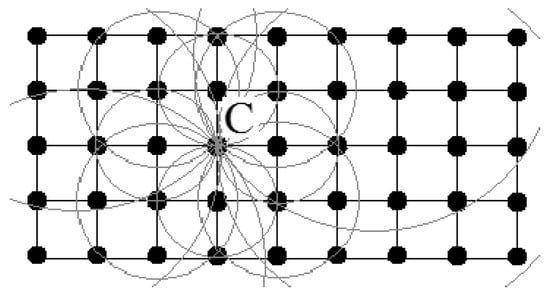
Figure 3.
Schematic sketch of how the constructive interference of electromagnetic (EM) fields, which are re-emitted by surrounding electrons, may increase the radiation intensity at point C in a material lattice. Thin circles represent the wavefronts of re-emitted fields.
To estimate a potential factor of enhancement, we must take into consideration several circumstances. Firstly, the nature of secondary emission by electrons is twofold: it may be a result of accelerated movement of an electron [30] and of an oscillating dipole which is formed by an electron and a positively charged atomic rest [29].
In the first case, all ~1.3 × 1024 cm−3 electrons of a material are sources of re-emission because the electric field Ei of the incident radiation moves an electron regardless of where it is located. The strength (amplitude) of an electric field, Ee, that is re-emitted by being driven with the acceleration electron decreases with distance R from that electron as [30]
where θ is the angle between the direction of the Hertzian vector and the direction of the observation. Correspondent movement is governed by the equation
where is the velocity of an electron, e and m are its charge and mass and Ei is the amplitude of the electric field of the incident radiation of frequency ω0. Accordingly, we have for the re-emitted field amplitude at the distance R from a point charge emitter
In the second case, an atom is considered as a set of dipole oscillators. These re-emit an EM wave to the electric field, the amplitude of which is decaying with R as [29]
where r(t) is the displacement of an electron from its equilibrium position at an orbit in an atom, which is driven by the electric field of the incident radiation Ei. This displacement may be described by the oscillator equation [31]
where γi is the coefficient, which characterizes a loss of oscillation energy due to inelastic collisions of an electron with surrounding particles and the material lattice, and ωg is the resonant frequency of an oscillator, the magnitude of which is determined by a bounding force between an electron and its atomic rest. When the radiation is monochromatic, a solution to Equation (6) is
It follows from Equation (7) that, since γi << ωg, ra maximizes when ω0 = ωg and decreases proportionally to 1/ωg2 when ωg >> ω0. It then follows from Equation (7) that the dipole-kind re-emission by the electrons, which occupy the deeper orbits, may be considered negligible since these have much higher energies than those bound with an atomic rest, i.e., much higher ωg. Consequently, in a Ge atom, the number of BEs, which are active in the dipole-kind interaction with NIR optical radiation, is limited to 4, giving the density of correspondent Bes, Nd = 4Na ≈ 1.6 × 1023 cm−3.
Let us evaluate the effect of the coherent summation at some point, C, in the p-Ge layer of the fields re-emitted by all involved electrons and dipoles in the SPAD. Consider in a medium a half-sphere of radius R with the thickness of wall δR. Its volume is
The number of emitters in this volume is
All these emitters are equidistant from some point, C, in the p-Ge layer (see Figure 4). An effective distance Rm in the body of the SPAD, from which a re-emitted radiation may have an essential magnitude at C, is of α−1. We then must account for the notion that the electric field of the incident radiation Ei drives the emitters in the plane parallel to the p-Ge layer. These emitters give rise to a re-emission of radiation with the electric field amplitude Ee dependent on θ (see Equations (4) and (5)). To account for this effect, we choose on the semi-sphere layer of a radius R a sub-volume δv = δsδR = R2δθδφδR, where δs is the cross-sectional area of the sub-volume. All emitters in such a volume will produce at C the fields of practically the same amplitude.
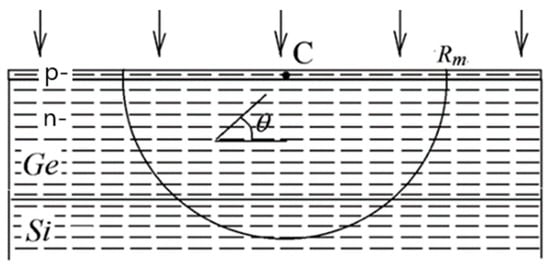
Figure 4.
Schematic sketch of the Ge (p- and n-) and Si layers in a SPAD, the re-emission from which contributes to an enhanced field at the point C in the p-Ge layer. Vertical arrows represent the propagation direction of the incident radiation, horizontal dashes represent electrons driven by the incident radiation, Rm is the effective absorption length of radiation and θ is the angle between the direction of electron oscillations and the direction from this electron to point C.
Multiplying δv by Ne and Ee from Equation (4) and integrating over R, θ and φ, we get the field, which may be induced at point C by the coherent summation of the fields re-emitted by all electrons in Ge and Si layers in the SPAD:
where a0 ≅ 2.8 × 10−8 cm is the Ge/Si lattice constant. The magnitude of |Fe(Rm)|2 determines a magnitude of W1 enhancement at point C when re-emission of all electrons in the irradiated volume is coherently summed. Substituting into Equation (10) the magnitudes of the corresponding parameters of Ge and Si (Ne ≈ 1024 cm−3, nGe ≅ 4,1, nSi ≅ 3.5 and Rm ≅ α−1 ≅ 2 μm), one would get |Fe|2 ≅ 2 × 109, which is clearly much less than the desirable ~1019.
Similarly, using Equations (5) and (7), presuming ω0 = ωg and taking into account that Rm >> a0, we get the enhancement factor in the case of re-emission by dipoles:
Among the parameters, magnitudes of which determine |Fd|2, the most uncertain one is γi. According to [30] its magnitude in semiconductors may vary in the range from ~1010 s−1 at a room temperature to ~107 s−1 at lower T. Substituting to Equation (11) magnitudes of e, m, n, c and ωg = Eg/ħ = 1015 s−1, we get
It follows from Equation (12) that at γi ≤ 2 × 109 s−1, which is a reasonable magnitude for Ge at T = 100–150 K, W1|Fd|2 ≥ 0.7 eV, even at W1 = 0.01ħω0 ≅ 10−21 J, i.e., this is just the energy sufficient for an electron to overcome the energy barrier of the forbidden zone in Ge. An important condition for the realization of such enhancement, which is ω0 = ωg, is the well-known Einstein condition ħω0 = Eg = ħωg.
The only problem, however, is that the conservation of energy in the case under consideration remains an enigma when Wi < Eg. A specific feature of heavily doped semiconductors, which is p-Ge used in SPADs [20], gives a clue for resolving this issue.
3.4. The Bandgap in a Heavily Doped p-Ge
In such materials, the typical for intrinsic semiconductors’ sharp zone boundaries (dashed straight lines in Figure 5a) is blurred and the “tails” of the allowed occupation states penetrate the forbidden zone, resulting in a substantially narrower effective bandgap Ege. [27]. The physical reason for this effect is the local fluctuations of the internal electric field in a material due to a generic inhomogeneity of the spatial distribution of a dopant at its high concentration [32]. The local shift of zone boundaries, which is induced by such fluctuations, is illustrated in Figure 5a by the two solid lines and the dashed curved lines. A deformation of zone boundaries, which is schematically depicted by two parallel solid lines, is typical for the case when the effective masses of charge carriers at zone boundaries coincide [27]. The local bandgap in this case does not change. As shown in [32], such a case takes place in p-Ge for indirect interband transitions. The radiation with λ = 1.31 µm (ħω0 ≅ 0.85 eV) falls in the range of direct transitions in Ge (Egd ≅ 0.85 eV). Since an effective mass of electrons at the center of the Brillouin zone is much less than that of holes, the amplitude of the conduction zone boundary deformation is essentially reduced [32] (the dashed curve). The shaded areas represent the “tails”, which are a result of averaging the field fluctuations. Figure 5b illustrates, schematically, the averaged densities of the allowed occupation states Nc,v(E) for electrons (c) and holes (v) for intrinsic (dash-dotted lines) and for highly doped (solid lines) material, and the intrinsic Egi and effective bandgap Ege.
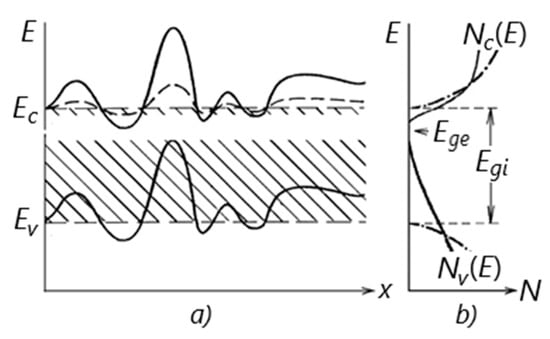
Figure 5.
(a) Spatial variation in the conduction and valence band boundaries, Ec,v, in a pure semiconductor (dashed straight lines) and in a heavily doped semiconductor (solid lines). (b) Effective densities of the allowed occupation states Nc,v(E) for electrons (c) and holes (v) for intrinsic (dash-dotted lines) and for highly doped (solid lines) material.
In particular, in Ge at Nd ≥ 1020 cм−3, the factor of the effective gap narrowing may be up to ~100 [27]. These circumstances allow us to account for why the appearance of a photoelectron resulting from the irradiation of a light pulse with sub-photon energy in the SPAD under consideration does not contradict the conservation of the energy principle in this interaction.
4. Conclusions
Classical macroscopic electrodynamics allows us to account for the photoelectric effect in a Ge-on-Si SPAD when the incident pulsed laser radiation is of sub-photon energy. The energy of the incident laser radiation, when transferred to a huge number of electrons in the Ge matrix, can concentrate on only one of these through the effect of constructive interference of the fields re-emitted by surrounding electrons. The conventional necessary condition for the photoelectric effect in a material, which reads as ω0 = Eg/ħ [23], comes to the model as a resonant condition for the Lorentz classical oscillator model. The conservation of the energy law in this interaction is upheld because of a substantial narrowing of the effective bandgap in the heavily doped p-Ge layer of the SPAD. Since the classical model presented in this work is linear with respect to the energy in an incident pulse Wi, the fact that the experimental data shown in Figure 2 demonstrate a smooth linear decrease in the detection efficiency with a decrease in Wi when Wi < 10 ħω and manifest no peculiarities at Wi ≅ 1 ħω is in good agreement with the developed model.
Funding
This research received no external funding.
Acknowledgments
The author would like to thank G. S. Buller and P. Vines for useful discussions.
Conflicts of Interest
The author declares no conflict of interest.
References
- Zhang, J.; Itzler, M.A.; Zbinden, H.; Pan, J.-W. Advances in InGaAs/InP single-photon detector systems for quantum communication. Light Sci. Appl. 2015, 4, e286. [Google Scholar] [CrossRef]
- Takesue, H.; Nam, S.W.; Zhang, Q.; Hadfield, R.H.; Honjo, T.; Tamaki, K.; Yamamoto, Y. Quantum key distribution over a 40-dB channel loss using superconducting single-photon detectors. Nat. Photonics 2007, 1, 343–348. [Google Scholar] [CrossRef]
- Buller, G.S.; Warburton, R.E.; Pellegrini, S.; Ng, J.S.; David, J.P.R.; Tan, L.J.J.; Krysa, A.B.; Cova, S. Single-photon avalanche diode detectors for quantum key distribution. IET Optoelectron. 2007, 1, 249–254. [Google Scholar] [CrossRef]
- Xiao, L.; Long, G.L.; Deng, F.G.; Pan, J.W. Efficient multiparty quantum-secret-sharing schemes. Phys. Rev. A 2004, 69, 052307. [Google Scholar] [CrossRef]
- Gisin, N.; Ribordy, G.; Tittel, W.; Zbinden, H. Quantum cryptography. Rev. Mod. Phys. 2002, 74, 145–195. [Google Scholar] [CrossRef]
- O’Brien, J.L. Optical quantum computing. Science 2007, 318, 1567–1570. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Sciarrino, F.; Laing, A.; Thompson, M.G. Integrated photonic quantum technologies. Nat. Photonics 2019, 14, 273–284. [Google Scholar] [CrossRef]
- Hall, D.; Liu, Y.-H.; Lo, Y.-H. Single photon avalanche detectors: Prospects of new quenching and gain mechanisms. Nanophotonics 2015, 4, 397–412. [Google Scholar] [CrossRef]
- Hemmati, H.; Biswas, A.; Djordjevic, I.B. Deep space optical communications: Future perspectives and applications. Proc. IEEE 2011, 99, 2020–2039. [Google Scholar] [CrossRef]
- Campbell, J.C. Recent advances in telecommunications avalanche photodiodes. J. Lightwave Tech. 2007, 25, 109–121. [Google Scholar] [CrossRef]
- Niclass, C.; Rochas, A.; Besse, P.-A.; Charbon, E. Design and characterization of a CMOS 3-D image sensor based on single photon avalanche diodes. IEEE J. Solid State Circuits 2005, 40, 1847–1854. [Google Scholar] [CrossRef]
- Warburton, R.E.; McCarthy, A.; Wallace, A.M.; Hernandez-Marin, S.; Hadfield, R.H.; Nam, S.W.; Buller, G.S. Subcentimeter depth resolution using a single-photon counting time-of-flight laser ranging system at 1550 nm wavelength. Opt. Lett. 2007, 32, 2266–2268. [Google Scholar] [CrossRef] [PubMed]
- Pawlikowska, A.M.; Halimi, A.; Lamb, R.A.; Buller, G.S. Single-photon three-dimensional imaging at up to 10 kilometers range. Opt. Express 2017, 25, 11919–11931. [Google Scholar] [CrossRef] [PubMed]
- Tobin, R.; Halimi, A.; McCarthy, A.; Laurenzis, M.; Christnacher, F.; Buller, G.S. Three-dimensional single-photon imaging through obscurants. Opt. Express 2019, 27, 4590–4611. [Google Scholar] [CrossRef]
- Llin, L.F.; Kirdoda, J.; Thorburn, F.; Huddleston, L.L.; Greener, Z.M.; Kuzmenko, K.; Vines, P.; Dumas, D.C.S.; Millar, R.W.; Buller, G.S.; et al. High sensitivity Ge-on-Si single-photon avalanche diode detectors. Opt. Lett. 2020, 45, 6406–6409. [Google Scholar] [CrossRef]
- Hadfield, R.H. Single-photon detectors for optical quantum information applications. Nat. Photonics 2009, 3, 696–705. [Google Scholar] [CrossRef]
- Buller, G.S.; Collins, R.J. Single-photon generation and detection. Meas. Sci. Technol. 2010, 21, 012002. [Google Scholar] [CrossRef]
- Eisaman, M.D.; Fan, J.; Migdall, A.; Polyakov, S.V. Invited Review Article: Single-photon sources and detectors. Rev. Sci. Instrum. 2011, 82, 071101. [Google Scholar] [CrossRef]
- Kang, Y.; Lo, Y.-H.; Bitter, M.; Kristjansson, S.; Pan, Z.; Pauchard, A. InGaAs-on-Si single photon avalanche photodetectors. Appl. Phys. Lett. 2004, 85, 1668–1670. [Google Scholar] [CrossRef]
- Warburton, R.E.; Intermite, G.; Myronov, M.; Allred, P.; Leadley, D.R.; Gallacher, K.; Paul, D.J.; Pilgrim, N.J.; Lever, L.J.M.; Ikonic, Z.; et al. Ge-on-Si Single-Photon Avalanche Diode Detectors: Design, Modeling, Fabrication, and Characterization at Wavelengths 1310 and 1550 nm. IEEE Trans. Electron Devices 2013, 60, 3807–3813. [Google Scholar] [CrossRef]
- Vines, P.; Kuzmenko, K.; Kirdoda, J.; Dumas, D.C.S.; Mirza, M.M.; Millar, R.W.; Paul, D.J.; Buller, G.S. High performance planar germanium-on-silicon single-photon avalanche diode detectors. Nat. Commun. 2019, 10, 1086. [Google Scholar] [CrossRef] [PubMed]
- Gol’tsman, G.N.; Okunev, O.; Chulkova, G.; Lipatov, A.; Semenov, A.; Smirnov, K.; Voronov, B.; Dzardanov, A.; Williams, C.; Sobolewski, R. Picosecond superconducting single-photon optical detector. Appl. Phys. Lett. 2001, 79, 705–707. [Google Scholar] [CrossRef]
- Einstein, A. Uber einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt. Ann. Phys. 1905, 17, 132–148. [Google Scholar] [CrossRef]
- Kirdoda, J.; Dumas, D.C.S.; Kuzmenko, K.; Vines, P.; Greener, Z.M.; Millar, R.W.; Mirza, M.M.; Buller, G.S.; Paul, D.J. Geiger Mode Ge-on-Si Single-Photon Avalanche Diode Detectors. In Proceedings of the 2019 IEEE 2nd British and Irish Conf. on Optics and Photonics (BICOP), London, UK, 11–13 December 2020. [Google Scholar] [CrossRef]
- Dash, W.; Newman, R. Intrinsic optical absorption in single-crystal germanium and silicon. Phys. Rev. 1955, 99, 1151–1155. [Google Scholar] [CrossRef]
- Bagaev, V.S.; Proshko, G.P.; Shotov, A.P. Infrared absorption in heavily doped germanium. Sov. Phys. Solid State 1963, 4, 2363–2368. [Google Scholar]
- Bonch-Bruevich, V.L.; Kalashnikov, S.G. Physics of Semiconductors; Nauka Press: Moscow, Russia, 1977. (In Russian) [Google Scholar]
- Cuttris, D.B. Relation Between Surface Concentration and Average Conductivity in Diffused Layers in Germanium. Bell Syst. Tech. J. 1961, 40, 509–523. [Google Scholar] [CrossRef]
- Tamm, I.E. Basics of Electricity Theory; OGIZ: Moscow, Russia, 1946. (In Russian) [Google Scholar]
- Jackson, J.D. Classical Electrodynamics, 3rd ed.; Willey & sons: New York, NY, USA, 1962. [Google Scholar]
- Lorentz, H.A. The Theory of Electrons and its Applications to the Phenomena of Light and Radiant Heat; Leipzig B.G.: Teubner, Germany, 1916. [Google Scholar]
- Keldish, L.V.; Proshko, G.P. Infrared absorption in heavily doped germanium. Sov. Phys. Solid State 1964, 5, 2481–2488. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).