Figure 1.
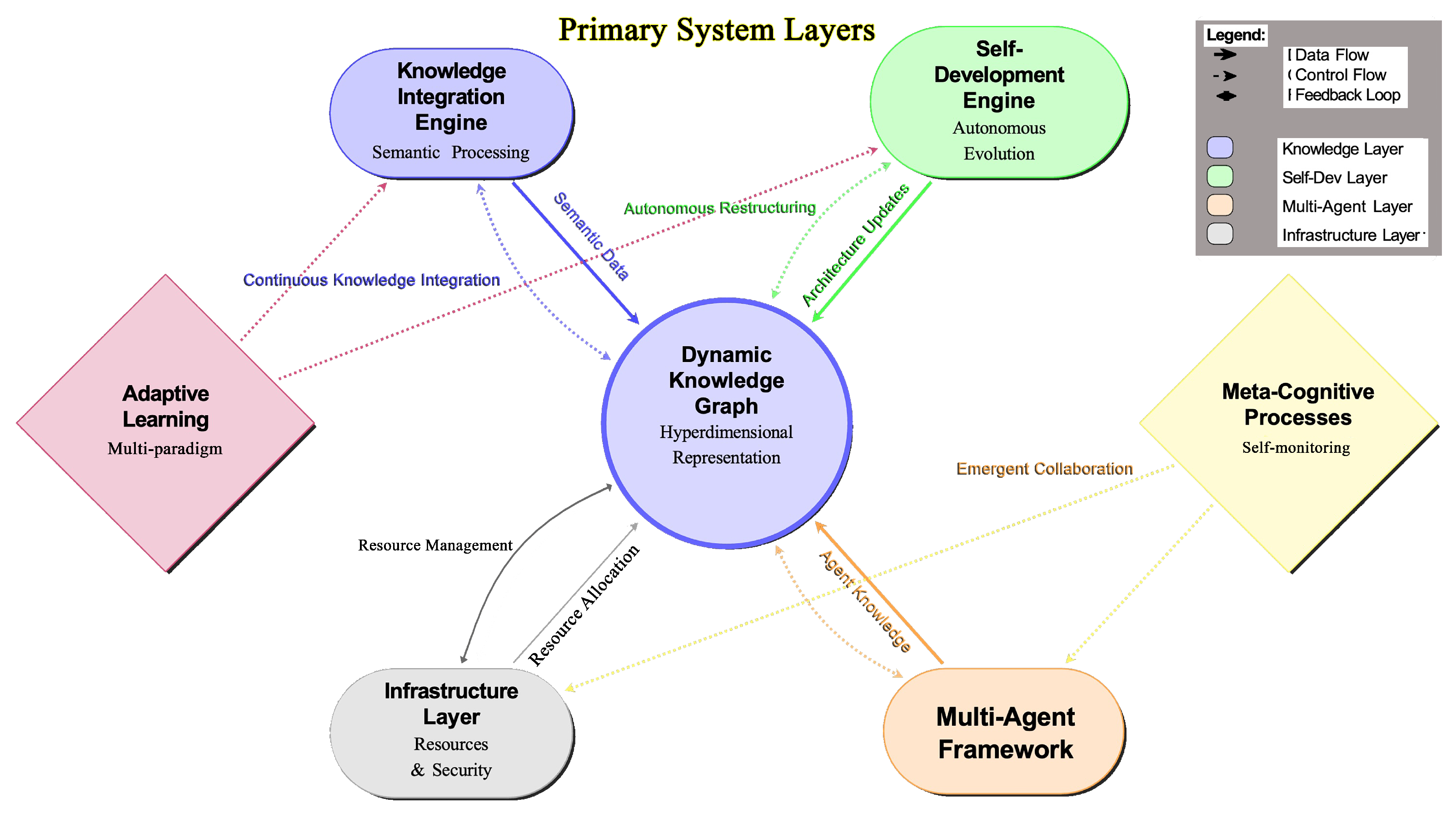
Core architectural components of Liquid AI showing the dynamic interaction between the Knowledge Integration Engine, Self-Development Module, Multi-Agent Coordinator, and supporting infrastructure. Components are color-coded by function with bidirectional data flows indicated by arrows. Arrows indicate bi-directional data flows among components, highlighting continuous feedback loops critical for maintaining coherence and adaptive system performance.
Figure 1.
Core architectural components of Liquid AI showing the dynamic interaction between the Knowledge Integration Engine, Self-Development Module, Multi-Agent Coordinator, and supporting infrastructure. Components are color-coded by function with bidirectional data flows indicated by arrows. Arrows indicate bi-directional data flows among components, highlighting continuous feedback loops critical for maintaining coherence and adaptive system performance.
Figure 2.
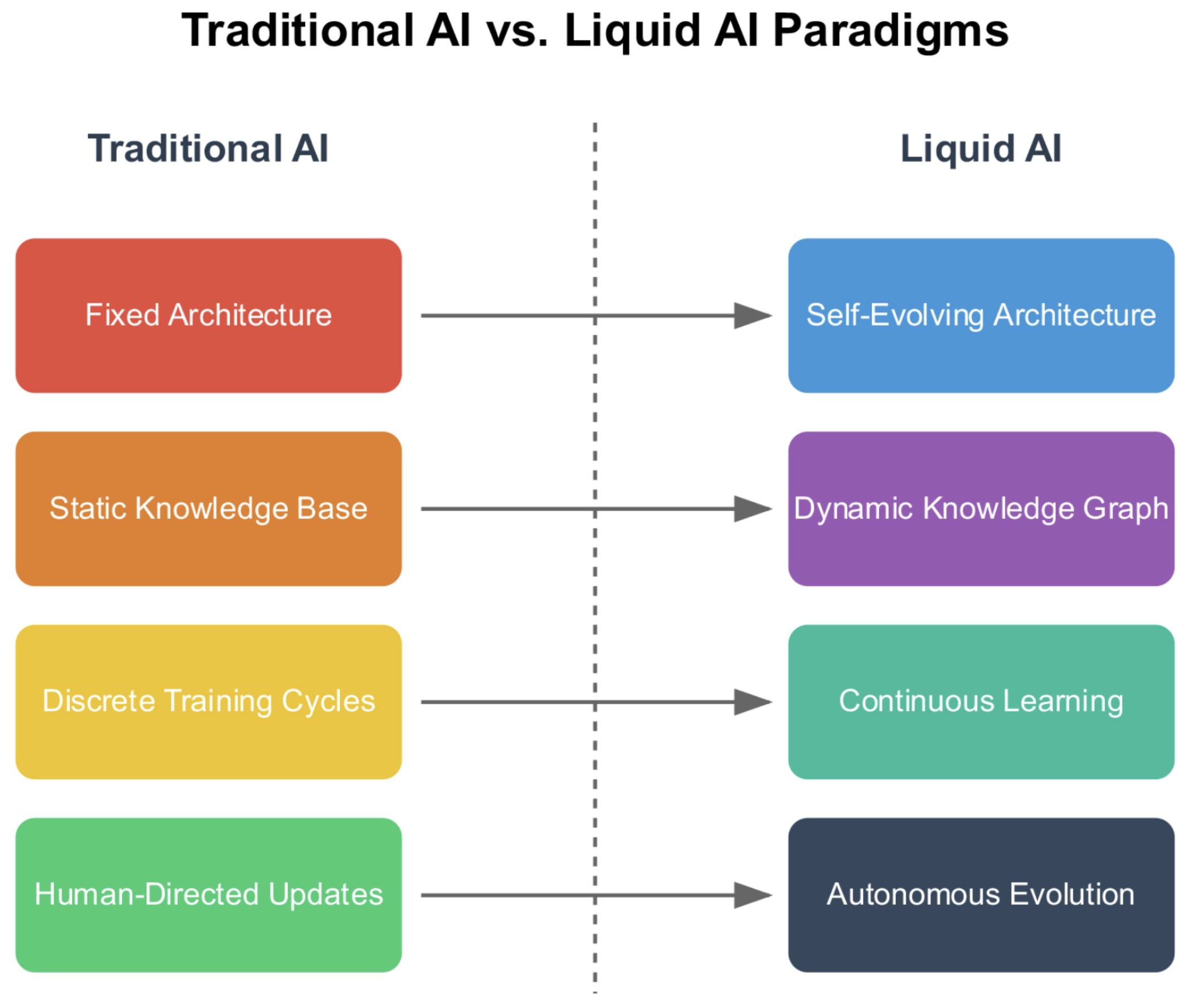
Comparative analysis of traditional AI versus Liquid AI paradigms. Systematic comparison between traditional AI and Liquid AI (right) approaches across four key dimensions: Fixed Architecture vs. Self-Evolving Architecture, Static Knowledge Base vs. Dynamic Knowledge Graph, Discrete Training Cycles vs. Continuous Learning, and Human-Directed Updates vs. Autonomous Evolution. Connecting arrows demonstrate the evolutionary progression from traditional to liquid paradigms.
Figure 2.
Comparative analysis of traditional AI versus Liquid AI paradigms. Systematic comparison between traditional AI and Liquid AI (right) approaches across four key dimensions: Fixed Architecture vs. Self-Evolving Architecture, Static Knowledge Base vs. Dynamic Knowledge Graph, Discrete Training Cycles vs. Continuous Learning, and Human-Directed Updates vs. Autonomous Evolution. Connecting arrows demonstrate the evolutionary progression from traditional to liquid paradigms.
Figure 3.
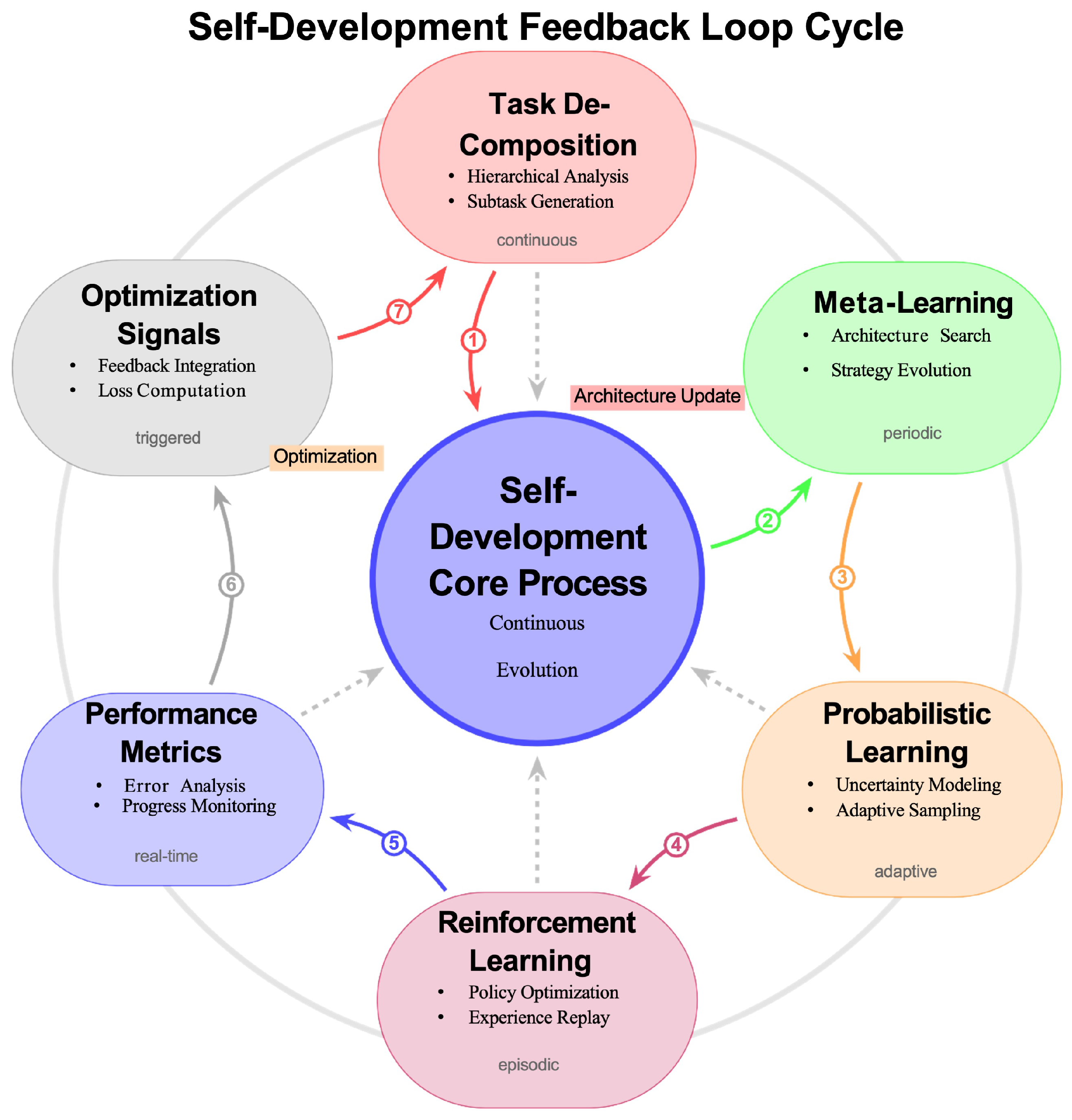
Self-development mechanisms and feedback loops in Liquid AI showing the continuous cycle of assessment, planning, execution, and reflection. The assessment phase evaluates current system performance and identifies gaps in capability relative to defined objectives. During planning, hierarchical Bayesian optimization and meta-learning strategies are employed to design and select optimal architectural modifications, aiming for incremental capability improvements. Execution involves dynamically applying these modifications to the architecture, guided by constraints to ensure system stability and performance continuity. In the reflection stage, the system critically analyzes outcomes, updating its internal models to inform future optimization cycles, thus enabling perpetual self-directed growth and evolution.
Figure 3.
Self-development mechanisms and feedback loops in Liquid AI showing the continuous cycle of assessment, planning, execution, and reflection. The assessment phase evaluates current system performance and identifies gaps in capability relative to defined objectives. During planning, hierarchical Bayesian optimization and meta-learning strategies are employed to design and select optimal architectural modifications, aiming for incremental capability improvements. Execution involves dynamically applying these modifications to the architecture, guided by constraints to ensure system stability and performance continuity. In the reflection stage, the system critically analyzes outcomes, updating its internal models to inform future optimization cycles, thus enabling perpetual self-directed growth and evolution.
Figure 4.
Federated multi-agent architecture showing emergent specialization patterns and communication pathways between heterogeneous agents. Distinct agent clusters represent specialized subgroups, each autonomously optimized for handling specific computational tasks, thereby maximizing collective efficiency and problem-solving capabilities. The communication pathways depicted as connecting lines illustrate adaptive, decentralized information exchange among agents, facilitating dynamic coordination and consensus-driven decision-making. Emergent specialization arises naturally from interactions and shared learning experiences, rather than explicit pre-defined roles, ensuring flexibility and resilience as tasks and computational demands evolve.
Figure 4.
Federated multi-agent architecture showing emergent specialization patterns and communication pathways between heterogeneous agents. Distinct agent clusters represent specialized subgroups, each autonomously optimized for handling specific computational tasks, thereby maximizing collective efficiency and problem-solving capabilities. The communication pathways depicted as connecting lines illustrate adaptive, decentralized information exchange among agents, facilitating dynamic coordination and consensus-driven decision-making. Emergent specialization arises naturally from interactions and shared learning experiences, rather than explicit pre-defined roles, ensuring flexibility and resilience as tasks and computational demands evolve.
Figure 5.
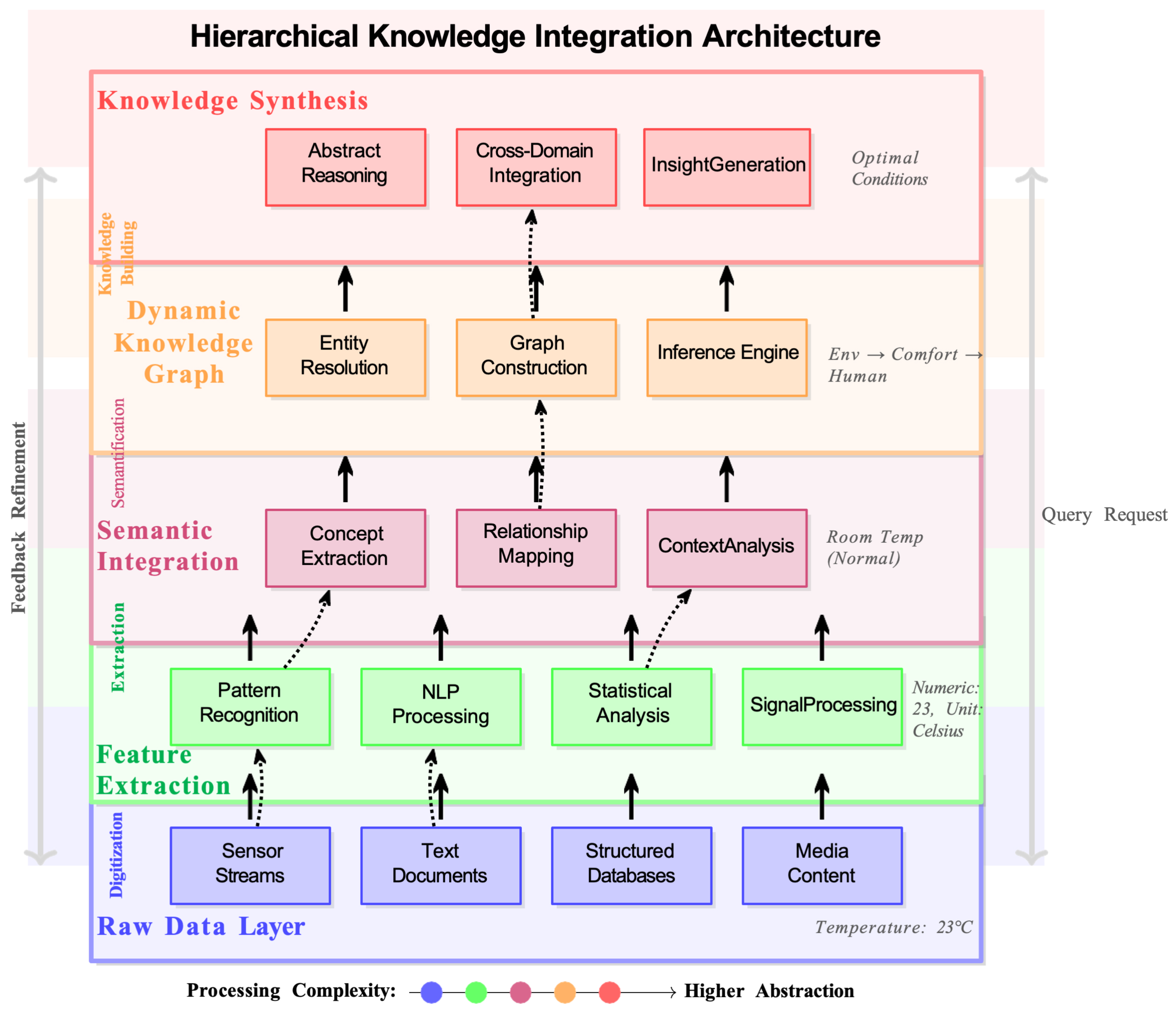
Knowledge integration layers showing the hierarchical organization from raw data through semantic concepts to abstract reasoning. The base layer illustrates the collection (“ingestion”) and initial processing of diverse data sources into structured representations. Intermediate layers demonstrate semantic integration, transforming raw information into meaningful concepts through hyperdimensional embedding and relational reasoning mechanisms. The top layer represents abstract reasoning, where the system synthesizes integrated concepts into generalized insights and decisions, enabling cross-domain inference and adaptive problem-solving capabilities. Arrows indicate upward propagation of information and downward feedback loops, ensuring continuous refinement and alignment of knowledge across hierarchical layers.
Figure 5.
Knowledge integration layers showing the hierarchical organization from raw data through semantic concepts to abstract reasoning. The base layer illustrates the collection (“ingestion”) and initial processing of diverse data sources into structured representations. Intermediate layers demonstrate semantic integration, transforming raw information into meaningful concepts through hyperdimensional embedding and relational reasoning mechanisms. The top layer represents abstract reasoning, where the system synthesizes integrated concepts into generalized insights and decisions, enabling cross-domain inference and adaptive problem-solving capabilities. Arrows indicate upward propagation of information and downward feedback loops, ensuring continuous refinement and alignment of knowledge across hierarchical layers.
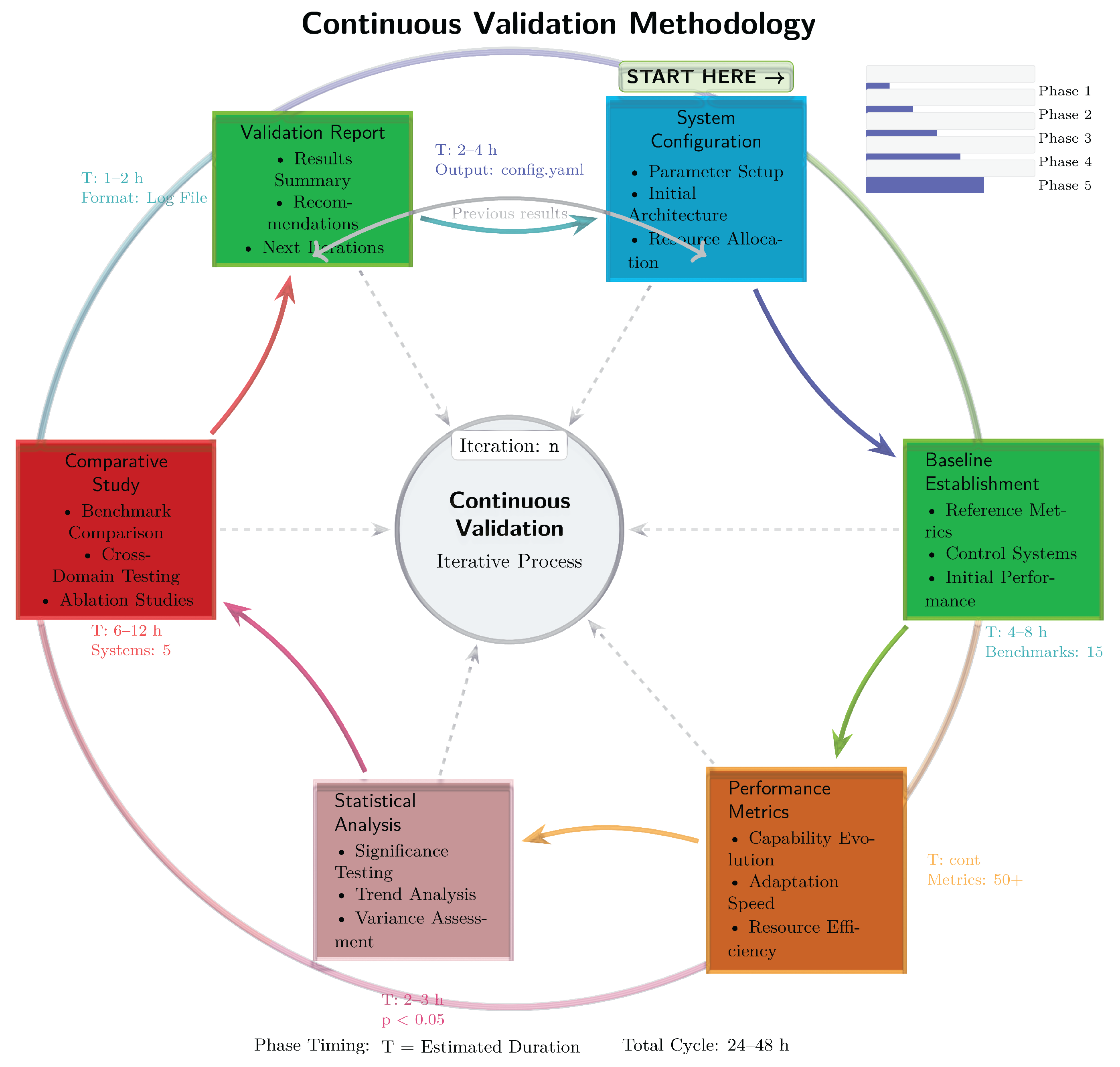
Figure 6.
Empirical validation methodology framework showing the iterative cycle of system configuration, baseline establishment, performance evaluation, and comparative analysis. System configuration includes selection and tuning of architectural parameters based on defined task requirements and computational resources. Baseline establishment involves capturing initial system performance metrics against which subsequent improvements are measured. Performance evaluation is conducted iteratively, leveraging comprehensive metrics to rigorously quantify gains in predictive accuracy, computational efficiency, and adaptive capability. The comparative analysis stage systematically compares results against prior performance and established benchmarks, facilitating continuous refinement and ensuring the Liquid AI framework achieves sustained, measurable improvements over successive iterations.
Figure 6.
Empirical validation methodology framework showing the iterative cycle of system configuration, baseline establishment, performance evaluation, and comparative analysis. System configuration includes selection and tuning of architectural parameters based on defined task requirements and computational resources. Baseline establishment involves capturing initial system performance metrics against which subsequent improvements are measured. Performance evaluation is conducted iteratively, leveraging comprehensive metrics to rigorously quantify gains in predictive accuracy, computational efficiency, and adaptive capability. The comparative analysis stage systematically compares results against prior performance and established benchmarks, facilitating continuous refinement and ensuring the Liquid AI framework achieves sustained, measurable improvements over successive iterations.
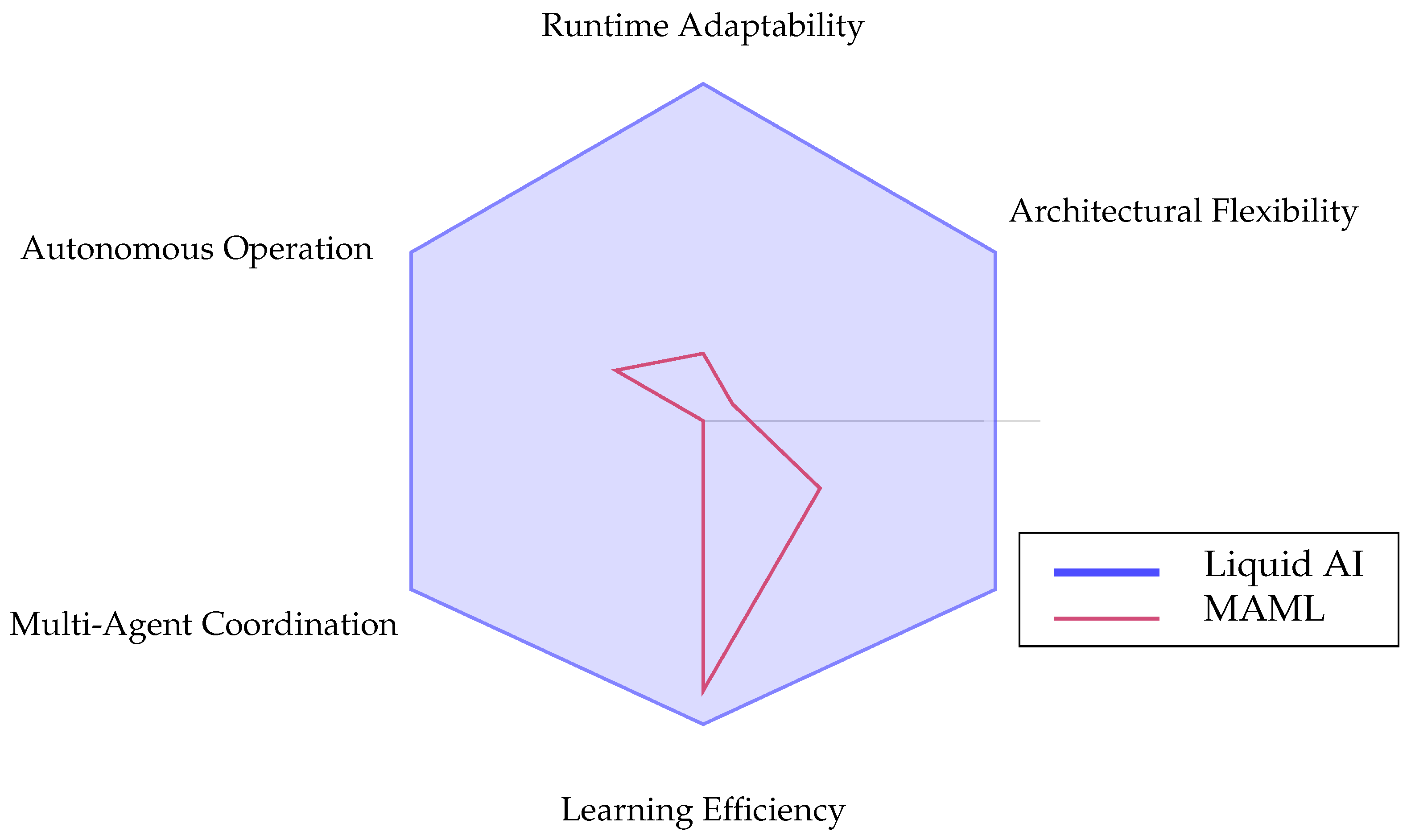
Figure 7.
Comparative analysis of adaptive AI systems across six key capability dimensions. Targeted capability dimensions for Liquid AI compared to existing approaches. Values represent theoretical design goals rather than measured performance. The radar chart visualizes relative performance across critical areas including runtime adaptability, architectural flexibility, knowledge integration, learning efficiency, multi-agent coordination, and autonomous operation.
Figure 7.
Comparative analysis of adaptive AI systems across six key capability dimensions. Targeted capability dimensions for Liquid AI compared to existing approaches. Values represent theoretical design goals rather than measured performance. The radar chart visualizes relative performance across critical areas including runtime adaptability, architectural flexibility, knowledge integration, learning efficiency, multi-agent coordination, and autonomous operation.
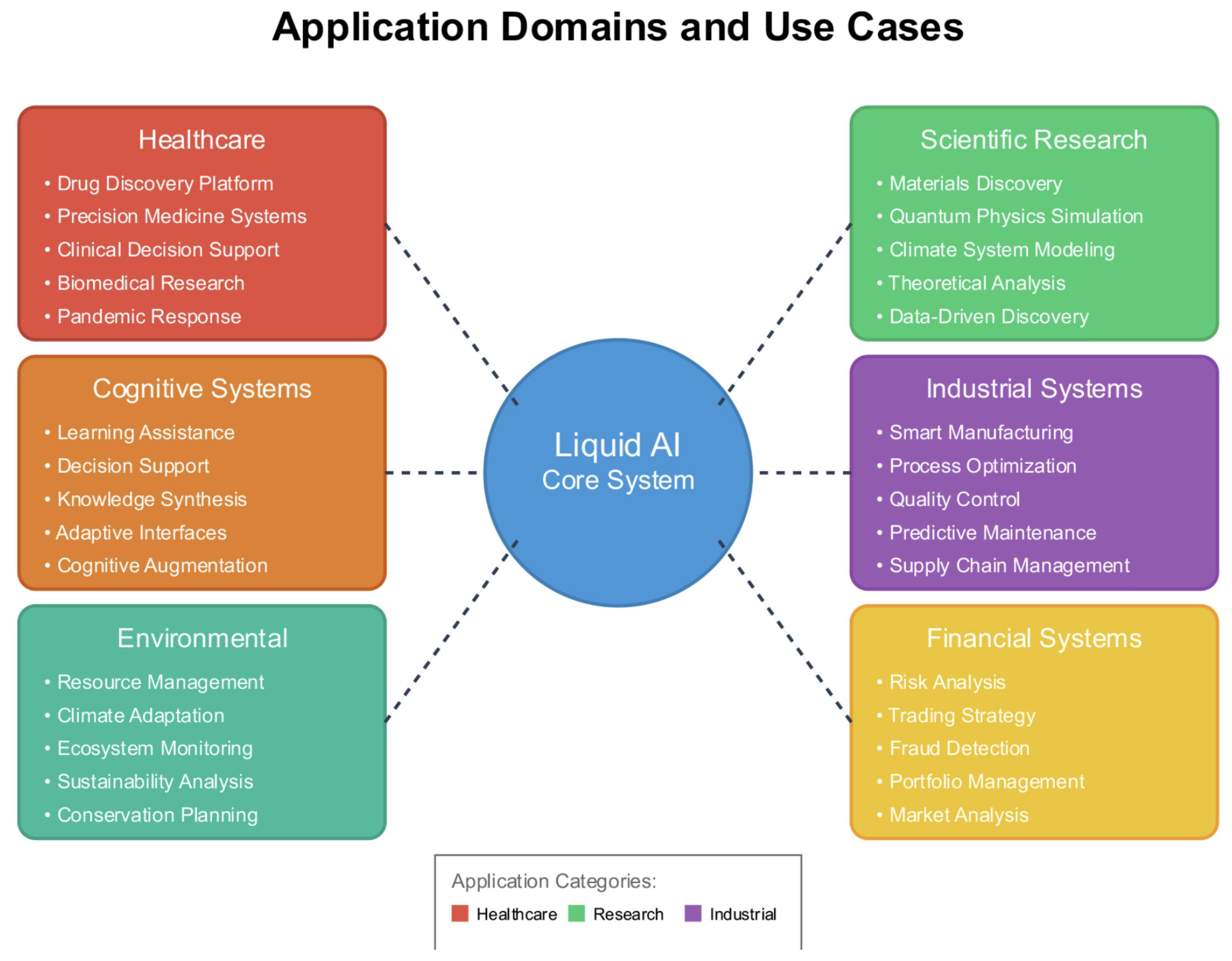
Figure 8.
Application domain and use cases of liquid AI. Systematic representation of six primary application domains: Healthcare (showing drug discovery, precision medicine, clinical analytics), Scientific Research (materials discovery, physics simulation, climate modeling), Industrial Systems (smart manufacturing, quality control, process optimization), Financial Systems (risk analysis, trading strategies, fraud detection), Environmental Management (resource management, climate adaptation, ecosystem monitoring), and Cognitive Systems (learning assistance, decision support, knowledge synthesis).
Figure 8.
Application domain and use cases of liquid AI. Systematic representation of six primary application domains: Healthcare (showing drug discovery, precision medicine, clinical analytics), Scientific Research (materials discovery, physics simulation, climate modeling), Industrial Systems (smart manufacturing, quality control, process optimization), Financial Systems (risk analysis, trading strategies, fraud detection), Environmental Management (resource management, climate adaptation, ecosystem monitoring), and Cognitive Systems (learning assistance, decision support, knowledge synthesis).
Figure 9.
Future research directions and implications. Comprehensive roadmap showing six key research areas arranged along a temporal progression: Theoretical Foundations (mathematical frameworks, convergence properties), Technical Implementation (scalable architecture, resource management), Safety and Ethics (value alignment, governance), Societal Impact (economic effects, policy frameworks), Interdisciplinary Studies (cognitive science, complex systems), and Future Applications (emerging technologies, new domains).
Figure 9.
Future research directions and implications. Comprehensive roadmap showing six key research areas arranged along a temporal progression: Theoretical Foundations (mathematical frameworks, convergence properties), Technical Implementation (scalable architecture, resource management), Safety and Ethics (value alignment, governance), Societal Impact (economic effects, policy frameworks), Interdisciplinary Studies (cognitive science, complex systems), and Future Applications (emerging technologies, new domains).
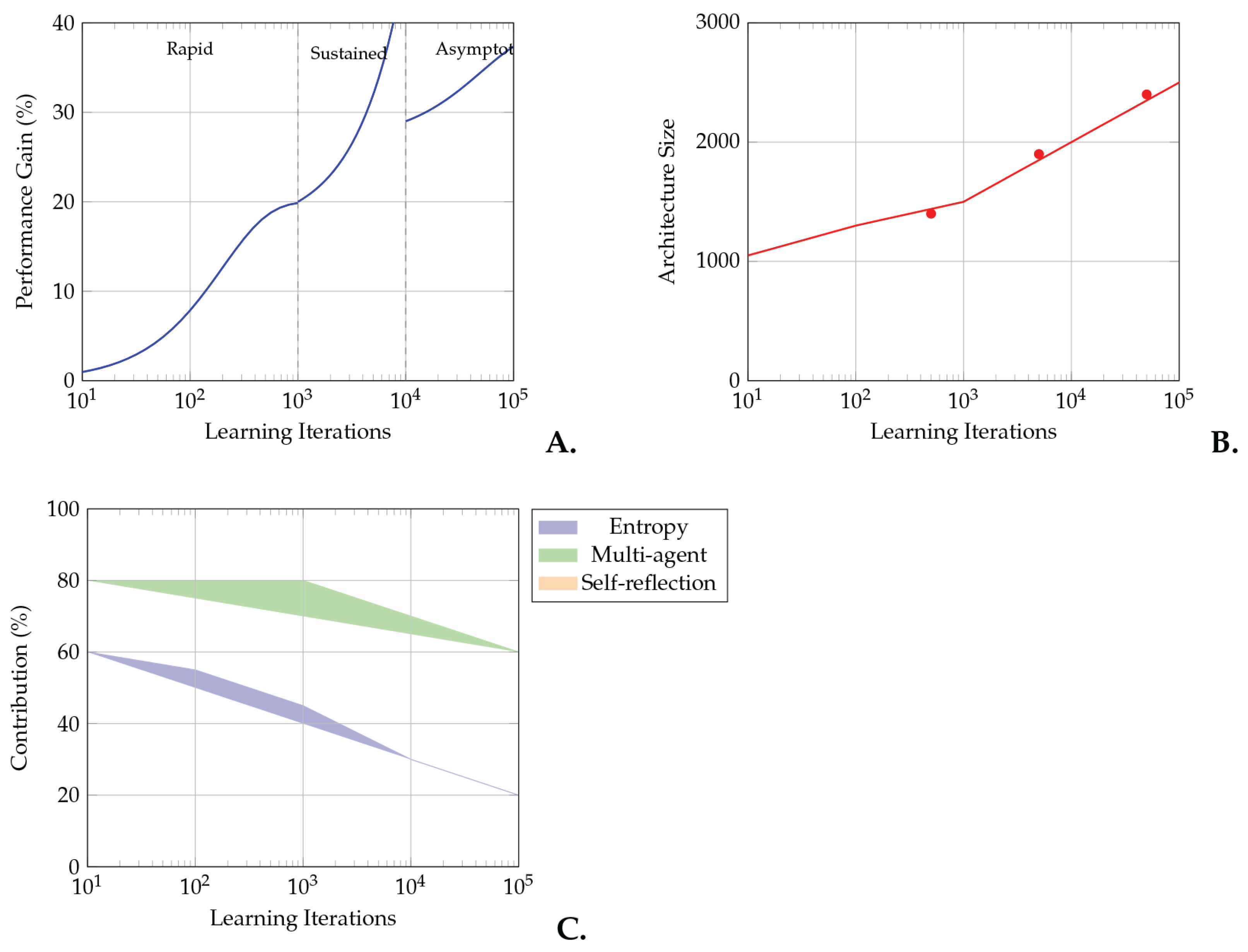
Figure 10.
Theoretical analysis of sustained capability improvement in Liquid AI. (A) Performance improvement trajectory showing three distinct phases: rapid initial learning (0–103 iterations), sustained improvement (103–104), and asymptotic convergence (>104). (B) Architectural complexity evolution demonstrating controlled growth with periodic efficiency optimizations. (C) Relative contributions of three primary feedback mechanisms, showing the shift from entropy-driven exploration to balanced multi-mechanism optimization.
Figure 10.
Theoretical analysis of sustained capability improvement in Liquid AI. (A) Performance improvement trajectory showing three distinct phases: rapid initial learning (0–103 iterations), sustained improvement (103–104), and asymptotic convergence (>104). (B) Architectural complexity evolution demonstrating controlled growth with periodic efficiency optimizations. (C) Relative contributions of three primary feedback mechanisms, showing the shift from entropy-driven exploration to balanced multi-mechanism optimization.
Table 1.
Comprehensive comparison of Liquid AI with existing adaptive AI methods.
Table 1.
Comprehensive comparison of Liquid AI with existing adaptive AI methods.
| Capability | Liquid AI | EWC | MAML | DARTS | PackNet | QMIX |
|---|
| |
(Ours)
|
[10]
|
[11]
|
[12]
|
[13]
|
[14]
|
|---|
|
Architectural Adaptation |
| Runtime Architecture Modification | ✓ | × | × | × | × | × |
| Topological Plasticity | ✓ | × | × | × | × | × |
| Autonomous Structural Evolution | ✓ | × | × | × | × | × |
| Pre-deployment Architecture Search | N/A | × | × | ✓ | × | × |
|
Learning Capabilities |
| Continual Learning | ✓ | ✓ | ✓ | × | ✓ | × |
| Catastrophic Forgetting Prevention | ✓ | ✓ | ✓ | N/A | ✓ | N/A |
| Cross-Domain Knowledge Transfer | ✓ | Limited | ✓ | × | Limited | × |
| Zero-Shot Task Adaptation | ✓ | × | ✓ | × | × | × |
| Self-Supervised Learning | ✓ | × | × | × | × | × |
|
Knowledge Management |
| Dynamic Knowledge Graphs | ✓ | × | × | × | × | × |
| Entropy-Guided Optimization | ✓ | × | × | × | × | × |
| Cross-Domain Reasoning | ✓ | × | Limited | × | × | × |
| Temporal Knowledge Evolution | ✓ | × | × | × | × | × |
|
Multi-Agent Capabilities |
| Emergent Agent Specialization | ✓ | N/A | N/A | N/A | N/A | × |
| Dynamic Agent Topology | ✓ | N/A | N/A | N/A | N/A | × |
| Collective Intelligence | ✓ | N/A | N/A | N/A | N/A | ✓ |
| Autonomous Role Assignment | ✓ | N/A | N/A | N/A | N/A | × |
|
Performance Characteristics |
| Sustained Improvement | ✓ | × | × | × | × | × |
| Resource Efficiency | Adaptive | Fixed | Fixed | Fixed | Fixed | Fixed |
| Scalability | Unlimited | Limited | Limited | Limited | Limited | Moderate |
| Interpretability | Dynamic | Low | Low | Moderate | Low | Low |
|
Deployment Flexibility |
| Online Adaptation | ✓ | Limited | Limited | × | Limited | Limited |
| Distributed Deployment | ✓ | × | × | × | × | ✓ |
| Hardware Agnostic | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ |
| Real-Time Operation | ✓ | ✓ | ✓ | × | ✓ | ✓ |
Table 2.
Ethical considerations for Liquid AI deployment.
Table 2.
Ethical considerations for Liquid AI deployment.
| Aspect | Challenge | Mitigation Strategy | Research Needs |
|---|
| Autonomy | Self-modification may lead to unintended behaviors | Bounded modification spaces, continuous monitoring | Formal verification methods for dynamic systems |
| Transparency | Evolving architectures complicate interpretability | Maintain modification logs, interpretable components | Dynamic explanation generation techniques |
| Accountability | Unclear responsibility for emergent decisions | Clear governance frameworks, audit trails | Legal frameworks for autonomous AI |
| Fairness | Potential for bias amplification | Active bias detection and mitigation | Fairness metrics for evolving systems |
| Privacy | Distributed knowledge may leak sensitive information | Differential privacy, secure computation | Privacy-preserving knowledge integration |
| Safety | Unpredictable emergent behaviors | Conservative modification bounds, rollback mechanisms | Safety verification for self-modifying systems |
| Control | Difficulty in stopping runaway evolution | Multiple kill switches, consensus requirements | Robust control mechanisms |