Learning and Reconstruction of Mobile Robot Trajectories with LSTM Autoencoders: A Data-Driven Framework for Real-World Deployment
Abstract
1. Introduction
2. Data Acquisition and Preprocessing
3. LSTM Autoencoder Architecture
- Start_Flag—set to 1 for the first row of each trajectory, 0 otherwise.
- End_Flag—set to 1 for the last row of each trajectory, 0 otherwise.
| Algorithm 1 Loading and preprocessing of trajectory data |
|
- The longest trajectory in the dataset defined the maximum sequence length.
- Shorter trajectories were padded with zeros until they matched this length.
- A masking mechanism was applied during training to ensure that padded values were ignored in loss computation and weight updates.
| Algorithm 2 Training of the LSTM autoencoder for trajectory reconstruction |
|
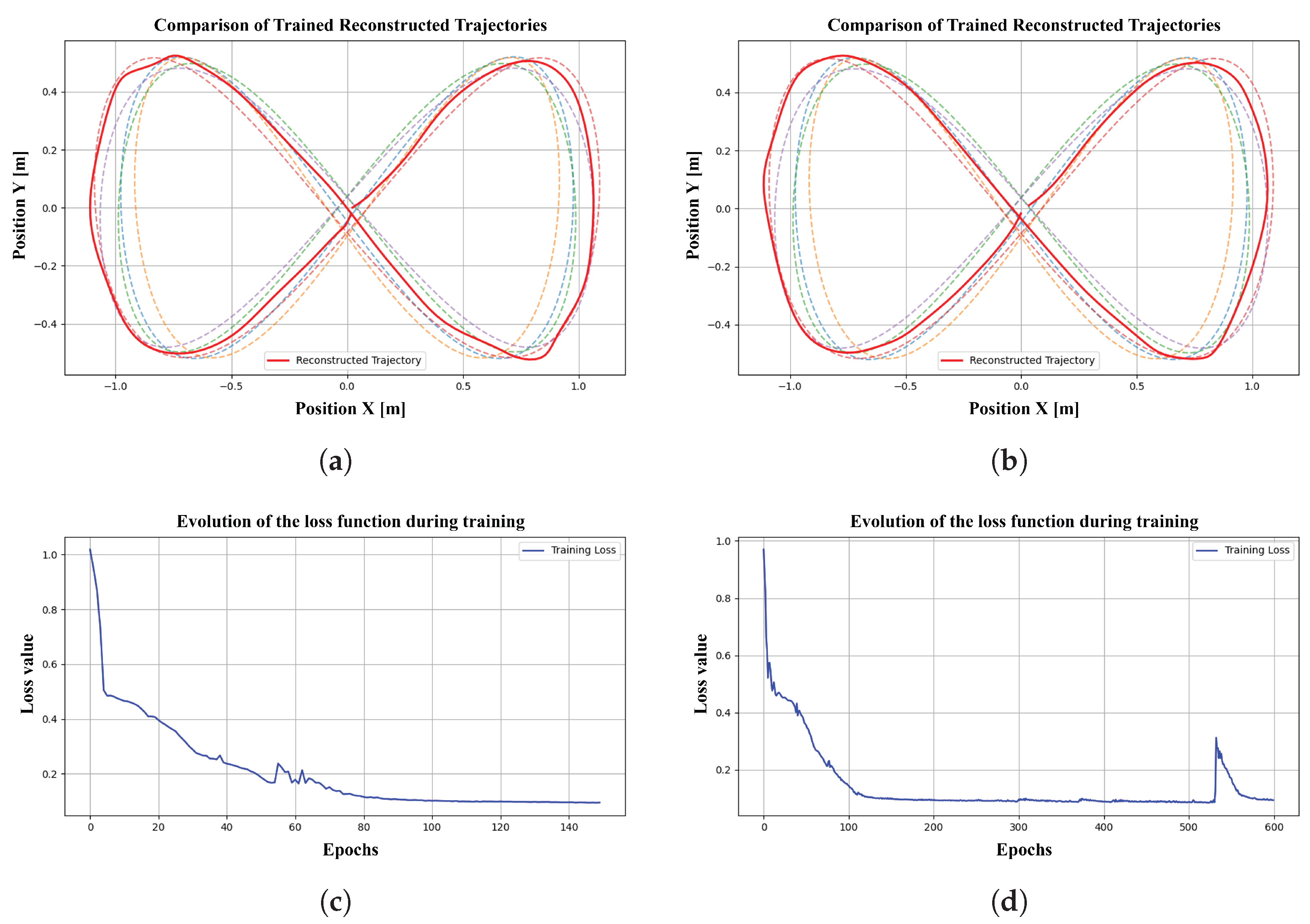
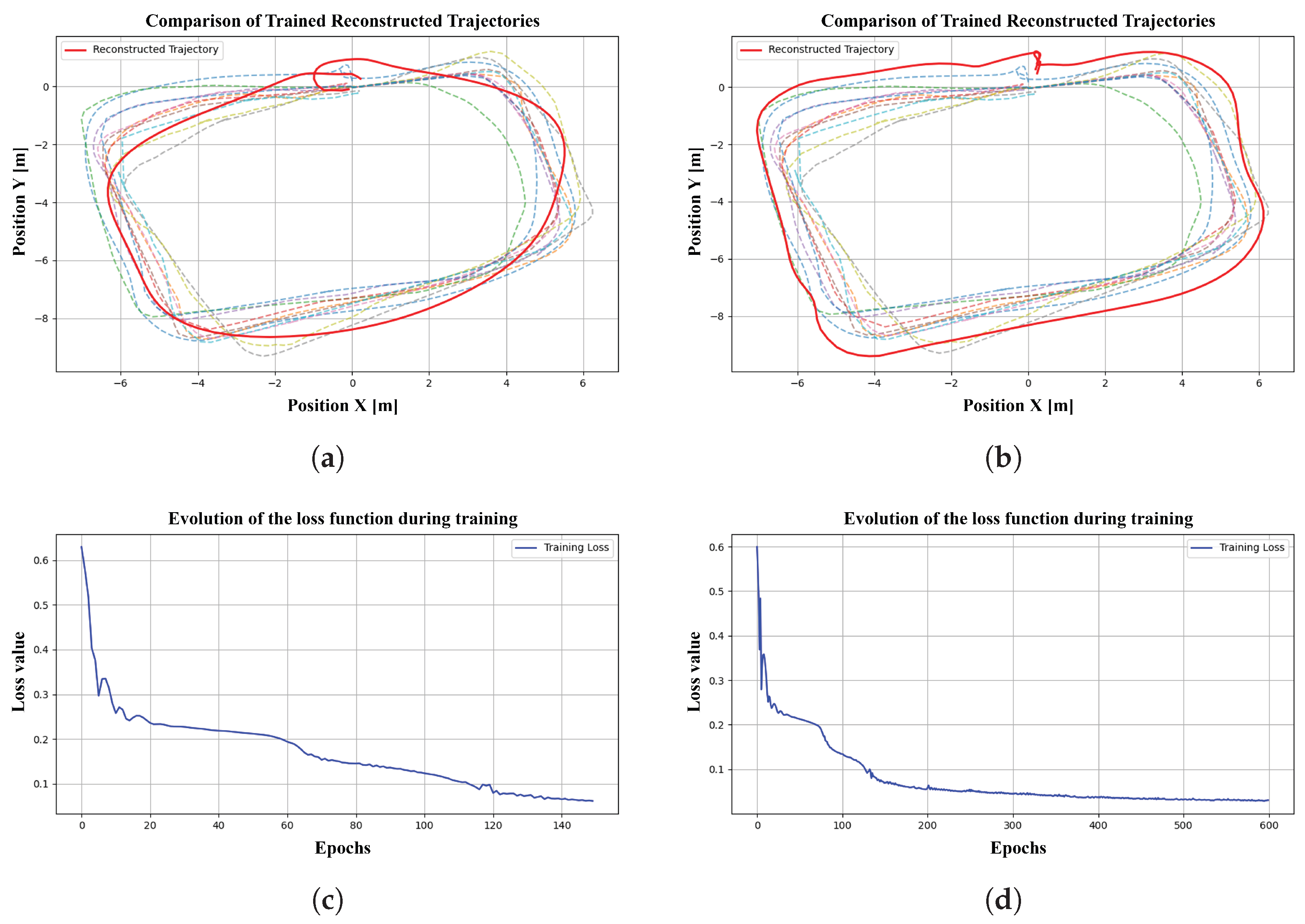
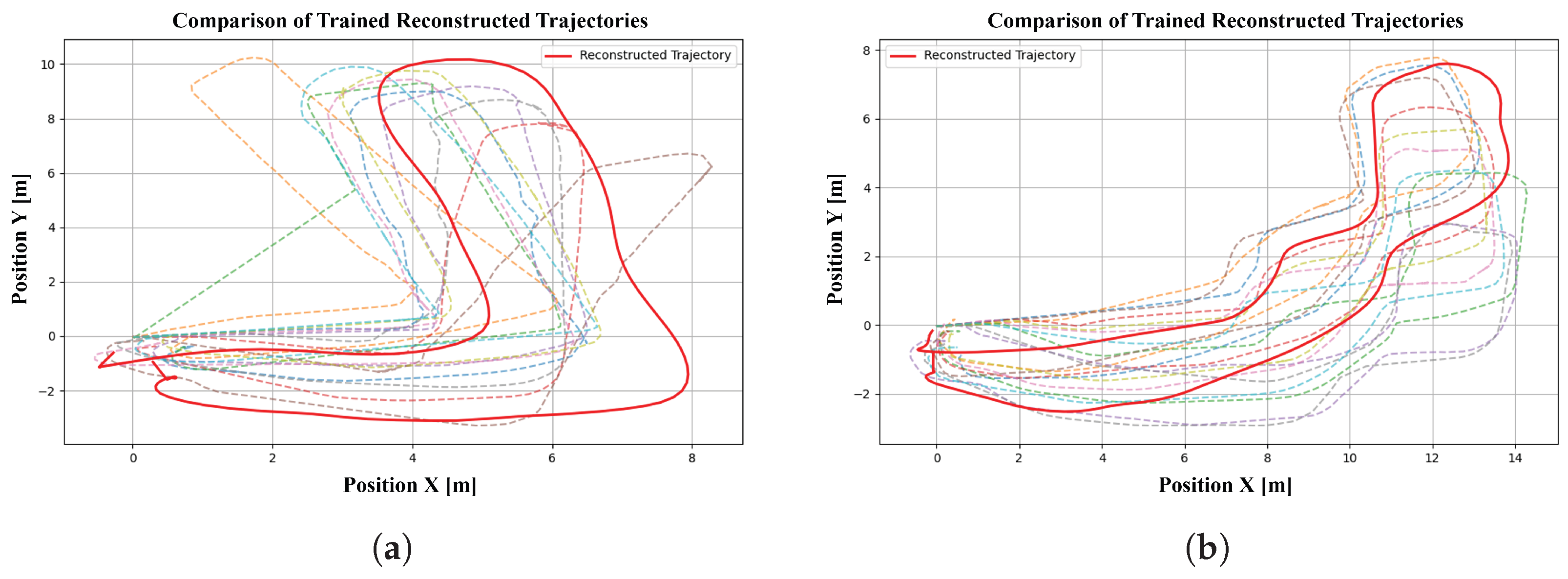
4. Experimental Results
4.1. Simulation Data
4.2. Real-World Data
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| IoRT | Internet of Robotic Things |
| LSTM | Long Short-Term Memory |
| RNN | Recurrent Neural Network |
| IMU | Inertial Measurement Unit |
| CSV | Comma-Separated Values |
| MSE | Mean Squared Error |
| L1 | L1 Loss (Mean Absolute Error) |
| AP | Access Point |
| MQTT | Message Queuing Telemetry Transport |
| MAC | Medium Access Control |
| PHY | Physical Layer |
| IEEE | Institute of Electrical and Electronics Engineers |
References
- Molina-Leal, A.; Gómez-Espinosa, A.; Escobedo Cabello, J.A.; Cuan-Urquizo, E.; Cruz-Ramírez, S.R. Trajectory Planning for a Mobile Robot in a Dynamic Environment Using an LSTM Neural Network. Appl. Sci. 2021, 11, 10689. [Google Scholar] [CrossRef]
- Liu, H.; Bianchin, G.; Pasqualetti, F. Secure Trajectory Planning Against Undetectable Spoofing Attacks. Automatica 2020, 113, 108655. [Google Scholar] [CrossRef]
- Li, X.; Li, M. The direction analysis on trajectory of fast neural network learning robot. IEEE Access 2021, 9, 125580–125589. [Google Scholar] [CrossRef]
- Yang, L.; Li, P.; Qian, S.; He, Q.; Miao, J.; Liu, M.; Hu, Y.; Memetimin, E. Path planning technique for mobile robots: A review. Machines 2023, 11, 980. [Google Scholar] [CrossRef]
- Hu, K.; Chen, Z.; Kang, H.; Tang, Y. 3D vision technologies for a self-developed structural external crack damage recognition robot. Autom. Constr. 2024, 159, 105262. [Google Scholar] [CrossRef]
- Hoeller, D.; Wellhausen, L.; Farshidian, F.; Hutter, M. Learning a State Representation and Navigation in Cluttered and Dynamic Environments. IEEE Robot. Autom. Lett. 2021, 6, 1091–1098. [Google Scholar] [CrossRef]
- Altan, S.; Sarıel, I. CLUE-AI: A Convolutional Three-Stream Anomaly Identification Framework for Robot Manipulation. IEEE Access 2023, 11, 12763–12775. [Google Scholar] [CrossRef]
- Liang, Y. Robot trajectory tracking control based on neural networks and sliding mode control. IEEE Access 2025, 13, 96740–96757. [Google Scholar] [CrossRef]
- Azzam, R.; Taha, T.; Huang, S.; Zweiri, Y. A Deep Learning Framework for Robust Semantic SLAM. In Proceedings of the 2020 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 4 February–9 April 2020; p. 9118181. [Google Scholar] [CrossRef]
- Keung, K.L.; Chow, K.H.; Lee, C. Collision avoidance and trajectory planning for autonomous mobile robot: A spatio-temporal deep learning approach. In Proceedings of the 2023 IEEE International Conference on Industrial Engineering and Engineering Management (IEEM), Singapore, 18–21 December 2023. [Google Scholar] [CrossRef]
- Dong, L.; He, Z.; Song, C.; Sun, C. A review of mobile robot motion planning methods: From classical motion planning workflows to reinforcement learning-based architectures. J. Syst. Eng. Electron. 2023, 34, 439–459. [Google Scholar] [CrossRef]
- Farajiparvar, P.; Ying, H.; Pandya, A. A brief survey of telerobotic time delay mitigation. Front. Robot. AI 2020, 7, 578805. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Jang-Jaccard, J.; Xu, W.; Sabrina, F.; Camtepe, S.; Boulic, M. Lstm-autoencoder based anomaly detection for indoor air quality time series data. arXiv 2022, arXiv:2204.06701. [Google Scholar] [CrossRef]
- Wei, S.; Lin, Y.; Wang, J.; Zeng, Y.; Qu, F.; Zhou, X.; Lu, Z. A robust tcphd filter for multi-sensor multitarget tracking based on a gaussian–student’s t-mixture model. Remote Sens. 2024, 16, 506. [Google Scholar] [CrossRef]
- Krish, V.; Mata, A.; Bak, S.; Hobbs, K.L.; Rahmati, A. Provable observation noise robustness for neural network control systems. Res. Dir.-Cyber-Phys. Syst. 2024, 2, e1. [Google Scholar] [CrossRef]
- Sarkar, M.; Ghose, D. Sequential learning of movement prediction in dynamic environments using lstm autoencoder. arXiv 2018, arXiv:1810.05394. [Google Scholar] [CrossRef]
- Chen, D.; Li, S.; Wu, Q. A novel supertwisting zeroing neural network with application to mobile robot manipulators. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 1776–1787. [Google Scholar] [CrossRef]
- Samuel, R.D.J.; Cuzzolin, F. Unsupervised anomaly detection for a smart autonomous robotic assistant surgeon (saras) using a deep residual autoencoder. IEEE Robot. Autom. Lett. 2021, 6, 7256–7261. [Google Scholar] [CrossRef]
- Chirayil Nandakumar, S.; Mitchell, D.; Erden, M.S.; Flynn, D.; Lim, T. Anomaly Detection Methods in Autonomous Robotic Missions. Sensors 2024, 24, 1330. [Google Scholar] [CrossRef] [PubMed]
- Sünderhauf, N.; Brock, O.; Scheirer, W.; Hadsell, R.; Fox, D.; Leitner, J.; Upcroft, B.; Abbeel, P.; Burgard, W.; Milford, M.; et al. The Limits and Potentials of Deep Learning for Robotics. Int. J. Robot. Res. 2018, 37, 1053–1077. [Google Scholar] [CrossRef]
- Chen, R. Anomaly Detection Model Based on Anomaly Representation Reinforcement and Path Iterative Modeling. Concurr. Comput. Pract. Exp. 2025, 37, e70245. [Google Scholar] [CrossRef]
- Qin, W.; Tang, J.; Lu, C.; Lao, S. Trajectory prediction based on long short-term memory network and kalman filter using hurricanes as an example. Comput. Geosci. 2021, 25, 1005–1023. [Google Scholar] [CrossRef]
- Zheng, Y.; Xu, Y.; Lu, Z. Pedestrian Trajectory Prediction Based on LSTM-NMPC. Int. J. Automot. Eng. 2025, 13575, 1009–1016. [Google Scholar] [CrossRef]
- Woo, H.; Ji, Y.; Tamura, Y.; Kuroda, Y.; Sugano, T.; Yamamoto, Y.; Yamashita, A.; Asama, H. Trajectory prediction of surrounding vehicles considering individual driving characteristics. Int. J. Automot. Eng. 2018, 9, 282–288. [Google Scholar] [CrossRef] [PubMed]
- Shen, Y.; Zheng, J.; Ye, L.; El-Farra, N. Online Local Modeling and Prediction of Batch Process Trajectories Using Just-In-Time Learning and LSTM Neural Network. J. Comput. Methods Sci. Eng. 2020, 20, 611–624. [Google Scholar] [CrossRef]
- Tang, G.; Lei, J.; Shao, C.; Hu, X.; Cao, W.; Men, S. Short-term prediction in vessel heave motion based on improved lstm model. IEEE Access 2021, 9, 58067–58078. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Cui, F.; Liu, Y.; Liu, Z.; Dong, J. Research into ship trajectory prediction based on an improved lstm network. J. Mar. Sci. Eng. 2023, 11, 1268. [Google Scholar] [CrossRef]
- Hangzhou Yushu Technology Co., Ltd. (Unitree Robotics). Unitree Go1: Bionic Companion Quadruped Robot. 2025. Available online: https://shop.unitree.com/products/unitreeyushutechnologydog-artificial-intelligence-companion-bionic-companion-intelligent-robot-go1-quadruped-robot-dog (accessed on 11 June 2025).
- NVIDIA Corporation. World’s Smallest AI Supercomputer: NVIDIA Jetson Xavier NX; NVIDIA Corporation: Santa Clara, CA, USA, 2025; Available online: https://www.nvidia.com/en-us/autonomous-machines/embedded-systems/jetson-xavier-nx/ (accessed on 11 June 2025).
- IEEE Std 802.11-2016; IEEE Standard for Information Technology—Telecommunications and Information Exchange Between Systems—Local and Metropolitan Area Networks—Specific Requirements—Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications. Institute of Electrical and Electronics Engineers (IEEE): New York, NY, USA, 2016. Available online: https://standards.ieee.org/standard/802_11-2016.html (accessed on 5 June 2025).
- ABB. Industrial Robots; ABB Ltd.: Zürich, Switzerland, 2024; Available online: https://new.abb.com/products/robotics/cs/roboty/prumyslove-roboty (accessed on 5 June 2025).
- Shi, L.; Ma, Y.; Lü, Y.; Chen, L. The application of computer intelligence in the cyber-physical business system integration in network security. Comput. Intell. Neurosci. 2022, 2022, 5490779. [Google Scholar] [CrossRef]
- Li, C.; Feng, G.; Jia, Y.; Li, Y.; Ji, J.; Miao, Q. Retad. Int. J. Data Warehous. Min. 2023, 19, 1–14. [Google Scholar] [CrossRef]
- Lu, F.; Zhang, Z.; Shui, C. Online trajectory anomaly detection model based on graph neural networks and variational autoencoder. J. Phys. Conf. Ser. 2024, 2816, 012006. [Google Scholar] [CrossRef]
- Zeng, W.; Xu, Z.; Cai, Z.; Chu, X.; Lu, X. Aircraft trajectory clustering in terminal airspace based on deep autoencoder and gaussian mixture model. Aerospace 2021, 8, 266. [Google Scholar] [CrossRef]
- Krejčí, J.; Babiuch, M.; Suder, J.; Krys, V.; Bobovský, Z. Latency-Sensitive Wireless Communication in Dynamically Moving Robots for Urban Mobility Applications. Smart Cities 2025, 8, 105. [Google Scholar] [CrossRef]

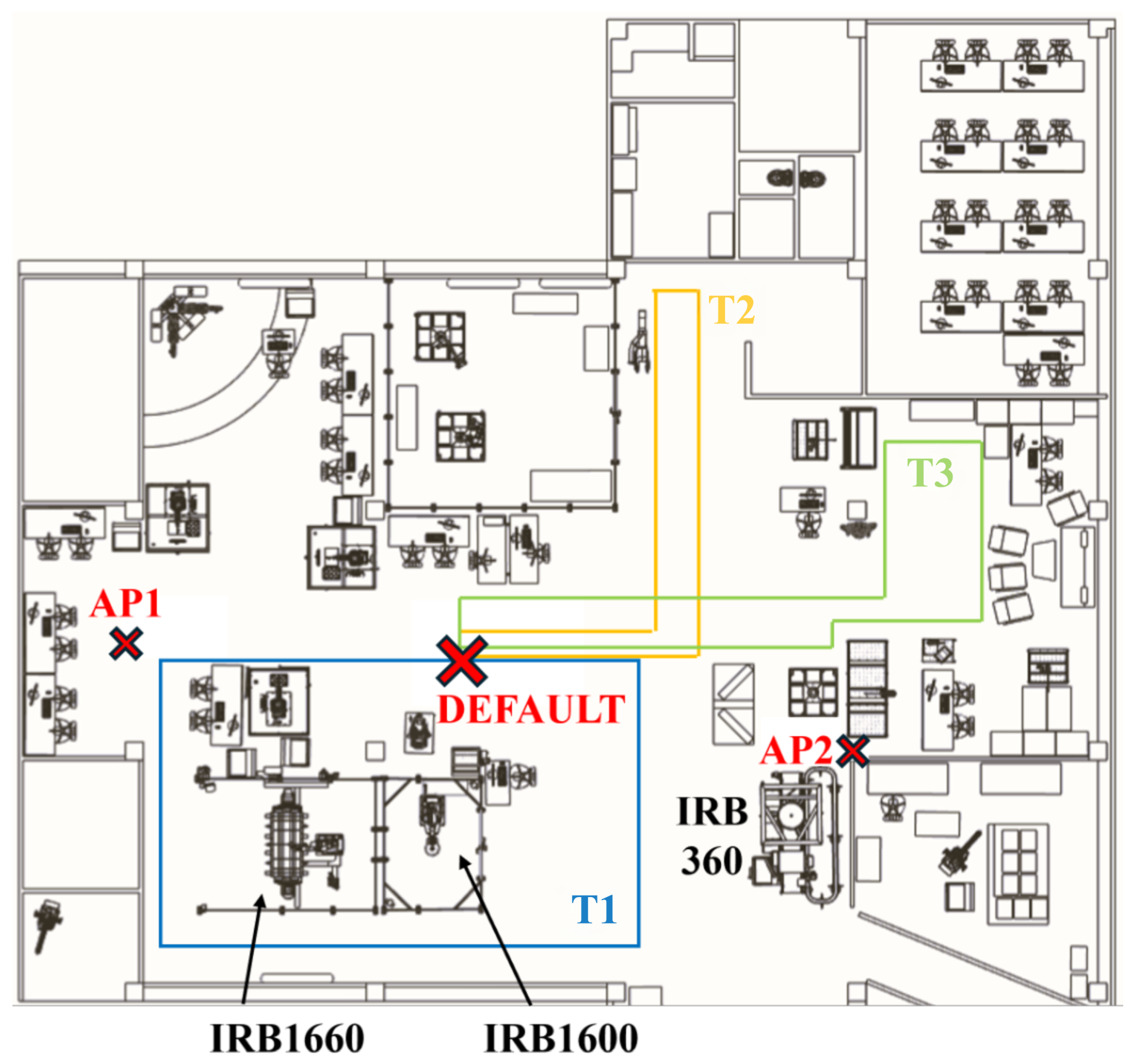
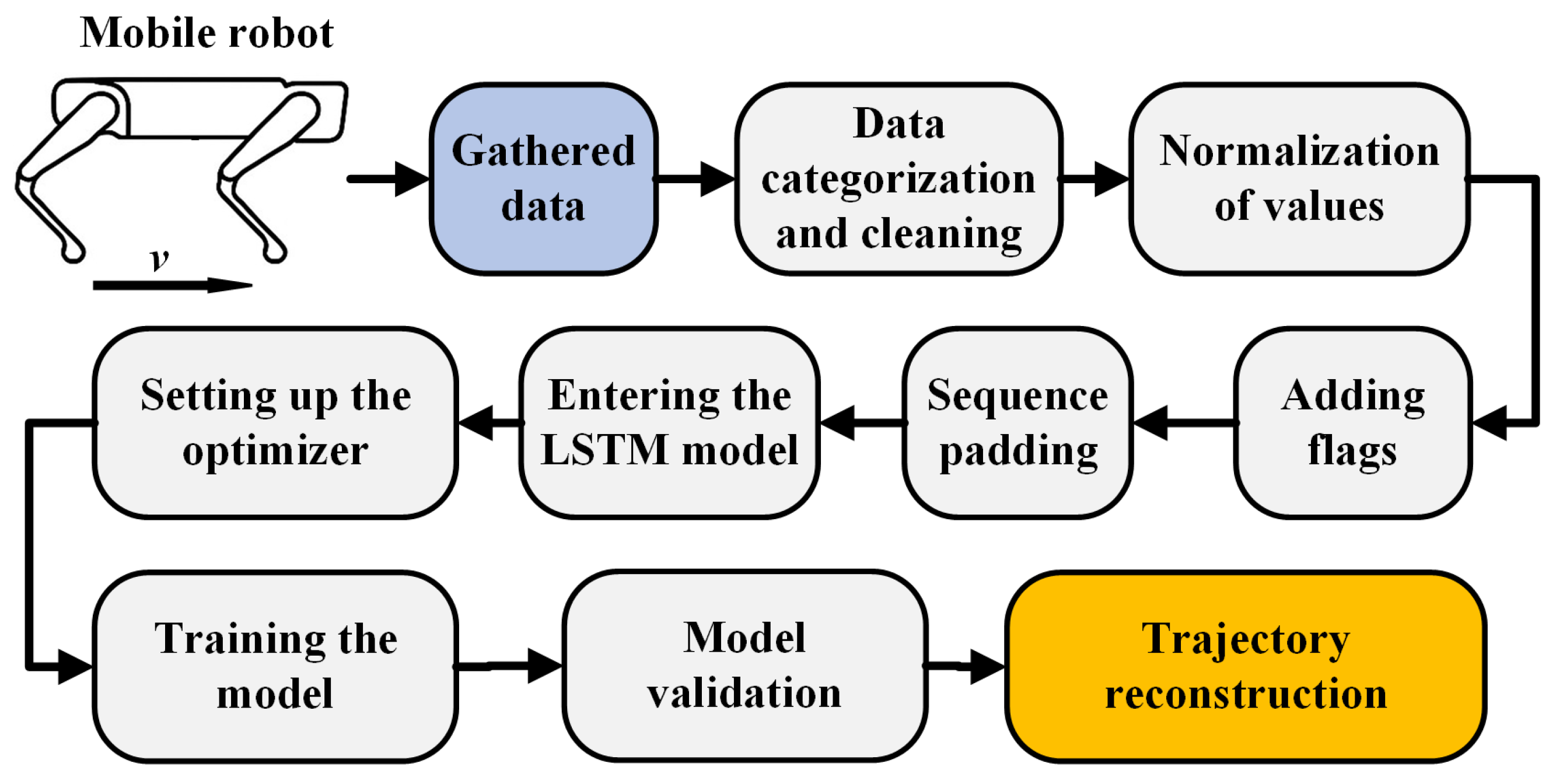
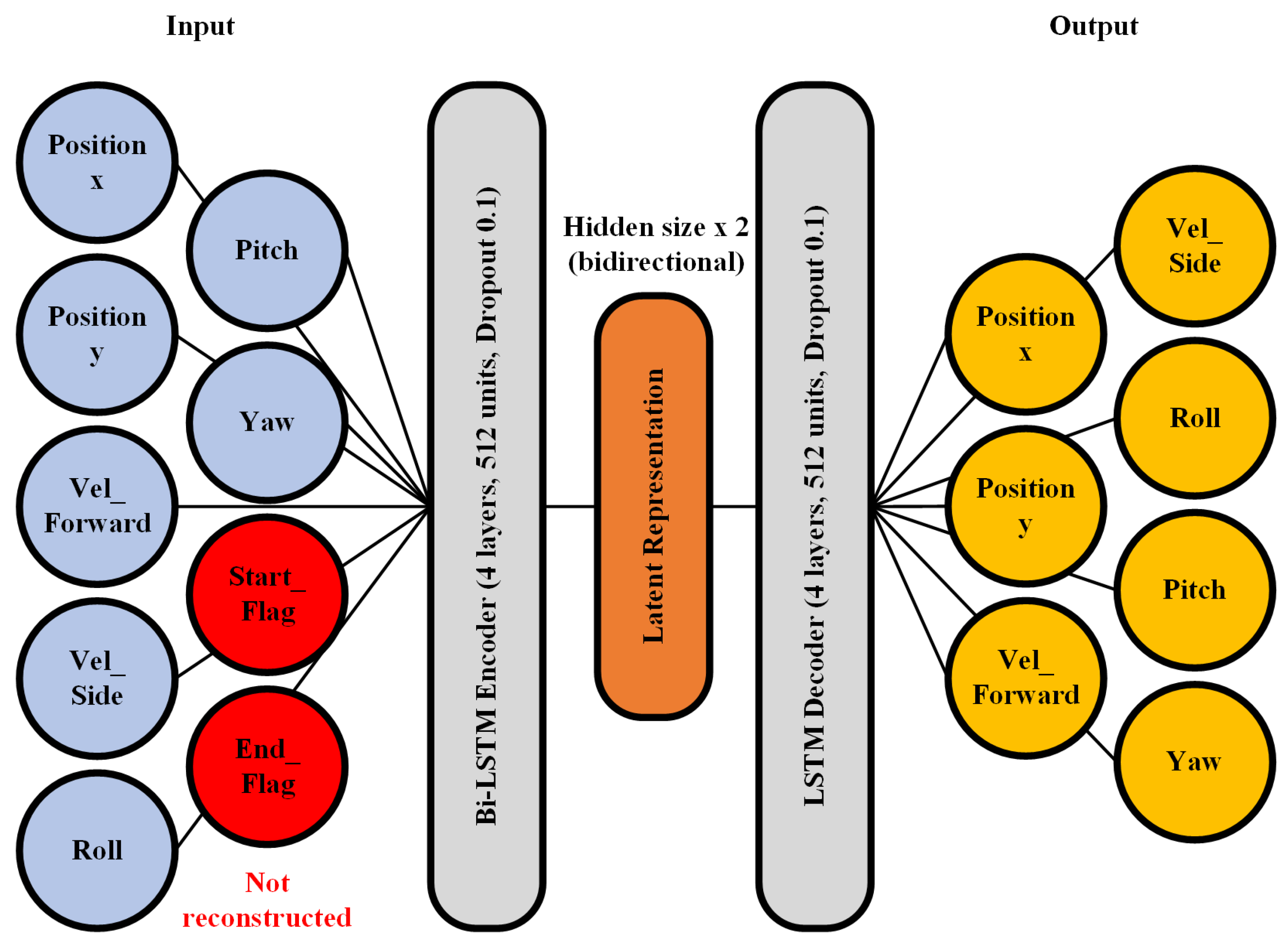
| Category | Variables and Description |
|---|---|
| Identifiers and metadata | Packet_id, Cloud_id—unique identifiers of data packets; Edge_Time, Cloud_Time—timestamps for synchronization between edge and cloud systems. |
| Network and communication data | Latency, Data_Loss—network performance metrics; RSSI, Bandwidth, MAC, Frequency—wireless connection parameters; data_received, data_size—size and integrity of transmitted messages. |
| Trajectory data (main input for the neural network) | Position_x, Position_y; Vel_Forward, Vel_Side, Vel_UpDown—velocity components in three directions; Roll, Pitch, Yaw—orientation angles (RPY). |
| RMSE Pos [m] | MAE Pos [m] | Hausdorff [m] | Velocity RMSE [m/s] | Yaw MAE [rad] | ||
|---|---|---|---|---|---|---|
| 0.3 | 0.0 | 0.98 | 0.71 | 2.47 | 0.13 | 0.66 |
| 0.3 | 0.3 | 0.79 | 0.62 | 1.81 | 0.12 | 0.59 |
| 0.3 | 0.6 | 0.79 | 0.60 | 1.95 | 0.11 | 0.56 |
| 0.7 | 0.0 | 0.87 | 0.63 | 2.29 | 0.13 | 0.61 |
| 0.7 | 0.3 | 0.86 | 0.66 | 1.94 | 0.12 | 0.63 |
| 0.7 | 0.6 | 0.82 | 0.62 | 1.86 | 0.12 | 0.68 |
| 1.0 | 0.0 | 0.93 | 0.67 | 2.51 | 0.12 | 0.62 |
| 1.0 | 0.3 | 1.85 | 1.31 | 4.41 | 0.14 | 0.95 |
| 1.0 | 0.6 | 0.88 | 0.67 | 2.12 | 0.13 | 0.72 |
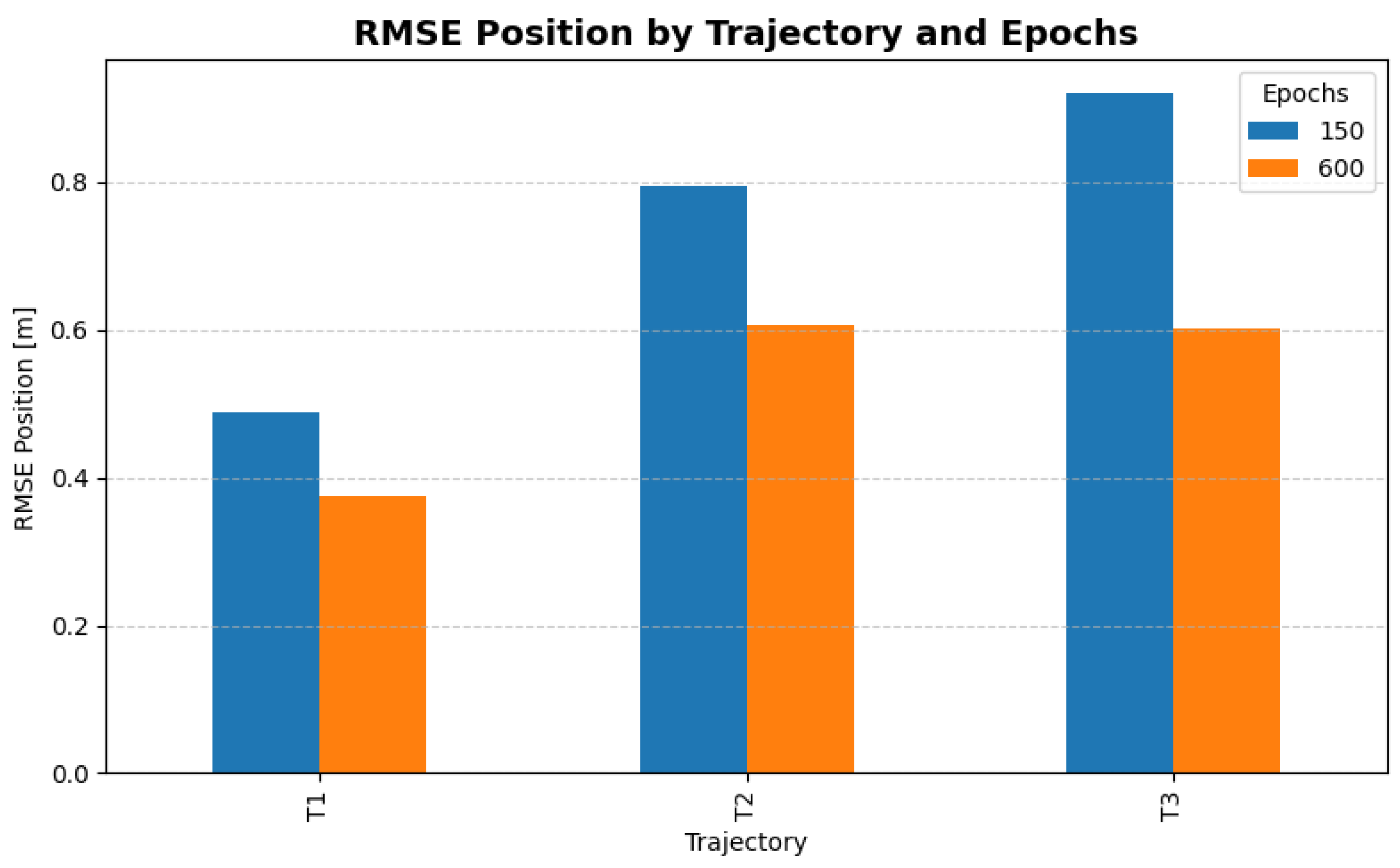
| Trajectory | Epochs | RMSE Pos [m] | MAE Pos [m] | Hausdorff [m] | Velocity RMSE [m/s] | Yaw MAE [rad] |
|---|---|---|---|---|---|---|
| T1 | 150 | 0.4888 | 0.4076 | 1.0604 | 0.0792 | 0.2214 |
| T1 | 600 | 0.3743 | 0.3200 | 0.7514 | 0.1355 | 0.2557 |
| T2 | 150 | 0.7950 | 0.6344 | 2.2889 | 0.1073 | 0.4468 |
| T2 | 600 | 0.6071 | 0.5769 | 1.6923 | 0.2579 | 0.2355 |
| T3 | 150 | 0.9197 | 0.7597 | 2.1954 | 0.1410 | 0.4852 |
| T3 | 600 | 0.6013 | 0.5233 | 1.0232 | 0.2004 | 0.1667 |
| Model | RMSE Pos [m] | MAE Pos [m] | Hausdorff [m] | Velocity RMSE [m/s] | Yaw MAE [rad] |
|---|---|---|---|---|---|
| Kalman | 0.2287 ± 0.0268 | 0.1620 ± 0.0236 | 0.5475 ± 0.1155 | 1.5628 ± 0.2209 | 0.2300 ± 0.0308 |
| LSTM-AE | 0.3426 ± 0.0375 | 0.2543 ± 0.0239 | 0.8089 ± 0.1868 | 0.0855 ± 0.0045 | 0.2598 ± 0.0481 |
| Seq2Seq-Attn | 3.1454 ± 0.3319 | 2.4639 ± 0.3240 | 7.6383 ± 0.8887 | 0.1588 ± 0.0050 | 1.2971 ± 0.0497 |
| Transformer | 0.3179 ± 0.0659 | 0.2663 ± 0.0476 | 0.7155 ± 0.1441 | 0.0215 ± 0.0027 | 0.1312 ± 0.0089 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krejčí, J.; Babiuch, M.; Krys, V.; Bobovský, Z. Learning and Reconstruction of Mobile Robot Trajectories with LSTM Autoencoders: A Data-Driven Framework for Real-World Deployment. AI 2025, 6, 302. https://doi.org/10.3390/ai6120302
Krejčí J, Babiuch M, Krys V, Bobovský Z. Learning and Reconstruction of Mobile Robot Trajectories with LSTM Autoencoders: A Data-Driven Framework for Real-World Deployment. AI. 2025; 6(12):302. https://doi.org/10.3390/ai6120302
Chicago/Turabian StyleKrejčí, Jakub, Marek Babiuch, Václav Krys, and Zdenko Bobovský. 2025. "Learning and Reconstruction of Mobile Robot Trajectories with LSTM Autoencoders: A Data-Driven Framework for Real-World Deployment" AI 6, no. 12: 302. https://doi.org/10.3390/ai6120302
APA StyleKrejčí, J., Babiuch, M., Krys, V., & Bobovský, Z. (2025). Learning and Reconstruction of Mobile Robot Trajectories with LSTM Autoencoders: A Data-Driven Framework for Real-World Deployment. AI, 6(12), 302. https://doi.org/10.3390/ai6120302






