Severity-Aware Drift Adaptation for Cost-Efficient Model Maintenance

Abstract

Objectives: This paper introduces an adaptive learning framework for handling concept drift in data by dynamically adjusting model updates based on the severity of detected drift. Methods: The proposed method combines multiple statistical measures to quantify distributional changes between recent and historical data windows. The resulting severity score drives a three-tier adaptation policy: minor drift is ignored, moderate drift triggers incremental model updates, and severe drift initiates full model retraining. Results: This approach balances stability and adaptability, reducing unnecessary computation while preserving model accuracy. The framework is applicable to both single-model and ensemble-based systems, offering a flexible and efficient solution for real-time drift management. Also, different transformation methods were reviewed, and quantile transformation was tested. By applying a quantile transformation, the Kolmogorov–Smirnov (KS) statistic decreased from 0.0559 to 0.0072, demonstrating effective drift adaptation.

1. Introduction

In real-world systems, data distributions rarely remain stable. Data drift, or covariate shift [1], occurs when input statistics change over time, threatening the reliability of models trained under the assumption of stable distributions. To manage such evolving data, it is important to recognize that data can be stored in multiple formats such as structured, semi-structured, and unstructured, depending on the application and the requirements for processing and analysis [2].

Undetected drift degrades accuracy and decision quality, which is critical in domains like finance, healthcare, and autonomous systems where outputs directly affect safety and outcomes. For instance, a credit scoring model trained on pre-pandemic data may perform inadequately during economic shifts unless changes in data patterns are identified and addressed [3].

Detecting and quantifying drift is now central to robust ML lifecycle management. Statistical and monitoring approaches [4] enable proactive retraining or adaptation, helping preserve long-term performance and reliability. Data drift can manifest in several distinct forms, each with different implications for machine learning model performance. The primary types of drift are generally categorized as covariate drift, prior probability drift, and concept drift. These drifts may occur independently or in combination, depending on changes in the data-generating process.

Covariate drift, also known as input drift, occurs when the distribution of the input features P(X) changes over time, while the relationship between inputs and outputs P(Y|X) remains stable. This type of drift is commonly encountered in real-world scenarios where external factors influence the input space. For example, in an e-commerce recommendation system, seasonal variation in user behavior may result in a shift in feature distributions, such as product views or click patterns, without altering the user preferences themselves [5].

Prior probability drift [6] refers to a change in the marginal distribution of the target variable P(Y) over time. This occurs even if the conditional distribution P(X|Y) remains unchanged. For instance, in medical diagnostics, the prevalence of certain conditions may change due to epidemiological factors, leading to a shift in label distributions [7]. If unaccounted for, this drift can introduce bias in model predictions and compromise decision accuracy.

Concept drift [8] arises when the input–output relationship P(Y|X) changes, shifting decision boundaries and reducing predictive power. For instance, fraudsters may adapt behaviors to evade detection [9]. Concept drift is considered the most disruptive form, as it indicates a fundamental change in the task the model is attempting to learn.

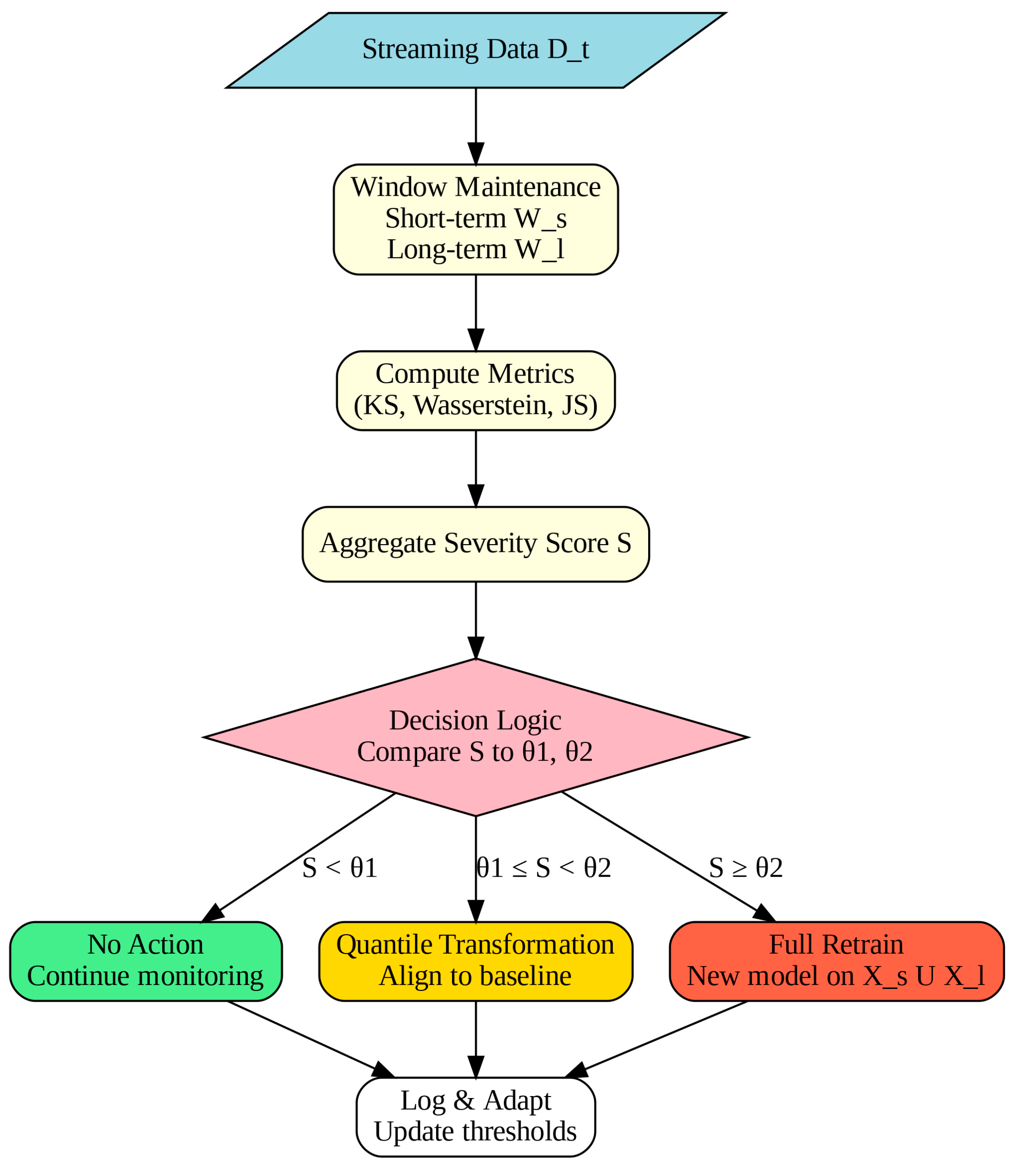
In this paper, an adaptive framework was proposed for handling concept drift in streaming data environments, focusing on dynamic model adaptation based on quantified drift severity. The core idea is to integrate a drift detection mechanism that continuously monitors changes in data distribution using multiple statistical measures like Kolmogorov–Smirnov, Wasserstein, and Jensen-Shannon divergence. These metrics are aggregated into a unified severity score that reflects the extent of distributional shift between short-term and long-term data windows. Unlike methods that retrain after every drift, our framework is severity-aware: minor drift is ignored, moderate drift triggers lightweight updates, and only severe drift requires full retraining. This adaptive policy reduces unnecessary computational overhead while maintaining high model performance over time. The framework can be implemented for both single-model and ensemble-based architectures and is designed to be modular, interpretable, and compatible with real-time learning systems. Quantile transformation was reviewed for updating low drift detected data.

The ROSE [10] algorithm proposes a robust ensemble learning framework specifically designed for online, imbalanced, and concept-drifting data streams. The method employs an ensemble of classifiers trained incrementally on random feature subsets to promote diversity and adaptability. Concept drift is addressed through an integrated online detection mechanism that triggers the creation of a background ensemble, enabling rapid adaptation when changes are detected. To manage class imbalance, ROSE maintains separate sliding windows for each class, ensuring sufficient representation of minority class instances during training. Additionally, the algorithm incorporates a self-adjusting bagging strategy that dynamically increases the sampling rate for difficult or minority class instances. Through the combination of these techniques, ROSE effectively handles challenges related to evolving data distributions, achieving a balance between predictive performance, computational efficiency, and memory usage in non-stationary environments.

The DAMSID method [11] presents a dynamic ensemble learning strategy tailored for imbalanced data streams affected by concept drift. The methodology is structured in three stages: ensemble learning, concept drift detection, and concept drift adaptation. In the ensemble learning stage, classifiers are sequentially trained on incoming data chunks and selectively maintained based on performance evaluations, with a particular focus on preserving high accuracy on minority classes. For drift detection, DAMSID employs a dynamic weighted performance monitoring mechanism, separately tracking classification performance for minority and majority classes and adjusting detection sensitivity according to the current class distribution. Upon detecting drift, the method initiates ensemble adaptation by discarding underperforming classifiers and reconstructing the ensemble using more recent data. This multi-stage process enables DAMSID to maintain robustness and predictive accuracy in dynamic, highly imbalanced streaming environments where both class distributions and decision boundaries may shift over time.

The proposed Self-Adaptive Ensemble (SA-Ensemble) framework [12] is designed to effectively handle user interest drift in data streams, structured around three interconnected components: topic-based drift detection (T-IDDM), adaptive weighted ensemble learning, and dynamic voting strategy selection. First, the T-IDDM component employs topic modeling (e.g., via LDA) to detect and quantify drift in user interest by comparing topic distributions across consecutive data chunks using statistical two-sample testing, enabling differentiation between real and virtual drift. Upon drift detection, the SA-Ensemble module adapts the ensemble: poorly performing base learners are pruned, and new ones are trained on the latest data, while resilient models are retained; it incorporates an adaptive weighted voting strategy in which a lightweight sub-model predicts labels based on topic context to estimate the current accuracy of ensemble members, thereby weighting votes accordingly. Lastly, robustness is enhanced through a dynamic voting strategy selection mechanism that evaluates predictions from majority voting, adaptive weighted voting, and the sub-model itself, selecting the most accurate strategy on a per-instance basis. This integrated process maintains high performance and resilience in the face of evolving user interest distributions.

The proposed Dynamic Ensemble Learning (DEL) framework [13] addresses predictive challenges in evolving data streams by integrating heterogeneous models, dynamic adaptation mechanisms, and concept drift handling techniques. The framework begins with the construction of an ensemble comprising diverse base learners, each offering distinct perspectives on the underlying data distribution. A dynamic weighting mechanism continuously adjusts the influence of each model based on real-time performance and sensitivity to concept drift. Base learners are incrementally updated using online learning techniques, such as stochastic gradient descent and online boosting, enabling continuous adaptation to new data. Concept drift is detected using statistical change detection methods, which trigger recalibration of the ensemble through reweighting and adaptive retraining. The DEL framework is evaluated through extensive experiments on benchmark datasets with simulated drift, using standard metrics such as accuracy, precision, recall, and F1-score. Furthermore, real-world case studies in finance, healthcare, and environmental monitoring demonstrate the practical applicability of DEL in supporting robust, real-time decision-making in dynamic environments.

The Fast Adapting Ensemble (FAE) algorithm [14] addresses both abrupt and gradual concept drift, with specific capability to handle recurring concepts in streaming data. Data are processed in fixed-size blocks, yet adaptation mechanisms are triggered even before a batch is fully received to ensure rapid response to drift. Explicit drift detection is implemented via a drift detector (e.g., DDM), which monitors the data stream and signals when significant distributional changes occur. To manage recurring concepts, FAE maintains a repository of inactive classifiers representing previously observed concepts; these classifiers can be reactivated immediately when their associated concepts reemerge. The algorithm’s performance is rigorously evaluated against established learning methods using benchmark datasets under various drift scenarios, demonstrating robust adaptability, high accuracy, and competitive runtime performance.

The challenge of concept drift in IoT data streams has been widely addressed through ensemble learning methods. For example, Yang et al. [15] proposed an lightweight framework that integrates offline classifiers with adaptive updating mechanisms to cope with both abrupt and gradual drift in highly imbalanced industrial IoT data. Their method leverages multiple learners to capture diverse drift patterns, while dynamically adjusting the ensemble to maintain predictive accuracy as new data arrives.

While the above approaches provide valuable strategies for handling data drift, many rely on frequent or full retraining of models once drift is detected. This creates significant computational and operational overhead, particularly in real-time or resource-constrained settings. What remains underexplored is a principled way of distinguishing between different levels of drift severity and tailoring the model’s response accordingly. Proposed framework addresses this gap by introducing a unified severity score that enables selective adaptation: instead of retraining at every drift event, the system applies lightweight transformations when drift is minor or moderate, and only escalates to full retraining under severe drift. This severity-aware strategy preserves predictive accuracy while reducing unnecessary updates, offering a more cost-efficient and practical alternative to traditional drift handling techniques.

2. Materials and Methods

Continuous data shifts affect model accuracy, but retraining after every drift is inefficient. Proposed approach quantifies drift severity with multiple statistical measures and responds proportionally, maintaining accuracy while avoiding unnecessary costs.

Inputs:

• Streaming data $D_t$ arriving over time.
• Short-term window size $W_s$, long-term window size $W_l$.
• Thresholds ${\theta }_1$, ${\theta }_2$ for severity.
• Current model M.

Outputs:

• Adaptive action: No Action, Partial Retrain, Full Retrain.

Procedure:

• Update Windows:

  ○

  Maintain a short-term window $X_s$, $Y_s$ of the most recent $W_s$ samples.

  ○

  Maintain a long-term window $X_l$, $Y_l$ of historical $W_l$ samples.

• Compute Drift Severity:

  ○

  For each distributional metric m ∈ {KS, Wasserstein, Jensen–Shannon}:

  $$d_m=m(P_s,P_l),$$

  (1)

  where $P_s$ and $P_l$ are the empirical distributions of $X_s$ and $X_l$.

  ○

  Aggregate into a single severity score:

  $$S=\alpha \times d\_ks+\beta \times d\_w+\gamma \times d\_jss,$$

  (2)

  with α, β, γ as weighting coefficients.

• Select Action Based on Severity:

  ○

  Low severity: ${S<\theta }_1$

  ▪

  Action = No update; continue monitoring.

  ○

  Moderate severity: ${\theta }_1\le S<{\theta }_2$

  ▪

  Action = Incremental Update: fine-tune M on $X_s$, $Y_s$ using small learning rate or online update step.

  ○

  High severity: ${S\ge \theta }_2$

  ▪

  Action = Full Retrain: discard M and train a new model on $X_s\cup X_l$

While the drift severity score is distributional in nature, its thresholds were designed with downstream model performance in mind. In preliminary sensitivity tests, scores below θ₁ (<0.05) did not yield measurable accuracy loss, whereas scores between θ₁ and θ₂ (0.05–0.1) typically coincided with minor but accumulating degradation (<2–3% accuracy drop on benchmark tasks). Scores above θ₂ (≥0.1) aligned with sharp declines in predictive stability, motivating full retraining. Thus, severity categories serve as operational proxies for acceptable versus unacceptable performance loss, providing a principled basis for retraining decisions. While current study emphasizes demonstrating the framework rather than exhaustive benchmarking, these mappings illustrate how thresholds can be operationalized in practice.

4.

Log and Adapt:

○

Record (S, action) for future threshold tuning.

○

Optionally update ${\theta }_1$, ${\theta }_2$ dynamically using historical S values.

To quantify distributional drift, multiple statistical metrics can be employed depending on the specific requirements of the analysis.

Figure 1 summarizes the workflow, highlighting the stages of window maintenance, drift quantification, aggregation, and adaptive action.

Initially, evaluation of the drift using the Kolmogorov–Smirnov (KS) statistic, Kullback–Leibler (KL) divergence, and the Anderson–Darling statistic was tested. However, this combination exhibited certain drawbacks: the Anderson–Darling statistic proved highly sensitive to sample size, often exaggerating drift in large datasets, while KL divergence suffered from asymmetry and instability in the presence of zero-probability bins. To address these issues, the Anderson–Darling statistic was replaced with the Wasserstein distance, which is more interpretable in terms of “average displacement” between distributions and less affected by differences in sample size. Furthermore, KL divergence was substituted with the Jensen–Shannon (JS) divergence, a symmetric and bounded measure that avoids zero-probability issues, providing a more robust and interpretable drift score.

Table A1. Drift metrics comparison.

Metric	What it Measures	Pros	Cons	Use Case
Kolmogorov–Smirnov (KS)	Max CDF difference	Simple, well-known	Less sensitive to tail differences	Quick general drift check
Anderson–Darling (AD)	Weighted CDF difference (emphasizes tails)	More sensitive than KS to differences in distribution tails	Highly sensitive to sample size, can exaggerate drift in large datasets	Detecting subtle tail changes, when sample size is moderate
Wasserstein distance (Earth Mover’s Distance)	Average distance between distributions	Intuitive distance measure	Computationally heavier	Good for quantifying practical difference
KL divergence	How much one dist differs from another	Information theoretic	Asymmetric, undefined if zero bins	Useful if distributions are PDFs
Jensen-Shannon divergence	Symmetric version of KL divergence	Symmetric, bounded (0–1)	Still needs PDFs	More stable than KL
Population Stability Index (PSI)	Measures population changes in bins	Popular in credit risk/model monitoring	Needs binning and care with bin edges	Used for scorecard drift
Energy distance/Maximum Mean Discrepancy (MMD)	Kernel-based distribution distance	Powerful, non-parametric	More complex	Good for multivariate data

presents detailed metrics comparison.

A single drift score in [0, 1] was obtained by combining normalized KS, Wasserstein, and Jensen–Shannon measures via a weighted average. Each metric was first scaled via min–max normalization based on historical drift observations to ensure comparability despite differing units and ranges. The weights were selected to balance sensitivity to both shape and location changes in the distribution, while avoiding dominance by any single metric. This aggregated score enables a consistent interpretation of drift magnitude, facilitating threshold-based categorization into “no drift,” “low drift,” and “significant drift” levels for operational decision-making.

After quantifying severity, we evaluated transformation methods to align new data with the historical baseline, aiming to reduce discrepancies before inference without full retraining. Several approaches were considered: (i) feature-wise importance reweighting [16], where sample weights are adjusted based on estimated density ratios between historical and current feature distributions; (ii) feature mapping through domain adaptation layers, which learn a transformation that minimizes distribution shift via statistical measures such as Maximum Mean Discrepancy (MMD) [17] or adversarial training; (iii) residual correction models [18], which adaptively adjust predictions based on recent residual errors; and (iv) calibration layers, which post-process output probabilities to better match observed frequencies in the new data.

After reviewing these options, the quantile transformation method [19] was selected for empirical testing. The mathematical formulations are provided in Appendix A.3. This approach non-parametrically maps the empirical cumulative distribution function (CDF) of the new data to that of the reference distribution, ensuring that each feature’s marginal distribution matches the baseline while preserving the rank order of observations. Unlike reweighting, it adjusts the feature space directly; unlike domain adaptation, it requires no extra model. The method is lightweight, deterministic, and robust to sample-size variation, making it suitable for rapid alignment when retraining is costly.

This transformation preserves the relative ranks of the new data while reshaping its distribution to resemble the historical (reference) one.

For implementation details, the pseudocode is included in Appendix A.2.

3. Results

3.1. Data Exploration

In data analysis and machine learning, tracking how variables evolve over time is key to maintaining relevant insights. The job market is one such domain, where salaries, demand, and skills shift with technology, economics, and organizational needs.

In this study, drift is examined within the context of a dataset on data science salaries, focusing on how compensation levels vary across time and between different experience levels. The observed drift reflects both covariate drift—changes in inputs such as experience level, job title, or company size—and prior probability drift, where category frequencies shift. Concept drift may also arise if external factors (e.g., market saturation or new tools) alter the relationship between experience and salary.

This case study investigates temporal trends and structural changes in the salary data, with particular attention paid to how distributions evolve across time and role seniority. By identifying and quantifying such drift, actionable insights can be derived to support more informed and adaptive decision-making in a rapidly changing labor market.

For the empirical study, the Data Science Job Salaries dataset published on Kaggle was used. The dataset contains 38,376 records covering salaries of data-related roles between 2020 and 2024. Each record includes attributes such as the reported salary in local currency, the standardized salary in USD, the work year, employment type, job title, company size, and location information. Importantly, this dataset is not a single-source collection but rather an aggregation of six independent salary surveys, which improves its diversity while also introducing potential inconsistencies across sources.

The temporal distribution of records is skewed toward recent years, with 20,548 entries in 2024, 13,319 in 2023, and substantially fewer observations in earlier years (e.g., 213 in 2020). This imbalance reflects the dataset’s crowdsourced nature and the rapid growth of the technology sector in recent years.

Salary values exhibit substantial variation: the average reported salary is approximately $148,762 USD, with a standard deviation of about $75,034 USD. The maximum salary exceeds $800,000 USD, while the minimum entries include zeros, which likely correspond to erroneous or incomplete submissions. These characteristics highlight the heterogeneity of the dataset and the importance of applying normalization and robustness checks in the drift analysis.

This dataset was selected for three reasons:

• Accessibility and size—it provides a relatively large sample that is publicly available and reproducible.
• Temporal coverage—the dataset spans multiple consecutive years, enabling year-over-year drift analysis.
• Heterogeneity—it captures a wide range of salaries and job contexts, which allows testing drift detection across diverse distributions.

While this dataset is not fully representative of all environments where drift adaptation is critical (e.g., high-frequency sensor data, streaming applications), it offers a practical and transparent benchmark for evaluating our severity-based drift scoring approach.

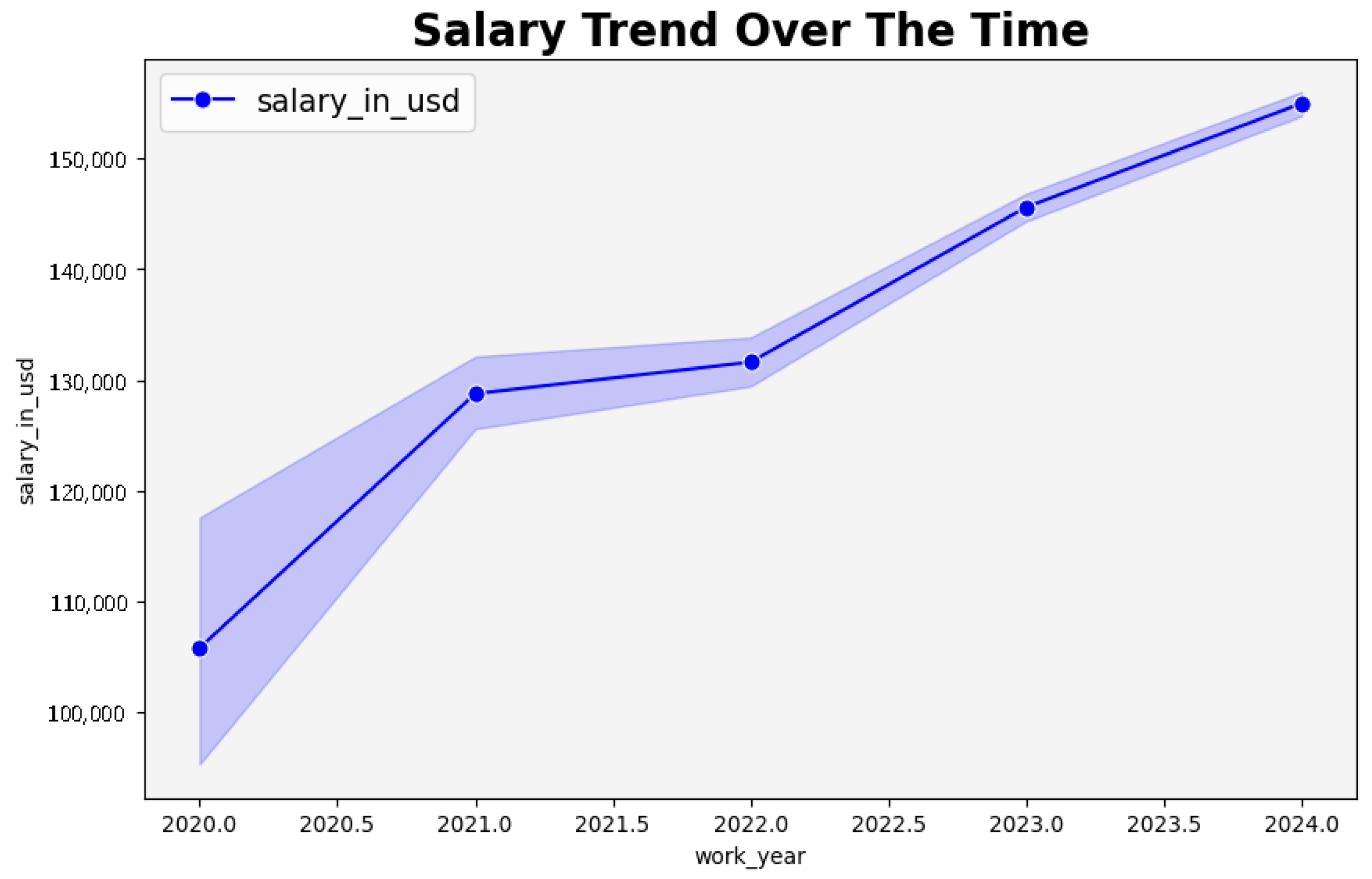
In Figure 2, the trend of data scientist salaries over time is depicted, showing a clear temporal shift. The observed pattern indicates drift, suggesting that the salary distribution changes notably across periods.

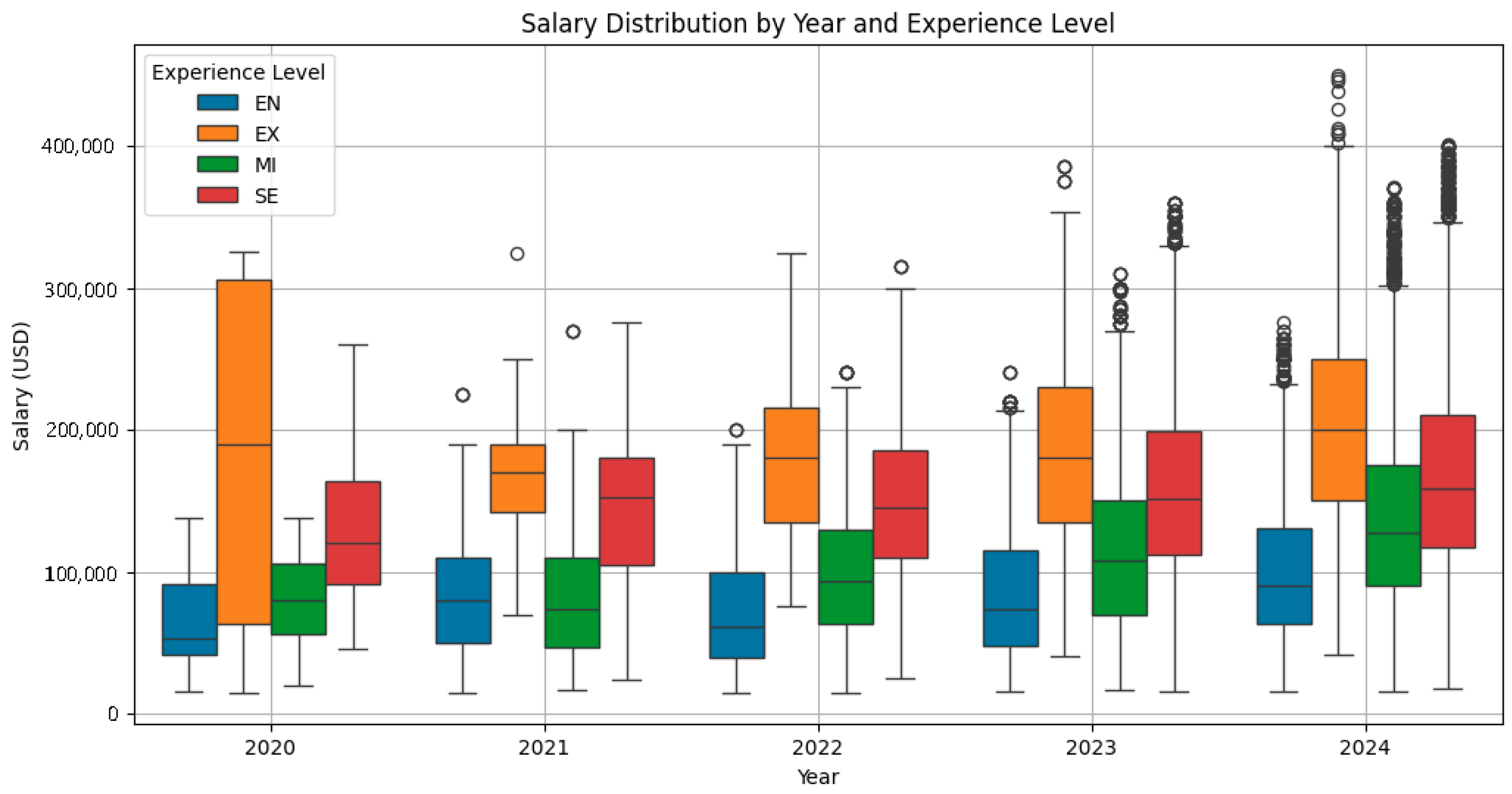
In Figure 3, boxplots illustrate the salary distribution by year and role level, revealing that the magnitude and direction of drift vary across levels. This indicates that salary dynamics are not uniform but depend on career stage.

To statistically confirm the observed drift, the Kolmogorov–Smirnov (KS) test [20] was applied to salary distributions from 2023 and 2024. The test yielded a KS statistic of 0.0559 (p < 0.0001), indicating a small but statistically significant difference in distribution shape, confirming measurable drift between the two years.

The Kolmogorov–Smirnov (KS) test was also applied separately for each role level to assess whether salary drift differs across career stages.

Table 1. KS test p-values for salary distribution drift by role level.

Years Compared	EN	EX	MI	SE
2020 vs. 2021	0.0011	0.0082	0.0764	0.0025
2021 vs. 2022	0.0008	0.0145	0.0000	0.0076
2022 vs. 2023	0.0003	0.2729	0.0000	0.0000
2023 vs. 2024	0.0000	0.0084	0.0000	0.0000

summarizes the results for all consecutive year comparisons.

Across most year-to-year comparisons, p-values < 0.05 indicate statistically significant distributional changes, confirming salary drift. However, the extent of drift is not uniform:

• Entry (EN) roles show consistent, significant drift in all comparisons.
• Executive (EX) roles exhibit significant drift in most years, but not between 2022 and 2023.
• Mid-level (MI) salaries are stable only between 2020 and 2021, with strong drift in later periods.
• Senior (SE) roles show significant drift in all but the 2020–2021 comparison.

This confirms that salary dynamics evolve differently by role level, with entry and mid-level positions experiencing the most persistent distributional shifts.

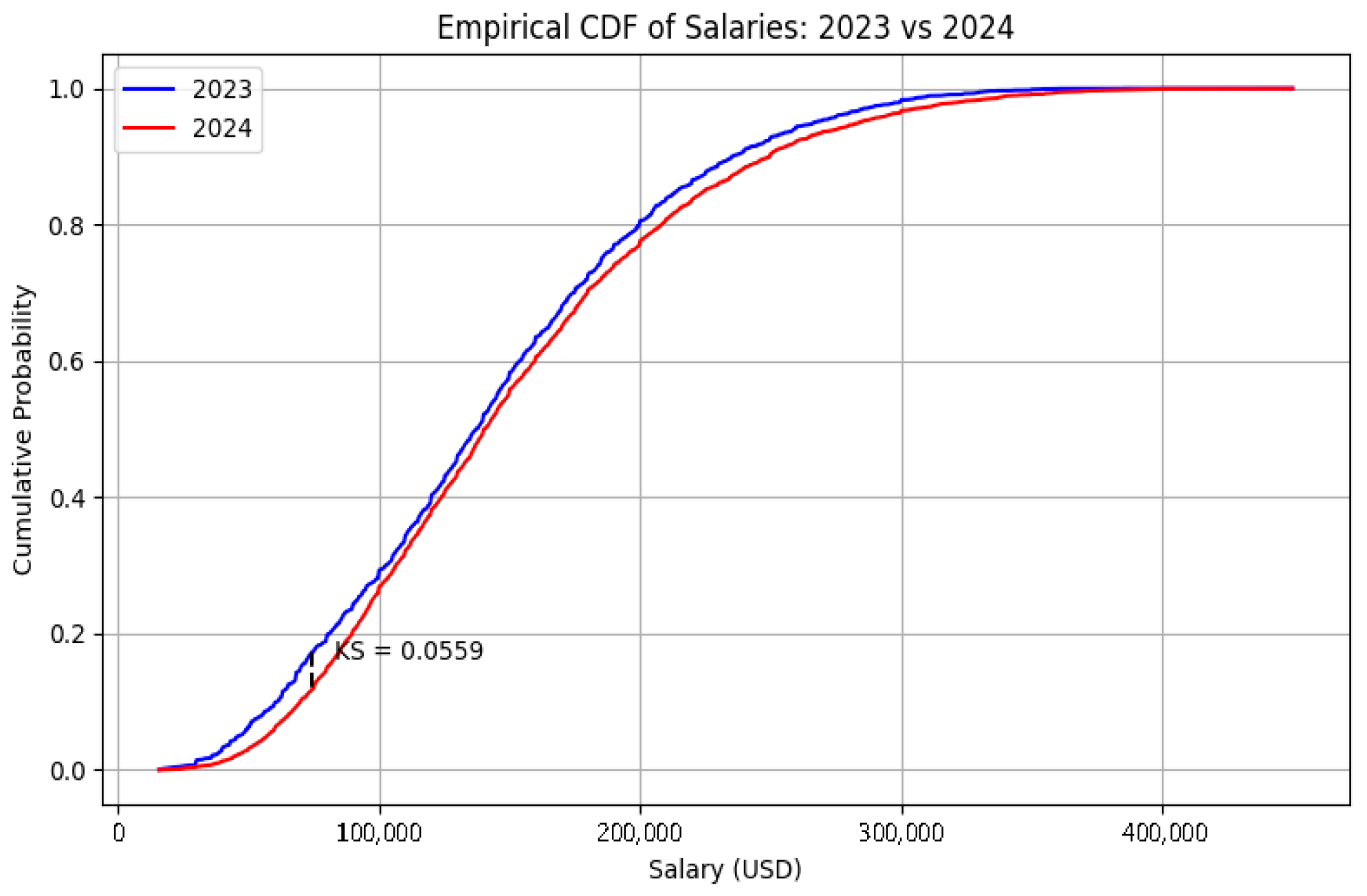
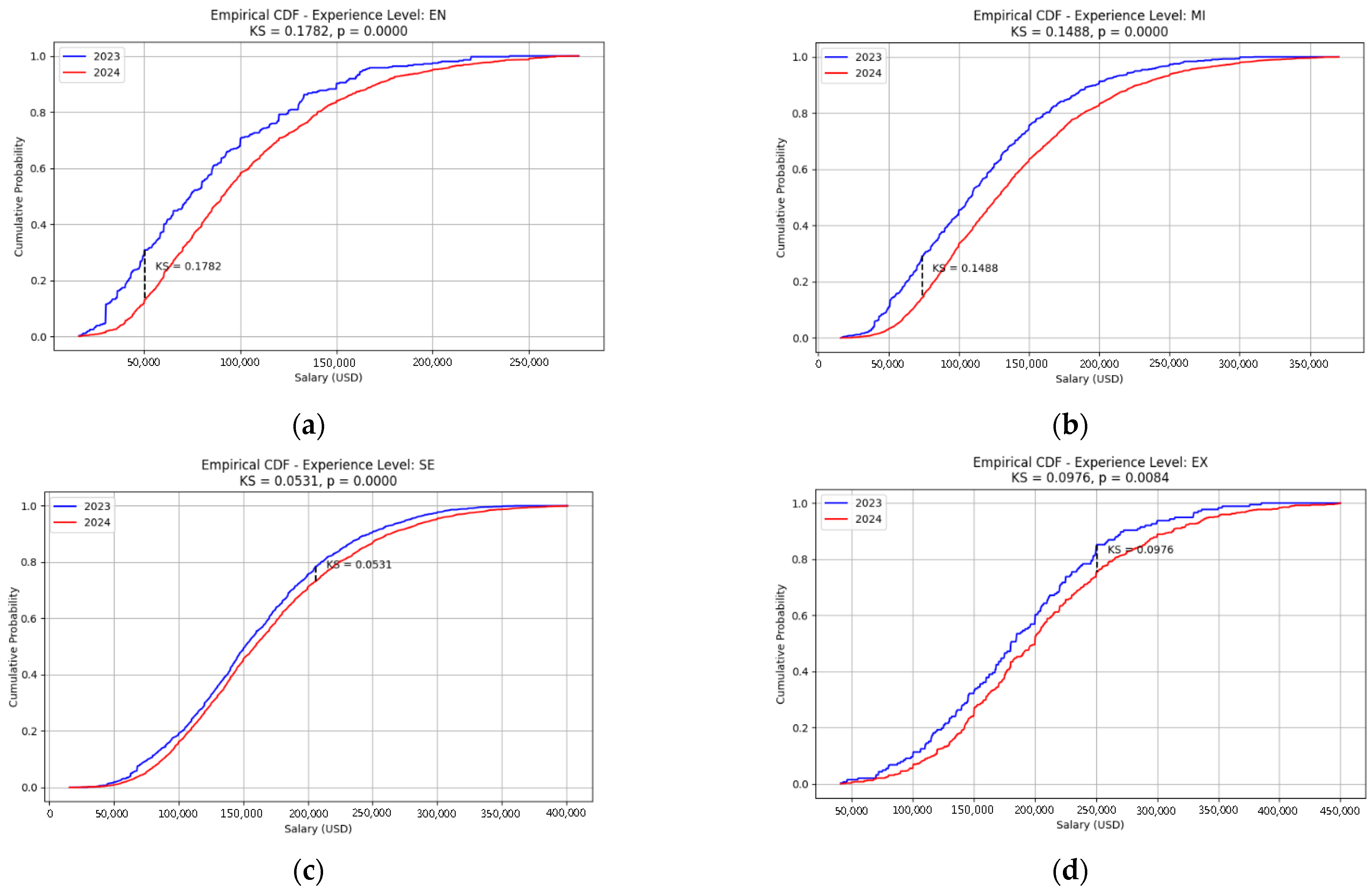
Another way to detect drift is using Empirical CDFs [21]. Figure 4 displays the Empirical Cumulative Distribution Functions (ECDFs) of salaries comparing 2023 and 2024 for the overall data and Figure 5 broken down by experience levels (EN, EX, MI, SE). The ECDF plots visualize the cumulative probability that a salary is less than or equal to a given value, highlighting differences in the salary distributions over time.

The overall ECDF (top plot) shows a small but noticeable shift between 2023 (blue) and 2024 (red) salaries, with a KS statistic of 0.0559, indicating some drift.

By experience level, the ECDFs reveal varying degrees of distributional change:

• Entry (EN) level shows a substantial shift with a KS statistic of 0.1782, indicating a significant increase in salary distribution between years.
• Executive (EX) level shows moderate drift with a KS statistic of 0.0976, confirming statistically significant but smaller changes.
• Mid-level (MI) also exhibits a pronounced shift (KS = 0.1488), reflecting notable salary adjustments.
• Senior (SE) level shows the smallest shift (KS = 0.0531), indicating relatively stable salary distributions compared to other levels.

Across all levels, p-values of 0.0000 or near zero confirm that these distributional differences between 2023 and 2024 are statistically significant. The varying KS statistics visually and quantitatively demonstrate that salary drift differs by role seniority, with the largest changes observed in Entry and Mid-level positions.

In addition to the primary analysis, two additional statistical metrics were used to assess the distributional differences in salary data between 2023 and 2024 across the four groups (EN, EX, MI, SE): the Kullback–Leibler [22] (KL) divergence and the Anderson-Darling (AD) test statistic.

The KL divergence, which measures the relative entropy or difference between two probability distributions, yielded the following values: EN = 0.2311, EX = 0.0645, MI = 0.1428, and SE = 0.0393. The overall KL divergence across all groups was found to be 0.0412, indicating a relatively small divergence between the salary distributions of the two years on aggregate.

The Anderson-Darling test [23], a non-parametric test used to evaluate whether two samples come from the same distribution, produced statistically significant results for all groups. The AD statistics were: EN = 88.5902, EX = 9.1434, MI = 203.8717, and SE = 58.5065, all with p-values equal to 0.0010. The overall Anderson-Darling statistic was 73.6193 with a p-value of 0.0010, strongly rejecting the null hypothesis of identical distributions between the 2023 and 2024 salary data.

These results collectively suggest that while the overall divergence measured by KL divergence is relatively low, the Anderson-Darling test detects statistically significant differences in the distributions across all groups, reflecting changes in the underlying salary distributions between the two years.

To investigate temporal changes in the salary distributions, the data across multiple years using three statistical metrics was compared: the Kolmogorov–Smirnov (KS) statistic, the Kullback–Leibler (KL) divergence, and the Anderson-Darling (AD) test statistic. The sample sizes and results for each year comparison against 2024 are summarized in

Table 2. Data drift comparison.

Years Compared
Comparing distributions for 2023 vs. 2024: Samples: 13,214 vs. 20,318 KS statistic: 0.0559, p-value: 0.0000 KL Divergence (2023 vs. 2024): 0.0412 Anderson–Darling statistic: 73.6193, p-value: 0.0010
Comparing distributions for 2022 vs. 2024: Samples: 2993 vs. 20,318 KS statistic: 0.1093, p-value: 0.0000 KL Divergence (2022 vs. 2024): 0.1421 Anderson–Darling statistic: 153.0022, p-value: 0.0010
Comparing distributions for 2021 vs. 2024: Samples: 1219 vs. 20,318 KS statistic: 0.1737, p-value: 0.0000 KL Divergence (2021 vs. 2024): 0.4136 Anderson–Darling statistic: 92.9645, p-value: 0.0010

:

Based on these results, the distributional shifts can be categorized as follows to simulate different levels of drift:

• No Drift—represented by the 2023 vs. 2024 comparison, where the KS statistic and KL divergence are relatively low, indicating minimal change between the salary distributions.
• Low Drift—represented by the 2022 vs. 2024 comparison, showing moderate increases in KS statistic and KL divergence, suggesting noticeable but not drastic changes.
• Strong Drift—represented by the 2021 vs. 2024 comparison, with the highest KS statistic and KL divergence values, indicating a substantial change in the distribution.

These categories allow modeling of drift severity in temporal salary data, useful for evaluating robustness of statistical methods or machine learning models to changing data distributions over time.

3.2. Weighted Drift Analysis

To obtain a single composite measure of distributional change, a Combined Drift Score by weighting the KS statistic (50%), KL divergence (30%), and the Anderson–Darling statistic normalized by the logarithm of the combined sample size (20%) was computed.

The KS statistic is sensitive to the largest differences between cumulative distribution functions (CDFs), the KL divergence quantifies the overall (asymmetrical) shift between distributions, and the Anderson-Darling statistic is particularly sensitive to differences in the tails of the distributions.

Drift severity was classified as No drift (<0.05), Low drift (<0.15), or Significant drift (≥0.15). The combined score results are shown in

Table 3. Combined score results comparison.

Comparison	KS	KL	AD	Combined Score	Drift Level
2023 vs. 2024	0.0559	0.0412	73.6193	1.4533	Significant
2022 vs. 2023	0.0793	0.0808	58.5182	1.2713	Significant
2021 vs. 2022	0.0821	0.1023	8.9058	0.2851	Significant

.

All year-to-year comparisons exceeded the threshold for Significant drift, indicating substantial changes in the underlying salary distributions across consecutive years. The largest drift was observed between 2023 and 2024 (score = 1.4533), driven primarily by a high normalized Anderson–Darling statistic, while the smallest—but still significant—drift occurred between 2021 and 2022 (score = 0.2851), where the Anderson–Darling contribution was comparatively low. While this confirms distributional changes over time, the uniformly significant results limit the ability to discriminate between different drift levels in current experimental setup, which requires distinguishing among no drift, low drift, and strong drift conditions.

To better capture and differentiate these levels, adjustment of the set of metrics was proposed:

• Keep KS test for a simple quick check.
• Replace Anderson–Darling with Wasserstein distance [24]—interpretable and less sample-size dependent.
• Use Jensen-Shannon divergence [25] instead of KL to avoid asymmetry and zero-probability issues.

The summary of changes are shown in

Table 4. Combined score metric decision.

Metric to Keep	Metric to Replace with	Why?
KS	-	Simple and interpretable
Anderson–Darling	Wasserstein distance	More stable with sample size
KL divergence	Jensen-Shannon divergence	Symmetric, more stable

.

Using the revised metrics—KS statistic, Wasserstein distance, and Jensen-Shannon divergence—the combined drift scores was recalculated for the yearly salary distribution comparisons. The results are summarized in

Table 5. Updated combined score results comparison.

Comparison	KS Statistic	Wasserstein Distance	Jensen-Shannon Divergence	Combined Drift Score	Drift Level
2023 vs. 2024	0.0559	7943.26	0.0148	2383.01	Significant
2022 vs. 2024	0.1093	21,564.75	0.0518	6469.49	Significant
2021 vs. 2024	0.1737	24,353.06	0.1502	7306.03	Significant

:

While the updated metrics produce a wider and more distributed range of drift scores—reflecting gradations in distributional changes—the absolute values of the combined scores vary greatly in magnitude. This wide scale complicates direct interpretation and comparison.

Therefore, to facilitate consistent classification and improve interpretability, the combined drift score requires normalization to a bounded range, such as [0, 1]. Normalizing the scores will enable straightforward thresholding and clearer distinction between no drift, low drift, and strong drift categories, thereby improving practical usability in monitoring and experimental evaluation.

3.3. Normalization of Drift Metrics and Results

To ensure comparability and interpretability of drift scores across different year-to-year salary distribution comparisons, normalization was applied to the individual metrics prior to combining them.

• Wasserstein distance normalization: The raw Wasserstein distance was divided by the range of combined salary values (max–min) from both samples. This scaling bounds the Wasserstein metric approximately between 0 and 1, making it invariant to absolute salary scale differences.
• Jensen-Shannon divergence: Computed on histograms with Freedman–Diaconis binning and smoothed with a small epsilon to avoid zeros, then squared to maintain values strictly between 0 and 1.
• KS statistic: Remains naturally between 0 and 1 and is retained without modification.
• The combined drift score is calculated as a weighted sum of the normalized KS statistic (weight 0.4), scaled Wasserstein distance (weight 0.3), and Jensen-Shannon divergence (weight 0.3). This weighted aggregation ensures the overall score ranges from 0 to 1.

The drift score is interpreted with thresholds:

• No drift: score < 0.05.
• Low drift: 0.05 ≤ score < 0.1.
• Significant drift: score ≥ 0.1.

The combined score results with normalized metrics are shown in

Table 6. Normalized metrics combined score results comparison.

Comparison	KS Statistic	Wasserstein (Scaled)	Jensen-Shannon	Combined Score	Drift Level
2023 vs. 2024	0.0559	0.0183	0.0148	0.0323	No drift
2022 vs. 2024	0.1093	0.0496	0.0518	0.0742	Low drift
2021 vs. 2024	0.1737	0.0560	0.1502	0.1313	Significant drift

.

The normalized combined scores reveal a clearer gradation of drift intensity, with the 2023 vs. 2024 comparison falling into the no drift category, 2022 vs. 2024 showing low drift, and 2021 vs. 2024 exhibiting significant drift.

As a complementary case study, experiments were conducted on the Housing in London dataset, originally published by the London Datastore. The dataset spans the period from January 1995 to January 2020, offering a long-term view of housing trends across London boroughs.

The dataset contains 13,549 records with the following main attributes:

• average_price—average property prices in GBP;
• houses_sold—number of residential property transactions;
• no_of_crimes—recorded crime counts;
• borough_flag—binary indicator distinguishing London boroughs from other administrative areas.

Descriptive statistics reveal considerable variation across these measures. The mean average property price is approximately £263,520 with a standard deviation of £187,618, while the maximum recorded value reaches over £1.46 million. The number of houses sold varies widely (mean ≈3894, max >132,000), reflecting the dynamic nature of the housing market. Crime counts average around 2158 incidents per period with notable dispersion (standard deviation ≈ 902). The borough_flag distribution (mean ≈0.73) reflects the dataset’s mix of borough-level and non-borough-level entries.

This dataset was selected because:

• Longitudinal coverage—it spans 25 years, allowing drift detection to be tested on long-term socio-economic processes.
• Multivariate structure—it includes economic (prices, transactions) and social (crime rates) indicators, enabling analysis of how different feature types drift jointly over time.
• Public provenance—sourced from an official open-data portal, ensuring transparency and reproducibility.

This dataset complements the salary dataset by providing a structurally different domain: structured temporal-economic data with geographic granularity, in contrast to individual-level survey data. Together, the two cases illustrate the flexibility of proposed drift severity scoring approach across diverse contexts.

One challenge with housing data is that adjacent years can show noisy differences due to changes in the mix of properties sold (e.g., regional distribution or property type). To address this, we anchor comparisons in a fixed year and then measure drift at increasing horizons. This approach highlights the cumulative effect of distributional change over time. As shown in

Table 7. Drift severity in housing dataset with 2010 as anchor year. Thresholds: No drift (<0.05), Low drift (0.05–0.15), Significant drift (≥0.15).

Comparison	KS Statistic	Wasserstein (Scaled)	Jensen-Shannon	Combined Score	Drift Level
2010 vs. 2011	0.0704	0.0105	0.0531	0.0472	No drift
2010 vs. 2012	0.1463	0.0237	0.0790	0.0893	Low drift
2010 vs. 2015	0.4611	0.1083	0.2012	0.2773	Significant drift

, the drift severity increases consistently with the time horizon: one-year comparisons remain in the No drift category, medium horizons show Low drift, and longer horizons reach Significant drift. This illustrates that proposed severity score scales meaningfully with temporal distance, even in noisy real-world datasets.

When comparing housing prices between 2010 and 2011, pooled analysis suggested No drift (combined score = 0.0472). However, when the same comparison was performed separately for each area, almost every region showed Significant drift (44 out of 45), with only one area showing Low drift.

Table 8. By-area drift severity for 2010 vs. 2011 (average_price).

Area	Combined Score	Drift Level
Yorks and the Humber	0.735	Significant drift
Richmond upon Thames	0.731	Significant drift
North East	0.715	Significant drift
Havering	0.147	Significant drift
Bexley	0.146	Significant drift
Enfield	0.097	Low drift

highlights the top-3 strongest and weakest cases.

This discrepancy shows that aggregated analysis can obscure important local changes: when subgroups shift in different ways, the overall distribution may appear stable even though strong drift occurs within subpopulations.

Drift assessment is most informative when performed at the level of detail that matches the model’s scope. For global models, aggregated (pooled) drift scores provide a useful overview, while for region- or subgroup-specific models, stratified detection offers more relevant insights. The proposed framework accommodates both approaches, allowing practitioners to compute severity scores for any subgroup of interest (e.g., by region, demographic, or device type) and align monitoring with the intended application.

As a direction for future work, it would be valuable to design summary statistics that integrate both global and subgroup perspectives. Such measures could capture overall distributional shifts while also reflecting variation across subpopulations, enabling a more balanced assessment in settings where both global accuracy and subgroup stability are critical.

To test proposed approach in a high-dimensional, non-economic domain, we used the Gas Sensor Array Drift Dataset at Different Concentrations, published by the UCI Machine Learning Repository. This dataset was originally collected by Vergara et al. as part of research on sensor drift phenomena, making it highly relevant for evaluating drift detection methods.

The dataset consists of 13,910 measurements of chemical gas concentrations collected over 10 batches. Each record includes:

• batch—indicating the measurement batch (1–10);
• class_id—the gas type identifier (6 classes of volatile organic compounds);
• concentration—concentration level (1–1000 ppm);
• f1–f128—128 continuous features representing the raw responses of an array of 16 chemical sensors across multiple feature extraction methods.

The data distribution is heterogeneous. Concentration values range from 1 ppm to 1000 ppm, while the sensor features span wide numeric scales. For instance, feature values (e.g., f1, f121) can range from highly negative values (e.g., −16,000) to large positive magnitudes (up to >670,000). The dataset thus reflects both the physical variability of sensor outputs and the challenges introduced by sensor drift. Sensor features exhibit large standard deviations (e.g., f1 std ≈ 69,845), skewness, and extreme outliers. Measurements cover multiple gases across batches, providing natural partitions for drift analysis.

This dataset was chosen because:

• Direct relevance—it was explicitly designed to study sensor drift, making it a natural benchmark.
• High dimensionality—with 128 features, it enables testing scalability and robustness of drift scoring.
• Temporal batching—the division into batches allows for evaluating drift both sequentially and cumulatively.

This dataset complements the salary and housing datasets by representing a real-world sensor scenario where drift is a known and critical challenge. It allows us to demonstrate that our severity-based scoring approach is not limited to socio-economic data but can generalize complex industrial and IoT settings.

Analysis was conducted in three steps:

• Feature-level drift detection: Each sensor feature was compared across time windows using the same statistical tests (KS, Wasserstein, Jensen–Shannon). Features were assigned a severity level (No drift, Low drift, Significant drift). This provides a fine-grained view of which sensors show the strongest distributional changes.
• Window-level aggregation: For each time window, we aggregated across features and computed the percentage of features in each drift category. This allows us to observe whether drift is sporadic or systemic across the sensor array.
• Stacked trend visualization: Finally, the drift dynamics over time using a stacked bar plot was presented, showing the evolution of No/Low/Significant drift categories across windows. This highlights not only which features drift, but also when drift is concentrated.

Key observation:

The gas dataset showed pervasive drift—with 93% of features flagged as Significant drift. Only a small fraction (7%) was categorized as Low drift, and none as No drift. This is consistent with the stacked plot, where almost every window is dominated by significant drift. At the same time, the framework identifies both the most unstable features (e.g., f121, f105, f113) and the relatively more stable ones (f32, f24, f10), demonstrating how it can pinpoint the where and when of changes, even in complex sensor data. Results are displayed on

Table 9. Top 5 most drifted and stable features.

Feature	Combined Score	Drift Level
f121	0.314	Significant drift
f105	0.313	Significant drift
f113	0.307	Significant drift
f57	0.298	Significant drift
f49	0.298	Significant drift
f32	0.056	Low drift
f24	0.059	Low drift
f10	0.067	Low drift
f56	0.081	Low drift
f96	0.081	Low drift

.

Table 10. Most and least drift-affected features in the gas dataset.

Target Window	Low Drift	No Drift	Significant Drift
(1,)	0.0%	38.3%	61.7%
(2,)	1.6%	47.7%	50.8%
(3,)	0.0%	0.8%	99.2%
(4,)	0.0%	4.7%	95.3%
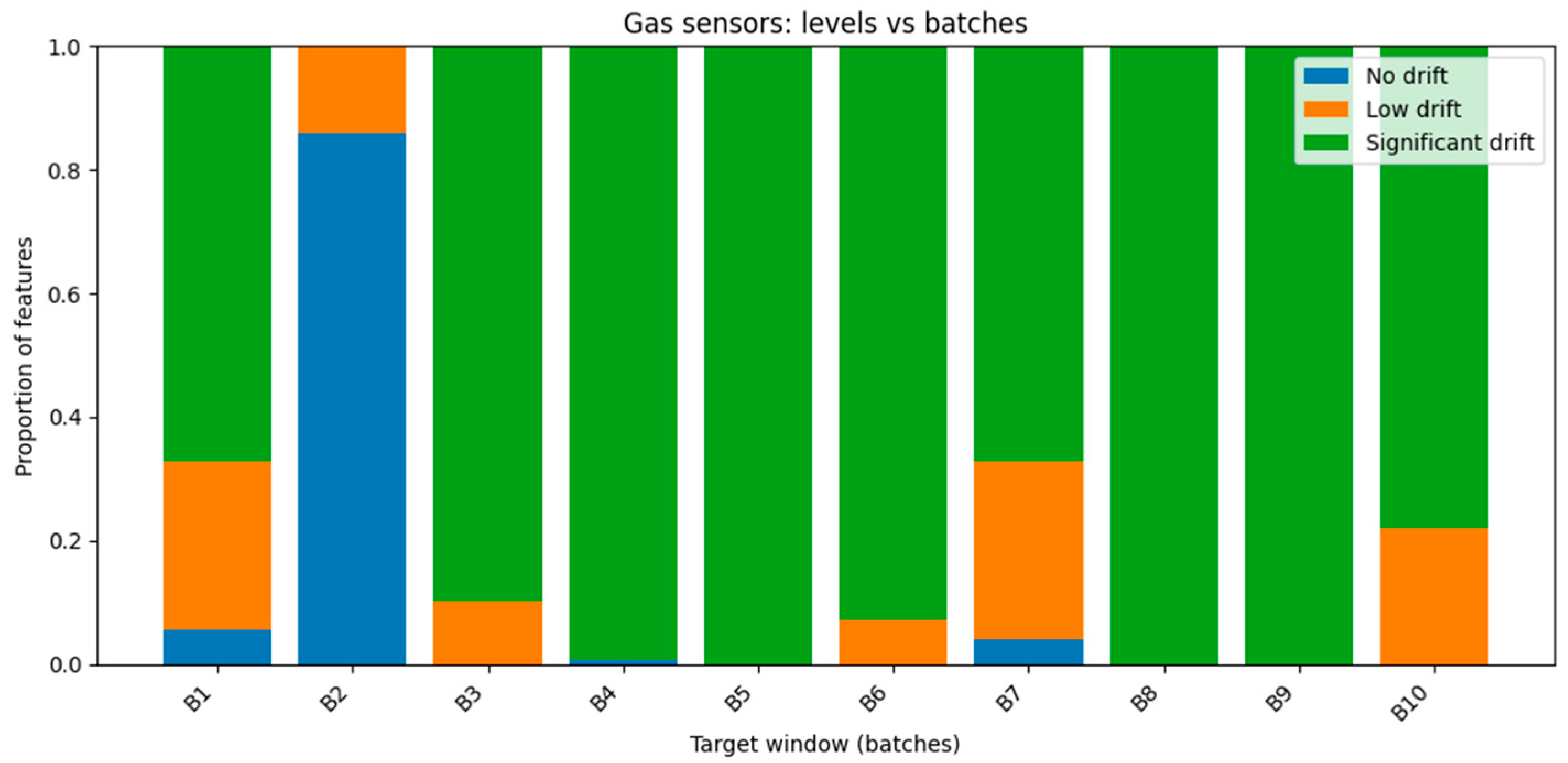
(5,)	0.0%	2.3%	97.7%

reports drift severity across different target windows in the gas sensor dataset. The dataset is organized into batches, where each batch corresponds to a controlled experimental run collected under fixed conditions (e.g., a particular time period and gas concentration setting). A target window in this analysis is defined as a single batch (window size = 1 batch). Thus, Window (1,) refers to the first batch after the baseline, Window (2,) to the second batch, and so on.

For each target window, drift severity was measured by comparing the feature distributions in that batch against the baseline distribution. The proportions of features falling into No drift, Low drift, and Significant drift categories are reported.

The results highlight a strong temporal progression:

• In the earliest windows ((1,) and (2,)), 38–48% of features remain stable (no drift), while roughly half already exhibit significant drift.
• Starting from Window (3,), significant drift dominates, exceeding 95% of features in later windows ((3,)–(5,)).
• Low drift is rarely observed, suggesting that feature distributions tend to change abruptly rather than gradually.

This confirms that gas sensor responses degrade or shift systematically across batches, with later experimental runs showing pronounced divergence from the baseline.

The stacked bar chart presented on Figure 6 shows the proportion of features categorized as no drift, low drift, and significant drift across sequential batches (B1–B10). While early batches contain a mix of drift severities, significant drift quickly becomes dominant, exceeding 90% of features in most later batches. A brief stabilization is observed in B2, but this effect does not persist. Overall, the chart highlights the pervasive and accelerating nature of drift in gas sensor data, with only transient windows of stability.

3.4. Limitations and Future Directions

The primary contribution of this work is a framework that enables rapid detection of data drift and its severity, providing a cost-efficient alternative to continuous model retraining. The experimental evaluation across diverse datasets (salary, housing prices, and gas sensors) highlights both the strengths and the current limitations of the approach.

First, data representativeness remains a challenge: some datasets (e.g., salary surveys) may not fully reflect real-world distributions, while others (e.g., housing or sensor data) exhibit imbalanced or limited samples that affect metric stability. Second, there is a trade-off in granularity: pooled analysis may suggest stability, whereas subgroup-level analysis (e.g., by region in housing data) reveals substantial drift. Third, the method is sensitive to temporal windowing, where small windows can produce noise and large windows can obscure short-term shifts. Fourth, small-sample effects occasionally yield unreliable statistical outputs (e.g., NaN values), leading to an overestimation of drift severity. Finally, the current implementation is restricted to continuous variables, and categorical drift detection has not yet been incorporated.

These limitations suggest several promising directions for future research. Expanding dataset diversity will help validate robustness across domains. Adaptive windowing strategies could automatically adjust temporal granularity, reducing reliance on fixed parameters. Hierarchical analysis at both global and subgroup levels would provide a more nuanced understanding of drift. Enhancing robustness to sparse data through Bayesian inference, bootstrapping, or resampling would mitigate instability in low-sample regimes. Extending the framework to categorical distributions represents an important next step to improve coverage. Finally, explicitly linking drift severity scores to model performance degradation would strengthen their utility in guiding retraining policies.

3.5. Parameter Selection and Justification

The construction of the Combined Drift Score required two key design decisions: the weighting of individual statistical metrics and the thresholds used to categorize drift severity. Both were guided by empirical experimentation and domain.

Weighting of metrics. The Kolmogorov–Smirnov (KS) statistic was initially assigned the largest weight (50%) because it is a widely established test for distributional differences and directly captures the maximum deviation between cumulative distributions. Kullback–Leibler (KL) divergence received a moderate weight (30%) to emphasize sensitivity to shifts in distributional mass while mitigating instability in sparse regions of the distribution. The Anderson–Darling (AD) statistic, normalized by the logarithm of the combined sample size to reduce sensitivity to sample size, was weighted lower (20%) to complement KS and KL by focusing on tail behavior. These coefficients were calibrated through repeated experiments to reflect which metrics most consistently aligned with observed and expert-validated distributional changes. The weighting scheme therefore balanced robustness, interpretability, and coverage of different distributional aspects.

Following further evaluation and refinement, the final Combined Drift Score is calculated as a weighted sum of the normalized KS statistic (40%), the scaled Wasserstein distance (30%), and the Jensen–Shannon (JS) divergence (30%). The KS statistics retained the largest share (40%) due to its established role as a non-parametric test for detecting distributional differences, particularly its sensitivity to maximum deviations between distributions. Wasserstein distance was assigned a moderate weight (30%) for its interpretability as the “average shift” between distributions, making it especially suitable for quantifying practical, real-world differences. JS divergence was also given a moderate weight (30%) because of its stability, bounded range (0–1), and symmetric treatment of distributions, complementing the directional sensitivity of KL divergence used earlier. Together, these weights were tuned through empirical testing to maximize robustness and consistency with observed drift phenomena, while ensuring that the combined score remains interpretable on a normalized [0, 1] scale. This scheme integrates complementary perspectives—maximum discrepancy, average shift, and symmetric divergence—yielding a balanced and reliable indicator of drift severity.

Thresholds for severity levels. To categorize the combined score into interpretable severity levels, we conducted experiments across multiple datasets (salary, housing, and gas sensor data). Results indicated that even relatively small deviations in the score (≥0.05) already signaled practically meaningful changes in the data distributions, with potential downstream effects on model performance. On this basis, thresholds were conservatively defined as: no drift (score < 0.05), low drift (0.05 ≤ score < 0.1), and significant drift (score ≥ 0.1). This conservative design reflects the principle that early detection of subtle drift is often more valuable than overlooking gradual shifts that may accumulate over time. While alternative thresholds could be adopted depending on application requirements, the chosen values provided a consistent and interpretable framework for our experiments.

Together, the weighting scheme and threshold definitions form a coherent approach to quantifying and categorizing distributional change. They ensure that the Combined Drift Score remains both sensitive to different types of drift and practically useful for guiding decisions about model retraining or transformation.

3.6. Data Transformation

Several approaches exist for mitigating the impact of distributional drift in input data, including z-score normalization, covariate reweighting, and domain-invariant representation learning. Among these, we employed the quantile transformation method as a statistically grounded and non-parametric approach that does not rely on fixed distributional assumptions. It preserves the rank structure of features while mapping them to a predefined target distribution (uniform or normal), thereby stabilizing feature behavior under non-linear, skewed, or multimodal shifts. Compared to standard scaling, quantile transformation adapts dynamically to the empirical distribution of incoming data, making it particularly effective for long-term or gradual drift scenarios. Its robustness and computational efficiency also make it suitable for both streaming and batch adaptation pipelines.

This transformation maps feature values to a uniform or normal distribution based on their empirical quantiles, effectively normalizing feature distributions without modifying the underlying model. This method posses both advantages and disadvantages, further details can be found in

Table 11. Review of quantile transformation method.

Advantages

Limitations

Model-agnostic: The transformation operates at the input level, requiring no changes or retraining of the existing predictive model. No retraining needed: Because the model processes transformed inputs seamlessly, this approach avoids costly retraining cycles. Non-parametric: It makes no assumptions about the underlying data distribution (e.g., Gaussian), adapting flexibly to various feature shapes. Effective for covariate drift: Particularly useful when the input feature distributions shift over time, helping stabilize model performance in the presence of covariate drift.

Univariate operation: The transformation is applied independently to each feature and does not capture or preserve dependencies or correlations between multiple features. Monotonicity constraint: While it preserves the order of feature values, applying quantile transforms blindly across correlated features may distort their relationships, potentially affecting model interpretability or performance. Sample size sensitivity: Accurate quantile estimation requires sufficiently large and representative samples; small sample windows may lead to noisy or unstable transformations. Does not address concept drift: Changes in the relationship between inputs and outputs (label or concept drift) are not mitigated by this method alone and require additional strategies.

.

Quantile Transformation algorithm

• Map the empirical CDF of the new data to the empirical CDF of old data feature-wise.
• For each feature or target:

  $$x_{new\_transformed}=F_{old}^{-1}\left(F_{new}\right(x_{new}\left)\right)$$

  (3)

  where $F_{new}$ and $F_{old}^{-1}$ are empirical CDFs of the feature in new and old data, respectively. This “warps” the new data distribution to look like the old.

The quantile transformation method was tested by mapping the 2024 salary distribution onto the 2023 distribution, aiming to reduce distributional differences while preserving the overall data structure. The transformation aligns the quantiles of the 2024 salaries with those of 2023, effectively normalizing for distributional shifts. The effect of quantile transformation is shown in

Table 12. Results before and after quantile transformation.

Metric	Before Transformation	After Transformation
KS Statistic	0.0559	0.0072
Wasserstein Distance	7943.26	170.93

.

The Kolmogorov–Smirnov (KS) statistic decreased substantially from 0.0559 to 0.0072, indicating a dramatic reduction in the maximum difference between the empirical cumulative distributions of the two years.

Similarly, the Wasserstein distance dropped sharply from 7943.26 to 170.93, reflecting a much smaller average shift in salary values after the transformation.

These results demonstrate that quantile transformation can effectively align distributions across years, mitigating covariate drift and helping maintain model robustness without retraining.

3.7. Time and Memory Complexity Analysis

At each time step, we maintain two per-feature sliding windows over the incoming stream—a short window of size $w_s$ and a long window of size $w_l$ (${total w= w}_s+ w_l$)—and compute a severity score by aggregating three divergences between the two windows: two-sample Kolmogorov–Smirnov (KS), 1-Wasserstein (W1), and Jensen–Shannon (JS). For exact computation from raw 1-D samples, per feature we sort the concatenated samples to obtain empirical CDFs and cumulative sums; KS and W1 are then obtained by a single linear scan, while JS is computed from histograms with $b$ bins. This yields a per-step time of $O(w\mathit{log}w+b)$ (equivalently $O(w_s\mathit{log}{w}_s+w_l\mathit{log}{w}_l+b)$) and memory $O(w+b)$ to hold (sorted) windows and counts.

Across $d$ features, the detection cost is therefore $T_{detect}= O\left(d\right(w\mathit{log}w+b\left)\right)$ with memory $O\left(d\left(w+b\right)\right)$. To reduce recomputation, we also report a streaming variant that maintains per-feature summaries: rolling histograms for JS and fixed-size quantile sketches for KS/W1 with summary size $q$ independent of $w$. Each new observation triggers constant-time amortized updates (inserting the new item and expiring the oldest), and the score is evaluated from the summaries in $O(q+b)$ time per feature. Consequently, streaming detection costs $T_{detect}= O\left(d\right(q+b\left)\right)$ with $O\left(1\right)$ amortized updates per arrival and memory O($O\left(d\right(q+b\left)\right)$. The aggregated divergences are finally combined into a unified severity score.

The proposed severity score is adaptive by design, allowing the system to respond proportionally to the detected level of drift rather than triggering full model retraining immediately. By integrating quantile transformation, the method normalizes heterogeneous feature distributions, ensuring robustness of drift detection across varying data scales. This adaptive mechanism enables incremental updates under moderate drift and reserves full retraining only for severe cases, thereby optimizing computational efficiency.

The quantile transformation step contributes a time complexity of $O(n\mathit{log}n)$—dominated by sorting operations—and a memory complexity of $O\left(n\right)$, as the transformed cumulative distribution must be retained for subsequent metric computation. These properties ensure that the adaptive severity score remains computationally feasible while preserving sensitivity to distributional changes across time.

In contrast, the ROSE framework exhibits a significantly higher computational burden. Its worst-case time complexity is $O\left(2k\lambda \left|S\right|\right)$, where k is the number of base classifiers, λ is the ensemble update rate, and |S| is the stream size. The memory complexity of ROSE is $O(\left(2krvlc\right)+(\left|w\right|f\left)\right)$, incorporating r-dimensional random subspace projections, tree structures, and per-class sliding windows. Therefore, the combined cost of detection + quantile transformation is markedly lower than ROSE’s ensemble-based overhead, underscoring the efficiency and scalability of the proposed adaptive scoring mechanism for online environments.

Naturally, purely statistical transformations such as quantile-based normalization cannot match the predictive accuracy of full model retraining or adaptive ensemble updates in all situations. However, their role is not to replace these mechanisms but to delay or reduce their frequency in cases where drift severity remains low or moderate. By relying on lightweight distributional adjustments, the system preserves stability and acceptable accuracy levels while substantially reducing computational and memory costs. In practice, this trade-off yields considerable efficiency gains: minor drifts can often be mitigated through transformation alone, whereas only the rare, severe drifts necessitate full adaptation. Thus, the framework achieves a balanced compromise between accuracy preservation and resource optimization, making it particularly effective for streaming or real-time deployment contexts.

4. Discussion

Concept drift remains one of the most critical challenges in maintaining reliable machine learning models in dynamic environments. Left unaddressed, drift can lead to gradual or sudden degradation in predictive performance, which in turn impacts decision quality, user trust, and operational efficiency. The framework proposed in this work directly addresses this challenge by introducing a severity-aware adaptation mechanism. By aggregating multiple complementary statistical metrics into a unified severity score, the method enables data-driven decisions about when and how to adapt the model. Selective adaptation—minor, moderate, or severe—triggers updates only when needed, reducing costs without sacrificing accuracy.

The approach not only optimizes resource usage but also enhances operational stability. For example, in real-world scenarios where model retraining incurs high financial or time costs, the ability to defer updates for negligible drift can yield significant efficiency gains. At the same time, the system remains vigilant against severe drift events, where rapid intervention is essential to prevent substantial performance loss. The adaptability of the thresholds, which may be either fixed or statistically tuned over time, further strengthens the robustness of the framework across different application domains.

An additional contribution of this work is the exploration of data transformation strategies to mitigate the effects of drift before triggering model adaptation. Different transformations can alter the feature space in ways that reduce the apparent severity or impact of drift, potentially postponing or even eliminating the need for costly retraining. In particular, quantile transformation reduced the KS statistic from 0.0559 to 0.0072, normalizing distributions and mitigating drift before adaptation. Such transformations can smooth distributional shifts—especially for skewed or heavy-tailed features—thereby enhancing resilience to gradual drift and potentially delaying the need for costly retraining.

While the current method focuses on the severity dimension of drift, future work can expand this decision process to incorporate drift type as well. Not all drift is created equal—covariate shift, prior probability shift, and conditional distribution change may require distinct adaptation strategies. A hybrid decision mechanism that considers both the magnitude and the nature of drift could further refine update policies, enabling even more precise trade-offs between adaptation cost and performance stability. Such an extension would open the door to truly intelligent, context-aware drift management systems that can operate effectively across a wide variety of dynamic data streams.

5. Conclusions

In summary, this study shows that careful, severity-driven adaptation offers a practical and cost-effective way to keep models performing well under drift. The framework updates models only when the benefits are expected to outweigh the costs and tries simple adjustments, like the quantile transformation, before making bigger changes. This makes the approach smarter and more efficient for machine learning in changing environments. The significant drop in the KS statistic after applying the quantile transformation highlights the value of targeted preprocessing in reducing drift effects. In the future, an important extension will be to adapt not only to the severity but also to the type of drift—such as covariate shift, prior probability shift, or concept shift—allowing for more precise and context-aware model updates. This could make the framework even more efficient and robust across a wide range of real-world scenarios.