Abstract
Modern semantic segmentation models require extensive pixel-level annotations, creating a significant barrier to practical deployment as labeling a single image can take hours of human effort. Active learning offers a promising way to reduce annotation costs through intelligent sample selection. However, existing methods rely on poorly calibrated confidence estimates, making uncertainty quantification unreliable. We introduce Conformal Risk Controlled Active Learning (CRC-AL), a novel framework that provides statistical guarantees on uncertainty quantification for semantic segmentation, in contrast to heuristic approaches. CRC-AL calibrates class-specific thresholds via conformal risk control, transforming softmax outputs into multi-class prediction sets with formal guarantees. From these sets, our approach derives complementary uncertainty representations: risk maps highlighting uncertain regions and class co-occurrence embeddings capturing semantic confusions. A physics-inspired selection algorithm leverages these representations with a barycenter-based distance metric that balances uncertainty and diversity. Experiments on Cityscapes and PascalVOC2012 show CRC-AL consistently outperforms baseline methods, achieving 95% of fully supervised performance with only 30% of labeled data, making semantic segmentation more practical under limited annotation budgets.
1. Introduction
Semantic segmentation, the task of assigning a semantic label to every pixel in an image, is fundamental to numerous computer vision applications, including autonomous driving [1], medical imaging [2], robotics [3], and aerial imaging [4]. Unlike image classification, which produces a single label per image, semantic segmentation requires dense, pixel-level predictions that capture fine-grained boundaries between objects and regions. This granularity is essential for applications requiring detailed scene understanding.
The remarkable success of deep learning in semantic segmentation comes at a significant cost: the need for vast amounts of meticulously labeled training data. Creating pixel-level annotations is extraordinarily labor-intensive compared to other vision tasks. For instance, annotating a single image from the Cityscapes dataset requires an average of 1.5 h of human effort [5], as each image contains urban street scenes with up to 30 object categories. This annotation bottleneck severely limits the scalability of supervised learning approaches and motivates methods that achieve high performance with minimal labeled data.
Active learning [6,7,8,9] offers a principled solution by strategically selecting which samples to annotate rather than relying on random sampling. The core insight is that not all training samples contribute equally to model performance. By iteratively selecting the most informative samples from a pool of unlabeled data, active learning can significantly reduce annotation requirements while maintaining model performance. The key challenge is designing an effective querying strategy that selects samples maximizing model improvement while minimizing annotation cost. The effectiveness of a querying strategy hinges on how it defines and measures sample informativeness.
Most strategies define informativeness through uncertainty estimates derived from model predictions, which makes the reliability of these estimates central to the effectiveness of active learning. A fundamental limitation of existing uncertainty estimation methods is their reliance on heuristic measures, such as those derived from softmax probabilities [10,11], or gradient magnitudes computed using pseudo-labels [12]. Despite their widespread use, these approaches fail to address the well-documented calibration problem in modern neural networks [13,14], where models tend to produce overconfident probability estimates even when their predictions are incorrect. This miscalibration is particularly severe in semantic segmentation for two reasons. First, the dense prediction setting requires thousands of per-pixel classifications for each image, with each classification being vulnerable to overconfidence. Second, severe class imbalance makes models systematically overconfident on frequent classes and underconfident on rare ones.
To address these fundamental calibration issues, conformal prediction [15,16,17] has been proposed as a theoretically grounded framework for uncertainty quantification with formal coverage guarantees. Unlike traditional approaches that output point estimates, conformal prediction constructs prediction sets that contain the true label with a specified confidence level. Conformal risk control [18] extends this framework beyond coverage by enabling guarantees on more general loss functions, thereby supporting complex outputs such as semantic segmentation. By calibrating the predictor on a held-out dataset, these approaches provide statistical guarantees independent of the underlying model architecture or data distribution. These properties make conformal prediction a strong foundation for developing reliable active learning strategies.
Despite these advances, only a handful of works [19,20,21] have applied conformal prediction to active learning, all focused exclusively on classification tasks. These techniques do not directly translate to the dense, pixel-level setting of semantic segmentation. A critical gap therefore remains: no existing method applies conformal prediction to active learning for semantic segmentation. The dense prediction nature of segmentation introduces unique challenges that classification-focused methods cannot address, including managing complex, interdependent pixel-level outputs and handling severe class imbalance. Our work fills this gap by introducing the first conformal prediction-based active learning framework specifically designed for semantic segmentation.
In this paper, we introduce Conformal Risk Controlled Active Learning (CRC-AL), the first active learning framework for semantic segmentation that provides statistical guarantees for uncertainty quantification through conformal prediction. Our key contribution is that conformal risk control, when applied independently to each semantic class, yields pixel-wise multi-class prediction sets that capture model uncertainty in a principled manner. Unlike heuristic uncertainty measures, these prediction sets provide statistical guarantees with calibrated, class-specific confidence. By calibrating classes independently at the same risk level, CRC-AL achieves more balanced uncertainty quantification across both frequent and rare classes, thus addressing intra-image class imbalance. Pixels with larger prediction sets correspond to regions of high uncertainty, where the model cannot confidently distinguish among classes.
CRC-AL transforms these prediction sets into two complementary representations for guiding sample selection. First, risk maps highlight uncertain image regions by identifying pixels where multiple classes remain plausible. Second, co-occurrence embeddings capture class confusion patterns, revealing which semantic categories the model struggles to distinguish. Together, these representations enable the identification of not only highly uncertain samples but also samples exhibiting diverse forms of uncertainty. To select informative yet diverse samples, we introduce the Top-Diverse-K algorithm, an extension of standard Top-K selection to high-dimensional space. Inspired by center-of-mass formulations in physics, it employs a barycenter-based distance metric that balances uncertainty weighting with spatial distribution in embedding space.
We validate our approach on Cityscapes [5] and PascalVOC2012 [22,23], where it consistently outperforms benchmark methods. CRC-AL achieves 95% of fully supervised performance using only 30% of the training data on both datasets, substantially reducing annotation requirements.
The main contributions of this work are as follows:
- We introduce the first active learning framework for semantic segmentation based on conformal prediction, providing principled uncertainty quantification with statistical guarantees.
- We propose a novel uncertainty representation that combines risk maps and class co-occurrence embeddings to capture both spatial and semantic uncertainty patterns.
- We develop a physics-inspired selection algorithm that balances sample informativeness with diversity through a barycenter-based distance metric.
- We provide comprehensive experimental validation, demonstrating significant improvements over benchmark methods across two fundamentally different datasets, and release our implementation to support future research.
The remainder of this paper is organized as follows. Section 2 reviews the related works. Section 3 introduces our CRC-AL framework. Section 4 describes experiments and benchmarking results, while Section 5 presents parameter sensitivity analysis. Section 6 provides an in-depth discussion of the findings, and Section 7 concludes the paper.
2. Related Works
2.1. Active Learning
Active learning methods are broadly categorized into uncertainty-based, diversity-based, and hybrid approaches. Uncertainty-based methods typically select samples using metrics such as entropy [24], margin [25], or least confidence [26]. While effective in classical settings with single-sample queries, deep neural networks require batch-mode selection, for which [10] proposed Top-K sampling. However, these strategies remain vulnerable to softmax overconfidence. Alternatives such as Monte Carlo dropout [27] and ensembles [28,29] attempt to mitigate this via predictive variance estimation, but these methods require dozens of forward passes per image, which is computationally prohibitive for high-resolution segmentation.
A second limitation of uncertainty-only methods is redundant sampling from similar high-uncertainty regions [30]. Diversity-based approaches attempt to mitigate this issue by ensuring that selected samples better represent the overall data distribution. CoreSet [31] formulates the objective as a K-Center clustering problem in the latent embedding space, while CDAL [32] introduces information-theoretic contextual diversity measures. However, these strategies often prioritize easy or uninformative samples that contribute little to model improvement.
Hybrid strategies attempt to balance both criteria. Ref. [33] proposed stochastic batch selection over groups of uncertain samples, with uncertainty computed using classical metrics. BADGE [12] employs gradient embeddings based on pseudo-labels, encoding uncertainty through gradient magnitudes while enforcing diversity via K-Means++ seeding. Nevertheless, these methods still rely on heuristic uncertainty measures and fail to address the underlying overconfidence problem.
In contrast, CRC-AL leverages conformal risk control to provide calibrated, class-wise uncertainty quantification with formal guarantees. Once calibrated, selection requires only a single forward pass per image, avoiding the high computational cost of ensemble- or dropout-based methods. The proposed Top-Diverse-K strategy further balances calibrated uncertainty with diversity, enabling more efficient and informative batch selection.
2.2. Active Learning for Semantic Segmentation
Active learning for semantic segmentation poses unique challenges due to its dense prediction nature and high annotation cost. Image-level methods query entire images for annotation [12,31,32,33,34,35,36], while region-level methods aim to improve efficiency by querying only parts of an image. Region-level methods consist of two groups. Patch-based approaches [11,37] divide images into fixed-size regions, whereas superpixel-based approaches [38,39] query irregular regions that better align with object boundaries. Although region-level selection can, in principle, reduce annotation costs, it introduces practical challenges such as interface complexity, boundary artifacts from partial labeling, and the need for specialized training procedures to handle incomplete annotations.
Despite extensive study, no consensus exists on which granularity is more cost-effective [40], partly due to differing annotation protocols and the lack of standardized cost metrics across studies. In this work, we adopt the standard image-level strategy for several reasons: (1) compatibility with conformal risk control, which requires complete class channels for calibration, (2) alignment with standard annotation workflows where full-image labels are the norm, and (3) avoiding the practical challenges of partial labeling such as boundary artifacts and specialized training procedures.
2.3. Active Learning with Conformal Prediction
Early work in this area explored transductive conformal prediction for classification tasks before the advent of deep learning [41,42,43]. Although effective for small-scale problems with simple classifiers, these methods required retraining for each unlabeled sample, making them computationally infeasible for deep neural networks.
The introduction of inductive conformal prediction with calibration sets enabled more practical implementations [15]. In this framework, the model is trained once on a training set; then, non-conformity scores are computed using a separate calibration set to construct prediction sets for unlabeled samples. ICP [20] applies this framework to pool-based active learning by using two key conformal metrics: credibility and confidence. ICP-CNN [19] extends this approach to convolutional networks, combining three selection criteria: informativeness, diversity, and information density. This multi-criteria approach balances uncertainty with representativeness. CPAL-LR [21] further refines sample relevance assessment on conformal scores. However, these methods are largely confined to classification tasks, leaving their adaptation to dense prediction problems such as semantic segmentation underexplored.
The dense prediction nature of semantic segmentation introduces unique challenges that traditional conformal prediction methods cannot address, particularly due to the strong correlations among pixels within an image. In this setting, the relevant notion of error is not simply miscoverage [17]. Conformal risk control addresses this by providing guarantees on expected loss rather than coverage, bounding errors at the image level (e.g., false negative rates) and producing outer confidence sets that exploit spatial structure. Yet no prior work has applied this framework to active learning. This gap motivates CRC-AL, which integrates conformal risk control into active learning for semantic segmentation.
3. Methodology
3.1. Problem Statement
Let denote the complete dataset of N images, where is an RGB image with height H and width W, and is the corresponding one-hot-encoded ground-truth segmentation mask with K classes. At any point in the active learning process, we partition into the labeled and unlabeled subsets and , where contains image–label pairs with revealed labels, and contains images whose labels remain hidden. The semantic segmentation task aims to learn a function that maps each input image to per-pixel softmax probabilities. The model is trained by minimizing the pixel-wise cross-entropy loss over the labeled data.
The goal of active learning is to iteratively select the most informative batches to maximize model performance while minimizing annotation cost. At each iteration, a batch is selected according to a querying strategy. This process is summarized in Algorithm 1. Initially, a learner model is trained on the initial labeled dataset . At iteration t, the current model is used to select a batch for annotation. After the oracle provides labels for images in , transforming them into labeled pairs , the datasets are updated: and . The model is then retrained on the expanded labeled dataset . This process continues until the annotation budget is exhausted or performance converges. The central challenge lies in developing a querying strategy that enhances model performance while keeping annotation costs low.
| Algorithm 1 Active learning algorithm for model improvement via strategic batch selection and retraining |
|
To address this, we introduce Conformal Risk Controlled Active Learning (CRC-AL), a novel active learning framework that enhances the querying strategy through principled uncertainty quantification, as illustrated in Figure 1. Our method consists of three integrated stages. First, we apply conformal risk control to calibrate class-specific thresholds that transform softmax outputs into binary prediction masks, allowing multiple class predictions per pixel. Second, these masks generate both image-level uncertainty scores through risk maps and embeddings from co-occurrence patterns, capturing class confusion structure. Finally, our Top-Diverse-K algorithm selects samples that balance high uncertainty with spatial diversity in the embedding space, incorporating previously labeled samples to ensure good coverage across iterations.
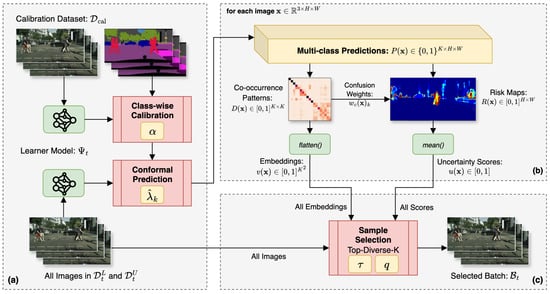
Figure 1.
Overview of the proposed CRC-AL method. (a) Conformal risk control calibration with risk level determines class-specific thresholds, which transform softmax probabilities into multi-class predictions (Section 3.2). (b) Uncertainty quantification through risk map generation and embedding construction from prediction co-occurrence patterns, capturing both image-level uncertainty and class confusion structure (Section 3.3). (c) Sample selection via the Top-Diverse-K algorithm, which jointly optimizes for high uncertainty and spatial diversity in the embedding space (Section 3.4).
3.2. Class-Wise Calibration
We formulate the multi-class semantic segmentation problem as K independent binary segmentation tasks, each distinguishing class k from all others. For each class , we define the binary segmentation output by extracting the k-th channel from the multi-class network, given by , where denotes the probability that pixel belongs to class k. Thus, represents the complete pixel-wise probability map for class k. The predicted binary mask is obtained by thresholding these probabilities with parameter :
Pixels with scores above are classified as belonging to class k. As increases, the threshold decreases, resulting in more pixels being classified as positive and thus expanding the predicted mask .
Let denote the calibration dataset, where is an RGB image and is its one-hot-encoded ground-truth mask with K classes. For each class k, we define the binary ground-truth mask by . Each element of equals 1 if pixel belongs to class k and 0 otherwise. It is important to note that is kept separate from the complete dataset , and the choice of calibration set is further examined in Section 5.3.
In calibration, we determine a threshold for each class such that the expected loss over the calibration set does not exceed a predefined risk level :
where is a loss function that is non-increasing in . We adopt the false negative rate (FNR) as the loss function:
where the numerator counts the number of true positive pixels, and the denominator counts the total number of positive pixels in the ground truth.
To satisfy the risk constraint with finite-sample correction, we compute the optimal threshold as
where is the set of calibration images containing at least one pixel of class k, and the empirical risk is
The correction term ensures, with high probability, that the empirical risk on the calibration set does not exceed the target level [17]. Figure 2 illustrates conformal risk control in practice.
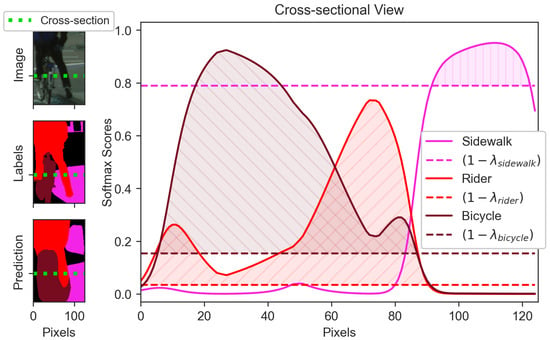
Figure 2.
Conformal risk control demonstration with three classes: Sidewalk, Rider, and Bicycle. The graph shows softmax scores along a horizontal cross-section of the image. Hatched regions (above thresholds) indicate where the conformal predictor includes each class with risk level at most . Although pixels around index 10 are classified as Bicycle via argmax, their softmax scores also exceed the Rider threshold, correctly including the true class in the prediction sets.
Calibrating a single threshold across all classes yields suboptimal performance due to class imbalance—frequent classes (e.g., Road) dominate calibration, while rare classes (e.g., Bus, Train) may be poorly calibrated. By calibrating each class independently at the same risk level , we ensure balanced performance across all classes regardless of frequency.
As illustrated in Figure 1a, we first determine the optimal thresholds for all classes using the class-wise calibration procedure described above, ensuring that each class satisfies the target risk level . Given these thresholds, we generate multi-class predictions for each image by stacking the binary prediction masks, defined as . At each pixel location , the prediction vector may contain multiple positive entries, indicating that several classes may simultaneously exceed their respective thresholds. Unlike standard argmax segmentation, these calibrated masks may overlap, reflecting conformal prediction sets that allow multiple plausible classes per pixel.
It is important to note that while each class-specific prediction mask satisfies the conformal risk control guarantee independently, the stacked prediction masks do not provide joint statistical guarantees across all classes simultaneously. For active learning, however, we use these prediction sets primarily as indicators of uncertainty rather than for their formal coverage properties. Calibrating each class independently with the same risk level helps ensure more balanced uncertainty quantification across frequent and rare classes. Pixels with larger prediction set sizes (i.e., ) indicate regions of high model uncertainty where the model cannot confidently distinguish among classes (Figure 2). This observation forms the foundation of our image-level uncertainty quantification strategy, as detailed in the following section.
3.3. Uncertainty Quantification
Not all classes contribute equally to image-level uncertainty within an image. For instance, pixels predicted as Bicycle often co-occur with Rider predictions, while Road predictions rarely co-occur with other classes. Here, co-occurrence refers to pixels satisfying , where the conformal predictor includes multiple classes in its prediction sets.
Figure 1b illustrates the process of computing uncertainty scores and embeddings. We first construct the co-occurrence matrix by counting pixel-wise class co-occurrences:
where . The matrix is symmetric, and each entry counts the number of pixels where classes k and are simultaneously predicted. In particular, the diagonal elements count the number of pixels where class k is predicted, regardless of whether other classes are also predicted at those pixels.
To account for class imbalance within images, we normalize the co-occurrence matrix to obtain the co-occurrence density matrix :
The k-th row of forms a categorical probability distribution over the class set , representing the relative likelihood that class k co-occurs with each other class. Diagonal entries represent the self-association strength of class k, equaling 1 when class k never co-occurs with other classes and decreasing as co-occurrences increase.
When the conformal predictor assigns multiple classes to a pixel location, indicating higher uncertainty, the resulting distributions become less peaked. We quantify this spread using Shannon entropy to compute class-wise confusion weights :
with the convention . Higher values of indicate greater uncertainty for class k. In particular, when class k either does not appear in the image or appears without any co-occurrences, and increases as co-occurrences become more diverse.
The risk map aggregates class-wise uncertainty at each pixel using these weights:
This produces a spatial uncertainty map highlighting regions where the model is most uncertain, as shown in Figure 3. Pixels with multiple predicted classes and those containing classes with high confusion weights contribute more to the risk map, effectively capturing both prediction ambiguity and class-specific uncertainty.
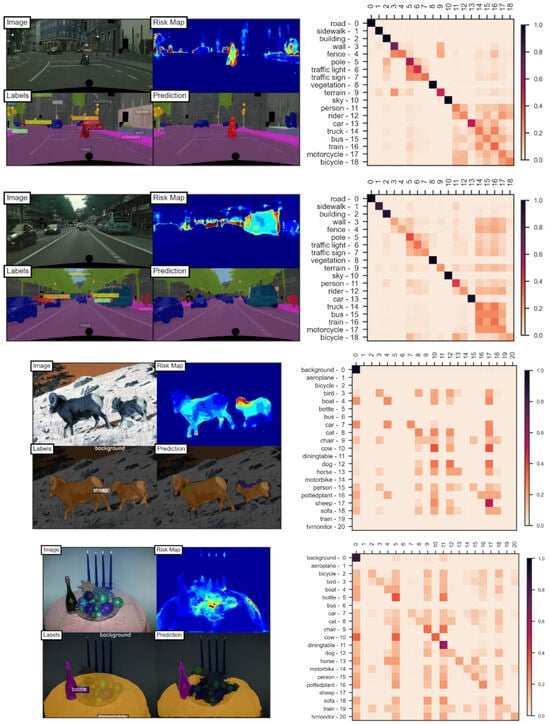
Figure 3.
Example risk maps and co-occurrence density matrices with . (Top) Cityscapes; (Bottom) PascalVOC2012. Risk maps highlight uncertain regions (warmer colors indicate higher uncertainty). Each matrix row shows the likelihood of a class co-occurring with others. Uncertainty scores are computed as the spatial average of risk maps, and embeddings are obtained by flattening the matrices.
The image-level uncertainty score is the spatial average of the risk map:
This aggregation provides a single interpretable score that summarizes the overall uncertainty across the entire image, enabling direct comparison and ranking of unlabeled samples.
When the co-occurrence density matrix is diagonal (no co-occurrences), the uncertainty score , indicating high model confidence. Such images require no further annotation and can be excluded from selection. However, two images may have similar uncertainty scores while exhibiting different class confusion patterns. To capture these differences, we construct image embeddings by flattening :
These embeddings represent images in a -dimensional space based on their class confusion structure, enabling diversity-aware sample selection.
3.4. Sample Selection
A common strategy in uncertainty-based active learning is Top-K selection, which iteratively selects the most uncertain samples [10,36]:
where is defined in Equation (10), denotes the set of unlabeled images and is the batch of already selected images (initially ). After each selection, we update and repeat until , where is the desired batch size. If multiple images attain the same maximum uncertainty score, the operator returns one of them arbitrarily.
While computationally efficient, this approach suffers from redundant sampling, particularly in datasets with limited diversity. Similar samples may all receive high uncertainty scores, leading to inefficient use of the annotation budget [30]. Conversely, pure diversity-based selection often queries easy, non-informative samples that contribute minimally to model improvement. To address these limitations, we extend Top-K selection to operate in the embedding space, balancing uncertainty and diversity through a principled distance metric.
To realize this idea, we adopt a physics-inspired formulation: each embedding represents a particle with mass , where and are given in Equations (11) and (10). Drawing from the two-body problem in classical mechanics [44], the distance from particle i to the barycenter (center of mass) of the two-particle system is given by . This distance is asymmetric except when . Specifically, when particle i has higher uncertainty than particle j (i.e., ), the distance from i to the barycenter is smaller than when .
Inspired by this physical analogy, we define a distance metric that quantifies the informativeness of sample j relative to sample i:
where is a trade-off parameter and is a small positive constant to prevent division by zero. This formulation yields a weighted geometric mean between spatial distance and relative uncertainty. When , the metric reduces to pure uncertainty weighting, disregarding spatial distance. Conversely, when , only spatial distance matters. The metric increases with both the spatial separation between samples and the relative uncertainty of sample j. Figure 4 provides a practical example of this metric.

Figure 4.
Illustration of the barycenter-based distance metric for sample selection. Sample A (blue) is labeled, while B (red), C (green), and E (purple) are unlabeled candidates. Circle sizes indicate uncertainty scores. Distances , , and represent the metrics from A to each candidate. The metric balances uncertainty (circle size) and diversity (spatial distance) to select C as the most informative sample when , avoiding the redundancy of nearby high-uncertainty sample B and the distant low-uncertainty sample E.
Building on this distance metric, Algorithm 2 introduces the Top-Diverse-K selection algorithm, which extends traditional Top-K selection by incorporating spatial diversity through the embedding space. The algorithm iteratively selects samples that maximize a combined distance criterion balancing average distance and minimum distance to previously selected samples. Starting with the images from the labeled set marked as traversed, the algorithm selects each subsequent sample according to
where is defined in Equation (13) and denotes the set of traversed samples (initially and ). After each selection, we update and . The process continues until . The first term promotes samples that are, on average, distant from the traversed set, encouraging diversity. The second term ensures a minimum separation from all traversed samples, preventing clustering around high-density regions. This dual criterion prevents scenarios where outliers dominate the average distance while ensuring selected samples span the embedding space effectively.
| Algorithm 2 Top-Diverse-K sample selection algorithm |
|
In the first iteration, when initially contains the images from , the algorithm evaluates the combined distance metric for all samples in relative to the samples in . It selects the sample that maximizes this metric, where larger values of indicate greater informativeness. Once selected, is added to both the traversed set and the selected batch . By updating , we treat as effectively labeled for subsequent selections. This ensures that future samples are chosen with respect to both the original labeled set and previously selected samples, maintaining a well-distributed selection across the embedding space. In the second iteration, the algorithm selects from the remaining unlabeled samples (where now ), evaluating distances to all samples in the updated traversed set . This iterative process continues, with each selected sample influencing subsequent selections to achieve both high uncertainty and spatial diversity.
The parameter controls the trade-off between uncertainty and diversity in sample selection. When , the algorithm reduces to standard Top-K selection based solely on uncertainty, as the spatial term becomes constant. Conversely, as approaches 1, spatial diversity increasingly dominates the selection criterion.
Figure 5 illustrates this behavior empirically. For small values, selected samples cluster in high-uncertainty regions of the embedding space. As increases, the selected batch becomes more spatially distributed while still favoring uncertain samples, achieving an effective balance between uncertainty scores and diversity. This adaptive behavior enables tuning the selection strategy based on dataset characteristics and annotation requirements.
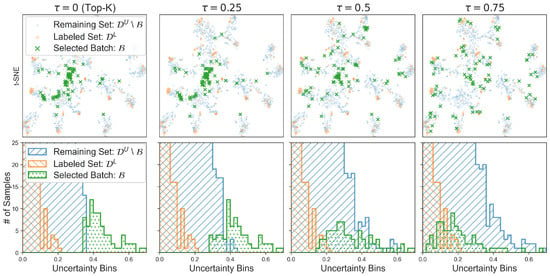
Figure 5.
Visualization of the parameter ’s impact on sample selection. (Top row) t-SNE [45] projections of the selected batch in the embedding space for increasing values of (left to right). Larger values yield more spatially distributed selections. (Bottom row) Uncertainty distributions of selected samples. The x-axis represents uncertainty scores and the y-axis shows sample counts per bin. As increases, the selection shifts from high-uncertainty clustering () to a broader uncertainty range with greater spatial diversity ().
4. Experiments
In this section, we present benchmarking experiments on two semantic segmentation datasets to demonstrate the effectiveness of our method compared to state-of-the-art baseline methods.
4.1. Datasets
Cityscapes [5] consists of real-world street scene images annotated with 19 semantic categories, including Road, Sidewalk, Building, Car, and Person. The training set contains 2975 images with fine-grained annotations, while the validation set includes 500 images. Cityscapes provides structured urban scenes with systematic class transition patterns (e.g., Road–Car, Building–Sky) and a moderate degree of visual similarity between images.
PascalVOC2012 [22] includes images with diverse object sizes, occlusions, and variations in lighting and backgrounds. It comprises 20 foreground object categories plus 1 background class, totaling 1464 training images and 1449 validation images. We use the extended version [23], which expands the training set to 10,582 images. PascalVOC2012 offers a wide range of object categories with varied contexts and exhibits severe class imbalance due to the dominant background class, making it particularly challenging for active learning methods.
Together, Cityscapes and PascalVOC2012 represent fundamentally different characteristics essential for validating active learning methods in terms of uncertainty- and diversity-aware sample selection. Used in combination, they provide a comprehensive evaluation across diverse data distributions and class structures that are representative of real-world semantic segmentation applications.
4.2. Implementation Details
We conduct experiments on a workstation equipped with an NVIDIA Tesla V100 GPU. Our codebase is built on top of the open-source MMSegmentation framework [46]. We evaluate two representative segmentation models: DeepLabV3 [47], a widely adopted CNN-based benchmark, and SegFormer [48], a transformer-based architecture chosen to ensure architectural diversity.
For Cityscapes, we employ DeepLabV3 [47] with a ResNet-18 [49] encoder. Training uses batch size 4 for 50 epochs with the Adam optimizer (learning rate: , weight decay: ). We apply polynomial learning rate decay (power = 0.9, minimum = ) with and . These hyperparameters are selected through a simple grid search, starting from MMSegmentation defaults and tuning on the fully labeled training set. Images are resized to .
For PascalVOC2012, we use SegFormer-B1 [48] with batch size 8, trained for 50 epochs using AdamW (initial learning rate: , final: , polynomial decay with power = 1.0, weight decay: 0.01, ). These hyperparameters are adopted from the original paper and its implementation in MMSegmentation. Images are resized to .
4.3. Evaluation Metrics
Following standard practice [47,48], segmentation performance is evaluated using the intersection-over-union (IoU) metric, defined as , where , , and denote true positives, false negatives, and false positives, respectively. In semantic segmentation, these quantities are defined at the pixel level and aggregated across the entire dataset for each class: is the number of pixels correctly predicted as belonging to the class, is the number of pixels belonging to the class in the ground truth but predicted as another class, and is the number of pixels incorrectly predicted as that class but belonging to another in the ground truth. The overall metric mean-IoU (mIoU) is obtained by averaging the IoU values across all classes, giving each class equal weight regardless of frequency.
We further assess performance using a pairwise penalty matrix (PPM) with two-sided t-tests, following [12]. For each pair of methods at each active learning iteration, we obtain seven per-seed mIoU scores, denoted by and . The t-statistic is computed as , where and . At the 95% confidence level (critical interval: ), two methods are considered significantly different when the corresponding statistic falls outside this range. For each pair , performance is compared after every iteration. If method i significantly outperforms method j (), a penalty score of is added to the PPM cell , where is the total number of iterations. Conversely, if method j significantly outperforms method i (), the penalty score is added to cell . Larger values in cell indicate that method i dominates j more consistently. The column-wise average summarizes overall performance, with lower values indicating stronger methods, as they are dominated less frequently across iterations.
4.4. Active Learning Setup
All methods begin with the same randomly selected initial labeled dataset and query an equal number of samples at each iteration t. We perform iterations following Algorithm 1, retraining the model from scratch using ImageNet [50] pre-trained weights and applying only horizontal flipping as data augmentation. Identical hyperparameters are used across all iterations and methods. Performance is evaluated in terms of mIoU on the validation set of each dataset, reported as mean ± standard deviation over seven runs with different random seeds. Table 1 summarizes the active learning setup for each dataset. These iteration counts and sampling percentages are sufficient for the models to approach 95% of the fully supervised mIoU on both datasets.

Table 1.
Active learning setup for Cityscapes and PascalVOC2012 datasets.
Unlike baseline methods, CRC-AL requires a calibration set for conformal risk control. Due to limited labeled data, we use the current iteration’s training set for calibration. Section 5.3 analyzes the impact of this choice.
4.5. Baseline Methods
We compare our method against a comprehensive set of baseline methods including uncertainty-based, diversity-based, and hybrid approaches. These methods were selected for their state-of-the-art performance and their compatibility with standard training procedures. All methods were implemented from scratch and adapted for semantic segmentation where necessary.
- Random: Selects samples uniformly at random, serving as a passive baseline.
- Entropy [10]: Employs Top-K selection based on average pixel-wise entropy across each image, quantifying prediction uncertainty through the Shannon entropy of the softmax distribution.
- CoreSet [31]: Solves the K-Center problem using 512-dimensional embeddings extracted from the network’s bottleneck layer via average pooling. Implements greedy selection where each sample maximizes the minimum Euclidean distance to previously selected samples.
- CDAL [32]: Constructs contextual diversity vectors capturing the spatial distribution of predicted classes within each image. Sample selection uses the CoreSet algorithm with symmetric KL divergence as the distance metric.
- BADGE [12]: Applies K-Means++ seeding in the gradient embedding space. Gradients are computed from the cross-entropy loss using pseudo-labels (argmax predictions) and dimensionality is reduced via average pooling to handle the large gradient space in segmentation tasks.
4.6. Benchmarking Results
We evaluate CRC-AL with parameters (calibration risk level) and (uncertainty–diversity trade-off) against five baseline methods across six active learning iterations. Figure 6 presents the results on both datasets.
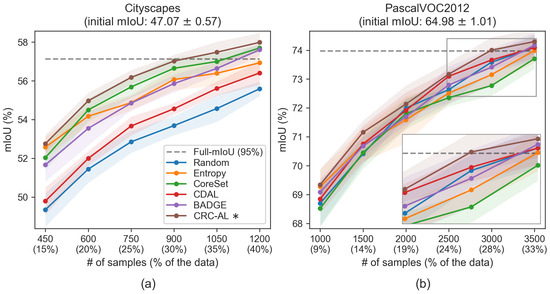
Figure 6.
* denotes the proposed method. Comparison of baseline methods with CRC-AL (, ). (a) Cityscapes and (b) PascalVOC2012 mIoU performance across active learning iterations. Initial scores () are shown above each plot. The dashed line indicates 95% of fully supervised performance; shaded regions show standard deviation over 7 runs.
Cityscapes results: As shown in Figure 6a and detailed in Table 2, CRC-AL demonstrates superior performance throughout all iterations, achieving the steepest learning curve among all methods. Starting from a shared baseline of mIoU with just 10% of the data (300 images), CRC-AL rapidly improves performance at each iteration. By iteration , it surpasses 56% mIoU, maintaining a clear margin over all baselines. The dashed line represents 95% of the mIoU achievable with the fully labeled training set, which CRC-AL approaches more rapidly than any competing method. Remarkably, CRC-AL achieves this 95% threshold using only 30% of the training data (900 images), while other methods require more extensive annotation to approach similar performance. The hierarchy is clearly established: CRC-AL consistently leads, followed by a competitive cluster of CoreSet and BADGE, entropy slightly behind, CDAL showing moderate effectiveness, and random sampling performing worst. These results confirm that conformal prediction-based uncertainty quantification identifies more informative samples than traditional softmax-based (entropy) or gradient-based (BADGE) methods, while the diversity-aware selection avoids redundancy and sustains performance improvements.

Table 2.
Cityscapes mIoU scores across iterations (initial mIoU: ). Bold values indicate the highest score at iteration t. Results show mean ± standard deviation over 7 runs.
PascalVOC2012 results: Figure 6b and Table 3 reveal more complex dynamics on this diverse object-centric dataset, where the background class exhibits highly varied textures. Starting from mIoU with only 500 labeled images, all methods show rapid initial improvement. CRC-AL consistently maintains an advantage, though with a smaller margin than on Cityscapes, reaching 74% mIoU at 28% data utilization (3000 images), where it achieves the 95% fully supervised threshold. Unlike Cityscapes, the performance hierarchy is less pronounced, with random sampling emerging as a surprisingly strong baseline. Except for CRC-AL, all methods fall below random at certain iterations based on average mIoU, although their results largely overlap once standard deviations are taken into account. Among the baselines, BADGE (gradient-embedding diversity), CDAL (contextual diversity), and entropy (softmax uncertainty) perform comparably to random, while CoreSet (pure representativeness) performs consistently worse, especially in later iterations. By the final iteration , all methods except CoreSet reaches or surpass the 95% fully supervised threshold, while CRC-AL reaches the threshold at . These results underscore CRC-AL’s robustness, demonstrating that it is the only method to sustain a consistent advantage across both iterations and dataset complexities.

Table 3.
PascalVOC2012 mIoU scores across iterations (initial mIoU: ). Bold values indicate the highest score at iteration t, while underlined values denote results below random sampling. Results show mean ± standard deviation over 7 runs.
Statistical significance: Figure 7 presents the aggregated pairwise penalty matrix (PPM) across two fundamentally different datasets, obtained by element-wise averaging. The diagonal entries are zero by definition, as methods cannot dominate themselves. The CRC-AL row shows that our approach significantly outperforms all competing methods, yielding near-maximum penalties across iterations. The bottom row further confirms CRC-AL’s dominance with , indicating that no method significantly outperforms it at any iteration under the 95% confidence level. BADGE () and entropy (), both uncertainty-driven methods, form a second tier with competitive performance. The matrix shows that BADGE and entropy do not significantly outperform one another, although BADGE is less frequently dominated by other methods. This suggests that gradient embeddings offer marginal yet consistent gains over softmax entropy. CoreSet () and CDAL (), focused solely on diversity, form a weaker third tier, outperforming only random sampling, which performs worst overall. CoreSet occasionally outperforms CDAL, while CDAL rarely dominates CoreSet, implying that visual representativeness can be more effective than contextual diversity in certain settings. Taken together, these results establish a stratified performance hierarchy—uncertainty-based methods outperform diversity-only strategies, while CRC-AL uniquely integrates both to deliver consistent superiority across datasets with markedly different characteristics.
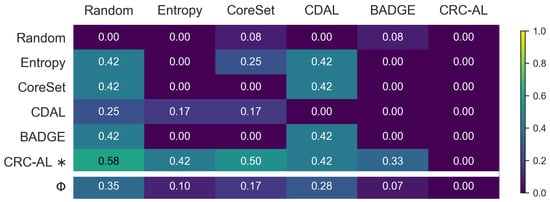
Figure 7.
* denotes the proposed method. Comparison of baseline methods with CRC-AL (, ), shown as the pairwise penalty matrix (PPM) aggregated across Cityscapes and PascalVOC2012. Lower scores indicate better performance. CRC-AL achieves , demonstrating consistent superiority at the 95% confidence level.
5. Sensitivity Analysis
5.1. Uncertainty–Diversity Balance
The trade-off parameter in the Top-Diverse-K algorithm governs the balance between uncertainty-driven and diversity-aware selection. Figure 8a illustrates its effect on Cityscapes with fixed at 0.05. Pure uncertainty sampling () performs poorly, indicating that uncertainty alone is insufficient and that diversity, captured through class confusion patterns, is essential for effective active learning. This poor performance arises from the dataset’s structured urban scenes where semantically related classes systematically co-occur, leading to redundant sampling of visually similar high-uncertainty regions without diversity awareness. While all values behave similarly in early iterations when the labeled set is small, their performance diverges as training progresses. Settings with degrade more noticeably, with performing better than but still suboptimal. This suggests that limited diversity incorporation helps, but stronger integration is required to maintain robust performance.
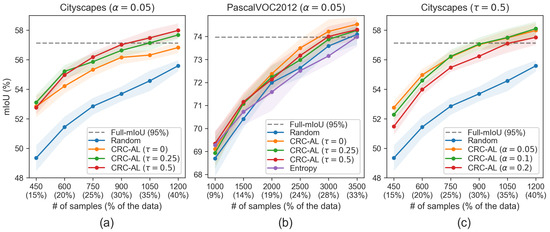
Figure 8.
Sensitivity analysis of CRC-AL parameters. (a) Effect of uncertainty–diversity trade-off on Cityscapes with . (b) Effect of on PascalVOC2012 with . (c) Effect of calibration risk level on Cityscapes with . The dashed line indicates 95% of fully supervised mIoU. Shaded regions show standard deviation over 7 runs. Random sampling and entropy are shown as baselines. The analysis identifies and as the most effective settings for practical active learning.
Figure 8b reveals contrasting behavior on PascalVOC2012. Here, all values consistently outperform random sampling, with even pure uncertainty sampling () showing reasonable performance. This contrasting behavior reflects PascalVOC2012’s inherent diversity, naturally distributing high-uncertainty samples across different regions of the embedding space. To understand this difference, we include entropy—which also uses pure uncertainty with Top-K selection—as a direct comparison. While entropy achieves results comparable to random sampling (consistent with our main results in Table 3), our method with outperforms both. This crucial observation demonstrates that conformal prediction provides superior uncertainty quantification compared to traditional entropy measures, offering better-calibrated confidence estimates even without diversity.
5.2. Risk Level Sensitivity
The risk level controls the statistical guarantee in conformal risk control, representing the acceptable upper bound on the false negative rate. The choice of involves a critical trade-off. With high values, the conformal predictor tolerates more risk, producing empty or smaller prediction sets. This leads to sparse risk maps where only the most ambiguous regions appear uncertain, and embeddings become nearly diagonal, indicating minimal class confusion. Such oversimplification treats most images as equally certain, reducing the discriminative power needed for effective active learning. Conversely, low values produce conservative predictions with larger prediction sets. This generates dense risk maps where extensive regions appear uncertain, potentially masking truly informative regions. The resulting embeddings capture spurious co-occurrences that may reflect statistical noise rather than meaningful class confusion patterns. Figure 9 shows example risk maps and co-occurrence density matrices for different values.
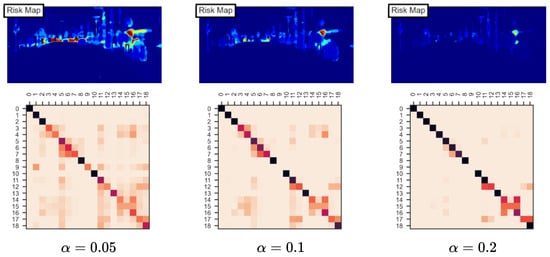
Figure 9.
Risk maps and co-occurrence matrices for . Low yields dense patterns, while high produces sparse, near-diagonal matrices, reducing discriminative power for active learning.
Figure 8c empirically validates these theoretical considerations on Cityscapes. With , we compare three values: 0.05, 0.1, and 0.2. The results reveal that and achieve similar performance throughout the active learning process, both substantially outperforming . The degraded performance at confirms that overly permissive risk levels fail to capture sufficient uncertainty for sample discrimination. Importantly, demonstrates superior performance in early iterations. This suggests that tighter statistical guarantees, while potentially introducing some noise, better identify the subtle uncertainties that distinguish truly informative samples when labeled data is scarce. The consistent advantage of lower values indicates that conservative calibration improves sample informativeness, with emerging as the most effective setting for practical active learning.
5.3. Impact of Calibration Set
Active learning assumes that labeled data is limited. Our method, based on conformal risk control, requires an additional labeled set for calibration. This introduces a challenge: deciding whether to allocate labeled data for calibration or use it to improve model performance. To address this, we conduct experiments to analyze the impact of the calibration set on overall active learning performance.
We use the Cityscapes dataset with a randomly selected initial labeled dataset containing 600 images and perform a single active learning iteration. The initial model is trained on . For the calibration set , we compare two configurations: (1) using the current labeled data , or (2) using a randomly sampled subset from the unlabeled pool with . Although labels in are typically hidden from the learner, we reveal them solely for calibration purposes to evaluate the conformal predictor.
After calibration, we select a batch containing 150 images for annotation. The model is then retrained on the combined dataset , where denotes the annotated batch. We evaluate the expected risk on both the Cityscapes validation split (500 images) and the remaining unlabeled data . Since these sets are not used during calibration, they remain unseen by the conformal predictor. Each experiment is repeated using five different random seeds.
Table 4 presents the mIoU scores and calibration performance, measured as the expected false negative rate (FNR) averaged across all classes. The differences in mIoU scores across configurations are minimal, although calibrating on unlabeled data performs slightly better when . This indicates that our method is not highly sensitive to the calibration set choice in terms of active learning performance.

Table 4.
Impact of calibration set choice on active learning performance. Calibration is performed on unseen unlabeled set () or labeled set () with . Reported values are mIoU after one iteration and empirical risk (FNR) on both validation and unlabeled test sets.
For calibration quality, using achieves risk levels close to the target risk level with minimal variation across both unseen evaluation sets. In contrast, calibrating on yields higher expected FNRs than ; however, these remain consistent across different evaluation sets.
This consistency is the critical observation: when using , although the absolute risk deviates from (0.182 vs. 0.05, and 0.280 vs. 0.10), the calibration produces stable predictions across both unseen evaluation sets, with nearly identical FNR values. This stability indicates that the calibration mechanism successfully learns relative uncertainty patterns even when the absolute thresholds are biased. The conformal predictor effectively identifies which pixels and classes are more uncertain than others, maintaining consistent uncertainty rankings across different data distributions.
For active learning, this relative ordering matters more than absolute calibration accuracy. The method correctly identifies uncertain regions and ambiguous class boundaries, enabling effective sample selection despite the shifted thresholds. The mIoU results confirm this, as both calibration strategies achieve similar performance (55.030 vs. 55.242 for ), showing that uncertainty quantification provides reliable guidance for active learning.
6. Discussion
Our experiments establish a clear performance hierarchy across benchmark datasets: CRC-AL consistently surpasses existing active learning baselines, maintaining the steepest learning curve throughout the annotation budget. The persistent gap between CRC-AL and competing methods underscores the effectiveness of conformal risk control in producing statistically grounded uncertainty quantification. Unlike conventional softmax-based uncertainty (entropy) or gradient-based heuristics (BADGE), CRC-AL identifies fundamentally more informative samples by capturing both relative uncertainty and semantic confusion at the class level. The resulting prediction sets, risk maps, and co-occurrence embeddings provide richer guidance for sample selection, while Top-Diverse-K enables a principled balance between uncertainty and diversity.
Dataset-specific analyses reveal that the advantages of CRC-AL hold under varied conditions but also highlight unique vulnerabilities of competing methods. On Cityscapes, where structured urban scenes generate strong co-occurrence among semantically related classes (e.g., Road–Car, Building–Sky), purely context- or representativeness-driven strategies (CDAL, CoreSet) fail to match the effectiveness of CRC-AL. CDAL’s reliance on contextual diversity is ill-suited to environments where many classes systematically co-occur, while CoreSet’s visual representativeness overlooks the semantic structure of uncertainty. In contrast, CRC-AL effectively exploits co-occurrence embeddings to prevent redundant queries and sustain annotation efficiency. On PascalVOC2012, with its object-centric and visually heterogeneous images, CoreSet even underperforms random sampling, as the background class dominates pixel statistics and misleads visual diversity metrics. CDAL partially mitigates this effect through its contextual measures. In contrast, entropy and BADGE remain vulnerable to severe class imbalance, causing their performance to converge with random sampling, which unexpectedly emerges as a strong baseline. Although CRC-AL is not immune to such imbalance—uncertainty estimates and embeddings degrade in the presence of overwhelming background pixels—it consistently maintains advantages over baselines, demonstrating robustness under adverse dataset conditions. Notably, no single baseline performs well across both datasets. In contrast, CRC-AL consistently achieves strong results on both Cityscapes and PascalVOC2012, underscoring its superior generalization across datasets with markedly different characteristics.
Overall, entropy and BADGE, both uncertainty-driven methods, show stronger performance than diversity-only strategies but remain limited by their reliance on heuristic uncertainty measures. Entropy suffers from softmax overconfidence, leading to unreliable estimates in class-imbalanced regions, while BADGE’s gradient-based embeddings improve diversity but can be unstable and sensitive to pseudo-label noise. Consequently, both methods achieve moderate gains but fail to consistently close the gap with CRC-AL. By calibrating each class independently at the same risk level , CRC-AL addresses these fundamental limitations through balanced uncertainty quantification across both frequent and rare classes. Compared to BADGE’s gradient embeddings, our co-occurrence embeddings introduce a different perspective by capturing statistically grounded semantic confusion patterns. These patterns encode both prediction ambiguity and class-specific uncertainty, enabling the selection of more informative samples in regions where the model struggles to distinguish between classes. CoreSet and CDAL lack any notion of uncertainty and select samples solely based on diversity. This limitation explains their weaker performance compared to uncertainty-driven methods, particularly on datasets with sufficient inherent diversity. Our Top-Diverse-K algorithm integrates co-occurrence embeddings with uncertainty weighting through a principled barycenter-based distance metric. In this way, it selects highly informative samples while maintaining a well-distributed batch, achieving an effective balance via the trade-off parameter . The clear stratification of values in the pairwise penalty matrix (Figure 7) underscores the importance of principled uncertainty quantification, with diversity serving as a secondary, complementary factor. By combining conformal prediction-based risk maps with co-occurrence embeddings, CRC-AL overcomes the limitations of existing methods, providing statistically guaranteed uncertainty quantification and sample selection that adapts effectively to dataset-specific class structures.
The parameter sensitivity analysis provides practical insights for deployment. The trade-off parameter effectively controls the uncertainty–diversity balance, with pure uncertainty sampling () leading to redundant selections and pure diversity losing informativeness. The robust performance at across both datasets suggests this balanced setting as a reliable default, while practitioners can adjust the parameter based on dataset characteristics—higher values for visually similar datasets (e.g., video sequences) and lower values for inherently diverse collections. Similarly, the calibration risk level consistently outperforms looser settings, particularly in early iterations where sample selection has the greatest impact on learning trajectories. These findings indicate that tighter statistical control enhances active learning by better identifying the subtle uncertainties that distinguish truly informative samples. Taken together, the analysis highlights and as robust defaults that can be applied across diverse semantic segmentation scenarios, reducing the need for extensive hyperparameter tuning.
An important practical consideration is the allocation of labeled data for calibration. Since conformal risk control requires a calibration set, practitioners must decide whether reserving part of the annotation budget for calibration is preferable to using it directly for training. Our calibration analysis indicates that even under this trade-off, CRC-AL remains highly competitive. Although absolute thresholds deviate from nominal values when calibration is performed on the labeled training set, the predictor preserves relative uncertainty rankings across unseen evaluation datasets. This stability ensures that informative samples are consistently prioritized, even when absolute risks diverge from theoretical expectations. For active learning, relative calibration quality is therefore more critical than strict adherence to error rates, aligning with the practical goal of guiding sample selection rather than providing formal risk certificates. The minimal performance difference between ideal and practical calibration further validates the practicality of CRC-AL in scenarios where separate calibration data may not be available.
Several limitations warrant discussion. First, extreme class imbalance still degrades performance—though CRC-AL handles it better than baselines, the background-dominated PascalVOC2012 results suggest room for improvement through adaptive reweighting or hierarchical calibration. Second, co-occurrence embeddings scale quadratically with the number of classes (), becoming computationally prohibitive for large K and vulnerable to the curse of dimensionality. For datasets with hundreds of classes, dimensionality reduction techniques or hierarchical class groupings may be necessary to maintain computational feasibility. In practice, dimensionality reduction techniques such as PCA can compress the embedding space to a manageable size while preserving the essential uncertainty structure, leveraging the observation that most class pairs seldom co-occur.
The proposed framework addresses a fundamental weakness of existing active learning approaches by embedding uncertainty quantification within a statistically grounded foundation. The empirical gains observed on two challenging benchmarks demonstrate both the methodological value and practical potential of CRC-AL, laying the groundwork for more reliable and annotation-efficient semantic segmentation systems.
7. Conclusions
In this paper, we introduced Conformal Risk Controlled Active Learning (CRC-AL), the first active learning framework for semantic segmentation based on conformal prediction theory. Our approach addresses a fundamental limitation in existing active learning methods: the reliance on poorly calibrated softmax probabilities that fail to reliably identify informative samples. By applying conformal risk control independently to each semantic class, we transform softmax outputs into statistically guaranteed prediction sets that reliably quantify model uncertainty. Our risk maps and co-occurrence embeddings capture both spatial and semantic uncertainty patterns, while the Top-Diverse-K algorithm effectively balances informativeness with diversity in sample selection.
Extensive experiments validate the effectiveness of our approach. CRC-AL consistently outperforms five state-of-the-art baselines across two fundamentally different datasets, achieving 95% of fully-supervised performance using only 30% of training data on both datasets. The superior performance over the benchmarking methods confirms that conformal prediction-based uncertainty quantification provides reliable guidance for active learning. The method’s robustness across structured street scenes and diverse object images demonstrates that statistical guarantees generalize better than heuristic confidence measures.
Future work will pursue theoretical studies on tighter bounds between conformal risk parameters and active learning performance, adaptive selection strategies, and extensions to other dense prediction tasks. Understanding the theoretical properties of class co-occurrence patterns under different data distributions could lead to more sophisticated embedding strategies. In addition, extensions toward joint calibration strategies could be explored to provide stronger formal guarantees across classes. We also plan to investigate adaptive schemes for the trade-off parameter that automatically adjust based on dataset characteristics and learning progress. The success of CRC-AL demonstrates that principled statistical methods can yield significant practical benefits, opening new avenues for uncertainty quantification in computer vision where annotation costs remain a critical bottleneck.
Author Contributions
Conceptualization, C.E. and N.K.U.; methodology, C.E.; software, C.E.; validation, C.E. and N.K.U.; visualization, C.E.; writing—original draft preparation, C.E.; writing—review and editing, C.E. and N.K.U.; supervision, N.K.U.; project administration, N.K.U. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data are available in publicly accessible repositories. The source code is openly available at https://github.com/ccerhan/AL-SEG (last accessed on 29 August 2025). The datasets can be accessed at the following links: Cityscapes (https://www.cityscapes-dataset.com/downloads, last accessed on 29 August 2025), PascalVOC2012 (https://www.kaggle.com/datasets/gopalbhattrai/pascal-voc-2012-dataset, last accessed on 29 August 2025), and PascalVOC2012 Augmented Patch (https://www2.eecs.berkeley.edu/Research/Projects/CS/vision/grouping/semantic_contours/benchmark.tgz, last accessed on 29 August 2025). No special access restrictions apply.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Tian, J.; Xin, P.; Bai, X.; Xiao, Z.; Li, N. An Efficient Semantic Segmentation Framework with Attention-Driven Context Enhancement and Dynamic Fusion for Autonomous Driving. Appl. Sci. 2025, 15, 8373. [Google Scholar] [CrossRef]
- Altini, N.; Lasaracina, E.; Galeone, F.; Prunella, M.; Suglia, V.; Carnimeo, L.; Triggiani, V.; Ranieri, D.; Brunetti, G.; Bevilacqua, V. A Comparison Between Unimodal and Multimodal Segmentation Models for Deep Brain Structures from T1- and T2-Weighted MRI. Mach. Learn. Knowl. Extr. 2025, 7, 84. [Google Scholar] [CrossRef]
- Czajka, M.; Krupka, M.; Kubacka, D.; Janiszewski, M.R.; Belter, D. A Comparison of Segmentation Methods for Semantic OctoMap Generation. Appl. Sci. 2025, 15, 7285. [Google Scholar] [CrossRef]
- Formichini, M.; Avizzano, C.A. A Comparative Analysis of Deep Learning-Based Segmentation Techniques for Terrain Classification in Aerial Imagery. AI 2025, 6, 145. [Google Scholar] [CrossRef]
- Cordts, M.; Omran, M.; Ramos, S.; Rehfeld, T.; Enzweiler, M.; Benenson, R.; Franke, U.; Roth, S.; Schiele, B. The Cityscapes Dataset for Semantic Urban Scene Understanding. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 3213–3223. [Google Scholar]
- Settles, B. Active Learning Literature Survey; Technical Report 1648; University of Wisconsin-Madison: Madison, WI, USA, 2009. [Google Scholar]
- Wu, M.; Li, C.; Yao, Z. Deep Active Learning for Computer Vision Tasks: Methodologies, Applications, and Challenges. Appl. Sci. 2022, 12, 8103. [Google Scholar] [CrossRef]
- Tharwat, A.; Schenck, W. A Survey on Active Learning: State-of-the-Art, Practical Challenges and Research Directions. Mathematics 2023, 11, 820. [Google Scholar] [CrossRef]
- Li, D.; Wang, Z.; Chen, Y.; Jiang, R.; Ding, W.; Okumura, M. A survey on deep active learning: Recent advances and new frontiers. IEEE Trans. Neural Networks Learn. Syst. 2025, 36, 5879–5899. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Shang, Y. A new active labeling method for deep learning. In Proceedings of the International Joint Conference on Neural Networks, Beijing, China, 6–11 July 2014; pp. 112–119. [Google Scholar]
- Golestaneh, S.A.; Kitani, K.M. Importance of Self-Consistency in Active Learning for Semantic Segmentation. arXiv 2020, arXiv:2008.01860v1. [Google Scholar] [CrossRef]
- Ash, J.T.; Zhang, C.; Krishnamurthy, A.; Langford, J.; Agarwal, A. Deep Batch Active Learning by Diverse, Uncertain Gradient Lower Bounds. arXiv 2019, arXiv:1906.03671. [Google Scholar]
- Han, Y.; Liu, D.; Shang, J.; Zheng, L.; Zhong, J.; Cao, W.; Sun, H.; Xie, W. BALQUE: Batch active learning by querying unstable examples with calibrated confidence. Pattern Recognit. 2024, 151, 110385. [Google Scholar] [CrossRef]
- Guo, C.; Pleiss, G.; Sun, Y.; Weinberger, K.Q. On calibration of modern neural networks. In Proceedings of the International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; pp. 1321–1330. [Google Scholar]
- Vovk, V.; Gammerman, A.; Shafer, G. Algorithmic Learning in a Random World; Springer: New York, NY, USA, 2005. [Google Scholar]
- Balasubramanian, V.; Ho, S.S.; Vovk, V. Conformal Prediction for Reliable Machine Learning: Theory, Adaptations and Applications; Newnes: Boston, MA, USA, 2014. [Google Scholar]
- Angelopoulos, A.N.; Bates, S. A Gentle Introduction to Conformal Prediction and Distribution-Free Uncertainty Quantification. arXiv 2022, arXiv:2107.07511. [Google Scholar] [CrossRef]
- Angelopoulos, A.N.; Bates, S.; Fisch, A.; Lei, L.; Schuster, T. Conformal Risk Control. In Proceedings of the Twelfth International Conference on Learning Representations, Vienna, Austria, 7–11 May 2024. [Google Scholar]
- Matiz, S.; Barner, K.E. Inductive conformal predictor for convolutional neural networks: Applications to active learning for image classification. Pattern Recognit. 2019, 90, 172–182. [Google Scholar] [CrossRef]
- Corrigan, A.; Hopcroft, P.; Narvaez, A.; Bendtsen, C. Batch mode active learning for mitotic phenotypes using conformal prediction. In Proceedings of the Ninth Symposium on Conformal and Probabilistic Prediction and Applications, PMLR, Online, 9–11 September 2020; Volume 128, pp. 229–243. [Google Scholar]
- Matiz, S.; Barner, K.E. Conformal prediction based active learning by linear regression optimization. Neurocomputing 2020, 388, 157–169. [Google Scholar] [CrossRef]
- Everingham, M.; Van Gool, L.; Williams, C.K.I.; Winn, J.; Zisserman, A. The Pascal Visual Object Classes (VOC) Challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Hariharan, B.; Arbeláez, P.; Bourdev, L.; Maji, S.; Malik, J. Semantic contours from inverse detectors. In Proceedings of the IEEE International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 991–998. [Google Scholar] [CrossRef]
- Lewis, D.D.; Catlett, J. Heterogeneous Uncertainty Sampling for Supervised Learning. In Machine Learning Proceedings; Morgan Kaufmann: San Francisco, CA, USA, 1994; pp. 148–156. [Google Scholar]
- Roth, D.; Small, K. Margin-Based Active Learning for Structured Output Spaces. In Proceedings of the Machine Learning: ECML 2006; Springer: Berlin/Heidelberg, Germany, 2006; pp. 413–424. [Google Scholar]
- Joshi, A.J.; Porikli, F.; Papanikolopoulos, N. Multi-class active learning for image classification. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 2372–2379. [Google Scholar]
- Gal, Y.; Islam, R.; Ghahramani, Z. Deep Bayesian Active Learning with Image Data. In Proceedings of the 34th International Conference on Machine Learning, PMLR, Sydney, Australia, 6–11 August 2017; Volume 70, pp. 1183–1192. [Google Scholar]
- Yang, L.; Zhang, Y.; Chen, J.; Zhang, S.; Chen, D.Z. Suggestive Annotation: A Deep Active Learning Framework for Biomedical Image Segmentation. In Proceedings of the Medical Image Computing and Computer Assisted Intervention—MICCAI; Springer International Publishing: Berlin/Heidelberg, Germany, 2017; pp. 399–407. [Google Scholar]
- Beluch, W.H.; Genewein, T.; Nurnberger, A.; Kohler, J.M. The Power of Ensembles for Active Learning in Image Classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 9368–9377. [Google Scholar]
- Mittal, S.; Niemeijer, J.; Cicek, O.; Tatarchenko, M.; Ehrhardt, J.; Schäfer, J.P.; Handels, H.; Brox, T. Realistic evaluation of deep active learning for image classification and semantic segmentation. Int. J. Comput. Vis. 2025, 133, 4294–4316. [Google Scholar] [CrossRef]
- Sener, O.; Savarese, S. Active Learning for Convolutional Neural Networks: A Core-Set Approach. In Proceedings of the International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018. [Google Scholar]
- Agarwal, S.; Arora, H.; Anand, S.; Arora, C. Contextual Diversity for Active Learning. In Proceedings of the Computer Vision—ECCV 2020; Springer International Publishing: Berlin/Heidelberg, Germany, 2020; pp. 137–153. [Google Scholar]
- Gaillochet, M.; Desrosiers, C.; Lombaert, H. Active learning for medical image segmentation with stochastic batches. Med Image Anal. 2023, 90, 102958. [Google Scholar] [CrossRef]
- Sinha, S.; Ebrahimi, S.; Darrell, T. Variational Adversarial Active Learning. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Seoul, Republic of Korea, 27–28 October 2019; pp. 5971–5980. [Google Scholar]
- Kim, K.; Park, D.; Kim, K.I.; Chun, S.Y. Task-aware variational adversarial active learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 19–25 June 2021; pp. 8162–8171. [Google Scholar]
- Yoo, D.; Kweon, I.S. Learning Loss for Active Learning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 93–102. [Google Scholar]
- Casanova, A.; Pinheiro, P.O.; Rostamzadeh, N.; Pal, C.J. Reinforced active learning for image segmentation. In Proceedings of the International Conference on Learning Representations, Addis Ababa, Ethiopia, 26–30 April 2020. [Google Scholar]
- Siddiqui, Y.; Valentin, J.; NieBner, M. ViewAL: Active learning with viewpoint entropy for semantic segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020. [Google Scholar]
- Cai, L.; Xu, X.; Liew, J.H.; Sheng Foo, C. Revisiting superpixels for active learning in semantic segmentation with realistic annotation costs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021. [Google Scholar]
- Mittal, S.; Niemeijer, J.; Schäfer, J.P.; Brox, T. Best Practices in Active Learning for Semantic Segmentation. In Pattern Recognition; Springer: Cham, Switzerland, 2024; pp. 427–442. [Google Scholar]
- Ho, S.S.; Wechsler, H. Query by transduction. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 1557–1571. [Google Scholar] [CrossRef]
- Balasubramanian, V.; Chakraborty, S.; Panchanathan, S. Generalized Query by Transduction for online active learning. In Proceedings of the IEEE 12th International Conference on Computer Vision Workshops, ICCV Workshops, Kyoto, Japan, 27 September–4 October 2009; pp. 1378–1385. [Google Scholar]
- Makili, L.E.; Sánchez, J.A.V.; Dormido-Canto, S. Active Learning Using Conformal Predictors: Application to Image Classification. Fusion Sci. Technol. 2012, 62, 347–355. [Google Scholar] [CrossRef]
- Goldstein, H.; Poole, C.P.; Safko, J.L. Classical Mechanics, 3rd ed.; Pearson: Upper Saddle River, NJ, USA, 2001. [Google Scholar]
- van der Maaten, L.; Hinton, G. Visualizing Data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
- MMSegmentation: OpenMMLab Semantic Segmentation Toolbox and Benchmark. 2020. Available online: https://github.com/open-mmlab/mmsegmentation (accessed on 13 October 2025).
- Chen, L.C.; Papandreou, G.; Schroff, F.; Adam, H. Rethinking Atrous Convolution for Semantic Image Segmentation. arXiv 2017, arXiv:1706.05587. [Google Scholar] [CrossRef]
- Xie, E.; Wang, W.; Yu, Z.; Anandkumar, A.; Alvarez, J.M.; Luo, P. SegFormer: Simple and Efficient Design for Semantic Segmentation with Transformers. arXiv 2021, arXiv:2105.15203. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. ImageNet: A large-scale hierarchical image database. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).