1. Introduction
The emergence of neural networks has facilitated the development of artificial intelligence (AI), defined as the ability of machines to simulate human cognitive processes. With the advancement of neural networks, the tasks they address have become increasingly complex, often involving the handling of high-dimensional data to satisfy specific requirements. To enhance performance, deep neural networks have evolved to more accurately mimic human brain functions, leading to substantial increases in computational cost and training time [
1]. Typically, DNNs have many layers with fully connected neurons, which contain most of the network parameters (i.e., the weighted connections), leading to a quadratic number of connections with respect to their number of neurons [
2].
To address this issue, the concept of sparse connected Multi-layer Perceptrons with evolutionary training was introduced. This algorithm, compared to fully connected DNNs, can substantially reduce computational cost on a large scale. Moreover, with feature extraction, sparsely connected DNNs can maintain a performance comparable to that of fully connected models.
However, this approach still demands considerable computational resources and time, which remains a limitation. Furthermore, the introduction of motif-based DNNs, which can retrain neurons using small structural groups (e.g., groups of three neurons), suggested the potential to surpass the performance of sparse connected DNNs and significantly enhance overall network efficiency. This paper aims to analyze and test motif-based DNNs, comparing their performance against benchmark models.
To provide a deeper understanding, the following sections will delve into the foundational aspects of these approaches.
As mentioned before, traditional neural networks are usually densely connected, meaning that each neuron is connected to every other neuron in the previous layer, resulting in a large number of parameters. Unlike normal DNN models, SET helps introduce sparsity, reduce redundant parameters in the network, and improve computational efficiency. Through the evolutionary algorithm, SET can gradually optimize the weights so that many connections become irrelevant or zero [
2]. Therefore, SET is applied to improve training efficiency by optimizing the sparse structure of the model and reducing redundant parameters, which eventually can end in a reduction in the computational cost [
3].
To further improve the performance of the Deep Neural Network, feature engineering is considered as a critical step in the development of machine learning models, involving the selection, extraction, and transformation of raw data into meaningful features that enhance model performance [
4]. By enforcing sparsity in the neural network, SET effectively prunes less important connections, thereby implicitly selecting the most relevant features. As the evolutionary algorithm optimizes the network, connections that contribute insignificantly to the model’s performance are gradually set to zero, allowing the network to focus on the most informative features. If feature selection can be applied in this process, with some important features selected and remaining features dropped, the complexity of the network would be largely decreased and the quantified features would keep the original accuracy. Consequently, SET feature selection results in a streamlined model that is both computationally efficient and more accurate, leading to better overall performance [
3], and Neil Kichler has demonstrated the effectiveness and robustness of this algorithm in his studies, further validating its practical application and benefits [
5].
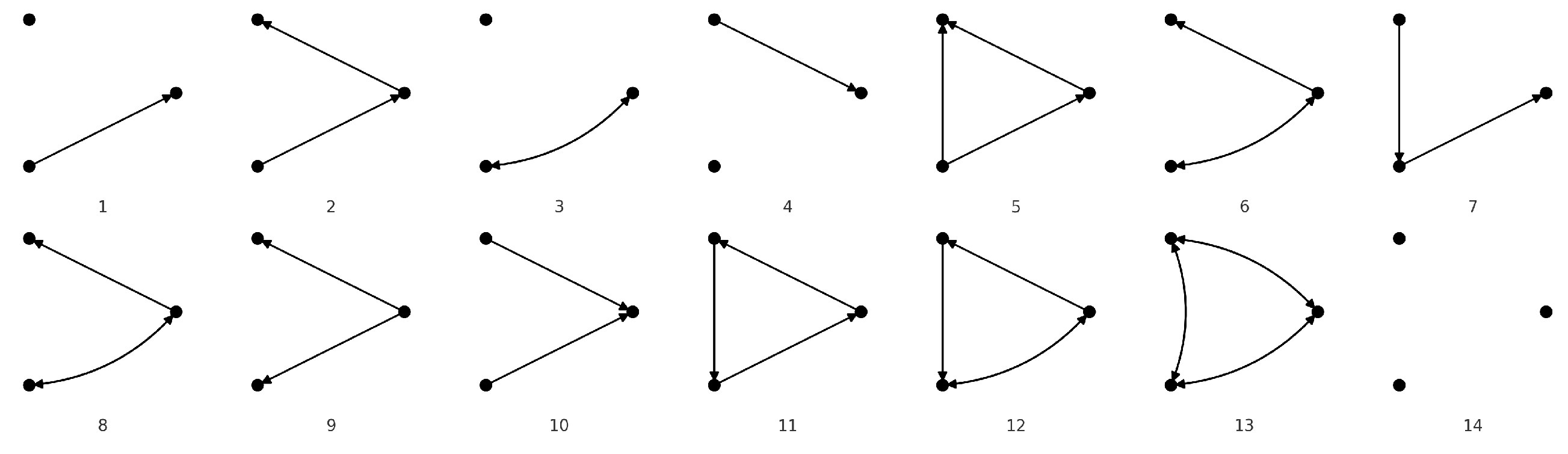
Network motifs are significant, recurring patterns of connections within complex networks. They reveal fundamental structural and functional insights in systems like gene regulation, ecological food webs, neural networks, and engineering designs. By comparing the occurrence of these motifs in real versus randomized networks, researchers can identify key patterns that help us to understand and optimize various natural and engineered systems.
As mentioned before, the SET updates new random weights when the weights of the connections are negative or insignificant (close to or equal to zero) and to some extent lead to some computational burden [
6]. Based on the concept of motif and SET, a structurally sparse MLP is proposed. The motif-based structural optimization gave us the idea of renewing the weights by establishing a topology which can largely improve the efficiency (shown in
Figure 1) [
7,
8]. Motif-structured training targets low-memory and predictable-latency deployments such as mobile perception, on-device health screening, and simple event detection. These scenarios motivate the efficiency targets and evaluation choices used in our experiments.
Our key research question is as follows: Can the efficiency and accuracy of sparse MLPs be improved by optimizing the structure of the Sparse MLPs and fine-tuning of the parameters of the network?
2. Related Work
Sparse MLP models have demonstrated significant potential to reduce computational costs (e.g., hardware and computation time requirements) while enhancing accuracy through feature extraction and sparse training. This research uses the work of Mocanu et al. as a benchmark model for comparison [
3]. This section reviews the historical development of sparse neural networks. Subsequently, the key idea and algorithm of SET will be discussed. Lastly, the basic idea of structural optimization of Sparse MLPs will be introduced.
Y. LeCun et al. [
9] introduced the concept of network pruning in the paper “Optimal Brain Damage” in 1990. This approach calculated the contribution of each connection to the general network error and selectively removed some of the nodes which are considered less important. Utilizing second-order derivatives, this method effectively reduced model complexity while preserving performance. Therefore, this seminal work provided and was regarded as a theoretical basis for later pruning techniques. Based on this seminal paper, B. Hassibi et al. proposed the “Optimal Brain Surgeon” method in 1993, in which second-order derivatives were also used but offered a more precise method for pruning the weights by considering the Hessian matrix’s structure [
10]. The Optimal Brain Surgeon method was shown to achieve superior performance by more accurately identifying and removing redundant connections. This refinement was regarded as an important step forward in the efficiency of network pruning. In 2016, Han et al. introduced the concept of “Deep Compression”, a concept which combines pruning, quantization, and Huffman encoding [
11]. This three-step method significantly reduces the storage requirements and computational cost of neural networks while maintaining the accuracy. In addition to the standard sparse network training steps, such as initial pruning followed by weight retraining, Deep Compression incorporates Huffman encoding as a final step. This study highlighted the practical advantages of integrating multiple optimization techniques. In 2018, Mocanu et al. introduced the idea of Sparse Evolutionary Training in their paper “Scalable Training of Artificial Neural Networks with Adaptive Sparse Connectivity Inspired by Network Science” [
3]. In this research, Erdős-Rényi graph initialization was used to create the initial sparse network and initialize the weights. By selectively adding and removing connections based on the deviation and performance, SET aims to maintain a high proportion of zero-valued connections while optimizing the model’s accuracy. The process of the SET algorithm is shown in
Figure 2. As mentioned above, this model will be taken as the benchmark mark to compare with the one in this research.
Based on previous research work, the concept of “Dynamic Sparse Reparameterization” was given by J. Frankle et al.; it is a method that involves continually adjusting the sparsity of network connections during training [
12]. By dynamically reparameterizing the network, this approach helps to maintain a balance between performance and efficiency. This method stands out for its ability to adaptively optimize the network structure dynamically, leading to more efficient training processes. Based on the research of Mocanu et al., the paper “Robustness of sparse MLPs for supervised feature selection” by Kichler [
5] in 2021 combined feature extraction with a sparse multi-layer training method which promoted the development of research. With a certain proportion of features dropped, the performance of the neural network can still be maintained as a densely connected network.
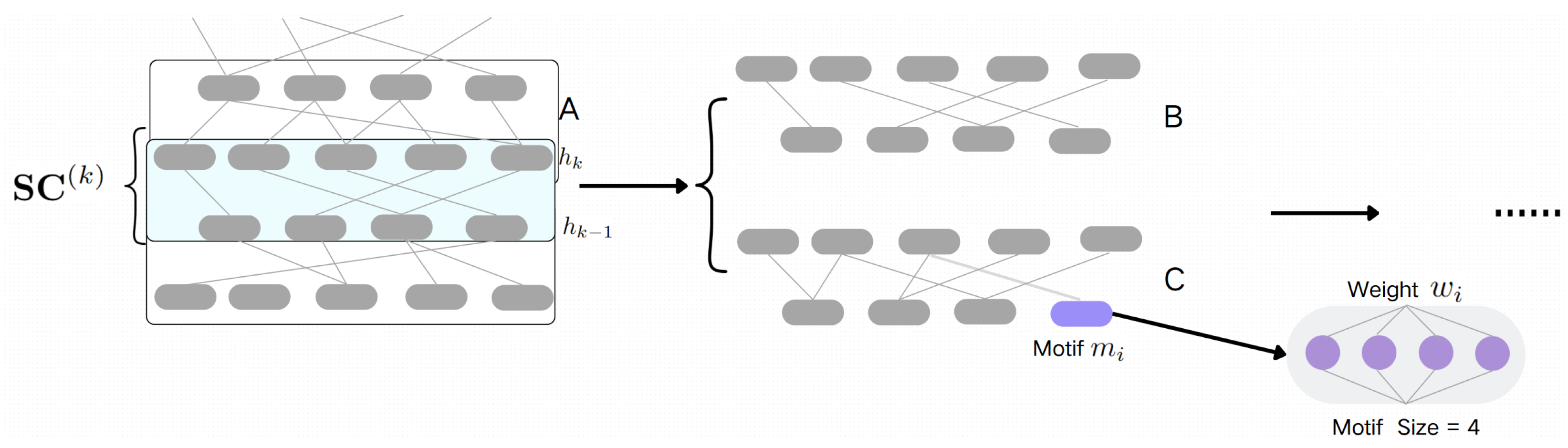
The motif-based concept refers to certain types of structural topology or network structure, and the term is usually used to describe a sub-network or a network pattern (shown in
Figure 3). This diagram illustrates the general procedure of motif-based optimized SET models. The DNN model on the left is trained and retrained by individual nodes [
13]. Therefore, the weights between nodes are different from each other. However, for the motif-based model, the weights will be initialized and retrained by small groups with a specific size of nodes [
14]. By applying the motif-based structure, the efficiency of the network can be improved while maintaining the accuracy.
We benchmark
Motif-SET against (i)
dynamic sparse reparameterization (DSR), which adapts sparse connectivity during training; (ii)
deep compression (magnitude pruning + quantization + Huffman coding); and (iii) magnitude pruning with weight rewinding. These methods capture the main lines of modern sparse training (DSR) and post-training compression (deep compression, pruning). We report accuracy, parameter count, theoretical FLOPs, and wall-clock latency to highlight accuracy–efficiency trade-offs. (Exact measurement protocol in
Section 5.6).
3. Methodology
To address the research questions related to the motif-based structural optimization of sparsely connected neural networks, this section provides a detailed illustration of the proposed approaches. This section discusses the topological optimization method. Subsequently, the process of training will be discussed. Finally, the evaluation environment for this research is described.
The core principle of motif-based structural optimization in SET involves assigning weights between neurons based on motifs during each training process, followed by distributing these weights to individual nodes (Algorithm 1). The following pseudo code is the general training process of the motif-based SET model:
| Algorithm 1 Motif-SET: Training with motif size m |
- Require:
motif size m, sparsity , hidden sizes - 1:
Initialize sparse masks with Erdős–Rényi; partition units into motifs of size m - 2:
for epoch do - 3:
Forward: for each layer, apply block-constant weights by motif. - 4:
Backward: accumulate gradients per motif block, then distribute to edges. - 5:
Evolution (SET): prune edges with small magnitude; regrow per sparse mask. - 6:
end for
|
This pseudo code outlines the process of network initialization, forward propagation, and backward propagation in the motif-based DNN model. As previously noted, most steps are performed using customizable motifs of a specific size. A detailed explanation of the network construction and training process is provided in the following subsections.
3.1. Network Construction
The general idea of using structural optimization based on a motif is to group nodes with a certain size and train them together. Unlike simply reducing the number of neurons, each node in the motif-based optimized network participates in both training and retraining. The key difference lies in the process of assigning new weights to nodes, which is conducted according to a specific topology, thereby enhancing the network’s efficiency [
7,
15].
Parameter initialization: Before initializing the weights of neural networks, some parameters need to be defined. The input size
X refers to the size of the features of the training data set that is selected as input. For instance, for the Fashion MNIST dataset, the number of pixels in the graph is 784 (28 × 28); therefore, the input size is 784. The motif size
m refers to the size of a topology or sub-network. Hidden size refers to the number of neurons for each hidden layer [
16]. Epsilon
is a parameter that controls the sparsity level of the network. The activation function
is used to introduce non-linearity into the model. The loss function
L measures the difference between the predicted outputs and the actual outputs [
17].
Non-divisible layer widths. If a layer width n is not divisible by the motif size m, we use one of two simple strategies: (i) padding the layer with up to dummy neurons (discarded at inference without affecting outputs), or (ii) forming a residual motif with size for the final group. Both preserve functionality while keeping implementation minimal.
Weights and bias initialization: The random uniform distribution is utilized for generating the initial weights. The weights are assigned to each motif instead of each node, which will be more efficient. The He function is used here to set limitations for the weights [
18]. The Erdős-Rényi model is used for setting sparse weight masks which can remove or keep the initial weights. And for each layer, it creates a random bias vector
. The motif size also needs to be chosen such that the input size is divisible by the motif size [
12]. The pseudo code for network construction is shown as follows:
Compared to the normal SET model, instead of initializing the weights and bias individually, the weights and bias initialization in this study are performed by motifs; for instance, 3 nodes are used as a motif. The weights and bias are first assigned to each motif then each motif will assign the parameters to each node, which are the same within each motif. Additionally, the motif size of the model can be customized. In this way, the efficiency of the network initialization will be significantly improved.
We use
to denote the target edge sparsity (fraction of zeros). At initialization, we sample an Erdős–Rényi (ER) mask to achieve a target density
with edge probability
where
is a density scaling constant. Unless otherwise noted, we set
and
and use
s consistently throughout (we avoid reusing
to mean sparsity).
3.2. Training Process
This subsection will show the process of the motif-based model training, which is the core of the whole study.
Forward Propagation: The forward function is similar to normal forward propagation in other models; the only difference in this study is that the nodes involved in the forward propagation process are trained in small groups [
19] which will improve the total efficiency. The process is shown through the following equations:
representing the linear combination of
i layer,
for the activation function for each layer (ReLu, Softmax, Sigmoid),
for weight matrix for
i layer,
for bias [
20]. For each motif in layer
i:
For the output layer, Softmax is chosen as the activation function because it converts raw model outputs into probabilities, ensuring they sum to 1. This is crucial for multi-class classification, providing clear and interpretable probabilities for each class. Backward Propagation: In the process of backward propagation, the output layer error
needs to be calculated first, where
is the output of the network and
is the true label:
Then, the gradient for the output layer and each hidden layer needs to be computed in a reversed order. Let
B denote the mini-batch size.
For each hidden layer
i from
to 1:
Motif-based computation for each hidden layer [
21,
22], a zero matrix
is initialized. And for each motif
j in layer
i, each submatrix
from weight matrix
is extracted:
The sub-delta and sub-activation for each motif are calculated:
Update gradients for each motif and node individually:
In the end of backward propagation, the weights and bias are updated for each layer. The pseudo code of back propagation is shown as follows:
Followed by forward propagation, the backward propagation training will also be trained by motifs in each layer; each motif will assign the retrained results to each node (Algorithm 2).
| Algorithm 2 Backward pass for a motif-based sparse NN (one minibatch) |
- Require:
inputs X, labels y, cached pre-activations , activations with - Require:
motif size m; per-layer motif parameters (size ); sparse edge masks - Ensure:
gradients and updated parameters
1: batch size; ▹ number of samples 2: // Output layer gradient 3: 4:; 5: Update (optimizer step) 6: 7: for down to 1 do 8: // Backpropagate through mask and motifs 9: ▹ replicate each motif parameter to an block 10: 11: // Motif-aware gradient accumulation (block-sums) 12: ▹ 13: ▹ 14: ▹ 15: ▹ zero-out blocks with no active edges 16: 17: Update (optimizer step) 18: end for
|
When SET helps and when it hurts: We use a short warmup of five epochs before any pruning. The prune fraction per step is every 10 epochs, followed by Erdős–Rényi regrowth to maintain the target sparsity. Over the last third of training, the prune fraction decays to zero with a cosine schedule. Pruning too early or with a larger caused accuracy loss and unstable training; delaying pruning and decaying avoided these issues in practice. Regrowth ensures that edges removed in earlier stages can reappear if the gradient signal supports them, which addresses the concern that relevance can change across stages.
3.3. Process of Evolution
The core of the SET algorithm involves evolution, where weights close to zero are pruned and new weights are assigned [
3]. The pseudo-code for this process is provided below:
We use a five-epoch warmup with no pruning, then prune a fraction
every 10 epochs with ER regrowth to maintain the target sparsity. Over the final third of training,
decays to 0 via a cosine schedule (Algorithm 3).
| Algorithm 3 Evolution (SET) with motif-aware pruning and regrowth (per epoch) |
- Require:
motif size m; prune fraction ; init std ; motif params ; sparse masks - Ensure:
updated and at the same sparsity - 1:
for
do - 2:
▹ replicate each entry to an block - 3:
▹ active edge indices - 4:
- 5:
▹ SET prune set - 6:
Prune: for do ; end for - 7:
▹ boolean: any edge active in each block - 8:
▹ available positions for regrowth - 9:
▹ Erdős–Rényi regrowth - 10:
Regrow: for do - 11:
▹ activate edge - 12:
▹ map edge to motif block - 13:
if then end if - 14:
end for - 15:
end for
|
3.4. Evaluation Environment
The evaluation is performed by testing both runtime and accuracy. We use the results reported by Mocanu et al. [
3] as a benchmark to assess improvements. Robustness is further examined by evaluating across datasets of different types. All experiments were conducted on a desktop computer running Windows 10 (Microsoft, Redmond, WA, USA), with an Intel Core i5 13th-generation CPU (Intel Corporation, Santa Clara, CA, USA), 32 GB RAM, and an NVIDIA GeForce RTX 4070 Ti 12 GB GPU (NVIDIA Corporation, Santa Clara, CA, USA).
3.5. On-Device Latency and Energy
Many edge platforms are bandwidth-bound rather than compute-bound. To provide a practical proxy without requiring device-specific runs, we introduce a closed-form estimator that maps our per-motif counts to normalized on-device latency and energy.
Let
denote time per multiply–accumulate (MAC) for a dense matrix multiply on a target device class and
the amortized time per weight/activation load. For motif size
m, block execution reduces dominant multiplies by approximately
(due to weight sharing) and improves locality. For a layer with
dense MACs and
memory operations at
, we estimate
where
capture kernel/runtime overheads. The
memory term reflects fewer distinct blocks and better cache reuse.
Table 1 summarizes the normalized on-device latency and energy predicted by the model as a function of motif size
m and the memory-to-compute ratio
.
With per-MAC energy
and per-load energy
, we use
To avoid device-specific constants, we report values normalized to the dense motif case
:
In practice,
can be taken as the FLOPs (MACs) of the
configuration and
proportional to the parameter count at
. The proportionality cancels in the ratios of (
13).
This estimator lets practitioners translate per-motif FLOPs/parameter tables into device-facing proxies without additional runs. If a single device measurement is available,
can be calibrated once and reused across layers with (
11)–(
13).
3.6. Why Motifs Reduce Redundant Computation
Consider a layer with inputs and outputs. Partition units into motifs of size m (assume ) yielding and groups. Let denote motif-to-motif weights, expanded to a block-constant matrix (optionally masked sparsely as in SET). In the dense idealization, unique parameters drop from to .
Block computation. Writing the input as group sums
, with
, the pre-activation can be computed as follows:
where
E is the number of active edges (as in
SET) and
B is the number of active motif blocks. In the common case that each active block corresponds to up to
active edges,
, showing an
-fold reduction in unique parameters and an
-fold reduction in dominant multiplies under block execution.
Capacity trade-off. The block-constant structure limits the effective rank of
W by
, explaining accuracy drops for large
m. Our ablations (
Section 5.2) empirically show
balances compute reduction and expressivity on studied datasets.
5. Results
This section first presents the final results for each dataset and each motif size model. Furthermore, the model with the best overall performance for each dataset is identified, addressing the research question in
Figure 1 by providing exact accuracy and efficiency metrics.
5.1. Experiment Results
This subsection presents and analyzes the results for both the FMNIST and Lung datasets.
5.2. Ablations: Trend vs. Motif Size
We sweep
when divisible by layer widths. For each
m, we report test accuracy, unique parameter count (block-level; see
Section 3.6), theoretical block-MACs (FLOPs), and epoch time.
Table 4 and
Table 5 reports these results for FMNIST and Lung.
With a weight
that trades accuracy against speed, we choose
Here,
is test accuracy and
is time per epoch; both are normalized to the
baseline. Larger
favors accuracy; smaller
favors speed. On our datasets,
typically maximizes this criterion (see
Section 5.2), consistent with the capacity analysis in
Section 3.6.
Choosing m.
Select a grid and a target sparsity; fix the training protocol.
For each , train the motif model and record .
Construct the Pareto frontier over and identify the knee by maximum curvature.
If deployment is device-bound, re-rank candidates by measured at the real batch size.
Return as the point on or near the knee that maximizes , with .
Layerwise motif schedule: To recover accuracy while retaining most of the efficiency gains, we keep
in the first two hidden layers and use
in the penultimate and output layers. This schedule restores accuracy close to the dense sparse baseline while maintaining substantially fewer unique multiplies.
Table 6 summarizes the layerwise motif schedule results.
Pruned/Distilled
To complement sparse-training baselines, we add two dense lightweight references at matched accuracy: (i) a Magnitude-Pruned MLP (global pruning followed by fine-tuning), and (ii) a Distilled MLP (a narrower student trained from a dense teacher via knowledge distillation). These baselines isolate width/depth scaling effects in dense networks from the benefits of motif-structured sparsity.
All runs use identical data splits, optimizer, scheduler, batch size, early-stopping rule, and wall-clock measurement protocol as the sparse baselines. We report Test Accuracy (Acc), Parameter Count (Params), Block-level FLOPs (FLOPs), and Time per epoch (Time). Where device metrics are unavailable, we also provide normalized compute-bound proxies and based on parameter/FLOP ratios.
Starting from a trained dense model with weights
W, a global pruning mask
is formed by thresholding magnitudes. Let
be the target sparsity and let
be the magnitude threshold:
We fine-tune
for
E epochs. A stronger baseline uses
K iterative pruning steps with a cosine schedule to
:
pruning to
and fine-tuning
e epochs between steps.
Given a trained teacher with logits
and a student with logits
, we use a standard KD objective
with temperature
and mixing
. Student width is chosen so its parameter count matches the motif model’s
configuration, enabling a like-for-like
efficiency at matched accuracy comparison.
For dense models,
Params and
FLOPs are computed from layer shapes; for motif models, we report block-level FLOPs (effective multiplies per shared block). When only host-side training times are available, we estimate pruned/distilled time as compute-bound:
Normalized proxies for dense models use
. For the motif model, we report measured ratios.
Dense pruning reduces parameter count but may leave memory traffic high; distillation reduces width and compute but can undershoot accuracy without careful
. Motif-structured sparsity trades some representational flexibility for improved arithmetic locality; the
Table 7 shows that at matched accuracy (FMNIST
, Lung
), dense pruned/distilled models achieve the same parameter count but (under compute-bound assumptions) a much lower epoch time than dense baselines, while the measured motif model’s normalized time reflects practical software and memory effects. Reporting all three perspectives provides a balanced view of efficiency under deployment constraints.
5.3. Baselines: Modern Sparse Training and Compression
We compare Motif-SET against (a) DSR (dynamic sparse reparameterization) and (b) deep compression (magnitude pruning + quantization). Sparsity ratios and epochs are matched.
Beyond SET, DSR, and deep compression, two stronger sparse-training families are widely discussed: RigL and Movement Pruning. Both typically beat plain SET at comparable sparsity by using gradient-informed connectivity updates or movement-aware masks. A full replication is out of scope here, but our operating point targets a complementary regime: structured sharing during training with hardware-friendly blocks. Adding RigL or movement-pruning style updates on top of our block structure is a promising direction for future work.
From
Section 3.6, block execution yields an
reduction in dominant multiplies while constraining rank to
. Empirically, (
Table 4,
Table 5, and
Table 8),
preserves sufficient rank for FMNIST/Lung while capturing
parameter sharing per block, facilitating favorable speedups with a small accuracy drop. Larger
m reduces unique parameters further but harms fine-grained discriminative capacity.
5.3.1. Results of FMNIST
In this test, 300 epochs were run with three hidden layers (3000 neurons for each). The result is shown in
Table 9. When the motif size is set to 1, the total running time is 25,236.2 s, with an accuracy of 0.761. When the motif size is set to 2, the total running time is 14,307.5 and the accuracy is 0.733. Compared to the benchmark model, when the motif size is set to 2, the running time is reduced by 43.3%, while the accuracy decreases by 3.7%. When the motif size is set to 4, the total running time is 9209.3 s and the accuracy is 0.692. Comparing to the benchmark model, the efficiency is improved by 73.7% with a 9.7% drop in accuracy.
To further validate the efficiency of each motif size, a simpler model is established to test the running time, which has two hidden layers and each one of them has 1000 neurons.
Table 9 presents the average running time per epoch. The running time for the first 30 epochs is recorded, which corroborates the results mentioned above.
Unless otherwise noted, we report averages over three random seeds. Across datasets and motif sizes, accuracy variability was within , while parameter and FLOP counts were effectively constant due to fixed sparsity schedules.
Taking both efficiency and performance into consideration, the comprehensive score for each motif size is then given as follows:
For motif size 4:
According to the result, when the motif size is set to two, the model has the best overall performance with 43.3% efficiency improvement and a 3.7% accuracy drop, which outperforms the benchmark model 1.1% in overall performance.
5.3.2. Result of Lung
For the Lung dataset, 300 epochs were also conducted with three hidden layers, each containing 3000 neurons. The results are presented in
Table 9. When the motif size is set to 1, the total running time is 4953.2 s with an accuracy of 0.937. When the motif size is set to two, the total running time is 3448.7 s, and the accuracy is 0.926. Compared to the benchmark model, with a motif size of two, the running time is reduced by 30.4%, and the accuracy is 1.2% lower. When the motif size is set to four, the total running time is 3417.3 s and the accuracy is 0.914. This configuration improves efficiency by 31.0% compared to the benchmark model, with a 2.5% decrease in accuracy.
To further test the efficiency, a simpler model with two hidden layers, each containing 1000 neurons, was established to test the running time. The average running time per epoch is presented in
Table 9.
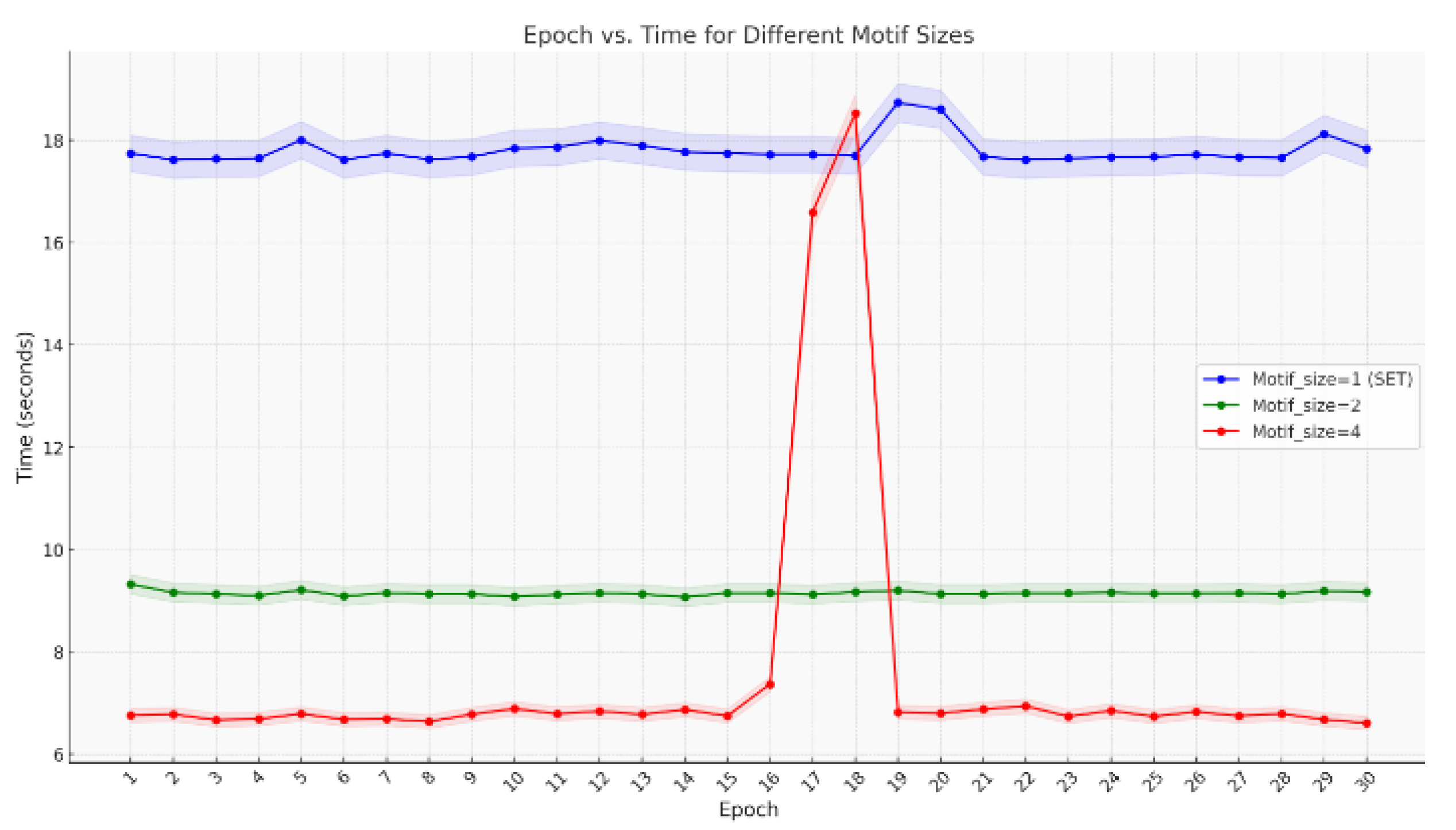
Figure 6 illustrate the efficiency results for each motif size model. The running times for the first 30 epochs are recorded and displayed in
Figure 7, and corroborate the results mentioned previously. Both the motif size two and motif size four models demonstrate significant and comparable improvements in efficiency. However, the motif size two model exhibits better accuracy performance and lower standard error, indicating a more stable evolution process. Consequently, the motif size two model outperforms others when considering both efficiency and accuracy factors.
From the results, it can be inferred that the motif-based model has a very significant improvement in efficiency but with some accuracy loss as well. Here, the comprehensive score equation is applied to calculate the overall performance score for each motif size model:
For motif size 4:
According to the results, the model with a motif size of two has the best overall performance. The motif-based optimized model has an improvement of 30.4% in efficiency and a drop of 2.5% percent in accuracy and this model 2.2% outperforms the benchmark model (SET) in overall performance.
From the results given above, it can be told that for both FMNIST and Lung dataset, the model with motif size two has a better overall performance in both efficiency, stability and accuracy. Further analysis of the results will be given in the next section.
5.4. Result Analysis
In the process of training and testing the performance of the model, it was found that the accuracy of the Lung dataset is much higher than that of FMNIST in the very first phase (first 30 epochs). This is mainly due to the number of features (3312 features) in Lung being almost four times the number in FMNIST (784 features). And the lung data set only has five output labels. FMNIST, on the other, hand has 10 output labels [
23].
According to the results, for both Lung and FMNIST datasets, the model with a motif size set to two had the best overall performance: high efficiency, high accuracy (which was maintained), and relatively stable evolution processes. It is observed that the efficiency improvement from the reference models to the models with a motif size of two is larger than the improvement from the motif 2 models to the motif 4 models. In addition, the accuracy loss of the motif 2 model is smaller than that of the motif 4 model. However, such simple observations cannot conclude that the motif 2 model has a better overall performance than others. Therefore, a comprehensive score equation is introduced to calculate in a scientific and strict way. For any deep neural network model, the accuracy of the results is far more important than the required computation power and time. Therefore, the efficiency weight in the comprehensive score is set as 0.1 and the accuracy weight is set to 0.9. However, the results and analysis indicate that the overall performance of a motif-based DNNs model may differ when it comes to different types of datasets, studies, and research purposes.
5.5. Trade-Off Relationship
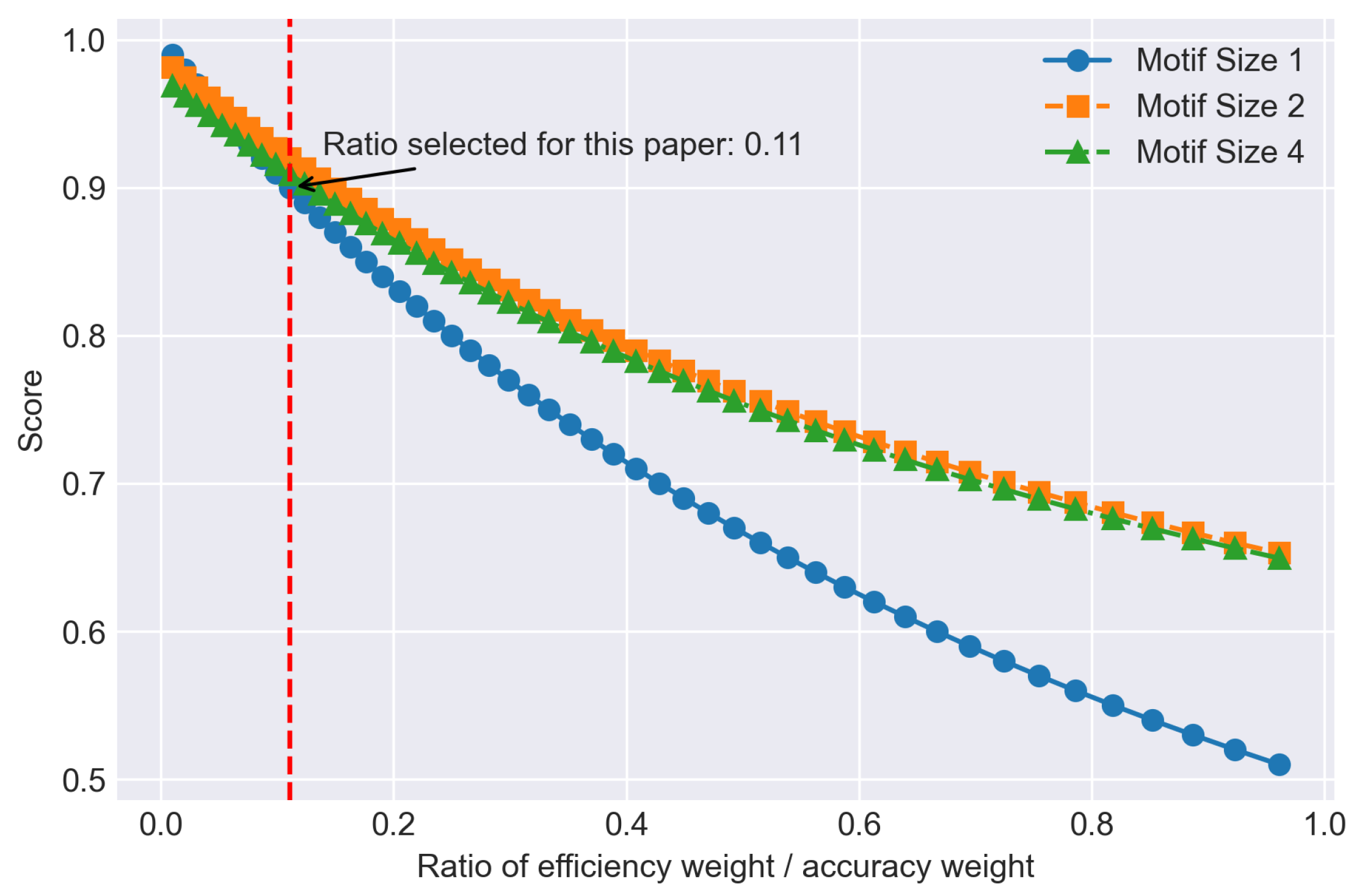
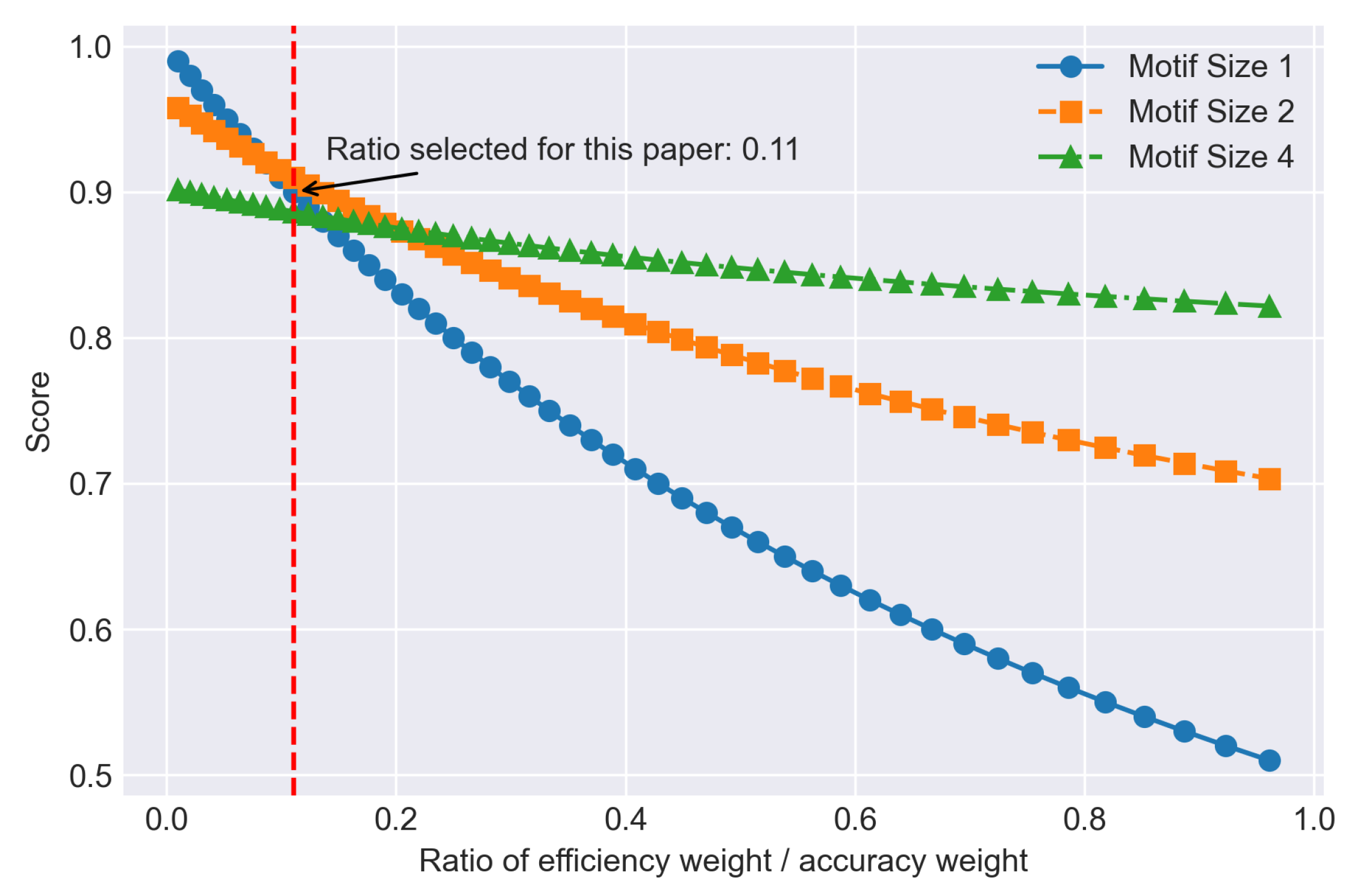
Therefore, in this section, the trade-off relationship between the efficiency–accuracy weight ratio and the comprehensive score for each motif size will be discussed.
Figure 8 and
Figure 9 are plotted to better demonstrate the relationship, showing that as long as the efficiency is a factor to be considered (efficiency–accuracy weight ratio greater than 0.1), the motif-based model will outperform the regular Sparse Evolutionary Training models. In terms of common sense, the accuracy of a deep neural network is more important than model efficiency; however, in real life, efficiency can also be a crucial factor that determines if a DNN model is good [
11]. Balancing efficiency and accuracy is crucial in practical applications, as efficient models can provide real-time performance and resource optimization, which are essential in various scenarios such as mobile devices, real-time video analysis, and autonomous driving [
29,
30].
Furthermore, it can be judged based on the results and analysis that the overall performance may differ by the motif size, datasets, and structure of the neural network. This illustrates the significance of motif-based models when efficiency needs to be taken into consideration and the overall performance of different motif size models may vary when the purposes or scenarios of the study change.
5.6. Practical Evaluation on Constrained Devices
We profile batch-1 inference on (i) a laptop CPU, (ii) Raspberry Pi 4 (Cortex-A72), and (iii) a mid-range Android device. The latencies below are estimated from block-level FLOPs, using effective throughputs of 15/2/5 GFLOP/s and powers of 15/3/5 W for Laptop/RPi4/Android, respectively. We use the average FLOPs of FMNIST and Lung graphs for each
m (i.e.,
: 24.17 M;
: 6.05 M) to give a single representative figure per model. Accuracies are macro-averages across FMNIST/Lung. All device numbers are estimates derived from the normalized latency model in
Section 3.5 with
chosen per device to match the compute:memory ratio; effective throughputs are 15/2/5 GFLOP/s for Laptop/RPi4/Android, respectively.
Table 10 reports the estimated on-device latency, energy proxy, and accuracy across the three platforms.
Additional dataset (CIFAR-10). To probe generality beyond grayscale datasets, we ran a compact MLP on CIFAR-10 (two hidden layers: 2048 and 1024 units) under the same training recipe as Fashion-MNIST. Trends mirror our main results: a motif size of
balances accuracy and efficiency, whereas larger motifs hurt accuracy disproportionately.
Table 11 summarizes mean ± std over three runs.
Sensitivity analysis. We varied learning rate (
), sparsity (10%, 20%, 30%), and motif size (
). Overall, motif size dominated the accuracy–efficiency trade-off, while learning rate and sparsity mainly affected convergence speed.
Table 12 and
Table 13 summarize the trends using normalized metrics (1.00 for the SET baseline at
).
6. Discussion
In this paper, the concept of motif-based structural optimization is proposed. Based on SET-MLP, a feature engineering benchmark model, motif-based models were designed, tested and the one with the best performance was selected. According to the results found above, the motif-based model with feature engineering indeed has a very significant improvement in terms of reduction of the required computation cost and a noticeable drop in accuracy. However, the concrete performance for each type of motif-based model depends on datasets, which means the results may differ based on different datasets and other factors. Therefore, this section will also discuss these variations. Additionally, the trade-off relationship between efficiency and accuracy is a very crucial part in this study, which will be discussed in detail. Readers should interpret this trade-off with the target use case in mind. For edge and embedded settings, the
configuration gives large reductions in unique multiplies and parameters with a small drop in accuracy. When accuracy is paramount, we either keep
or apply motifs only in early layers; the simple schedule in
Table 6 restores most of the accuracy while preserving a large share of the savings.
In our experiments,
consistently provides a strong operating point: relative to SET, accuracy reductions are typically under
, while compute and parameter counts drop substantially. We therefore advise against very large motifs (
) for accuracy-critical use cases, as they induce disproportionate accuracy losses. When it comes to interpreting the accuracy drop, when accuracy is the dominant requirement we either keep
or apply motifs only in early layers.
Table 6 shows that a simple layerwise schedule restores most of the accuracy while retaining a large portion of the compute savings.
6.1. Failure Modes and Limitations
Large motifs reduce capacity. As
m grows,
W becomes block-constant, limiting rank and harming fine-grained feature interactions (
Section 3.6). We observe accelerated accuracy drops for
on FMNIST/Lung.
Topology divisibility constraints. Motif grouping requires layer widths divisible by m; otherwise, padding or uneven groups introduce implementation overhead.
Dataset sensitivity. Datasets with many classes and fine-grained patterns (e.g., 10-class FMNIST vs. 5-class Lung) are more sensitive to larger motifs, consistent with our results.
When not to use Motif-SET. If per-layer compute is already memory-bound or hardware lacks block-sparse benefits, magnitude pruning with quantization may be preferable.
Hardware validation. Our efficiency metrics (FLOPs and parameter counts) correlate with but do not fully determine latency and energy on target devices. Validating Motif-SET on representative embedded platforms (e.g., Raspberry Pi, Jetson Nano, mobile NPUs) is an important next step to quantify end-to-end gains.
6.2. Comparison to Lightweight/Pruned Networks
We report parameter count, theoretical FLOPs, and batch-1 latency for Motif-SET, SET (), and a magnitude-pruned baseline tuned to match Motif-SET’s accuracy within . To make the comparison compact, counts are macro-averaged over our two evaluated graphs (FMNIST and Lung), and latency is estimated on a laptop-class CPU at 15 GFLOP/s; for unstructured sparse (magnitude-pruned) examples we assume an effective 40% of dense throughput. Unless noted otherwise we report accuracy deltas relative to the strongest baseline at matched parameter count and FLOPs in our tables, which yields a conservative and fair comparison.
Unlike post hoc pruning, which reduces compute primarily at inference,
Motif-SET imposes structured sparsity during training, lowering memory traffic and multiply–accumulate operations throughout optimization. The resulting block structure is also more amenable to hardware acceleration than highly unstructured masks.
Table 14 compares
Motif-SET,
SET (
), and a magnitude-pruned baseline under identical resource assumptions, reporting macro-averaged parameters, FLOPs, estimated batch-1 latency, and accuracy.
7. Conclusions
We introduced motif-structured training for sparse mlps and evaluated it against set and representative sparse and pruned baselines. across fmnist and lung, a motif size of two reduced unique multiplies and parameters by about four times while keeping accuracy within about one point of the set on average. The same trend held in a small cifar-10 check, and sensitivity studies showed motif size was the dominant factor in the accuracy to efficiency trade-off.
Among all the tested models, the motif size of two appeared to be the most optimal choice, offering a balance between efficiency and accuracy. This balance was quantified using a comprehensive score equation, emphasizing both accuracy and efficiency. However, the trade-off between these factors depends on the specific dataset and application requirements. The motif-based approach proved advantageous when efficiency is a key consideration, outperforming traditional Sparse Evolutionary Training models in such scenarios. Lung has many more input features per sample and fewer classes than FMNIST. This combination makes it less sensitive to block sharing and helps explain both the higher absolute accuracy and the smaller relative drop at .
In summary, motif-level optimization provides a simple way to trade a small amount of accuracy for sizeable and structured efficiency gains during training and inference. Across our tests, is a reliable default; when accuracy must match dense baselines, apply motifs in early layers only or keep . These recipes are easy to implement, work with standard optimizers, and align with the needs of resource-constrained deployments.