Support Vector Machines to Propose a Ground Motion Prediction Equation for the Particular Case of the Bojorquez Intensity Measure INp
Abstract
1. Introduction
- To propose the first Ground Motion Prediction Equation (GMPE) for the INp intensity measure, which directly incorporates ground motion spectral shape.
- To employ a Support Vector Regression (SVR) model for its superior robustness against outliers compared to traditional linear regression models.
- To provide a generalized expression for INp that is applicable across a wide range of periods and validated through a rigorous cross-validation analysis.
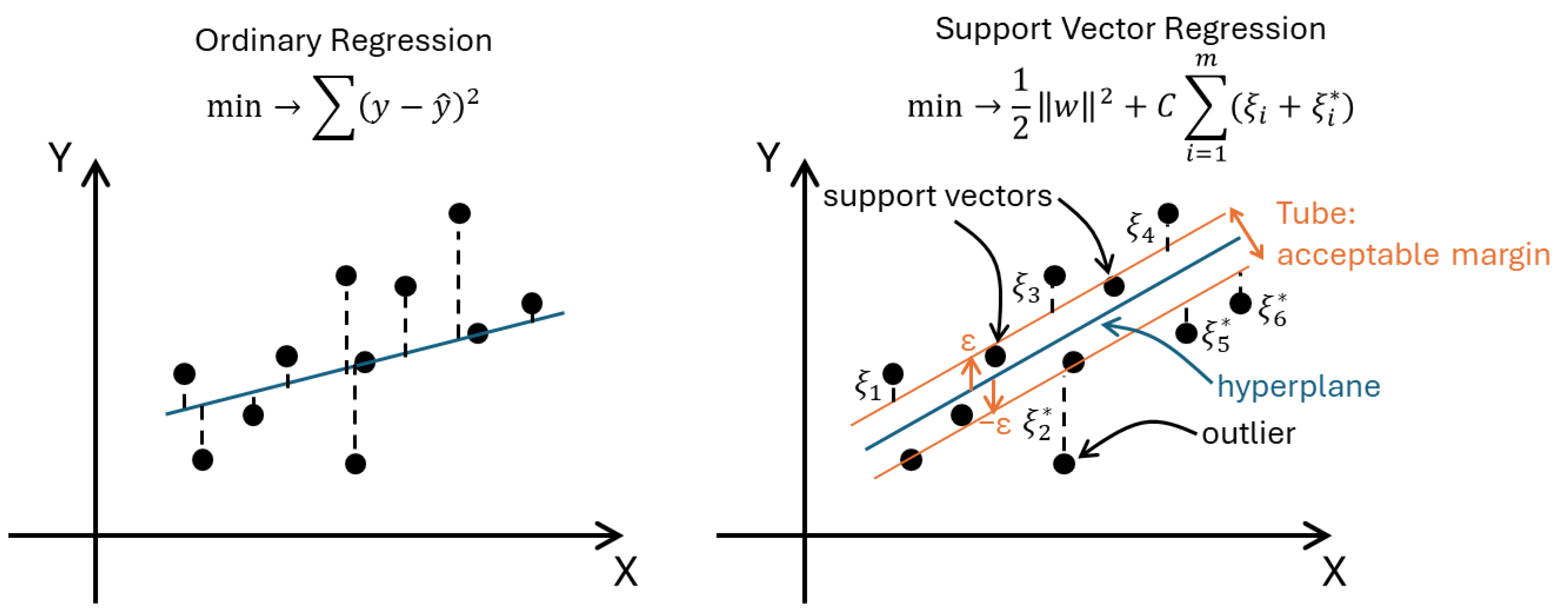
2. Support Vector Regression
- Initialization: The algorithm starts by initializing all the Lagrange multipliers to zero.
- Iterative Optimization:
- Select the first pair of multipliers (, ): It searches for a pair of multipliers that violates the KKT conditions. This is the multiplier that is currently the “furthest” of its optimal value; for example, it has the largest prediction error.
- Select the second pair of multipliers (, ): After finding the first, it then chooses a second multiplier that is likely to make the largest possible change to the first. This is done to speed up the convergence process.
- Analytical Solution: Once the two pairs of multipliers, (, ) and (, ), are chosen, SMO solves a simple 2 × 2 sub-problem to find the optimal values for this pair. This sub-problem has a simple analytical solution, which avoids the need for complex, time-consuming numerical methods.
- Updating Parameters and Repetition: After solving the sub-problem, the algorithm updates the values of (, ) and (, ). It then updates a parameter called the “bias” or b, which is essential for defining the regression function. The process from Step 2 is repeated until all α values converge and the KKT conditions are met for all data points.
- End: Step 2 is repeated until all Lagrange multipliers satisfy the KKT conditions within a predefined tolerance. At this point, the algorithm converges, and the SVR optimization problem has been solved.
- Step 1: Obtain the weight vector () and Bias (b). The SMO algorithm, used by scikit-learn, solves the dual optimization problem to find the Lagrange multipliers ( and ). Once these multipliers are found, they are used to compute the weight vector w and the bias b. The weight vector contains the coefficients for each independent variable in the GMPE. It is calculated with Equation (4).
- Step 2: Formulate the Final GMPE. Once the weight vector and the bias b have been calculated, the final GMPE can be expressed in a traditional linear form. The predicted value of INp is simply the dot product of the vector and the input vector , plus the bias term. The equation for the GMPE could be expressed as , where is the input vector containing the values of your independent variables (e.g., magnitude, distance).
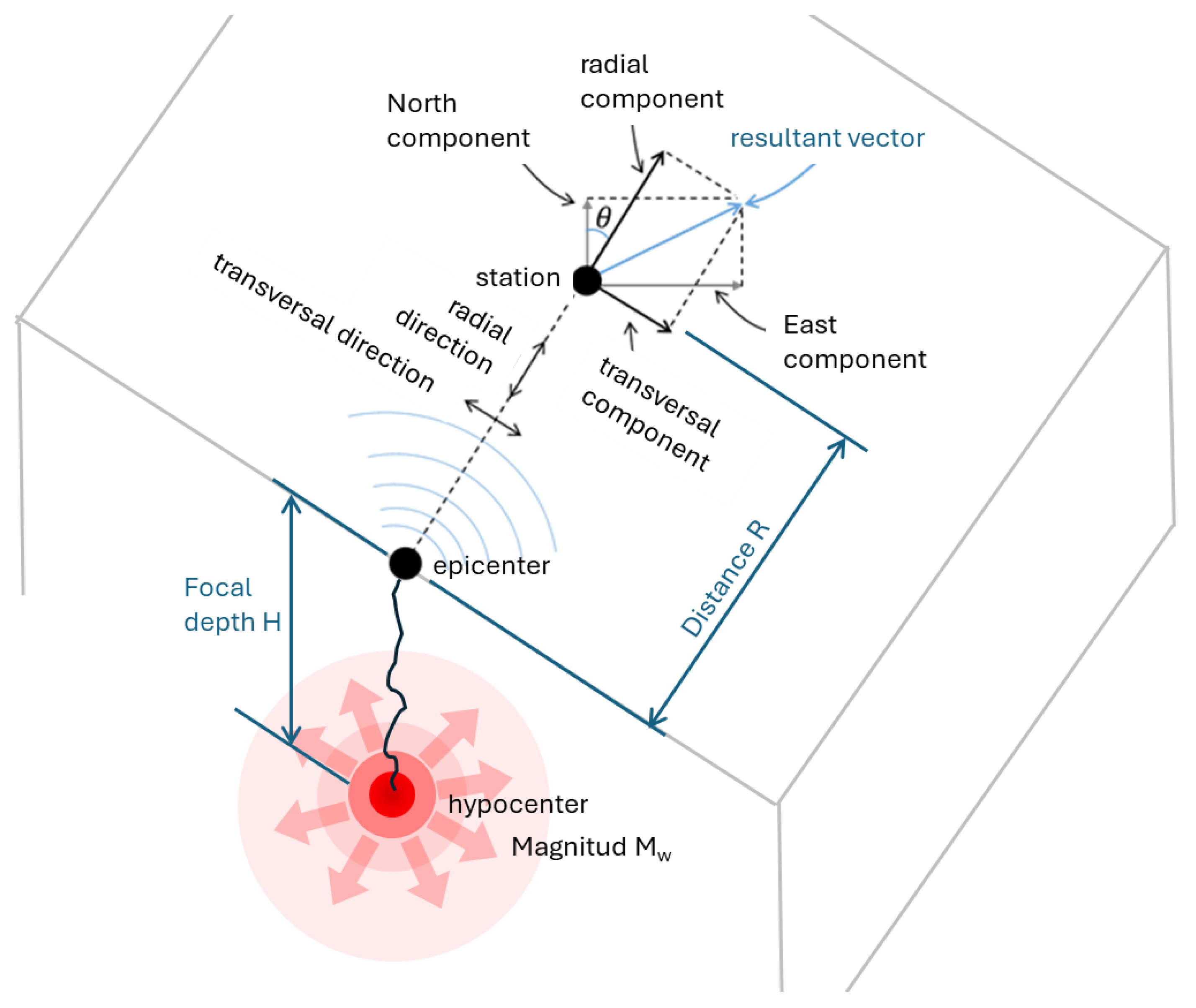
3. The Generalized Bojorquez Intensity Measure IBg and the Particular Case INp
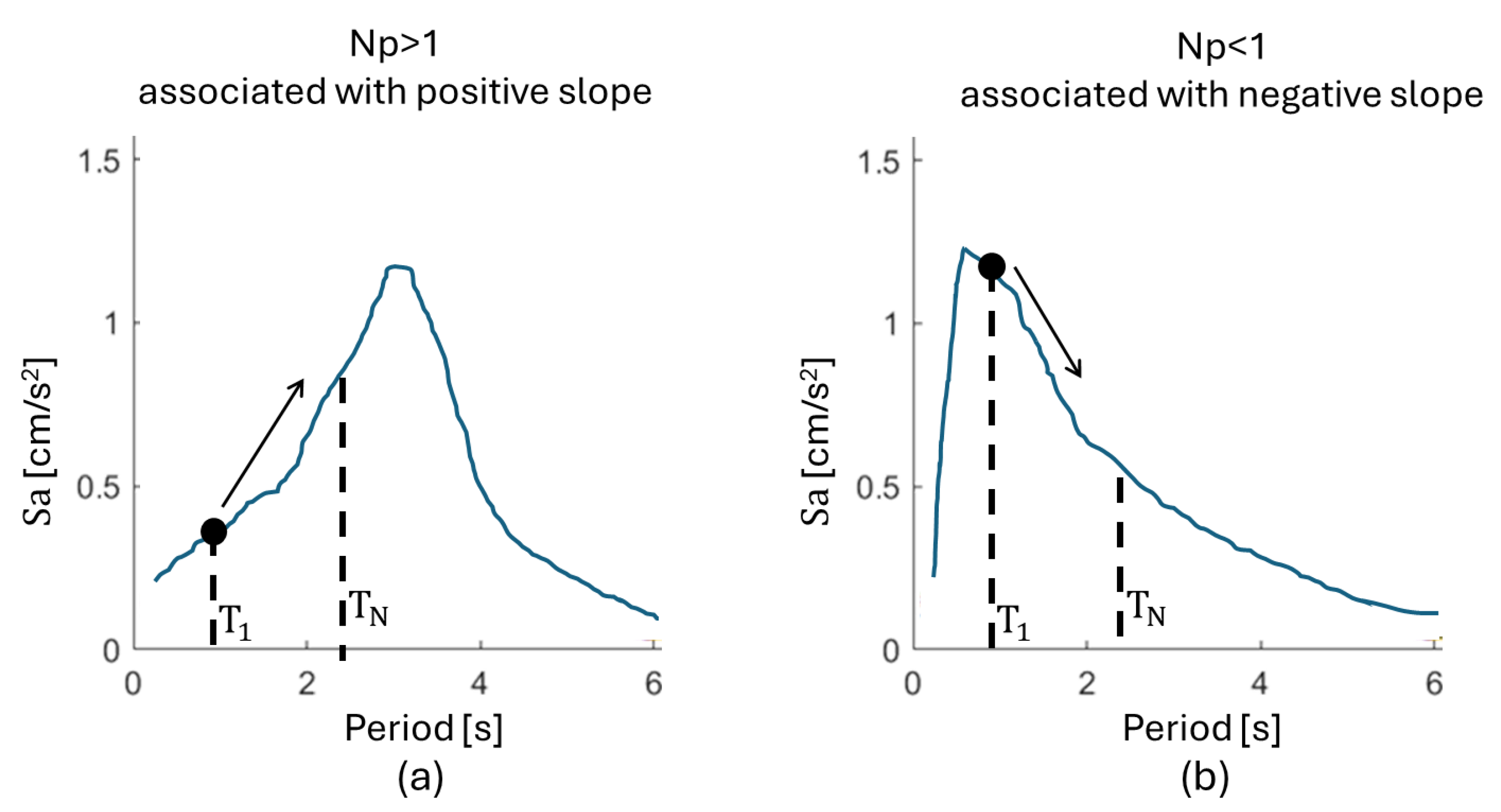
The Particular Case INp
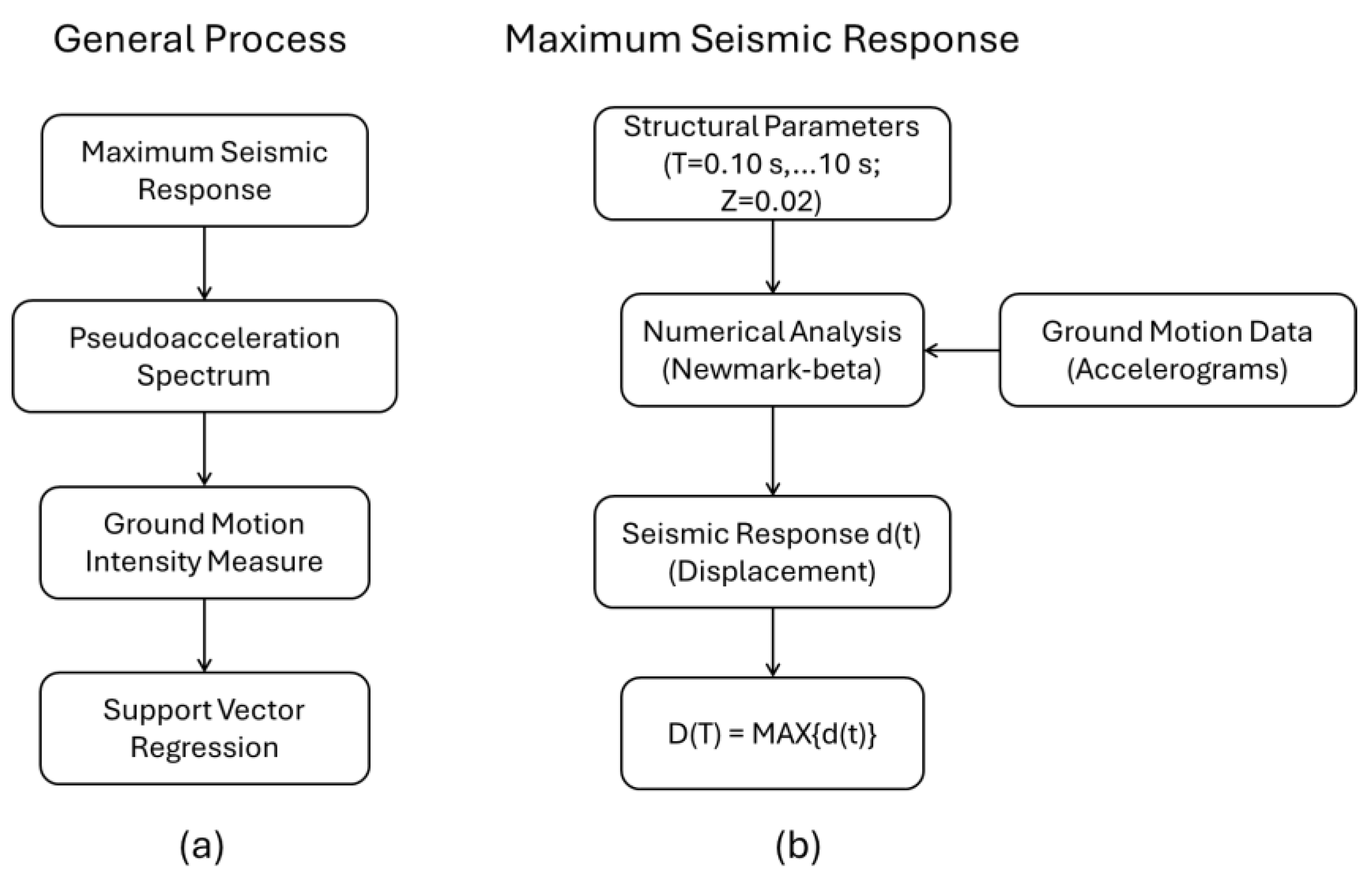
4. Methodology
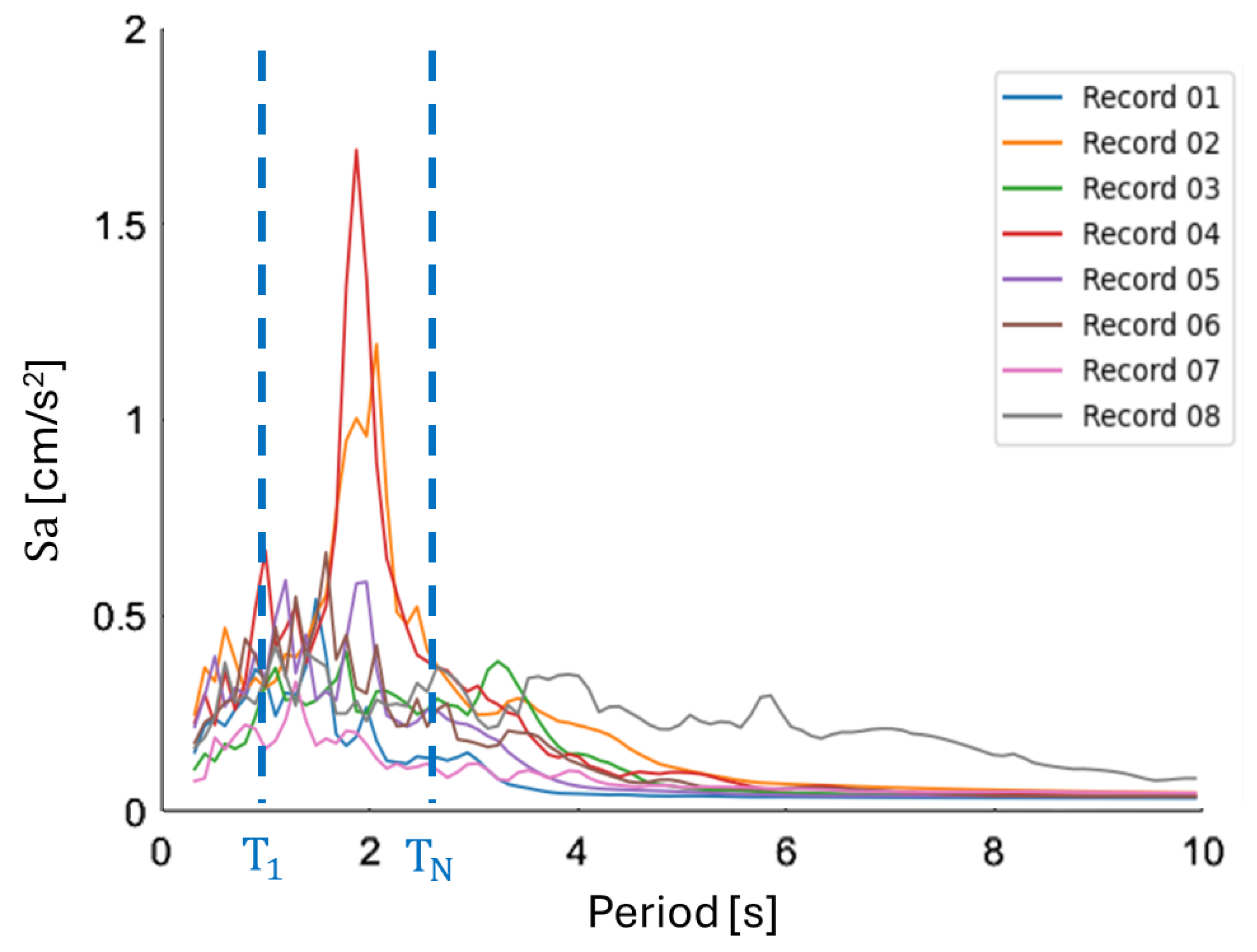
Selected Seismic Ground Motion Records
5. Numerical Results
6. Model Limitations, Generalization and Application in Engineering Practice
7. Conclusions
- (1)
- The Support Vector Regression (SVR) model demonstrated high predictive accuracy for periods shorter than 3 s. A grid search procedure was employed to optimize the hyperparameters C and ε (C = [0.1, 1, 10, 100] and ε = [0.1, 1, 10, 100]). The model’s performance was quantitatively confirmed with a coefficient of determination (R2) close to 0.80 and a Mean Squared Error (MSE) of 0.15, showing a strong correlation between the model’s predictions and the actual observed values.
- (2)
- The unified, generalized expression developed for the entire dataset proved to be a practical and valuable tool. It exhibited an acceptable coefficient of determination (R2) of 0.75 and a Mean Squared Error (MSE) of 0.32 for periods ranging from 0.1 to 5 s. This generalized equation provides a simple yet effective way for engineers and practitioners to estimate INp across a wide range of structural periods.
- (3)
- A comparison with ordinary linear regression (MSE = 0.37, R2 = 0.71) demonstrated the superior predictive performance of SVR. The versatility of SVR, through its adjustable hyperparameters C and ε, provides greater robustness, particularly against outliers.
- (4)
- To address concerns about the limited dataset, a rigorous cross-validation analysis was performed. The results showed a minimal variation in error across all data splits. This finding is crucial as it confirms that the model’s predictive accuracy is not dependent on a specific data split and that it possesses a strong capacity for generalization within the studied range.
- (5)
- This work not only introduces a novel GMPE but also validates the use of Support Vector Regression as a robust and effective method for developing these equations. Our findings offer a more sophisticated tool for seismic risk assessment, which can lead to more reliable estimations of seismic demand and, consequently, safer structural designs.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| GMPE | Ground Motion Prediction Equation |
| SVM | Support Vector Machine |
| SVR | Support Vector Regression |
| MSE | Mean Squared Error |
| IM | Intensity Measures |
| PGA | Peak Ground Acceleration |
| KKT | Karush-Kuhn-Tucker |
| SMO | Sequential Minimal Optimization |
| SDOF | Single-Degree-of-Freedom |
| MDOF | Multi-Degree-of-Freedom |
| UNAM | Universidad Nacional Autónoma de México |
| CU | Ciudad Universitaria |
References
- Mehanny, S.S.; Cordova, P.P. Development of a Two-Parameter Seismic Intensity Measure and Probabilistic Design Procedure. J. Eng. Appl. Sci. 2004, 51, 233–252. [Google Scholar]
- Kazantzi, A.K.; Vamvatsikos, D. Intensity Measure Selection for Vulnerability Studies of Building Classes. Earthq. Eng. Struct. Dyn. 2015, 44, 2677–2694. [Google Scholar] [CrossRef]
- Supplement 3 for Minimum Design Loads and Associated Criteria for Buildings and Other Structures (ASCE/SEI 7-22). In Minimum Design Loads and Associated Criteria for Buildings and Other Structures; ASCE: Reston, VA, USA, 2021.
- Arzola, I.; Carlos, J.; Fortunio, C.; Energies, C. Manual de Diseño de Obras Civiles—Diseño Por Sismo CFE-IIE Versión; ResearchGate: London, UK, 2015; Volume 1. [Google Scholar]
- Asgarian, B.; Nojoumi, R.M.; Alanjari, P. Performance-Based Evaluation of Tall Buildings Using Advanced Intensity Measures (Case Study: 30-Story Steel Structure with Framed-Tube System). Struct. Des. Tall Spec. Build. 2014, 23, 81–93. [Google Scholar] [CrossRef]
- Baker, J.W.; Cornell, C.A. A Vector-Valued Ground Motion Intensity Measure Consisting of Spectral Acceleration and Epsilon. Earthq. Eng. Struct. Dyn. 2005, 34, 1193–1217. [Google Scholar] [CrossRef]
- Bojórquez, E.; Ruiz, S.E.; Rodríguez-Castellanos, A.; Orellana, M.A.; Reyes-Salazar, A.; Bojórquez, J. Bayesian Analysis-Based Ground Motion Prediction Equations for Earthquake Input Energy. Soil Dyn. Earthq. Eng. 2023, 173, 108115. [Google Scholar] [CrossRef]
- Grigoriu, M. Do Seismic Intensity Measures (IMs) Measure Up? Probabilistic Eng. Mech. 2016, 46, 80–93. [Google Scholar] [CrossRef]
- Kostinakis, K.; Fontara, I.K.; Athanatopoulou, A.M. Scalar Structure-Specific Ground Motion Intensity Measures for Assessing the Seismic Performance of Structures: A Review. J. Earthq. Eng. 2018, 22, 630–665. [Google Scholar] [CrossRef]
- Zaker Esteghamati, M.; Huang, Q. Evaluating the Impact of Higher-Mode and Inelastic Dynamic Responses of Concrete Frames on the Performance of Seismic Intensity Measures. Structures 2023, 56, 105029. [Google Scholar] [CrossRef]
- Bojórquez, E.; Iervolino, I. Spectral Shape Proxies and Nonlinear Structural Response. Soil Dyn. Earthq. Eng. 2011, 31, 996–1008. [Google Scholar] [CrossRef]
- Baker, J.W.; Cornell, C.A. Vector-Valued Intensity Measures Incorporating Spectral Shape for Prediction of Structural Response. J. Earthq. Eng. 2008, 12, 534–554. [Google Scholar] [CrossRef]
- Bojórquez, E.; Carvajal, J.; Ruiz, S.E.; Bojórquez, J. Reliability-Based Ductility Reduction Factors Surfaces Using the Generalized Bojorquez Ground Motion Intensity Measure IBg. Results Eng. 2024, 23, 102756. [Google Scholar] [CrossRef]
- Cordova, P.; Deierlein, G.; Mehanny, S.S.F.; Cornell, C.A. Development of A Two-Parameter Seismic Intensity Measure and Probabilistic Assessment Procedure. In Proceedings of the Second US-Japan Workshop on Performance-Based Earthquake Engineering Methodology for Reinforced Concrete Building Structures, Berkeley, CA, USA, 11–13 September 2000. [Google Scholar]
- Eads, L.; Miranda, E.; Lignos, D.G. Average Spectral Acceleration as an Intensity Measure for Collapse Risk Assessment. Earthq. Eng. Struct. Dyn. 2015, 44, 2057–2073. [Google Scholar] [CrossRef]
- Buratti, N. A Comparison of the Performances of Various Ground–Motion Intensity Measures. In Proceedings of the 15th World Conference on Earthquake Engineering, Lisbon, Portugal, 24–28 September 2012. [Google Scholar]
- Chen, Z.; Sun, X.; Feng, D.C.; Wu, G. Selection of Optimal Vector-Valued Seismic Intensity Measures for Fragility Analysis of Self-Centering Prestressed RC Structures. Bull. Earthq. Eng. 2024, 22, 1515–1538. [Google Scholar] [CrossRef]
- Javadi, E.; Yakhchalian, M. Selection of Optimal Intensity Measure for Seismic Assessment of Steel Buckling Restrained Braced Frames under Near-Fault Ground Motions. J. Rehabil. Civ. Eng. 2019, 7, 16. [Google Scholar] [CrossRef]
- Phan, H.N.; Paolacci, F.; Nguyen, V.M.; Hoang, P.H. Ground Motion Intensity Measures for Seismic Vulnerability Assessment of Steel Storage Tanks with Unanchored Support Conditions. J. Press. Vessel. Technol. Trans. ASME 2021, 143, 061904. [Google Scholar] [CrossRef]
- Rajabnejad, H.; Hamidi, H.; Naseri, S.A.; Abbaszadeh, M.A. Effect of Intensity Measure on the Response of a 3D-Structure under Different Ground Motion Duration. Int. J. Eng. Trans. B Appl. 2021, 34, 2219–2237. [Google Scholar] [CrossRef]
- Bojórquez, E.; Leyva, H.; Bojórquez, J.; Reyes-Salazar, A.; Mollaioli, F.; Barraza, M.; Torres, I. Optimal Acceleration and Energy-Based Record Selection Using Artificial Intelligence Approaches and NP. J. Earthq. Eng. 2023, 28, 582–601. [Google Scholar] [CrossRef]
- Modica, A.; Stafford, P.J. Vector Fragility Surfaces for Reinforced Concrete Frames in Europe. Bull. Earthq. Eng. 2014, 12, 1725–1753. [Google Scholar] [CrossRef]
- De Biasio, M.; Grange, S.; Dufour, F.; Allain, F.; Petre-Lazar, I. A Simple and Efficient Intensity Measure to Account for Nonlinear Structural Behavior. Earthq. Spectra 2014, 30, 1403–1426. [Google Scholar] [CrossRef]
- Tsioulou, A.; Galasso, C. Information Theory Measures for the Engineering Validation of Ground-Motion Simulations. Earthq. Eng. Struct. Dyn. 2018, 47, 1095–1104. [Google Scholar] [CrossRef]
- Kadas, K.; Yakut, A. Regression-Based Evaluation of Novel Intensity Measures under Alternative Ground Motion Record Sets. J. Phys. Conf. Ser. 2024, 2647, 252004. [Google Scholar] [CrossRef]
- Abrahamson, N.; Atkinson, G.; Boore, D.; Bozorgnia, Y.; Campbell, K.; Chiou, B.; Idriss, I.M.; Silva, W.; Youngs, R. Comparisons of the NGA Ground-Motion Relations. Earthq. Spectra 2008, 24, 45–66. [Google Scholar] [CrossRef]
- Arroyo, D.; García, D.; Ordaz, M.; Mora, M.A.; Singh, S.K. Strong Ground-Motion Relations for Mexican Interplate Earthquakes. J. Seismol. 2010, 14, 769–785. [Google Scholar] [CrossRef]
- Boore, D.M.; Joyner, W.B.; Fumal, T.E. Estimation of Response Spectra and Peak Accelerations from Western North American Earthquakes: An Interim Report; U.S. Geological Survey: Reston, VA, USA, 1993.
- Campbell, K.W.; Bozorgnia, Y. NGA-West2 Ground Motion Model for the Average Horizontal Components of PGA, PGV, and 5% Damped Linear Acceleration Response Spectra. Earthq. Spectra 2014, 30, 1087–1115. [Google Scholar] [CrossRef]
- Dávalos, H.; Miranda, E. A Ground Motion Prediction Model for Average Spectral Acceleration. J. Earthq. Eng. 2021, 25, 319–342. [Google Scholar] [CrossRef]
- Jaimes, M.A.; Ramirez-Gaytan, A.; Reinoso, E. Ground-Motion Prediction Model from Intermediate-Depth Intraslab Earthquakes at the Hill and Lake-Bed Zones of Mexico City. J. Earthq. Eng. 2015, 19, 1260–1278. [Google Scholar] [CrossRef]
- Molas, G.L.; Yamazaki, F. Attenuation of Earthquake Ground Motion in Japan Including Deep Focus Events. Bull.-Seismol. Soc. Am. 1995, 85, 1343–1358. [Google Scholar] [CrossRef]
- Ordaz, M.; Reyes, C. Earthquake Hazard in Mexico City: Observations versus Computations. Bull. Seismol. Soc. Am. 1999, 89, 1379–1383. [Google Scholar] [CrossRef]
- Chen, S.; Liu, X.; Fu, L.; Wang, S.; Zhang, B.; Li, X. Physics Symbolic Learner for Discovering Ground-Motion Models via NGA-West2 Database. Earthq. Eng. Struct. Dyn. 2024, 53, 138–151. [Google Scholar] [CrossRef]
- Barbur, V.A.; Montgomery, D.C.; Peck, E.A. Introduction to Linear Regression Analysis. Statistician 1994, 43, 339. [Google Scholar] [CrossRef]
- Guenther, N.; Schonlau, M. Support Vector Machines. Stata J. 2016, 16, 917–937. [Google Scholar] [CrossRef]
- Zhang, F.; O’Donnell, L.J. Support Vector Regression. In Machine Learning: Methods and Applications to Brain Disorders; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Karush, W.; Kuhn, H.W.; Tucker, A.W.; Luptácik, M. Karush–Kuhn–Tucker Conditions. In Mathematical Optimization and Economic Analysis; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-Learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Platt, J.C.; Labs, R. Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines Review. In Advances in Kernel MethodsSupport Vector Learning; MIT Press: Cambridge, MA, USA, 1997; Volume 208. [Google Scholar]
- Giovenale, P.; Cornell, C.A.; Esteva, L. Comparing the Adequacy of Alternative Ground Motion Intensity Measures for the Estimation of Structural Responses. Earthq. Eng. Struct. Dyn. 2004, 33, 951–979. [Google Scholar] [CrossRef]
- Huang, C.; Galasso, C. Ground-Motion Intensity Measure Correlations Observed in Italian Strong-Motion Records. Earthq. Eng. Struct. Dyn. 2019, 48, 1634–1660. [Google Scholar] [CrossRef]
- Auvinet, G.; Juárez, M. Geotechnical Characterization of Mexico City Subsoil. In Proceedings of the 2011 Pan-Am CGS Geotechnical Conference, Toronto, ON, Canada, 2 October 2011. [Google Scholar]
- Singh, S.K.; Cruz-Atienza, V.; Pérez-Campos, X.; Iglesias, A.; Hjörleifsdóttir, V.; Reinoso, E.; Ordaz, M.; Arroyo, D. Deadly Intraslab Mexico Earthquake of 19 September 2017 (Mw 7.1): Ground Motion and Damage Pattern in Mexico City. Seismol. Res. Lett. 2018, 89, 2193–2203. [Google Scholar] [CrossRef]
- Singh, S.K.; Ordaz, M.; Pérez-Campos, X.; Iglesias, A. Intraslab versus Interplate Earthquakes as Recorded in Mexico City: Implications for Seismic Hazard. Earthq. Spectra 2015, 31, 795–812. [Google Scholar] [CrossRef]
- Jaimes, M.A.; Reinoso, E.; Ordaz, M. Comparison of Methods to Predict Response Spectra at Instrumented Sites given the Magnitude and Distance of an Earthquake. J. Earthq. Eng. 2006, 10, 887–902. [Google Scholar] [CrossRef]
- Ordaz, M.; Singh, S.K.; Arciniega, A. Bayesian Attenuation Regressions: An Application to Mexico City. Geophys. J. Int. 1994, 117, 335–344. [Google Scholar] [CrossRef]
- Lermo, J.; Santoyo, M.A.; Jaimes, M.A.; Antayhua, Y.; Chavacán, M. Local Earthquakes of the Mexico Basin in Mexico City: κ, Q, Source Spectra, and Stress Drop. Bull. Seismol. Soc. Am. 2016, 106, 1423–1437. [Google Scholar] [CrossRef]

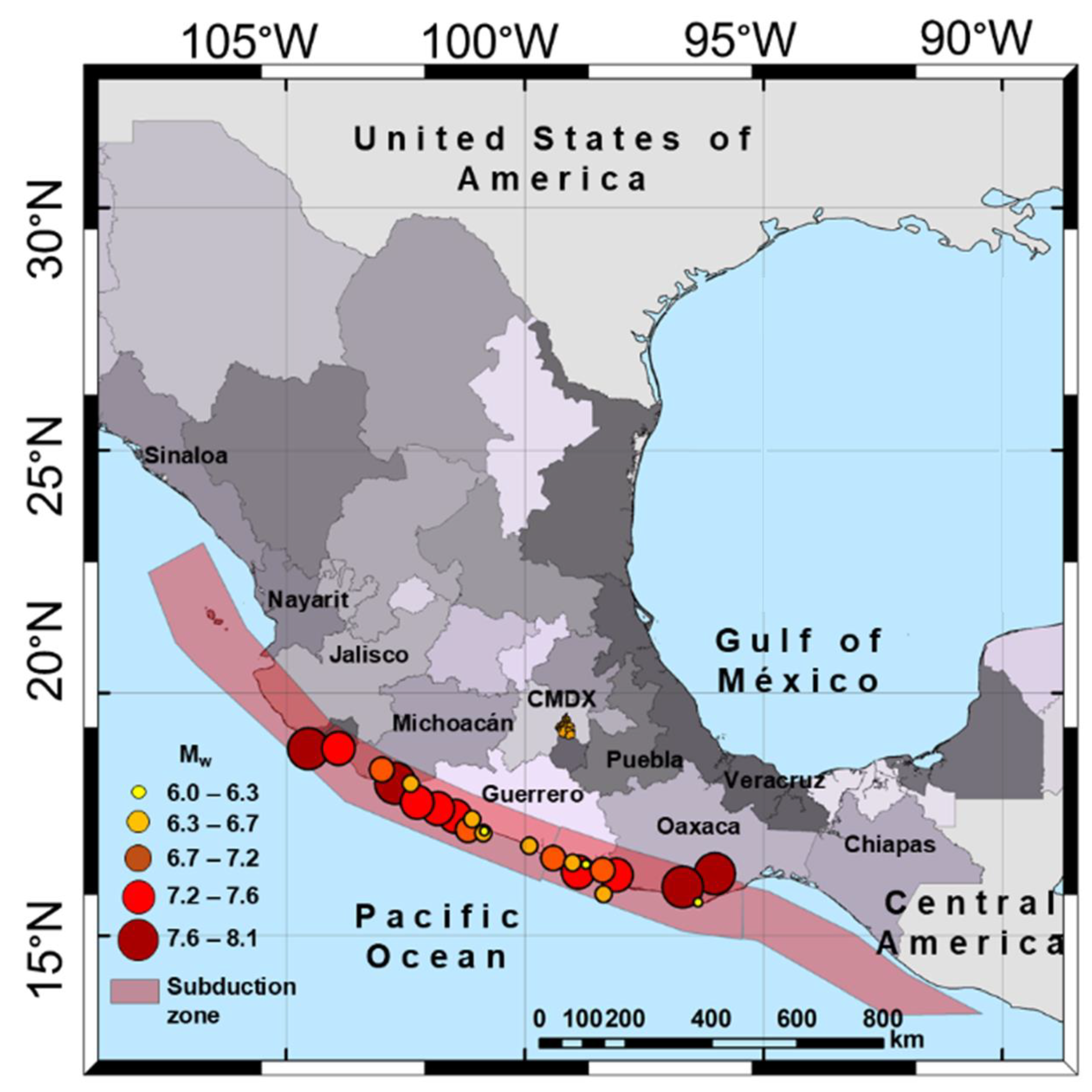
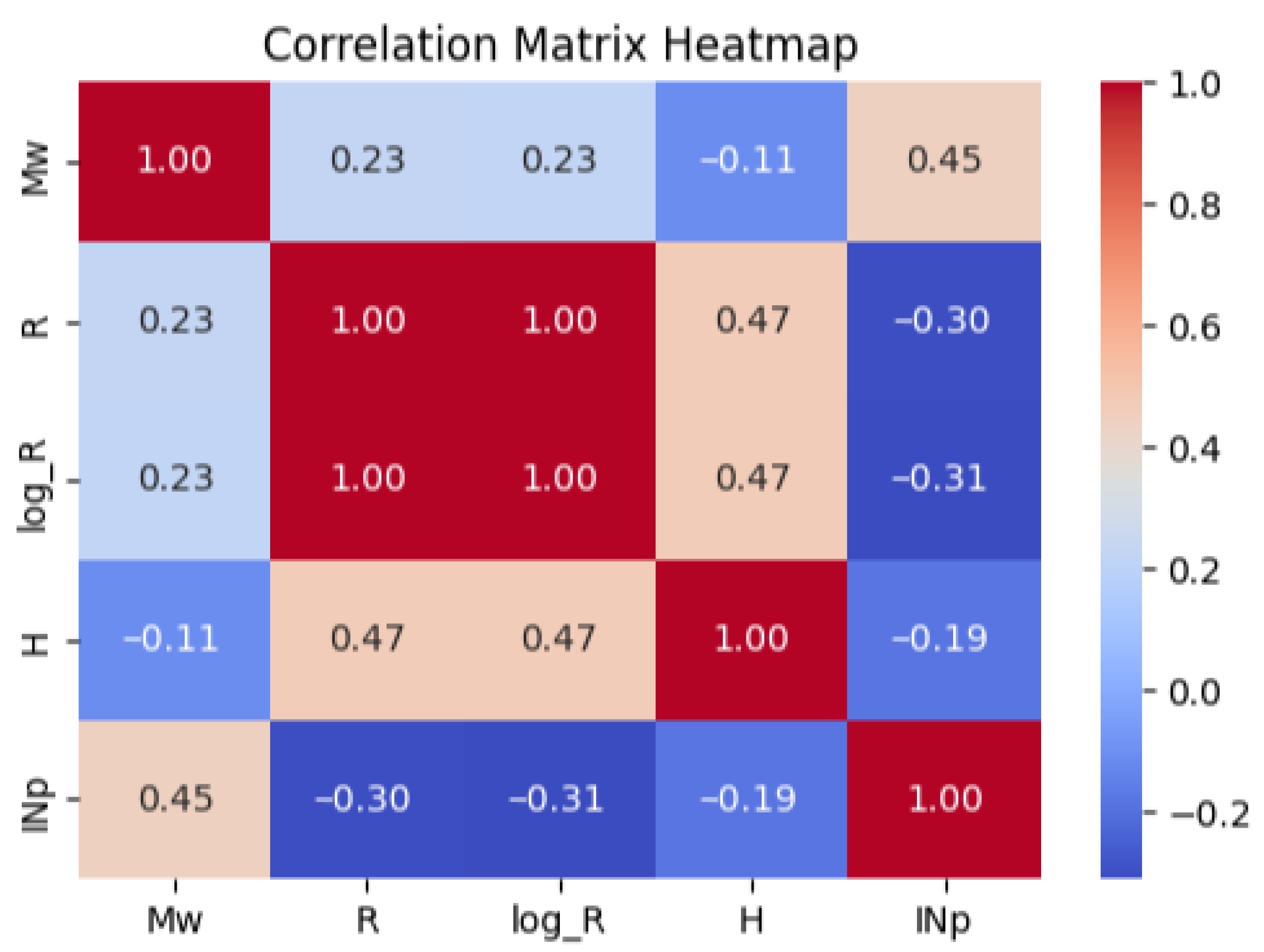

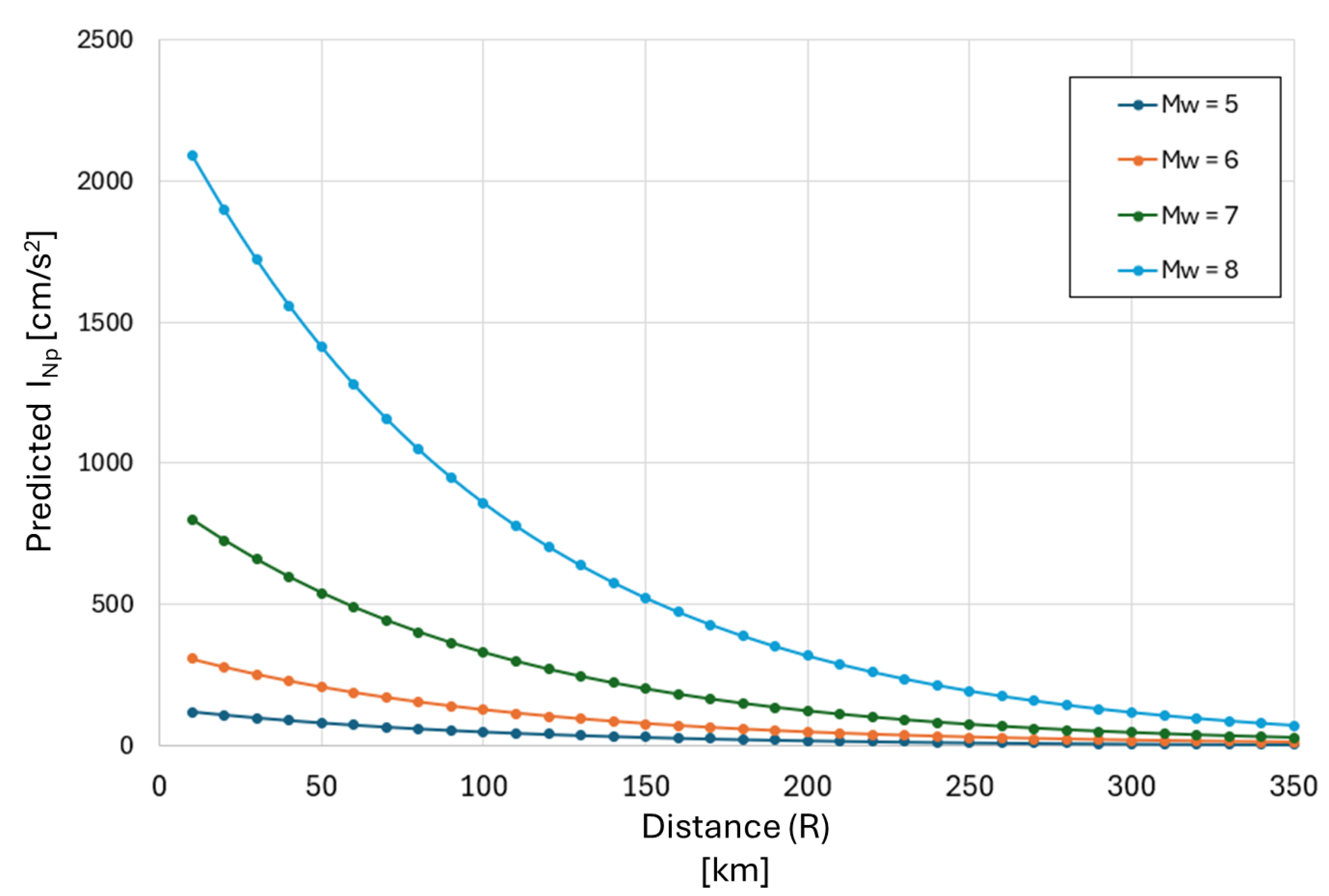
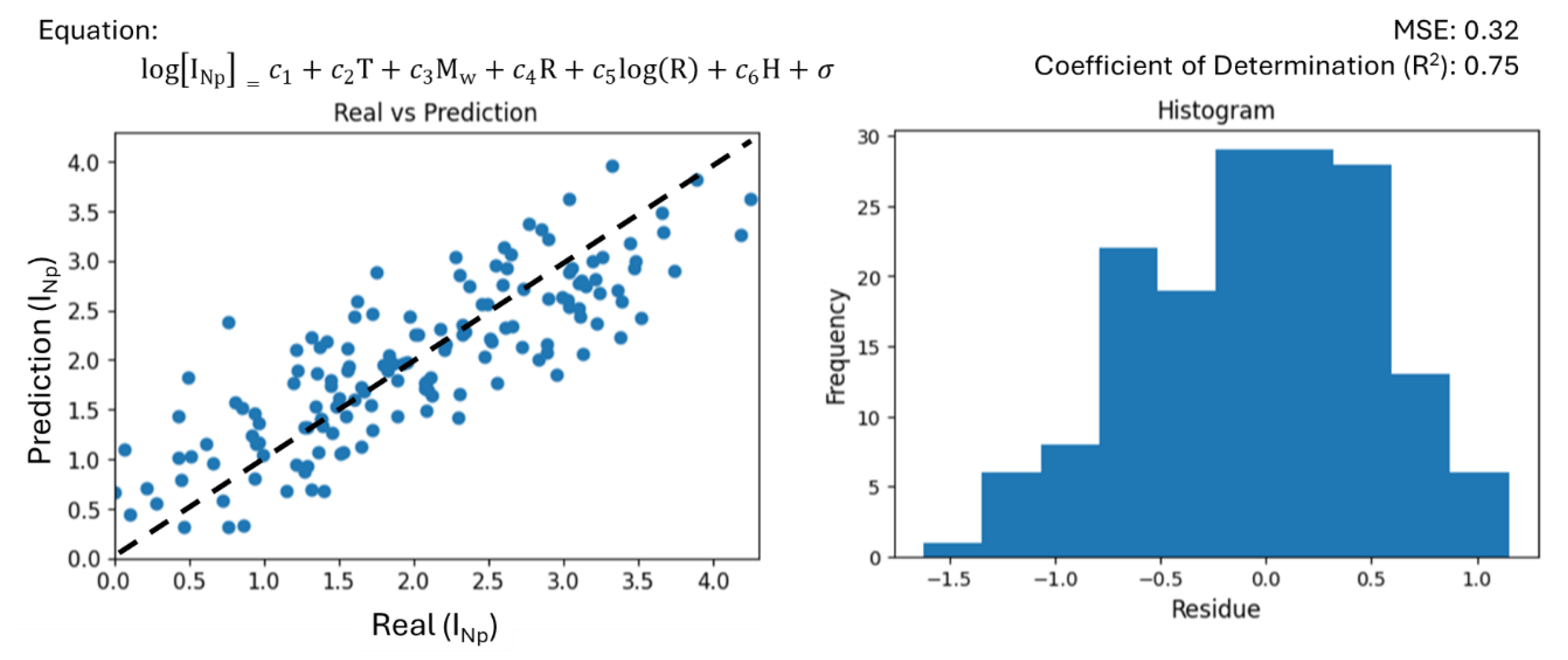
| ID | Date | R (km) | H (km) | ID | Date | R (km) | H (km) | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 23 August 1965 | 7.8 | 466 | 16 | 13 | 31 May 1990 | 6.1 | 304 | 21 |
| 2 | 2 August 1968 | 7.4 | 326 | 33 | 14 | 15 May 1993 | 6.0 | 320 | 20 |
| 3 | 19 March 1978 | 6.4 | 285 | 16 | 15 | 24 October 1993 | 6.7 | 310 | 19 |
| 4 | 29 November 1978 | 7.8 | 414 | 19 | 16 | 14 September 1995 | 7.3 | 320 | 22 |
| 5 | 14 March 1979 | 7.6 | 287 | 20 | 17 | 9 October 1995 | 8.0 | 530 | 27 |
| 6 | 25 October 1981 | 7.3 | 330 | 20 | 18 | 15 July 1996 | 6.6 | 301 | 20 |
| 7 | 7 June 1982 | 6.9 | 304 | 15 | 19 | 19 July1997 | 6.7 | 394 | 15 |
| 8 | 7 June 1982 | 7.0 | 303 | 15 | 20 | 3 February 1998 | 6.3 | 509 | 33 |
| 9 | 19 September 1985 | 8.1 | 295 | 15 | 21 | 9 August 2000 | 6.5 | 380 | 33 |
| 10 | 21 September 1985 | 7.6 | 318 | 15 | 22 | 20 March 2012 | 7.4 | 329 | 16 |
| 11 | 30 April 1986 | 7.0 | 409 | 16 | 23 | 18 April 2014 | 7.2 | 304 | 10 |
| 12 | 25 April 1989 | 6.9 | 290 | 19 | 24 | 8 May 2014 | 6.4 | 398 | 17 |
| Index | Period T (s) | Magnitude | Distance | Depth | INp (cm/s2) | ||
|---|---|---|---|---|---|---|---|
(km) | (km) | ||||||
| 0 | 0.1 | 7.8 | 466 | 6.144186 | 16 | 5.613024 | 1.72509 |
| 1 | 0.11 | 7.8 | 466 | 6.144186 | 16 | 5.888786 | 1.77305 |
| 2 | 0.12 | 7.8 | 466 | 6.144186 | 16 | 6.236613 | 1.830437 |
| ... | ... | ... | ... | ... | ... | ... | ... |
| 11,290 | 4.98 | 6.4 | 298 | 5.697093 | 17 | 1.406041 | 0.340778 |
| 11,291 | 4.99 | 6.4 | 298 | 5.697093 | 17 | 1.389247 | 0.328762 |
| 11,292 | 5 | 6.4 | 298 | 5.697093 | 17 | 1.330535 | 0.285581 |
| T | MSE | R2 | Intercept | Coef Mw | Coef R | Coef log(R) | Coef H | Std Dev |
|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.08 | 0.85 | −0.50 | 0.86 | −0.01 | 0.01 | 0.01 | 0.29 |
| 0.2 | 0.11 | 0.82 | −0.24 | 0.91 | −0.01 | 0.04 | 0.00 | 0.33 |
| 0.3 | 0.12 | 0.82 | −0.16 | 0.91 | −0.01 | −0.01 | 0.01 | 0.33 |
| 0.5 | 0.13 | 0.77 | −0.59 | 0.96 | −0.01 | 0.01 | 0.00 | 0.35 |
| 1.0 | 0.11 | 0.81 | −1.49 | 1.02 | −0.01 | 0.01 | 0.01 | 0.32 |
| 2.0 | 0.18 | 0.77 | −2.86 | 1.02 | −0.01 | 0.09 | 0.03 | 0.42 |
| 3.0 | 0.22 | 0.72 | −3.74 | 0.95 | −0.01 | 0.09 | 0.01 | 0.47 |
| 4.0 | 0.29 | 0.61 | −4.54 | 0.94 | 0.00 | 0.07 | 0.00 | 0.54 |
| 5.0 | 0.39 | 0.52 | −5.05 | 0.92 | 0.00 | 0.05 | 0.00 | 0.62 |
| ID | MSE Training Data | MSE Evaluation Data |
|---|---|---|
| 1 | 0.3450 | 0.3520 |
| 2 | 0.3145 | 0.3235 |
| 3 | 0.3320 | 0.3420 |
| 4 | 0.3214 | 0.3315 |
| 5 | 0.3351 | 0.3452 |
| 6 | 0.3170 | 0.3260 |
| 7 | 0.3443 | 0.3533 |
| 8 | 0.3246 | 0.3335 |
| 9 | 0.3330 | 0.3410 |
| 10 | 0.3302 | 0.3413 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bojórquez, E.; Payán-Serrano, O.; Bojórquez, J.; Rodríguez-Castellanos, A.; Ruiz, S.E.; Reyes-Salazar, A.; Chávez, R.; Leyva, H.; Velarde, F. Support Vector Machines to Propose a Ground Motion Prediction Equation for the Particular Case of the Bojorquez Intensity Measure INp. AI 2025, 6, 254. https://doi.org/10.3390/ai6100254
Bojórquez E, Payán-Serrano O, Bojórquez J, Rodríguez-Castellanos A, Ruiz SE, Reyes-Salazar A, Chávez R, Leyva H, Velarde F. Support Vector Machines to Propose a Ground Motion Prediction Equation for the Particular Case of the Bojorquez Intensity Measure INp. AI. 2025; 6(10):254. https://doi.org/10.3390/ai6100254
Chicago/Turabian StyleBojórquez, Edén, Omar Payán-Serrano, Juan Bojórquez, Ali Rodríguez-Castellanos, Sonia E. Ruiz, Alfredo Reyes-Salazar, Robespierre Chávez, Herian Leyva, and Fernando Velarde. 2025. "Support Vector Machines to Propose a Ground Motion Prediction Equation for the Particular Case of the Bojorquez Intensity Measure INp" AI 6, no. 10: 254. https://doi.org/10.3390/ai6100254
APA StyleBojórquez, E., Payán-Serrano, O., Bojórquez, J., Rodríguez-Castellanos, A., Ruiz, S. E., Reyes-Salazar, A., Chávez, R., Leyva, H., & Velarde, F. (2025). Support Vector Machines to Propose a Ground Motion Prediction Equation for the Particular Case of the Bojorquez Intensity Measure INp. AI, 6(10), 254. https://doi.org/10.3390/ai6100254









