Attention-Based Multi-Agent RL for Multi-Machine Tending Using Mobile Robots

Abstract

Robotics can help address the growing worker shortage challenge of the manufacturing industry. As such, machine tending is a task collaborative robots can tackle that can also greatly boost productivity. Nevertheless, existing robotics systems deployed in that sector rely on a fixed single-arm setup, whereas mobile robots can provide more flexibility and scalability. We introduce a multi-agent multi-machine-tending learning framework using mobile robots based on multi-agent reinforcement learning (MARL) techniques, with the design of a suitable observation and reward. Moreover, we integrate an attention-based encoding mechanism into the Multi-Agent Proximal Policy Optimization (MAPPO) algorithm to boost its performance for machine-tending scenarios. Our model (AB-MAPPO) outperforms MAPPO in this new challenging scenario in terms of task success, safety, and resource utilization. Furthermore, we provided an extensive ablation study to support our design decisions.

1. Introduction

The manufacturing industry is increasingly turning to robotic automation to mitigate workforce shortages and enhance operational efficiency [1]. Among the most common applications is machine tending, which involves automating the loading and unloading of parts from production machines [2]. Traditionally, this task relies on fixed robotic systems, where dedicated robotic arms serve individual machines. While effective, fixed setups lack flexibility and often require continuous human oversight, limiting scalability in dynamic production environments.

A more adaptable solution involves mobile manipulators that can autonomously navigate between multiple machines and storage areas, maximizing resource utilization and improving overall productivity. However, deploying a fleet of mobile robots introduces complex challenges in coordination and control. Current industry solutions, such as Amazon’s warehouse automation, employ a centralized control model, where a single server orchestrates task assignment, trajectory planning, and collision avoidance. While this approach ensures optimized fleet operations, it presents several drawbacks, including single points of failure, high communication overhead, and limited adaptability in unstructured environments [3].

An alternative approach is decentralized multi-agent control, where robots make local, independent decisions based on their surroundings. However, it also comes with its own challenges in terms of partial observability (the agent may not be able to observe the full environment state) and non-stationarity (as the change in the environment state also depends on the other agent’s actions) [4]. Reinforcement learning (RL) offers a promising framework for such autonomous decision-making, leveraging trial-and-error learning to refine robot behaviors [5]. Recent advances in deep reinforcement learning (DRL), supported by powerful GPU-based computation, have further enhanced the feasibility of RL-based autonomous control.

Despite its potential, most multi-agent reinforcement learning (MARL) research has focused on simulated environments, such as Starcraft Multi-Agent Challenge (SMAC) [6,7], Soccer [8], and simplified coordination tasks like goal coverage and formation control [9,10,11]. These scenarios, while valuable for theoretical exploration, fail to capture the real-world complexities of deployable multi-robot systems in industrial applications.

Motivated by the huge advancements and potential of artificial intelligence and data-driven techniques, this paper presents a novel reinforcement learning model tailored to a realistic manufacturing scenario, where decentralized mobile robots autonomously manage both task assignment and navigation for machine tending. In short, our main contributions are as follows:

• Address a realistic machine-tending scenario with decentralized execution, part picking, and delivery;
• Design a novel dense reward function specifically for this scenario;
• Design an attention-based encoding technique and incorporate it into a working new model (AB-MAPPO).

Finally, we also provide an ablation study in the additional material to verify the effect of various design decisions.

The rest of the paper is organized as follows: the next section (Section 2: Background and Related Work) covers related works on machine tending in general and more specifically on the use of reinforcement learning for machine tending. Then, the problem of multi-agent, multi-machine tending is formally defined in Section 3: Problem Definition, followed by Section 4 detailing the methodology implemented in this research. Section 5 describes the details of the experimental setup, conducted experiments, and obtained results. An ablation study for observation and reward design is reported in Section 6, followed by the conclusion and possible future directions of the study.

2. Background and Related Work

2.1. Machine Tending

Despite substantial research and development efforts in both academia and industry [12], the gap between automation demands and the available commercial products is still wide and requires further work to be reduced.

Due to the complexity of the machine-tending problem, different researchers focused on different specific areas. For instance, Jia et al. [13] focused on recognizing the state of the machine by first detecting a specific computer numerical control (CNC) machine and then using text detection and recognition techniques to obtain the status from its display.

Al-Hussaini et al. [14] developed a semi-autonomous mobile manipulator that, given a task from the operator, generates the execution plan. It also estimates the risk of the plan execution and provides a simulation of the plan for the operator to approve it to be executed autonomously or to teleoperate the robot. In addition, Heimann et al. [2] presented an ROS2-based mobile manipulator solution with a focus on evaluating the system precision in reaching the machine location and reaching inside the machine. Moreover, Chen et al. [15] proposed a centralized method for multi-agent task assignment and path planning, where task assignment is informed by the task completion cost. Behbahani et al. [16] used a learning-from-demonstration approach to teach a physical fixed robot to tend to one machine in a simplified tabletop setup.

In a different direction, Burgess-Limerick et al. [17] developed a controller to allow a mobile manipulator to perform a pick-and-place task on the move in a dynamic environment, reducing the overall task execution time.

2.2. RL for Machine Tending

RL has been explored for various robotic tasks such as pick and place, navigation, collision avoidance, locomotion, and quadcopter control [5,18,19]. However, RL for machine tending is not a well-explored area of research, except for some works such as [20], where they used Proximal Policy Optimization (PPO) [21] and Deep Deterministic Policy Gradient (DDPG) [22] to teach a single mobile manipulator to navigate to the location of a table that has the object to pick. Despite targeting a one-agent and one-machine setup, their work is still far from being deployable in reality because it does not address part dropping, learning to navigate when the part is ready, or navigating multiple times to pick and place multiple parts.

On the other hand, multi-agent reinforcement learning (MARL) is a growing research area that focuses on extending RL to multi-agent setups to expand its potential use. Two notable works in this area are Multi-agent Proximal Policy Optimization (MAPPO) [23] and Multi-Agent Deep Deterministic Policy Gradient (MADDPG) [24], which extended PPO and Deep Deterministic Policy Gradient (DDPG), respectively. Further works have extended MARL techniques by integrating the attention mechanism [25] to enhance performance [26,27]. However, to the best of our knowledge, one of the only works presenting a MARL solution for machine tending is [28]. This pioneering work introduces a multi-agent framework for integrated job scheduling and navigation for shop floor management, exhibiting robustness under processing delays and failures. However, their implementation assumes the agents can accumulate parts from various machines without unloading them, as if they had infinite onboard storage, making the solution non-deployable in the real world. They also depend on a central server for communication and marginal control.

Distinct from prior models, our work addresses multi-agent, multi-machine tending by encompassing task assignment, the navigation to machines with ready parts, and transporting these parts to designated storage areas. This approach more realistically reflects real-world manufacturing scenarios, pushing MARL closer to full deployment on machine-tending tasks. Moreover, our work can be integrated with low-level controllers like [17] to facilitate actual deployment in real robots.

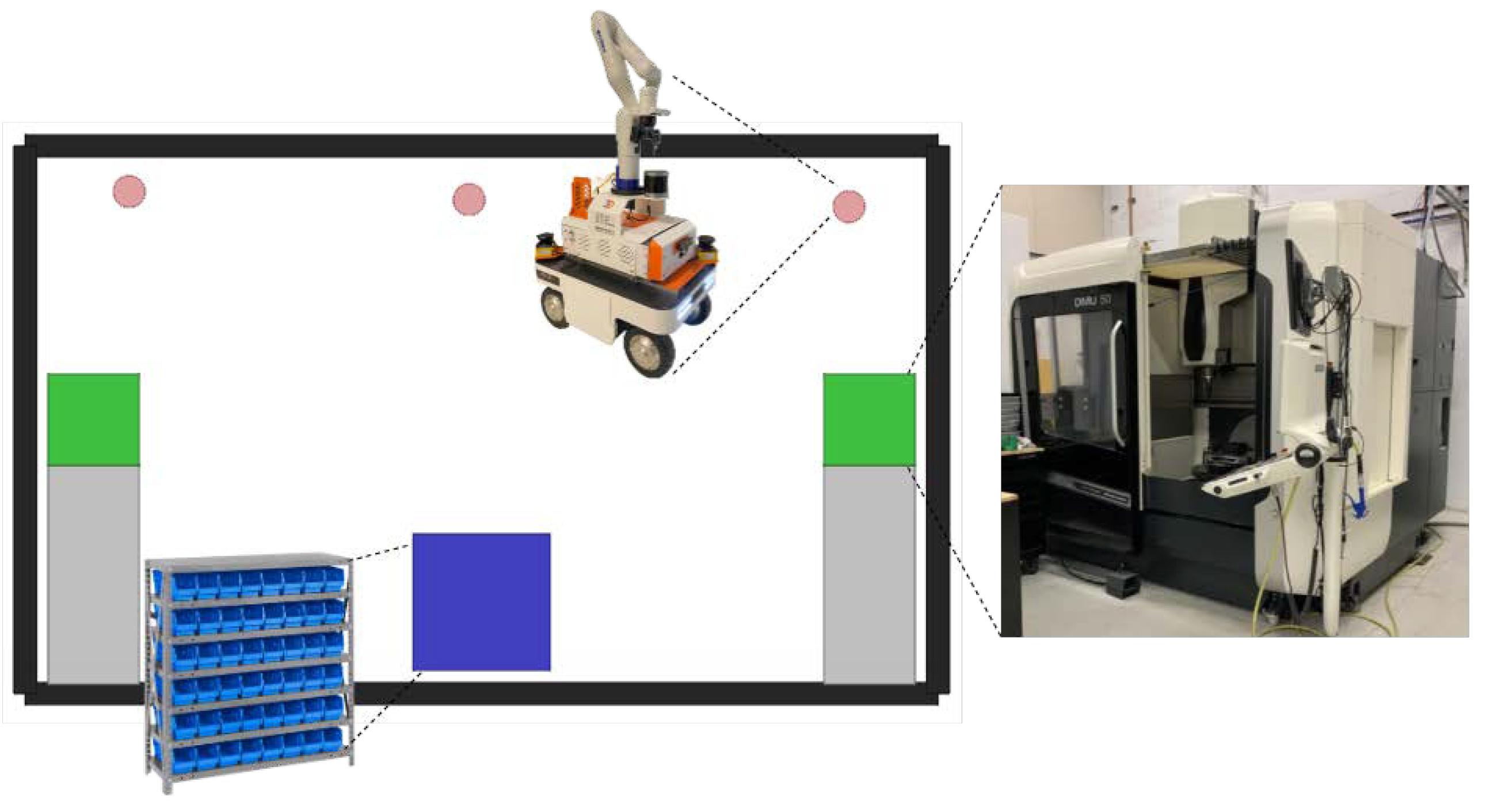
3. Problem Definition

The multi-agent, multi-machine-tending problem involves coordination, navigation, and object manipulation, where N agents service M machines, managing tasks from feeding raw materials to delivering finished parts to storage. The problem’s constraints include the following:

• Coordination: Agents autonomously determine their targets to optimize machine usage and minimize collision risks.
• Navigation: Agents must navigate efficiently to and from machines, while maintaining safety by avoiding collisions with other agents and static obstacles while transporting parts to the storage area.
• Cooperative–Competitive Dynamics: Agents compete for parts; the first to arrive at a machine can claim the part, requiring others to wait for the next availability.
• Temporal Reasoning: Agents must sequence their actions correctly, ensuring machines are fed or parts are collected and delivered at appropriate times.

More formally, we assume a team of N robots $\{R_i$, $i\in \{0,1,\dots ,N-1\}\}$, moving in an ${\mathbb{R}}^2$ space, with respect to a fixed global frame ${\varphi }_{xy}^g$. Each robot position can be expressed by $P_{A_i}\left(t\right)=[x_{A_i}\left(t\right),y_{A_i}\left(t\right)]\in {\mathbb{R}}^2$. The robots are tending to M machines $\{M_j, j\in \{0,1,\dots ,M-1\}\}$, with fixed positions $P_{M_j}=[x_{M_j}, y_{M_j}]\in {\mathbb{R}}^2$ for a time horizon of H time steps. At any given time step t, there will be K machines with ready parts ($0<=K<=M$) and L robots available for picking parts (robots have a limited capacity of one part at a time). Once a part is collected from a machine, there is a production delay of P time steps before it can produce another part, and when a robot delivers a part, it will be directly available for picking another. We define coordination as the L robots independently assigning themselves to the K machines. Navigation is defined as taking a collision-free path from robot i’s current position ($P_{A_i}$) to the position of the selected ready machine j ($P_{M_j}$). Cooperative–competitive refers to the competition cases where $L>K$. On the other hand, temporal reasoning refers to the logical sequential order of events. For example, if a machine produced a part at time step p, then a robot can collect it at time step c where $p+1<=c<=H$.

Object manipulation is acknowledged but not addressed in this study, focusing on the four constraints mentioned above. Key assumptions include instantaneous pick-and-place actions (as supported by prior studies [17]) and external management of raw material supply.

4. Methodology

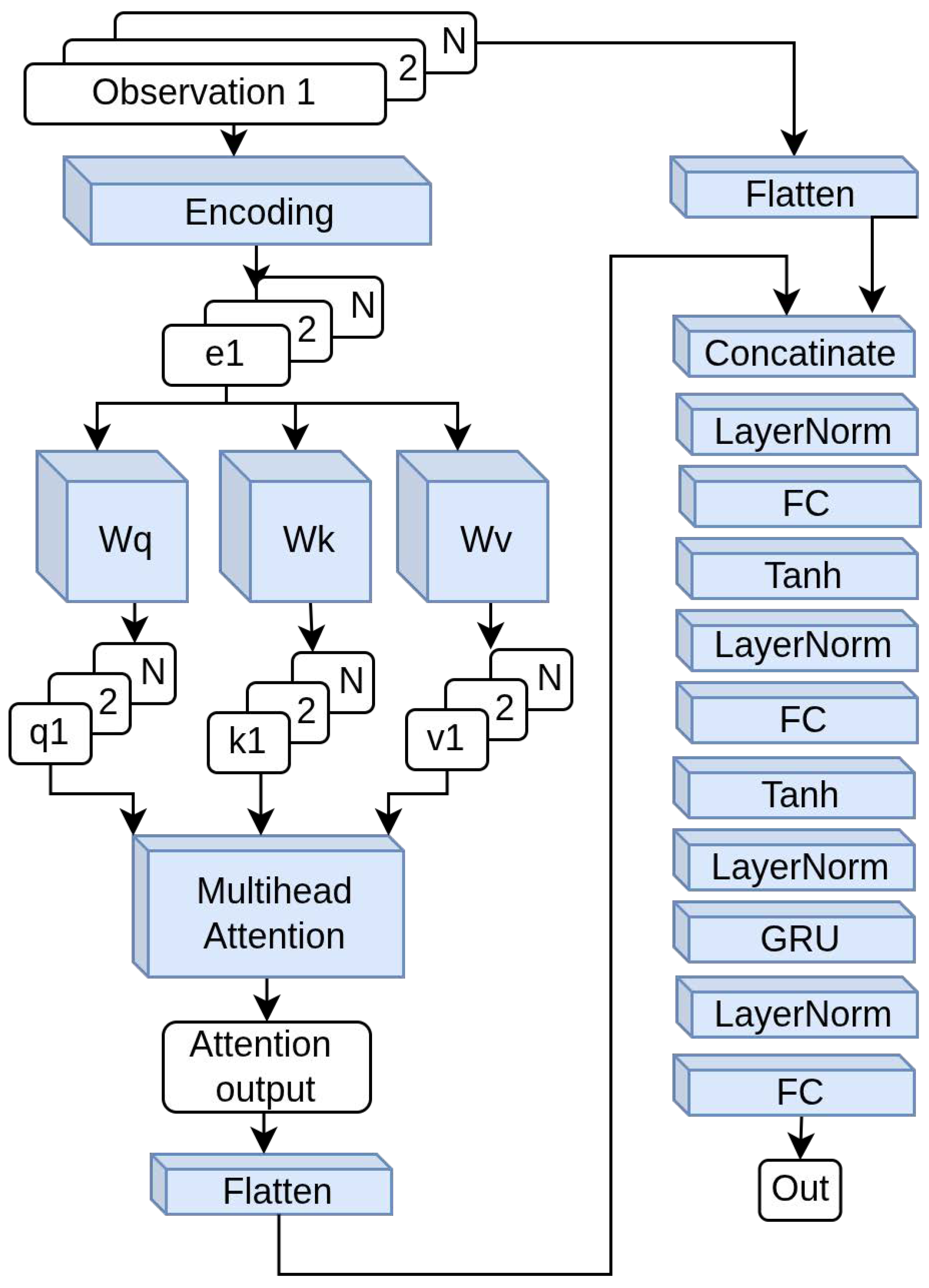
4.1. MAPPO Backbone

MAPPO, a prominent multi-agent reinforcement learning algorithm introduced by Yu et al. [23], operates on a dual-network architecture comprising an actor and a critic. The actor network, or policy, executes actions aimed at maximizing accumulated discounted rewards. The critic provides an estimate of the value of the current state, to be used for variance reduction.

This algorithm is designed for a decentralized partially observable Markov decision process (DEC-POMDP), characterized by the number of agents (n); the global state space ($\mathcal{S}$); the local observation space for agents ($\mathcal{O}$), with each agent i having a local observation $o_i$ derived from the global state s; the action space ($\mathcal{A}$), where each agent acts according to a policy ${\pi }_{\theta }\left(o_i\right)$, with $\theta$ representing the learnable parameters of the policy; the probability of transitioning from state s to state $\acute{s}$ given the joint actions $A=(a_1,a_2,\dots ,a_n)$ of the agents ($\mathcal{P}\left(\acute{s}\right|s, A)$); and the shared reward function for the joint actions of the agents ($R(s,A)$). MAPPO’s objective is to maximize the expected sum of discounted rewards, formulated as follows:

$$J\left(\theta \right)={\mathbb{E}}_{A^t,s^t}[\sum _t{\gamma }^{t}R(s^t,A^t)]$$

(1)

where $\gamma$ is the discount factor that prioritizes immediate rewards over future ones.

The algorithm employs a centralized training but decentralized execution (CTDE) approach, where the critic, accessible only during training, utilizes global information across all agents. In contrast, the actor operates solely on local observations during both training and execution phases.

In our implementation, given that our agents are homogeneous, we adopt parameter-sharing to streamline the learning process. However, our scenario deviates from standard MAPPO applications as it encompasses both cooperative and competitive elements. Thus, we have explored strategies involving both individual rewards and shared rewards to accommodate the competitive dynamics among agents.

4.2. Novel Attention-Based Encoding for MAPPO

We introduce AB-MAPPO, an upgraded MAPPO architecture with the integration of a novel attention-based encoding mechanism, into the critic network. This enhancement allows the actor to make decisions based on more accurately estimated values from the critic, thereby improving its performance indirectly as well. Figure 1 illustrates the design of our attention-based encoding mechanism for the critic. The left part of the figure depicts the main novelty in this architecture (observation splitting by agent, agent observation encoding and projection, multi-head attention between encoded agents’ observations, and finally concatenation with the original observation). This design enables the critic to leverage all agents’ observations to develop a representation that encapsulates both spatial and temporal dynamics effectively.

Spatial information is captured through encoding and multi-head attention mechanisms. Temporal information is processed using a Gated Recurrent Unit (GRU). Initially, each agent’s observation $o_i$ is transformed into an encoded vector $e_i$ using shared learnable parameters $W_e$ and $b_e$, ($e_i=W_e\ast o_i+b_e$). Then, each encoded vector $e_i$ is mapped to three vectors: query ($q_i=W_q\ast e_i$), key ($k_i=W_k\ast e_i$), and value ($v_i=W_v\ast e_i$), where $W_q$, $W_k$, and $W_v$, are learnable parameters.

The query vectors of all agents are stacked together to build one query, and the same is performed for the keys and value vectors.

$$\begin{array}{cc}\hfill Q& =stack(q_1,q_2,\dots ,q_N)\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill K& =stack(k_1,k_2,\dots ,k_N)\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill V& =stack(v_1,v_2,\dots ,v_N)\hfill \end{array}$$

(4)

These vectors are subsequently processed by a multi-head attention module, which learns the inter-agent attention dynamics. The output from the multi-head attention module, based on the seminal paper by Vaswani et al. [25], is computed as follows:

$$\begin{array}{cc}\hfill M_{out}& =Concat(hea{d}_1,\dots ,hea{d}_H)W^o\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill hea{d}_j& =Attention(Q{W}_j^Q,K{W}_j^K,V{W}_j^V)\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill Attention(Q,K,V)& =softmax(Q{K}^T/\sqrt{d_k})V\hfill \end{array}$$

(7)

where $W^o,W^Q,W^K$, and $W^V$ are learnable parameters, and H represents the number of heads used (in this case, three). The matrix $Q{K}^T$ captures the relevance scores (the degree to which each agent’s updated observation representation should attend to the observations of all agents, including its own). Then, those scores are scaled by $d_k$ (the key vector dimension) and normalized by a softmax function to produce the attention weights. Those weights are used to form a weighted combination of the agents’ value representations V. This allows each agent’s observation to selectively integrate information from all agents, including itself, based on contextual importance.

The attention module’s output is then flattened and concatenated with the original observation and passed through a sequence of fully connected layers (FCs), normalization (Norm), a GRU, and a final FC layer to produce the value estimate. This series of layers’ configuration follows a standard, open-source implementation of MAPPO. For the actor, we retained the standard configuration, which includes a similar series of FCs, Norms, and a GRU layer, differing only in the final output layer, which matches the number of possible actions.

4.3. Observation Design

In addressing the multi-agent, multi-machine-tending problem, designing an efficient observation scheme that captures essential information while excluding superfluous details was crucial. After extensive empirical testing to determine the optimal data inclusion by trying different observation options (more about it in Section 6), each agent’s observation was crafted to include the following:

• The agent’s absolute position and a “has part” flag indicating whether it has picked up a part but not yet placed it.
• The relative positions of each machine, accompanied by a flag indicating the readiness of a part at each location.
• The relative position of the storage area.
• The relative positions of other agents, along with their respective “has part” flags.

All positional data represent the central point of entities, normalized to scale values between 0 and 1 to facilitate processing.

4.4. Reward Design

Inspired by the rewards used typically in navigation tasks to encourage reaching a specific goal while avoiding collisions [29], we tailored our reward structure to enhance navigation and efficiency specifically for machine-tending tasks:

1. Base Rewards:

• Pick Reward ($R_{pi}$): Granted when an agent without a part reaches a machine with a ready part.
• Place Reward ($R_{pl}$): Awarded when an agent with a part reaches the storage area to place the part.
• Collision Penalty ($R_c$): Incurred upon collision with agents, walls, machines, or the storage area.

2. Distance-based Rewards:

• Progress towards the closest machine with a ready part ($R_{pm}$) and the storage area ($R_{ps}$) is rewarded to provide continuous feedback. The rewards are calculated based on the reduction in distance to the target ($d_m^t$) between consecutive steps, scaled by a factor ($pr$).

  $$R_{pm}^t=\left\{\begin{array}{cc}pr\ast (d_m^{t-1}-d_m^t)\hfill & \mathrm{if}\mathrm{the}\mathrm{agent}\mathrm{has}\mathrm{no}\mathrm{part}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

  (8)

  $$R_{ps}^t=\left\{\begin{array}{cc}pr\ast (d_s^{t-1}-d_s^t)\hfill & \mathrm{if}\mathrm{the}\mathrm{agent}\mathrm{has}\mathrm{part}\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

  (9)

3. Utilization Penalty ($R_u$):

• To discourage idle machines, a penalty is applied for uncollected parts ($p_{un}$) at each step, calculated based on the number of steps a part (i) remains uncollected ($n{s}_i$) multiplied by a scaling factor (u).

  $$R_u=\left\{\begin{array}{cc}{p}_{un}\ast u\hfill & \mathrm{if}\mathrm{fixed}\mathrm{uncollected}\mathrm{penalty}\hfill \\ \sum n{s}_i\ast u\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

  (10)

4. Time Penalty ($R_t$):

• Imposed to encourage movement, particularly when no other rewards or penalties are being applied.

  $$R_t=\left\{\begin{array}{cc}tp\hfill & \mathrm{if}{R}_{pi},R_{pl},\mathrm{and}{R}_u\mathrm{are}0\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

  (11)

The cumulative reward for an agent is the sum of all the above components:

$$R_T=R_{pi}+R_{pl}+R_c+R_{pm}+R_{ps}+R_u+R_t$$

(12)

The reader can refer to

Table A1. Model and training parameters.

Parameter	Value
Reward Sharing	False
Pick Reward	15
Place Reward	30
Collision Penalty	−10
Distance Rewards Scale	10
Fixed Uncollected Parts Penalty	True
Uncollected Penalty	−1
Time Penalty	−0.01
Encoding vector Size	18
Object embedding Size	18
Number of Attention Heads	3
Attention Embedding Size	18
Learning Rate	7 × ${10}^{-4}$
Optimizer	Adam

in Appendix A for the details of the reward terms’ values and scaling factors.

5. Experiments

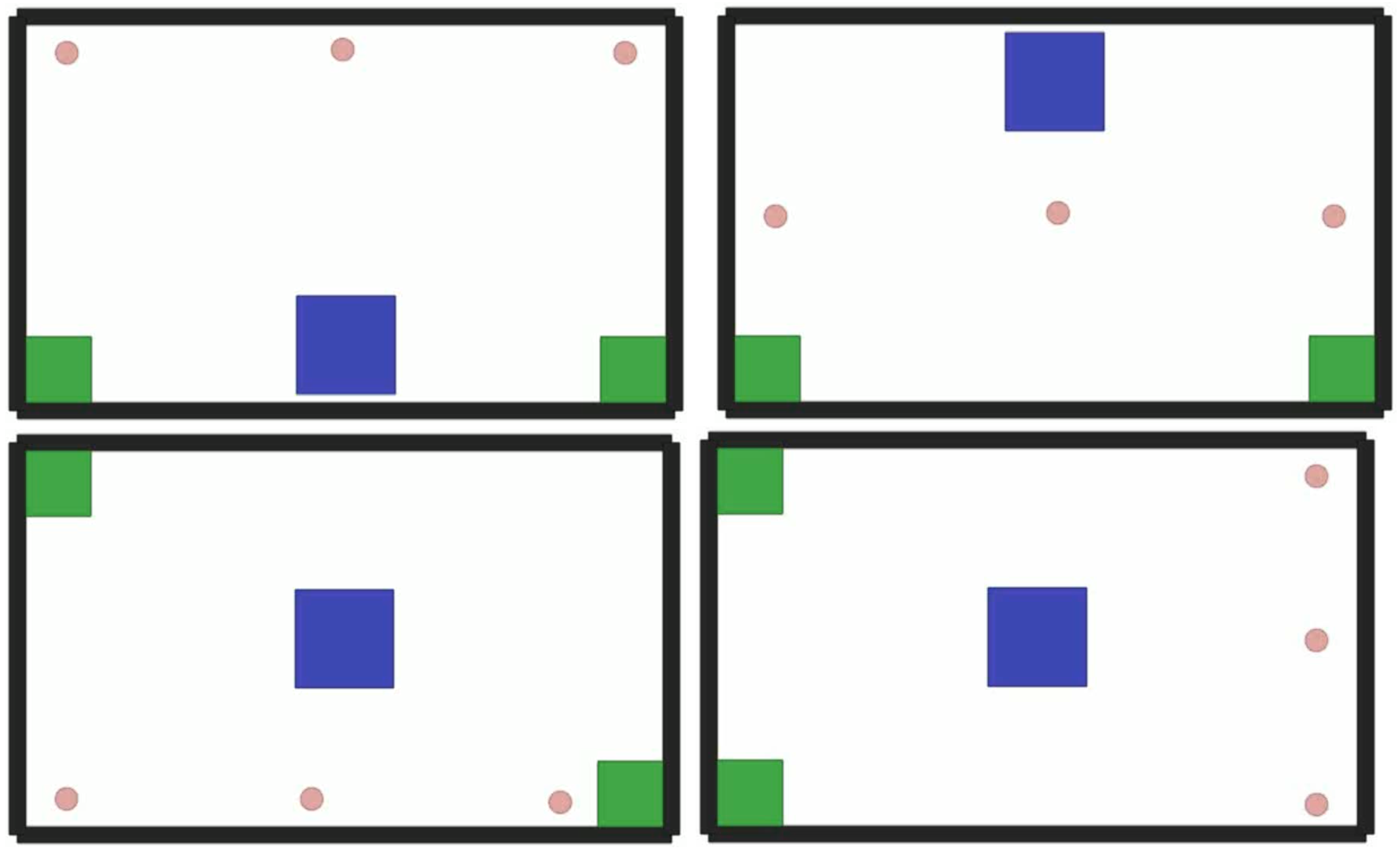
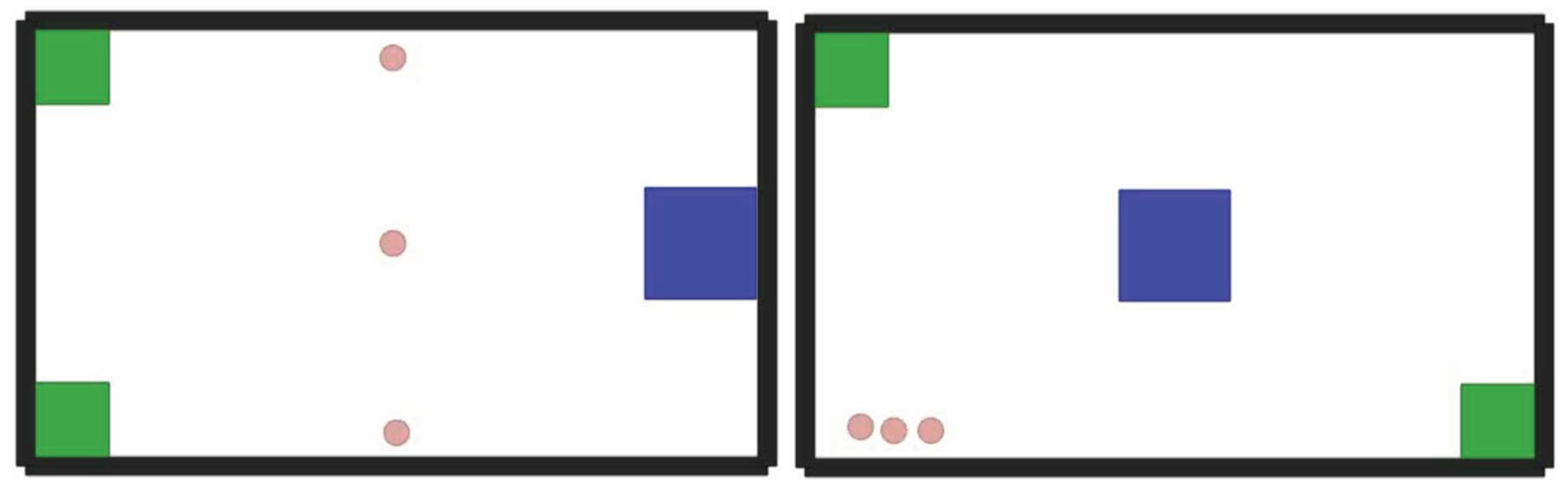
5.1. Simulation Setup

For our experiments, we leveraged the Vectorized Multi-Agent Simulator (VMAS) [30], specifically designed for efficient multi-agent reinforcement learning (MARL) benchmarking. VMAS integrates a 2D physics engine and supports the well-known Gym simulation environment interface. Its architecture allows for straightforward customization and expansion, facilitating the development of new and more complex scenarios.

Figure 2 illustrates the multi-agent multi-machine-tending scenario we developed. In this setup, three agents, depicted in red, initiate from their designated idle positions at the top of the environment. The production machines are highlighted in green, with machine blockers in gray obstructing direct access to the machines from one side. The storage area is marked in blue, and the walls outlining the environment are shown in black. Dotted lines in the figure point to the actual robot (our RanGen robot, composed of a Kinova Gen3 arm on top of an AgileX Ranger Mini mobile base), machines (CNC Universal Milling Machine DMU 50), and storage shelves that we are planning to use for real deployment. Despite using a simplified representation of the objects, the task itself is more oriented toward a real-world industrial application than the game-like environments typically used for the evaluation of MARL solutions [31,32]. Moreover, unlike some environments that use a simplified discrete grid representation of the world and actions [33], this environment represents objects’ states (positions and velocities) as continuous values, making it more challenging and closer to the real world. We refer the readers to

Table A2. Simulation setup details.

Parameter	Value
Machine mass	1 Kg (the default value in VMAS)
Machine length	20 cm
Machine width	20 cm
Agent mass	1 Kg
Agent radius	3.5 cm
Storage mass	1 Kg
Storage length	0.3
Storage width	0.3
Collidables	Agents, walls, machine blockers, machines, storage
Positions noise	Zero
Velocity damping	Zero

for more information about our simulation setup.

In VMAS, agents’ actions are represented as physical forces $f_x$ and $f_y$. The physics engine takes into account this input force and other factors like the velocity damping, gravity, and forces due to the collisions with other objects [30]. We used five discrete actions: 0: no force (translated internally to $f_x=0, f_y=0$), 1: leftward acceleration ($f_x=-1, f_y=0$), 2: rightward acceleration ($f_x=1, f_y=0$), 3: downward acceleration ($f_x=0, f_y=-1$), and 4: upward acceleration ($f_x=0, f_y=1$). This holonomic motion is also supported by our intended mobile base (the AgileX Ranger Mini).

Each episode in our simulation environment spans 200 time steps, during which agents aim to collect and deliver as many parts as possible. Agents are restricted to carrying only one part at a time; an agent must deliver its current part before picking up another. Additionally, once a part is collected from a machine, there is a production delay of 20 steps before the next part is available from the same machine.

5.2. Evaluation Procedure

Our evaluation framework is designed to assess both task effectiveness and resource efficiency through various criteria:

1. Task Success Factors:

• Total Number of Collected Parts: Measures the efficiency of part collection by agents.
• Total Number of Delivered Parts: Assesses the effectiveness of the delivery process.

2. Safety Factor:

• Total Number of Collisions: Calculated as the cumulative collisions across all agents, indicating the safety of navigation and interaction.

3. Resource Utilization Factors:

• Machine Utilization (MU):

  $$M{U}_i={\displaystyle \frac{P_i}{P_{imax}}},Avr\left(MU\right)={\displaystyle \frac{\sum M{U}_i}{M}}$$

  (13)

  where $M{U}_i$ represents the utilization rate of machine i, calculated by dividing the number of parts collected from machine i ($P_i$) by the maximum parts it could have produced ($P_{imax}$). The average utilization across all machines ($Avr\left(MU\right)$) is then determined by averaging the $M{U}_i$ values for all machines (M).
• Agent Utilization (AU):

  $$A{U}_i={\displaystyle \frac{P_i}{(P_{max}/N)}},Avr\left(AU\right)={\displaystyle \frac{\sum A{U}_i}{N}}$$

  (14)

  where $A{U}_i$ is the utilization for agent i, based on the number of parts it collected ($P_i$) relative to the average expected parts per agent ($P_{max}/N$). The average utilization for all agents ($Avr\left(AU\right)$) is the mean of $A{U}_i$ values across all agents (N).

To stabilize the training, we use 32 parallel environments, each running 375 episodes. So, each model’s interaction with the environment spanned a total of 12,000 episodes, with performance metrics averaged over the last 4000 episodes to assess stability and effectiveness. The experiments were replicated 10 times using different random seeds to ensure reliability, with results reported as both average and standard deviation values.

5.3. Results and Adaptability

MAPPO was selected as the baseline of comparison for this work, since MAPPO has been shown to perform generally better than multiple state-of-the-art methods in different environments (including QMix and MADDPG in MPE and QPlex, CWQMix, AIQMix, and RODE in SMAC) [23].

Table 1. Evaluation results for our model (AB-MAPPO) compared to MAPPO, showing the mean and standard deviation of the number of collected parts, delivered parts, collisions, and average machine and agent utilization; the ones with * are found to be statistically significant.

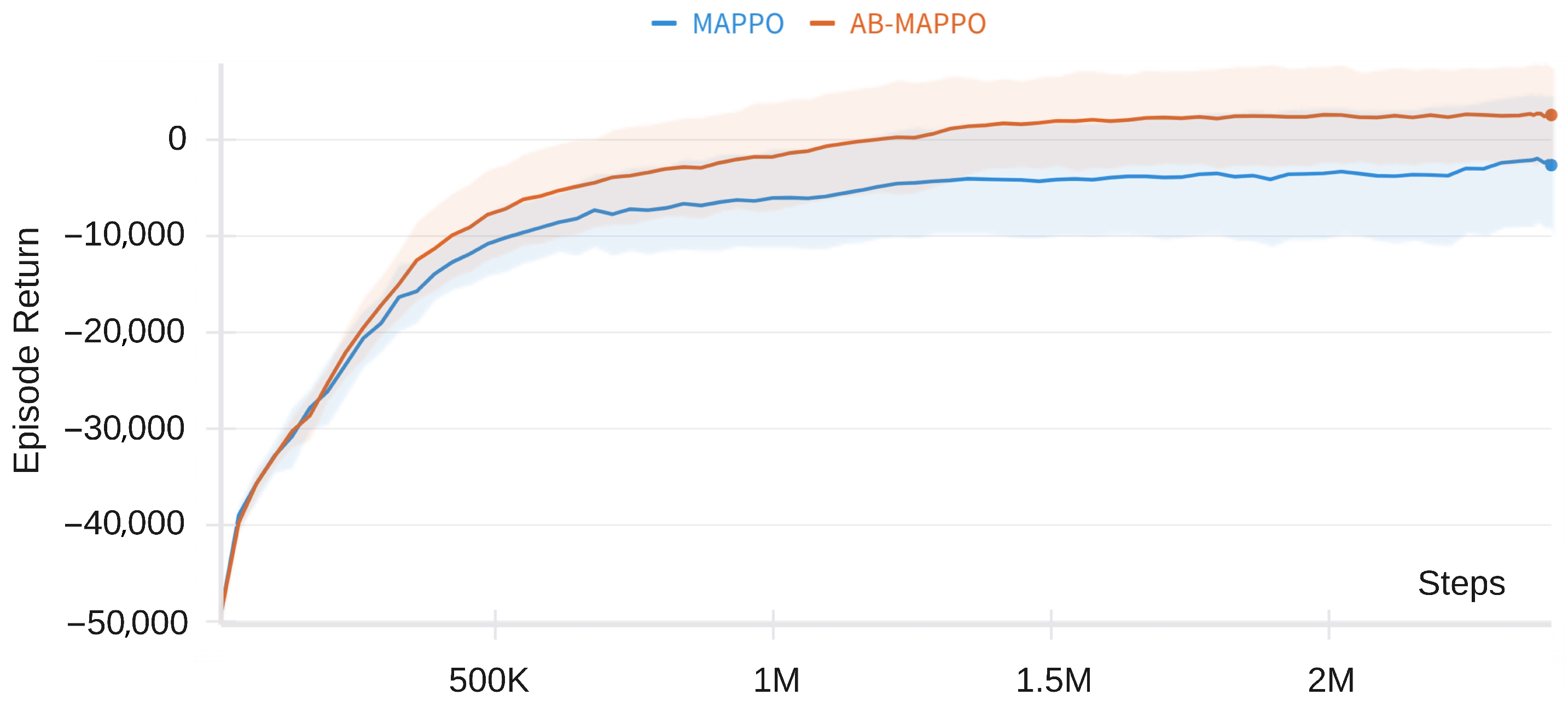
Model	MAPPO	AB-MAPPO
Collected *	10.73(1.7)	12.63(1.39)
Delivered *	9.79(1.69)	10.96(1.13)
Collisions	2.16(0.6)	1.92(0.84)
Avr(MU) *	0.54(0.02)	0.63(0.01)
Avr(AU) *	0.54(0.03)	0.63(0.06)

presents a comparative analysis of AB-MAPPO against the standard MAPPO in the same setup shown in Figure 2, reported as the mean and (standard deviation) over 10 different seeds. The data demonstrate that AB-MAPPO significantly surpasses MAPPO across all evaluated metrics. Notably, it achieves an 11% reduction in collisions, enhancing safety. Furthermore, it exhibits an 18% increase in parts collection and a 12% improvement in parts delivery. Additionally, the model boosts average machine utilization and agent utilization by 9% each, indicating a more efficient use of resources. The improvements in parts collection, parts delivery, machines utilization, and agents utilization were found to be statistically significant using the nonparametric Wilcoxon test. For collision reduction, we may be able to demonstrate significance with more seeds, or else explain it.

The total episode return (average total rewards collected by all agents per episode) for AB-MAPPO in comparison to MAPPO is shown in Figure 3. In the beginning, the two models have similar performance, but at around 250 thousand steps, our model starts to outperform MAPPO, and the gap between the two gradually continues to increase.

Furthermore, we performed a two-sided Mann-Whitney U Test to investigate the difference in collected reward over all the episodes (n1 = n2 = 10, median1 = −9019, median2 = −4719, U = 23.0, p-value = 0.045, rank-biserial correlation = −0.54). Before that, we performed a Shapiro-Wilk normality test and found that the data were non-normally distributed, justifying the Mann-Whitney Test. The values of U and P both indicate that the difference in the result is statistically significant. The rank-biserial correlation value indicates a statistically significant increase in the reward collection.

To assess the adaptability of our model to various industrial settings, we conducted training and evaluation in multiple environment layouts without adjusting the model hyperparameters. This approach was designed to test whether the model could be effectively deployed in different setups with the same number of agents and machines but different layout arrangements without requiring layout-specific tuning, but again, the framework can also be finetuned for a specific factory layout to achieve even better performance. This was performed to evaluate if the model and reward design are just tied to a specific layout or can be used in other layouts too. The experiments maintained consistent dimensions for the environment, machines, agents, and storage area, varying only the layout configurations. For each experiment, the model was allowed to interact with a single environment for 18,200 episodes.

Figure 4 displays examples of environment layouts where the model demonstrated robust performance. Conversely, Figure 5 highlights layouts where the model’s performance was comparatively weaker.

Empirical testing revealed that our model performs optimally when the distance between the machines and the storage area is minimized. This configuration facilitates quicker part deliveries, enhancing overall efficiency. In contrast, a larger distance from the agents’ initial positions to the machines does not significantly impact performance, suggesting that initial agent placement is less critical.

However, significantly increasing the distance between the machines and the storage area adversely affects performance. We attribute this decline to the increased challenge agents face in locating the storage area after part collection, necessitating exploration over a larger area. The placement of the storage area—whether centrally or peripherally—does not markedly influence performance. Nevertheless, starting agents in close proximity to one another can impede their learning due to an increased incidence of collisions at the outset, which the collision penalty exacerbates by discouraging exploration.

Furthermore, for the two layouts with less optimal performance, we believe the reward parameters tuning can play a crucial role in enhancing performance. For instance, in the current setup, with machines far from each other or far from the storage area, agents may find it more rewarding if all of them focus on one machine, or may not even be incentivized enough to find the other machine. A possible solution would be to increase the uncollected parts penalty or even use the increasing uncollected part penalty option, where the agents will be penalized more for the parts that stayed longer.

6. Ablation Study

This ablation study was run without training stabilization, to focus on the observation and reward design rather than stabilizing the training. However, the final model, as presented in Section 5.2, leverages stabilized training. Since the goal was to design a good observation and reward, the baseline MAPPO was used to conduct those experiments. In each experiment, the model was allowed to interact with the environment for 18,200 episodes, where the last 200 episodes were used for evaluation, and each experiment was repeated three times with different randomization seeds.

6.1. Experiments on Observation Design

To develop an effective observation strategy for our model, we initially assessed various observation configurations using MAPPO to determine their impact on performance.

Table 2. Evaluation results for various observation components: showing the mean and standard deviation of the number of collected parts, delivered parts, collisions, and average machine and agent utilization.

Exp	Collected	Delivered	Collisions	Avr(MU)	Avr(AU)
Baseline(B)	7.66(0.7)	6.29(0.7)	13.47(4.2)	0.38(0.2)	0.38(0.0)
B + Ready steps (PRS)	1.26(0.1)	0.01(0.0)	10.25(3.3)	0.06(0.0)	0.06(0.0)
B − Velocity (RV)	9.25(1.1)	7.8(1.1)	13.96(1.8)	0.46(0.1)	0.46(0.0)
B − Normalization (RN)	7.78(1.2)	6.24(1.3)	8.67(2.5)	0.39(0.2)	0.39(0.1)
B + Corner rep. (PCR)	9.18(0.5)	7.74(0.5)	7.72(1.3)	0.46(0.2)	0.46(0.0)
B + Blockers info. (PBI)	8.15(1.0)	6.64(1.0)	9.22(1.9)	0.41(0.3)	0.41(0.0)
B − Walls info. (RWI)	7.49(0.1)	5.78(0.2)	9.78(2.0)	0.38(0.3)	0.37(0.1)

presents a baseline experiment (B), which incorporates all observation components detailed in Section 4.3, including all agents’ velocities and the relative positions of the walls.

Subsequent experiments each modify a single aspect of the baseline observation to isolate and measure its effect on performance: experiment (PRS) adds the time elapsed since a part became ready at a machine but remained uncollected, (RV) excludes agents’ velocity data, (RN) removes the normalization step from the observation process, (PCR) changes the representation of entities from the center point to the positions of two opposite corners, (PBI) includes the positions of machine blockers, and (RWI) omits the walls’ positions from the observation. This systematic approach allows us to identify the most influential observation factors and optimize the model’s input data for better learning outcomes and performance.

Our experimental findings indicate that certain observation modifications enhance model performance while others may impede it. Specifically, the inclusion of wall and machine blocker observations, the use of two-corner representations for entities, and normalization procedures significantly improved parts delivery outcomes. Conversely, tracking agents’ velocities and the duration since parts became ready without collection appeared to hinder learning. In terms of safety, the two-corner representation and normalization generally reduced the number of collisions, suggesting that more detailed information in the observation helps in avoiding mishaps. Interestingly, the inclusion of wall observations did not demonstrate a clear benefit and appeared not to affect safety positively.

Furthermore, enhancements in parts delivery correlated well with improvements in both machine and agent utilization rates. This suggests that factors contributing positively to operational efficiency also tend to optimize resource usage.

6.2. Experiments on Reward Design

This section continues our evaluation by focusing on the different components of the reward structure to determine their impacts on performance. Utilizing the same base experiment setup as before, all reward components outlined in (12) were initially included, along with reward sharing where all agents receive the pick-or-place reward if at least one agent successfully picks up or places a part, respectively. Subsequent experiments each isolate and modify a specific reward feature to analyze its effects. Experiment (RT) eliminates the time penalty, (RRS) removes reward sharing, (RUP) omits the uncollected parts penalty, (IUP) applies an increasing uncollected parts penalty as described in the latter part of (10), and (RDR) removes the distance-based reward.

Table 3. Evaluation results for various reward components, showing the mean and standard deviation of the number of collected parts, delivered parts, collisions, and average machine and agent utilization.

Exp	Collected	Delivered	Collisions	Avr(MU)	Avr(AU)
Baseline(B)	7.66(0.7)	6.29(0.7)	13.47(4.2)	0.38(0.2)	0.38(0.0)
B − Time Penalty (RT)	6.72(1.8)	5.4(1.9)	18.33(9.0)	0.34(0.0)	0.34(0.0)
B − Reward Sharing (RRS)	8.44(0.7)	7.39(0.5)	27.25(9.8)	0.42(0.2)	0.42(0.1)
B − Utilization Penalty (RUP)	4.79(0.6)	3.46(0.2)	6.58(2.1)	0.24(0.1)	0.24(0.0)
B + Increasing Util. Pen. (IUP)	1.55(0.1)	0.28(0.2)	167.48(53.7)	0.08(0.0)	0.08(0.0)
B − Distance Rewards (RDR)	6.57(2.6)	4.99(3.4)	7.57(4.6)	0.33(0.2)	0.33(0.1)

details these comparisons.

Generally, the removal of any reward component negatively impacted productivity and resource utilization. Notably, not sharing rewards and applying a fixed penalty for uncollected parts yielded better results. From a safety perspective, fewer reward terms led to increased safety, except in the case of the time penalty. Sharing rewards and using fixed penalties for uncollected parts also resulted in fewer collisions.

6.3. Experiments on Combinations of Options

Additionally, we assessed the performance of combining the most effective observation and reward options.

Table 4. Combining the best-performing options: Mean (stddev).

Exp	Collected	Delivered	Collisions	Avr(MU)	Avr(AU)
RV + PBI	9.03(1.4)	7.56(1.5)	11.59(1.1)	0.45(0.2)	0.45(0.1)
RV + RRS	10.2(1.0)	8.74(0.8)	15.02(1.0)	0.51(0.1)	0.51(0.1)
RV + PCR	9.8(0.7)	8.16(1.0)	7.64(2.0)	0.49 (0.2)	0.49(0.1)
RV + PCR + RSS + RRS	8.51(0.6)	7.43(0.5)	21.26(1.6)	0.43(0.4)	0.43(0.1)

presents these results. Not all combinations led to performance enhancements. For instance, Exp1, which combines removing velocity observation (RV) with observing machine blockers’ positions (PBI), did not improve outcomes. However, Exp2, which combines RV with remove reward sharing (RRS), showed enhanced performance, as did Exp3, which pairs no velocity observation (RV) with two-corner entity representation (PCR). Contrarily, combining all selected options (RV, PCR, RSS, and not observing machine blockers (RBI)) in Exp4 did not yield better results. Ultimately, the setup from Exp2 was chosen as the optimal configuration for our observation and reward strategy.

7. Conclusions

This study applies multi-agent reinforcement learning to a challenging real-world industrial scenario (machine tending). It aims to leverage the full potential of multiple mobile robots and artificial intelligence to help advance the manufacturing sector. We introduced AB-MAPPO, incorporating MAPPO with a novel attention-based encoding to significantly improve feature representation. These innovations establish a new baseline and pave the way for future advancements. Rigorously tested across diverse environments and supported by a comprehensive ablation study, AB-MAPPO demonstrated its efficacy and adaptability. However, we believe there are still some limitations in this work for it to be more applicable to the industry, such as scalability, robustness to noise, and loosening the assumptions. Looking forward, we plan to extend these innovations to more dynamic scenarios, including real-time material feeding and interactive object manipulation, to bridge the gap between theoretical research and practical applications. Furthermore, we are considering integrating a low-level controller that converts velocity commands to robot wheel velocity commands, so that our model can focus on high-level control.