Development of an Attention Mechanism for Task-Adaptive Heterogeneous Robot Teaming
Abstract
1. Introduction
- •
- A novel multi-robot teaming method, innerATT, is developed to guide the flexible cooperation among heterogeneous robots as the task complexity varies in target number, target type, and robot work status.
- •
- A theoretical analysis is conducted to validate the robustness of innerATT in guiding flexible cooperation, providing a theoretical foundation for implementing innerATT in general disturbance-involved multi-robot teaming in future similar research.
- •
- A deep reinforcement learning-based simulation framework, which integrates the simulation platform of a multi-agent particle environment, the multi-agent deep reinforcement learning algorithms, and robot models, is developed to provide a standard pipeline for simulating flexible robot teaming.
2. Related Work
3. Materials and Methods
3.1. Inner Attention-Supported Adaptive Cooperation
3.1.1. Heterogeneous Teaming Supported by Multi-Agent Reinforcement Learning with Centralized Training and Decentralized Execution
3.1.2. Robot Inner Attention for Team Adaptability Modeling
3.1.3. Theoretical Analysis of innerATT’s Robustness
3.2. Experiment Settings
4. Results and Discussion
4.1. Adapting to Task Varieties
4.2. Adapting to Robot Availability
5. Conclusions
- Summary. This study introduces a novel inner attention mechanism, innerATT, designed to facilitate adaptive cooperation among multi-heterogeneous robots in response to varying task requirements. Through the deployment of scenarios with diverse task configurations, such as a single task, a double task, and dynamically mixed tasks, the efficacy of the innerATT model in promoting flexible team formation is empirically confirmed. The model adeptly navigates the challenge of distributing limited robot resources across fluctuating task demands.
- Potential Application. Additionally, the theoretical framework of this model offers potential for broad application, including the coordination of ground and aerial vehicles, as well as integration between vehicular units and human operatives. Consequently, the attention-driven flexible teaming model unveiled in this research holds substantial promise for practical implementation across a spectrum of multi-robot applications, ranging from disaster response to wildlife conservation and the management of airport traffic flows.
- Novelty. While building upon foundational research in multi-agent reinforcement learning [52,53], our work introduces a distinctive approach by focusing on the strategic formation and adaptability of robot teams to task demands and environmental changes, utilizing innerATT for adaptive cooperation. This unique contribution addresses unexplored challenges in the field, extending beyond the scope of prior studies, and highlights the innovative potential of attention mechanisms in enhancing HMRS operations.
- Practical Challenges. The primary goal of this research is to assess the feasibility of using attention mechanisms to flexibly assemble heterogeneous robot teams. Given the differences between simulated environments and their real-world counterparts, the model developed in this study might not perform identically in practical settings. Nonetheless, the model acts as an essential initial step for further development and adjustment to actual conditions. It is vital to acknowledge the difficulties in applying simulation-based methods in real environments. The unpredictability and sensor inaccuracies inherent in real-world scenarios necessitate thorough validation and improvement of any theoretical model. Consequently, our future endeavors aim to narrow the gap between simulation outcomes and real-world implementation. This will include a comprehensive analysis and the integration of specific sensors (e.g., LIDARs, cameras, GPS) for various applications, alongside the examination of robust communication protocols to facilitate efficient team coordination amidst the challenges of bandwidth and latency in operational environments. Additionally, future research will explore robot behavior analysis and the creation of models to measure and improve human trust in heterogeneous multi-robot systems with the goal of enhancing their real-world efficacy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| HMRS | Heterogeneous Multi-Robot System |
| inner-ATT | Inner Attention |
| MAAC | Multi-Agent Actor–Critic |
| UAV | Unmanned Aerial Vehicle |
| TD | Temporal Difference |
| PPO | Proximal Policy Optimization |
References
- Matos, A.; Martins, A.; Dias, A.; Ferreira, B.; Almeida, J.M.; Ferreira, H.; Amaral, G.; Figueiredo, A.; Almeida, R.; Silva, F. Multiple robot operations for maritime search and rescue in euRathlon 2015 competition. In Proceedings of the OCEANS 2016-Shanghai, Shanghai, China, 10–13 April 2016; pp. 1–7. [Google Scholar]
- Mouradian, C.; Yangui, S.; Glitho, R.H. Robots as-a-service in cloud computing: Search and rescue in large-scale disasters case study. In Proceedings of the 2018 15th IEEE Annual Consumer Communications and Networking Conference (CCNC), Las Vegas, NV, USA, 12–15 January 2018; pp. 1–7. [Google Scholar]
- Beck, Z.; Teacy, N.R.; Rogers, A.C. Online planning for collaborative search and rescue by heterogeneous robot teams. Association of Computing Machinery. In Proceedings of the AAMAS’16: International Conference on Agents and Multiagent Systems, Singapore, 9–13 May 2016. [Google Scholar]
- Alotaibi, E.T.S.; Al-Rawi, H. Multi-robot path-planning problem for a heavy traffic control application: A survey. Int. J. Adv. Comput. Sci. Appl. 2016, 7, 10. [Google Scholar]
- Digani, V.; Sabattini, L.; Secchi, C.; Fantuzzi, C. Towards decentralized coordination of multi robot systems in industrial environments: A hierarchical traffic control strategy. In Proceedings of the 2013 IEEE 9th International Conference on Intelligent Computer Communication and Processing (ICCP), Cluj-Napoca, Romania, 5–7 September 2013; pp. 209–215. [Google Scholar]
- Digani, V.; Sabattini, L.; Secchi, C.; Fantuzzi, C. Hierarchical traffic control for partially decentralized coordination of multi agv systems in industrial environments. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014; pp. 6144–6149. [Google Scholar]
- Broecker, B.; Caliskanelli, I.; Tuyls, K.; Sklar, E.I.; Hennes, D. Hybrid insect-inspired multi-robot coverage in complex environments. In Proceedings of the Conference Towards Autonomous Robotic Systems, London, UK, 3–5 July 2019; pp. 56–68. [Google Scholar]
- Kolling, A.; Carpin, S. Multi-robot surveillance: An improved algorithm for the graph-clear problem. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasaena, CA, USA, 19–23 May 2008; pp. 2360–2365. [Google Scholar]
- Easton, K.; Burdick, J. A coverage algorithm for multi-robot boundary inspection. In Proceedings of the 2005 IEEE International Conference on Robotics and Automation, Barcelona, Spain, 18–22 April 2005; pp. 727–734. [Google Scholar]
- Zhu, A.M.; Yang, S.X. An improved SOM-based approach to dynamic task assignment of multi-robot. In Proceedings of the World Congress on Intelligent Control and Automation, Jinan, China, 7–9 July 2010; pp. 2168–2173. [Google Scholar]
- Fazli, P.; Davoodi, A.; Mackworth, A.K. Multi-robot repeated area coverage. Auton. Robot. 2013, 34, 251–276. [Google Scholar] [CrossRef]
- Boardman, M.; Edmonds, J.; Francis, K.; Clark, C.M. Multi-robot boundary tracking with phase and workload balancing. In Proceedings of the International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 3321–3326. [Google Scholar]
- Zhu, D.Q.; Huang, H.; Yang, S.X. Dynamic task assignment and path planning of multi-AUV system based on an improved self-organizing map and velocity synthesis method in three-dimensional underwater workspace. IEEE Trans. Cybern. 2013, 43, 504–514. [Google Scholar]
- Vergnano, A.; Thorstensson, C.; Lennartson, B.; Falkman, P.; Pellicciari, M.; Leali, F.; Biller, S. Modeling and optimization of energy consumption in cooperative multi-robot systems. IEEE Trans. Autom. Sci. Eng. 2012, 9, 423–428. [Google Scholar] [CrossRef]
- Parker, L.E. Adaptive heterogeneous multi-robot teams. Neurocomputing 1999, 28, 75–92. [Google Scholar] [CrossRef]
- Kim, J.; Cauli, N.; Vicente, P.; Damas, B.; Bernardino, A.; Santos-Victor, J.; Cavallo, F. Cleaning tasks knowledge transfer between heterogeneous robots: A deep learning approach. J. Intell. Robot. Syst. 2020, 98, 191–205. [Google Scholar] [CrossRef]
- Prorok, A.; Hsieh, M.A.; Kumar, V. Fast redistribution of a swarm of heterogeneous robots. In Proceedings of the 9th EAI International Conference on Bio-inspired Information and Communications Technologies (formerly BIONETICS), New York City, NY, USA, 3–5 December 2015; pp. 249–255. [Google Scholar]
- Saribatur, Z.G.; Patoglu, V.; Erdem, E. Finding optimal feasible global plans for multiple teams of heterogeneous robots using hybrid reasoning: An application to cognitive factories. Auton. Robot. 2019, 43, 213–238. [Google Scholar] [CrossRef]
- Atay, N.; Bayazit, B. Mixed-Integer Linear Programming Solution to Multi-Robot Task Allocation Problem; Washington University: St. Louis, MO, USA, 2006. [Google Scholar]
- Darrah, M.; Nil, W.; Stolarik, B. Multiple UAV Dynamic Task Allocation Using Mixed Integer Linear Programming in a SEAD Mission; Infotech at Aerospace: Arlington, VA, USA, 2005; p. 7165. [Google Scholar]
- Mosteo, A.R.; Montano, L. Simulated annealing for multi-robot hierarchical task allocation with flexible constraints and objective functions. In Proceedings of the Workshop on Network Robot Systems: Toward Intelligent Robotic Systems Integrated with Environments, Beijing, China, 10 October 2006. [Google Scholar]
- Juedes, D.; Drews, F.; Welch, L.; Fleeman, D. Heuristic resource allocation algorithms for maximizing allowable workload in dynamic, distributed real-time systems. In Proceedings of the International Parallel and Distributed Processing Symposium, Santa Fe, NM, USA, 26–30 April 2004; p. 117. [Google Scholar]
- Kmiecik, W.; Wojcikowski, M.; Koszalka, L.; Kasprzak, A. Task allocation in mesh connected processors with local search meta-heuristic algorithms. In Proceedings of the Asian Conference on Intelligent Information and Database Systems, Hue City, Vietnam, 24–26 March 2010; pp. 215–224. [Google Scholar]
- Iijima, N.; Sugiyama, A.; Hayano, M.; Sugawara, T. Adaptive task allocation based on social utility and individual preference in distributed environments. Procedia Comput. Sci. 2017, 112, 91–98. [Google Scholar] [CrossRef]
- Lope, D.; Javier, D.; Quiñonez, Y. Response threshold models and stochastic learning automata for self-coordination of heterogeneous multi-tasks distribution in multi-robot systems. Robot. Auton. Syst. 2012, 61, 714–720. [Google Scholar] [CrossRef]
- Elfakharany, A.; Yusof, R.; Ismail, Z. Towards multi-robot Task Allocation and Navigation using Deep Reinforcement Learning. J. Phys. Conf. Ser. 2020, 1447, 012045. [Google Scholar] [CrossRef]
- Fan, T.X.; Long, P.X.; Liu, W.X.; Pan, J. Fully distributed multi-robot collision avoidance via deep reinforcement learning for safe and efficient navigation in complex scenarios. arXiv 2018, arXiv:1808.03841. [Google Scholar]
- Noureddine, D.B.; Gharbi, A.; Ahmed, S.B. Multi-agent Deep Reinforcement Learning for Task Allocation in Dynamic Environment. In Proceedings of the 12th International Conference on Software Technologies, ICSOFT 2017, Madrid, Spain, 24–26 July 2017; pp. 17–26. [Google Scholar] [CrossRef]
- Luo, T.Z.; Subagdja, B.; Wang, D.; Tan, A. Multi-Agent Collaborative Exploration through Graph-based Deep Reinforcement Learning. In Proceedings of the 2019 IEEE International Conference on Agents (ICA), Jinan, China, 18–21 October 2019; pp. 2–7. [Google Scholar]
- Harnett, B.M.; Doarn, C.R.; Rosen, J.; Hannaford, B.; Broderick, T.J. Evaluation of unmanned airborne vehicles and mobile robotic telesurgery in an extreme environment. Telemed.-Health 2008, 14, 539–544. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Chen, W. Self-healing for mobile robot networks with motion synchronization. In Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Diego, CA, USA, 29 October–2 November 2007; pp. 3107–3112. [Google Scholar]
- Liu, Z.; Ju, J.; Chen, W.; Fu, X.Y.; Wang, H. A gradient-based self-healing algorithm for mobile robot formation. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 3395–3400. [Google Scholar]
- Mathews, N.; Christensen, A.L.; O’Grady, R.; Mondada, F.; Dorigo, M. Mergeable nervous systems for robots. Nat. Commun. 2017, 8, 439. [Google Scholar] [CrossRef] [PubMed]
- Mathews, N.; Christensen, A.L.; Stranieri, A.; Scheidler, A.; Dorigo, M. Supervised morphogenesis: Exploiting morphological flexibility of self-assembling multirobot systems through cooperation with aerial robots. Robot. Auton. Syst. 2019, 112, 154–167. [Google Scholar] [CrossRef]
- Pelc, A.; Peleg, D. Broadcasting with locally bounded byzantine faults. Inf. Process. Lett. 2005, 93, 109–115. [Google Scholar] [CrossRef]
- Saulnier, K.; Saldana, D.; Prorok, A.; Pappas, G.J.; Kumar, V. Resilient flocking for mobile robot teams. IEEE Robot. Autom. Lett. 2017, 2, 1039–1046. [Google Scholar] [CrossRef]
- Liu, R.; Jia, F.; Luo, W.; Chandarana, M.; Nam, C.; Lewis, M.; Sycara, K.P. Trust-Aware Behavior Reflection for Robot Swarm Self-Healing. In Proceedings of the 18th International Conference on Autonomous Agents and MultiAgent Systems, Montreal, QC, Canada, 13–17 May 2019; pp. 122–130. [Google Scholar]
- Foerster, R.M.; Schneider, W.X. Task-Irrelevant Features in Visual Working Memory Influence Covert Attention: Evidence from a Partial Report Task. Vision 2019, 3, 42. [Google Scholar] [CrossRef] [PubMed]
- Aly, A.; Griffiths, S.; Stramandinoli, F. Metrics and benchmarks in human-robot interaction: Recent advances in cognitive robotics. Cogn. Syst. Res. 2017, 43, 313–323. [Google Scholar] [CrossRef]
- Huber, A.; Weiss, A. Developing human-robot interaction for an industry 4.0 robot: How industry workers helped to improve remote-HRI to physical-HRI. In Proceedings of the Companion of the 2017 ACM/IEEE International Conference on Human-Robot Interaction, Vienna, Austria, 6–9 March 2017; pp. 137–138. [Google Scholar]
- Anzalone, S.M.; Boucenna, S.; Ivaldi, S.; Chetouani, M. Evaluating the engagement with social robots. Int. J. Soc. Robot. 2015, 7, 465–478. [Google Scholar] [CrossRef]
- Daglarli, E.; Daglarli, S.F.; Gunel, G.O.; Kose, H. Improving human-robot interaction based on joint attention. Appl. Intell. 2017, 47, 62–82. [Google Scholar] [CrossRef]
- So, W.C.; Wong, M.K.; Lam, W.Y.; Cheng, C.H.; Yang, J.H.; Huang, Y.; Ng, P.; Wong, W.L.; Ho, C.L.; Yeung, K.L. Robot-based intervention may reduce delay in the production of intransitive gestures in Chinese-speaking preschoolers with autism spectrum disorder. Mol. Autism. 2018, 9, 34. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.C.; Lu, Z.Q. Learning attentional communication for multi-agent cooperation. In Proceedings of the Neural Information Processing Systems, Montreal, QC, Canada, 3–8 December 2018; pp. 7254–7265. [Google Scholar]
- Geng, M.Y.; Xu, K.L.; Zhou, X.; Ding, B.; Wang, H.M.; Zhang, L. Learning to cooperate via an attention-based communication neural network in decentralized multi-robot exploration. Entropy 2019, 21, 294. [Google Scholar] [CrossRef] [PubMed]
- Capitan, J.; Spaan, M.T.; Merino, L.; Ollero, A. Decentralized multi-robot cooperation with auctioned POMDPs. Int. J. Robot. Res. 2018, 32, 650–671. [Google Scholar] [CrossRef]
- Iqbal, S.; Sha, F. Actor-attention-critic for multi-agent reinforcement learning. Int. Conf. Mach. Learn. 2019, 97, 2961–2970. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Abbeel, O.P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. In Proceedings of the Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 6379–6390. [Google Scholar]
- Patkin, M.L.; Rogachev, G.N. Construction of multi-agent mobile robots control system in the problem of persecution with using a modified reinforcement learning method based on neural networks. IOP Conf. Ser. Mater. Sci. Eng. 2018, 32, 012018. [Google Scholar] [CrossRef]
- Gupta, J.K.; Egorov, M.; Kochenderfer, M. Cooperative multi-agent control using deep reinforcement learning. In International Conference on Autonomous Agents and Multiagent Systems; Springer: Berlin/Heidelberg, Germany, 2017; pp. 66–83. [Google Scholar]
- Hsieh, Y.L.; Cheng, M.H.; Juan, D.C.; Wei, W.; Hsu, W.L.; Hsieh, C.J. On the robustness of self-attentive models. In Proceedings of the Association for Computational Linguistics, Florence, Italy, 28 July–2 August 2019; pp. 1520–1529. [Google Scholar]
- Hu, S.; Shen, L.; Zhang, Y.; Tao, D. Learning Multi-Agent Communication from Graph Modeling Perspective. In The Twelfth International Conference on Learning Representations; ICLR: Appleton, WI, USA, 2023. [Google Scholar]
- Seraj, E.; Wang, Z.; Paleja, R.; Martin, D.; Sklar, M.; Patel, A.; Gombolay, M. Learning efficient diverse communication for cooperative heterogeneous teaming. In Proceedings of the 21st International Conference on Autonomous Agents and Multiagent Systems, Auckland, New Zealand, 9–13 May 2022; pp. 1173–1182. [Google Scholar]

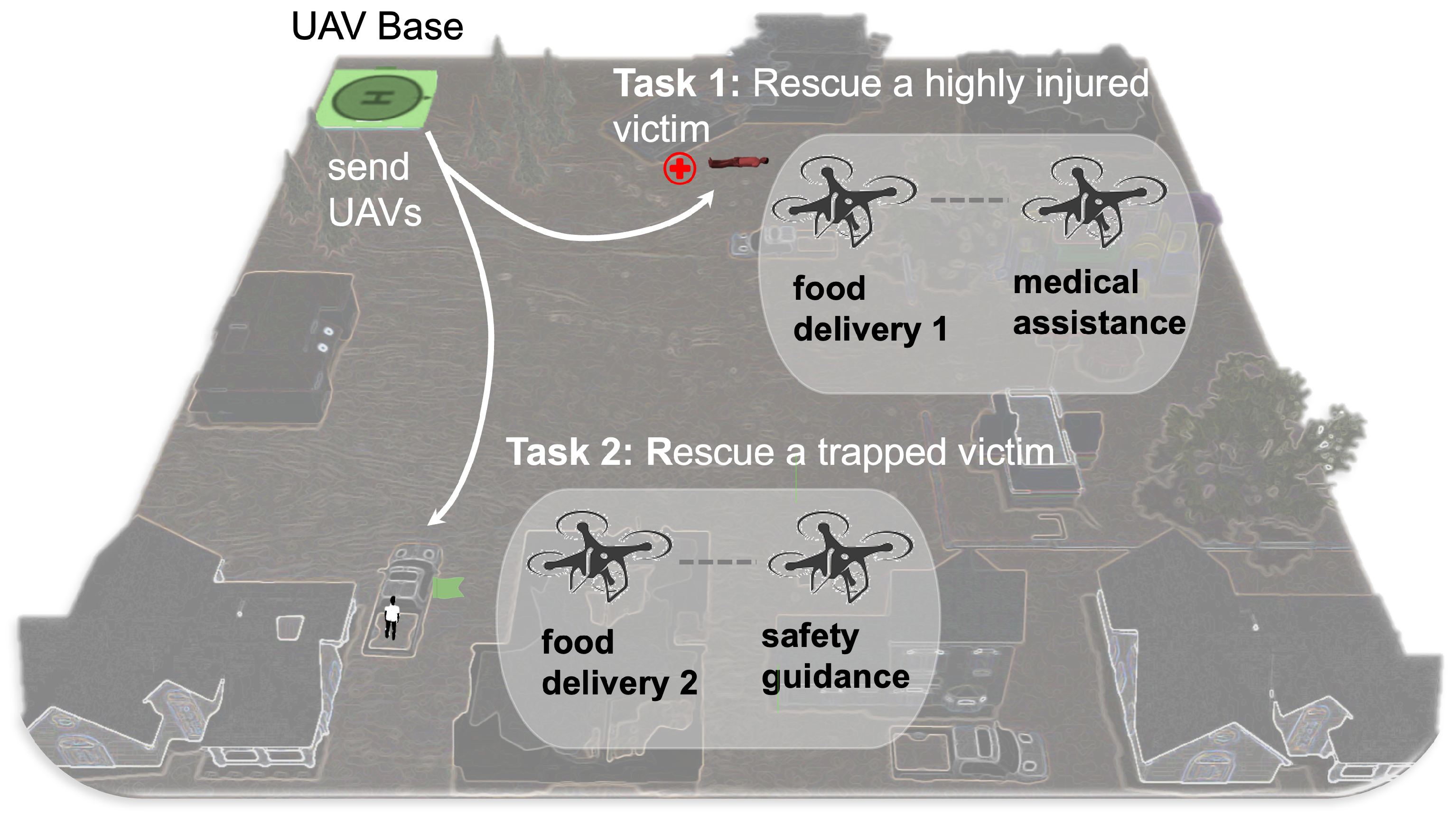


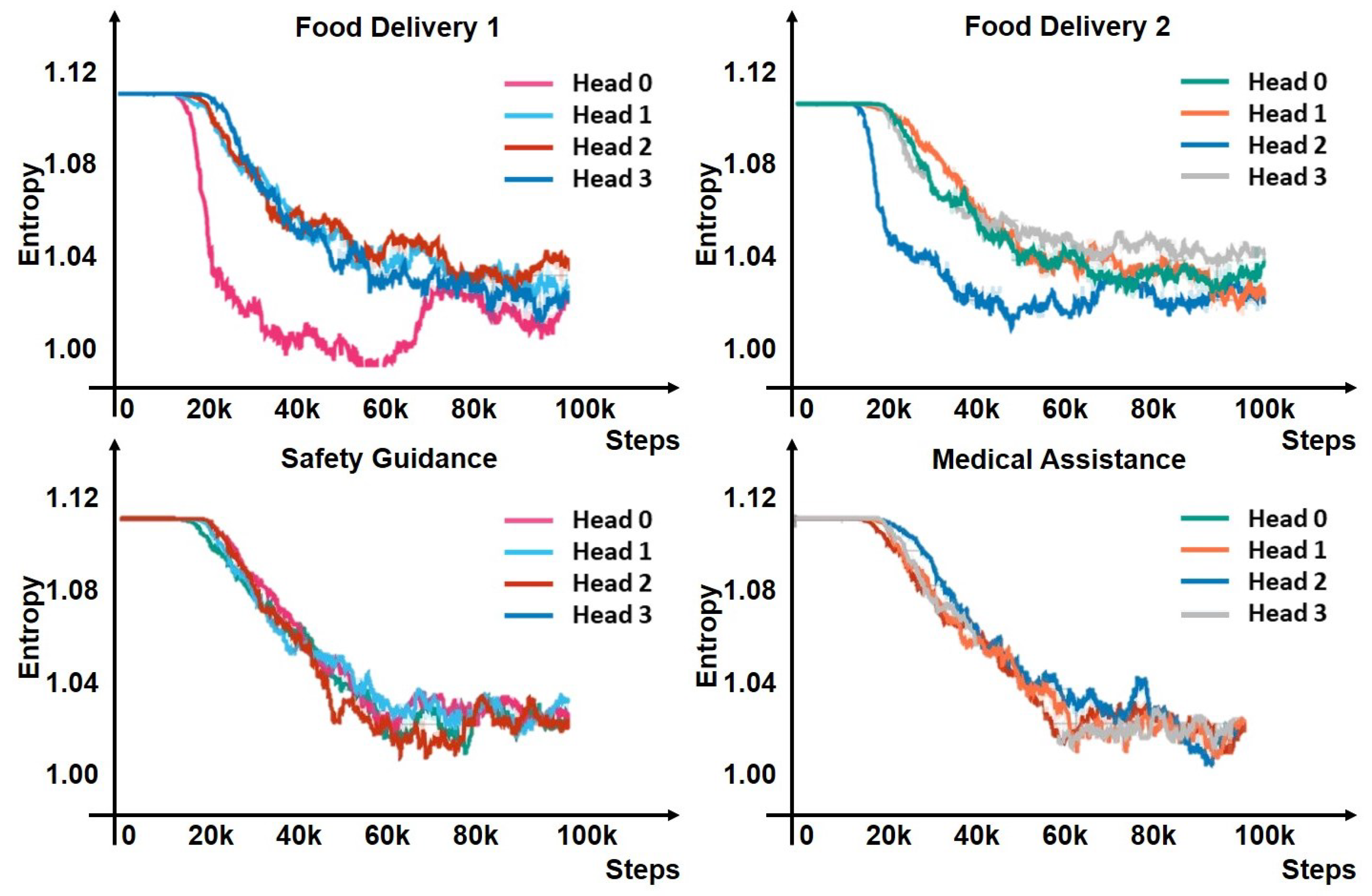

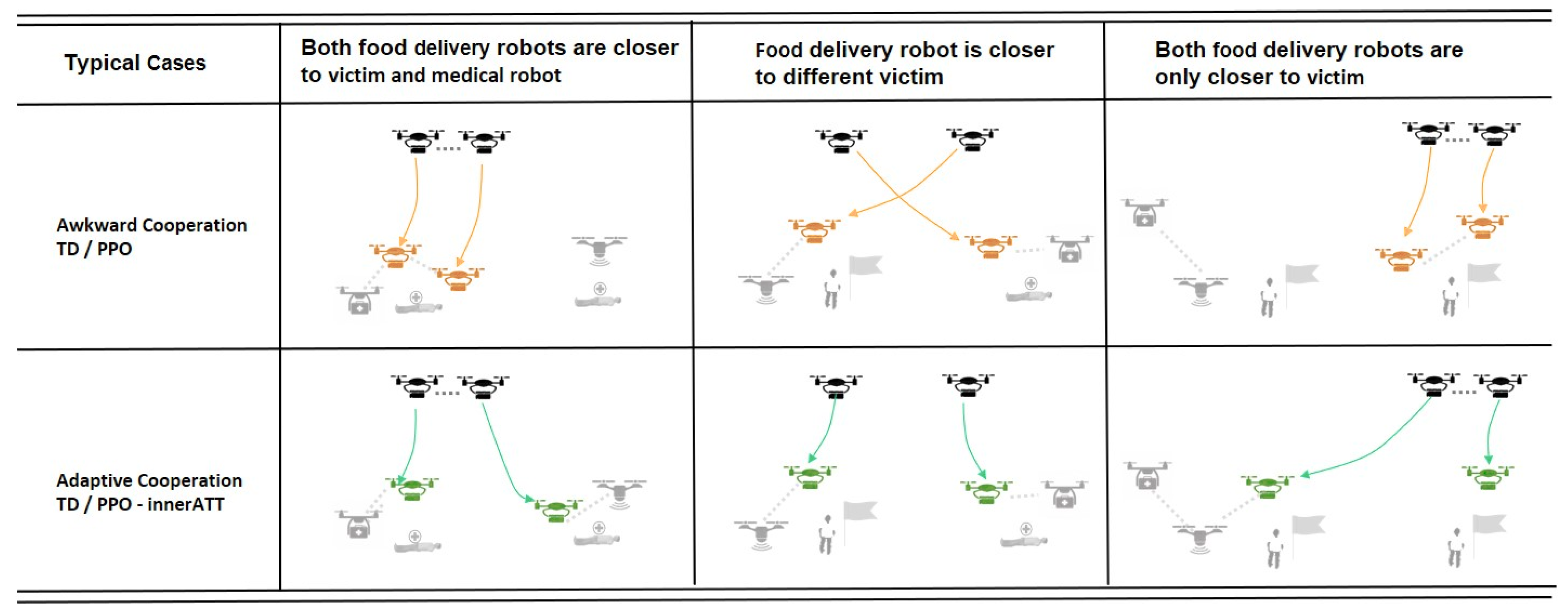
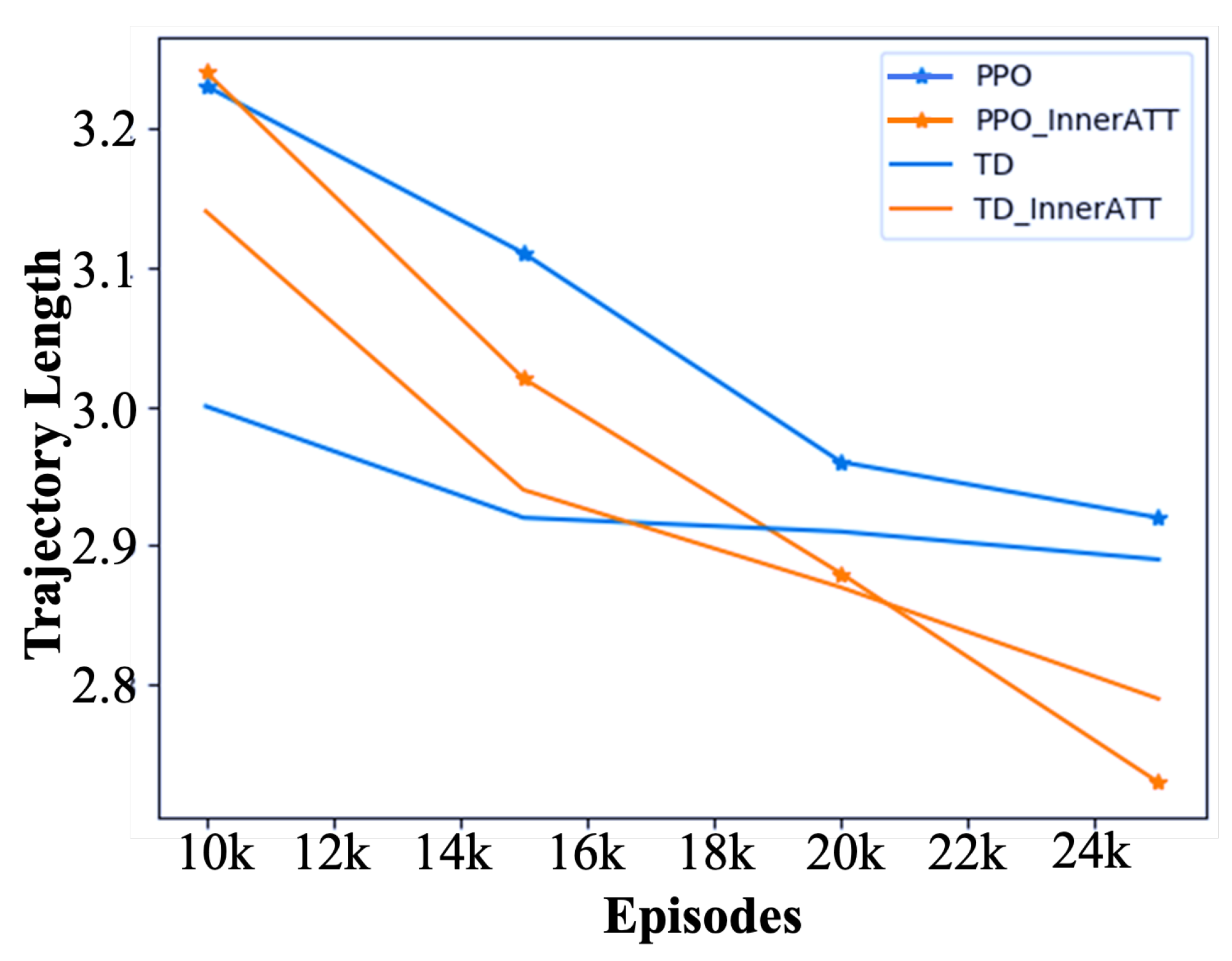

| Type | Speed | Mass | Ability |
|---|---|---|---|
| Food Delivery | 1.0 m/s | 1.0 kg | Food |
| Safety Guidance | 1.5 m/s | 0.5 kg | Information |
| Medical Assistance | 1.5 m/s | 0.5 kg | Medicine |
| Food | Food | |||
|---|---|---|---|---|
| Delivery 1 | Delivery 2 | (a = 0.05) | ||
| Task 1 | TD-innerATT | 0.47 | 0.53 | 0.36 < 3.84 |
| TD | 0.82 | 0.18 | 81.9 > 3.84 | |
| Task 2 | TD-innerATT | 0.56 | 0.44 | 1.44 < 3.84 |
| TD | 0.18 | 0.82 | 81.9 > 3.84 | |
| Task 1 | PPO-innerATT | 0.48 | 0.52 | 0.16 < 3.84 |
| PPO | 0.32 | 0.68 | 25.9 > 3.84 | |
| Task 2 | PPO-innerATT | 0.45 | 0.55 | 1.00 < 3.84 |
| PPO | 0.73 | 0.27 | 42.3 > 3.84 |
| Food Delivery 1 | Food Delivery 2 | ||
|---|---|---|---|
| Task 1 | TD-innerATT | 0.17 | 0.17 |
| TD | 0.43 | 0.40 | |
| Task 2 | TD-innerATT | 0.22 | 0.16 |
| TD | 0.45 | 0.49 | |
| Task 1 | PPO-innerATT | 0.26 | 0.30 |
| PPO | 0.44 | 0.46 | |
| Task 2 | PPO-innerATT | 0.30 | 0.18 |
| PPO | 0.47 | 0.44 |
| Food | Food | |||
|---|---|---|---|---|
| Delivery 1 | Delivery 2 | (a = 0.05) | ||
| Task 1 | TD-innerATT | 0.51 | 0.49 | 0.04 < 3.84 |
| TD | 0.82 | 0.18 | 81.9 > 3.84 | |
| Task 2 | TD-innerATT | 0.57 | 0.43 | 0.36 < 3.84 |
| TD | 0.17 | 0.83 | 87.1 > 3.84 | |
| Task 1 | PPO-innerATT | 0.51 | 0.49 | 0.04 < 3.84 |
| PPO | 0.34 | 0.66 | 20.4 > 3.84 | |
| Task 2 | PPO-innerATT | 0.47 | 0.53 | 0.36 < 3.84 |
| PPO | 0.72 | 0.28 | 38.7 > 3.84 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; Huang, C.; Liu, R. Development of an Attention Mechanism for Task-Adaptive Heterogeneous Robot Teaming. AI 2024, 5, 555-575. https://doi.org/10.3390/ai5020029
Guo Y, Huang C, Liu R. Development of an Attention Mechanism for Task-Adaptive Heterogeneous Robot Teaming. AI. 2024; 5(2):555-575. https://doi.org/10.3390/ai5020029
Chicago/Turabian StyleGuo, Yibei, Chao Huang, and Rui Liu. 2024. "Development of an Attention Mechanism for Task-Adaptive Heterogeneous Robot Teaming" AI 5, no. 2: 555-575. https://doi.org/10.3390/ai5020029
APA StyleGuo, Y., Huang, C., & Liu, R. (2024). Development of an Attention Mechanism for Task-Adaptive Heterogeneous Robot Teaming. AI, 5(2), 555-575. https://doi.org/10.3390/ai5020029






