Abstract
Recently, some effort went into explaining intransparent and black-box models, such as deep neural networks or random forests. So-called model-agnostic methods typically approximate the prediction of the intransparent black-box model with an interpretable model, without considering any specifics of the black-box model itself. It is a valid question whether direct learning of interpretable white-box models should not be preferred over post-hoc approximations of intransparent and black-box models. In this paper, we report the results of an empirical study, which compares post-hoc explanations and interpretable models on several datasets for rule-based and feature-based interpretable models. The results seem to underline that often directly learned interpretable models approximate the black-box models at least as well as their post-hoc surrogates, even though the former do not have direct access to the black-box model.
1. Introduction
Machine learning methods are widely used in various domains and applications such as healthcare, finance, etc. In many cases, the learned models are so-called black-box models, meaning that the learned representation is not easily interpretable. Hence, the predictions they make are not easily comprehensible to humans.
The necessity of having some explanations to understand how the model works led to substantial research on explaining learned models [1]. One can distinguish between local explanations, which try to approximate the black-box model in the vicinity of an example that should be explained (e.g., [2,3]), or global models, which try to capture the behavior of the entire black-box model in an interpretable surrogate. Recently, several approaches have been investigated which try to construct global models from local explanations (e.g., [4,5]). Furthermore, one can distinguish between model-specific explanation methods, which are tailored to specific types of black-box models such as deep neural networks (e.g., [6]), and model-agnostic explanation methods, which do not make any assumptions about the nature of the learned black-box model (e.g., [2]).
While the importance of explaining black-box models is not deniable in high stake decision problems, various challenges and issues have renewed the interest in learning interpretable models, such as decision trees or rule sets, in the first place.
The obvious problem is that post-hoc explanation methods only approximate the underlying black-box model so that the found explanations often do not accurately reflect the behavior of the model they are meant to explain. This is typically captured by monitoring the fidelity of the surrogate model, i.e., the degree to which it follows the underlying model. In addition, if the explanation works ideally without any errors, it might use completely different features, which means that the explanation is not faithful to the computations in the black-box model. Furthermore, there might be flaws in black-box models, and in this situation, troubleshooting gets more complicated since both explanations and black-box models must be maintained. For these and other reasons, it has been argued that more efforts should be devoted to learning more accurate interpretable models [7].
Motivated by this observation, this paper evaluates to what extent post-hoc explanations can be replaced with directly learned interpretable methods unaware of the underlying black-box models. The goal is to investigate whether the performance of an interpretable model is accurate enough to be used as a replacement for model-agnostic methods or, conversely, to see how much information is lost when doing so. To reach this goal, the performance of local and global explanation methods will be evaluated by putting the theories to the test, thereby assessing the validity of the assumption. We conduct a series of experiments to evaluate and compare the performance of several interpretable models to explain black-box models. Our results on rule-based and feature-based explanatory models seem to confirm our hypothesis.
2. Related Work
Numerous research studies have been conducted on the explainability and interpretability of black-box models. We refer to [8,9,10] for general surveys and only briefly recapitulate the most relevant works for our study. In particular, we are interested in comparing works in two major categories: directly learning interpretable methods and post-hoc explanation methods.
2.1. Direct Learning of Interpretable Models
Directly learning interpretable methods are a subset of algorithms that create interpretable models without the need for an underlying black-box model. Linear regression, logistic regression, and decision trees are the most common interpretable models. We are primarily interested in learning logical rules [11], for which Ripper (Repeated Incremental Pruning to Produce Error Reduction) is still a state-of-the-art method that is very hard to beat [12]. For the case of feature-based explanations, we will consider GA2Ms as an interpretable (white box) model based on Generalized Additive Models. It is designed to have high accuracy compared to the state-of-the-art machine learning models while keeping the intelligibility, and explainability [13].
2.2. Local Explanations of Black-Box Models
Post-hoc explanation methods can either provide a global explanation of the entire black-box model (global surrogate) or a local explanation for a given example (local surrogate). Some of the best-known methods are model-agnostic, i.e., they work for any type of underlying black-box model.
Shap [3] is an algorithm based on game theory that provides explanations for predictions in the form of post-hoc weights that reflect the importance of an input value for the final prediction. Ribeiro et al. [2] proposed Local Interpretable Model agnostic Explanation (LIME), which focuses on explaining individual predictions of the black-box model. Although LIME is in principle independent of the type of interpretable model used for explanations, it is typically also used for feature-weight-based explanations. LOcal Rule-based Explanations (LORE) is a variant of LIME, which is specifically tailored to rules as local surrogate models [14]. It provides interpretable and locally faithful explanations by applying a local interpretable predictor on a synthetical neighborhood generated by a genetic algorithm. The algorithm then derives a meaningful explanation in the form of rules from the local interpretable predictor. Model Agnostic Supervised Local Explanations (MAPLE) is a hybrid system that may serve as both, a highly accurate tree-based predictive model, as well as a feature-based local explanatory model [15].
2.3. Combining Local Explanations into Global Models
While interpretable models are typically global, i.e., they provide a method for classifying every possible instance in the data space, post-hoc explanations are typically local, i.e., they pertain only to the example for which they were generated. Rule-based models are particularly interesting in this context because a global model is typically a rule set or a rule list consisting of individual rules, which may be viewed as local models [16,17]. More generally, recently, several works have focused on combining local explanations into global models, which facilitates comparison between local and global models.
For example, Yang et al. [18] proposed Global Interpretation via Recursive Partitioning (GIRP), a method to build a global interpretation tree for a wide range of machine learning models based on their local explanations. This method recursively partitions the input variable space by maximizing the contribution of input variables averaged from local explanations between the divided spaces. The method’s output is a binary so-called interpretation tree, which describes a set of decision rules that approximates the original model. van der Linden et al. [19] proposed Global Aggregations of Local Explanation (GALE) as an approach to provide insight into the global decision-making process. This paper tries to understand to what extent local explanations are able to provide global insights on a black-box model. For this purpose, local explanations from the LIME algorithm are analyzed and aggregated using several approaches to evaluate how they are able to represent global insight. Finally, Setzu et al. [4] proposed the GLobal to loCAL eXplainer (GLocalX), a “local-first” model-agnostic explanation method. This method aims to use local explanation methods and their benefits for producing a global explanation. The algorithm starts from local explanations in decision rules and iteratively generates global explanations by aggregating them.
3. Methods and Experimental Setup
3.1. Problem Statement
This study addresses the validation of the idea proposed by Rudin [7] that research should focus more on interpretable models rather than explaining black-box models. To this end, we select and compare pairs of a model-agnostic post-hoc explanation method and an independent, directly trained interpretable method, which both produce the same syntactic class of models. More precisely, as shown in Figure 1, we learn a black-box model from a data set and training set. With training set consisting of n examples where each example has m features and a label . We then employ common methods from explainable AI to approximate with an interpretable model . In parallel, we directly learn a syntactically comparable model from the same data and compare it to .
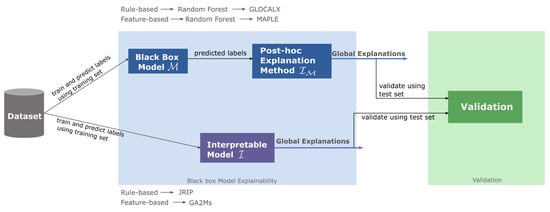
Figure 1.
Experimental setup for comparing post-hoc explanations to directly trained interpretable models.
Thus, the research question that we investigate is to what extent an interpretable model that has been directly learned from data can approximate an independently learned black-box model , and how much of this fidelity is lost compared to an interpretable model , which had access to . One would, of course, expect that has a higher fidelity (and consequently maybe also a higher accuracy) than , because had access to M, whereas was trained independently. However, both are trained on the same data, so that implicit correlations may emerge.
Moreover, it is well-known that interpretable models are often less accurate than because they typically only approximate the underlying black-box model . This approximation is often measured in terms of fidelity, i.e., how well approximates the predictions of .
Thus, we intend to find out how the two models , and are compared not only in terms of commonly used parameters such as their complexity or the accuracy of the respective models but also in terms of this fidelity.
Furthermore, different ways of explaining a model might exist according to the so-called Rashomon effect [20], which, in a nutshell, states that in particular with structured models such as trees or rules, there are often multiple different models which explain the data equally well. We are interested in understanding whether there are differences in the explanations provided by our selected interpretation methods for a model.
Generally, we focus on rule-based and feature-based methods, whereby we compare the methods with respect to the logical rules they learn and the latter according to the feature weights that are attributed to them. The following sections will introduce the selected methods and algorithms we are interested in.
3.2. Rule-Based Interpretability Methods
GLocalX and JRip are selected as model-agnostic and interpretable models, respectively. Both methods generate explanations in the form of rulesets, which are our preference as they produce more compact models and are very close to human reasoning language [11].
JRip [12] is a classic rule learning algorithm that generates rules by executing three main steps; grow, prune, and optimize. Before learning each individual rule, JRip splits the examples it covers into two sets, a growing set from which the next rule is learned and a pruning set used to simplify the learned rule. The rule set is further optimized by re-learning individual rules in the context of other rules when a sufficient number of positive examples have been covered.
GLocalX [4] generates global explanations for a black-box model using local explanations created by a local surrogate model such as LORE [14], and the predicted labels from a black-box model. The algorithm takes a set of local explanations as input, and then tries to iteratively merge and combine them to provide more general rules. At each iteration, it sorts the local explanations into a queue according to their similarities and samples a batch of data to merge the candidate explanations. The merge operation gets executed once a pair of explanations with the closest similarity is popped from the queue. The merge function consists of cut and join operators, which allow the algorithm to generalize a set of explanations while balancing fidelity and complexity. To merge two local explanations and , the join and cut operators apply to non-conflicting and conflicting explanations, respectively. Thus, join generalizes explanations at the cost of fidelity while cut specializes explanations at the cost of generality. If the result of the merge function satisfies simplicity and accuracy constraints, a merged pair is kept, and and would be replaced by the merged pair. Finally, explanations with low fidelity are filtered out using the parameter that indicates a per-class trimming threshold.
3.3. Feature-Based Interpretability Methods
Among various feature-based methods on interpretability, GA2Ms [13] is selected as a glass-box model, intelligible algorithm, and MAPLE is selected as a post-hoc method.
GA2Ms and MAPLE are based on linear models and provide feature weights that explain the contribution of the features in the prediction.
GA2Ms algorithm is based on Generalized Additive Models (GAM) which is a generalized linear model. GAM considers that the model could be the sum of arbitrary functions instead of simple weights.
GA2Ms extends GAM, including terms that capture the interaction of features values:
The method starts by building up a small tree for each feature separately in a boosting fashion so that each tree is only related to one feature. This procedure will be repeated for a fixed number of iterations, so that eventually, for each feature, we obtain an ensemble of trees. In the next step, the generated trees for each feature are summarized in a graph by recording the prediction of each tree in a graph. At the end of this step, there is a graph for each feature that builds the model. Since GA2Ms is an additive model, we can easily reason the contribution of each feature to the prediction [13].
As for the prediction in GA2Ms each function , for each feature acts like a lookup table that returns a term contribution. The returned term contributions are added up, and the final predictions are calculated by passing them through function g. The additivity enables GA2Ms to give us the impact of each feature on the prediction.
MAPLE uses classical linear modeling and a tree interpretation of tree ensembles as a supervised neighborhood approach and feature selection method to detect global and example-based explanations. The algorithm first identifies the training points in the training set that are most relevant to the prediction. It then assigns similarity weights to each training point by calculating how often and x are put in the same leaf node in trees as defined in (2)
The weights of the training points are then used in the linear model to make a prediction and a local explanation by solving the linear regression problem in
3.4. Experimental Setup
The two experiments were performed on some commonly used datasets, mostly from the UCI collection of machine learning databases [21]. All the datasets are binary classification problems. In the adult dataset, the task is to determine whether a person earns over 50 K a year. The compas two-year dataset contains recidivism risk score that predicts a person’s likelihood of committing a crime in the next two years. The German dataset records whether a loan applicant has good or bad credit risk. The NHANES I dataset is a follow-up mortality data from the National Health and Nutrition Examination Survey epidemiologic follow-up study. The credit card fraud dataset contains credit card transactions labeled as legitimate or fraudulent transactions. Finally, the Bank dataset is from a direct marketing campaign of a Portuguese banking institution, where the goal is to predict whether the client will subscribe to a term deposit.
3.5. Experimental Setup on Rule-Based Models
To prepare the experiments, we follow the same procedure as in [4]. As the preprocessing step in the experiment, the dataset is separated into three parts: 60% of the data is dedicated to training the black-box model , 20% is for training GLocalX and the last 20% is used as unseen data for validation .
As pointed out in Section 3.2, GLocalX requires a black-box model and a local explanation method to extract the global rules. To this end, we use random forests [22] as a black-box model to predict the labels for the 20% training data for GLocalX. We use the LORE algorithm to find local explanations of each sample in the same partition. An overview of the required blocks is shown in Figure 2.
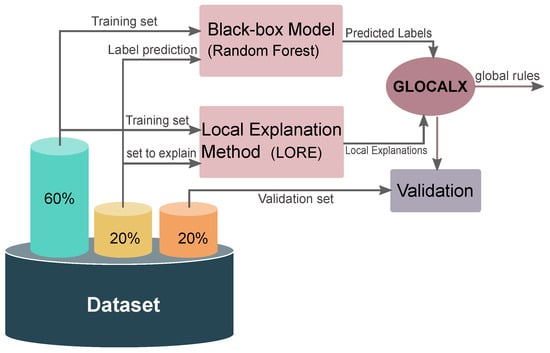
Figure 2.
An overview of experiment setup for GLocalX.
For the experiments with JRip, we employ the first 80% of the dataset as the training data. Note that JRip internally also splits the data into growing set and pruning set, which is quite similar to the internal split of GLocalX.
Since rule-based interpretability methods provide label prediction, the evaluation is done through accuracy and fidelity. In addition, the number of rules is considered another evaluation metric.
4. Results and Discussion
This section describes the results of rule-based and feature-based models experiments.
4.1. Results on Rule-Based Models
In order to evaluate the performance of the glass-box model JRip as a substitute for the explanatory model GLocalX, we tried various values for the parameter of GLocalX, and compared the resulting rule set against a rule set that can be directly obtained from JRip. Table 1 shows the results of JRip and all parameters on the adult dataset.

Table 1.
Evaluation on adult dataset.
As can be seen, for the adult dataset, GLocalX obtained its best results in terms of fidelity and the number of rules with . Hence this value is selected for further discussion. By comparing the GLocalX results to the JRip in Table 1, we see that both methods obtain a quite comparable performance in terms of accuracy and fidelity: the most accurate theory in terms of accuracy and fidelity learned by GLocalX (for ) has lower accuracy than JRip, which, however, learns a somewhat more complex rule set. However, even if we take a look at a rule set with a comparable complexity (), the result is still quite similar to the previous observation: Even though JRip has not seen the underlying black-box model, it seems to deliver a better explanation of the model than GLocalX, in the sense that it has a higher fidelity to the black-box model than GLocalX, despite the fact that GLocalX tried to mimic the black-box model, while JRip learned an independent rule set.
Table 2 shows the results for all datasets, with the best for each dataset. We can see that both algorithms obtain a quite comparable performance in the number of rules and accuracy, with, again, slight advantages for JRip.

Table 2.
Summary of Evaluation on datasets.
To better understand the rules, Table 3 compares the rules learned by GLocalX and JRip for the adult data set. Even though there are some common features such as “age”, “capital-gain”, and “marital-status” in the global rules of both GLocalX, and JRip, in general, very different rules were learned, which had similar fidelity as global explanations. This is an instantiation of a phenomenon known as the Rashomon effect [20], namely that very different models can obtain a similar predictive accuracy and that small changes in a dataset may often lead to significant changes in a learned symbolic model. However, here we see this phenomenon from a novel angle: Very different rules may provide different explanations with the same fidelity to an underlying black-box model.

Table 3.
Rules learned on adult.
Furthermore, the trade-off between interpretability and accuracy states that models with high interpretability might have lower accuracy. By comparing the rules provided by GLocalX and JRip in terms of the rule length and number of conditions for each rule, we see that in general GLocalX generates shorter rules with smaller number of conditions than JRip. Thus, as a simple inference, GLocalX can be more understandable for human since it generates shorter and simpler rules. However, JRip obtains higher accuracy while generating more complex rules. It is noteworthy to mention that the interpretability and understandability of rules can be evaluated from different perspectives and it needs to be studied deeply.
4.2. Results on Feature-Based Interpretability Methods
As mentioned in previous sections, GA2Ms and MAPLE are selected as feature-based interpretability methods. Again, we aim to evaluate the performance of the two methods in terms of their stand-alone performance (accuracy) as well as their similarity to a black-box model (fidelity). We will first show the contribution of features to the prediction by plotting the feature importance ranks provided by GA2Ms and MAPLE. Since the MAPLE algorithm does not give global feature importance in the form of weights, we use the average linear regression weights for each feature as the feature importance.
The detailed results of the feature importance plot and feature importance ranks for GA2Ms and MAPLE methods on the adult are tabulated and shown graphically in Figure 3. By comparing the results from MAPLE and GA2Ms methods, we see that “age” and “capital_gain” have high contributions to the prediction. Some features such as "marital_status” in MAPLE have low contributions while in GA2Ms they highly contribute to the prediction which, again, illustrates the Rashomon effect, i.e., different feature weights can be provided as explanations.
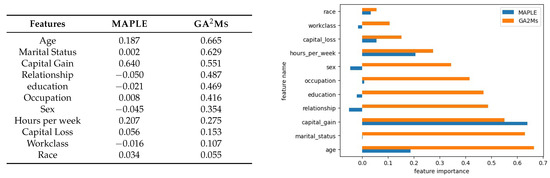
Figure 3.
MAPLE and GA2Ms feature importance for adult dataset.
In order to compare both methods with respect to fidelity, we need to have an identical prediction method for both MAPLE and GA2Ms. To that end, we use normalized feature importance weights from the two methods GA2Ms and MAPLE as and . Then, for each explanation method, we use (4) to calculate the value for each sample in the dataset.
In (4), for each sample in the dataset, weights derived from MAPLE and GA2Ms are multiplied by the features. To convert probabilities to binary labels, we tune the threshold using the ROC curve and as defined in (5):
where TPR and FPR are true positive and false positive rates, respectively. The obtained values are then used to measure accuracy and fidelity by computing the AUC.
In this way, the accuracy and fidelity of the two methods are again evaluated on different datasets, and the results are shown in Table 4. The results confirm that in all the datasets, GA2Ms has higher accuracy and fidelity compared to MAPLE, again underlining the hypothesis behind this work, namely that directly learned interpretable models may provide excellent explanations for black-box models, even if they have not seen this model, simply because well-trained interpretable and black-box models will necessarily correlate with each other.

Table 4.
GA2Ms and MAPLE fidelity and accuracy evaluation on datasets.
5. Conclusions
Interpretable machine learning has gained importance in various problems and applications. The key idea behind many approaches that aim at explaining a black-box model is to approximate it globally or locally with an interpretable surrogate model. However, in this approximation, much of the predictive quality of the original model is lost, and it is unclear whether the surrogate model is actually sufficiently faithful to the black-box model. In this work, we showed that maybe somewhat surprisingly, interpretable models, which have not seen the black-box model, may be equally faithful to the black-box model as the surrogate models that have been learned from them.
In particular, we selected GLocalX and JRip as post-hoc and interpretable rule-based methods, and MAPLE and GA2Ms as post-hoc and interpretable feature-based methods, respectively. According to the experiment’s results, the performance of interpretable models in terms of accuracy and fidelity is as good as post-hoc methods. However, various explanations can be provided by the two methods in the form of rules or feature importance. Thus, interpretable models can be used instead of post-hoc methods. In addition, differences in explanations provided by rule-based and feature-based methods can be another research topic in the future to measure the efficiency of different explanations on a dataset and determine the most efficient explanation.
Author Contributions
Conceptualization, P.M. and J.F.; Investigation, P.M.; Methodology, P.M.; Software, P.M.; Supervision, J.F.; Validation, J.F.; Writing—original draft, P.M.; Writing—review & editing, J.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created in this study.
Acknowledgments
Supported by Johannes Kepler Open Access Publishing Fund and the federal state of Upper Austria.
Conflicts of Interest
The authors declare no conflict of interest.
Correction Statement
This article has been republished with a minor correction to the Acknowledgments statement. This change does not affect the scientific content of the article.
References
- Guidotti, R.; Monreale, A.; Ruggieri, S.; Turini, F.; Giannotti, F.; Pedreschi, D. A Survey of Methods for Explaining Black Box Models. ACM Comput. Surv. 2019, 51, 93. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why Should I Trust You?”: Explaining the Predictions of Any Classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD); Krishnapuram, B., Shah, M., Smola, A.J., Aggarwal, C.C., Shen, D., Rastogi, R., Eds.; ACM: San Francisco, CA, USA, 2016; pp. 1135–1144. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S. A Unified Approach to Interpreting Model Predictions. In Advances in Neural Information Processing Systems 30, Proceedings of the NIPS 2017, Long Beach, CA, USA, 4–9 December 2017; Guyon, I., von Luxburg, U., Bengio, S., Wallach, H.M., Fergus, R., Vishwanathan, S.V.N., Garnett, R., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2017; pp. 4765–4774. [Google Scholar]
- Setzu, M.; Guidotti, R.; Monreale, A.; Turini, F.; Pedreschi, D.; Giannotti, F. GLocalX—From Local to Global Explanations of Black Box AI Models. Artif. Intell. 2021, 294, 103457. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.G.; Chen, H.; DeGrave, A.J.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S. From Local Explanations to Global Understanding with Explainable AI for Trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef] [PubMed]
- Montavon, G.; Binder, A.; Lapuschkin, S.; Samek, W.; Müller, K. Layer-Wise Relevance Propagation: An Overview. In Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Samek, W., Montavon, G., Vedaldi, A., Hansen, L.K., Müller, K., Eds.; Springer: Berlin/Heidelberg, Germany, 2019; pp. 193–209. [Google Scholar] [CrossRef]
- Rudin, C. Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 2019, 1, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Molnar, C. Interpretable Machine Learning. 2019. Available online: https://christophm.github.io/interpretable-ml-book/ (accessed on 1 September 2022).
- Samek, W.; Montavon, G.; Vedaldi, A.; Hansen, L.K.; Müller, K. (Eds.) Explainable AI: Interpreting, Explaining and Visualizing Deep Learning; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2019; Volume 11700. [Google Scholar] [CrossRef]
- Jair Escalante, H.; Escalera, S.; Guyon, I.; Baró, X.; Güçlütürk, Y.; Güçlü, U.; van Gerven, M.A.J. (Eds.) Explainable and Interpretable Models in Computer Vision and Machine Learning; The Springer Series on Challenges in Machine Learning; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar] [CrossRef]
- Fürnkranz, J.; Gamberger, D.; Lavrač, N. Foundations of Rule Learning; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Cohen, W.W. Fast Effective Rule Induction. In Machine Learning Proceedings 1995, Proceedings of the Twelfth International Conference on Machine Learning, Tahoe City, CA, USA, 9–12 July 1995; Prieditis, A., Russell, S., Eds.; Morgan Kaufmann: San Francisco, CA, USA, 1995; pp. 115–123. [Google Scholar] [CrossRef]
- Lou, Y.; Caruana, R.; Gehrke, J.; Hooker, G. Accurate intelligible models with pairwise interactions. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), Chicago, IL, USA, 11–14 August 2013; pp. 623–631. [Google Scholar]
- Guidotti, R.; Monreale, A.; Giannotti, F.; Pedreschi, D.; Ruggieri, S.; Turini, F. Factual and Counterfactual Explanations for Black Box Decision Making. IEEE Intell. Syst. 2019, 34, 14–23. [Google Scholar] [CrossRef]
- Plumb, G.; Molitor, D.; Talwalkar, A. Model Agnostic Supervised Local Explanations. In Advances in Neural Information Processing Systems 31, Proceedings of the NeurIPS 2018, Montreal, QC, Canada, 3–8 December 2018; Bengio, S., Wallach, H.M., Larochelle, H., Grauman, K., Cesa-Bianchi, N., Garnett, R., Eds.; Curran Associates Inc.: Red Hook, NY, USA, 2018; pp. 2520–2529. [Google Scholar]
- Fürnkranz, J. From Local to Global Patterns: Evaluation Issues in Rule Learning Algorithms. In Local Pattern Detection; Morik, K., Boulicaut, J.F., Siebes, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2005; pp. 20–38. [Google Scholar]
- Knobbe, A.J.; Crémilleux, B.; Fürnkranz, J.; Scholz, M. From Local Patterns to Global Models: The LeGo Approach to Data Mining. In From Local Patterns to Global Models: Proceedings of the ECML/PKDD-08 Workshop (LeGo-08); Knobbe, A.J., Ed.; University and State Library Darmstadt: Darmstadt, Germany, 2008; pp. 1–16. [Google Scholar]
- Yang, C.; Rangarajan, A.; Ranka, S. Global Model Interpretation Via Recursive Partitioning. In Proceedings of the 20th IEEE International Conference on High Performance Computing and Communications; the 16th IEEE International Conference on Smart City; the 4th IEEE International Conference on Data Science and Systems (HPCC/SmartCity/DSS), Exeter, UK, 28–30 June 2018; pp. 1563–1570. [Google Scholar] [CrossRef]
- van der Linden, I.; Haned, H.; Kanoulas, E. Global Aggregations of Local Explanations for Black Box models. arXiv 2019, arXiv:1907.03039. [Google Scholar]
- Breiman, L. Statistical modeling: The two cultures. Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Dua, D.; Graff, C. UCI Machine Learning Repository.University of California, Irvine, School of Information and Computer Sciences. 2017. Available online: http://archive.ics.uci.edu/ml (accessed on 3 April 2023).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).