A Four-Stage Algorithm for Community Detection Based on Label Propagation and Game Theory in Social Networks

Abstract

Over the years, detecting stable communities in a complex network has been a major challenge in network science. The global and local structures help to detect communities from different perspectives. However, previous methods based on them suffer from high complexity and fall into local optimum, respectively. The Four-Stage Algorithm (FSA) is proposed to reduce these issues and to allocate nodes to stable communities. Balancing global and local information, as well as accuracy and time complexity, while ensuring the allocation of nodes to stable communities, are the fundamental goals of this research. The Four-Stage Algorithm (FSA) is described and demonstrated using four real-world data with ground truth and three real networks without ground truth. In addition, it is evaluated with the results of seven community detection methods: Three-stage algorithm (TS), Louvain, Infomap, Fastgreedy, Walktrap, Eigenvector, and Label propagation (LPA). Experimental results on seven real network data sets show the effectiveness of our proposed approach and confirm that it is sufficiently capable of identifying those communities that are more desirable. The experimental results confirm that the proposed method can detect more stable and assured communities. For future work, deep learning methods can also be used to extract semantic content features that are more beneficial to investigating networks.

1. Introduction

Complex systems can be modeled as networks that are composed of subnets called communities, which are denser and more connected than the other parts of the network.

The structures of communities are directly related to the functions of a network. Identifying these structures is expected to yield helpful intuitions about the functional organization of the specific network. Community detection has been the most important topic in complex networks in recent decades, and one that has attracted many researchers, aiming to discover groups of nodes based on modular tendencies. The ability to detect communities provides deeper insight into the functionality of groups and how the networks are formed.

Different studies have various perspectives on detecting network communities, such as partitioning methods, modularity-based methods, factorization-based methods, etc. [1,2]. Some methods consider the global structure and the whole network’s perspective, such as Infomap [3], Louvain [4], Fastgreedy [5], etc. while in many cases, they suffer from high cost and complexity.

On the other hand, some methods consider the local structure and extract the local information of the nodes [1,2,3,4]. These methods conquer the limitations of global structure-based methods. However, due to the significant development and growth of social networks, and the lack of access to global structure information, these types of algorithms may fall into a local minimum and may not have the desired accuracy, despite their low time complexity.

Therefore, creating a balance between global and local information, accuracy and time complexity is one of the crucial issues in community detection. Another important point is to achieve established and assured communities. In general, the environment of complex networks in terms of the relationships and interactions between their members can be considered as a game in which nodes as players or agents try to join or leave a community based on similar characteristics. On one hand, we can consider a cooperative environment as one where individuals with similar features interact with each other, they constitute the communities and attempt to promote the community’s utility. On the other hand, it can also be considered a competitive space in which agents try to join or leave their communities and enhance their profits. A logical approach is necessary to interpret these relations. By borrowing game theoretical concepts from economics, this issue can easily be analyzed.

Game theory is a very useful mathematical means for studying strategic conditions and modeling the competition and cooperation between decision-makers to provide rational and optimal solutions in complicated situations. Generally, game theory is divided into two categories: cooperative and non-cooperative. A game that focuses on the member’s cooperation is classified as a cooperative game [6], where every individual tries to improve the coalition’s utility. Conversely, in non-cooperative games, individuals attempt to increase their own utilities and ignore the group’s profits.

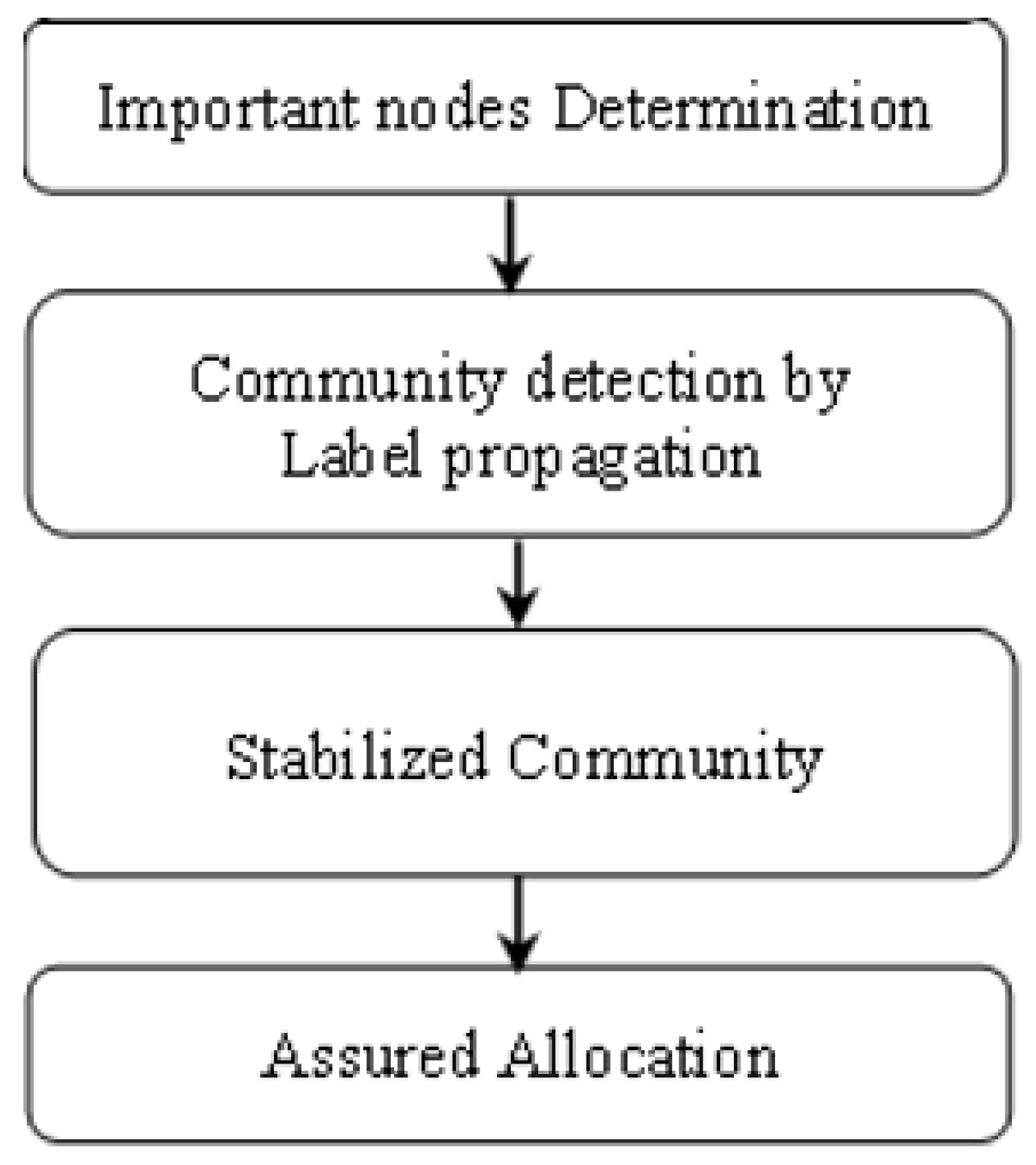
Hence, we came up with the idea to take into account both global and local information structures and cooperative and non-cooperative games to extract more satisfactory and assured communities. The proposed algorithm includes four stages: finding the important and central vertices, propagating the labels and identifying initial communities, merging these communities, and finally stabilizing them and assuring the nodes’ allocation.

Taking this algorithm into account, the overall efficiency of the proposed algorithm increased, and the computational cost diminished remarkably. The subsequent parts of this paper are organized as follows: In Section 2, the literature about various approaches to community detection problems is reviewed. The basic concepts are mentioned in Section 3. The proposed model is brought up in Section 4. Analysis of the experimental results is discussed in Section 5, and finally concluding remarks and future works are presented in Section 6.

2. Related Work

A community is a subset of elements close to each other within their group rather than to the rest of the network. According to [1], approximately, the nodes of the same community exhibit similar characteristics, functions, and/or roles.

Community detection is one of the most fascinating research topics which has attracted the attention of many scientists in several fields, such as biology, statistics, economics, and computer science [1]. In general, community detection is an NP-Complete problem [2,3]. Various studies in the literature have tried extracting communities according to the global structure and whole network’s perspectives, like Infomap [3], Louvain [4], Fastgreedy [5], etc., while in many cases, they suffer high cost and complexity.

Conversely, some methods consider the local structure and extract the local information of the nodes, and do not focus on the global knowledge of the network. Therefore, they are not as robust as the global algorithms. In addition, these types of methods may be caught into a local optimum. In contrast, they demonstrate less time complexity than global methods and are applicable to large-scale networks.

Some of the local algorithms are based on clustering, [5,6,7,8,9,10,11,12,13,14,15,16,17,18]. However, these approaches have some limitations, such as poor cluster descriptors and their high sensitivity to initial phase settings.

So, considering both global and local structures in community detection can be useful in eliminating the limitations of each method [19].

It is also noticeable that the communities detected based on the above-mentioned approaches may not be sufficiently qualified, to the extent that some nodes may be assigned to unreliable groups.

To circumvent this problem, game theoretical approaches to identifying communities have been proposed.

They have imagined the community detection issue as a game, in which each member rationally chooses a community and maximizes its score. Members of a community also attempt to enhance the group’s utility.

Many approaches address the problem of community detection by using the non-cooperative game theory, and some others employ the cooperative one. Along the cooperative line, where individuals form a group based on the similarity of their communal interests, Mcsweeney et al. [20] considered each node as a player in a hedonic game, which tries to form fair and stable community structures. Zhou et al. [21], suggested the Shapley value to detect communities of a given social network. Additionally, they proposed a coalitional game for investigating communities based on the topological structure of nodes [16]. Hajibagheri and his colleagues [22] imagined each node as a rational individual trying to maximize the Shapley value. They considered community structure as Nash equilibrium. Two approaches from cooperative game theory based on the Myerson value and hedonic games were recommended in [23]. Both of them detected communities with different resolutions. Xu Zhou et al. [24] considered nodes as players who try to enhance the utility of their coalition by participating in a cooperative game. They proposed an edge weight computation for calculating the Shapley value of nodes and coalitions.

Regarding the non-cooperative aspect, according to Chen et al. [25], the utility of an agent is determined as gain and loss functions based on the modularity and community membership fee, respectively. Finally, the community structure was revealed by the local equilibrium of the game. Additionally, the authors in [26] regarded each vertex as an agent trying to join a community and assumed its utility as a linear function. Nash’s stability guarantees the stability of communities. A framework based on the iterative game has been proposed in [27] for detecting communities in social networks. They considered nodes as rational agents who play the game to enhance their utilities. To reveal community structure, a weighted potential game was defined in [23]. Communities become stable as they reach the Nash equilibrium point. Zhao et al. [28] suggested Co-game, a game-theoretic approach for extracting community in real networks. This method produces finer-grained partitions in the detection process by combining individual games and equilibrium.

An algorithm, based on game theory for detecting communities in online social networks, was also proposed by Vincezo Moscato et al. [29]. They modeled the process of community formation as a game, in which each node as a player aims to maximize its goal. A new approach based on both cooperative and non-cooperative games for detecting communities was suggested by [30], which considered nodes as players in cooperative games who attempt to enhance the group’s utility while engaging in a non-cooperative game to improve their utility.

In the first phase, this method, similarly to a hierarchical agglomerative method, considers a cooperative game in which individuals in a social network are modeled as rational players and aims to improve the utility of the group by cooperating with other players to form coalitions. In large datasets, this method, like other local and agglomerating approaches, typically suffers from high computational complexity.

The main problem with the existing approaches to game-theory-based community detection is that the game is initially started with single nodes. The main problem with the existing approaches to game-theory-based community detection is that the game is initially started with single nodes, with a large amount of comparisons between them, which in turn increases the computational cost, while in our approach the game is just considered for some extracted initial communities, thus leading to fewer comparisons between the nodes.

3. Basic Concepts

3.1. The Necessity of Representing the Network

Given a network ${\mathrm{G}=(\mathrm{V}, \mathrm{E}), \mathrm{V}=\{\mathrm{v}}_1{, \mathrm{v}}_2{, \mathrm{v}}_3{, \dots , \mathrm{v}}_{\mathrm{N}}\}$ is a set of nodes, where N is the number of nodes. $E={\left\{e_{ij}\right\}}_{i,j=1}^N$ consists of the set of edges, where $e_{ij }$ encodes the edge between $v_i$ and $v_j$.

3.2. Community Detection

The community detection is to extract K communities, i.e., $C=\left\{C_1, C_2,\dots , C_k\right\}$, such that K ≪ N and ${\cup }_{k=1}^K C_k=V$. If these communities are non-empty, mutually exclusive subsets of V, i.e., $\forall i,j \in \left\{1,2,\dots ,K\right\}, i \ne j, C_{i }\cap C_{j }=\varnothing$, this is non-overlapping community detection, and nodes only can join one community. Conversely, this is entitled as overlapping communities, where nodes can join more than one community.

3.3. Sorensen Index

Sorensen–Dice coefficient, in short, the “Sorensen Index” [26], is a statistic that measures the similarity between two nodes by dividing the size of the intersection of their neighbor’s sets by the total number of their members (Equation (1)). The Sorensen index considers the degree of the two nodes and the number of their common neighbors.

The Sorensen index output is between 0 and 1:

$$S_{Sorenson}\left(u,v\right)=\frac{2\times \left|N_u\cap N_v\right|}{d_u+d_v}$$

(1)

where $N_u,N_v$, and $d_u,d_v$ are the neighbor sets and the degree of node i, respectively.

3.4. Game Theory Background

Game theory is a very useful mathematical means for studying strategic conditions between decision-makers to provide rational solutions in complicated situations. The environment of the relationships and interactions between the members of complex networks can be considered as a game in which nodes as players try to join or leave a community based on similar characteristics, where the decisions of one player influence the other player’s payoffs [25].

Let $u_i$ be the utility function of node$i\in V$. For each community, $C_i\in C , u_{i }\left(C_i\right)$ demonstrates the utility of node i by being in the community$C_i$. Each node (player) tries to join a community and enhance its utility. It should be noted that the utility of any node depends on the community to which it belongs.

4. The Proposed Model

As mentioned before, the four-stage algorithm (FSA) has considered both global and local information structures with regard to the network. An overview of the proposed method can be seen in Figure 1.

Let us say, in the first step of the proposed algorithm, important nodes are determined according to their degree and relative distance. In the second step, the initial communities are detected based on the label propagation method. Next, the extracted communities are stabilized by the cooperative game, and finally, the non-cooperative game is applied to these clusters to ensure a rational allocation of nodes to the established communities.

So, identifying central nodes, label propagation, stabilizing the extracted communities, and ensuring the rational allocation of nodes to the established communities, can be considered the main characteristics of our approach.

Out of the above stages, the first two stages have been observed in previous works [25,27].

However, to be assured that the extracted communities would be stable, the third stage has been added based on the idea of a cooperative game. However, there are cases where a limited number of nodes may exist that could affiliate with a variety of different communities. In these cases, the fourth stage, which is based on the idea of a non-cooperative game, would help us to ensure the rational allocation of these nodes to the deserving/properly established communities.

One of the main problems of community detection is to discover communities which are sufficiently qualified. Therefore, inventing an algorithm that can assign nodes to reliable groups is one of the most important topics in complex networks, such as social networks. Therefore, the proposed algorithm attempts to obtain high-quality and reliable communities by relying on cooperative and non-cooperative games.

4.1. Important Nodes Determination

Important nodes in a community have a high degree of surrounding neighbors. Approximately, the nodes with this characteristic are more likely to be the communities’ centers. Speaking intuitively, the distances between important nodes are often far apart. Therefore, it can be assumed that the distance between two important nodes is not less than the average network distance. The average distance of graph G is [25]:

$$Avd=\frac{2}{n\left(n-2\right)}{{\displaystyle \sum }}_{u,v\in V}d\left(u,v\right)$$

(2)

where d(u,v) is the shortest distance between u and v.

Then, rank all nodes by their degrees; B = $\left\{v_1, v_2, \dots , v_n\right\}$.

Then, let $C$ be the set of important nodes. Initially, the highest-ranking node is settled in $C$:

$$\begin{gathered} C=\left\{v_1\right\} \\ \forall { \mathrm{v}}_{\mathrm{j}}\in \mathrm{B} \&{ \mathrm{v}}_{\mathrm{j}}\notin \mathrm{C}, \forall { \mathrm{v}}_{\mathrm{i}}\in \mathrm{C}, \mathrm{if} \mathrm{d}\left({\mathrm{v}}_{\mathrm{i}},{\mathrm{v}}_{\mathrm{j}}\right)\ge \mathrm{Avd}, then \mathrm{C}\cup \left\{{\mathrm{v}}_{\mathrm{j}}\right\}. \end{gathered}$$

Repeat this until the distance between two nodes is not greater than the average distance of the graph (Equation (2)).

4.2. Community Detection by Label Propagation

Nodes in a community have similar characteristics and common interests and are more connected to each other than the rest of the network.

Having identified the important nodes in the network, the remaining nodes join the communities according to the Sorensen index, which is a useful index for comparing similarities between the samples [26].

Now, if we assume that every important node in C corresponds to an identified community, then we label every node $u\in V-C$ as the node $v\in C$ if $u \mathrm{and} v$ are neighbors:

$$\begin{array}{c}{S}_{Sorenson}\left(u,v\right)=max max S_{Sorenson}\left(v_i,v_j\right)\\ v_i\in C ,v_j\in N \left(v_i\right)\end{array}$$

(3)

So, label u according to v. Repeat this process until all nodes have been labeled and assigned to the initial communities.

4.3. Stabilized Community

After the initial communities were formed by Label propagation, it is worth observing that some communities have only one member—in other words, they are sparse and do not have suitable quality—and these single nodes should join other communities with more nodes. For the sake of improving the quality, it is necessary to merge and reduce the initial communities. In this regard, we utilized the advantages of cooperative (coalitional form) games with a transferable utility, which is assumed that the earnings of a coalition (utility) can be distributed among the individuals in any conceivable way [28].

The reason for using cooperative game theory is that members of a community, based on their commitment towards the entire community, try to obtain a higher utility through cooperation. In other words, nodes in a network are modeled as logical agents (players), which try to form coalitions (communities) and cooperate to improve the group’s utility.

Coalitions with single or fewer nodes join larger groups according to the utility measurement. The community, which gains the highest utility, is selected as the final community, and the single node, or the group with fewer members, joins it. Merging operations will continue until the utility no longer improved the utility of the merged coalitions. In this situation, the game has reached an equilibrium, and accordingly no coalition is willing to merge with the others. In this way, the number of communities will reduce, and high-quality coalitions will be obtained. In other words, the communities are stabilized.

Given $S_i$ be a coalition of G = <V, E>. The utility function $u\left(S_i\right)$of S is:

$$u\left(S_i\right)={\sum }_{S\in S}(\frac{e\left(S_i\right)}{\left|E\right|}-{\left(\frac{D\left(S_i\right)}{2.\left|E\right|}\right)}^2)$$

(4)

where |E| is the total number of edges in G, $e\left(S_i\right)$ is the number of edges that connect nodes within $S_i$, and $D\left(S_i\right)$ is the sum of the degrees of the nodes within $S_i$. $u\left(S_i\right)$ is based on Newman’s modularity metric (Q) [25]. The modularity metric is one of the famous metrics that has been used in many kinds of research to measure the quality of the community structure in networks. The main idea of this index is based on comparing edge density within communities with the expected number in a random network. Thus, the value of 1 means that a network community structure has the highest possible strength [29].

Stable coalitions: A community is a stable coalition which is not eager to participate in the merged operation to improve its utility. In other words, $S_{i }$ tries to join $S_j$ if $u\left(S_i\right)>u\left(S_i+S_j\right) \forall S_j\ne S_i$ then it prefers to stay in the previous situation and with no further will to join $S_j$.

Utility increment: In the merge operation of $S_j$, let $S_{ij}$ be a super-coalition of $S_i$ obtained by the merged operation, so the utility increment of $S_i$ is defined by $\Delta u\left( S_i, S_{ij}\right)=u\left(S_i, S_{ij}\right)-u\left(S_i\right)$. It means that the utility of $S_i$ should increase within the merging coalition.

Generally, if $\Delta u\left( S_i, S_{ij}\right)>0$ and $\Delta u\left( S_j, S_{ij}\right)>0$ and then two communities are joined, the newly joined communities are added to a new list ${\rm Y}=\left\{C_1, C_2, \dots , C_n\right\}$ which includes stable coalitions.

Stable coalitions are products of an equilibrium state for coalitions in which no group of agents has an interest in further merging operations.

It should be noted that coalitions with at least one edge in between are merged.

4.4. Assured Allocation

Having attained the set of stabilized communities, the non-cooperative game then takes place. The nodes may not be in their exact coalition. In this game, each node is considered a selfish agent, which attempts to join or leave a coalition from γ (stabilized communities’ structure) based on its utility measurement. If by joining a coalition its utility increases, then it will leave the current coalition and join the new one.

Utility function of an agent: Let $x\in V$, $C_{i }\in \gamma$ the utility function is as [25]:

$$u_x\left(C_i\right)=\frac{e\left(x, C_i\right) }{d\left(x\right)}$$

(5)

$e\left(x, C_i\right)$ is the number of edges between x and coalition $C_i$. $d\left(x\right)$ is the degree of x. $u_x\left(C_i\right)$ measures the closeness between x and the targeted community $C_i$. The higher value of$u_x\left(C_i\right)$, the more similarity that exists between x and$C_i$.

Join and Leave: node x joins the community$C_i$

$$\begin{gathered} C_i \leftarrow C_i+\left\{x\right\} \\ \mathrm{If} x \notin C_i \mathrm{and} u_x\left(C_i\right) \ge \alpha , x \mathrm{joins} C_i. \end{gathered}$$

Node x leaves its community $C_n$ and joins community$C_i$:

$$\begin{gathered} C_n \leftarrow C_n-\left\{x\right\} \\ \mathrm{if} x \in C_n\mathrm{and} u_x\left(C_n\right)<\beta . \end{gathered}$$

α and β are the lower and upper bounds of the utility value of x, respectively.

The Four-Stage Algorithm (FSA) is described in

Table 1. The pseudo-code for Four-Stage Algorithm (FSA).

Important nodes Determination

$1:\mathrm{Input}: \mathrm{An} \mathrm{undirected} \mathrm{and} \mathrm{unweighted} \mathrm{network} \mathrm{G}=\left(\mathrm{V},\mathrm{E}\right)$ 2: Output: The important node’s set $\mathrm{C}=\{{\mathrm{v}}_1$,${ \mathrm{v}}_2, \dots ,{ \mathrm{v}}_{\mathrm{n}}$} 3:$\mathrm{C}=\left\{{\mathrm{v}}_1\right\}$ 4:$\mathrm{for} \mathrm{all} \left({\mathrm{v}}_{\mathrm{j} }\in \mathrm{V},{ \mathrm{v}}_{\mathrm{j} }\notin \mathrm{C}\right)\mathrm{do}$ 5: $\mathrm{if} \left(\mathrm{d}\left({\mathrm{v}}_{\mathrm{j} },{ \mathrm{v}}_{\mathrm{i} }\right)\ge \mathrm{Avd}\right)$ 6:    $\mathrm{C}=\mathrm{C}\cup \left\{{\mathrm{v}}_{\mathrm{j} }\right\}$ 7: end if 8:Return C 9:end for

Community Detection (Label Propagation)

$1:\mathrm{Input}: \mathrm{Ranking} \mathrm{nodes} \mathrm{C}=\{{\mathrm{v}}_1$,${ \mathrm{v}}_2, \dots ,{ \mathrm{v}}_{\mathrm{n}}$} 2: Output: The communities $\mathrm{S}=\{{\mathrm{S}}_1$,${ \mathrm{S}}_2, \dots ,{ \mathrm{S}}_{\mathrm{n}}$} 3:${\mathrm{S}}_{\mathrm{i}}=\left\{{\mathrm{v}}_{{\mathrm{i}}_{\mathrm{j}}}\right\},{ \mathrm{v}}_{{\mathrm{i}}_{\mathrm{j}}}\in \mathrm{C}$ 4:$\mathrm{for} \mathrm{all} \left(\mathrm{u}\in \mathrm{S} \mathrm{and} \mathrm{v}\in \mathrm{V}-\mathrm{C}\right)\mathrm{do}$ 5: $\mathrm{if} \left({\mathrm{S}}_{\mathrm{Sorenson}} \left(\mathrm{u},\mathrm{v}\right)=\mathrm{true}\right)$ 6:    ${\mathrm{S}}_{\mathrm{i}}={\mathrm{S}}_{\mathrm{i}}\cup \left\{\mathrm{v}\right\}$ 7:    end if $8: \mathrm{S}=\mathrm{S}\cup {\mathrm{S}}_{\mathrm{i}}$ 9: Return S 10:end for

Community Combination (Cooperative game)

$1:\mathrm{Input}: \mathrm{The} \mathrm{initial} \mathrm{communities} \mathrm{S}=\{{\mathrm{S}}_1$,${ \mathrm{S}}_2, \dots ,{ \mathrm{S}}_{\mathrm{n}}$} 2:Output: $\mathrm{Reduced} \mathrm{and} \mathrm{stabilized} \mathrm{communities} \mathsf{\gamma }=\{{\mathrm{C}}_1$,${ \mathrm{C}}_2, \dots ,{ \mathrm{C}}_{\mathrm{n}}$} $3:\mathsf{\gamma }=\left\{\right\}$ 4: $\mathrm{for} \mathrm{all} \left({\mathrm{S}}_{\mathrm{i}},{ \mathrm{S}}_{\mathrm{j}}\in {\mathrm{S} \mathrm{and} \mathrm{S}}_{\mathrm{i}}\ne { \mathrm{S}}_{\mathrm{j}}\right)\mathrm{do}$ 5:   $\mathrm{if} \Delta \mathrm{u}\left({\mathrm{S}}_{\mathrm{ij}}\right)>\Delta \mathrm{u}\left({\mathrm{S}}_{\mathrm{j}}\right)\& \Delta \mathrm{u}\left({\mathrm{S}}_{\mathrm{j}}\right)>0 \mathrm{then}$ 6:     $\mathsf{\gamma }=\{$ ${\mathrm{S}}_{\mathrm{ij}}\}-\left\{{\mathrm{S}}_{\mathrm{i}}\right\}-\left\{{\mathrm{S}}_{\mathrm{j}}\right\}$ 7:    else 8:     Return $\mathsf{\gamma }$ 9:    end else 10: end if 11: end for (Repeat until no coalition willing to join the other one to improve itself)

Assured Allocation (non-Cooperative game)

$1:\mathrm{Input}: \mathrm{The} \mathrm{reduced} \mathrm{and} \mathrm{stabilized} \mathrm{communities} \mathrm{achieved} \mathrm{by} \mathrm{cooperative} \mathrm{game} \mathsf{\gamma }=\{{\mathrm{C}}_1$,${ \mathrm{C}}_2, \dots ,{ \mathrm{C}}_{\mathrm{n}}$} 2:Output: $\mathrm{Assured} \mathrm{node} \mathrm{allocation} \mathrm{and} \mathrm{final} \mathrm{stable} \mathrm{community} \mathrm{structure} \mathrm{C}=\{{\mathrm{C}}_1$,${ \mathrm{C}}_2, \dots ,{ \mathrm{C}}_{\mathrm{n}}$} $3:\mathsf{\delta }=\left\{\right\}$ 4:$\mathrm{for} \mathrm{all} \left(\mathrm{x}\in { \mathrm{C}}_{\mathrm{i}}\right)\mathrm{do}$ $5: \mathsf{\delta }=\mathrm{C}-{\mathrm{C}}_{\mathrm{i}}$ 6:     $\mathrm{for} \mathrm{all} \left({\mathrm{C}}_{\mathrm{j}} \in \mathsf{\delta }\right) \mathrm{do}$ $7: \mathrm{if} \left(\Delta {\mathrm{u}}_{\mathrm{x}}\left({\mathrm{C}}_{\mathrm{i}}\right)\right)>\mathsf{\omega }$ 8:          ${\mathrm{C}}_{\mathrm{j}}={\mathrm{C}}_{\mathrm{j}}+\left\{\mathrm{x}\right\}$ 9:       end if $10: \mathrm{if} \left(\Delta {\mathrm{u}}_{\mathrm{x}}\left({\mathrm{C}}_{\mathrm{j}}\right)\right)<\mathsf{\epsilon }$ 11:        ${\mathrm{C}}_{\mathrm{i}}={\mathrm{C}}_{\mathrm{i}}-\left\{\mathrm{x}\right\}$ 12:    end if 13: Return ${\mathrm{C}}_{\mathrm{i}} ,{ \mathrm{C}}_{\mathrm{j}}$ 14:end for (Repeat until nodes do not eager to join new community and leave their current communities)

.

As mentioned before, after identifying the important nodes in the network, the remaining nodes join the initial communities according to the Sorensen similarity index.

The cooperative game initiates between these communities. Given $S_i$,$S_j$ two communities in S, if the utility of joining these two communities ($S_{ij}$) is greater than the utility of each of them, then the joining operation occurs and $S_{ij}$ is added to a new list Υ, and the two communities are merged. Once equilibrium has been achieved, the utility of each group cannot be demonstrated. The stable communities are then identified; however, some nodes may not satisfy their utilities, and they begin to play the non-cooperative game to improve their utilities.

Each node evaluates the other communities and calculates its utility if it joins them. If the value is more than ω and lower than ε, the node leaves its current position and joins the new community. The algorithm ends when the agents are not interested in joining other communities to improve their utility values and are interested in staying in their current situation.

Since the cooperative game runs on the results of the initial clustering rather than singleton nodes, the complexity is reduced. In addition, because the non-cooperative game applied on the stabilized clusters has been achieved by the cooperative game, the nodes are most likely to be in their exact coalitions and therefore there would have been no intention to change membership in their community due to improving their utilities.

5. Analysis of the Experimental Results

To evaluate the capabilities and effectiveness of the proposed approach, the experiments are conducted on real networks with/without the ground truth and the benchmark network of Lancichinetti and Fortunato [9]. The outcomes of the four-stage algorithm are compared by seven other community detection methods: Three-stage algorithm (TS) [25], Louvain [4], Infomap [3], Fastgreedy [5], Walktrap [30], Eigenvector [31], and Label propagation (LPA) [32].

Before debating on the experimental results, two famous functions for evaluating the proposed algorithm are introduced as follows:

Normalized Mutual Information (NMI): This is a well-known approach for evaluating the performance of community detection algorithms, which determines the amount of similarity between the partition proposed by the algorithm and the desired partition [5]. The NMI between two identical partitions is 1 [33].

The standard normalized mutual information (NMI) metric defined in [33], is determined as follows:

$$I_{norm }\left(X,Y\right)=\frac{2I\left(X,Y\right)}{H\left(x\right)+H\left(Y\right)}$$

(6)

where I(X, Y) is the mutual information between X and Y. H(X) and H(Y) are the entropy of X, Y. If the communities of X and Y are independent, then knowing X does not provide information about Y, therefore NMI(X, Y) = 0.

Modularity: This is a famous evaluation index, proposed by Newman and Girvan [34], for measuring the quality of the community structure in networks. The main idea of this index is based on comparing edge density within communities with the expected number in a random network.

The definition of modularity is:

$$\mathrm{Q}=\frac{1}{2m} \Sigma ij(A_{ij}-\frac{d\left(v_i\right) d\left(v_j\right)}{2m})\delta \left(C_i, C_j\right)$$

(7)

where m is the total number of edges, $A_{ij}$ is the adjacency matrix, $d\left(v_i\right)$ is the degree of the $v_i$, and δ is an indicator function which is 1 if i and j are in the same community ($C_i$ = C_j) and output 0 if they are in different communities.

The modularity value ranges between 0 and 1. If the whole graph is assumed as a community, the modularity value would be zero. A higher value of Q indicates a better community structure.

5.1. Real Networks with Ground Truth

In this research, the following four real networks with ground truth are used to test the efficiency and accuracy of the proposed algorithm.

Dolphin Network [34]: This network includes 62 nodes and 159 edges, which represent the relationships between two groups of dolphins.

Zachary Karate Club Network [4]: It consists of 34 nodes and 79 edges that were set between the individuals who intend to join one of the two clubs.

American College Football Network [35]: This network originates from the United States college football. It consists of 115 nodes and 616 edges. The team represented as nodes and edges have defined the regular season games between two related teams.

Polbooks network [5]: It includes 105 nodes and 882 links. The network consists of the US political books’ data which were recorded in 2005 by Adamic and Glance.

Table 2. The performance for each step of the FSA algorithm in the networks with ground truth.

Dataset	NMI			Modularity
	Label Propagation	Cooperative Game	Non-Cooperative Game	Label Propagation	Cooperative Game	Non-Cooperative Game
Karate	0.3428	06948	0.8737	0.0015	0.2797	0.2890
Dolphin	0.2672	0.4888	0.8649	0.0119	0.2864	0.2991
Polbooks	0.3363	0.5036	0.8701	0.0064	0.0785	0.0884
Football	0.6845	0.5003	0.7261	0.0058	0.3705	0.3924

shows the NMI and the modularity values of only Label propagation, after applying the cooperative game and finally after running the non-cooperative game in the four real networks with ground truth.

Table 2 indicates that the Label propagation method does not work properly in this situation. Because some obtained communities have low quality and are sparse, they need to merge with the other strong ones to qualify for the final communities. After applying the cooperative game to the Label propagation results, the NMI value and the modularity were improved due to the cluster merging process and stabilization point achievement.

As we may see, after running the non-cooperative game on the results of the cooperative approach, promising results were obtained. Once the equilibrium point is achieved, the condition of all nodes and communities stabilizes.

Figure 2 and Figure 3 show the modularity and NMI values for the applied algorithms in the four real networks, respectively.

As can be seen, the Four-Stage Algorithm (FSA) yielded better results in terms of NMI, particularly for the karate and polbooks networks. In addition, for the other datasets, the four-stage algorithm remains competitive.

In terms of modularity, the Four-Stage Algorithm (FSA) is better than other methods in dolphin, Football, and polbooks networks.

According to the results in

Table 3. Shows that the FSA algorithm has detected a close number of communities to the ground truth.

Methods		Networks	Karate	Dolphin	Polbooks	Football
	Evaluation Approaches
Ground Truth	Q		0.37	0.38	0.41	0.55
	C		2	2	3	12
FSA	Q		0.37	0.44	0.53	0.61
	NMI		0.87	0.89	87	0.9
	C		2	2	4	10
TS	Q		0.42	0.38	0.52	0.6
	NMI		0.71	0.89	0.55	0.9
	C		4	2	4	10
Louvain	Q		0.42	0.52	0.52	0.6
	NMI		0.59	0.48	0.51	88
Fast Greedy	Q		0.38	0.5	0.5	0.55
	NMI		0.69	0.61	0.53	0.7
Infomap	Q		0.4	0.52	0.52	0.6
	NMI		0.7	0.5	0.49	0.92
LPA	Q		0.4	0.5	0.5	0.6
	NMI		0.7	0.69	0.57	0.92
Eigenvector	Q		0.39	0.49	0.49	0.47
	NMI		0.68	0.45	0.71	0.52
Walktrap	Q		0.35	0.49	0.51	0.6
	NMI		0.5	0.54	0.54	0.9

, in most cases, the FSA method works much better than other clustering methods in the NMI and modularity. TS algorithm is in second place in this list, which has extracted four communities for the polbooks dataset, while the number of communities is two in the ground truth.

5.2. Real Networks without Ground Truth

Additionally, to evaluate the efficiency and accuracy of the four-stage and seven other algorithms, three real networks without ground truth are investigated as follows:

Lesmis network [36]: This undirected network contains co-occurrences of characters in Victor Hugo’s novel “Les Misérables”, as compiled by Donald Ervin Knuth. Nodes represent characters and the edge between two nodes shows that these two characters appeared in the same chapter of the book.

Adjnoun network [31]: A network of common adjective and noun adjacencies for the novel “David Copperfield” by Charles Dickens, as described by M. Newman. Nodes represent the most common adjectives and nouns in the novel. Edges connect each pair of words that are in adjacent positions in the text of the book.

Jazz network [37]: is the collaboration network between jazz musicians. The nodes are jazz musicians and the edges indicate the cooperation of two musicians in a band.

Table 4. The performance and the number of extracted communities in real networks without ground truth.

Networks	FSA		TS		Louvain		FastGreedy		Infomap		LPA		Eigenvector		Walktrap
	C	Q	C	Q	C	Q	C	Q	C	Q	C	Q	C	Q	C	Q
Lesmis	6	0.55	6	0.54	6	0.56	5	0.50	9	0.55	8	0.53	6	0.55	8	0.52
Adjnoun	7	0.31	7	0.29	7	0.29	7	0.29	2	0.01	10	0.24	1	0.00	25	0.22
Jazz	3	0.45	3	0.44	4	0.44	4	0.44	7	0.28	3	0.39	2	0.28	11	0.44

represents the results of the modularity (Q) [38] and the number of detected communities (C) in real datasets without ground truth. In the Lesmis dataset, the maximum modularity, Q = 0.56, belongs to the Louvain algorithm, while in the Adjnoun and Jazz datasets, the proposed method has a more promising result.

The number of extracted communities in Table 4 reveals that in the Lesmis dataset, FSA, TS, Louvain, and eigenvector achieve good results. FSA, TS, Louvain, and Fastgreedy detected an identical number of communities in the Adjnoun network, and in the Jazz network, the FSA algorithm detected three communities that are close to TS, Louvain, and Fastgreedy, However, its larity has been slightly improved in two recent datasets. Walktrap has performed very differently in these networks than the other algorithms.

5.3. Time Analysis of the Proposed Algorithm

The calculated running time (in seconds) for the FSA algorithm and other algorithms in real-world datasets is shown in

Table 5. Comparison of the runtime (in seconds) of the proposed algorithm in real datasets.

Networks	FSA	Louvain	Infomap	LPA	Walktrap
Karate	0.0007	0.1061	0.0200	0.0041	0.0039
Football	0.0009	0.1082	0.0170	0.0032	0.0059
Dolphin	0.0010	0.1078	0.0181	0.0023	0.0041
Polbooks	0.0014	0.1101	0.0208	0.0031	0.0049
Lesmis	0.0011	0.1090	0.0095	0.0029	0.0051
Jazz	0.0034	0.1890	0.1098	0.0078	0.0090
Adjnoun	0.0021	0.1001	0.0971	0.0034	0.0058

. All of the experiments are implemented on a desktop PC with an Intel Core i7 CPU (3.4 GHz) and 8 GB RAM.

5.4. Benchmark Networks

In this section, a series of benchmark networks are applied according to the method of Lancichinetti, Fortunato, and Raddichi (LFR) [9]. These networks have power law distributions and to some extent are suitable for evaluating the performance of community detection algorithms [39,40,41,42,43,44,45].

The parameters used in this research are the same as [9] except the number of nodes in the network (n) which is considered as n = 50, 100, 150, 200.

The power law exponent for the size of communities: β = 1.

As seen in

Table 6. The performance for each step of the FSA algorithm in the benchmark networks.

	NMI			Modularity
n	Label Propagation	Coalition	Individual	Label Propagation	Coalition	Individual
50	0.3224	0.9049	0.9321	0.0244	0.5008	0.6127
100	0.4029	0.9267	0.9526	0.0010	0.5320	0.5340
150	0.4849	0.9602	0.9731	0.0168	0.6972	0.7321
200	0.5413	0.8387	0.9606	0.0299	0.6896	0.7487

, the NMI value for the label propagation method is lower than the other steps.

In the cooperative game deployment step, the NMI value and the modularity were improved due to the merging process and reaching the stabilizing communities. Finally, using the non-cooperative game step, promising values of NMI and modularity were obtained, as each node tries to improve its utility and stabilize its position in the communities.

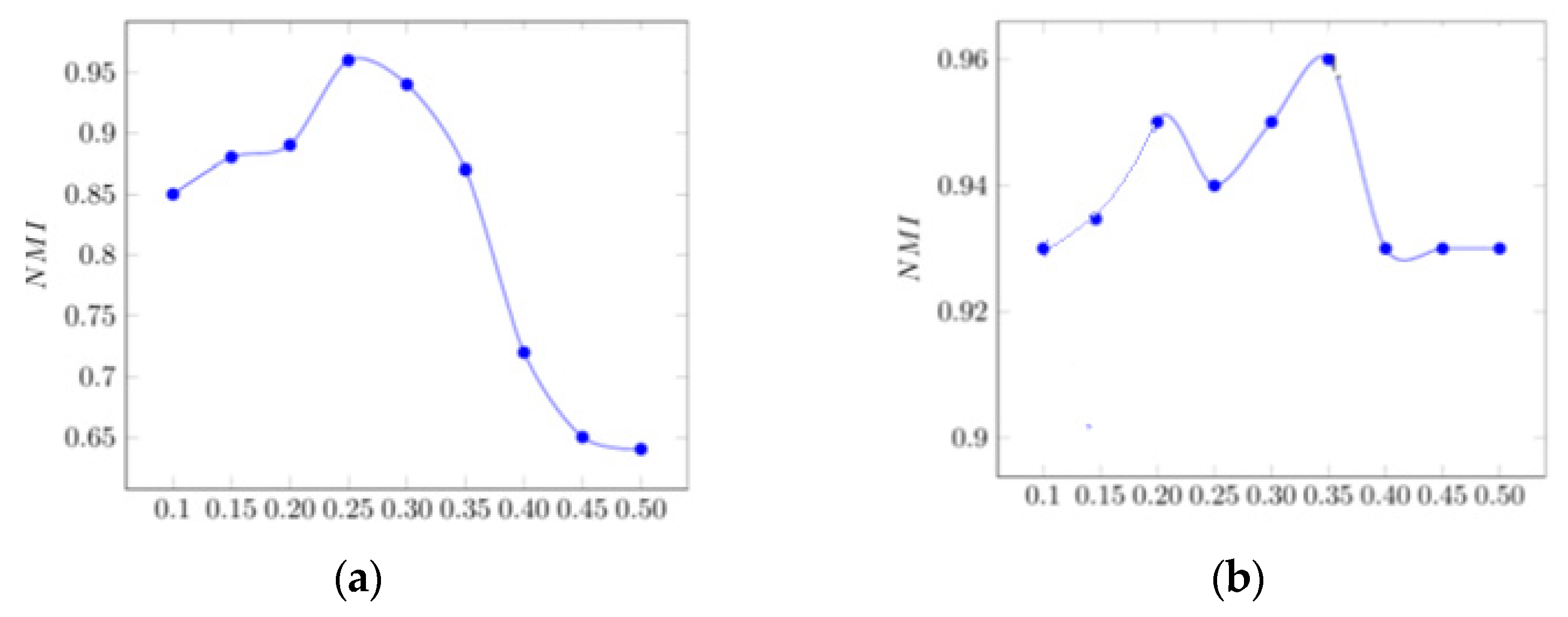
According to Figure 4a, initially, with the increase in ε, the probability of removing nodes from the clusters increases, and those nodes which have fewer connections with each cluster are removed. As a result, the NMI value will increase.

However, after a while, when the ε value exceeds the threshold (approximately 0.24), nodes that have more intra-cluster communications will also be removed from that cluster and the NMI value will subsequently decrease sharply.

In Figure 4b, the optimal value of ω is approximately 0.35, and for the higher values, the NMI value will practically not change, and nodes will rarely join the clusters.

6. Concluding Remarks and Future Works

In this paper, we suggested a powerful and effective community detection approach that incorporates global and local information into community detection. First, important nodes in the networks are determined and then label propagation is applied to find the initial clusters. However, some sparse clusters require merging with other strong types and their situation stabilizes; therefore, a cooperative game is used Ultimately, this guarantees a rational allocation of nodes to established communities, where a non-cooperative game is performed on each node.

The experimental results confirm the performance of our approach and demonstrate that cooperative and non-cooperative game approaches boost each other to detect more stables and assured communities.

We evaluated the proposed method on several standard real networks and benchmark datasets and compared the performance of the FSA method with other algorithms. There are several advantages of the proposed method, including the formation of high-quality communities, solving the problem of community quality dependency on the inappropriately selected node, and allocate nodes to their stable communities.

The proposed method can respond successfully to a wide range of real-world issues like real business recommendations, precision marketing, etc. The application of the FSA algorithm in healthcare is settled by its fundamental idea; it can be applied to the diagnosis and treatment of diseases in general, and mental diseases in particular. It can be used to identify the patients, enhance their conditions, and detect the contagion of the disease. By using this method, it is possible to easily solve the challenges of the supply and demand side, which improves the condition of patients.

Additionally, it is also suitable for recommending and finding friends on social networks.

The proposed algorithm has high performance in small- and medium-size data sets. Although it has limitations in large datasets, where the number of extracted communities is large, it takes time to detect suitable communities once we use game theory, especially when it comes to considering non-cooperative games.

Furthermore, it can only detect non-overlapping communities from unweighted and undirected networks.

For future work, some solutions, such as deep learning methods, can be used to extract features that are more beneficial to large networks, especially those with semantic content. Furthermore, overlapping communities and weighted networks would be considered.