Deep Learning Based Wildfire Event Object Detection from 4K Aerial Images Acquired by UAS
Abstract
1. Introduction
- (1)
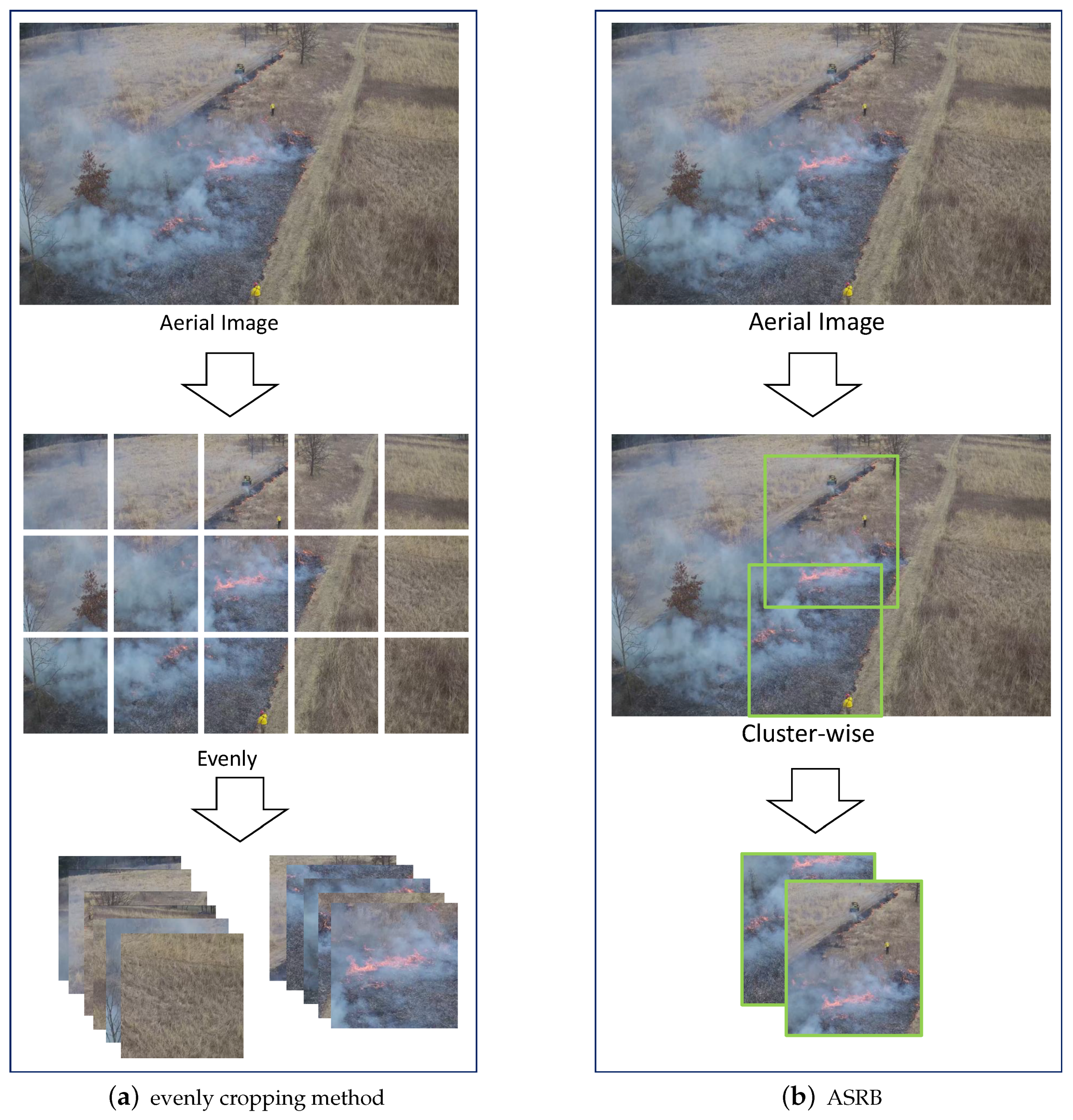
- Aerial UAS imagery are usually acquired in high-resolution. However, the promising results from CNN-based object detectors are from low-resolution images (600 px × 400 px). The results from high-resolution aerial images are far from satisfactory because of the small and sparse objects.
- (2)
- CNN-based detectors heavily rely on well-annotated datasets. The fire can be amorphous and cannot be annotated with a single rectangle bounding box. Therefore, it is time-consuming to label the fire from high resolution images. To our best knowledge, there is no available public aerial fire dataset.
- We compiled a large-scale aerial dataset, heavily annotated for fire, persons, and vehicles. The dataset contains 1400 images from 4K videos taken with a ZenMuse XT2 sensor from Purdue Wildlife Area (West Lafayette, IN, USA) on a DJI M600 drone over a controlled burn covering approximately two hectares.
- We provide a fast and accurate coarse-to-fine pipeline to detect the small objects in 4K images. By a carefully designed CNN model, we can locate the center point of the objects and reduce the image size into low resolution with no loss of the objects.
- In this work, we applied the deep learning models in 4K aerial fire detection. In addition, compared to other fire detectors using special sensors, we can not only predict the fire with state-of-art accuracy, but also provide predictions for other objects such as persons or vehicles.
2. Related Work
2.1. Object Detection Using Deep Learning
2.1.1. Two-Stage Object Detectors
2.1.2. One-Stage Object Detectors
2.2. Detection of Small Objects in High-Resolution Aerial Images
2.3. Fire Detection via Machine Learning and Deep Learning Methods
3. Dataset Specification
3.1. Overview of the Dataset
3.2. Category Selection and Annotation Methods
4. Methodology
4.1. Adaptive Sub-Region Select Block (ARSB)
| Algorithm 1 Iterative Bounding-Box Merge (IBBM) |
| Input: Bounding boxes of an image , classes of the bounding boxes , desired bounding box height and width , non max merge threshold Output: Merged bounding boxes
|
4.2. Fine Object Detection
4.3. Fusion of the Final Results
5. Experiments
5.1. Implementation Details
5.2. Evaluation Metric
5.3. Baseline Methods
5.4. Ablation Study
5.4.1. The Baseline from Original Yolov3
5.4.2. The Improvement from Yolo_crop
5.4.3. Improvement by Our Methods
5.5. Limitations
6. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Evarts, B. Fire Loss in the United States during 2017. 2018. Available online: https://www.darley.com/documents/inside_darley/NFPA_2017_Fire_Loss_Report.pdf (accessed on 22 April 2020).
- Apvrille, L.; Tanzi, T.; Dugelay, J.L. Autonomous drones for assisting rescue services within the context of natural disasters. In Proceedings of the 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), Beijing, China, 16–23 August 2014; pp. 1–4. [Google Scholar]
- Eyerman, J.; Crispino, G.; Zamarro, A.; Durscher, R. Drone Efficacy Study (DES): Evaluating the Impact of Drones for Locating Lost Persons in Search and Rescue Events; European Emergency Number Association: Brussels, Belgium, 2018. [Google Scholar]
- Qiu, T.; Yan, Y.; Lu, G. An autoadaptive edge-detection algorithm for flame and fire image processing. IEEE Trans. Instrum. Meas. 2012, 61, 1486–1493. [Google Scholar] [CrossRef]
- Redmon, J.; Divvala, S.; Girshick, R.; Farhadi, A. You only look once: Unified, real-time object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 779–788. [Google Scholar]
- Liu, W.; Anguelov, D.; Erhan, D.; Szegedy, C.; Reed, S.; Fu, C.Y.; Berg, A.C. Ssd: Single shot multibox detector. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 21–37. [Google Scholar]
- Lowe, D.G. Distinctive image features from scale-invariant keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Felzenszwalb, P.F.; Girshick, R.B.; McAllester, D.; Ramanan, D. Object detection with discriminatively trained part-based models. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 32, 1627–1645. [Google Scholar] [CrossRef]
- Uijlings, J.R.; Van De Sande, K.E.; Gevers, T.; Smeulders, A.W. Selective search for object recognition. Int. J. Comput. Vis. 2013, 104, 154–171. [Google Scholar] [CrossRef]
- Pinheiro, P.O.; Collobert, R.; Dollár, P. Learning to segment object candidates. In Advances in Neural Information Processing Systems; NIPS: Montreal, QC, Canada, 2015; pp. 1990–1998. [Google Scholar]
- Ren, S.; He, K.; Girshick, R.; Sun, J. Faster r-cnn: Towards real-time object detection with region proposal networks. In Advances in Neural Information Processing Systems; NIPS: Montreal, QC, Canada, 2015; pp. 91–99. [Google Scholar]
- Szegedy, C.; Ioffe, S.; Vanhoucke, V.; Alemi, A.A. Inception-v4, inception-resnet and the impact of residual connections on learning. In Proceedings of the Thirty-First, AAAI Conference on Artificial Intelligence, San Francisco, CA, USA, 4–9 February 2017; pp. 4278–4284. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Lin, T.Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2961–2969. [Google Scholar]
- Redmon, J.; Farhadi, A. YOLO9000: Better, faster, stronger. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 7263–7271. [Google Scholar]
- Fu, C.Y.; Liu, W.; Ranga, A.; Tyagi, A.; Berg, A.C. Dssd: Deconvolutional single shot detector. arXiv 2017, arXiv:1701.06659. [Google Scholar]
- Ren, J.; Chen, X.; Liu, J.; Sun, W.; Pang, J.; Yan, Q.; Tai, Y.W.; Xu, L. Accurate single stage detector using recurrent rolling convolution. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5420–5428. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef] [PubMed]
- Sommer, L.W.; Schuchert, T.; Beyerer, J. Fast deep vehicle detection in aerial images. In Proceedings of the 2017 IEEE Winter Conference on Applications of Computer Vision (WACV), Santa Rosa, CA, USA, 24–31 March 2017; pp. 311–319. [Google Scholar]
- Lu, Y.; Javidi, T.; Lazebnik, S. Adaptive object detection using adjacency and zoom prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 2351–2359. [Google Scholar]
- Alexe, B.; Heess, N.; Teh, Y.W.; Ferrari, V. Searching for objects driven by context. In Advances in Neural Information Processing Systems; NIPS: Lake Tahoe, NV, USA, 2012; pp. 881–889. [Google Scholar]
- Rŭžička, V.; Franchetti, F. Fast and accurate object detection in high resolution 4K and 8K video using GPUs. In Proceedings of the 2018 IEEE High Performance Extreme Computing Conference (HPEC), Waltham, MA, USA, 25–27 September 2018; pp. 1–7. [Google Scholar]
- Yang, F.; Fan, H.; Chu, P.; Blasch, E.; Ling, H. Clustered Object Detection in Aerial Images. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–3 November 2019. [Google Scholar]
- Zhao, Y.; Ma, J.; Li, X.; Zhang, J. Saliency detection and deep learning-based wildfire identification in UAV imagery. Sensors 2018, 18, 712. [Google Scholar] [CrossRef] [PubMed]
- Sudhakar, S.; Vijayakumar, V.; Kumar, C.S.; Priya, V.; Ravi, L.; Subramaniyaswamy, V. Unmanned Aerial Vehicle (UAV) based Forest Fire Detection and monitoring for reducing false alarms in forest-fires. Comput. Commun. 2020, 149, 1–16. [Google Scholar] [CrossRef]
- Chen, T.H.; Wu, P.H.; Chiou, Y.C. An early fire-detection method based on image processing. In Proceedings of the 2004 International Conference on Image Processing, 2004—ICIP’04, Singapore, 24–27 October 2004; Volume 3, pp. 1707–1710. [Google Scholar]
- Çelik, T.; Özkaramanlı, H.; Demirel, H. Fire and smoke detection without sensors: Image processing based approach. In Proceedings of the 2007 15th European Signal Processing Conference, Poznan, Poland, 3–7 September 2007; pp. 1794–1798. [Google Scholar]
- Mueller, M.; Karasev, P.; Kolesov, I.; Tannenbaum, A. Optical flow estimation for flame detection in videos. IEEE Trans. Image Process. 2013, 22, 2786–2797. [Google Scholar] [CrossRef] [PubMed]
- Kamalakannan, J.; Chakrabortty, A.; Bothra, G.; Pare, P.; Kumar, C.P. Forest Fire Prediction to Prevent Environmental Hazards Using Data Mining Approach. In Proceedings of the 2nd International Conference on Data Engineering and Communication Technology, Pune, India, 15–16 December 2017; pp. 615–622. [Google Scholar]
- Mahmoud, M.A.I.; Ren, H. Forest Fire Detection and Identification Using Image Processing and SVM. J. Inf. Process. Syst. 2019, 15, 159–168. [Google Scholar]
- Zhang, Q.; Xu, J.; Xu, L.; Guo, H. Deep convolutional neural networks for forest fire detection. In Proceedings of the 2016 International Forum on Management, Education and Information Technology Application, Guangzhou, China, 30–31 January 2016; pp. 568–575. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Advances in Neural Information Processing Systems; NIPS: Lake Tahoe, NV, USA, 2012; pp. 1097–1105. [Google Scholar]
- Sharma, J.; Granmo, O.C.; Goodwin, M.; Fidje, J.T. Deep convolutional neural networks for fire detection in images. In Proceedings of the International Conference on Engineering Applications of Neural Networks, Athens, Greece, 25–27 August 2017; pp. 183–193. [Google Scholar]
- Muhammad, K.; Ahmad, J.; Lv, Z.; Bellavista, P.; Yang, P.; Baik, S.W. Efficient deep CNN-based fire detection and localization in video surveillance applications. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 1419–1434. [Google Scholar] [CrossRef]
- Muhammad, K.; Khan, S.; Elhoseny, M.; Ahmed, S.H.; Baik, S.W. Efficient fire detection for uncertain surveillance environment. IEEE Trans. Ind. Inform. 2019, 15, 3113–3122. [Google Scholar] [CrossRef]
- Jadon, A.; Omama, M.; Varshney, A.; Ansari, M.S.; Sharma, R. FireNet: A Specialized Lightweight Fire & Smoke Detection Model for Real-Time IoT Applications. arXiv 2019, arXiv:1905.11922. [Google Scholar]
- Redmon, J.; Farhadi, A. Yolov3: An incremental improvement. arXiv 2018, arXiv:1804.02767. [Google Scholar]
- Neubeck, A.; Van Gool, L. Efficient non-maximum suppression. In Proceedings of the 18th International Conference on Pattern Recognition (ICPR’06), Hong Kong, China, 20–24 August 2006; Volume 3, pp. 850–855. [Google Scholar]
- Everingham, M.; Van Gool, L.; Williams, C.K.; Winn, J.; Zisserman, A. The pascal visual object classes (voc) challenge. Int. J. Comput. Vis. 2010, 88, 303–338. [Google Scholar] [CrossRef]
- Lin, T.; Maire, M.; Belongie, S.J.; Bourdev, L.D.; Girshick, R.B.; Hays, J.; Perona, P.; Ramanan, D.; Dollár, P.; Zitnick, C.L. Microsoft COCO: Common Objects in Context. arXiv 2014, arXiv:1405.031. [Google Scholar]

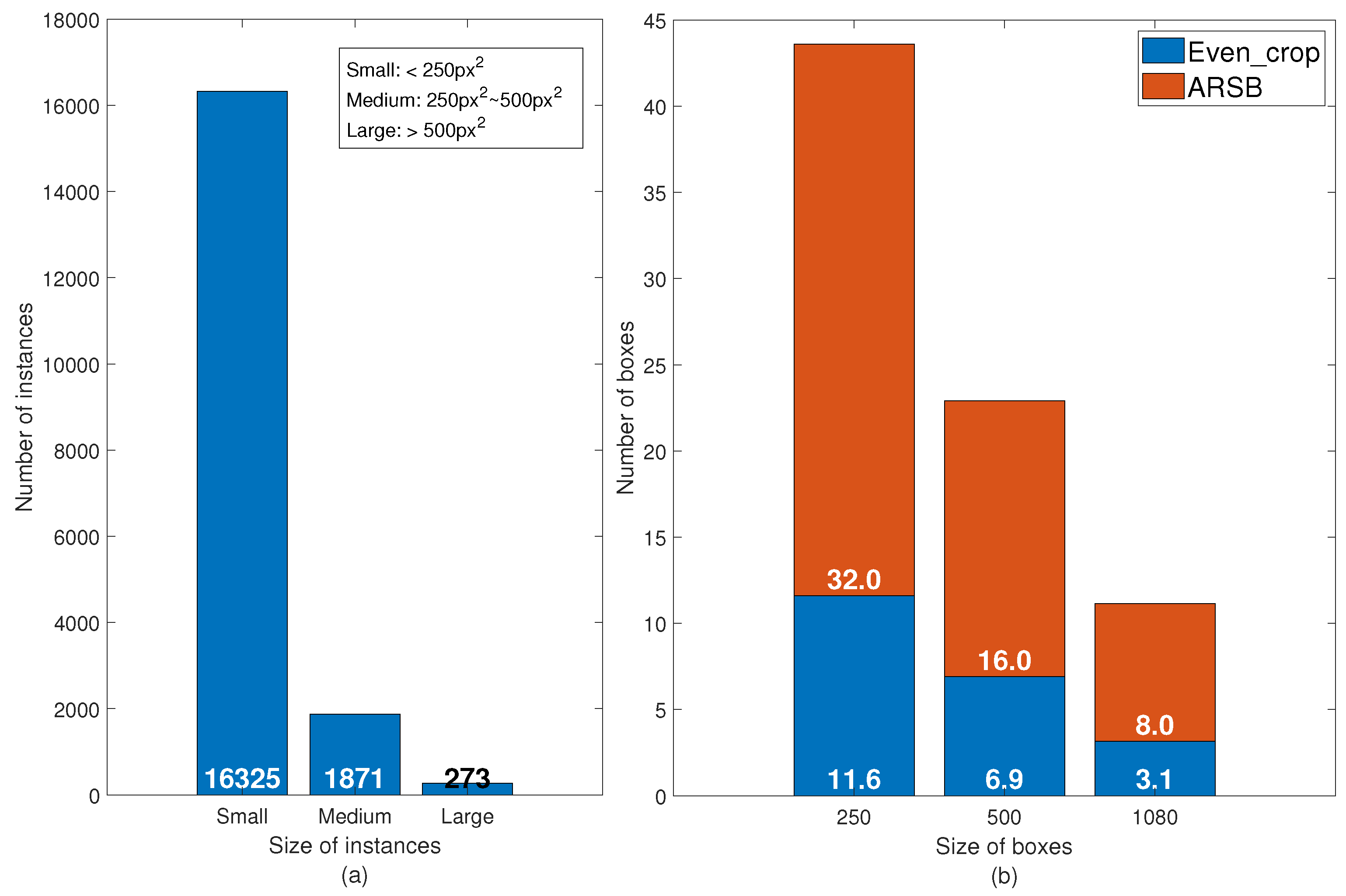

| Scale | Cluster Centers |
|---|---|
| small | |
| medium | |
| large |
| Method | Size | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Car | Person | Fire | Car | Person | Fire | Car | Person | Fire | |||||
| yolo_ori | - | 0.63 | 0.63 | 0.38 | 0.55 | 0.42 | 0.37 | 0.09 | 0.29 | 0.07 | 0.05 | 0.01 | 0.04 |
| 540 | 0.80 | 0.86 | 0.56 | 0.74 | 0.72 | 0.75 | 0.32 | 0.60 | 0.45 | 0.35 | 0.08 | 0.29 | |
| yolo_crop | 720 | 0.88 | 0.83 | 0.53 | 0.75 | 0.85 | 0.73 | 0.27 | 0.62 | 0.56 | 0.34 | 0.09 | 0.33 |
| 1080 | 0.87 | 0.85 | 0.57 | 0.76 | 0.87 | 0.72 | 0.36 | 0.65 | 0.68 | 0.30 | 0.07 | 0.35 | |
| 540 | 0.41 | 0.73 | 0.62 | 0.59 | 0.47 | 0.85 | 0.39 | 0.57 | 0.20 | 0.23 | 0.14 | 0.19 | |
| ARSB_pad | 720 | 0.64 | 0.79 | 0.60 | 0.68 | 0.71 | 0.80 | 0.23 | 0.58 | 0.39 | 0.30 | 0.03 | 0.24 |
| 1080 | 0.91 | 0.88 | 0.50 | 0.76 | 0.75 | 0.79 | 0.35 | 0.63 | 0.67 | 0.31 | 0.11 | 0.37 | |
| 540 | 0.59 | 0.95 | 0.58 | 0.71 | 0.60 | 0.91 | 0.18 | 0.56 | 0.45 | 0.35 | 0.07 | 0.29 | |
| ARSB_crop | 720 | 0.76 | 0.86 | 0.56 | 0.73 | 0.78 | 0.80 | 0.11 | 0.57 | 0.44 | 0.34 | 0.04 | 0.27 |
| 1080 | 0.91 | 0.84 | 0.59 | 0.78 | 0.88 | 0.76 | 0.37 | 0.67 | 0.82 | 0.41 | 0.12 | 0.45 | |
| Method | Frame per Second () | |
|---|---|---|
| yolo_ori [39] | 0.29 | 50.6 |
| yolo_crop | 0.65 | 1.92 |
| ARSB_pad | 0.66 | 20.6 |
| ARSB_crop | 0.67 | 7.44 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tang, Z.; Liu, X.; Chen, H.; Hupy, J.; Yang, B. Deep Learning Based Wildfire Event Object Detection from 4K Aerial Images Acquired by UAS. AI 2020, 1, 166-179. https://doi.org/10.3390/ai1020010
Tang Z, Liu X, Chen H, Hupy J, Yang B. Deep Learning Based Wildfire Event Object Detection from 4K Aerial Images Acquired by UAS. AI. 2020; 1(2):166-179. https://doi.org/10.3390/ai1020010
Chicago/Turabian StyleTang, Ziyang, Xiang Liu, Hanlin Chen, Joseph Hupy, and Baijian Yang. 2020. "Deep Learning Based Wildfire Event Object Detection from 4K Aerial Images Acquired by UAS" AI 1, no. 2: 166-179. https://doi.org/10.3390/ai1020010
APA StyleTang, Z., Liu, X., Chen, H., Hupy, J., & Yang, B. (2020). Deep Learning Based Wildfire Event Object Detection from 4K Aerial Images Acquired by UAS. AI, 1(2), 166-179. https://doi.org/10.3390/ai1020010






