Abstract
This study delves into an in-depth examination of the biomechanical characteristics of various materials commonly utilized in the fabrication of artificial ankle joints. Specifically, this research focuses on the design of an ankle joint resembling the salto-talaris type, aiming to comprehensively understand its performance under different loading conditions. Employing advanced finite element analysis techniques, this investigation rigorously evaluates the stresses and displacements experienced by the designed ankle joint when subjected to varying loads. Furthermore, this study endeavors to identify the vibrating frequencies associated with these displacements, offering valuable insights into the dynamic behavior of the ankle joint. Notably, the analysis extends to studying random frequencies across three axes of motion, enabling a comprehensive assessment of directional deformities that may arise during joint function. To validate the effectiveness of the proposed design, a comparative analysis is conducted against the star ankle design, a widely recognized benchmark in ankle joint prosthetics. This comparative approach serves dual purposes: confirming the accuracy of the findings derived from the salto-talaris design and elucidating the relative efficacy of the proposed design in practical application scenarios.
1. Introduction
The ankle joint serves as a crucial link between the leg and foot, facilitating load transfer that is essential for activities like standing, walking, running, and jumping, crucial for balance and stability [1]. It absorbs external forces’ impact during these activities, owing to its robust skeletal, biomechanical, and cartilaginous structural characteristics [1]. Despite the challenges in treating various types of arthritis, collaborative efforts among surgeons, physicians, and researchers have led to the development of treatment modalities, including surgical and non-surgical approaches [2]. However, the limited efficacy of non-surgical treatments in pain alleviation often necessitates surgical interventions, with Total Ankle Replacement being the preferred procedure [2,3].
Moreover, the ankle joint exhibits dynamic mechanical activity beyond passive functions, particularly evident during efforts to increase walking speed [3]. Technological advancements have transformed ankle joint disorder treatment, replacing traditional approaches with artificial joint replacements [4]. Yet initial attempts at ankle joint replacement have faced challenges, including increased problems and difficulties [5].
Current biomechanical studies prioritize developing joints that mimic natural movement, possess extended lifespans, and employ high-quality, biocompatible materials to minimize inflammatory reactions [4]. However, ankle joint replacement is not devoid of drawbacks, with complications such as loosening, infection, anesthesia-related issues, and nerve injury persisting in many patients even years after surgery [6,7]. These challenges underscore the imperative of understanding ankle joint biomechanics to develop artificial joints that optimize mobility while minimizing adverse effects.
Consequently, there is a pressing need for the development of artificial ankle joints with enhanced characteristics or quasi-archetypal designs. Suggestions or designs for ankle joints must consider factors like walking speed and jumping, necessitating an understanding of vibrating frequencies and deformities in multiple directions. Such insights can pave the way for the creation of ankle joints that function more effectively and efficiently [8].
2. Basic Components of the Human Ankle
The ankle essentially consists of three bones: the tibia, fibula, and talus [8,9]. The talus is usually called the ankle bone and its top part is located inside a bowl-like structure that is made of two parts, which are the fibula and the lower part of the tibia. The lower part of the ankle, however, is supported by the calcaneus and generally is called the heel bone. According to these parts, the legs of human beings can move up and down so easily due to the link to these three basic bones that is similar to a joint. In addition to this, there exists a material similar to oil, named the articular cartilage, to present a level that is quasi-void of friction when bones move. The articular cartilage must be quite thin and hard to support the weight of the body. Figure 1a [10] shows the overall structure of the ankle joint. In addition to this, ligaments and tendons are considered significant soft tissues to perform the movement of the ankle; as ligaments play a key role in linking bones, tendons are the soft tissues used to join bones and muscles [11]. Tendons are located on both sides of the ankle joint and avail a capacity to make bones well joined. Tendons also support the ankle joint at the same time, and there are miscellaneous types of tendons that perform different tasks. For example, the Achilles tendon can be used while jumping, running, or walking. Figure 1b elaborates on ligaments and tendons.
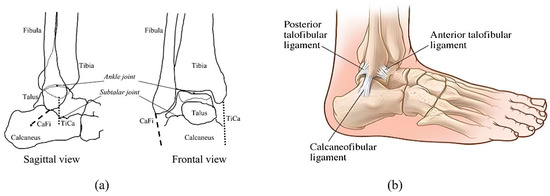
Figure 1.
(a) Overall structure of ankle joint; (b) ligaments and tendons.
3. Replacement of the Entire Salto-Talaris Ankle Joint
The artificial salto-talaris joint is one of the most used artificial ankle joints and is considered a complete substitute for the non-constrained ankle, where it can be planted surgically. Generally speaking, the carrier can move freely on more than one surface. Such a design consists of three parts: a leg component (tibia) which is metal and enters inside the shinbone, a metal ankle component (talar) fixed from the bottom to the bones, and finally, a plastic component fixed to the tibia, as is elaborated in Figure 2. According to this, the lower part of the plastic component (carrier) slides over the upper surface of the ankle component (Talar), and a cylinder with the shinbone component helps fasten the apparatus to the bone.
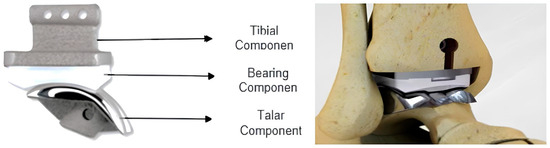
Figure 2.
Parts of the artificial ankle joint salto-talaris.
4. Materials and Methods
Based on the aforementioned studies and research, a significant challenge in designing the three-dimensional archetype of an artificial ankle joint lies in selecting a material that exhibits lower stresses, higher resistance to deformity, and lower density. This selection aims to attain desired mechanical properties while also assessing the impact of load distribution along the length of prosthetic limbs on unexpected movement conditions. Furthermore, prioritizing mechanical strength and durability is essential for ensuring safety. Metallic materials, commonly used under load-bearing conditions, may exhibit toxicity and susceptibility to corrosion-induced breakage [12]. To address this, a comparative analysis among five different materials will be conducted during simulated load conditions (ranging from 50 to 100 kg) to evaluate their performance. These materials are as follows:
- First: Metal materials:
- Stainless steel (SS316L):
Austenitic chromium–nickel stainless steel is heat-resistant with high corrosion resistance, comparable to chromium–nickel steel when exposed to several kinds of harmful chemicals such as seawater, salt water solutions, and the like.
- Titanium–aluminum–vanadium alloys (Ti-6A1-4V):
Alfa beta titanium alloys have high energy and excellent erosion resistance. They are used in biomedicine. This specification refers to their chemical structure: up to almost 90% titanium, 6%, aluminum, 4% vanadium, 0.25% (maximally) iron, and 0.2% (maximally) oxygen. They possess distinct energy characteristics, a low flexibility factor, and malleability, and are amenable to temperature treatment.
- B-type titanium alloys (Ti-13Nb-13Zr):
These are new titanium alloys developed to suit medical implant applications. These alloys are characterized by low ductility, high energy, excellent hot and cold formability, and high corrosion resistance [13].
- Cobalt–chromium molybdenum alloys (Co-Cr-Mo):
Cobalt–chromium molybdenum alloys consist of 26–30% Cr, 5–7% Mo, and less than 0.35% carbon with some basic cobalt. This alloy can be manufactured by casting, striking, and pressing. Its features include high strength and fatigue resistance, a low to medium elastic modulus, and high abrasion resistance.
- Second: Polymeric materials:
- Polyethylene (Ultra-High-Molecular-Weight Polyethylene) (UHMWPE):
This is the polymer material of choice in ankle replacements. Due to a range of features including corrosion resistance and biocompatibility, it remains the gold standard to date. It has very long polymer chains that tend to transfer the load more effectively toward the polymer backbone by enhancing intermolecular activities [14].
Table 1 reveals the mechanical characteristics of these items [15,16,17]. On the other hand, the vibration frequency values (frequency [Hz]) are calculated; the random vibration of the three directions (x, y, and z) is also achieved. This is to analyze the findings, identify the appropriate item to implement the artificial ankle joint, and select the archetypal design. The significance of this research stems from studying the biomechanics and its influence on the leg and the ankle to prevent the side effects observed following the surgery; all this is through manipulating the finite element method that concludes with these criteria.

Table 1.
Mechanical properties of the SS316L, TI-6AL-4V, TI-13ZR, CO-CR-MO, and UHMWPE materials.
4.1. Selecting Materials for Each Element of the Components of an Artificial Ankle
The artificial ankle joint consists of three parts:
- Tibial Component: Polymeric item (UHMWPE), Ti-6A1-4V alloy, SS316L alloy, Co-Cr-Mo alloys, and Ti-13 Nb-13Zr alloys.
- Bearing Component: UHMWPE.
- Talar Component: Polymeric item (UHMWPE), Ti-6A1-4V alloy, SS316L alloy, Co-Cr-Mo alloys, and Ti-13 Nb-13Zr alloys.
4.2. Three-Dimensional Design of the Artificial Salto-Talaris Ankle Joint
The three-dimensional prototype of the artificial ankle joint was drawn via CATIA software (V5R18, Dassault Systèmes, Vélizy-Villacoublay, France). There are three parts to this design. The tibial component consists of an empty tube that is soon inserted into the lower part of the leg; it is fastened from below with the bearing component that looks like a semi-circle bow. One apparent feature is that it moves on all levels; when it slides higher toward the talar, the bow looks concave in order to fix it to the upper part of the ankle, and from above the component, it is possible to fasten the bearing component. These measures are designed as is apparent in Table 2 [16]. Figure 3 elaborates on the three-dimensional archetype of the salto-talaris artificial ankle joint.

Table 2.
Measures of design of the artificial ankle joint.
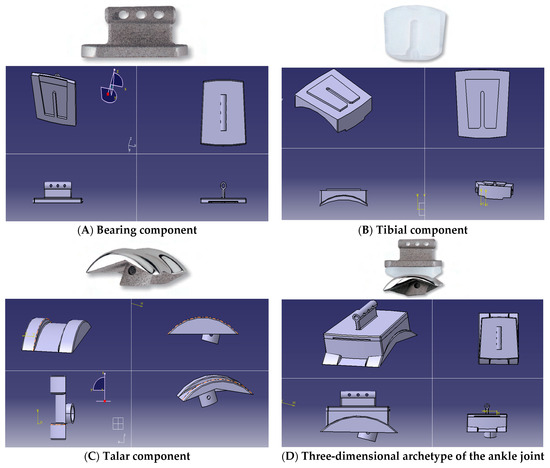
Figure 3.
(A–C) Components with three dimensional archetype of the artificial (D) salto-talaris ankle joint.
4.3. FEA of the Salto-Talaris Ankle Joint
Each part of the ankle joint components has to be capable of holding both tensile and compressive loads successively. On the other hand, pressures and deviations are supposed to be within the permissible limits. A perfect contact pair is formulated in our study. However, parts of the components are always bonded to each other. The archetype is exported as an igs file, and such a file can be imported into the environment of Ansys software (v. 19 R1, ANSYS, Inc., Canonsburg, PA, USA) in order to open an archetype. Finally, the archetype was prepared for analysis, where 11,188 elements were structured with 21,829 nodes accordingly. With the help of ANSYS, miscellaneous dimensional conditions are identified in addition to conducting an analysis. Figure 4 elaborates on the finite element archetype of the implant, as well as the dimensional conditions suggested for the archetype prior to analysis.
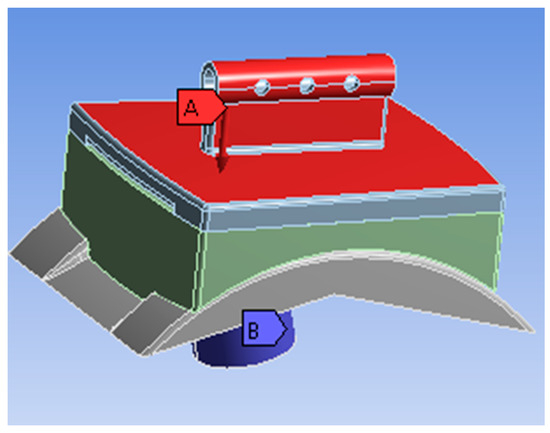
Figure 4.
Loads and boundary conditions.
5. Results
5.1. Conditions of Natural Walking
Figure 5 and Figure 6 disclose the results of the displacement and stress compared to von Mises stress under the conditions of natural walking of the five items with the help of the ANSYS software, provided that the patient’s weight is 50 kg. It has been observed that the item UHMWPE has the lowest stress value compared to von Mises stress, contrasting other manipulated items when the highest stress reaches 38.968 MPa, whereas the sliding value of this item is the highest, reaching 0.2745 mm. Accordingly, it seems that the UHMWPE item is the best in light of the resulting stresses. We can also observe that TI-13Nb-13ZR alloys possess a maximum stress reaching 54.043 MPa, and a maximum displacement of 0.020894 mm. Thus, this alloy is considered the best to use following UHMWPE according to the resulting stresses. In terms of displacement values, we notice that the Co-Cr-Mo material has an upper stress of up to 56.476 MPa and a low displacement of 0.016551 mm compared to the rest of the materials, as the results indicate that the biomechanical response intensifies at the front of the artificial ankle joint, which contributes to the pressure observed at the front of the joint. The highest point allows us to improve the pressure location, manipulate the direction, and improve the displacement properties of each material. Other effects of the patient’s weights and different loads are elaborated in Table 3 and Figure 7 and Figure 8.
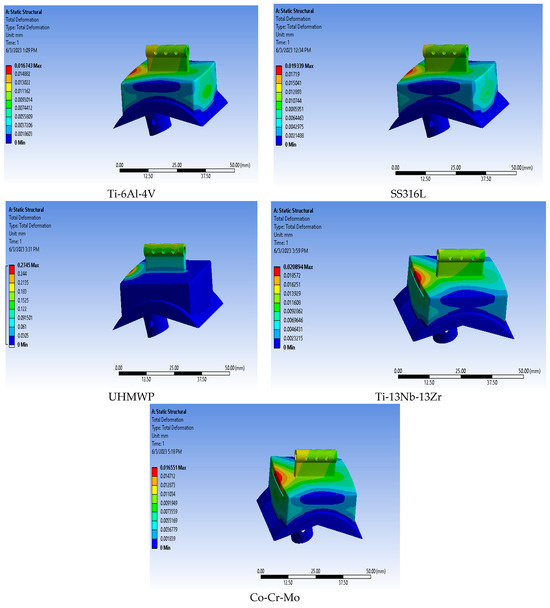
Figure 5.
Results of displacement analysis under normal walking conditions.
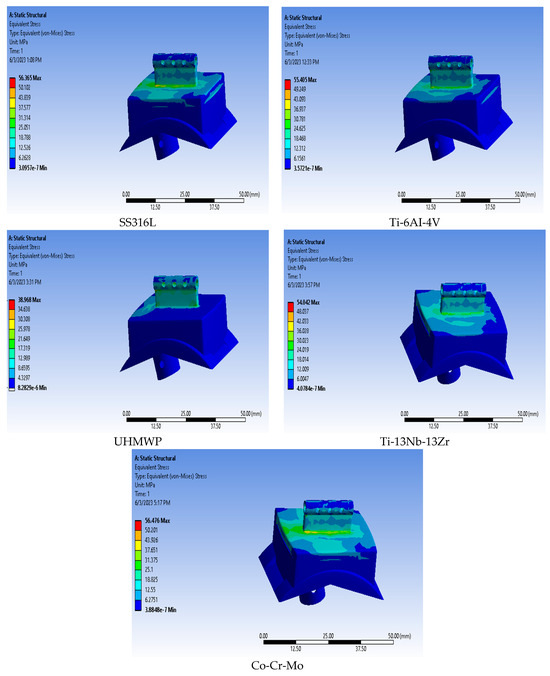
Figure 6.
Results of the von Mises stress analysis.

Table 3.
Summary of the results of salto-talaris joint under natural walking conditions.
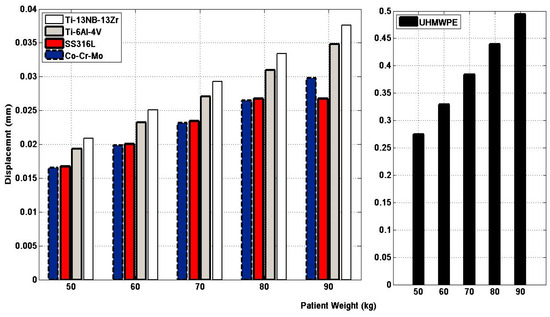
Figure 7.
Displacement values for the studied materials under normal walking conditions for the studied materials.
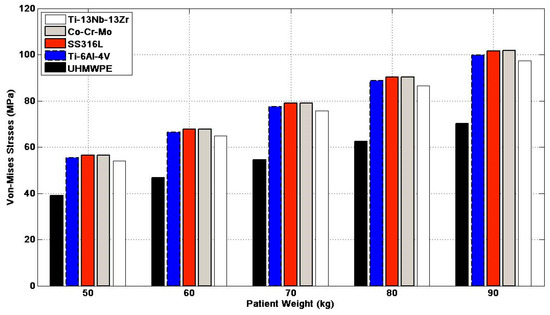
Figure 8.
Von Mises stress of the studied materials during normal walking of the materials used in the ankle industry.
5.2. Under the Effect of Loading
Concerning the stress resulting from the artificial ankle joint under the influence of loading, we still need to conduct a lot of analyses to confirm that the ankle joint could meet the expectations of the vast majority, like walking, running, and jumping, since these will lead to miscellaneous stresses upon the ankle joint. Figure 9 and Figure 10 and Table 4 disclose displacement values and von Mises’ stress of the researched items within the loading conditions; the results showed that the UHMWPE material had the lowest von Mises stress value by 194.84 MPa, while the displacement value was high by 1.3725 mm at a force of 10,000 N. The Ti-13Nb-13Zr material also showed the lowest stress after the UHMWPE material, and it was found that the Co-Cr-Mo material was better in terms of displacement, but had higher pressures compared to other materials. We could confirm the significance of using UHMWPE items in manufacturing the ankle joint, since it reveals low stress values when compared to other items used with higher values of displacement.
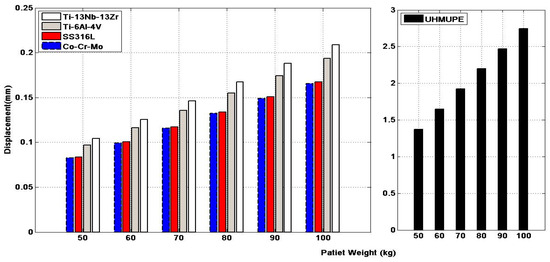
Figure 9.
Diagram of displacement of the implanting items under loading conditions.
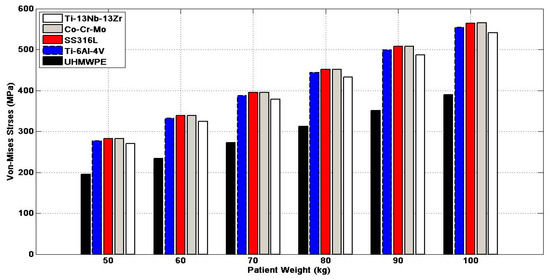
Figure 10.
Diagram of von Mises stresses of the implanting items under loading.

Table 4.
Results of von Mises stresses and displacement of the items used in manufacturing the ankle joint under loading conditions.
5.3. Analyzing the Vibrating Behaviour
Vibration analysis is meant to study the dynamic characteristics of skeletons under the effect of vibrating stimulus in the ankle joint, where it is fastened exclusively from one side. To complete this study, the boundary conditions used are similar to what has been previously mentioned above. An analysis was conducted to trace the total deformity in six positions. The concluding results of the values of frequency and total deformities are elaborated in Figure 11, Figure 12, Figure 13, Figure 14 and Figure 15 and in Table 5, Table 6, Table 7, Table 8 and Table 9 of the implanting items in this study. According to these results, it transpires that the frequency values of the item UHMWPE are low compared to other manipulated items: an amount of 155.774 Hz. By contrast, the values of the total deformity of this item are much higher compared to other researched items (16.365 mm). This is due to the low values of the density and flexibility of the UHMWPE compared to other items. From this, we observe that this item is the best to avoid the frequency stimulus.
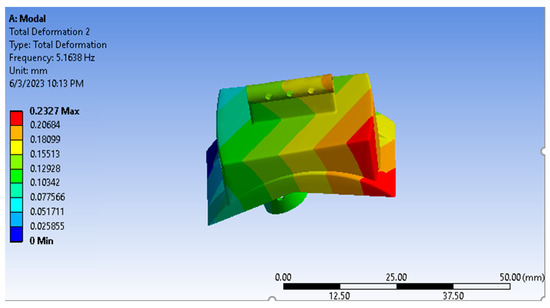
Figure 11.
Vibration results of Ti-6A1-4V part.
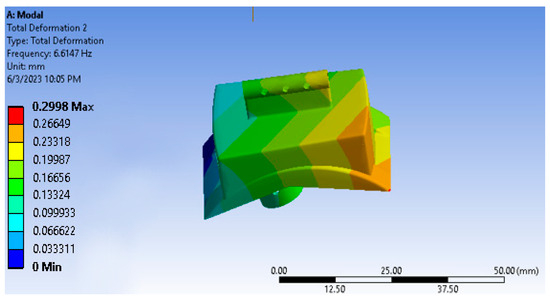
Figure 12.
Vibration results of the Ti-13Nb-13Zr part.
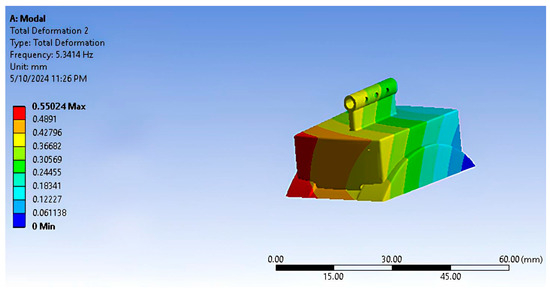
Figure 13.
Vibration results of the Co-Cr-Mo part.
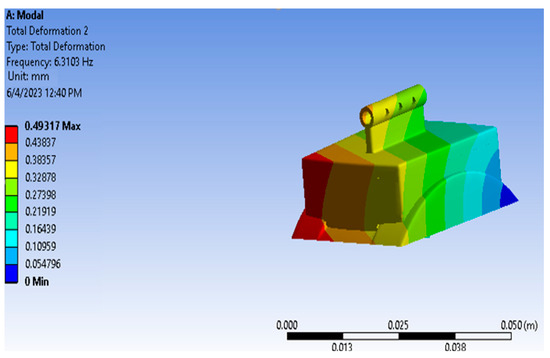
Figure 14.
Vibration results of the SS316L part.
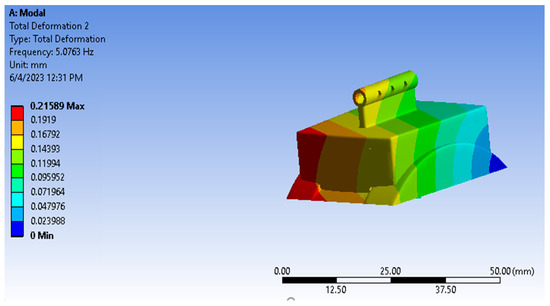
Figure 15.
Vibration results of the UHMWPE part.

Table 5.
Values of frequency and total deformation of Ti-6A1-4V joint.

Table 6.
Values of frequency and total deformation of Ti-13Nb-13Zr part.

Table 7.
Values of frequency and total deformation of Co-Cr-Mo part.

Table 8.
Values of frequency and total deformation of SS316L part.

Table 9.
Values of frequency and total deformation of UHMWPE part.
After concluding with the vibration analysis using ANSYS, random vibration can be simulated, which is the vibration according to three directions (x, y, z). This is an attempt to reach the value of the deformity in these directions. It is also possible to identify the deformity by linking to the aforementioned vibration analysis by recording the displacement values (displacement [mm2]/Hz]) and appropriate frequencies. Contrariwise, PSD displacement was selected, and we recorded the results of the analysis, as is apparent in Table 10 and Figure 16, with a probability value of 68.269%. The material UHMWPE is the best in terms of directional deformation according to three directions (x, y, z) compared to other materials; the material Co-Cr-Mo was the best in terms of directional deformation after UHMWPE. As a conclusion, it is still the best item to use under the loading conditions specific to jumping and at high speed in uneven areas (rough places or slopes).

Table 10.
The final results of the higher directional deformation of each item on the axes x, y, and z when exposed to vibration.
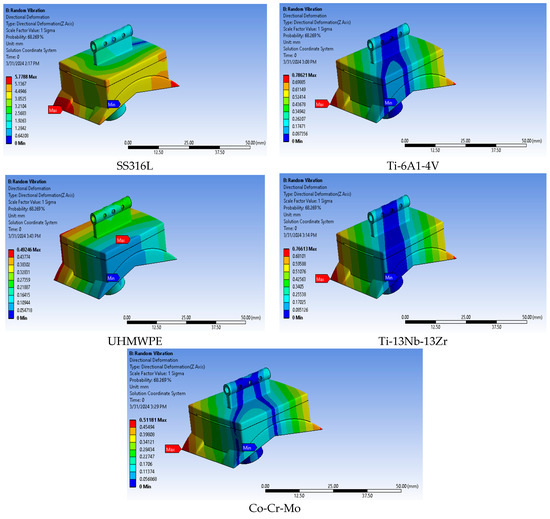
Figure 16.
Directional deformation along three (XYZ) axes of the studied materials.
5.4. Confirming the Correct Design Analysis
In addition, the ability of the model to restore the original state in the absence of applied forces or loading conditions was verified. The elastic strain method was used during the analysis using ANSYS, as elastic strain is a very essential factor to measure whether a model is practical or not. The elastic strain is shown in the Figure 17. However, we observe that the maximum elastic strain in this design reaches 4.4484 × 10−2 mm/mm, and that the minimal elastic strain is 2.01 × 10−8 mm/mm. We also observe the non-existence of any red regions in the design of the archetype. This proves that such a design has the capacity to restore its original status [3].
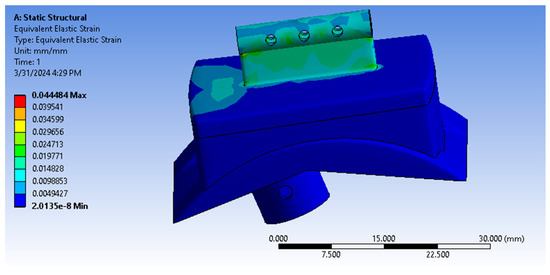
Figure 17.
Analysis of the equivalent elastic strains.
In addition, in order to obtain the optimal design of the artificial ankle joint, this design (salto-talaris) was compared with the star ankle design [15]. To perfectly achieve this, measures and results of the star ankle design were recorded and applied to the salto-talaris design in compliance with forces of 2000 N, 2500 N, 3000 N, and 3500 N. Figure 18 reveals both aforementioned designs. The results of analyzing the von Mises stresses and displacements of the items Ti-6A-4V and Co-Cr-Mo are elaborated in Figure 19. Whilst the results for the material Ti-6Al-4V for the salto-talaris design showed an amount of 55.405 MPa, for the star ankle design, it showed an amount of 57.952 MPa, and the displacement for the salto-talaris design showed 0.0193 mm, while for the star ankle, it showed 0.0612 mm. However, we can confirm that the values of displacement and higher stress (equivalent to von Mises stress) in designing salto-talaris joints are lower in comparison with the star ankle design of both items [3].
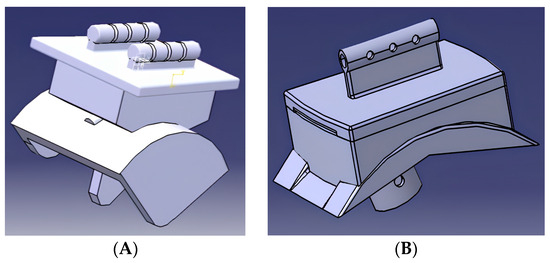
Figure 18.
A comparison between designs of the artificial ankle joints: (A) Star Ankle, and (B) Salto-Talaris.
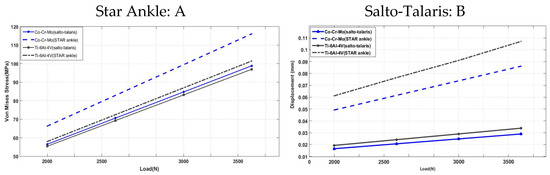
Figure 19.
A comparison between values of displacement and maximal stress equivalent to von Mises via the use of the designs of salto-talaris and star ankle.
6. Discussion
The finite element method (FEM) serves as a robust numerical technique that is extensively utilized for intricate numeric analyses under complex conditions and geometries [18]. It finds broad application in assessing ankle and foot models’ performance under various loading and material conditions [19], as well as in evaluating the stability of prosthetic ankle joints [20]. Ankle joint designs often feature intricate geometries, posing challenges in deriving analytical solutions for stress distribution and optimal material selection. Total ankle joint replacements have emerged as the preferred treatment for joint failure, aiming to restore range of motion, thus garnering increasing significance. Numerous studies investigate artificial joint performance, spanning both experimental approaches and finite element analyses.
The long-term success or failure of such transplants heavily relies on distributed pressure. Current biomechanical studies aim to develop joints that maintain the natural range of motion and have prolonged lifespans by designing them with ideal shapes and introducing high-quality materials to their manufacture to prevent inflammatory reactions [3]. Similar findings were corroborated by Manvi et al. [15] in their study on designs and material selection. They revealed that implant groups exert higher forces and energy to maintain the implant in the predetermined position of the prosthesis. Their study also highlighted that the top and front of the ankle experience the highest stress, crucial for joint treatment and enhancement. The UHMWPE material emerged as superior in stress resistance, albeit displaying higher displacement values attributed to its structural hierarchy. Jian Yu et al. [17] showed the effect of implant materials for total ankle joint replacement (TAR) in order to reduce stress on the components of the joint. The materials were compared, showing that the UHMWPE polymeric material is better in terms of stress values, which confirms to us UHMWPE’s suitability for joint composition, as well as the validity of our results [17].
Under impact loading, artificial ankle joints typically endure stress levels equal to five times the body’s weight during walking [16,19], escalating to approximately ten times during running [21,22], and two to twelve times during jumping. The importance of utilizing UHMWPE elements in ankle joint manufacturing is evident, given their low pressure values compared to other elements, despite exhibiting higher displacement values, facilitating appropriate design and material selection under different loads.
Following vibration analysis using ANSYS, random vibrations in three directions (x, y, z) can be simulated, aiding in designing distortion-resistant joints under varying loading conditions. However, despite its significance, such studies often receive inadequate attention. Elastic strain analysis is pivotal in evaluating design practicality, as evidenced by the absence of red spots, indicating the design’s ability to restore its original state. Ştefan-Cătălin Popescu et al. [23] showed that the importance of comparing design and model predictions was compared to loading and displacement conditions, which leads to selecting the best preoperative ankle model and improving the kinematic state in our research. A comparison between the salto-talaris and star ankle designs revealed lower displacement and stress values in the former, affirming its superiority in terms of lesser displacement values and higher equivalent stress. This confirms that the proposed design is the best. This approach offers exciting prospects for improving patient care and optimizing prosthetic joint replacements. We remain optimistic that future research will improve and extend these findings, ultimately improving treatments for individuals with inflammation and joint laxity. In conclusion, the design can be developed in all conditions, including walking, running, jumping, and walking in rough places, which also allows for the selection and development of the appropriate material within these conditions.
This study has several limitations that should be considered for the future optimization of computational resources while maintaining fundamental analysis. The materials selected for comparison may not represent the full range of materials available for artificial ankle joints. Although this research includes different types of metal alloys and one polymeric material, there may be other materials with different properties that could be relevant. Work on developing a new material with low density and high properties is expected in the future. Another limitation of this study is also the lack of inclusion of bone modeling for simplification purposes. While bones are an integral part of the study of biomechanics, their exclusion simplifies the analysis and can be justified depending on the specific focus of the study or the desired level of computational complexity. This choice allows for a comprehensive analysis of stress distribution and biomechanical interactions from all sides, providing a comprehensive view of the effect of the implant on the surrounding bone. This allows us to validate the bone density distributions determined for healthy ankle bones by the bone remodeling model via bone densitometry devices; thereby, bone remodeling results can be analyzed and compared with the true bone density of the specimen.
7. Conclusions
In this research, we introduced significant insights into the design of artificial ankle joints using the CATIA software, aiming to ensure accurate pattern design and enhance reader understanding. Through extensive analyses conducted in ANSYS, leveraging the finite element method (FEM), we have validated the design and compared various materials for ankle joint manufacturing. Furthermore, thorough investigations into the characteristics of skeletons under vibrational stimuli, including random vibrations derived from vibration analysis, have been undertaken.
Based on our conclusive findings, we can now develop an archetype design devoid of directional deformities under diverse load conditions such as running, jumping, or brisk walking on uneven surfaces. Additionally, material selection for joint fabrication can be informed by the stress values and frequency characteristics observed in the joint structure. Notably, UHMWPE material exhibits lower stress values and offers superior usability compared to other materials, albeit with higher displacement values. Conversely, TI-13-Nb-13ZR material demonstrates elevated stress levels but with minimal displacement. Meanwhile, Ti-6A1-4V material presents higher stress and displacement values, albeit less than SS316L and Co-Cr-Mo. The opportunity to develop novel materials with lower density and enhanced characteristics, coupled with continued refinement of the design to prioritize human comfort, represents promising avenues for future research endeavors. Addressing these limitations could pave the way for more effective and comfortable artificial ankle joint designs, further advancing the field of biomechanics and joint replacement technology.
Author Contributions
Software, formal analysis, data curation validation, and writing—original draft: H.M.N. and M.A.; conceptualization, methodology, and supervision: T.O.; conceptualization, data curation, and visualization: M.I. and Y.Z.; resources, supervision, and writing—review and editing: A.I. and D.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data that support the findings of this study are available upon reasonable request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Janice, J.E.; Winter, D.A. Kinetic Analysis of the Lower Limbs During Walking: What Informati Can Be Gained from a Three- Dimensional Model? J. Biomech. 1995, 28, 753–758. [Google Scholar]
- Faldini, C.; Mazzotti, A.; Belvedere, C.; Durastanti, G.; Panciera, A.; Geraci, G.; Leardini, A. A New Ligament-Compatible Patient-Specific 3D-Printed Implant and Instrumentation for Total Ankle Arthroplasty: From Biomechanical Studies to Clinical Cases. J. Orthop. Traumatol. 2020, 21, 16. [Google Scholar] [CrossRef] [PubMed]
- Zhao, T.R.; Vahora, M.; Li, Z.J. Computer Aided Artificial Ankle Joints Design. J. Orthop. Traumatol. 2018, 5, 82–87. [Google Scholar]
- Nunley, A.J.; Walton, D. Ankle Arthrodesis in Case Competencies in Orthopaedic Surgery; Elsevier: Amsterdam, The Netherlands, 2016. [Google Scholar]
- Vickerstaff, J.A.; Miles, A.W.; Cunningham, J.L. A Brief History of Total Ankle Replacement and a Review of the Current Status. Med. Eng. Phys. 2007, 29, 1056–1064. [Google Scholar] [CrossRef] [PubMed]
- Hermus, J.P.S. Complications in Total Ankle Replacement. Foot Ankle Clin. 2024, 29, 157–163. [Google Scholar] [CrossRef] [PubMed]
- Yu, J.; Zhao, D.; Chen, W.M.; Chu, P.; Wang, S.; Zhang, C.; Huang, J.; Ma, X. Finite Element Stress Analysis of the Bearing Component and Bone Resected Surfaces for Total Ankle Replacement with Different Implant Material Combinations Fudan. BMC Musculoskelet. Disord. 2022, 45, 1783–1789. [Google Scholar] [CrossRef]
- Mrcsa, R.K.; Siddique, M.S. Stresses in the Ankle Joint and Total Ankle Replacement Design. Foot Ankle Surg. 2011, 17, 58–63. [Google Scholar] [CrossRef]
- Zhang, Y. Computational Modelling of Biomechanics and Biotribology for an Artificial Ankle Joint. In Computational Modelling of Biomechanics and Biotribology in the Musculoskeletal System; Elsevier: Amsterdam, The Netherlands, 2021; pp. 499–515. ISBN 9780128195314. [Google Scholar]
- Leardini, A.; Connor, J.O.; Giannini, S. Biomechanics of the Natural, Arthritic, and Replaced Human Ankle Joint, Alberto Leardini. J. Foot Ankle Res. 2014, 7, 8–20. [Google Scholar] [CrossRef] [PubMed]
- Earll, M.; Wayne, J.; Brodrick, C.; Vokshoor, A.; Adelaar, R. Contribution of the Deltoid Ligament to Ankle Joint Contact Characteristics: A Cadaver Study. Foot Ankle Int. 1996, 17, 317–324. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Yang, C.; Zhao, H.; Qu, S.; Li, X.; Li, Y. New Developments of Ti-Based Alloys for Biomedical Applications. Materials 2014, 7, 1709–1800. [Google Scholar] [CrossRef] [PubMed]
- Schneider, S.G.; Nunes, C.A.; Rogero, S.O.; Higa, O.Z.; Bressiani, J.C. Mechanical Properties and Cytotoxic Evaluation of the Ti-3Nb-13Zr Alloy. Biomecánica 2000, 8, 84–87. [Google Scholar] [CrossRef]
- Shen, F.-W. Ultrahigh-Molecular-Weight Polyethylene (UHMWPE) in Joint Replacement. In Biomedical Polymers; CRC Press: Boca Raton, FL, USA, 2007; ISBN 9781420044515. [Google Scholar]
- Manvi, M.; Pradeepa, S.K.; Savadi, R. Finite Element Analysis on Stainles Steel and Titanium Alloy Used as Ankle Joint Replacement Implant Materials. Int. J. Eng. Dev. Res. 2016, 4, 586–592. [Google Scholar]
- Oliveira, D.S.; Rodrigues, S. Biomechanics of the Total Ankle Arthroplasty Stres Analysis and Bone Remodeling. Master’s Thesis, Tecnico Lisboa, Lisboa, Portugal, 2013; pp. 72–363. [Google Scholar]
- Jian, Y.; Dahang, Z.; Chen, W.; Chu, M.; Wang, P. Finite Element Stress Analysis of the Bearing Component and Bone Resected Surfaces for Total Ankle Replacement with Different Implant Material Combinations. BMC Musculoskelet. Disord. 2022, 45, 70. [Google Scholar]
- Nazha, H.M.; Szávai, S.; Juhre, D. An Overview of Mathematical Methods Applied in the Biomechanics of Foot and Ankle–Foot Orthosis Models. J 2023, 7, 1–18. [Google Scholar] [CrossRef]
- Bischoff, J.E.; Dharia, M.; Hertzler, J.S. Evaluation of Total Ankle Arthroplasty Using Highly Crosslinked Ultrahigh Molecular-Weight Polyethylene Subjected to Physiological Loading. Foot Ankle Int. 2019, 40, 880–887. [Google Scholar] [CrossRef] [PubMed]
- Stauffer, R.N.; Chao, E.Y.; Brewster, R.C. Force and Motion Analysis of the Normal, Diseased, and Prosthetic Ankle Joint. Clin. Orthop. Relat. Res. 1977, 127, 189–196. [Google Scholar] [CrossRef]
- Miller, M.C.; Smolinski, P.; Conti, S.; Galik, K. Stresses in Polyethylene Liners in a Semiconstrained Ankle Prosthesis. J. Biomech. Eng. 2004, 126, 636–640. [Google Scholar] [CrossRef] [PubMed]
- Burdett, R.G. Forces Predicted at the Ankle during Running. Med. Sci. Sports Exerc. 1982, 14, 308–316. [Google Scholar] [CrossRef] [PubMed]
- Popescu, Ş.C. Mechanical Analysis of Scandinavian Total Ankle Replacement Prostheses through Finite Element. Int. J. Mechatron. Appl. Mech. 2018, 4, 27–31. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).