Extending Applications of Generalizability Theory-Based Bifactor Model Designs
Abstract
1. Introduction
2. Background
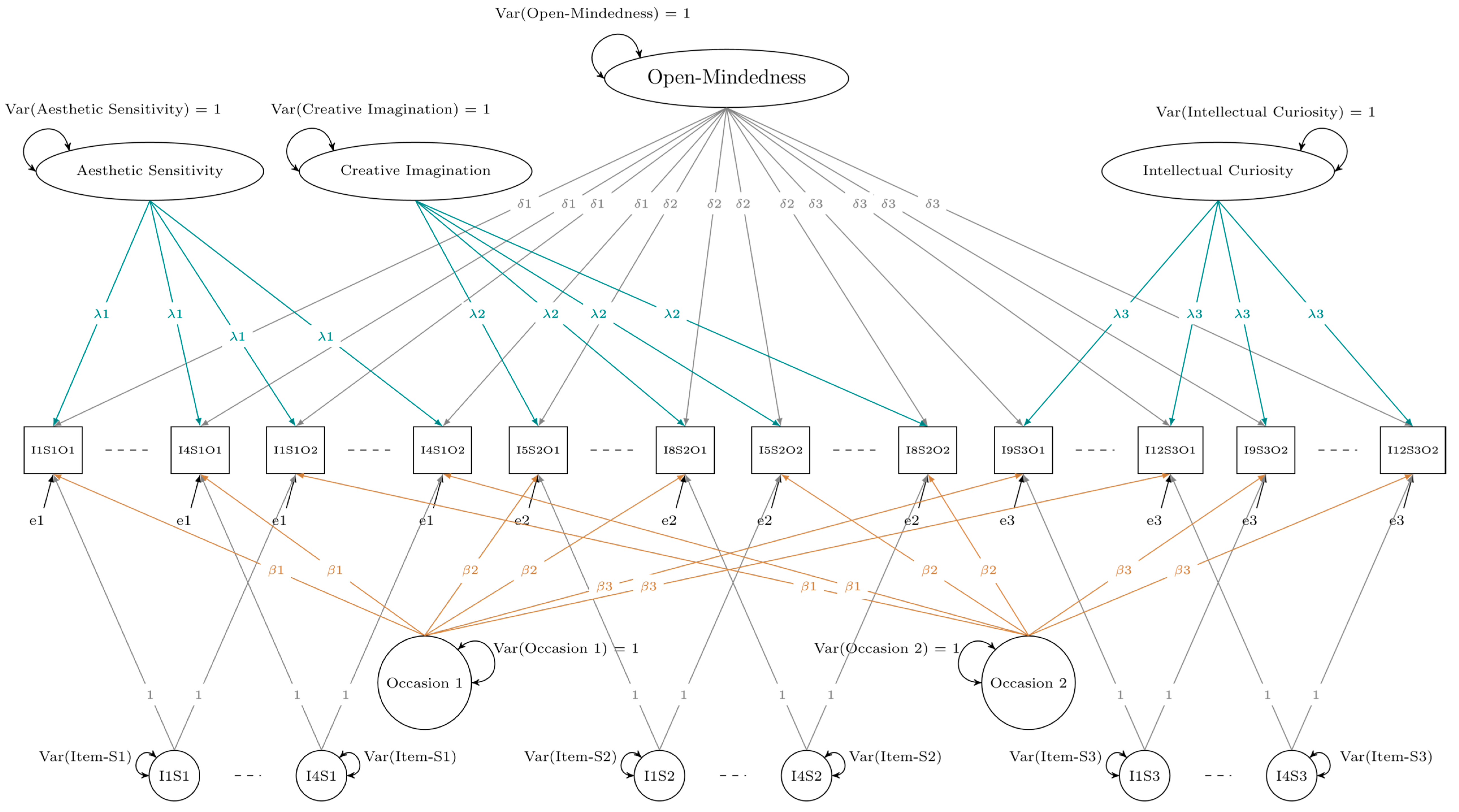
2.1. GT-Based Bifactor Structural Equation Modeling
2.2. Indices of Generalizability, Dependability, Measurement Error, Viability, and Added Value
2.3. Confidence Intervals
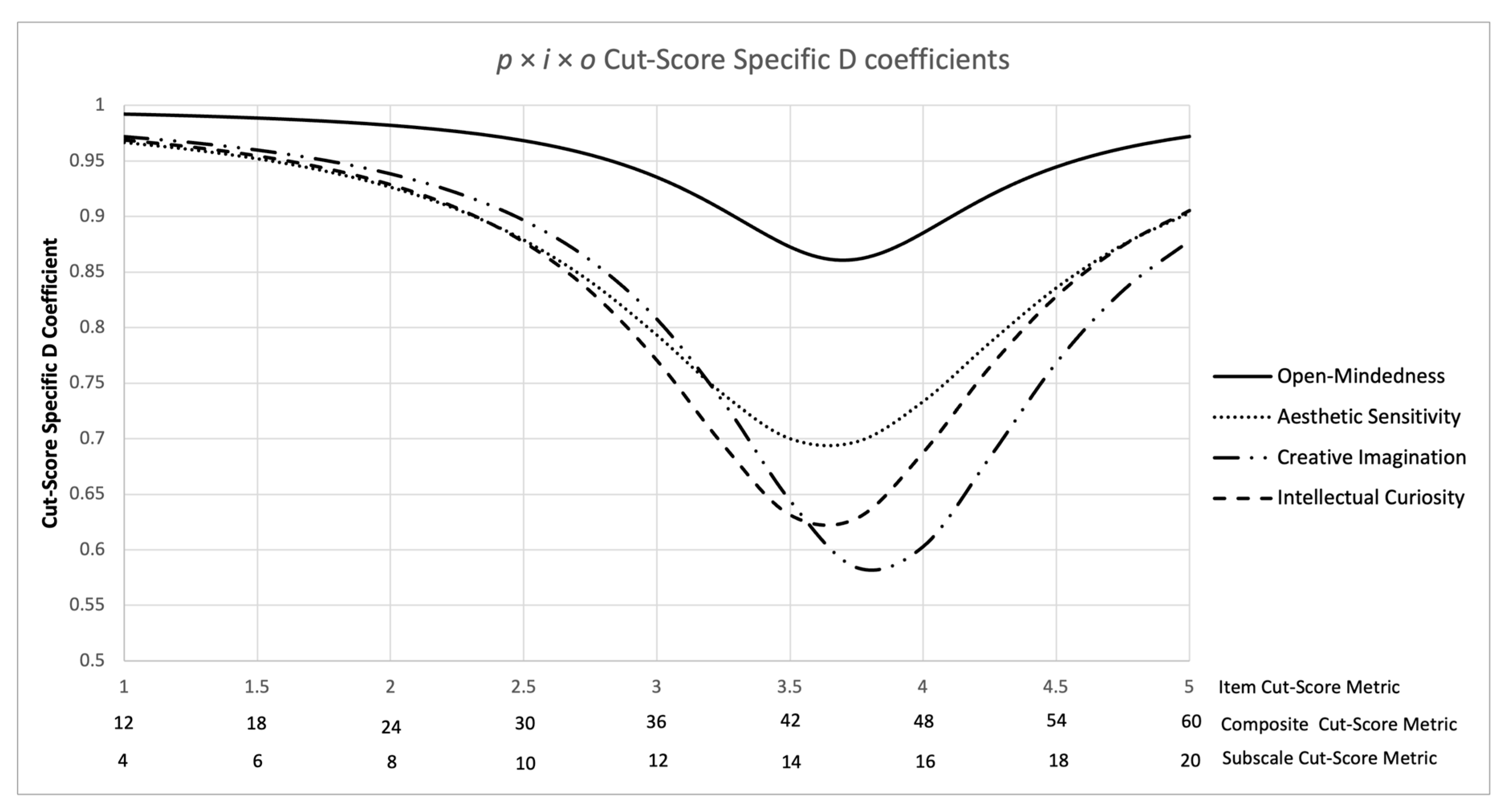
2.4. Changing Measurement Procedures
3. Purpose
4. Methods
4.1. Sample, Procedures, and Measures
4.2. Analyses
5. Results
5.1. Descriptive Statistics and Conventional Reliability Estimates
5.2. GT Bifactor Designs including Both Item and Occasion Effects
5.3. GT Bifactor Designs including Just Item and Just Occasion Effects
6. Discussion
6.1. Overview
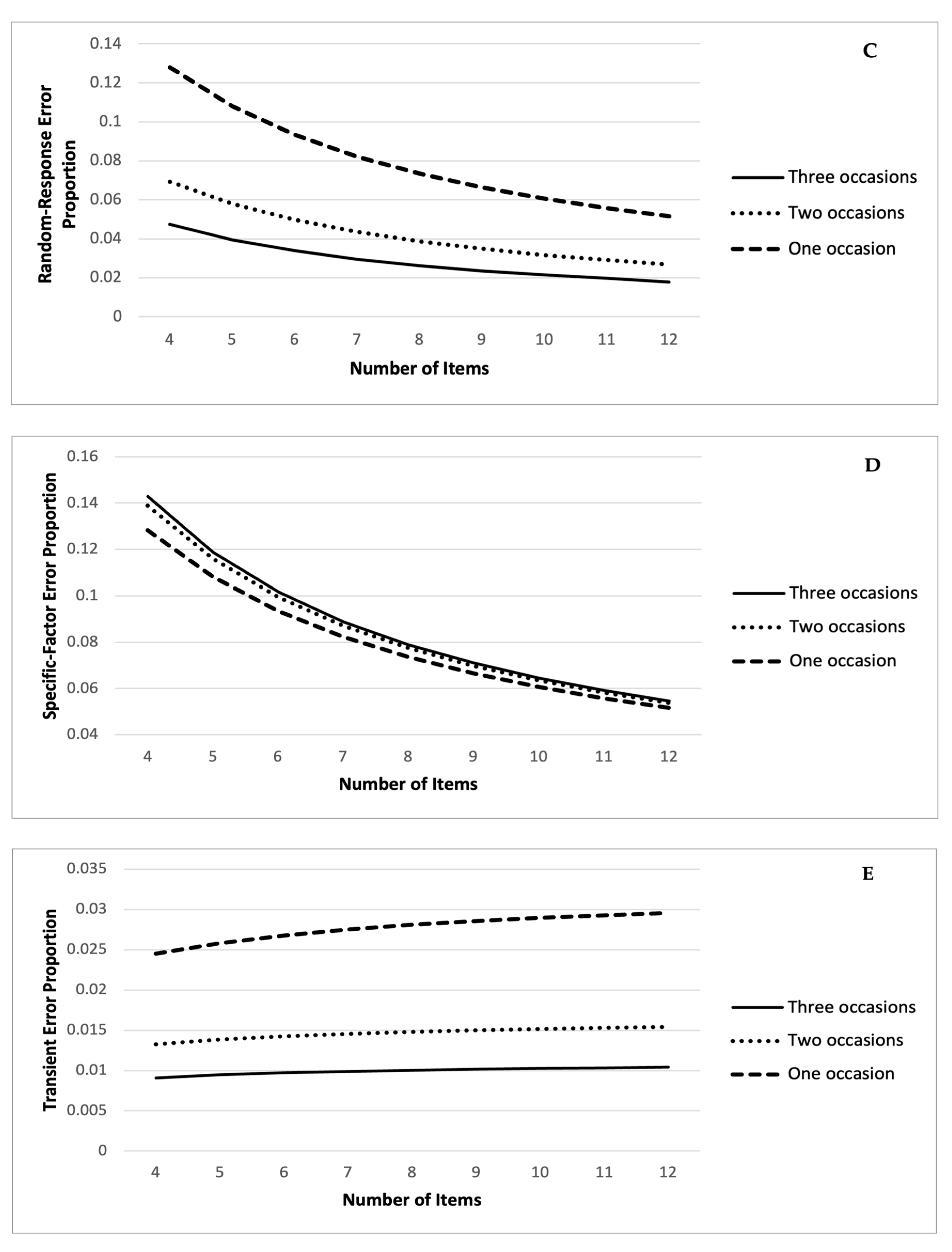
6.2. Relative Differences in Scores and Effects of Measurement Error
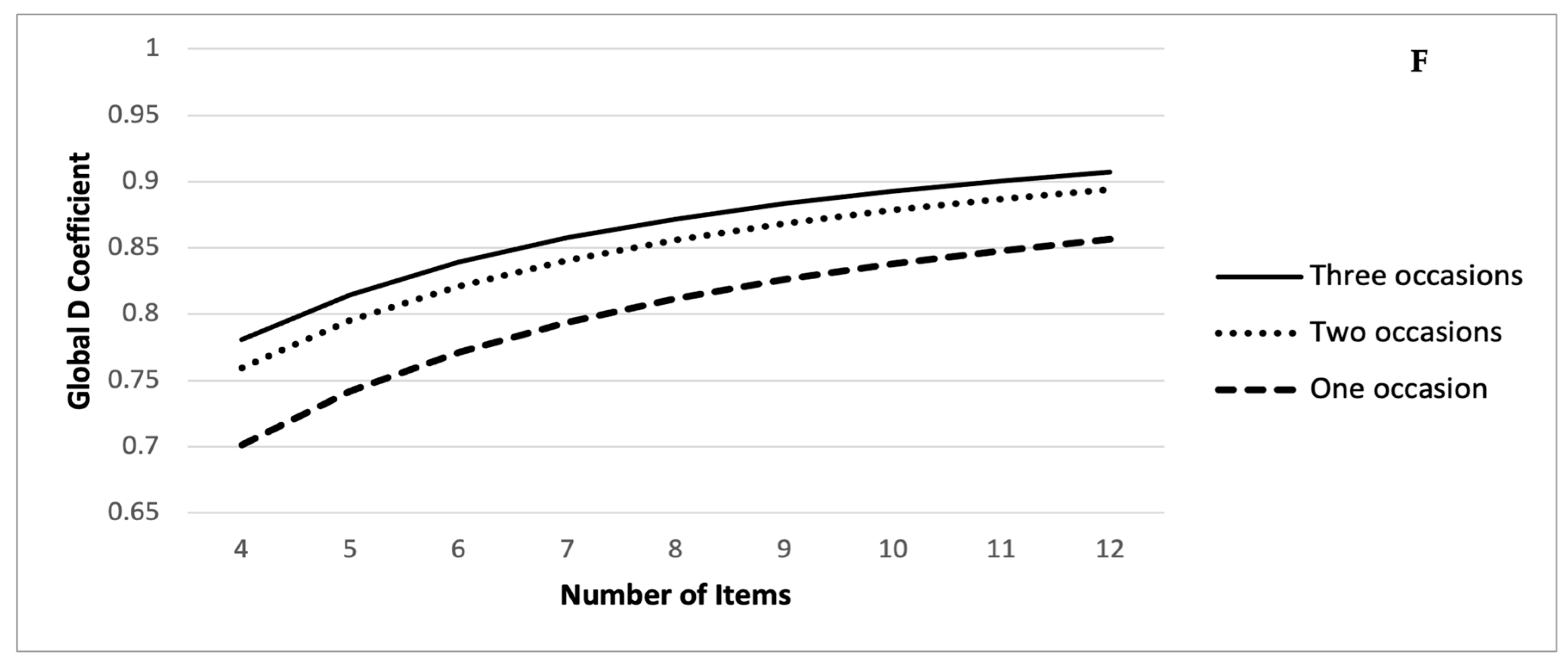
6.3. Absolute Differences in Item and Occasion Mean Scores
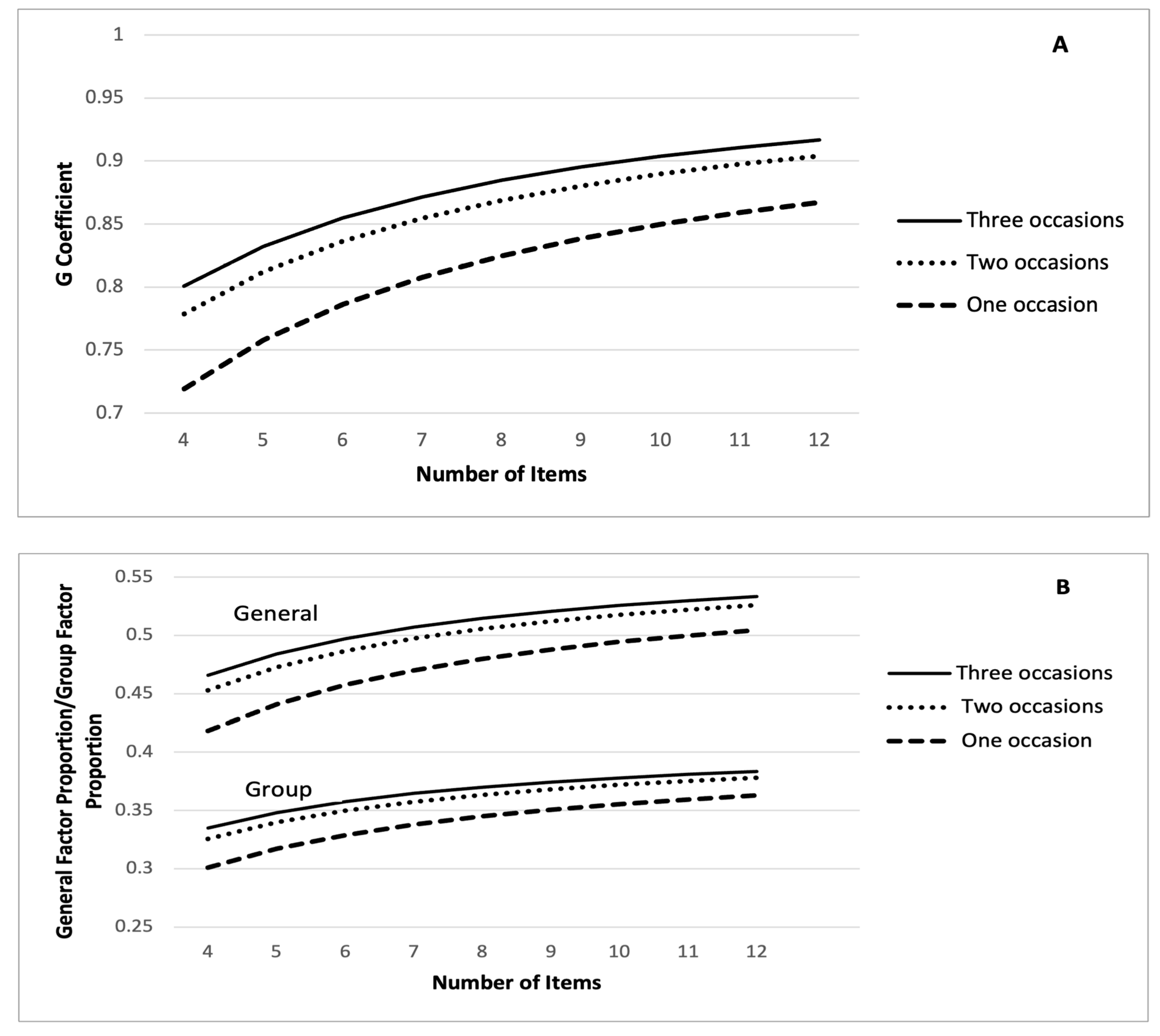
6.4. Scale Viability and Added Value
6.5. Restricting Universes of Generalization
7. Summary and Future Extensions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cronbach, L.J.; Rajaratnam, N.; Gleser, G.C. Theory of generalizability: A liberalization of reliability theory. Br. J. Stat. Psychol. 1963, 16, 137–163. [Google Scholar] [CrossRef]
- Andersen, S.A.W.; Nayahangan, L.J.; Park, Y.S.; Konge, L. Use of generalizability theory for exploring reliability of and sources of variance in assessment of technical skills: A systematic review and meta-analysis. Acad. Med. 2021, 96, 1609–1619. [Google Scholar] [CrossRef] [PubMed]
- Anderson, T.N.; Lau, J.N.; Shi, R.; Sapp, R.W.; Aalami, L.R.; Lee, E.W.; Tekian, A.; Park, Y.S. The utility of peers and trained raters in technical skill-based assessments a generalizability theory study. J. Surg. Educ. 2022, 79, 206–215. [Google Scholar] [CrossRef] [PubMed]
- Kreiter, C.; Zaidi, N.B. Generalizability theory’s role in validity research: Innovative applications in health science education. Health Prof. Educ. 2020, 6, 282–290. [Google Scholar] [CrossRef]
- Chen, D.; Hebert, M.; Wilson, J. Examining human and automated ratings of elementary students’ writing quality: A multivariate generalizability theory application. Am. Educ. Res. J. 2022, 59, 1122–1156. [Google Scholar] [CrossRef]
- Lightburn, S.; Medvedev, O.N.; Henning, M.A.; Chen, Y. Investigating how students approach learning using generalizability theory. High. Educ. Res. Dev. 2021, 41, 1618–1632. [Google Scholar] [CrossRef]
- Shin, J. Investigating and optimizing score dependability of a local ITA speaking test across language groups: A generalizability theory approach. Lang. Test. 2022, 39, 313–337. [Google Scholar] [CrossRef]
- Kumar, S.S.; Merkin, A.G.; Numbers, K.; Sachdev, P.S.; Brodaty, H.; Kochan, N.A.; Trollor, J.N.; Mahon, S.; Medvedev, O. A novel approach to investigate depression symptoms in the aging population using generalizability theory. Psychol. Assess. 2022, 34, 684–696. [Google Scholar] [CrossRef]
- Moore, L.J.; Freeman, P.; Hase, A.; Solomon-Moore, E.; Arnold, R. How consistent are challenge and threat evaluations? A generalizability analysis. Front. Psychol. 2019, 10, 1778. [Google Scholar] [CrossRef]
- Truong, Q.C.; Krägeloh, C.U.; Siegert, R.J.; Landon, J.; Medvedev, O.N. Applying Generalizability theory to differentiate between trait and state in the Five Facet Mindfulness Questionnaire (FFMQ). Mindfulness 2020, 11, 953–963. [Google Scholar] [CrossRef]
- Lafave, M.R.; Butterwick, D.J. A generalizability theory study of athletic taping using the technical skill assessment instrument. J. Athl. Train. 2014, 49, 368–372. [Google Scholar] [CrossRef] [PubMed]
- LoPilato, A.C.; Carter, N.T.; Wang, M. Updating generalizability theory in management research: Bayesian estimation of variance components. J. Manag. 2015, 41, 692–717. [Google Scholar] [CrossRef]
- Ford, A.L.B.; Johnson, L.D. The use of generalizability theory to inform sampling of educator language used with preschoolers with autism spectrum disorder. J. Speech Lang. Hear. Res. 2021, 64, 1748–1757. [Google Scholar] [CrossRef]
- Holzinger, K.J.; Harman, H.H. Comparison of two factorial analyses. Psychometrika 1938, 3, 45–60. [Google Scholar] [CrossRef]
- Holzinger, K.J.; Swineford, F. The bi-factor method. Psychometrika 1937, 2, 41–54. [Google Scholar] [CrossRef]
- Cucina, J.; Byle, K. The bifactor model fits better than the higher order model in more than 90% of comparisons for mental abilities test batteries. J. Intell. 2017, 5, 27. [Google Scholar] [CrossRef]
- Feraco, T.; Cona, G. Differentiation of general and specific abilities in intelligence. A bifactor study of age and gender differentiation in 8- to 19-year-olds. Intelligence 2022, 94, 101669. [Google Scholar] [CrossRef]
- Garn, A.C.; Webster, E.K. Bifactor structure and model reliability of the Test of Gross Motor Development—3rd edition. J. Sci. Med. Sport. 2021, 24, 255–283. [Google Scholar] [CrossRef]
- Panayiotou, M.; Santos, J.; Black, L.; Humphrey, N. Exploring the dimensionality of the Social Skills Improvement System using exploratory graph analysis and bifactor-(S-1) modeling. Assessment 2022, 29, 257–271. [Google Scholar] [CrossRef]
- Blasco-Belled, A.; Rogoza, R.; Torrelles-Nadal, C.; Alsinet, C. Emotional intelligence structure and its relationship with life satisfaction and happiness: New findings from the bifactor model. J. Happiness Stud. 2020, 21, 2031–2049. [Google Scholar] [CrossRef]
- Anglim, J.; Morse, G.; De Vries, R.E.; MacCann, C.; Marty, A. Comparing job applicants to non–applicants using an item–level bifactor model on the Hexaco Personality Inventory. Eur. J. Pers. 2017, 31, 669–684. [Google Scholar] [CrossRef]
- Biderman, M.D.; McAbee, S.T.; Chen, Z.J.; Hendy, N.T. Assessing the evaluative content of personality questionnaires using bifactor models. J. Pers. Assess. 2018, 100, 375–388. [Google Scholar] [CrossRef]
- Hörz-Sagstetter, S.; Volkert, J.; Rentrop, M.; Benecke, C.; Gremaud-Heitz, D.J.; Unterrainer, H.-F.; Schauenburg, H.; Seidler, D.; Buchheim, A.; Doering, S.; et al. A bifactor model of personality organization. J. Pers. Assess. 2021, 103, 149–160. [Google Scholar] [CrossRef] [PubMed]
- Vispoel, W.P.; Lee, H.; Xu, G.; Hong, H. Integrating bifactor models into a generalizability theory structural equation modeling framework. J. Exp. Educ. 2022. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Lee, H.; Xu, G.; Hong, H. Expanding bifactor models of psychological traits to account for multiple sources of measurement error. Psychol. Assess. 2022, 32, 1093–1111. [Google Scholar] [CrossRef]
- Longo, Y.; Jovanović, V.; Sampaio de Carvalho, J.; Karaś, D. The general factor of well-being: Multinational evidence using bifactor ESEM on the Mental Health Continuum-Short Form. Assessment 2020, 27, 596–606. [Google Scholar] [CrossRef]
- Burns, G.L.; Geiser, C.; Servera, M.; Becker, S.P.; Beauchaine, T.P. Application of the bifactor S-1 model to multisource ratings of ADHD/ODD symptoms: An appropriate bifactor model for symptom ratings. J. Abnorm. Child Psych. 2020, 48, 881–894. [Google Scholar] [CrossRef]
- Gomez, R.; Vance, A.; Gomez, R.M. Validity of the ADHD bifactor model in general community samples of adolescents and adults, and a clinic-referred sample of children and adolescents. J. Atten. Disord. 2018, 22, 1307–1319. [Google Scholar] [CrossRef]
- Willoughby, M.T.; Fabiano, G.A.; Schatz, N.K.; Vujnovic, R.K.; Morris, K.L. Bifactor models of attention deficit/hyperactivity symptomatology in adolescents: Criterion validity and implications for clinical practice. Assessment 2019, 26, 799–810. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Hong, H.; Lee, H. Benefits of doing generalizability theory analyses within structural equation modeling frameworks: Illustrations using the Rosenberg Self-Esteem Scale [Teacher’s corner]. Struct. Equ. Model. 2023. [Google Scholar] [CrossRef]
- Soto, C.J.; John, O.P. The next Big Five Inventory (BFI-2): Developing and assessing a hierarchical model with 15 facets to enhance bandwidth, fidelity, and predictive power. J. Pers. Soc. Psychol. 2017, 113, 117–143. [Google Scholar] [CrossRef]
- Reise, S.P.; Bonifay, W.E.; Haviland, M.G. Scoring and modeling psychological measures in the presence of multidimensionality. J. Pers. Assess. 2013, 95, 129–140. [Google Scholar] [CrossRef]
- Rodriguez, A.; Reise, S.P.; Haviland, M.G. Applying bifactor statistical indices in the evaluation of psychological measures. J. Pers. Assess. 2016, 98, 223–237. [Google Scholar] [CrossRef]
- Rodriguez, A.; Reise, S.P.; Haviland, M.G. Evaluating bifactor models: Calculating and interpreting statistical indices. Psychol. Methods 2016, 21, 137–150. [Google Scholar] [CrossRef] [PubMed]
- Le, H.; Schmidt, F.L.; Putka, D.J. The multifaceted nature of measurement artifacts and its implications for estimating construct-level relationships. Organ. Res. Methods 2009, 12, 165–200. [Google Scholar] [CrossRef]
- Thorndike, R.L. Reliability. In Educational Measurement; Lindquist, E.F., Ed.; American Council on Education: Washington, DC, USA, 1951; pp. 560–620. [Google Scholar]
- Schmidt, F.L.; Le, H.; Ilies, R. Beyond alpha: An empirical investigation of the effects of different sources of measurement error on reliability estimates for measures of individual differences constructs. Psychol. Methods 2003, 8, 206–224. [Google Scholar] [CrossRef]
- Geiser, C.; Lockhart, G. A comparison of four approaches to account for method effects in latent state-trait analyses. Psychol. Methods 2012, 17, 255–283. [Google Scholar] [CrossRef]
- Steyer, R.; Ferring, D.; Schmitt, M.J. States and traits in psychological assessment. Eur. J. Psychol. Assess. 1992, 8, 79–98. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Xu, G.; Schneider, W.S. Interrelationships between latent state-trait theory and generalizability theory in a structural equation modeling framework. Psychol. Methods 2022, 27, 773–803. [Google Scholar] [CrossRef]
- Brennan, R.L.; Kane, M.T. An index of dependability for mastery tests. J. Educ. Meas. 1977, 14, 277–289. [Google Scholar] [CrossRef]
- Kane, M.T.; Brennan, R.L. Agreement coefficients as indices of dependability for domain-referenced tests. Appl. Psychol. Meas. 1980, 4, 105–126. [Google Scholar] [CrossRef]
- Jorgensen, T.D. How to estimate absolute-error components in structural equation models of generalizability theory. Psych 2021, 3, 113–133. [Google Scholar] [CrossRef]
- Little, T.D.; Siegers, D.W.; Card, A. A non-arbitrary method or identifying and scaling latent variables in SEM and MACS models. Struct. Equ. Modeling 2006, 13, 59–72. [Google Scholar] [CrossRef]
- Reise, S.P. The rediscovery of bifactor measurement models. Multivar. Behav. Res. 2012, 47, 667–696. [Google Scholar] [CrossRef]
- Haberman, S.J. When can subscores have value? J. Educ. Behav. Stat. 2008, 33, 204–229. [Google Scholar] [CrossRef]
- Haberman, S.J.; Sinharay, S. Reporting of subscores using multidimensional item response theory. Psychometrika 2010, 75, 209–227. [Google Scholar] [CrossRef]
- Sinharay, S. Added value of subscores and hypothesis testing. J. Educ. Behav. Stat. 2019, 44, 25–44. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Lee, H.; Hong, H.; Chen, T. Applying Multivariate Generalizability Theory to Psychological Assessments. Psychol. Methods 2022. submitted. [Google Scholar]
- Feinberg, R.A.; Wainer, H. A simple equation to predict a subscore’s value. Educ. Meas. 2014, 33, 55–56. [Google Scholar] [CrossRef]
- Rosseel, Y. lavaan: An R package for structural equation modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- Rosseel, Y.; Jorgensen, T.D.; Rockwood, N. Package ‘Lavaan’. R Package Version (0.6–15). 2023. Available online: https://cran.r-project.org/web/packages/lavaan/lavaan.pdf (accessed on 27 April 2023).
- Jorgensen, T.D.; Pornprasertmanit, S.; Schoemann, A.M.; Rosseel, Y. semTools: Useful Tools for Structural Equation Modeling. R Package Version 0.5–6. 2022. Available online: https://CRAN.R-project.org/package=semTools (accessed on 9 February 2023).
- John, O.P.; Donahue, E.M.; Kentle, R.L. The Big Five Inventory—Versions 4a and 54; University of California, Berkeley, Institute of Personality and Social Research: Berkeley, CA, USA, 1991. [Google Scholar]
- Revelle, W. Psych: Procedures for Psychological, Psychometric, and Personality Research. R Package Version (2.3.3). 2023. Available online: https://cran.r-project.org/web/packages/psych/index.html (accessed on 27 April 2023).
- Vispoel, W.P.; Lee, H.; Hong, H. Analyzing multivariate generalizability theory designs within structural equation modeling frameworks. Struct. Equ. Model. 2023, in press. [Google Scholar]
- Morris, C.A. Optimal Methods for Disattenuating Correlation Coefficients under Realistic Measurement Conditions with Single-Form, Self-Report Instruments (Publication No. 27668419). Ph.D. Thesis, University of Lowa, Lowa City, IA, USA, 2020. [Google Scholar]
- Reeve, C.L.; Heggestad, E.D.; George, E. Estimation of transient error in cognitive ability scales. Int. J. Select. Assess. 2005, 13, 316–332. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Morris, C.A.; Kilinc, M. Applications of generalizability theory and their relations to classical test theory and structural equation modeling. Psychol. Methods 2018, 23, 1–26. [Google Scholar] [CrossRef] [PubMed]
- Vispoel, W.P.; Morris, C.A.; Kilinc, M. Practical applications of generalizability theory for designing, evaluating, and improving psychological assessments. J. Pers. Assess. 2018, 100, 53–67. [Google Scholar] [CrossRef]
- Vispoel, W.P.; Morris, C.A.; Kilinc, M. Using generalizability theory with continuous latent response variables. Psychol. Methods 2019, 24, 153–178. [Google Scholar] [CrossRef] [PubMed]
- Marcoulides, G.A. Estimating variance components in generalizability theory: The covariance structure analysis approach [Teacher’s corner]. Struct. Equ. Modeling 1996, 3, 290–299. [Google Scholar] [CrossRef]
- Raykov, T.; Marcoulides, G.A. Estimation of generalizability coefficients via a structural equation modeling approach to scale reliability evaluation. Int. J. Test. 2006, 6, 81–95. [Google Scholar] [CrossRef]
- Enders, C.K.; Bandalos, D.L. The relative performance of full information maximum likelihood estimation for missing data in structural equation models. Struct. Equ. Model. 2001, 8, 430–457. [Google Scholar] [CrossRef]
- Huebner, A.; Skar, G.B. Conditional standard error of measurement: Classical test theory, generalizability theory and many-facet Rasch measurement with applications to writing assessment. Pract. Assess. Res. Eval. 2021, 26, 1–20. [Google Scholar]
- Vispoel, W.P.; Xu, G.; Kilinc, M. Expanding G-theory models to incorporate congeneric relationships: Illustrations using the Big Five Inventory. J. Pers. Assess. 2021, 103, 429–442. [Google Scholar] [CrossRef]
- Ark, T.K. Ordinal Generalizability Theory Using an Underlying Latent Variable Framework. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2015. Available online: https://open.library.ubc.ca/soa/cIRcle/collections/ubctheses/24/items/1.0166304 (accessed on 9 February 2023).
| Composite | Subscale |
|---|---|
| Formula |
|---|
| Value-added ratio , where U = universe score. |
| Formula |
|---|
| Value-added ratio , where U = universe score. |
| Formula |
|---|
| Value-added ratio , where U = universe score. |
| Occasion/Index | Composite/Subscale | ||||
|---|---|---|---|---|---|
| Open- Mindedness | Aesthetic Sensitivity | Creative Imagination | Intellectual Curiosity | Subscale Average | |
| Number of Items | 12 | 4 | 4 | 4 | 4 |
| Time 1 | |||||
| Mean: Scale (Item) | 44.483 (3.707) | 14.576 (3.644) | 15.375 (3.844) | 14.532 (3.633) | 14.828 (3.707) |
| SD: Scale (Item) | 8.145 (0.679) | 3.693 (0.923) | 3.005 (0.751) | 3.230 (0.808) | 3.309 (0.827) |
| Alpha | 0.837 | 0.730 | 0.671 | 0.725 | 0.709 |
| Time 2 | |||||
| Mean: Scale (Item) | 44.290 (3.691) | 14.553 (3.638) | 15.185 (3.796) | 14.553 (3.638) | 14.763 (3.691) |
| SD: Scale (Item) | 8.212 (0.684) | 3.719 (0.930) | 3.036 (0.759) | 3.071 (0.768) | 3.275 (0.819) |
| Alpha | 0.855 | 0.769 | 0.696 | 0.723 | 0.729 |
| Test-retest | 0.856 | 0.828 | 0.793 | 0.759 | 0.794 |
| Variance Component | Composite/Subscale | ||||
|---|---|---|---|---|---|
| Open- Mindedness | Aesthetic Sensitivity | Creative Imagination | Intellectual Curiosity | Subscale Average | |
| 0.323 (0.314, 0.333) | 0.355 (0.326, 0.386) | 0.274 (0.254, 0.296) | 0.343 (0.316, 0.371) | 0.324 | |
| 0.043 (0.039, 0.049) | 0.256 (0.224, 0.289) | 0.116 (0.089, 0.147) | 0.015 (0.000, 0.062) | 0.129 | |
| 0.126 (0.116, 0.137) | 0.436 (0.381, 0.491) | 0.328 (0.272, 0.384) | 0.373 (0.317, 0.428) | 0.379 | |
| 0.035 (0.024, 0.048) | 0.021 (0.005, 0.048) | 0.056 (0.027, 0.095) | 0.033 (0.011, 0.065) | 0.036 | |
| 0.127 (0.115, 0.140) | 0.435 (0.370, 0.500) | 0.361 (0.291, 0.431) | 0.348 (0.281, 0.415) | 0.381 | |
| 0.020 (0.017, 0.025) | 0.074 (0.054, 0.099) | 0.014 (0.007, 0.026) | 0.094 (0.071, 0.121) | 0.061 | |
| 0.001 (0.000, 0.014) | 0.003 (0.000, 0.042) | 0.003 (0.000, 0.042) | 0.003 (0.000, 0.042) | 0.003 | |
| 0.000 (0.000, 0.001) | 0.000 (0.000, 0.004) | 0.001 (0.000, 0.006) | 0.000 (0.000, 0.005) | 0.001 | |
| Design/Scale | Index (CI) | ||||||
|---|---|---|---|---|---|---|---|
| G (US) | Gen | Grp | SFE | TE | RRE | TRelE | |
| Design 1: i(s) = 4, o = 1 | |||||||
| Open-Mindedness | 0.789 (0.764, 0.811) | 0.696 (0.670, 0.718) | 0.093 (0.084, 0.105) | 0.068 (0.062, 0.074) | 0.075 (0.051, 0.102) | 0.068 (0.061, 0.075) | 0.211 (0.189, 0.236) |
| Aesthetic Sensitivity | 0.719 (0.692, 0.740) | 0.418 (0.378, 0.456) | 0.301 (0.266, 0.335) | 0.128 (0.111, 0.145) | 0.024 (0.006, 0.056) | 0.128 (0.109, 0.147) | 0.281 (0.260, 0.308) |
| Creative Imagination | 0.632 (0.583, 0.673) | 0.444 (0.402, 0.483) | 0.188 (0.145, 0.234) | 0.133 (0.109, 0.156) | 0.090 (0.043, 0.149) | 0.146 (0.117, 0.174) | 0.368 (0.327, 0.417) |
| Intellectual Curiosity | 0.628 (0.585, 0.667) | 0.601 (0.531, 0.646) | 0.027 (0.000, 0.103) | 0.163 (0.136, 0.187) | 0.057 (0.019, 0.110) | 0.152 (0.121, 0.180) | 0.372 (0.333, 0.415) |
| Subscale Average | 0.659 | 0.487 | 0.172 | 0.141 | 0.057 | 0.142 | 0.341 |
| Design 2: i(s) = 4, o = 2 | |||||||
| Open-Mindedness | 0.849 (0.834, 0.864) | 0.750 (0.730, 0.766) | 0.100 (0.090, 0.113) | 0.073 (0.067, 0.079) | 0.040 (0.027, 0.056) | 0.037 (0.033, 0.040) | 0.151 (0.136, 0.166) |
| Aesthetic Sensitivity | 0.779 (0.758, 0.796) | 0.453 (0.413, 0.492) | 0.326 (0.288, 0.363) | 0.139 (0.121, 0.156) | 0.013 (0.003, 0.031) | 0.069 (0.059, 0.080) | 0.221 (0.204, 0.242) |
| Creative Imagination | 0.716 (0.677, 0.751) | 0.503 (0.461, 0.543) | 0.213 (0.166, 0.263) | 0.150 (0.124, 0.176) | 0.051 (0.024, 0.087) | 0.083 (0.066, 0.099) | 0.284 (0.249, 0.323) |
| Intellectual Curiosity | 0.701 (0.667, 0.735) | 0.671 (0.597, 0.714) | 0.030 (0.000, 0.115) | 0.182 (0.153, 0.208) | 0.032 (0.011, 0.063) | 0.085 (0.067, 0.101) | 0.299 (0.265, 0.333) |
| Subscale Average | 0.732 | 0.542 | 0.190 | 0.157 | 0.032 | 0.079 | 0.268 |
| Design 3: i(s) = 4, o = 3 | |||||||
| Open-Mindedness | 0.872 (0.860, 0.883) | 0.769 (0.752, 0.783) | 0.102 (0.093, 0.116) | 0.075 (0.069, 0.081) | 0.028 (0.019, 0.038) | 0.025 (0.023, 0.028) | 0.128 (0.117, 0.140) |
| Aesthetic Sensitivity | 0.801 (0.781, 0.818) | 0.466 (0.425, 0.505) | 0.335 (0.296, 0.374) | 0.143 (0.125, 0.161) | 0.009 (0.002, 0.021) | 0.048 (0.040, 0.055) | 0.199 (0.182, 0.219) |
| Creative Imagination | 0.750 (0.714, 0.782) | 0.526 (0.483, 0.567) | 0.223 (0.175, 0.275) | 0.157 (0.130, 0.184) | 0.035 (0.017, 0.061) | 0.058 (0.046, 0.069) | 0.250 (0.218, 0.286) |
| Intellectual Curiosity | 0.729 (0.698, 0.762) | 0.698 (0.622, 0.741) | 0.031 (0.000, 0.119) | 0.190 (0.159, 0.216) | 0.022 (0.007, 0.044) | 0.059 (0.047, 0.070) | 0.271 (0.238, 0.302) |
| Subscale Average | 0.760 | 0.563 | 0.197 | 0.163 | 0.022 | 0.055 | 0.240 |
| Design 4: i(s) = 8, o = 1 | |||||||
| Open-Mindedness | 0.846 (0.819, 0.870) | 0.747 (0.718, 0.771) | 0.099 (0.090, 0.112) | 0.036 (0.033, 0.040) | 0.081 (0.055, 0.109) | 0.037 (0.033, 0.040) | 0.154 (0.130, 0.181) |
| Aesthetic Sensitivity | 0.825 (0.793, 0.846) | 0.480 (0.432, 0.524) | 0.345 (0.307, 0.383) | 0.074 (0.064, 0.083) | 0.028 (0.006, 0.064) | 0.073 (0.062, 0.084) | 0.175 (0.154, 0.207) |
| Creative Imagination | 0.734 (0.675, 0.783) | 0.515 (0.464, 0.564) | 0.219 (0.168, 0.271) | 0.077 (0.063, 0.091) | 0.104 (0.051, 0.172) | 0.085 (0.067, 0.102) | 0.266 (0.217, 0.325) |
| Intellectual Curiosity | 0.745 (0.692, 0.789) | 0.713 (0.623, 0.769) | 0.032 (0.000, 0.121) | 0.097 (0.080, 0.112) | 0.068 (0.023, 0.129) | 0.090 (0.071, 0.108) | 0.255 (0.211, 0.308) |
| Subscale Average | 0.768 | 0.569 | 0.199 | 0.082 | 0.067 | 0.083 | 0.232 |
| Design 5: i(s) = 8, o = 2 | |||||||
| Open-Mindedness | 0.899 (0.883, 0.913) | 0.793 (0.772, 0.810) | 0.106 (0.096, 0.119) | 0.039 (0.035, 0.042) | 0.043 (0.029, 0.059) | 0.019 (0.018, 0.021) | 0.101 (0.087, 0.117) |
| Aesthetic Sensitivity | 0.869 (0.849, 0.884) | 0.506 (0.460, 0.549) | 0.363 (0.322, 0.404) | 0.078 (0.067, 0.088) | 0.015 (0.003, 0.034) | 0.039 (0.033, 0.045) | 0.131 (0.116, 0.151) |
| Creative Imagination | 0.811 (0.769, 0.845) | 0.569 (0.520, 0.616) | 0.241 (0.189, 0.296) | 0.085 (0.069, 0.100) | 0.058 (0.027, 0.098) | 0.047 (0.037, 0.056) | 0.189 (0.155, 0.231) |
| Intellectual Curiosity | 0.809 (0.772, 0.840) | 0.774 (0.683, 0.822) | 0.035 (0.000, 0.132) | 0.105 (0.087, 0.121) | 0.037 (0.012, 0.073) | 0.049 (0.039, 0.058) | 0.191 (0.160, 0.228) |
| Subscale Average | 0.830 | 0.616 | 0.213 | 0.089 | 0.036 | 0.045 | 0.170 |
| Design 6: i(s) = 8, o = 3 | |||||||
| Open-Mindedness | 0.918 (0.906, 0.928) | 0.810 (0.792, 0.825) | 0.108 (0.097, 0.122) | 0.040 (0.036, 0.043) | 0.029 (0.020, 0.040) | 0.013 (0.012, 0.015) | 0.082 (0.072, 0.094) |
| Aesthetic Sensitivity | 0.885 (0.868, 0.898) | 0.515 (0.470, 0.559) | 0.370 (0.328, 0.412) | 0.079 (0.068, 0.089) | 0.010 (0.002, 0.023) | 0.026 (0.022, 0.030) | 0.115 (0.102, 0.132) |
| Creative Imagination | 0.840 (0.806, 0.868) | 0.590 (0.540, 0.637) | 0.250 (0.196, 0.306) | 0.088 (0.072, 0.104) | 0.040 (0.019, 0.069) | 0.032 (0.026, 0.039) | 0.160 (0.132, 0.194) |
| Intellectual Curiosity | 0.833 (0.803, 0.860) | 0.797 (0.704, 0.842) | 0.036 (0.000, 0.136) | 0.108 (0.090, 0.125) | 0.025 (0.008, 0.050) | 0.034 (0.027, 0.040) | 0.167 (0.140, 0.197) |
| Subscale Average | 0.852 | 0.634 | 0.219 | 0.092 | 0.025 | 0.031 | 0.148 |
| Design 7: i(s) = 12, o = 1 | |||||||
| Open-Mindedness | 0.867 (0.839, 0.892) | 0.765 (0.736, 0.791) | 0.102 (0.092, 0.115) | 0.025 (0.023, 0.027) | 0.083 (0.057, 0.112) | 0.025 (0.022, 0.028) | 0.133 (0.108, 0.161) |
| Aesthetic Sensitivity | 0.867 (0.833, 0.889) | 0.505 (0.454, 0.552) | 0.363 (0.323, 0.402) | 0.052 (0.044, 0.059) | 0.030 (0.007, 0.067) | 0.051 (0.043, 0.059) | 0.133 (0.111, 0.167) |
| Creative Imagination | 0.776 (0.711, 0.828) | 0.545 (0.488, 0.597) | 0.231 (0.178, 0.286) | 0.054 (0.044, 0.064) | 0.110 (0.054, 0.181) | 0.060 (0.047, 0.072) | 0.224 (0.172, 0.289) |
| Intellectual Curiosity | 0.795 (0.736, 0.841) | 0.760 (0.661, 0.821) | 0.034 (0.000, 0.129) | 0.069 (0.057, 0.079) | 0.072 (0.025, 0.138) | 0.064 (0.050, 0.077) | 0.205 (0.159, 0.264) |
| Subscale Average | 0.813 | 0.603 | 0.209 | 0.058 | 0.071 | 0.058 | 0.187 |
| Design 8: i(s) = 12, o = 2 | |||||||
| Open-Mindedness | 0.917 (0.900, 0.931) | 0.809 (0.788, 0.826) | 0.108 (0.097, 0.122) | 0.026 (0.024, 0.029) | 0.044 (0.030, 0.060) | 0.013 (0.012, 0.015) | 0.083 (0.069, 0.100) |
| Aesthetic Sensitivity | 0.904 (0.883, 0.918) | 0.526 (0.478, 0.572) | 0.378 (0.336, 0.420) | 0.054 (0.046, 0.061) | 0.015 (0.004, 0.036) | 0.027 (0.023, 0.031) | 0.096 (0.082, 0.117) |
| Creative Imagination | 0.848 (0.805, 0.882) | 0.595 (0.543, 0.645) | 0.253 (0.198, 0.309) | 0.059 (0.048, 0.070) | 0.060 (0.028, 0.102) | 0.033 (0.026, 0.039) | 0.152 (0.118, 0.195) |
| Intellectual Curiosity | 0.853 (0.815, 0.883) | 0.816 (0.718, 0.866) | 0.037 (0.000, 0.138) | 0.074 (0.061, 0.085) | 0.039 (0.013, 0.076) | 0.034 (0.027, 0.041) | 0.147 (0.117, 0.185) |
| Subscale Average | 0.868 | 0.646 | 0.222 | 0.062 | 0.038 | 0.031 | 0.132 |
| Design 9: i(s) = 12, o = 3 | |||||||
| Open-Mindedness | 0.934 (0.923, 0.945) | 0.825 (0.806, 0.839) | 0.110 (0.099, 0.124) | 0.027 (0.024, 0.029) | 0.030 (0.020, 0.041) | 0.009 (0.008, 0.010) | 0.066 (0.055, 0.077) |
| Aesthetic Sensitivity | 0.917 (0.901, 0.928) | 0.533 (0.486, 0.579) | 0.384 (0.340, 0.427) | 0.055 (0.047, 0.062) | 0.010 (0.002, 0.024) | 0.018 (0.015, 0.021) | 0.083 (0.072, 0.099) |
| Creative Imagination | 0.875 (0.842, 0.901) | 0.614 (0.562, 0.664) | 0.261 (0.205, 0.318) | 0.061 (0.050, 0.073) | 0.041 (0.019, 0.071) | 0.022 (0.018, 0.027) | 0.125 (0.099, 0.158) |
| Intellectual Curiosity | 0.874 (0.845, 0.898) | 0.836 (0.738, 0.883) | 0.038 (0.000, 0.141) | 0.076 (0.062, 0.088) | 0.026 (0.009, 0.053) | 0.024 (0.019, 0.028) | 0.126 (0.102, 0.155) |
| Subscale Average | 0.889 | 0.661 | 0.227 | 0.064 | 0.026 | 0.021 | 0.111 |
| Design/Scale | Index (CI) | |||||||
|---|---|---|---|---|---|---|---|---|
| Global D (US) | Gen | Grp | TRelE | I | O | IO | Overall MDs | |
| Design 1: i(s) = 4, o = 1 | ||||||||
| Open-Mindedness | 0.778 (0.747, 0.798) | 0.687 (0.656, 0.707) | 0.091 (0.082, 0.103) | 0.209 (0.186, 0.232) | 0.011 (0.009, 0.013) | 0.002 (0.000, 0.029) | 0.000 (0.000, 0.001) | 0.013 (0.010, 0.040) |
| Aesthetic Sensitivity | 0.701 (0.662, 0.720) | 0.408 (0.365, 0.443) | 0.293 (0.256, 0.326) | 0.274 (0.251, 0.299) | 0.021 (0.016, 0.028) | 0.003 (0.000, 0.046) | 0.000 (0.000, 0.001) | 0.025 (0.018, 0.067) |
| Creative Imagination | 0.625 (0.566, 0.663) | 0.439 (0.391, 0.475) | 0.186 (0.142, 0.230) | 0.364 (0.318, 0.410) | 0.006 (0.003, 0.010) | 0.005 (0.000, 0.063) | 0.000 (0.000, 0.002) | 0.010 (0.005, 0.069) |
| Intellectual Curiosity | 0.600 (0.547, 0.636) | 0.574 (0.500, 0.615) | 0.026 (0.000, 0.098) | 0.356 (0.312, 0.394) | 0.039 (0.029, 0.050) | 0.005 (0.000, 0.065) | 0.000 (0.000, 0.002) | 0.044 (0.033, 0.103) |
| Subscale Average | 0.642 | 0.474 | 0.169 | 0.331 | 0.022 | 0.004 | 0.000 | 0.026 |
| Design 2: i(s) = 4, o = 2 | ||||||||
| Open-Mindedness | 0.839 (0.819, 0.852) | 0.740 (0.718, 0.755) | 0.099 (0.089, 0.111) | 0.149 (0.134, 0.164) | 0.012 (0.010, 0.014) | 0.001 (0.000, 0.016) | 0.000 (0.000, 0.000) | 0.013 (0.011, 0.028) |
| Aesthetic Sensitivity | 0.759 (0.731, 0.776) | 0.442 (0.400, 0.478) | 0.318 (0.279, 0.353) | 0.216 (0.198, 0.236) | 0.023 (0.017, 0.030) | 0.002 (0.000, 0.025) | 0.000 (0.000, 0.001) | 0.025 (0.019, 0.049) |
| Creative Imagination | 0.710 (0.663, 0.742) | 0.498 (0.453, 0.536) | 0.211 (0.163, 0.260) | 0.281 (0.245, 0.319) | 0.006 (0.003, 0.012) | 0.003 (0.000, 0.037) | 0.000 (0.000, 0.001) | 0.009 (0.005, 0.044) |
| Intellectual Curiosity | 0.668 (0.628, 0.700) | 0.640 (0.565, 0.679) | 0.029 (0.000, 0.109) | 0.285 (0.250, 0.317) | 0.044 (0.033, 0.055) | 0.003 (0.000, 0.037) | 0.000 (0.000, 0.001) | 0.046 (0.036, 0.082) |
| Subscale Average | 0.712 | 0.526 | 0.186 | 0.261 | 0.024 | 0.002 | 0.000 | 0.027 |
| Design 3: i(s) = 4, o = 3 | ||||||||
| Open-Mindedness | 0.861 (0.846, 0.871) | 0.760 (0.740, 0.773) | 0.101 (0.091, 0.114) | 0.126 (0.115, 0.138) | 0.012 (0.010, 0.014) | 0.001 (0.000, 0.011) | 0.000 (0.000, 0.000) | 0.013 (0.011, 0.023) |
| Aesthetic Sensitivity | 0.781 (0.757, 0.797) | 0.454 (0.413, 0.491) | 0.327 (0.288, 0.364) | 0.194 (0.177, 0.213) | 0.024 (0.017, 0.031) | 0.001 (0.000, 0.018) | 0.000 (0.000, 0.000) | 0.025 (0.019, 0.043) |
| Creative Imagination | 0.743 (0.703, 0.773) | 0.522 (0.476, 0.560) | 0.221 (0.172, 0.272) | 0.248 (0.215, 0.283) | 0.007 (0.003, 0.012) | 0.002 (0.000, 0.026) | 0.000 (0.000, 0.001) | 0.008 (0.005, 0.034) |
| Intellectual Curiosity | 0.695 (0.659, 0.727) | 0.665 (0.590, 0.705) | 0.030 (0.000, 0.113) | 0.258 (0.225, 0.287) | 0.045 (0.034, 0.057) | 0.002 (0.000, 0.026) | 0.000 (0.000, 0.001) | 0.047 (0.037, 0.073) |
| Subscale Average | 0.740 | 0.547 | 0.193 | 0.234 | 0.025 | 0.002 | 0.000 | 0.027 |
| Design 4: i(s) = 8, o = 1 | ||||||||
| Open-Mindedness | 0.839 (0.804, 0.861) | 0.741 (0.706, 0.763) | 0.099 (0.089, 0.111) | 0.153 (0.128, 0.179) | 0.006 (0.005, 0.007) | 0.002 (0.000, 0.031) | 0.000 (0.000, 0.000) | 0.008 (0.006, 0.037) |
| Aesthetic Sensitivity | 0.812 (0.762, 0.832) | 0.472 (0.420, 0.513) | 0.339 (0.298, 0.375) | 0.172 (0.149, 0.203) | 0.012 (0.009, 0.016) | 0.004 (0.000, 0.053) | 0.000 (0.000, 0.001) | 0.016 (0.011, 0.065) |
| Creative Imagination | 0.728 (0.654, 0.773) | 0.511 (0.450, 0.555) | 0.217 (0.165, 0.267) | 0.264 (0.211, 0.320) | 0.003 (0.002, 0.006) | 0.005 (0.000, 0.073) | 0.000 (0.000, 0.001) | 0.009 (0.003, 0.076) |
| Intellectual Curiosity | 0.723 (0.653, 0.763) | 0.692 (0.594, 0.743) | 0.031 (0.000, 0.116) | 0.247 (0.201, 0.297) | 0.024 (0.018, 0.030) | 0.006 (0.000, 0.078) | 0.000 (0.000, 0.001) | 0.029 (0.021, 0.100) |
| Subscale Average | 0.754 | 0.558 | 0.196 | 0.228 | 0.013 | 0.005 | 0.000 | 0.018 |
| Design 5: i(s) = 8, o = 2 | ||||||||
| Open-Mindedness | 0.892 (0.872, 0.905) | 0.787 (0.763, 0.803) | 0.105 (0.095, 0.118) | 0.100 (0.086, 0.116) | 0.006 (0.005, 0.007) | 0.001 (0.000, 0.017) | 0.000 (0.000, 0.000) | 0.007 (0.006, 0.023) |
| Aesthetic Sensitivity | 0.856 (0.826, 0.870) | 0.498 (0.450, 0.539) | 0.358 (0.315, 0.397) | 0.129 (0.114, 0.149) | 0.013 (0.009, 0.017) | 0.002 (0.000, 0.029) | 0.000 (0.000, 0.000) | 0.015 (0.011, 0.042) |
| Creative Imagination | 0.805 (0.754, 0.837) | 0.565 (0.511, 0.609) | 0.240 (0.186, 0.293) | 0.188 (0.153, 0.229) | 0.004 (0.002, 0.007) | 0.003 (0.000, 0.042) | 0.000 (0.000, 0.001) | 0.007 (0.003, 0.046) |
| Intellectual Curiosity | 0.786 (0.738, 0.815) | 0.752 (0.658, 0.796) | 0.034 (0.000, 0.128) | 0.185 (0.154, 0.220) | 0.026 (0.019, 0.033) | 0.003 (0.000, 0.044) | 0.000 (0.000, 0.001) | 0.029 (0.022, 0.069) |
| Subscale Average | 0.816 | 0.605 | 0.211 | 0.168 | 0.014 | 0.003 | 0.000 | 0.017 |
| Design 6: i(s) = 8, o = 3 | ||||||||
| Open-Mindedness | 0.912 (0.896, 0.921) | 0.804 (0.784, 0.818) | 0.107 (0.097, 0.121) | 0.081 (0.071, 0.093) | 0.006 (0.005, 0.008) | 0.001 (0.000, 0.011) | 0.000 (0.000, 0.000) | 0.007 (0.006, 0.018) |
| Aesthetic Sensitivity | 0.872 (0.849, 0.884) | 0.507 (0.461, 0.549) | 0.365 (0.322, 0.405) | 0.114 (0.101, 0.129) | 0.013 (0.010, 0.017) | 0.001 (0.000, 0.019) | 0.000 (0.000, 0.000) | 0.015 (0.011, 0.033) |
| Creative Imagination | 0.835 (0.794, 0.861) | 0.586 (0.534, 0.631) | 0.249 (0.194, 0.303) | 0.159 (0.131, 0.192) | 0.004 (0.002, 0.007) | 0.002 (0.000, 0.029) | 0.000 (0.000, 0.000) | 0.006 (0.003, 0.033) |
| Intellectual Curiosity | 0.809 (0.772, 0.835) | 0.774 (0.681, 0.817) | 0.035 (0.000, 0.131) | 0.162 (0.136, 0.191) | 0.026 (0.020, 0.034) | 0.002 (0.000, 0.030) | 0.000 (0.000, 0.000) | 0.029 (0.022, 0.057) |
| Subscale Average | 0.839 | 0.623 | 0.216 | 0.145 | 0.014 | 0.002 | 0.000 | 0.016 |
| Design 7: i(s) = 12, o = 1 | ||||||||
| Open-Mindedness | 0.862 (0.825, 0.885) | 0.761 (0.724, 0.784) | 0.101 (0.091, 0.114) | 0.132 (0.106, 0.159) | 0.004 (0.003, 0.005) | 0.002 (0.000, 0.032) | 0.000 (0.000, 0.000) | 0.006 (0.004, 0.036) |
| Aesthetic Sensitivity | 0.856 (0.802, 0.877) | 0.498 (0.442, 0.542) | 0.358 (0.314, 0.395) | 0.131 (0.108, 0.164) | 0.009 (0.006, 0.011) | 0.004 (0.000, 0.056) | 0.000 (0.000, 0.001) | 0.013 (0.008, 0.064) |
| Creative Imagination | 0.770 (0.688, 0.818) | 0.540 (0.474, 0.589) | 0.229 (0.174, 0.282) | 0.222 (0.167, 0.285) | 0.002 (0.001, 0.004) | 0.006 (0.000, 0.077) | 0.000 (0.000, 0.001) | 0.008 (0.002, 0.079) |
| Intellectual Curiosity | 0.776 (0.697, 0.819) | 0.743 (0.632, 0.798) | 0.034 (0.000, 0.125) | 0.201 (0.153, 0.256) | 0.017 (0.012, 0.021) | 0.006 (0.000, 0.083) | 0.000 (0.000, 0.001) | 0.023 (0.015, 0.099) |
| Subscale Average | 0.801 | 0.594 | 0.207 | 0.185 | 0.009 | 0.005 | 0.000 | 0.015 |
| Design 8: i(s) = 12, o = 2 | ||||||||
| Open-Mindedness | 0.912 (0.890, 0.925) | 0.805 (0.780, 0.821) | 0.107 (0.097, 0.121) | 0.083 (0.068, 0.099) | 0.004 (0.003, 0.005) | 0.001 (0.000, 0.017) | 0.000 (0.000, 0.000) | 0.005 (0.004, 0.021) |
| Aesthetic Sensitivity | 0.894 (0.862, 0.907) | 0.520 (0.470, 0.564) | 0.374 (0.330, 0.414) | 0.095 (0.081, 0.115) | 0.009 (0.007, 0.012) | 0.002 (0.000, 0.030) | 0.000 (0.000, 0.000) | 0.011 (0.008, 0.039) |
| Creative Imagination | 0.843 (0.789, 0.875) | 0.592 (0.534, 0.639) | 0.251 (0.195, 0.306) | 0.151 (0.117, 0.193) | 0.002 (0.001, 0.005) | 0.003 (0.000, 0.043) | 0.000 (0.000, 0.000) | 0.006 (0.002, 0.046) |
| Intellectual Curiosity | 0.835 (0.784, 0.863) | 0.798 (0.697, 0.845) | 0.036 (0.000, 0.134) | 0.144 (0.114, 0.180) | 0.018 (0.014, 0.023) | 0.003 (0.000, 0.046) | 0.000 (0.000, 0.000) | 0.022 (0.015, 0.064) |
| Subscale Average | 0.857 | 0.637 | 0.220 | 0.130 | 0.010 | 0.003 | 0.000 | 0.013 |
| Design 9: i(s) = 12, o = 3 | ||||||||
| Open-Mindedness | 0.930 (0.915, 0.939) | 0.820 (0.800, 0.834) | 0.109 (0.099, 0.123) | 0.065 (0.055, 0.077) | 0.004 (0.004, 0.005) | 0.001 (0.000, 0.012) | 0.000 (0.000, 0.000) | 0.005 (0.004, 0.016) |
| Aesthetic Sensitivity | 0.907 (0.884, 0.918) | 0.528 (0.480, 0.571) | 0.379 (0.335, 0.421) | 0.082 (0.071, 0.098) | 0.009 (0.007, 0.012) | 0.001 (0.000, 0.020) | 0.000 (0.000, 0.000) | 0.011 (0.008, 0.030) |
| Creative Imagination | 0.871 (0.830, 0.895) | 0.611 (0.556, 0.658) | 0.259 (0.203, 0.315) | 0.124 (0.098, 0.157) | 0.003 (0.001, 0.005) | 0.002 (0.000, 0.030) | 0.000 (0.000, 0.000) | 0.005 (0.002, 0.033) |
| Intellectual Curiosity | 0.856 (0.818, 0.879) | 0.819 (0.720, 0.863) | 0.037 (0.000, 0.137) | 0.123 (0.099, 0.151) | 0.019 (0.014, 0.024) | 0.002 (0.000, 0.032) | 0.000 (0.000, 0.000) | 0.021 (0.016, 0.051) |
| Subscale Average | 0.878 | 0.653 | 0.225 | 0.110 | 0.010 | 0.002 | 0.000 | 0.012 |
| Design/Scale | Index (CI) | |||||
|---|---|---|---|---|---|---|
| ECV | EUV | ECV/EUV | PRMSE(s) | PRMSE(c) | VAR | |
| Design 1: i(s) = 4, o = 1 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.531, 8.412) | |||
| Aesthetic Sensitivity | 0.582 (0.534, 0.629) | 0.418 (0.371, 0.466) | 1.391 (1.145, 1.699) | 0.719 (0.692, 0.740) | 0.634 (0.607, 0.658) | 1.135 (1.094, 1.178) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.784, 3.206) | 0.632 (0.583, 0.673) | 0.624 (0.594, 0.652) | 1.012 (0.928, 1.096) |
| Intellectual Curiosity | 0.957 (0.839, 1.000) | 0.043 (0.000, 0.161) | 22.170 (5.229, 2026.368) | 0.628 (0.585, 0.667) | 0.687 (0.648, 0.712) | 0.914 (0.855, 1.000) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.659 | 0.648 | 1.020 |
| Design 2: i(s) = 4, o = 2 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.534, 8.417) | |||
| Aesthetic Sensitivity | 0.582 (0.534, 0.629) | 0.418 (0.371, 0.466) | 1.391 (1.144, 1.696) | 0.779 (0.758, 0.796) | 0.683 (0.660, 0.703) | 1.140 (1.106, 1.177) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.785, 3.200) | 0.716 (0.677, 0.751) | 0.672 (0.645, 0.697) | 1.065 (0.995, 1.137) |
| Intellectual Curiosity | 0.957 (0.840, 1.000) | 0.043 (0.000, 0.160) | 22.170 (5.231, 2028.344) | 0.701 (0.667, 0.735) | 0.740 (0.702, 0.761) | 0.948 (0.899, 1.028) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.732 | 0.698 | 1.051 |
| Design 3: i(s) = 4, o = 3 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.532, 8.421) | |||
| Aesthetic Sensitivity | 0.582 (0.534, 0.630) | 0.418 (0.370, 0.466) | 1.391 (1.145, 1.702) | 0.801 (0.781, 0.818) | 0.701 (0.679, 0.720) | 1.142 (1.110, 1.179) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.783, 3.209) | 0.750 (0.714, 0.782) | 0.690 (0.664, 0.714) | 1.086 (1.021, 1.155) |
| Intellectual Curiosity | 0.957 (0.840, 1.000) | 0.043 (0.000, 0.160) | 22.170 (5.248, 2038.343) | 0.729 (0.698, 0.762) | 0.759 (0.722, 0.779) | 0.961 (0.915, 1.039) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.760 | 0.717 | 1.063 |
| Design 4: i(s) = 8, o = 1 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.531, 8.420) | |||
| Aesthetic Sensitivity | 0.582 (0.534, 0.629) | 0.418 (0.371, 0.466) | 1.391 (1.145, 1.697) | 0.825 (0.793, 0.846) | 0.680 (0.650, 0.706) | 1.213 (1.172, 1.256) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.786, 3.205) | 0.734 (0.675, 0.783) | 0.670 (0.637, 0.700) | 1.096 (1.002, 1.186) |
| Intellectual Curiosity | 0.957 (0.840, 0.999) | 0.043 (0.001, 0.160) | 22.170 (5.250, 1964.877) | 0.745 (0.692, 0.789) | 0.737 (0.694, 0.765) | 1.011 (0.944, 1.097) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.768 | 0.696 | 1.107 |
| Design 5: i(s) = 8, o = 2 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.531, 8.415) | |||
| Aesthetic Sensitivity | 0.582 (0.533, 0.629) | 0.418 (0.371, 0.467) | 1.391 (1.143, 1.697) | 0.869 (0.849, 0.884) | 0.723 (0.698, 0.744) | 1.203 (1.171, 1.238) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.784, 3.201) | 0.811 (0.769, 0.845) | 0.712 (0.683, 0.738) | 1.139 (1.069, 1.209) |
| Intellectual Curiosity | 0.957 (0.839, 1.000) | 0.043 (0.000, 0.161) | 22.170 (5.218, 2044.612) | 0.809 (0.772, 0.840) | 0.783 (0.743, 0.805) | 1.034 (0.985, 1.108) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.830 | 0.739 | 1.125 |
| Design 6: i(s) = 8, o = 3 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.533, 8.420) | |||
| Aesthetic Sensitivity | 0.582 (0.533, 0.630) | 0.418 (0.370, 0.467) | 1.391 (1.143, 1.700) | 0.885 (0.868, 0.898) | 0.738 (0.715, 0.758) | 1.199 (1.169, 1.233) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.785, 3.207) | 0.840 (0.806, 0.868) | 0.727 (0.699, 0.751) | 1.156 (1.094, 1.219) |
| Intellectual Curiosity | 0.957 (0.839, 1.000) | 0.043 (0.000, 0.161) | 22.170 (5.214, 2033.926) | 0.833 (0.803, 0.860) | 0.799 (0.759, 0.820) | 1.042 (1.000, 1.114) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.852 | 0.755 | 1.132 |
| Design 7: i(s) = 12, o = 1 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.527, 8.420) | |||
| Aesthetic Sensitivity | 0.582 (0.534, 0.630) | 0.418 (0.370, 0.466) | 1.391 (1.144, 1.699) | 0.867 (0.833, 0.889) | 0.697 (0.666, 0.724) | 1.244 (1.203, 1.287) |
| Creative Imagination | 0.702 (0.640, 0.762) | 0.298 (0.238, 0.360) | 2.357 (1.781, 3.206) | 0.776 (0.711, 0.828) | 0.687 (0.652, 0.718) | 1.130 (1.032, 1.223) |
| Intellectual Curiosity | 0.957 (0.839, 1.000) | 0.043 (0.000, 0.161) | 22.170 (5.220, 2101.003) | 0.795 (0.736, 0.841) | 0.755 (0.711, 0.784) | 1.052 (0.981, 1.138) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.813 | 0.713 | 1.142 |
| Design 8: i(s) = 12, o = 2 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.529, 8.419) | |||
| Aesthetic Sensitivity | 0.582 (0.534, 0.629) | 0.418 (0.371, 0.466) | 1.391 (1.144, 1.698) | 0.904 (0.883, 0.918) | 0.737 (0.712, 0.759) | 1.227 (1.196, 1.261) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.783, 3.205) | 0.848 (0.805, 0.882) | 0.726 (0.696, 0.752) | 1.168 (1.098, 1.238) |
| Intellectual Curiosity | 0.957 (0.840, 1.000) | 0.043 (0.000, 0.160) | 22.170 (5.236, 2032.403) | 0.853 (0.815, 0.883) | 0.798 (0.757, 0.821) | 1.068 (1.020, 1.141) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.868 | 0.754 | 1.155 |
| Design 9: i(s) = 12, o = 3 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.535, 8.414) | |||
| Aesthetic Sensitivity | 0.582 (0.534, 0.630) | 0.418 (0.370, 0.466) | 1.391 (1.144, 1.699) | 0.917 (0.901, 0.928) | 0.751 (0.728, 0.771) | 1.221 (1.192, 1.254) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.783, 3.202) | 0.875 (0.842, 0.901) | 0.740 (0.712, 0.765) | 1.183 (1.123, 1.245) |
| Intellectual Curiosity | 0.957 (0.840, 1.000) | 0.043 (0.000, 0.160) | 22.170 (5.262, 2048.940) | 0.874 (0.845, 0.898) | 0.814 (0.773, 0.835) | 1.074 (1.034, 1.144) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.889 | 0.768 | 1.159 |
| Design/Scale | Index (CI) | ||||
|---|---|---|---|---|---|
| G Coefficient Denominator Partitioning | Global D Coefficient Denominator Partitioning | ||||
| US (G) | TRelE (G) | US (G-D) | TRelE (G-D) | MD (G-D) | |
| Persons × Items | |||||
| Design 1: i(s) = 4 | |||||
| Open-Mindedness | 0.864 (0.859, 0.869) | 0.136 (0.131, 0.141) | 0.854 (0.849, 0.860) | 0.135 (0.129, 0.140) | 0.011 (0.009, 0.013) |
| Aesthetic Sensitivity | 0.744 (0.730, 0.759) | 0.256 (0.241, 0.270) | 0.728 (0.713, 0.743) | 0.251 (0.236, 0.264) | 0.021 (0.016, 0.029) |
| Creative Imagination | 0.722 (0.700, 0.745) | 0.278 (0.255, 0.300) | 0.717 (0.695, 0.740) | 0.277 (0.254, 0.298) | 0.006 (0.003, 0.011) |
| Intellectual Curiosity | 0.685 (0.665, 0.713) | 0.315 (0.287, 0.335) | 0.657 (0.637, 0.686) | 0.303 (0.276, 0.321) | 0.040 (0.030, 0.051) |
| Subscale Average | 0.717 | 0.283 | 0.701 | 0.277 | 0.022 |
| Design 2: i(s) = 8 | |||||
| Open-Mindedness | 0.927 (0.924, 0.930) | 0.073 (0.070, 0.076) | 0.921 (0.918, 0.925) | 0.073 (0.070, 0.076) | 0.006 (0.005, 0.007) |
| Aesthetic Sensitivity | 0.853 (0.844, 0.863) | 0.147 (0.137, 0.156) | 0.842 (0.832, 0.852) | 0.145 (0.136, 0.154) | 0.012 (0.009, 0.017) |
| Creative Imagination | 0.838 (0.824, 0.854) | 0.162 (0.146, 0.176) | 0.835 (0.820, 0.851) | 0.161 (0.146, 0.175) | 0.003 (0.002, 0.007) |
| Intellectual Curiosity | 0.813 (0.799, 0.832) | 0.187 (0.168, 0.201) | 0.793 (0.778, 0.814) | 0.183 (0.164, 0.196) | 0.024 (0.018, 0.031) |
| Subscale Average | 0.835 | 0.165 | 0.824 | 0.163 | 0.013 |
| Design 3: i(s) = 12 | |||||
| Open-Mindedness | 0.950 (0.948, 0.952) | 0.050 (0.048, 0.052) | 0.946 (0.944, 0.948) | 0.050 (0.048, 0.052) | 0.004 (0.003, 0.005) |
| Aesthetic Sensitivity | 0.897 (0.890, 0.904) | 0.103 (0.096, 0.110) | 0.889 (0.882, 0.897) | 0.102 (0.095, 0.109) | 0.009 (0.007, 0.012) |
| Creative Imagination | 0.886 (0.875, 0.897) | 0.114 (0.103, 0.125) | 0.884 (0.873, 0.895) | 0.114 (0.102, 0.124) | 0.002 (0.001, 0.005) |
| Intellectual Curiosity | 0.867 (0.856, 0.882) | 0.133 (0.118, 0.144) | 0.852 (0.840, 0.868) | 0.131 (0.116, 0.141) | 0.017 (0.013, 0.022) |
| Subscale Average | 0.883 | 0.117 | 0.875 | 0.116 | 0.009 |
| Persons × Occasions | |||||
| Design 1: o = 1 | |||||
| Open-Mindedness | 0.856 (0.832, 0.878) | 0.144 (0.122, 0.168) | 0.862 (0.838, 0.867) | 0.143 (0.121, 0.167) | 0.002 (0.000, 0.030) |
| Aesthetic Sensitivity | 0.847 (0.819, 0.869) | 0.153 (0.131, 0.181) | 0.741 (0.707, 0.755) | 0.152 (0.129, 0.179) | 0.003 (0.000, 0.048) |
| Creative Imagination | 0.764 (0.717, 0.804) | 0.236 (0.196, 0.283) | 0.718 (0.672, 0.740) | 0.235 (0.192, 0.280) | 0.005 (0.000, 0.064) |
| Intellectual Curiosity | 0.791 (0.747, 0.828) | 0.209 (0.172, 0.253) | 0.681 (0.636, 0.708) | 0.208 (0.168, 0.250) | 0.005 (0.000, 0.069) |
| Subscale Average | 0.801 | 0.199 | 0.713 | 0.198 | 0.004 |
| Design 2: o = 2 | |||||
| Open-Mindedness | 0.923 (0.908, 0.935) | 0.077 (0.065, 0.092) | 0.929 (0.910, 0.945) | 0.077 (0.065, 0.092) | 0.001 (0.000, 0.016) |
| Aesthetic Sensitivity | 0.917 (0.901, 0.930) | 0.083 (0.070, 0.099) | 0.790 (0.768, 0.803) | 0.082 (0.069, 0.099) | 0.002 (0.000, 0.026) |
| Creative Imagination | 0.866 (0.835, 0.891) | 0.134 (0.109, 0.165) | 0.765 (0.733, 0.783) | 0.133 (0.108, 0.164) | 0.003 (0.000, 0.037) |
| Intellectual Curiosity | 0.883 (0.855, 0.906) | 0.117 (0.094, 0.145) | 0.731 (0.700, 0.754) | 0.117 (0.093, 0.144) | 0.003 (0.000, 0.039) |
| Subscale Average | 0.889 | 0.111 | 0.762 | 0.111 | 0.003 |
| Design 3: o = 3 | |||||
| Open-Mindedness | 0.947 (0.937, 0.956) | 0.053 (0.044, 0.063) | 0.954 (0.934, 0.974) | 0.053 (0.044, 0.063) | 0.001 (0.000, 0.011) |
| Aesthetic Sensitivity | 0.943 (0.931, 0.952) | 0.057 (0.048, 0.069) | 0.809 (0.789, 0.822) | 0.057 (0.048, 0.068) | 0.001 (0.000, 0.018) |
| Creative Imagination | 0.907 (0.884, 0.925) | 0.093 (0.075, 0.116) | 0.784 (0.756, 0.804) | 0.093 (0.075, 0.116) | 0.002 (0.000, 0.026) |
| Intellectual Curiosity | 0.919 (0.898, 0.935) | 0.081 (0.065, 0.102) | 0.750 (0.723, 0.775) | 0.081 (0.064, 0.101) | 0.002 (0.000, 0.027) |
| Subscale Average | 0.923 | 0.077 | 0.781 | 0.077 | 0.002 |
| Design/Scale | Index (CI) | |||||
|---|---|---|---|---|---|---|
| ECV | EUV | ECV/EUV | PRMSE(s) | PRMSE(c) | VAR | |
| Persons × Items | ||||||
| Design 1: i(s) = 4 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.532, 8.421) | |||
| Aesthetic Sensitivity | 0.582 (0.533, 0.630) | 0.418 (0.370, 0.467) | 1.391 (1.143, 1.701) | 0.744 (0.730, 0.759) | 0.633 (0.606, 0.657) | 1.175 (1.122, 1.240) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.786, 3.202) | 0.722 (0.700, 0.745) | 0.608 (0.577, 0.636) | 1.186 (1.114, 1.275) |
| Intellectual Curiosity | 0.957 (0.839, 1.000) | 0.043 (0.000, 0.161) | 22.170 (5.218, 2050.789) | 0.685 (0.665, 0.713) | 0.670 (0.629, 0.701) | 1.021 (0.960, 1.124) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.717 | 0.637 | 1.127 |
| Design 2: i(s) = 8 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.532, 8.419) | |||
| Aesthetic Sensitivity | 0.582 (0.533, 0.630) | 0.418 (0.370, 0.467) | 1.391 (1.143, 1.699) | 0.853 (0.844, 0.863) | 0.679 (0.650, 0.706) | 1.255 (1.203, 1.320) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.785, 3.202) | 0.838 (0.824, 0.854) | 0.653 (0.619, 0.683) | 1.284 (1.215, 1.368) |
| Intellectual Curiosity | 0.957 (0.840, 1.000) | 0.043 (0.000, 0.160) | 22.170 (5.251, 2043.285) | 0.813 (0.799, 0.832) | 0.720 (0.674, 0.753) | 1.130 (1.070, 1.227) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.835 | 0.684 | 1.223 |
| Design 3: i(s) = 12 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.531, 8.422) | |||
| Aesthetic Sensitivity | 0.582 (0.534, 0.630) | 0.418 (0.370, 0.466) | 1.391 (1.144, 1.699) | 0.897 (0.890, 0.904) | 0.696 (0.666, 0.724) | 1.288 (1.236, 1.352) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.787, 3.205) | 0.886 (0.875, 0.897) | 0.669 (0.634, 0.701) | 1.324 (1.256, 1.407) |
| Intellectual Curiosity | 0.957 (0.840, 0.999) | 0.043 (0.001, 0.160) | 22.170 (5.231, 1986.216) | 0.867 (0.856, 0.882) | 0.738 (0.691, 0.772) | 1.175 (1.116, 1.270) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.883 | 0.701 | 1.262 |
| Persons × Occasions | ||||||
| Design 1: o = 1 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.532, 8.423) | |||
| Aesthetic Sensitivity | 0.582 (0.533, 0.630) | 0.418 (0.370, 0.467) | 1.391 (1.143, 1.699) | 0.847 (0.819, 0.869) | 0.634 (0.608, 0.656) | 1.337 (1.293, 1.384) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.783, 3.205) | 0.764 (0.717, 0.804) | 0.603 (0.576, 0.628) | 1.267 (1.187, 1.348) |
| Intellectual Curiosity | 0.957 (0.839, 1.000) | 0.043 (0.000, 0.161) | 22.170 (5.223, 2041.584) | 0.791 (0.747, 0.828) | 0.650 (0.618, 0.674) | 1.217 (1.154, 1.294) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.801 | 0.629 | 1.274 |
| Design 2: o = 2 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.536, 8.422) | |||
| Aesthetic Sensitivity | 0.582 (0.533, 0.630) | 0.418 (0.370, 0.467) | 1.391 (1.144, 1.701) | 0.917 (0.901, 0.930) | 0.683 (0.662, 0.702) | 1.343 (1.310, 1.380) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.786, 3.203) | 0.866 (0.835, 0.891) | 0.650 (0.626, 0.671) | 1.333 (1.276, 1.393) |
| Intellectual Curiosity | 0.957 (0.840, 1.000) | 0.043 (0.000, 0.160) | 22.170 (5.265, 2027.910) | 0.883 (0.855, 0.906) | 0.700 (0.671, 0.720) | 1.262 (1.218, 1.322) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.889 | 0.678 | 1.313 |
| Design 3: o = 3 | ||||||
| Open-Mindedness | 0.882 (0.867, 0.894) | 0.118 (0.106, 0.133) | 7.509 (6.529, 8.418) | |||
| Aesthetic Sensitivity | 0.582 (0.534, 0.629) | 0.418 (0.371, 0.466) | 1.391 (1.145, 1.698) | 0.943 (0.931, 0.952) | 0.701 (0.681, 0.719) | 1.346 (1.315, 1.380) |
| Creative Imagination | 0.702 (0.641, 0.762) | 0.298 (0.238, 0.359) | 2.357 (1.784, 3.209) | 0.907 (0.884, 0.925) | 0.667 (0.644, 0.687) | 1.360 (1.311, 1.412) |
| Intellectual Curiosity | 0.957 (0.840, 1.000) | 0.043 (0.000, 0.160) | 22.170 (5.240, 2012.269) | 0.919 (0.898, 0.935) | 0.718 (0.690, 0.737) | 1.279 (1.242, 1.335) |
| Subscale Average | 0.747 | 0.253 | 8.639 | 0.923 | 0.695 | 1.328 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vispoel, W.P.; Lee, H.; Chen, T.; Hong, H. Extending Applications of Generalizability Theory-Based Bifactor Model Designs. Psych 2023, 5, 545-575. https://doi.org/10.3390/psych5020036
Vispoel WP, Lee H, Chen T, Hong H. Extending Applications of Generalizability Theory-Based Bifactor Model Designs. Psych. 2023; 5(2):545-575. https://doi.org/10.3390/psych5020036
Chicago/Turabian StyleVispoel, Walter P., Hyeryung Lee, Tingting Chen, and Hyeri Hong. 2023. "Extending Applications of Generalizability Theory-Based Bifactor Model Designs" Psych 5, no. 2: 545-575. https://doi.org/10.3390/psych5020036
APA StyleVispoel, W. P., Lee, H., Chen, T., & Hong, H. (2023). Extending Applications of Generalizability Theory-Based Bifactor Model Designs. Psych, 5(2), 545-575. https://doi.org/10.3390/psych5020036





