Abstract
Detecting and understanding DTF is very important under various DIF conditions. In this study, the performance of DTF, DRF, SIBTEST, and CSIBTEST approaches in detecting DIF effects was investigated using a simulation study and a real dataset. It was observed that different DIF conditions (uniform, non-uniform), the proportion of DIF items in the test, the DIF size, and the DIF effect (balanced, unbalanced) affected the performance of the methods, and especially in the case of the non-uniform DIF condition, the power rates of sDTF, sDRF, and SIBTEST statistics were low. In addition, according to the DTF estimations with the balanced/unbalanced DIF effect condition, in some cases, the effect of DIF on the overall test could be negligible. However, it was clearly emphasized in this study that DTF analyses should accompany DIF studies since DTF analysis may change with different DIF and test conditions.
1. Introduction
Differential item functioning (DIF), differential bundle functioning (DBF), and differential test functioning (DTF) are important concepts in the field of educational and psychological testing. DIF refers to the situation where an item on a test functions differently for different groups of test-takers, even if they have the same level of ability. DBF occurs when items that contain small amounts of DIF can provide a significant differential effect at the level of clusters or bundles of items at the cumulative level. DTF occurs if true differences on the latent variable are held constant across two or more groups, but the function relating expected test scores to the latent variable differs across groups [1]. Several researchers have devoted considerable attention to the study of DTF because the effects of DIF on overall test scores may be negligible or it might be that there are large DIF effects in one direction for some items, but these effects are canceled out by DIF in the opposite direction for other items [1,2,3,4,5,6]. In some cases, examining the DTF in isolation or in combination with DIF analyses can be meaningful and informative for test administrators [1]. According to some researchers e.g., [4,5], DTF may be more critical than DIF because decisions are made based on the result of an entire test rather than the result of an individual item. If the DTF appears negligible, in some situations there is no need to discard items with DIF [1,7].
Numerous statistics have been developed to detect DTF using different approaches. Chalmers et al. [1] described the area-based signed (sDTF) and unsigned (uDTF) approaches, which have subtle but important differences compared to sample-based statistics proposed by Raju et al. [8]. Similarly, Chalmers [9] has described the differential response functioning (DRF) statistics (compensatory and non-compensatory statistics) by extending and improving the statistics of area-based DTF measures. DRF provides compensatory differential response functioning statistics (sDRF) and non-compensatory differential response functioning statistics (uDRF) when testing DIF, DBF, and DTF, and provides an effective approach to diagnose conditional differential functioning (i.e., at specific θ values), which are straightforward for isolated hypothesis testing, as well as graphically presenting the range of differences between the response functions [9]. The DRF statistics can be interpreted as IRT generalizations of the item bias test (SIBTEST) [10,11] and its non-compensatory counterpart, Crossing-SIBTEST (CSIBTEST) [9,12]. The two-step differential item and test (DFIT) statistics are also the most widely used approaches to study DTF [8,13]. However, each of these methods has its own strengths and limitations, and for this reason, different researchers have investigated the DTF estimation performance of the methods with different test conditions by various Monte Carlo simulation studies [1,7,9,14,15]. The main objective of this study is to compare methods, including area-based signed (sDTF) and unsigned (uDTF) approaches [1], DRF statistics [9], and SIBTEST [10,11] and CSIBTEST [9,12], by simulating data from models with known IRT parameters and examining DTF estimation results under different test conditions. Numerous test conditions, DIF conditions and models (e.g., 3PL models), and methods/approaches have been specifically defined for optimal DIF detection using simulation studies. For example, for reference and focus groups, the sample size of the test (balanced/unbalanced, large (e.g., N = 1000 or 2500), or relatively small (e.g., N = 250 or 500)), the length of the test (n = 10, 20, or 40), the DIF direction (balanced/unbalanced), DIF type (uniform, non-uniform DIF), or the DIF size (e.g., small (0.25) large (0.60)). In this study, similar to previous studies [1,9,14,16], we simulated important DIF and test conditions that may have a significant impact on the detection of the DIF effect.
The performance of the sDTF and uDTF statistics was investigated using the 3PL and the graded response model by Chalmers et al. [1]. The performance of the statistics was examined with different test conditions (e.g., sample size, test length, DIF direction, and DIF effect size). The results showed that the performance of both DTF statistics was better with larger sample sizes (e.g., N = 3000), larger DIF effect sizes, and shorter test lengths (e.g., n = 10). Rejection rates were highest when there was DIF in both the slope (a) and the intercept (d) parameters. However, when the slope parameters alone contained DIF, the likelihood of detecting a significant sDTF was five times less than when the d parameters alone contained DIF [1]. The DRF statistics were compared to the SIBTEST and CSIBTEST by Chalmers [9], and the results of these studies indicated that DRF statistics were more optimal effect size estimates of marginal response bias than the SIBTEST family and were the most optimal when studying differential bundle and test bias. The DRF statistics were also compared to the SIBTEST and differential functioning of items and tests (DFIT) frameworks in another study [14]. The results from the DBF and DTF simulations clearly demonstrated that the DRF framework is superior in terms of Type I error control and power to detect DTF and DBF. The results of the study indicated that the DFIT framework demonstrated extremely liberal Type I error rates. The simulation study showed that more than ten anchor items are required to obtain acceptable Type I error rates with SIBTEST, and the dDRF family of statistics provided the highest power in the item bundles studied. Among all studied compensatory statistics, the sDRF family demonstrated the lowest power rates for the type of composite response bias generated. Recently, the performance of the area-based signed (sDTF) and unsigned (uDTF) was compared to a number of effect size statistics, including the DIF variance estimate from a random effects model, both unweighted () and weighted () [16], Cohen’s d for the between-group average DIF [17,18], the average variance associated with DIF from logistic regression [17,19] and the Doebler´s statistics [20], including a measure of the variance in differences between group difficulty parameters (), and a standardized DIF variance measure (S−DIF−V) for the difference between group difficulty parameters [15]. The results of this study indicated that across study conditions, , , and d were consistently the most accurate measures of the DIF effects. Although DTF statistics have been investigated in simulation studies with different test conditions, there are inconsistencies in the performance of DTF estimation statistics for some test conditions. For example, non-compensatory statistics have been proposed as an effective DTF estimation technique when the non-uniform DIF is due to slope parameters only, while inflated Type I error rates have also been emphasized for these statistics in the non-DIF case. It may be essential to evaluate these statistics in the absence and in the presence of DIF due to slope parameters. Similarly, in the case of unidirectional (unbalanced)/bidirectional (balanced) DIF, it may be important to consider how the power rates of the DTF statistics may differ under different test conditions.
1.1. Statistics for Differential Test Functioning
Chalmers et al. [1] described two area-based statistics for detecting DTF, referred to as sDTF (signed) and uDTF (unsigned) measures of the DTF. These DTF statistics were defined based on the group-specific test score function. These DTF measures were described as follows in Equation (1), Equation (2), and Equation (3), respectively:
where represents the participant’s value on the latent variable, is a weighting function with the property that , and , are the reference and focus group item parameters. The sample estimation sDTF is obtained by evaluating the function in Equation (1), where is a quadrature node and is the associated weight. Equation (1) expresses the average amount of test-scoring bias between the response curves and the range from −TS to TS, where TS represents the highest possible test score. The negative values indicate that the reference group scored lower than the focus group on average and the positive values indicate that the focus group had lower mean scores. The uDTF captures the average area between the two test curves and ranges from 0 to TS, because the area between the curve equals zero when the test-scoring functions have exactly the same functional form. (Equation (4)) is defined as a suitable standardized effect size metric for better interpretation, and it represents the percent scoring difference for the overall test:
1.2. Statistics for Differential Response Functioning
The effect size estimates with DRF were defined by Chalmers [9] as follows:
and
where S(·) are the scoring equations used to evaluate the model-implied difference between the focal and reference groups. The f(θ) terms can either be estimated from the posterior via an empirical histogram approach (default) or can use the best-fitting prior distribution that is obtained post-convergence (default is a Gaussian distribution). Similar to DTF statistics, compensatory differential response function statistics (sDRF), non-compensatory differential response function statistics (uDRF) and dDRF statistics have been described in Equation (5), Equation (6), and Equation (7), respectively.
Another important issue to consider when determining the DIF effect, or when measuring DTF and DBF statistics, is how differences across response functions should be aggregated considering the θ parameters. Integrating (or marginalizing) over the latent trait distributions is often carried out to help automate the detection of differential item, bundle, and test effects, rather than focusing on particular θ locations. In the case where the response functions between the groups intersect at one or more locations of θ, practitioners must decide whether the total differential effects should be allowed to compensate across the response functions or whether a definition based on the total magnitude of the difference should be adopted. Based on this framework, it has been argued that, across latent trait distributions, differences between latent trait values can be canceled out if the functions intersect in one or more locations (compensatory) or they are not canceled out (non-compensatory). In the literature, non-compensatory item bias is the primary target for differential function statistics. [14].
Differential response functioning statistics have been obtained as sample-based instantiations of the compensatory and non-compensatory response bias functions and the estimations. These statistics have been described by Chalmers [9] and have been referred to as the compensatory and non-compensatory differential response functioning statistics, or CDRF and NCDRF, respectively. The overall details of the model-based compensatory and non-compensatory bias measures have been discussed by Chalmers [8]. In addition, DRF statistics share a common lineage with a number of previously proposed statistics, such as SIBTEST [11], CSIBTEST [12], and Wainer’s [21] standardized impact measures for DIF and DFIT statistics [8,22]. The SIBTEST was designed to detect DIF at both the item and test levels [11], and it may be defined as a bridge between CTT and IRT in that it uses traditional non-parametric statistical mathematics with an IRT approach to analysis [7]. It obtains the marginal density by conditioning on the unweighted sum scores from a set of anchors (matching subsets) items, which are restricted to be monotonically related to the measured latent trait in order to compute coefficient α [23]. The compensatory response bias in the studied item set (suspect item set) is approximated after applying a regression-correction technique to equate the observed scores. SIBTEST and CSIBTEST statistics are closely related to the CDRF and NCDRF, respectively. The differences between them are explained by Chalmers [9] as follows: SIBTEST requires only observed scores to be used in computations, while CDRF utilizes fitted probabilistic item response models and the marginal distribution of the latent trait directly. Both CSIBTEST and NCDRF statistics are non-compensatory response bias measures, but they slightly differ in their population definitions. DRF, SIBTEST, CSIBTEST, and DTF statistics were used in this study.
2. Materials and Methods
The aim of this study was to investigate the performance of the effect size measures for the detection of the DTF. A Monte Carlo simulation study was conducted to evaluate and compare the DRF (sDRF, uDRF, dDRF), SIBTEST, CSIBTEST, and DTF (sDTF, uDTF) statistics. Similar to the DIF detection methods, the performance of the DTF methods are influenced by factors such as DIF type (i.e., uniform or non-uniform), DIF magnitude (i.e., low, medium), test length, sample size (i.e., equal or unequal), equal/unequal ability distributions, direction of the DIF (e.g., balanced, unbalanced), and percentages of the DIF items. The performance of DTF statistics was investigated by Chalmers et al. [1] using different sample sizes (500, 1000, and 3000), test lengths (30, 40, and 50 items for the 3PLM design, and 20, 25, and 30 items for the GRM design), and different test conditions, such as DIF types (e.g., DIF in intercepts, in slope, and in both parameters) and DIF directions. The results of this study highlighted the particularly poor performance of DTF statistics in detecting the non-uniform DIF effect. The performance of DRF statistics was compared with SIBTEST and CBISTEST with different test lengths (20, 30, and 40), sample sizes (500 to 3000), number of anchor items (five and ten anchors), and different latent ability distributions [9], and this study emphasized that DRF statistics outperformed SIBTEST and CSIBTEST. Overall, the performance of DTF statistics needs to be examined in terms of different IRT models, especially in terms of 2PL, which is the preferred model for the majority of IRT applications. In addition, the performance of DTF and DRF statistics may also be examined, especially with respect to the non-uniform DIF effect. In particular, the direction of DIF and the effect of the sample ratio, the differences in ability between the focal and reference groups, should be investigated in the presence and absence of DIF. This study provides a comparison of DTF and DRF statistics with SIBTEST and CSIBTEST using various DIF conditions (balanced/unbalanced DIF), DIF sizes (low, medium), and DIF types (uniform and non-uniform) in a simulation study. This study also provides a comparison of the Type I error rates of the statistics in the absence of DIF conditions. Simulated data were generated using the two-parameter logistic (2PL) model [24]. Similar to the previous studies [1], the intercepts (d) were drawn from a standard normal distribution (d~N (0, 1)), and the slope parameters (a) were drawn from a log-normal distribution (a~log N (0.2, 0.2)). The ability parameters (θ) was set to a standardized normal distribution (~N (0, 1)). In addition, similar to the previous studies [7,15], the group mean differences in the latent trait (impact) were also evaluated in this study. The mean abilities of the reference and focus groups were varied by 0/0 and 0/−1.0 to simulate no and large differences, respectively. The item parameters of the DIF and anchor items are included in the Supplementary Materials (Table S1).
Balanced/unbalanced DIF is an important test characteristic that was expected to impact DTF detection and has been highlighted in several studies [1,7,15,25]. In some balanced DIF cases, the effects of the DIF items on the test-scoring functions cancel out to create a negligible DTF [1]. The sample sizes of the reference and focus groups were simulated at a variety of levels, and equal and unequal sample sizes (R250/F250, R500/F500, R1000/F1000 and R2000/F2000, R1000/250, R1000/F500, R2000/250, R2000/F500) were used to evaluate the DTF methods. In addition to these general test factors, the percentage (0%, 10%, and 20%), magnitude (low (0.25), medium (0.50)), and type of DIF effect (uniform, non-uniform DIF) were simulated. One test length was used in this study (I = 20). The uniform DIF condition was simulated by generating data with the DIF magnitude added to the intercept (d) parameters. The non-uniform DIF condition for the DIF pattern was created by generating data with DIF magnitude added to only the slope parameters (a), without differences in the intercept parameters (d). Two different DIF percentages with 20 items were used in the simulation study. When the DIF percentage was 10%, 18 items were considered as anchor items and 2 items were generated as DIF items. Similarly, for 20% DIF items, 16 items were generated as anchor items and 4 items were generated as DIF items. In the case of unidirectional (unbalanced) DIF and when the DIF percentage was 10%, both items had higher intercept/slope values for the reference group, while in the case of bidirectional (balanced) DIF, the DIF magnitude was added to a single item for both groups, creating a balanced DIF situation.
2.1. Data Analysis and Evaluation Measures
The Type I error and power rates or reject rates (correct identification of DTF) for the statistics were evaluated. In addition to the Type I error and power rates, the mean effect size values and the empirical standard errors for the effect sizes were evaluated to investigate the study outcomes. Similar to the previous studies [1,15], 1000 replications were implemented, and for each combination of the study conditions, the standard deviation of each effect size measure, and likewise, the mean effect size value for each effect size statistic, were calculated across the 1000 parameter estimates for each combination of conditions. The overall analysis of the simulation study was performed using the statistical software R [26], mirt [27], and the doParallel package [28]. The integration range for was set to [−6, 6], with 1000 independent imputations. Unless specified otherwise, all detection rates were calculated using a nominal α rate of 0.05, and the liberal Bradley robustness criteria [29] (0.025 < type I error < 0.075) was used to interpret Type I errors.
2.2. Real Data Illustration
The real data used for this study consisted of VERA 8 (Vergleichsarbeiten) [30], a mathematics test that was administered to 8th grade students in Germany. The results of the VERA tests were used to inform teachers about their students’ relative performance in Germany. The DIF effect of the VERA 8 mathematics test (Booklet 2) was examined using the DTF measures that were also used in the simulation study. Language groups (German, non-German (those students whose everyday language is not German)) were used to evaluate DIF at the item and test levels. Since the symmetrical treatment of groups can be advantageous when evaluating DIF across two groups, in the study, weighted sampling was used, and the sample sizes of both the German and non-German students were equal, at 1248. Before the DTF analyses, DIF analyses were performed with multigroup IRT, and the uniform and non-uniform DIF items that were derived from slope, intercept, and both slope and intercept parameters are reported in Table S2, Table S3, and Table S4, respectively.
3. Results
3.1. When No Items Contained DIF
The empirical p-values for the statistics were compared to the nominal α values 0.1, 0.05, and 0.01 in the study, and the results of the Type I error rates in the absence of the DIF condition are presented in Table 1. According to the results in the table, the lowest Type I error rates were obtained with sDRF, sDTF, and SIBTEST, and the highest were estimated with uDRF. Table 1 indicates that in the test condition where the mean ability distributions of the reference and focus groups were equal and zero, the Type I error rates for all statistics were not systematically affected by the sample size. In the test condition where the mean ability distributions were not equal, larger Type I error rates were estimated, especially with small and unbalanced sample sizes. However, in the test condition where the sample size was large (R5000/F5000), similar Type I error rates were also estimated from unequal ability distributions for sDTF, sDRF, and uDRF. However, for SIBTEST and CSIBTEST, the Type I error rates were higher for the unequal mean ability distribution condition. When the p < 0.05 condition was examined, the Type I error rates for sDTF, sDRF, and SIBTEST were consistently inside the liberal Bradley robustness criteria (0.025 < type I error < 0.075). The inflated type I error rates were obtained for CSIBTEST, especially for uDRF. For uDRF, in particular, these values were not within an acceptable range. In the case of unequal ability distributions, Type I error rates were slightly higher for sDTF, sDRF, and SIBTEST than in the case of equal ability distributions, but still inside the Bradley robustness criteria, whereas Type I error rates for CSIBTEST and uDRF were not inside the Bradley robustness criteria. The mean and standard errors of the DTF effect size statistics in the absence of the DIF condition are provided in Table 2 and Table 3, respectively. When the standard error rates in the no DIF condition were examined, it was observed that larger standard errors were estimated with small sample sizes (250/250) and unbalanced sample sizes (e.g., 1000/250, 2000/250) for all the statistics when the ability distributions were equal, and the smallest errors were obtained in the test condition when the sample size was 5000/5000. Standard errors of similar values were estimated for sDRF, sDTF, SIBTEST, and CSIBTEST, and similar values were also estimated for uDTF, uDRF, and dDRF. However, in the test condition where the ability distributions were not equal, the standard errors for all statistics increased.

Table 1.
Type I error rates when no DIF items contained DIF.

Table 2.
Mean effect size values when no items contained DIF.

Table 3.
The empirical standard errors when no items contained DIF.
3.2. The Results of DTF Statistics When the Items Contained Uniform DIF
In this study, in addition to the Type I error rates, the power rates of the statistics for the DTF detection were also calculated. The DTF power rates of the statistics are reported in Table 4 with different test conditions for the uniform DIF condition. In the unidirectional (unbalanced)/ bidirectional (balanced) DIF conditions, we examined the power rates estimated by DTF statistics for different DIF magnitudes and proportions. In the case of unidirectional (unbalanced) DIF, with balanced and large sample sizes, power rates were 1.0 or close to this value and increased for all statistics when the DIF size increased from 0.25 to 0.50 and the DIF proportions increased from 0.10 to 0.20. Additionally, it was observed that the highest power rates (e.g., in the case where the DIF magnitude was 0.25) were predicted by the uDRF statistic, although it varied by sample size. It should be noted again that the uDRF statistic (see Table 1) also provided high rejection rates in the no DIF condition. In the bidirectional (balanced) DIF condition, the obtained power rates resembled the Type I error rates in the no DIF condition and did not change considerably with increasing the DIF magnitude or with increasing the DIF rates. However, it was observed here that the power rates also tended to increase with larger sample sizes.

Table 4.
Power rate estimates for DTF statistics when the items contained uniform DIF.
3.3. The Results of DTF Statistics When the Items Contained Non-Uniform DIF
In this study, the performance of DTF statistics with uniform DIF as well as with non-uniform DIF was analyzed. When the DIF effect was unidirectional (unbalanced), the non-uniform DIF power rates with sDTF, sDRF, or SIBTEST were quite low, and showed no systematic pattern depending on the test conditions (e.g., when DIF magnitude increased (from 0.25 to 0.50) or when DIF proportions increased (from 0.10 to 0.20)). However, uDRF and CSIBTEST statistics yielded power rates consistent with the test conditions. For example, when the sample size, DIF magnitude, and DIF percentage increased, the power rates of the uDRF and CSIBTEST statistics increased, and the power rates obtained with uDRF were higher than the power rates obtained with CSIBTEST. In the test condition where the DIF effect was bidirectional (balanced), power rates were lower in the case of non-uniform DIF, where only the slope parameter contained DIF. For sDTF, sDRF, and SIBTEST, there was no difference in the power rates with increasing DIF magnitude values, except in the test conditions where the sample size was larger (2000/2000 and 5000/5000). In summary, the results in Table 4, Table 5, Table 6 and Table 7 indicated that all statistics had very high power to detect a uniform DIF effect and Type I error rates within acceptable ranges in the absence of DIF, especially when the sample size was large (e.g., 1000 to 5000), the DIF size was moderate (0.50), the DIF conditions were unbalanced, and the percentage of DIF items was high (20%) (except CSIBTEST and uDRF, which showed extreme Type I error rates in the absence of DIF). In practice, it can be said that in the presence of an unbalanced DIF effect, almost all statistics provided higher performance rates for the detection of a uniform DIF. However, in the case of a non-uniform DIF effect, the performance of the statistics was quite different. The non-uniform DIF effect could be reasonably detected only with non-compensatory statistics (uDRF and CSIBTEST), even with an unbalanced DIF, large sample size, and a medium DIF size. Researchers may prefer these statistics when examining a non-uniform DIF effect, but it should be noted that it was also identified in this study that these statistics led to higher Type I error rates in the absence of DIF. This was also observed with the real dataset application, as presented below.

Table 5.
Power rate estimates for DTF statistics when the items contained non-uniform DIF.

Table 6.
The mean effect size values and the empirical standard errors for DTF statistics when the items contained uniform/non-uniform DIF.

Table 7.
The results of the real data illustrations.
3.4. The Results of Mean Effect Size Values and the Empirical Standard Errors for DTF Statistics When the Items Contained Uniform/Non-Uniform DIF
These results are presented in Table 6. When examining the test condition where the DIF effect was unidirectional (unbalanced), it was found that for all statistics, the mean values of the estimated effect size yielded larger values when the magnitude and percentage of the DIF were larger. However, the increase in all statistics applicable to the uniform DIF was not valid for the non-uniform DIF condition. For example, when examining the mean effect size values estimated with the non-uniform DIF type, the increase was only seen in the values estimated with the uDTF, %uDTF, uDRF, dDRF, and CSIBTEST statistics when the DIF effect was unbalanced. However, when the DIF effect was balanced, similar to the uniform DIF condition, there was no systematic and significant increase in mean effect size values with the increasing DIF magnitude in the non-uniform DIF condition. Empirical standard errors for effect sizes by DIF magnitude and type are also presented in Table 6. The combination of DIF magnitude and DIF direction had no effect on the empirical standard errors. Since the mean standard errors were estimated in the test condition where the sample size was 5000, equal for the reference and focus groups, they resembled those estimated in Table 3, where the ability distributions were equal, and the sample size was 5000/5000.
3.5. The Results of the Real Data Illustrations
In the last part of the study, the performance of DTF statistics was examined using a real dataset. In the real dataset, the sample sizes were equal, at 1248. In order to determine the effects of uniform and non-uniform DIF conditions on the performance of the DTF statistic, DIF items in the intercept, slope, and both intercept and slope parameters were identified, and the DTF statistics were calculated. When the values reported in Table 7 and Figure 1 were examined, it was first found that the DTF estimated by the DTF statistics (sDTF, uDTF) was not statistically significant (p > 0). Similarly, no significant effect was found for either the uniform or non-uniform DIF conditions. This can be clearly seen from the graphs shown in Figure 1. The test characteristic curves (TCC) of both groups are shown in Figure 1a. Since the number of items in the tests was 52, the graph shows the expected total score from 0 to 52. The TCCs can only cross if both statistics have the same value. However, as the graph shows, in this study, the TCCs for German and non-German students crossed. This can be better interpreted using the marked DTF plot together with the confidence limits presented in Figure 1b. The black curve on this graph shows how sDTFθ varied with ability, and the 95% confidence limits on sDTF are shown as a grey area, while the red line indicates sDTFθ = 0. Examining this graph, when values were less than zero (, the sDTF was negative and the test favored non-German students (focus group), and when values were greater than zero (, sDTF was positive and the test favored German students (reference group). The situation was also indicated by the crossing TCCs. In contrast to the DTF statistics, the p-values in Table 7 indicated that the DIF effect determined by the DRF, SIBTEST, and CSIBTEST statistics was significant. When these statistics were examined, it was observed that both uniform and non-uniform DIF conditions, as determined by the DIF conditions in the intercept and/or slope parameters, had a significant effect.
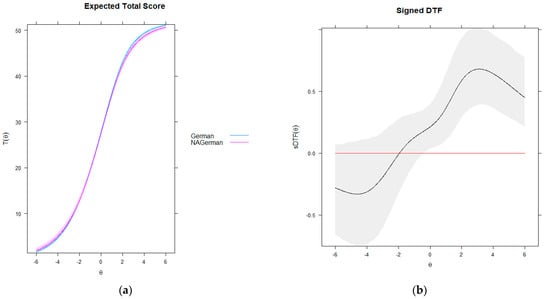
Figure 1.
Empirical test-scoring functions with imputed confidence intervals: (a) Expected total score and (b) signed DTF.
4. Discussion
Methods and statistics for determining DIF/DTF have their own strengths and limitations, as often discussed in the literature. This simulation study examined the various methods and statistics commonly used in DTF measurement under different test conditions and with a real data application. In the first step of the study, the Type I error values in the no DIF case were examined under conditions where the sample sizes and the means of the group ability distributions were different. The results obtained in this part of the study demonstrated that the Type I error rates for all statistics were not affected by the sample size. These results were consistent with the approach described by Chalmers et al. [1]. However, it is important to note that the Type I error rates obtained for uDRF and CSIBTEST were quite high, even in the no DIF condition (e.g., when p < 0.05), and consistently outside the liberal Bradley robustness criteria (especially for uDRF). In the no DIF condition, where the means of group ability distributions were different, the Type I error rates for SIBTEST and CSIBTEST increased. In the case where no item contained DIF, standard errors were influenced by differences in the sample size and mean group ability distributions. In particular, values increased with small and unbalanced sample sizes.
In the second part of the simulation study, the effect of DIF items was investigated with different DIF conditions. In the study, uniform and non-uniform DIF were created by simply adding DIF magnitude to the intercept and slope parameters, respectively. In the case of uniform DIF, when the estimation statistics with unbalanced DIF were examined, it was observed that the power rates of the techniques were high and increased as the sample sizes, DIF magnitude, and the number of questions with DIF (percentage) increased. However, in the balanced DIF condition, the power rates did not change systematically depending on the test conditions. The highest power rates were obtained with uDRF, SIBTEST, and CSIBTEST. However, it should be noted that high Type I error rates were also estimated with these statistics in the no DIF condition. However, the performances of sDTF, sDRF, and SIBTEST statistics were not effective when the DIF effect was only due to the slope parameters; in other words, in the case of non-uniform DIF. The power rates estimated with these statistics did not vary systematically with DIF magnitude, proportion, or sample size, and they were also quite low. In contrast, uDRF and CSIBTEST yielded substantial and high-power rates. However, as mentioned before, the Type I error rates of these statistics in the no DIF condition should be considered.
The performance of the DTF statistic, which was also analyzed with a real dataset, was also consistent with the results of the simulation study. One of the main findings was that under the uniform DIF condition (considering only the DIF effect in the intercept parameters), no significant DTFs were estimated with any statistics except uDRF. In the non-uniform DIF condition (DIF in slope parameters only), a significant effect was observed with SIBTEST and CSIBTEST, but the effect was not statistically significant with the other statistics. This is again consistent with simulation studies, especially with the CSIBTEST findings. When we examined the items where the non-uniform DIF effect was due to both the slope and intercept parameters, it was found that the DIF effect was significant at the test level with sDRF and uDRF, and SIBTEST and CSIBTEST.
Considering all the findings in this study, these statistics were generally effective in identifying uniform DIF. However, non-uniform DIF should be investigated with different test conditions. Similar to the effect of DIF at the item level, it is important to investigate the effects of DIF items at the test level and evaluate their performance under different test conditions. In addition, only unidimensional 2PL models were used in this study, and the performance of these models can also be separately examined, especially for non-uniform DIF detection in multidimensional models.
5. Conclusions
The detection of DIF is an important step to improve the psychometric properties of achievement tests and scales developed in many fields (e.g., educational sciences, psychology, medicine) [31]. Many researchers from different fields have developed different DIF determination techniques for analyzing DIF in test or scale items. Differential item functioning (DIF) analysis refers to procedures that evaluate whether an item’s characteristics differ for different groups of examinees after controlling for overall differences in performance. Two types of DIF are often differentiated: uniform DIF and non-uniform DIF [32]. The basic definition of DIF, test fairness, and the basic overview of DIF have been explained in numerous studies e.g., [33,34,35,36]. DIF detection has been widely applied in the context of IRT models and observed score approaches. Based on both approaches, various methods for DIF detection have been proposed in the literature. Researchers have aimed to identify optimal DIF detection methods using simulation studies and the application of real datasets.
However, despite the vast literature on methods for detecting DIF, relatively little research has been conducted on the effects of DIF on subsequent outcomes, which is at least as important as the accurate identification of items with DIF. This study examined the performance of commonly used statistics for detecting the DIF effect under different DIF types (uniform, non-uniform), DIF conditions, and test conditions. One of the most important findings of the study was the superiority of non-compensatory statistics in detecting non-uniform DIF, but also their inflated Type I error rates in the absence of DIF. It was therefore recommended that studies be conducted to determine the effect of non-uniform DIF. It was also emphasized that the DIF and test conditions are very important in determining the DIF effect, and it was suggested to consider, in particular, the conditions in which the DIF effect is balanced and unbalanced. Moreover, this study emphasized that similar to DIF analyses, the DIF effect should be determined by researchers. The aggregative effect of DIF items on test scores, or the cumulative DIF effect of item sets, have an important effect on the improvement of the psychometric properties of tests or scales.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/psych5020032/s1, Table S1: The item parameters used for data generation. Table S2: Non-uniform DIF items in a real dataset (slope parameters only). Table S3: Uniform DIF items in a real dataset (intercept parameters only). Table S4: Non-uniform DIF items in a real dataset (both intercept and slope parameters).
Funding
This research was funded by Ministry of Science, Research and the Arts Baden-Württemberg with BRIGITTE-SCHLIEBEN-LANGE-PROGRAMM and Heidelberg University of Education within the framework of internal research funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The empirical datasets analyzed for this study cannot be made available because the dataset is an official dataset that requires approval from the “Institute for Educational Analyses Ba-den-Württemberg (IBBW)” at poststelle@ibbw.kv.bwl.de and the “Institute for Quality Development in Education (IQB)” at https://www.iqb.hu-berlin.de/institut/staff. All R codes used in this study will be available via e-mail in case of interest.
Acknowledgments
I gratefully thank Christian Rietz and Maya Machunsky for their contributions and suggestions.
Conflicts of Interest
The author declares no conflict of interest.
References
- Chalmers, R.P.; Counsell, A.; Flora, D.B. It might not make a big DIF: Improved Differential Test Functioning statistics that account for sampling variability. Educ. Psychol. Meas. 2016, 76, 114–140. [Google Scholar] [CrossRef]
- Drasgow, F. Study of the measurement bias of two standardized psychological tests. J. Appl. Psychol. 1987, 72, 19–29. [Google Scholar] [CrossRef]
- DeMars, C.E. An analytic comparison of effect sizes for differential item functioning. Appl. Meas. Educ. 2011, 24, 189–209. [Google Scholar] [CrossRef]
- Stark, S.; Chernyshenko, O.S.; Drasgow, F. Examining the effects of differential item functioning and differential test functioning on selection decisions: When are statistically significant effects practically important? J. Appl. Psychol. 2004, 89, 497–508. [Google Scholar] [CrossRef]
- Pae, T.; Park, G. Examining the relationship between differential item functioning and differential test functioning. Lang. Test. 2006, 23, 475–496. [Google Scholar] [CrossRef]
- Flora, D.; Curran, P.; Hussong, A.; Edwards, M. Incorporating measurement nonequivalence in a cross-study latent growth curve analysis. Struct. Equ. Model. A Multidiscip. J. 2008, 15, 676–704. [Google Scholar] [CrossRef]
- Hunter, C. A Simulation Study Comparing Two Methods ff Evaluating Differential Test Functioning (DTF): DFIT and the Mantel-Haenszel/Liu-Agresti Variance. Ph.D. Thesis, Georgia State University, Atlanta, GA, USA, 2014. Available online: https://core.ac.uk/download/pdf/71425819.pdf (accessed on 3 April 2023).
- Raju, N.S.; van der Linden, W.J.; Fleer, P.F. IRT-based internal measures of differential functioning of items and tests. Appl. Psychol. Meas. 1995, 19, 353–368. [Google Scholar] [CrossRef]
- Chalmers, R.P. Model-Based Measures for Detecting and Quantifying Response Bias. Psychometrika 2018, 83, 696–732. [Google Scholar] [CrossRef]
- Chang, H.-H.; Mazzeo, J.; Roussos, L. DIF for polytomously scored items: An adaptation of the SIBTEST procedure. J. Educ. Meas. 1996, 33, 333–353. [Google Scholar] [CrossRef]
- Shealy, R.; Stout, W. A model-based standardization approach that separates true bias/DIF from group ability differences and detects test bias/DTF as well as item bias/DIF. Psychometrika 1993, 58, 159–194. [Google Scholar] [CrossRef]
- Li, H.-H.; Stout, W. A new procedure for detection of crossing DIF. Psychometrika 1996, 61, 647–677. [Google Scholar] [CrossRef]
- Oshima, T.C.; Raju, N.S.; Flowers, C.P.; Slinde, J.A. Differential bundle functioning using the DFIT framework: Procedures for identifying possible sources of differential functioning. Appl. Meas. Educ. 1998, 11, 353–369. [Google Scholar] [CrossRef]
- Chalmers, R.P. A differential response functioning framework for understanding item, bundle, and test bias. Unpublished. Ph.D. Thesis, York University, Toronto, ON, Canada, October 2016. Available online: https://yorkspace.library.yorku.ca/xmlui/handle/10315/33431 (accessed on 3 April 2023).
- Finch, W.H.; French, B.F. Effect Sizes for Estimating Differential Item Functioning Influence at the Test Level. Psych 2023, 5, 133–147. [Google Scholar] [CrossRef]
- Camilli, G.; Penfield, R.A. Variance estimation for Differential Test Functioning based on Mantel-Haenszel statistics. J. Educ. Meas. 1997, 34, 123–139. [Google Scholar] [CrossRef]
- Finch, W.H.; French, B.F.; Hernandez, M.F. Quantifying Item Invariance for the Selection of the Least Biased Assessment. J. Appl. Meas. 2019, 20, 13–26. [Google Scholar]
- Hasselblad, V.; Hedges, L.V. Meta-analysis of screening and diagnostic tests. Psychol. Bull. 1995, 117, 167–178. [Google Scholar] [CrossRef]
- Zumbo, B.D.; Thomas, D.R. A Measure of Effect Size for a Model-Based Approach for Studying DIF (Working Paper of the Edgeworth Laboratory for Quantitative Behavioral Science); Canada University of Northern British Columbia: Prince George, BC, Canada, 1997. [Google Scholar]
- Doebler, A. Looking at DIF from a new perspective: A structure-based approach acknowledging inherent indefinability. Appl. Psychol. Meas. 2019, 43, 303–321. [Google Scholar] [CrossRef] [PubMed]
- Wainer, H. Model-based standardized measurement of an item’s differential impact. In Differential Item functioning; Holland, P.W., Wainer, H., Eds.; Lawrence Erlbaum Associates, Inc.: Hillsdale, NJ, USA, 1993; pp. 123–135. [Google Scholar]
- Oshima, T.C.; Raju, N.S.; Flowers, C.P. Development and demonstration of multidimensional IRT-based internal measures of differential functioning of items and tests. J. Educ. Meas. 1997, 34, 253–272. [Google Scholar] [CrossRef]
- Guttman, L. A basis for analyzing test-retest reliability. Psychometrika 1945, 10, 255–282. [Google Scholar] [CrossRef]
- Lord, F.M.; Novick, M.R. Statistical Theory of Mental Test Scores; Addison-Wesley: Reading, MA, USA, 1968. [Google Scholar]
- Robitzsch, A. Robust and Nonrobust Linking of Two Groups for the Rasch Model with Balanced and Unbalanced Random DIF: A Comparative Simulation Study and the Simultaneous Assessment of Standard Errors and Linking Errors with Resampling Techniques. Symmetry 2021, 13, 2198. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022; Available online: https://www.R-project.org/ (accessed on 3 April 2023).
- Chalmers, R.P. Mirt: A multidimensional item response theory package for the R environment. J. Stat. Softw. 2012, 48, 1–29. [Google Scholar] [CrossRef]
- Corporation, M.; Weston, S. DoParallel: Foreach Parallel Adaptor for the ‘Parallel’ Package, R package version 1.0.14; 2018. Available online: https://CRAN.R-project.org/package=doParallel (accessed on 3 April 2023).
- Bradley, J.V. Robustness? Br. J. Math. Stat. Psychol. 1978, 31, 144–152. [Google Scholar] [CrossRef]
- Schult, J.; Wagner, S. VERA 8 in Baden-Württemberg 2019. In Beiträge zur Bildungsberichterstattung; Institut für Bildungsanalysen Baden-Württemberg: Stuttgart, Germany, 2019; Available online: https://ibbw.kultus-bw.de/site/pbs-bw-km-root/get/documents_E56497547/KULTUS.Dachmandant/KULTUS/Dienststellen/ibbw/Systemanalysen/Bildungsberichterstattung/Ergebnisberichte/VERA_8/Ergebnisse_VERA8_2019.pdf (accessed on 3 April 2023).
- Lee, S. Lord’s Wald test for detecting DIF in multidimensional IRT models. Unpublished. Ph.D. Thesis, The State University of New Jersey, New Jersey, NJ, USA, 2015. Available online: https://doi.org/doi:10.7282/T3JH3P13 (accessed on 3 April 2023).
- Wang, C.; Zhu, R.; Xu, G. Using Lasso and Adaptive Lasso to Identify DIF in Multidimensional 2PL Models. Multivar. Behav. Res. 2023, 58, 387–407. [Google Scholar] [CrossRef] [PubMed]
- Zumbo, B.D. Three Generations of DIF Analyses: Considering Where It Has Been, Where It Is Now, and Where It Is Going. Lang. Assess. Q. 2007, 4, 223–233. [Google Scholar] [CrossRef]
- Camilli, G. Test Fairness. In Educational Measurement, 4th ed.; Brennan, R., Ed.; American Council on Education and Praeger: Westport, CT, USA, 2006; pp. 221–256. [Google Scholar]
- Penfield, R.D.; Camilli, G. Differential item functioning and item bias. In Handbook of Statistics; Rao, C.R., Sinharay, S., Eds.; Routledge: Oxford, UK, 2007; Volume 26, pp. 125–167. [Google Scholar]
- Martinková, P.; Drabinová, A.; Liaw, Y.L.; Sanders, E.A.; McFarland, J.L.; Price, R.M. Checking Equity: Why Differential Item Functioning Analysis Should Be a Routine Part of Developing Conceptual Assessments. CBE Life Sci. Educ. 2017, 16, rm2. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).