Learning Engagement as a Moderator between Self-Efficacy, Math Anxiety, Problem-Solving Strategy, and Vector Problem-Solving Performance
Abstract
:1. Introduction
1.1. Math Anxiety
1.2. Self-Efficacy
1.3. Problem-Solving Strategy
1.4. Learning Engagement
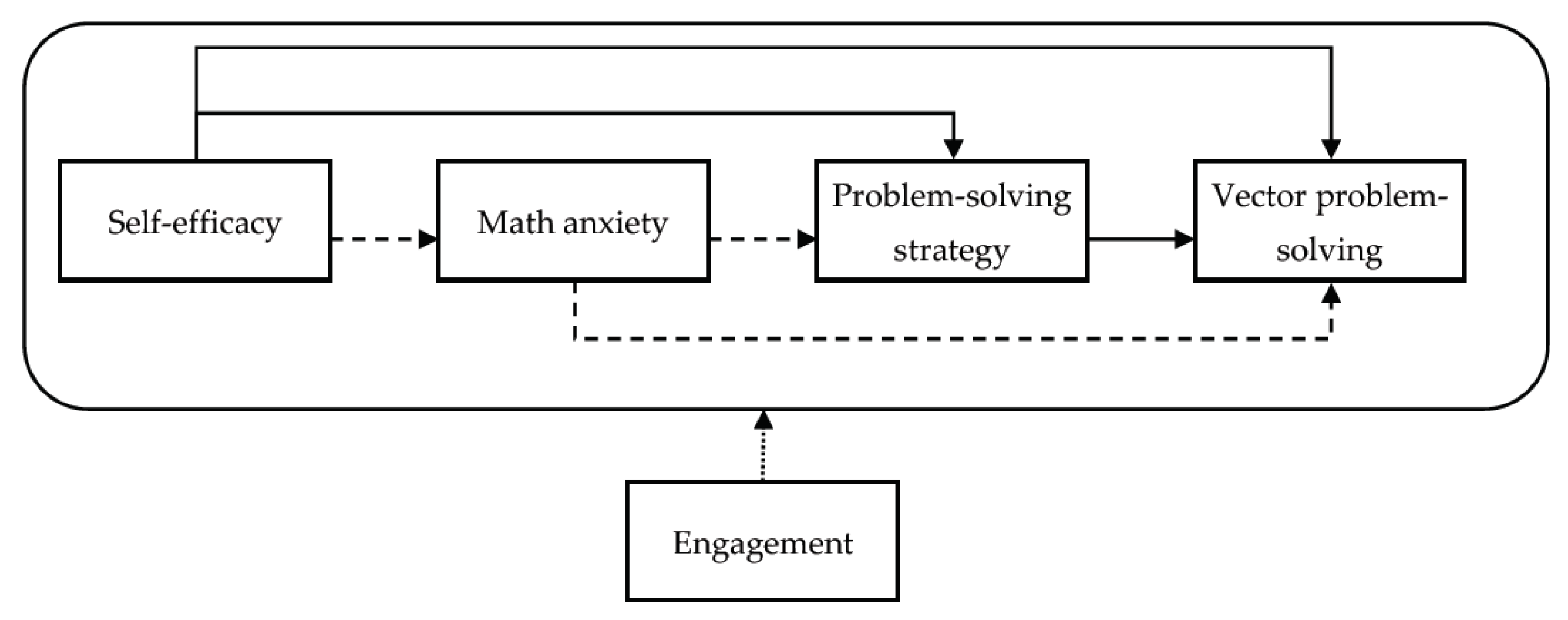
1.5. The Current Study
- Hypothesis 1: Self-efficacy is negatively related to math anxiety and positively related to problem-solving strategy and vector problem-solving performance.
- Hypothesis 2: Math anxiety is negatively related to problem-solving strategy and vector problem-solving performance.
- Hypothesis 3: Problem-solving strategy is positively related to vector problem-solving performance.
- Hypothesis 4: The combination of the level of learning engagement and instability has a significant moderate effect on the association between Hypothesis 1 to Hypothesis 3.
2. Methods
2.1. Participants and Procedure
2.2. Measures
2.2.1. Math Anxiety
2.2.2. Self-Efficacy
2.2.3. Problem-Solving Strategy
2.2.4. Level of Learning Engagement and Instability
2.2.5. Vector Problem-Solving Performance
2.3. Data Analysis
- Model 1: a model that does not impose equal constraints.
- Model 2: a model that imposes equal constraints on the intercept.
- Model 3: a model that imposes equal constraints on intercept and variance.
- Model 4: a model that imposes equal constraints on intercept, variance, and path coefficient.
3. Results
3.1. Preliminary Analysis
3.2. Descriptive Statistics
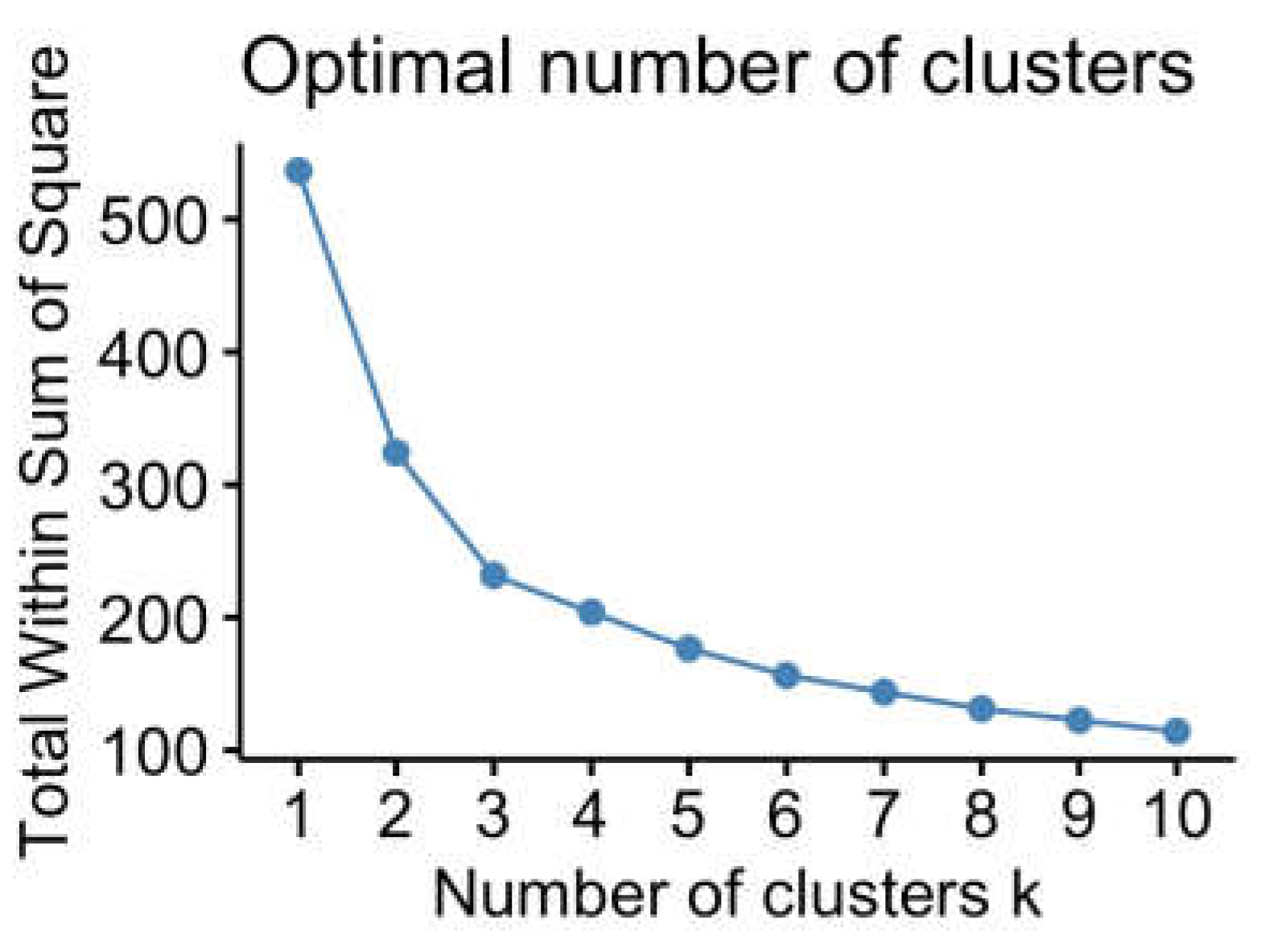
3.3. Combination of Level and Instability of Learning Engagement
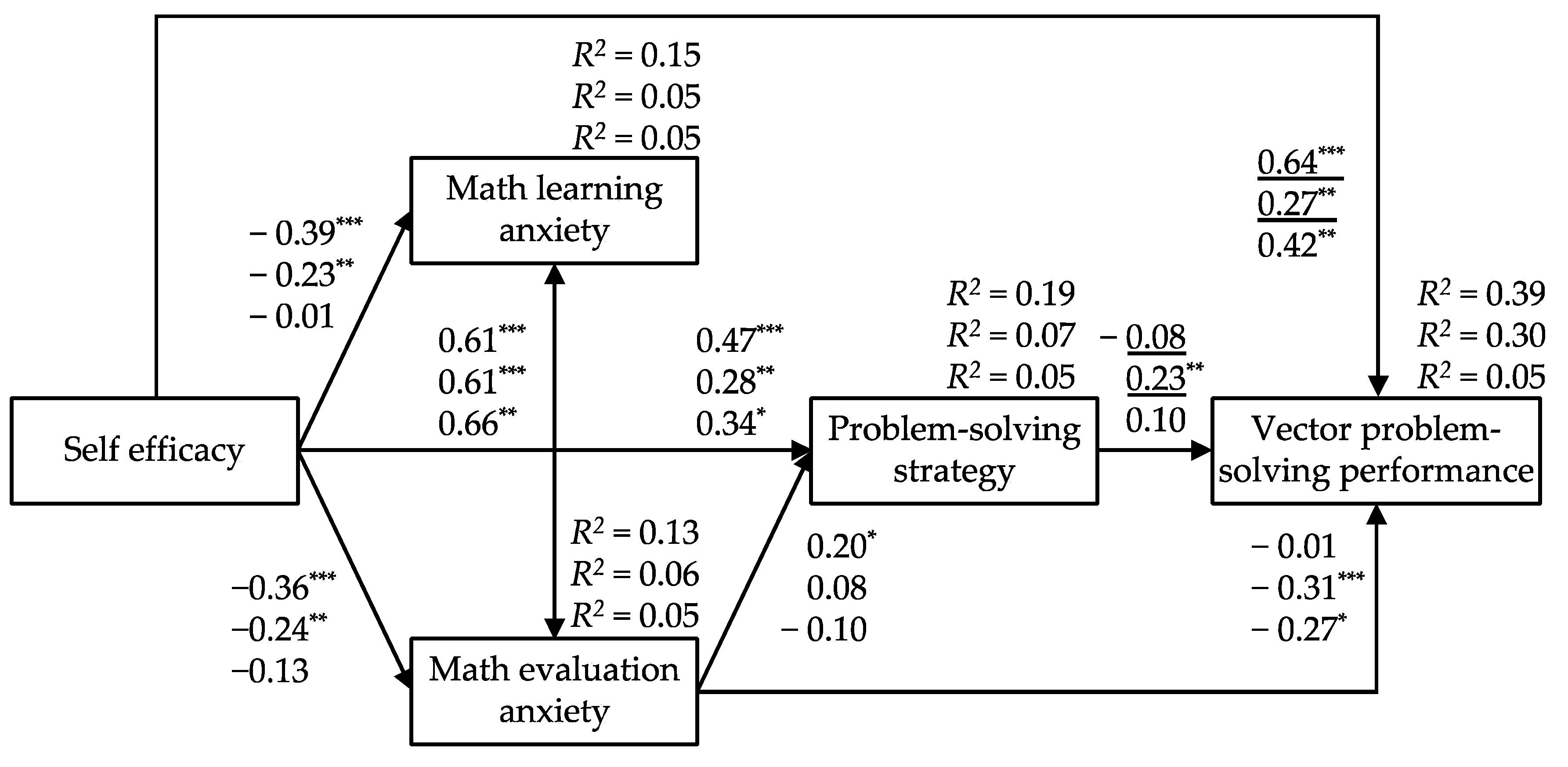
3.4. Multiple-Group Structural Equation Modelling
4. Discussion
4.1. Implications for Education
4.2. Limitations
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ministry of Education, Culture, Sports, Science, and Technology in Japan. The Course of Study for Mathematics in High School. Available online: https://www.mext.go.jp/content/1407073_05_1_2.pdf (accessed on 12 July 2022).
- National Council of Teachers of Mathematics. Principles and Standards for School Mathematics, 1st ed.; National Council of Teachers of Mathematics: Reston, VA, USA, 2000. [Google Scholar]
- Victorian Curriculum and Assessment Authority. Victorian Curriculum: Mathematics. Available online: https://victoriancurriculum.vcaa.vic.edu.au/mathematics/introduction/rationale-and-aims (accessed on 12 July 2022).
- Kumakura, H. A study on geometry teaching at senior high school which attach importance to connection of junior high school: Focus on teaching vector. Bull. Fac. Educ. Shizuoka Univ. Educ. Res. Ser. 2005, 36, 101–116. [Google Scholar]
- Barniol, P.; Zavala, G. Test of understanding of vectors: A reliable multiple-choice vector concept test. Phys. Rev. Spec. Top.-Phys. Educ. Res. 2014, 10, 010121. [Google Scholar] [CrossRef]
- Kawazoe, M.; Okamoto, M. The infuence of students’ mental representation on understanding of liner independency of spatial vectors. J. Jpn. Soc. Math. Educ. 2016, 98, 17–24. [Google Scholar]
- Latifa, B.R.A.; Purwaningsih, E.; Sutopo, S. Identification of students’ difficulties in understanding of vector concepts using test of understanding of vector. J. Phys. Conf. Ser. 2021, 2098, 012018. [Google Scholar] [CrossRef]
- Liu, D.; Kottegoda, Y. Disconnect between undergraduates’ understanding of the algebraic and geometric aspects of vectors. Eur. J. Phys. 2019, 40, 035702. [Google Scholar] [CrossRef]
- Poynter, A. Effect as a Pivot between Actions and Symbols: The Case of Vector. Ph.D. Thesis, University of Warwick, Coventry, UK, July 2004. [Google Scholar]
- Shimizu, Y. Relation between knowledge of vector in high school students, achievement goals, and engagement. Jpn. J. Educ. Technol. 2020, 43, 351–362. [Google Scholar]
- Wutchana, U.; Emarat, N. Students’ understanding of graphical vector addition in one and two dimensions. Int. J. Phys. Chem. Educ. 2011, 3, 102–111. [Google Scholar] [CrossRef]
- Gutieérrez, A.; Leder, G.C.; Boero, P. The Second Handbook of Research on the Psychology of Mathematics Education: The Journey Continues, 1st ed.; Sense Publishers: Rotterdam, The Netherlands, 2016. [Google Scholar]
- Mayer, R.E. Cognitive, metacognitive, and motivational aspects of problem solving. Instr. Sci. 1998, 26, 49–63. [Google Scholar] [CrossRef]
- Schoenfeld, A.H. Mathematical Problem Solving; Academic Press: New York, NY, USA, 1985. [Google Scholar]
- Hembree, R. Experiments and relational studies in problem solving: A meta-analysis. J. Res. Math. Educ. 1992, 23, 242–273. [Google Scholar] [CrossRef]
- Barroso, C.; Ganley, C.M.; McGraw, A.L.; Gerr, A.A.; Hart, S.A.; Daucourt, M.D. A meta-analysis of the relation between math anxiety and math achievement. Psychol. Bull. 2021, 147, 134–168. [Google Scholar] [CrossRef]
- Lee, J. Universals and specifics of math self-concept, math self-efficacy, and math anxiety across 41 PISA 2003 participating countries. Learn. Individ. Differ. 2009, 19, 355–365. [Google Scholar] [CrossRef]
- OECD. PISA 2012 Results: Ready to Learn (Volume III): Students’ Engagement, Drive and Self-Beliefs, 1st ed.; OECD Publishing: Paris, France, 2013. [Google Scholar]
- Richardson, F.C.; Suinn, R.M. The mathematics anxiety rating scale: Psychometric data. J. Couns. Psychol. 1972, 19, 551–554. [Google Scholar] [CrossRef]
- Hembree, R. The nature, effects, and relief of mathematics anxiety. J. Res. Math. Educ. 1990, 21, 33–46. [Google Scholar] [CrossRef]
- Ma, X. A Meta-Analysis of the relationship between anxiety toward mathematics and achievement in mathematics. J. Res. Math. Educ. 1999, 30, 520–540. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, N.; Kong, Q.P. The Relationship between math anxiety and math performance: A meta-analytic investigation. Front. Psychol. 2019, 10, 1613. [Google Scholar] [CrossRef] [Green Version]
- Hill, F.; Mammarella, I.C.; Devine, A.; Caviola, S.; Passolunghi, M.C.; Szűcs, D. Maths anxiety in primary and secondary school students: Gender differences, developmental changes and anxiety specificity. Learn. Individ. Differ. 2016, 48, 45–53. [Google Scholar] [CrossRef]
- Ramirez, G.; Shaw, S.T.; Maloney, E.A. Math anxiety: Past research, promising interventions, and a new interpretation framework. Educ. Psychol. 2018, 53, 145–164. [Google Scholar] [CrossRef]
- Eysenck, M.W.; Derakshan, N.; Santos, R.; Calvo, M.G. Anxiety and cognitive performance: Attentional control theory. Emotion 2007, 7, 336–353. [Google Scholar] [CrossRef] [Green Version]
- Caviola, S.; Toffalini, E.; Giofrè, D.; Ruiz, J.M.; Szűcs, D.; Mammarella, I.C. Math performance and academic anxiety forms, from sociodemographic to cognitive aspects: A meta-analysis on 906,311 participants. Educ. Psychol. Rev. 2022, 34, 363–399. [Google Scholar] [CrossRef]
- Finell, J.; Sammallahti, E.; Korhonen, J.; Eklöf, H.; Jonsson, B. Working Memory and its mediating role on the relationship of math anxiety and math performance: A meta-analysis. Front. Psychol. 2022, 12, 798090. [Google Scholar] [CrossRef]
- Bandura, A. Social Foundations of Thought and Action: A Social Cognitive Theory; Prentice Hall: Englewood Cliffs, NJ, USA, 1986. [Google Scholar]
- Bandura, A. Social cognitive theory of mass communication. In Media Effects: Advances in Theory and Research, 2nd ed.; Bryant, J., Zillmann, D., Eds.; Routledge: New York, NY, USA, 2002; pp. 121–153. [Google Scholar]
- Jiang, Y.; Song, J.; Lee, M.; Bong, M. Self-efficacy and achievement goals as motivational links between perceived contexts and achievement. Educ. Psychol. 2014, 34, 92–117. [Google Scholar] [CrossRef]
- Pajares, F.; Graham, L. Self-efficacy, motivation constructs, and mathematics performance of entering middle school students. Contemp. Educ. Psychol. 1999, 24, 124–139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Siefer, K.; Leuders, T.; Obersteiner, A. Which task characteristics do students rely on when they evaluate their abilities to solve linear function tasks?: A task-specific assessment of self-efficacy. Front. Psychol. 2021, 12, 596901. [Google Scholar] [CrossRef] [PubMed]
- Schwarzer, R.; Jerusalem, M. Generalized Self-Efficacy scale. In Measures in Health Psychology: A User’s Portfolio. Causal and Control Beliefs, 1st ed.; Weinman, J., Wright, S., Johnston, M., Eds.; Nfer-Nelson: Windsor, UK, 1995; pp. 35–37. [Google Scholar]
- Kranzler, J.H.; Pajares, F.M. An exploratory factor analysis of the mathematics self-efficacy scale—Revised (MSES-R). Meas. Eval. Couns. Dev. 1997, 29, 215–228. [Google Scholar] [CrossRef]
- Sartawi, A.; Alsawaie, O.N.; Dodeen, H.; Tibi, S.; Alghazo, I.M. Predicting mathematics achievement by motivation and self-efficacy across gender and achievement levels. Interdiscip. J. Teac. Learn. 2012, 2, 59–77. [Google Scholar]
- Pajares, F.; Kranzler, J. Self-efficacy beliefs and general mental ability in mathematical problem-solving. Contemp. Educ. Psychol. 1995, 20, 426–443. [Google Scholar] [CrossRef]
- Pérez-Fuentes, M.D.C.; Núñez, A.; del Mar Molero, M.; Gázquez, J.J.; Rosário, P.; Núñez, J.C. The role of anxiety in the relationship between self-efficacy and math achievement. Psicol. Educ. 2020, 26, 137–143. [Google Scholar] [CrossRef] [Green Version]
- Azar, H.K.; Lavasani, M.G.; Malahmadi, E.; Amani, J. The role of self-efficacy, task value, and achievement goals in predicting learning approaches and mathematics achievement. Procedia Soc. Behav. Sci. 2010, 5, 942–947. [Google Scholar] [CrossRef] [Green Version]
- Roick, J.; Ringeisen, T. Students’ math performance in higher education: Examining the role of self-regulated learning and self-efficacy. Learn. Individ. Differ. 2018, 65, 148–158. [Google Scholar] [CrossRef]
- Pekrun, R. The control-value theory of achievement emotions: Assumptions, corollaries, and implications for educational research and practice. Educ. Psychol. Rev. 2006, 18, 315–341. [Google Scholar] [CrossRef]
- Gick, M.L. Problem-solving strategies. Educ. Psychol. 1986, 21, 99–120. [Google Scholar] [CrossRef]
- Cowan, R. Does it all add up? Changes in children’s knowledge of addition combinations, strategies, and principles. In The Development of Arithmetic Concepts and Skills: Constructing Adaptive Expertise, 1st ed.; Baroody, A.J., Dowker, A., Eds.; Lawrence Erlbaum Associates Publishers: Mahwah, NJ, USA, 2003; pp. 35–74. [Google Scholar]
- Polya, G. How to Solve It; a New Aspect of Mathematical Method, 1st ed.; Princeton University Press: Princeton, NJ, USA, 1945. [Google Scholar]
- Ishida, J. Effects of teaching mathematical problem solving strategy. J. Jpn. Soc. Math. Educ. 1992, 74, 27–32. [Google Scholar]
- Beilock, S.L.; Decaro, M.S. From poor performance to success under stress: Working memory, strategy selection, and mathematical problem solving under pressure. J. Exp. Psychol. Learn. Mem. Cogn. 2007, 33, 983–998. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramirez, G.; Chang, H.; Maloney, E.A.; Levine, S.C.; Beilock, S.L. On the relationship between math anxiety and math achievement in early elementary school: The role of problem solving strategies. J. Exp. Child Psychol. 2016, 141, 83–100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fredricks, J.A.; Blumenfeld, P.C.; Paris, A.H. School engagement: Potential of the concept, state of the evidence. Rev. Educ. Res. 2004, 74, 59–109. [Google Scholar] [CrossRef]
- Christenson, S.L.; Reschly, A.L.; Wylie, C. Handbook of Research on Student Engagement, 1st ed.; Springer Science + Business Media: New York, NY, USA, 2012. [Google Scholar]
- Skinner, E.A.; Kindermann, T.A.; Furrer, C.J. A motivational perspective on engagement and disaffection: Conceptualization and assessment of children’s behavioral and emotional participation in academic activities in the classroom. Educ. Psychol. Meas. 2009, 69, 493–525. [Google Scholar] [CrossRef] [Green Version]
- Fung, F.; Tan, C.Y.; Chen, G. Student engagement and mathematics achievement: Unraveling main and interactive effects. Psychol. Sch. 2018, 55, 815–831. [Google Scholar] [CrossRef]
- Putwain, D.W.; Symes, W.; Nicholson, L.J.; Becker, S. Achievement goals, behavioural engagement, and mathematics achievement: A mediational analysis. Learn. Individ. Differ. 2018, 68, 12–19. [Google Scholar] [CrossRef] [Green Version]
- Ghelichli, Y.; Seyyedrezaei, S.H.; Barani, G.; Mazandarani, O. The mediating role of self-regulation between student engagement and motivation among Iranian EFL learners: A structural equation modeling approach. J. Mod. Res. Eng. Lang. Stud. 2021, 9, 179–200. [Google Scholar]
- Reeve, J.; Lee, W. Students’ classroom engagement produces longitudinal changes in classroom motivation. J. Educ. Psychol. 2014, 106, 527–540. [Google Scholar] [CrossRef] [Green Version]
- Umemoto, T.; Ito, T. The relationship between self-efficacy, intrinsic value, and emotional engagement: Using a cross-lagged panel model. Jpn. J. Educ. Technol. 2016, 40, 75–84. [Google Scholar]
- Wu, Y.-J.; Chen, Y.-H.; Kiefer, S.M.; Carstensen, C.H. Learning strategies as moderators between motivation and mathematics performance in east Asian students: Latent class analysis. SAGE Open 2021, 11, 21582440211061382. [Google Scholar] [CrossRef]
- Okada, R.; Ito, T.; Umemoto, T. Global level and instability of motivation: Relations with motivational traits and self-motivational strategies. Educ. Psychol. Forum Rep. 2013, FR-2013-01, 1–11. [Google Scholar]
- Umemoto, T.; Inagaki, T. Interactive effects of level and instability of situational motivation for learning during class. Kansai Univ. J. Higher Educ. 2021, 12, 87–98. [Google Scholar]
- Ichimura, M. A study of the measure of instability of self-esteem. Jpn. J. Personal. 2012, 20, 204–216. [Google Scholar] [CrossRef] [Green Version]
- Kernis, M.H.; Grannemann, B.D.; Barclay, L.C. Stability and level of self-esteem as predictors of anger arousal and hostility. J. Personal. Soc. Psychol. 1989, 56, 1013–1022. [Google Scholar] [CrossRef]
- Fujii, Y. A study on mathematics anxiety rating scale (MARS). Jpn. J. Educ. Psychol. 1994, 42, 448–454. [Google Scholar] [CrossRef] [Green Version]
- Pajares, F.; Miller, M.D. Role of self-efficacy and self-concept beliefs in mathematical problem solving: A path analysis. J. Educ. Psychol. 1994, 86, 193–203. [Google Scholar] [CrossRef]
- Seo, M. Academic help-seeking and question-generating in mathematics: Role of strategies to check failures in problem solving. Jpn. J. Educ. Psychol. 2005, 53, 441–455. [Google Scholar] [CrossRef]
- Ichikawa, S.; Haebara, T.; Sugisawa, T.; Seo, M.; Kiyokawa, S.; Inuzuka, M.; Murayama, K.; Uesaaka, Y.; Kobayashi, H.; Shinogaya, K. Development of COMPASS: Componential assessment for basic competence and study skills in mathematics. Cogn. Stu. Bull. Jpn. Cogn. Sci. Soc. 2009, 16, 333–347. [Google Scholar]
- Reeve, J.; Tseng, C.-M. Agency as a fourth aspect of students’ engagement during learning activities. Contemp. Educ. Psychol. 2011, 36, 257–267. [Google Scholar] [CrossRef]
- Jikkyo Shuppan. New Edition Mathematics B, 1st ed.; Jikkyo Shuppan: Tokyo, Japan, 2018. [Google Scholar]
- Suken Shuppan. Revised Edition Mathematics B, 1st ed.; Suken Shupan: Tokyo, Japan, 2017. [Google Scholar]
- Tokyo Shoseki. New Edition Mathematics B, 1st ed.; Tokyo Shoseki: Tokyo, Japan, 2014. [Google Scholar]
- Fornell, C.; Larcker, D.F. Evaluating structural equation models with unobservable variables and measurement error. J. Mark. Res. 1981, 18, 39–50. [Google Scholar] [CrossRef]
- Tsui, J.M.; Mazzocco, M.M. Effects of math anxiety and perfectionism on timed versus untimed math testing in mathematically gifted sixth graders. Roeper Rev. 2007, 29, 132–139. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Skinner, E.A.; Pitzer, J.R. Developmental dynamics of student engagement, coping, and everyday resilience. In Handbook of Research on Student Engagement, 1st ed.; Christenson, S.L., Reschly, A.L., Wylie, C., Eds.; Springer Science + Business Media: New York, NY, USA, 2012; pp. 21–44. [Google Scholar]
- Bandura, A. Self-Efficacy: The Exercise of Control, 1st ed.; Freeman: New York, NY, USA, 1997. [Google Scholar]
- Usher, E.L.; Pajares, F. Sources of self-efficacy in school: Critical review of the literature and future directions. Rev. Educ. Res. 2008, 78, 751–796. [Google Scholar] [CrossRef]
- Senko, C. Achievement goal theory: A story of early promises, eventual discords, and future possibilities. In Handbook of Motivation at School, 2nd ed.; Wentzel, K.R., Miele, D.B., Eds.; Routledge: New York, NY, USA, 2016; pp. 75–95. [Google Scholar]
| Variable | Sub-Scales | Number of Items | Example Item |
|---|---|---|---|
| Math anxiety | Math learning anxiety | 4 | When I take a math class, I am… |
| Math evaluation anxiety | 4 | When I think about tomorrow’s math, I am… | |
| Self-efficacy | 6 | I solve Q1 | |
| Problem-solving strategy | 4 | I would use formulae and theorems | |
| Level of learning engagement and instability | Behavioural engagement | 3 | I work as hard as I can on mathematics learning |
| Emotional engagement | 3 | I enjoy learning mathematics | |
| Cognitive engagement | 3 | I try to connect what I am learning with my knowledge | |
| Vector problem-solving performance | 6 | are perpendicular. | |
| Q1 | are perpendicular. |
| Q2 | Show that the diagonals of a rhombus are orthogonal using the concept of vector. |
| Q3 | In △ABC, if P, Q, and R are the midpoints of AB, BC, and CA, respectively, then show that the centres of gravity of △ABC and △PQR are congruent. |
| Q4 | is true for a point P inside △ABC, then show and illustrate where P is located. |
| Q5 | In △ABC, if point P divides the line segment OA in the ratio 2:5, point Q divides the line segment OB in the ratio 3:1, and point R is the intersection of line AQ and line BP, answer the following questions. . Q5.2: If point R is the intersection of the straight line OR and the side A, then answer AD: DB. |
| Variable | CFI | TLI | RMSEA | SRMR |
|---|---|---|---|---|
| 1. Self-efficacy | 0.96 | 0.93 | 0.11 | 0.04 |
| 2. Math anxiety | 0.95 | 0.92 | 0.12 | 0.05 |
| 3. Problem-solving strategy | 0.99 | 0.96 | 0.09 | 0.02 |
| 4. Learning engagement | 0.96–1.00 | 0.92–0.99 | 0.03–0.09 | 0.02–0.09 |
| 5. Vector problem-solving performance | 1.00 | 1.00 | 0.02 | 0.06 |
| Variable | ω | CR | AVE |
|---|---|---|---|
| 1. Math learning anxiety | 0.88 | 0.88 | 0.64 |
| 2. Math evaluation anxiety | 0.92 | 0.92 | 0.74 |
| 3. Self-efficacy | 0.92 | 0.89 | 0.66 |
| 4. Problem-solving strategy | 0.89 | 0.89 | 0.66 |
| 5. Behavioural engagement | 0.83–0.87 | 0.82–0.86 | 0.60–0.68 |
| 6. Emotional engagement | 0.88–0.93 | 0.88–0.93 | 0.72–0.81 |
| 7. Cognitive engagement | 0.69–0.87 | 0.69–0.87 | 0.42–0.69 |
| 8. Vector problem-solving performance | 0.77 | 0.77 | 0.38 |
| Variable | N | M | SD | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1. Behavioural engagement level | 240 | 5.12 | 0.65 | — | |||||||||
| 2. Behavioural engagement instability | 238 | 0.38 | 0.22 | −0.48 | — | ||||||||
| 3. Emotional engagement level | 240 | 4.30 | 0.92 | 0.59 | −0.31 | — | |||||||
| 4. Emotional engagement instability | 238 | 0.57 | 0.32 | −0.13 | 0.47 | −0.30 | — | ||||||
| 5. Cognitive engagement level | 240 | 4.86 | 0.68 | 0.77 | −0.37 | 0.70 | −0.23 | — | |||||
| 6. Cognitive engagement instability | 238 | 0.44 | 0.24 | −0.23 | 0.49 | −0.30 | 0.56 | −0.40 | — | ||||
| 7. Self-efficacy | 217 | 2.22 | 1.07 | 0.16 | −0.12 | 0.30 | −0.06 | 0.26 | −0.15 | — | |||
| 8. Math learning anxiety | 218 | 3.19 | 1.26 | −0.19 | 0.07 | −0.35 | 0.15 | −0.26 | 0.20 | −0.30 | — | ||
| 9. Math evaluation anxiety | 218 | 4.77 | 1.34 | −0.09 | 0.14 | −0.27 | 0.21 | −0.16 | 0.22 | −0.31 | 0.66 | — | |
| 10. Problem-solving strategy | 229 | 4.53 | 0.95 | 0.39 | −0.22 | 0.34 | −0.06 | 0.41 | −0.14 | 0.41 | −0.07 | −0.03 | — |
| 11. Vector problem-solving performance | 241 | 1.61 | 1.76 | 0.28 | −0.20 | 0.29 | −0.11 | 0.33 | −0.16 | 0.55 | −0.26 | −0.30 | 0.36 |
| Variable | Cluster 1 ( n = 110) | Cluster 2 ( n = 73) | Cluster 3 ( n = 51) | F | η2 | Multiple Comparison | |||
|---|---|---|---|---|---|---|---|---|---|
| M | SD | M | SD | M | SD | ||||
| 1. Behavioural engagement level | 5.15 | 0.43 | 5.66 | 0.31 | 4.30 | 0.54 | 154.89 * | 0.57 | 2 > 1 > 3 |
| 2. Behavioural engagement instability | 0.41 | 0.21 | 0.29 | 0.22 | 0.44 | 0.22 | 9.89 * | 0.08 | 1 = 3 > 2 |
| 3. Emotional engagement level | 4.12 | 0.50 | 5.29 | 0.42 | 3.26 | 0.75 | 221.24 * | 0.66 | 2 > 1 > 3 |
| 4. Emotional engagement instability | 0.65 | 0.33 | 0.45 | 0.26 | 0.58 | 0.34 | 9.15 * | 0.07 | 1 > 2 |
| 5. Cognitive engagement level | 4.86 | 0.36 | 5.50 | 0.34 | 3.94 | 0.48 | 251.87 * | 0.69 | 2 > 1 > 3 |
| 6. Cognitive engagement instability | 0.50 | 0.26 | 0.33 | 0.18 | 0.47 | 0.22 | 12.33 * | 0.10 | 1 = 3 > 2 |
| Variable | Medium and Unstable | High and Stable | Low and Unstable | F | η2 | Multiple Comparison | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | M | SD | n | M | SD | n | M | SD | ||||
| 1. Self-efficacy | 102 | 2.15 | 0.93 | 68 | 2.56 | 1.18 | 44 | 1.73 | 0.75 | 9.67 ** | 0.08 | 2 > 1 = 3 |
| 2. Math learning anxiety | 104 | 3.19 | 1.23 | 67 | 2.83 | 1.11 | 44 | 3.78 | 1.36 | 8.03 ** | 0.07 | 3 > 1 = 2 |
| 3. Math evaluation anxiety | 104 | 4.83 | 1.34 | 67 | 4.47 | 1.37 | 44 | 5.11 | 1.20 | 3.31 * | 0.03 | 3 > 2 |
| 4. Problem-solving strategy | 106 | 4.46 | 0.91 | 72 | 4.94 | 0.75 | 44 | 4.01 | 1.06 | 15.42 ** | 0.12 | 2 > 1 > 3 |
| 5. Vector problem-solving | 110 | 1.53 | 1.65 | 73 | 2.27 | 2.04 | 50 | 0.80 | 1.09 | 11.56 ** | 0.09 | 2 > 1 > 3 |
| Variable | Medium and Unstable | High and Stable | Low and Unstable | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | 1 | 2 | 3 | 4 | |
| 1. Self-efficacy | — | — | — | |||||||||
| 2. Math learning anxiety | −0.21 | — | −0.40 | — | −0.03 | — | ||||||
| 3. Math evaluation anxiety | −0.27 | 0.64 | — | −0.40 | 0.68 | — | 0.12 | 0.66 | — | |||
| 4. Problem-solving strategy | 0.29 | 0.14 | 0.07 | — | 0.40 | −0.15 | −0.07 | — | 0.33 | −0.05 | 0.03 | — |
| 5. Vector problem-solving performance | 0.43 | −0.23 | −0.31 | 0.32 | 0.66 | −0.17 | −0.17 | 0.32 | 0.23 | −0.23 | −0.32 | 0.17 |
| Model | AIC | BIC | χ2 | df | Δχ2 | CFI | TLI | RMSEA | SRMR |
|---|---|---|---|---|---|---|---|---|---|
| Model 1 | 2529.80 | 2691.40 | 4.29 | 6 | - | 1.00 | 1.00 | 0.00 | 0.02 |
| Model 2 | 2384.00 | 2514.50 | 14.29 | 14 | 10.00 | 1.00 | 1.00 | 0.02 | 0.05 |
| Model 3 | 2392.10 | 2496.50 | 38.34 | 22 | 24.06 * | 0.92 | 0.89 | 0.11 | 0.12 |
| Model 4 | 2398.20 | 2457.00 | 72.51 | 36 | 34.17 * | 0.83 | 0.86 | 0.13 | 0.17 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shimizu, Y. Learning Engagement as a Moderator between Self-Efficacy, Math Anxiety, Problem-Solving Strategy, and Vector Problem-Solving Performance. Psych 2022, 4, 816-832. https://doi.org/10.3390/psych4040060
Shimizu Y. Learning Engagement as a Moderator between Self-Efficacy, Math Anxiety, Problem-Solving Strategy, and Vector Problem-Solving Performance. Psych. 2022; 4(4):816-832. https://doi.org/10.3390/psych4040060
Chicago/Turabian StyleShimizu, Yuno. 2022. "Learning Engagement as a Moderator between Self-Efficacy, Math Anxiety, Problem-Solving Strategy, and Vector Problem-Solving Performance" Psych 4, no. 4: 816-832. https://doi.org/10.3390/psych4040060
APA StyleShimizu, Y. (2022). Learning Engagement as a Moderator between Self-Efficacy, Math Anxiety, Problem-Solving Strategy, and Vector Problem-Solving Performance. Psych, 4(4), 816-832. https://doi.org/10.3390/psych4040060






