Abstract
Industrial control systems (ICS) are increasingly vulnerable to evolving cyber threats due to the convergence of operational and information technologies. This research presents a robust cybersecurity framework that integrates machine learning-based anomaly detection with advanced cryptographic techniques to protect ICS communication networks. Using the ICS-Flow dataset, we evaluate several ensemble models, with XGBoost achieving 99.92% accuracy in binary classification and Decision Tree attaining 99.81% accuracy in multi-class classification. Additionally, we implement an LSTM autoencoder for temporal anomaly detection and employ the ADWIN technique for real-time drift detection. To ensure data security, we apply AES-CBC with HMAC and AES-GCM with RSA encryption, which demonstrates resilience against brute-force, tampering, and cryptanalytic attacks. Security assessments, including entropy analysis and adversarial evaluations (IND-CPA and IND-CCA), confirm the robustness of the encryption schemes against passive and active threats. A hardware implementation on a PYNQ Zynq board shows the feasibility of real-time deployment, with a runtime of 0.11 s. The results demonstrate that the proposed framework enhances ICS security by combining AI-driven anomaly detection with RSA-based cryptography, offering a viable solution for protecting ICS networks from emerging cyber threats.
1. Introduction
Industrial control systems (ICS) represent important key infrastructure, facilitating areas such as energy, water supply, and manufacturing [1]. The integration of operational and information technologies has enhanced efficiency while simultaneously raising cyber risks, such as DDoS and multi-stage attacks. These vulnerabilities pose significant threats to critical services, requiring enhanced security measures beyond standard defenses. While there have been significant advancements in artificial intelligence (AI) [2] and cryptography, there are still some issues. Machine learning algorithms detect anomalies but often fall short on integrating cryptography [3]. Deep learning enhances the detection of threats but has a problem with adaptive learning and security protocols, while offering limited hardware integration possibility on lightweight supports [4]. Cryptographic methods augment data security but infrequently use AI-based detection. Addressing these deficiencies demands a comprehensive approach that integrates an adaptive threat response, AI–cryptography collaboration, and cross-protocol security [5,6]. This research presents a complete innovative ICS security architecture that combines AI-driven anomaly detection with post-quantum cryptography methods utilizing this dataset. It uses ensemble models for attack classification, an autoencoder for anomaly detection, and adaptive algorithms for real-time threat response. Secure communication is offered through Advanced Encryption Standard-Cipher Block Chaining (AES-CBC) with Hash-based Message Authentication Code (HMAC) and Advanced Encryption Standard-Galois/Counter Mode (AES-GCM) with Rivest–Shamir–Adleman (RSA) encryption, verified to be robust. Hardware testing confirms real-time feasibility. The paper discusses relevant work, dataset information, methodologies, results, and future research directions.
2. Literature Review
ICS forms the technological base for crucial infrastructure sectors, including power generation, water treatment, and manufacturing. The integration of operational technology (OT) and information technology (IT) has made ICS networks more susceptible to advanced cyber threats. Researchers utilized numerous techniques, especially for machine learning-based anomaly detection, cryptographic frameworks, hybrid security mechanisms, and privacy-preserving computation. This literature review gathers data from 20 pertinent studies, conceptually categorizing them while defining their contributions and limits, especially related to cryptographic integration, adaptive threat management, and cross-protocol resilience. Traditional machine learning methods have proven essential in ICS anomaly identification. The authors in [7] investigated supervised models, including Random Forest and Support Vector Machine (SVM), on real-life ICS traffic and determined they were effective for detection, although without addressing encryption or cryptanalysis robustness. Similarly, the XGBoost classifier, a widely used technique applied to many different classification tasks [8], has been utilized on the Electra dataset [9], attaining outstanding precision while lacking cryptographic integration and intensive dataset validation expanded the topic by a comparative analysis of Supervisory Control and Data Acquisition (SCADA) testbeds, but lacked in adaptive learning capabilities and dataset variety. Recent studies have transitioned to deep learning and transfer learning methodologies. A residual Convolutional Neural Network (CNN) architecture with 1D-to-2D data transformation [10] is developed for anomaly detection and transfer learning, which lead to improved accuracy against unknown assaults. The effectiveness of CNN-based frameworks in achieving high accuracy and reduced computational complexity has also been demonstrated in the medical imaging domain [11]. Still, it did not include LSTM-based adaptive learning or cryptographic resilience. The authors in [12] presented a few-shot learning framework employing a large and deep neural network, demonstrating significant adaptability to domain shifts; however, it was deficient in secure communication protocols and cryptanalysis evaluation. Exploration has also been carried out with lightweight and rule-based detection models. The authors in [13] employed Logical Analysis of Data (LAD) for rule-based classification, offering explainability and minimum determining costs, although lacking support for adaptive threat evolution. The research in [14] concentrated on detecting stealthy attacks using Random Forest and Decision Tree models, even though it failed to incorporate encryption or secure communication protocols. Unsupervised and predictive methodologies have attracted attention for their adaptability in dynamic environments. CNN-LSTM autoencoders with adaptive thresholding are proposed in [15], enabling detailed anomaly scoring; however, they failed to enable multi-dataset training or encryption. A correlation-aware LSTM architecture using Pearson correlation [16] is proposed to monitor and predict multi-stage ICS assaults; nevertheless, this approach additionally displayed deficiencies in cryptographic integration and adversarial resilience.
To enhance contextual learning, the authors in [17] used process mining techniques to find workflow deviations using ICS event logs. It offered interpretability but was lacking in integration with encryption and adaptive detection. The ICS-Flow dataset, consist of flow records, labels, and attack scenarios, was contributed in [18] as a thorough benchmark. Although useful in model assessment, it lacks cryptographic safeguards and adversarial robustness tests. The issue of dataset dependency in CNN-based models has also been highlighted in digital image forensics, where comparative studies have shown that model performance varies significantly depending on the dataset used [19]. Several studies have tackled ICS security through symmetric, asymmetric, and hybrid encryption algorithms. Similarly, recent work on BESS-enabled smart grids highlights that storage systems integrated with IoT and cloud infrastructures face parallel cybersecurity and resilience challenges, requiring advanced encryption, anomaly detection, and power quality assurance measures [20]. A layered cryptographic framework spanning field devices, networks, and enterprise layers is proposed in [21]; however, it lacks formal cryptanalysis or validate it using actual datasets. The authors in [22] implemented AES and RSA in a SCADA testbed, providing practical insights; nevertheless, it was restricted to the DNP3 protocol without generalization across other protocols. The authors in [23] presented SelEnc, a selective encryption technique designed for improving real-time ICS performance by encrypting only critical payloads; however, it lacked anomaly detection and resilience validation features. The work in [24] advanced the domain by integrating AES with CP-ABE and blockchain logging, providing accurate access control and auditability. However, despite the diffusion of blockchain-based technologies [25], these are still lacking in AI-based threat detection and secure communication protocols. Efforts using ECC and identity-based frameworks provided lightweight alternatives. In [26], the researchers implemented ECC for mutual authentication, significantly diminishing key overhead; however, it was not verified with real-world ICS data. An AI-assisted encryption and authentication architecture utilizing secret sharing is proposed in [27], which offers dynamic key generation but fails to include cryptanalysis testing or adaptive detection. ChaCha20-Poly1305 is implemented in IEC61850 systems [28], offering low-latency alternatives to AES while neglecting secure key rotation and intrusion detection methods.
Homomorphic encryption has developed as a viable approach for safeguarding ICS computations. A modified RSA/ElGamal system is utilized for secure control signal processing [29], excluding the need for private key storage and resisting reverse engineering. Still, it failed to circumvent AI-driven detection or key rotation. In latency-sensitive environments, the authors in [30] established a recursive watermarking technique to ensure data integrity on fieldbus networks such as Profinet and CAN. It accomplished sub-millisecond determination of replay and injection attacks without any kind of encryption overhead. The solution limited itself to a specific use case (ship control systems) and did not involve significant dataset validation or encryption for long-term security. Strengthening cybersecurity in automated systems and ICS has been the subject of recent research. By emphasizing important weaknesses that frequently go unnoticed when cyber and physical systems are taken into consideration separately, the authors in [31] offer an optimization methodology to discover worst-case intrusions in ICS. In order to reduce dangers like illegal access and data breaches, the study tackles cybersecurity issues in robotics, with a strong emphasis on secure design, authentication, and cooperation [32]. A federated learning-based intrusion detection system for ICS [33] has been developed, which lowers communication and computing expenses while increasing accuracy. In a similar vein, the work in [34] offers a federated learning-driven cybersecurity framework for IoT, which strikes a balance between edge device processing, real-time threat detection, and privacy. A model predictive control approach for ICPSs based on digital twins is examined in [35], which successfully counteracts fake data injection assaults. While the work in [36] uses digital twin technology to improve cybersecurity in Cyber–Physical Production Systems (CPPSs), increasing asset visibility and mitigating vulnerabilities, the authors of [37] explore the application of digital twins in smart microgrids, emphasizing automation, security, and resilience. Although significant contributions were made, various limitations persist throughout the analyzed studies. A significant number of machine learning-based works (e.g., [7,13,14]) failed to include cryptographic techniques or secure communication protocols. Secondly, many studies (e.g., [9,38]) utilized static models without provisions for adaptive learning or concept drift detection. Third, cryptographic research (e.g., [22,24]) often neglected to perform resilience assessments against COA (Ciphertext-Only Attack), CCA (Chosen Ciphertext Attack), or side-channel attacks. The overview of the proposed work is shown in Figure 1 and it addresses all the drawbacks and the highlights, and the major contributions of the paper are as follows:
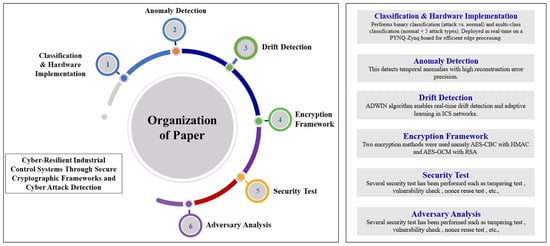
Figure 1.
Overall structure and flow of the paper, highlighting each major module from classification to adversary analysis.
- The study employs machine learning models, including XGBoost and Random Forest, for binary intrusion detection in ICS networks using the ICS-Flow dataset. XGBoost achieved a peak accuracy of 99.92%, effectively distinguishing between normal and malicious traffic with high precision and minimal error.
- For multi-class attack detection, models like Decision Tree and Artificial Neural Network (ANN) were used, with Decision Tree achieving the highest accuracy of 99.81%. The model was deployed on a PYNQ-Zynq board, confirming its real-time feasibility with an inference time of just 0.11 s, suitable for edge-based ICS applications.
- ADWIN was used for real-time drift detection, allowing the model to adapt to changes in ICS network traffic and effectively handle emerging threats.
- An LSTM-based autoencoder detected temporal anomalies by using reconstruction error, successfully identifying 23 anomalies from 500 cases based on time-series patterns.
- A dual encryption approach was implemented—AES-CBC with HMAC for integrity, and AES-GCM combined with RSA for secure key exchange and built-in authentication. This framework ensures both data confidentiality and secure communication in ICS environments.
- The encryption methods were rigorously tested through entropy analysis, brute-force complexity, tampering checks, and vulnerability scoring. Results confirmed high randomness, data integrity, and resistance to brute-force and collision attacks, ensuring robust cryptographic strength.
- Formal adversarial evaluations confirmed AES-CBC as IND-CPA-secure but vulnerable to IND-CCA attacks. In contrast, AES-GCM with RSA satisfied both IND-CPA and IND-CCA security guarantees, demonstrating strong resilience against advanced cryptographic attacks.
3. Dataset Description
The ICS-Flow dataset [18] is purposely designed for machine learning-based intrusion detection in ICS network. It contains network traffic logs, process state variables, attack logs, and labeled network flows for binary intrusion detection and multi-class attack classification. The dataset consists of multiple components that include raw network captures, labeled network flows, process state logs, and attack logs. This dataset consists of 45,718 entries, with 64 features representing network traffic data for ICS. This dataset includes key attributes in Table 1 such as source and destination addresses, MAC addresses, IPs, protocol types, timestamps, and various network flow rates. It also contains statistical metrics like packet counts, byte sums, payload sizes, and TCP-related features such as sequence numbers, window sizes, and acknowledgment delays.

Table 1.
Feature categories and descriptions.
These attributes provide insights into network behavior, aiding intrusion detection and security analysis. The dataset consists of multiple components that include raw network captures, labeled network flows, process state logs, and attack logs shown in Table 2.

Table 2.
Dataset components and their descriptions.
The dataset is labeled with binary and multi-class attack classifications based on two strategies: Injection Timing (IT) and Network Security Tools (NST). Classes and their impacts are given in Table 3 and the distribution is given in Figure 2. IT_B_Label and NST_B_Label features classify traffic as usual or attack, while the IT_M_Label and NST_M_Label specify attack types such as port-scan, DDoS, Man-in-the-Middle, and replay attacks. This labeled structure supports the development of machine learning models for anomaly detection and cyber threat monitoring in ICS environments. This moderate imbalance could potentially influence model performance, particularly precision and recall metrics. While the imbalance was not explicitly corrected through resampling methods such as SMOTE or undersampling, we addressed it by monitoring classification performance using precision, recall, and F1-score. These metrics provided a more balanced evaluation across all classes. We acknowledge that integrating balancing techniques in future work may further improve robustness.

Table 3.
Class descriptions and impacts.
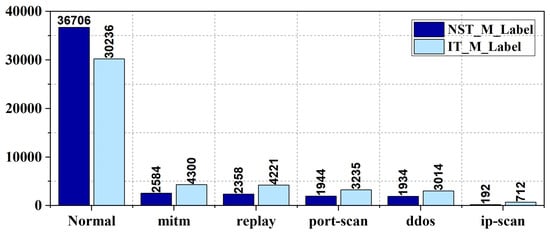
Figure 2.
Class-wise data distribution comparison between IT and NST datasets.
4. Proposed Methodologies
The proposed methodologies form a robust cybersecurity framework for industrial control systems, combining advanced machine learning techniques for anomaly detection with secure cryptographic protocols to protect network communications. Using this dataset, the approach includes ensemble learning models for classifying network traffic, a sequence-based autoencoder for detecting temporal anomalies, and adaptive algorithms for real-time drift detection. Additionally, two encryption strategies namely AES-CBC with HMAC for integrity and confidentiality, and a hybrid AES-GCM with RSA for secure key exchange and authentication were implemented to ensure data security. These methods collectively enable accurate threat identification and resilient communication, validated through hardware deployment for real-time feasibility. The proposed framework ensures architectural cohesion by tightly integrating anomaly detection with cryptographic protection. Detected threats from the machine learning models are not only identified but also securely managed through immediate encryption and key exchange protocols. This design ensures that detection and protection mechanisms operate in a continuous, unified pipeline, providing a comprehensive security approach for ICS networks. While the obtained accuracies exceed 99%, we acknowledge the potential risk of overfitting, especially in closed datasets like ICS-Flow. This concern aligns with the literature, where similarly high accuracies have been reported under controlled conditions. The dataset includes attack types such as port scanning, IP scanning, replay, DDoS, and MITM, reflecting real-world ICS threats. While this work does not explicitly adopt a formal threat modeling framework such as STRIDE or MITRE ATT&CK for ICS, the model is designed to detect and mitigate adversarial behaviors aligned with these categories. The classification models address network-based reconnaissance and flooding attempts (e.g., scan and DDoS), while the temporal autoencoder is capable of identifying anomalies such as replay and injection attacks. Future work may formalize this alignment using structured threat modeling frameworks to further contextualize the defensive scope.
4.1. XGBoost for Binary Classification
XGBoost is a stable ensemble learning method designed for improving predictive accuracy using sequential tree boosting [39]. The model gradually improves predictions via lowering the following objective function as specified in Equation (1):
represents the actual value or target label for the ith data point. denotes the input feature vector corresponding to the ith data point. is the predicted value for the ith data point, which is generated by the model. refers to the model function at the tth iteration of boosting, which updates the prediction, represents the loss function (log-loss for classification), and by Equation (2), is the regularization term controlling model complexity:
where T indicates the total number of tree leaves, represents regularization parameter, and denotes the weight provided to each leaf. The architecture of the XGBoost classifier showing the ensemble of Decision Tree is shown in Figure 3.
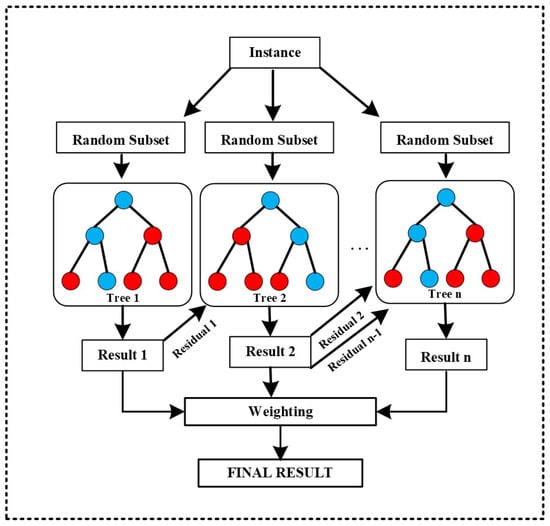
Figure 3.
Architecture of the XGBoost classifier showing the ensemble of Decision Trees, (blue circles as decision nodes and red circles as leaf nodes).
XGBoost increases the objective function by a second-order Taylor expansion as provided in Equation (3):
where and denote the first and second derivatives of the loss function. This enables effective tree formation while minimizing computing complexity.
An early stop mechanism is used to avoid overfitting. The validation loss is measured using Equation (4), and training ends if no improvement appears over a certain amount of cycles:
where represents the number of validation samples.
The trained model has been evaluated using accuracy, precision, recall, and F1-score. The confusion matrix additionally provides insights on classification performance, calculated by Equation (5):
where , , , and denote true positives, true negatives, false positives, and false negatives, respectively. The model’s performance is additionally evaluated by classification reports and visualization techniques, notably heatmaps.
4.2. Decision Tree for Multi-Classification
A Decision Tree (DT) is a hierarchical model used for classification and regression [40,41]. It divides data according to feature values to generate decision nodes, which produce final predictions at the leaf nodes. The splitting criterion is determined by measures such as Gini impurity and entropy.
The Gini impurity measures the impurity of a node, as determined by Equation (6):
where represents the probability of class i in a given node, and c represents the threshold constant.
Entropy is an additional impurity metric utilized in information gain computations, defined as per Equation (7):
A split is used to enhance the information gain (IG), which measures the decrease in entropy according to Equation (8):
Let S be the original dataset, represent the subsets obtained from the splitting, and represent the proportion of instances in each subset, represents the entropy of set .
The model uses recursive partitioning, and for a classification problem, the ultimate class prediction at a leaf node is determined as , where is the predicted class and is the proportion of samples belonging to class i in that node. The structure of a Decision Tree classifier with root, decision, and leaf nodes is shown in Figure 4. Pruning methods, especially cost-complexity pruning, maximize tree depth and accuracy by minimizing as shown in Equation (9):
Here, denotes the sample count in node t, denotes its impurity, and is a regularization parameter that determines tree complexity.
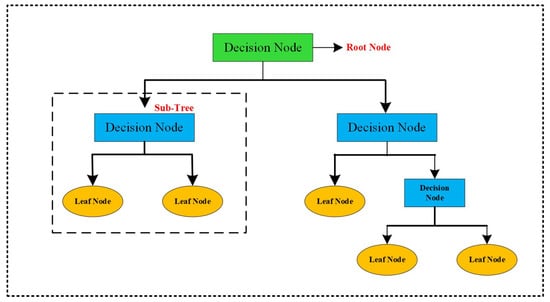
Figure 4.
Structure of a Decision Tree classifier with root, decision, and leaf nodes.
4.3. Sequence-Based Learning for Temporal Anomaly Detection
An LSTM-based autoencoder [42] encodes sequential data into a latent representation and simultaneously reconstructs the original sequence. The architecture of the LSTM-based autoencoder includes an encoder and a decoder. The encoder uses LSTM cells to store temporal dependencies, with its final hidden state functioning as the latent vector . At each timestep t, an LSTM cell performs the computation using Equation (10):
where represents the weight matrix associated with the feature transformation function. represents the weight matrix associated with the classification function. The ∘ (circle) operator denotes the element-wise multiplication (Hadamard product) between two matrices or vectors and LSTM autoencoder architecture for anomaly detection using reconstruction error thresholding is shown in Figure 5.
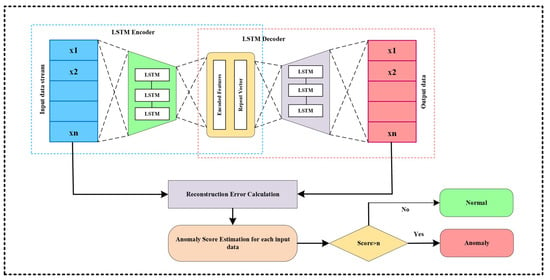
Figure 5.
LSTM autoencoder architecture for anomaly detection using reconstruction error thresholding.
The decoder reconstructs the sequence by initially duplicating the latent vector (often using a RepeatVector layer) and thereafter inputting it into other LSTM layers, culminating in a TimeDistributed dense layer to generate the output sequence . The model is trained by minimizing the reconstruction error, often measured by the Mean Squared Error (MSE) as shown in Equation (11):
In anomaly detection, after training on normal data, sequences demonstrating a reconstruction error exceeding a predefined threshold are classified as anomalies.
4.4. Adaptive and Incremental Learning for Drift Detection
ADWIN (Adaptive Windowing) is an algorithm for drift detection [43] that aims to recognize alterations in the statistical characteristics of a data stream in real time. It maintains a variable-sized window of recent data points and perpetually observes the mean of the values within this window. Upon detecting a substantial alteration in the mean, ADWIN reduces the window by excluding older data, thereby adjusting to the new distribution.
Let the current window W be divided into two adjacent subwindows and with sizes and and empirical means and , respectively. ADWIN employs a statistical test grounded in Hoeffding’s inequality to ascertain whether the disparity between these two means is statistically significant. The threshold for this test is determined by Equation (12):
In this context, serves as a confidence parameter that regulates the detection’s sensitivity. If the absolute difference between the means meets the condition , the algorithm determines that a change (or drift) has transpired. The older segment of the window is removed, and the window is changed to include only data from the new distribution. ADWIN can quickly adapt to unexpected shifts by dynamically changing the window size while maintaining robustness against noise in the data stream. This flexibility makes it an invaluable instrument for real-time drift detection across various applications.
The LSTM-based autoencoder and ADWIN drift detection module are designed to complement the core classification models rather than operate in isolation. In the proposed framework, the classification models (XGBoost for binary classification and Decision Tree for multi-class) serve as the primary detection mechanisms for known threats. The LSTM autoencoder operates in parallel, analyzing temporal patterns to detect unseen or evolving anomalies based on reconstruction error. ADWIN monitors data streams for concept drift and can dynamically signal model retraining or flag inconsistent patterns, ensuring that the classifiers remain robust over time. While these components are functionally decoupled, they interact logically in the pipeline classifiers handle known patterns, the autoencoder handles temporal novelty, and ADWIN ensures continuous adaptation. This layered design ensures robustness against both static and dynamic threat profiles.
4.5. Encryption Methodology
Encryption transforms data into a secure format to prevent unauthorized access [44]. The ICS-Flow dataset utilizes encryption to safeguard the security and integrity of industrial control system (ICS) network traffic, shielding it from cyberattacks and unauthorized tampering. This research includes two encryption approaches: AES-CBC with HMAC and a hybrid AES-GCM with RSA.
4.5.1. AES-CBC Encryption with HMAC
AES-CBC encryption [45] with HMAC integrates two cryptographic components—AES for confidentiality and HMAC for integrity—into a resilient framework that ensures data confidentiality and tamper evidence. The encryption flow diagram is shown in Figure 6 and the corresponding pseudocode is given in Algorithm 1.
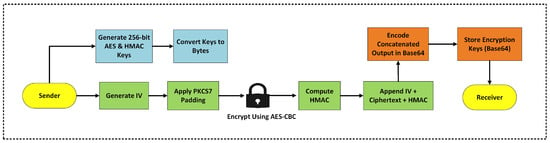
Figure 6.
Step-by-step encryption workflow using AES-CBC with HMAC for secure data transmission.
Encryption in CBC Mode: AES is a symmetric block cipher that operates on fixed-size data blocks, typically 128 bits in length. If a plaintext P is not a multiple of the block size, a padding method like PKCS7 is implemented. When the block size is b bytes and the plaintext length ℓ is not divisible by b, the padded plaintext is constructed as shown in Equation (13):
AES in Cipher Block Chaining (CBC) mode utilizes an Initialization Vector (IV) and encrypts each block by integrating it with the preceding ciphertext block. Let represent the i-th segment of the padded plaintext, assign a random vector of size b, and indicate the AES encryption function utilizing key K. The encryption procedure is delineated by Equations (14) and (15):
where ⊕ indicates bitwise XOR. The decryption procedure replicates these steps with the AES decryption function as shown in Equations (16) and (17):
HMAC for Ensuring Data Integrity: An HMAC (Hash-based Message Authentication Code) is generated to protect the ciphertext against undetected modifications. HMAC employs a cryptographic hash function (e.g., SHA-256) combined with a secret key . For a message m (namely, the concatenation of the IV and ciphertext), HMAC is shown in Equation (18):
In this context, H denotes the hash function, for instance, SHA-256 and ⊕ symbol denotes the bitwise XOR (exclusive OR) operation. The key is generated from the original key by padding it according to the block size B. If the length of K is less than B, it is padded with zeros to achieve the necessary size, in accordance with Equation (19):
If the key K exceeds B in length, it is initially hashed using H and subsequently padded as necessary. Additionally, opad (outer padding) and ipad (inner padding) are fixed byte sequences utilized in the HMAC calculation. Typically, opad comprises the byte 0x5c repeated B times, whereas ipad consists of the byte 0x36 reiterated B times. The symbol ‖ denotes concatenation, indicating that values are sequentially processed as part of the hashing process.
The HMAC is calculated across the message , where C is the entire ciphertext formed from all blocks according to Equation (20):
Combined Encryption with Integrity: The final output combines the IV, ciphertext, and HMAC. The complete encrypted message M is expressed in Equation (21):
To enable storage or transmission, M is commonly encoded using Base64 or an alternate binary-to-text encoding method.
The main differences from existing methods include the use of a random Initialization Vector (IV) for added security, PKCS7 padding for variable message lengths, and block chaining (similar to CBC mode) for enhanced security. Additionally, a HMAC tag is computed for integrity verification, ensuring the authenticity of the encrypted message. The final message concatenates the IV, ciphertext, and HMAC tag, and is optionally encoded for safe transmission, ensuring both confidentiality and integrity.
| Algorithm 1 Modified AES_Encrypt_HMAC |
|
4.5.2. AES-GCM Encryption
AES-GCM (Galois/Counter Mode) is an authenticated encryption technique that ensures confidentiality and integrity. In AES-GCM [46], the plaintext P is encrypted using counter mode, while an authentication tag is generated by Galois field multiplication-based hashing. This dual mechanism provides encryption alongside validation that the data remain unaltered. The encryption flow diagram is shown in Figure 7 and the corresponding pseudocode is given in Algorithm 2.
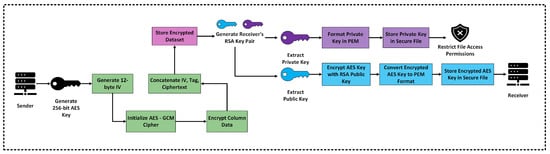
Figure 7.
Hybrid encryption workflow using AES-GCM and RSA key pair for secure dataset protection.
Counter Mode Encryption: AES operating in counter mode converts the block cipher into a stream cipher. With a symmetric key K (e.g., 256 bits) and a randomly generated Initialization Vector (IV) of 12 bytes (96 bits), the encryption procedure produces a sequence of counter blocks . The initial counter block can be expressed as in Equation (22):
where ‖ indicates concatenation and represents a predetermined initial counter (often assigned a value of 1). For each plaintext block (where ), the counter is incremented according to Equation (23):
The ciphertext block is calculated using Equation (24):
where ⊕ denotes the bitwise XOR operation, and denotes the AES encryption of the counter using key K.
Authentication Tag Calculation: AES-GCM ensures integrity by calculating an authentication tag T for both the related data (if present) and the ciphertext. A hash subkey H is initially produced by encrypting a zero block, as demonstrated in Equation (25):
A GHASH function is subsequently applied to the data, yielding an intermediate value , where A represents the related data (which may be empty) and denotes the concatenated ciphertext. The authentication tag is computed as defined in Equation (26):
The final encrypted message produced by AES-GCM is: .
| Algorithm 2 Modified AES-GCM with RSA |
|
RSA Encryption for Key Exchange: RSA is an asymmetric cryptographic system that enables secure key exchange. This approach uses RSA to encrypt the AES symmetric key, ensuring that only the designated recipient can decrypt it using their private key.
RSA Key Generation: RSA key generation includes the selection of two substantial prime numbers p and q. The modulus n is determined by . Euler’s quotient function is calculated by Equation (27):
A public exponent e (often e = 65,537) is selected such that . The private exponent d is calculated to fulfill the condition . The public key comprises , while the private key is denoted as d.
RSA Key Encryption: RSA encryption is utilized to securely transport the AES key K. If K is treated as an integer inside the interval , RSA encryption utilizing OAEP padding is calculated according to Equation (28):
The ciphertext c (with appropriate padding) is transmitted to the receiver, who employs their private key d to recover K by utilizing Equation (29):
where the operator represents the remainder.
Combined Hybrid Encryption Approach: The hybrid encryption approach involves the sender encrypting the dataset with AES-GCM and securing the symmetric key with RSA. The procedure is outlined as follows:
- Data Encryption: The sender encrypts the plaintext data using AES-GCM. The format of the encrypted output is , where C is generated by counter mode encryption, denotes the Initialization Vector, and T represents the authentication tag that ensures data integrity.
- Key Encryption: The AES symmetric key K is encrypted with the receiver’s RSA public key, resulting in utilizing OAEP padding for enhanced security.
- Transmission: The encrypted dataset and the RSA-encrypted symmetric key are sent to the recipient.
- Decryption: The recipient initially employs their RSA private key to decode and obtain the symmetric key K using the equation . Subsequently, using K, the receiver decrypts by reversing the AES-GCM procedure, validating the tag T, and retrieving the original dataset.
This mathematically rigorous hybrid technique utilizes the speed and efficiency of AES-GCM for encrypting substantial data volumes and the secure key distribution attributes of RSA. The resultant system offers robust assurances for both confidentiality and integrity, ensuring that the data remains secure and unaltered during storage and transmission.
In practical terms, the hybrid encryption scheme uses RSA solely for encrypting the symmetric AES key, while AES-GCM handles the bulk of the dataset encryption. This design minimizes computational overhead since asymmetric encryption is not applied to large volumes of data. AES-GCM was chosen for its efficiency, built-in authentication, and high throughput. The use of RSA addresses the secure key distribution challenge in untrusted or distributed environments, especially where pre-shared keys are not feasible. Therefore, the hybrid approach ensures both secure communication and efficient performance. While precise runtime or throughput measurements were not included, our empirical testing confirmed that encryption introduced no noticeable degradation in system responsiveness. Future work may include detailed benchmarking of cryptographic overhead. The proposed AES-GCM with RSA approach presents key improvements over traditional encryption methods. First, we encrypt the AES key employing RSA-OAEP for secure key exchange, proposing stronger security compared to traditional symmetric key techniques. The integration of RSA for key exchange and AES-GCM for encryption, along with the employment of AES-CTR mode for block encryption and GHASH for authentication, provides both confidentiality and data integrity. Moreover, we generate a random 96-bit IV for each data block, decreasing vulnerabilities associated with IV reuse. These improvements enhance security, key management, and data integrity.
5. Experimental Setup, Results and Discussion
This section focuses the efficient use of machine learning models in identifying anomalies and classifying network traffic within ICS communication, as well as in temporal anomaly detection. Several encryption techniques, such as AES-CBC and hybrid AES-GCM with RSA, were tested for security through testing key length, tampering resistance, and vulnerability assessments and adversary indistinguishability analysis were also performed. The studies are conducted on a GPU workstation equipped with an Intel Core i9 processor, Intel Corporation, Santa Clara, CA, USA, (3.6 GHz), 32 GB of RAM, and an NVIDIA GeForce RTX 4060 GPU setup (NVIDIA Corporation, Santa Clara, CA, USA).
In the tests executed for both binary and multi-class classification, we evaluated multiple data splits to assess the performance of different models under diverse training and testing conditions. The data was divided into four configurations: 80/20, 70/30, 70/20/10, and 80/15/5, where the first number specifies the ratio of training data, and the second and third numbers specify the testing and validation divisions, respectively. Using these divisions, we have assessed how each model performs with variable quantities of training data and its capability to generalize across diverse datasets. The experiments were conducted utilizing four popular machine learning models, namely XGBoost, Random Forest, Extra Trees, and Decision Tree, to assess their effectiveness in both binary classification (differentiating between normal and attack traffic) and multi-class classification (determining diverse types of attacks). The machine learning models—XGBoost, Random Forest, Extra Trees, and Decision Tree—were chosen for this analysis due to their distinctive advantages in classification tasks. XGBoost was selected for its outstanding performance in catching complex patterns through gradient boosting, delivering high accuracy and efficiency. Random Forest and Extra Trees were used for their robust ensemble techniques that decrease overfitting and improve generalization, making them well-suited for handling noisy data. Decision Tree was chosen for its simplicity, interpretability, and computational efficiency, delivering clear decision-making paths while preserving strong performance on simpler datasets. These models were selected to provide a comprehensive comparison of ensemble methods and single-model methods, ensuring a well-rounded evaluation of classification performance. The results for both studies were comprehensively analyzed, concentrating on key performance parameters such as accuracy, precision, recall, and F1-score, yielding insights into the strengths and limitations of each model under diverse data configurations.
5.1. Binary Classification
Binary classification is a supervised learning method used to classify data into two distinct classes, such as attack or normal. The performance of various algorithms is shown in Table 4, where various metrics are provided for each model across different dataset splits. The confusion matrices obtained for various models for binary-class classification are shown in Figure 8. In the binary classification task, XGBoost consistently delivers exceptional performance across all dataset splits, achieving near-perfect results with accuracy, precision, recall, and F1-score all reaching approximately 0.9999. This outstanding performance can be attributed to XGBoost’s ensemble approach, which uses multiple Decision Trees connected in a boosting framework. By iteratively correcting errors and capturing complex relationships in the data, XGBoost reduces overfitting and improves predictive performance. Its gradient boosting technique optimizes forecasts by focusing on misclassified instances, enabling it to effectively handle complex patterns, making it highly reliable for tasks that require both high accuracy and fast inference, such as anomaly detection or intrusion detection. The model’s ability to generalize well across varying data distributions further contributes to its superior performance. Similarly, Random Forest and Extra Trees also exhibit strong performance, with accuracy values close to 0.9999 across all splits. These models leverage the power of ensemble learning by combining multiple Decision Trees, which enhances robustness and reduces overfitting, particularly in noisy data environments. However, they slightly lag behind XGBoost due to their reliance on averaging or voting techniques, which may not capture complex feature interactions as effectively as XGBoost’s boosting method. In addition, their inference times are slightly higher than XGBoost, which may be a consideration in real-time applications. On the other hand, Decision Tree performs well but shows slightly lower performance in certain splits, particularly in the 80/20 and 70/20/10 splits, where its accuracy drops to around 0.9994. Despite achieving impressive results, a single Decision Tree can struggle with capturing complex patterns in the data compared to ensemble methods. This makes it less effective for tasks requiring high generalization, especially when the data is more intricate or noisy. While Decision Trees offer computational efficiency and simplicity, their performance is outpaced by ensemble methods like XGBoost and Random Forest, which are better suited for handling complex classification tasks.

Table 4.
Performance metrics in (%) obtained for binary class classification using various ML models.
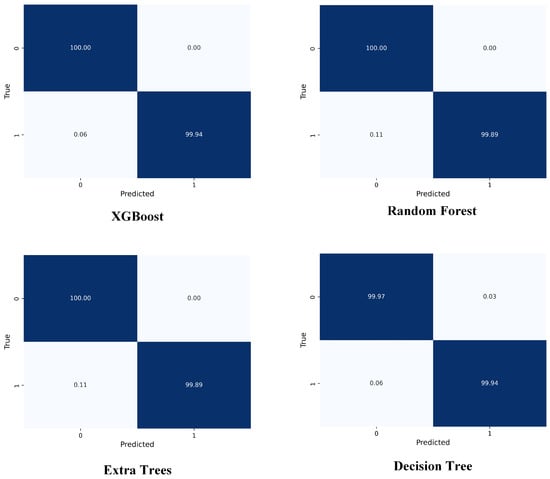
Figure 8.
Confusion matrices obtained for various models for binary classification.
5.2. Multi-Class Classification
Multi-class classification is a supervised learning method used for classifying data into more than one category. The performance of different models is shown in Table 5 and their confusion matrices in Figure 9. In the multi-class classification task, XGBoost continues to deliver exceptional performance across all dataset splits, achieving near-perfect results with accuracy, precision, recall, and F1-score. Its ability to capture complex interactions between multiple classes allows it to generalize effectively across diverse data distributions, making it a reliable choice for applications that demand high classification accuracy and robustness. The ensemble approach of XGBoost, which integrates multiple Decision Trees and refines predictions iteratively, improves its ability to handle complex, multi-class tasks effectively. Random Forest and Extra Trees also demonstrate outstanding performance, with accuracy values above 0.9999 across all splits. Both models benefit from ensemble learning techniques that reduce overfitting and enhance generalization. Random Forest uses bootstrapping to deliver tree diversity, while Extra Trees enhances robustness by considering more random splits, making them well-suited for noisy data. While these models do not quite outperform XGBoost in overall performance, they still yield excellent results and remain reliable for multi-class classification tasks, especially when interpretability is a priority. Decision Tree, while simpler than the ensemble models, performs remarkably well, achieving near-perfect accuracy and F1-scores (around 0.9996 to 0.9999) across different dataset splits. This makes it competitive with the ensemble models, as it strikes a balance between computational efficiency and performance. Its performance in multi-class classification is on par with Random Forest and Extra Trees, demonstrating that Decision Trees are capable of handling complex patterns while maintaining high generalization. It remains a practical choice for situations where simplicity, interpretability, and efficiency are valued, particularly when dealing with less complex datasets.

Table 5.
Performance metrics in (%) obtained for multi-class classification using various ML models.
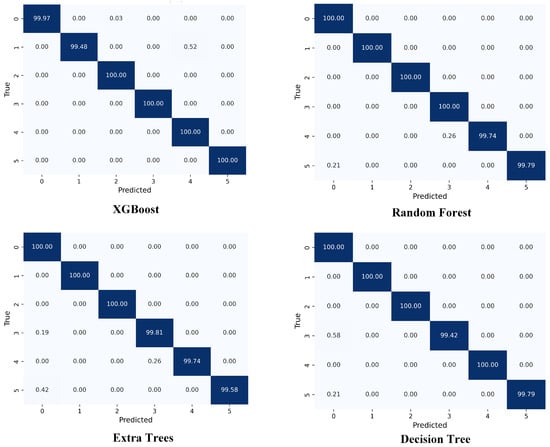
Figure 9.
Confusion matrices obtained for various models for multi-class classification.
5.3. Hardware Validation of Decision Tree for Multi-Class Classification
To determine the feasibility of implementing our proposed model in real-world contexts, we conducted an experimental assessment by deploying the Decision Tree model on PYNQ, utilizing the Xilinx Zynq board, an edge computing device, as seen in Figure 10. The model’s performance was evaluated based on its execution time for the specified purpose. The training time took 1.03 s and testing took 0.11 s. The hardware configuration and results showed that the Decision Tree model could actually run well on the edge device, indicating its applicability for real-time use in smart meter environments. In future work, we plan to enhance our system’s performance through the creation of a dedicated machine learning model structure for FPGA-based acceleration. This approach will leverage hardware-specific optimizations, specifically parallelism, pipelining, and low-latency computation, to achieve faster inference speeds and improved energy efficiency. Through adaptation of the model structure to accommodate FPGA limitations, we anticipate enhanced efficiency, thus supporting deployment for extensive real-time ICS uses.

Figure 10.
Real-time hardware deployment of the Decision Tree model on PYNQ Zynq board for multi-class classification in ICS networks.
5.4. Sequential Data Learning Through LSTM Autoencoder
An LSTM-based autoencoder that obtained the time-series data of normal packets and correctly identified abnormal packets. The reconstruction error peaks shown in Figure 11 illustrate the model’s capability to recognize temporal anomalies. Normal sequences were classified according to reconstruction error that dropped below the threshold value. A major differentiation occurred between anomalous sequences and normal sequences, as the reconstruction error for anomalous sequences was significantly high. The analysis of reconstruction error utilizes latent representation and threshold-based anomaly classification, defining the top 5% as anomalies. By this approach, 23 anomalies were detected among 500 cases.
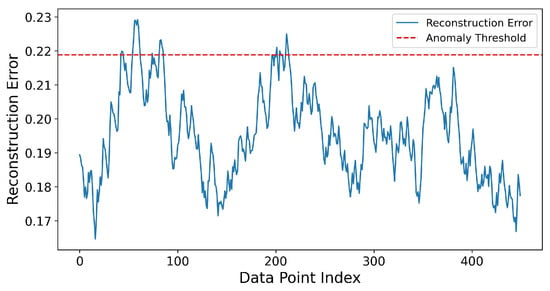
Figure 11.
Reconstruction error plot showing anomaly detection using LSTM autoencoder.
5.5. Drift Detection Using ADWIN
In this study, Adaptive Windowing (ADWIN) was used for real-time drift detection to handle the dynamic nature of data deviations and evolving patterns. ADWIN is a sliding window algorithm that acclimates to transitions in the underlying data distribution. It dynamically alters its window size to lower the impact of recent concept drifts, which is essential for continuous learning in environments where data distributions may change over time. The results of the drift detection are shown in Figure 12, where the red dots indicate the points where drift was detected in the sPackets data stream. These drift points describe moments when there was a substantial change in the distribution of data, signaling a potential shift in the underlying behavior of the network. The model successfully determined these distribution changes, demonstrating its capability to detect concept drift in real-time. By using ADWIN, the system adapts to these changes, allowing it to learn from new data and respond to emerging threats continuously. This adaptive learning mechanism guarantees that the model can handle divergences in the data stream, making it appropriate for long-term deployment in real-world systems such as intrusion detection networks or anomaly detection systems. The hyperparameters used for each model in the study are given in Table 6.
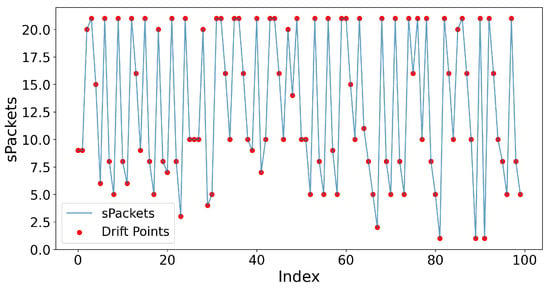
Figure 12.
Real-time drift detection in sPackets using ADWIN, with drift points marked in red.

Table 6.
Hyperparameters used for each model in the study.
5.6. Encryption and Security Test
The current research develops and verifies two encryption methods: AES-CBC and hybrid AES-GCM with RSA encryption, using multiple security evaluation methods.
5.6.1. AES-CBC
The AES encryption technique proved effective in safeguarding and accurately restoring the dataset, thereby ensuring data confidentiality. Specifically, the AES CBC mode—a commonly adopted symmetric encryption algorithm—was utilized to encrypt the data securely. To maintain data integrity, a HMAC was generated and associated with the encrypted content. Upon decryption, the HMAC was successfully verified, confirming that the data had not been tampered with during storage or transmission. This method offers robust security, but it is required for the safe exchange of symmetric encryption keys between the sender and the recipient. This crucial exchange can be especially important in this environment where trust cannot be taken for granted. Furthermore, because AES-CBC lacks built-in authentication, including a standalone integrity-checking mechanism like HMAC is needed. Despite these challenges, this encryption method remains highly effective in scenarios where both the sender and receiver must securely share the key and where separate integrity verification is acceptable. The mean comparison shown in Figure 13 highlights a major difference between the original and encrypted data. This reflects the expected transformation caused by the encryption process, which varies depending on the type of data. As depicted in Figure 14, the comparison between the original and decrypted data shows a 100% match rate across all columns, demonstrating that the decryption process was entirely accurate. Furthermore, Figure 15 compares the string lengths of the original, encrypted, and decrypted data, reinforcing the effectiveness of the approach. These results confirm that the encryption and decryption processes faithfully preserve the original data without any loss or corruption across all examined fields.
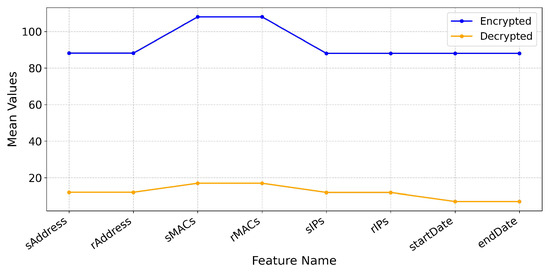
Figure 13.
Mean values of original and encrypted data for AES-CBC across different columns.
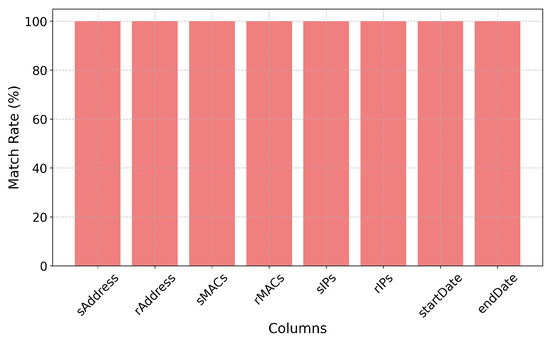
Figure 14.
Match percentage between original and decrypted values using AES-CBC and AES-GCM with RSA.
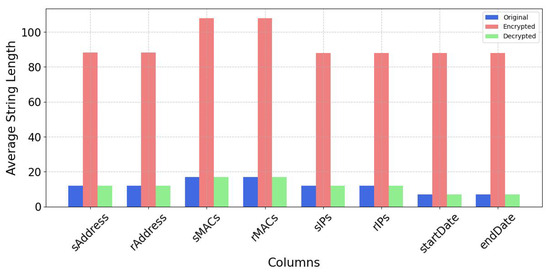
Figure 15.
Average string length comparison before encryption, after AES-CBC encryption, and after decryption.
5.6.2. Security Test for AES Encryption
This section deals with various security tests performed to validate the AES encryption.
Key Length and Entropy Analysis
The AES-CBC method of encryption uses a symmetric key K with a length of bits. The key space size is denoted by , suggesting that there are potential keys. A brute-force attack requires that an adversary attempts all keys, and with current machines (about operations per second), the estimated time complexity is denoted by Equation (30).
which is computationally infeasible. To further validate the randomness of the key generation, we analyze its Shannon entropy. The entropy of a perfectly random n-bit key using Equation (31)
where for a uniform key distribution, , leading to 256 bits. Additionally, the Figure 16 shows the entropy of the encrypted data with all the features with value of 15.16 bits. This confirms that the key selection process maintains maximal unpredictability, ensuring strong cryptographic security.
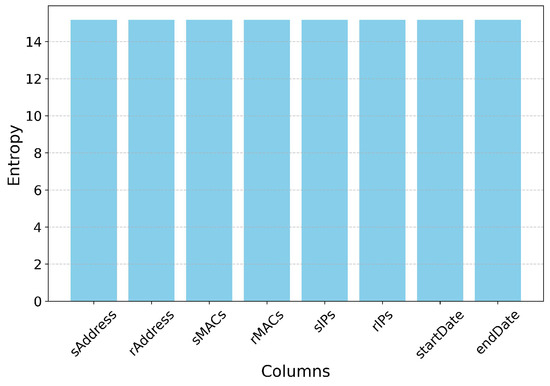
Figure 16.
Entropy of encrypted values across columns using AES-CBC and AES-GCM with RSA.
Tampering Test
The AES-CBC encryption method is used alongside with an HMAC-SHA256 function to ensure data integrity. For an arbitrary message M of length , the HMAC is computed in Equation (32):
where is a cryptographic hash function (SHA-256 in this case), (64 bytes), and (64 bytes). The probability of an adversary forging a valid HMAC without knowledge of K is upper-bounded by which is practically negligible. During decryption, the received HMAC is compared to the computed HMAC using Equation (33)
and decryption is only permitted if . If the HMAC verification fail, decryption stops, thus preventing any changed ciphertext from being decrypted.
Vulnerability Testing
The uniqueness of the Initialization Vector (IV) is an essential component of AES-CBC security. Initializing vectors (IVs) are randomly chosen from a set of possible values. The probability of IV collisions after q encryptions conforms to the Birthday Paradox, is expressed in Equation (34):
which is insignificant yet nonzero. To assess encryption security, a vulnerability function V is calculated using the equation
where denotes the entropy of the encrypted data. The empirical results show that bits and , resulting in a vulnerability score of 0.1. This suggests a minimal yet existent security risk, underscoring the significance of IV management.
Brute-Force Attack
The brute-force complexity increases significantly with the various key length of sizes 128, 192 and 256 bits as shown in Figure 17. Specifically, the 256-bit key length has a considerably higher brute-force complexity compared to the 128-bit and 192-bit key lengths. This implies that longer key lengths provide greater security against brute-force attacks, as the number of possible key combinations that need to be tested grows exponentially with the key length.
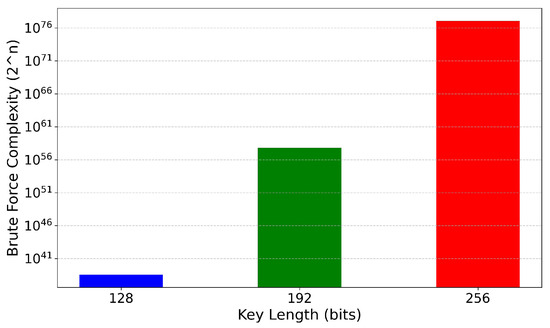
Figure 17.
Brute-force complexity for AES with 128, 192, and 256-bit key lengths.
5.6.3. Hybrid Encryption
The new hybrid encryption mechanism, which has been introduced, improves the original AES-based method by using asymmetric encryption for key exchange and AES-GCM for data encryption. The data was successfully encrypted with AES-GCM, ensuring high confidentiality and integrity. The symmetric key used for encryption was then securely encrypted with RSA-OAEP using a 2048-bit key. The recipient could decrypt the dataset by first using their private RSA key to get the AES key, and then using it for decryption. This is a superior method compared to the first one because it avoids the use of pre-shared symmetric keys as it allows their secure transfer using RSA encryption, and thus it is more appropriate for secure communication over untrusted networks. Unlike AES-CBC, which has an additional HMAC for integrity verification, this has its own built-in authentication using its tag method, offering greater protection against data tampering. This method offers better security, protects against key compromise, and guarantees higher data confidentiality, integrity, and validity than the previous method. The comparision of mean values between encrypted and decrypted data across features using AES-GCM with RSA is shown in Figure 18.
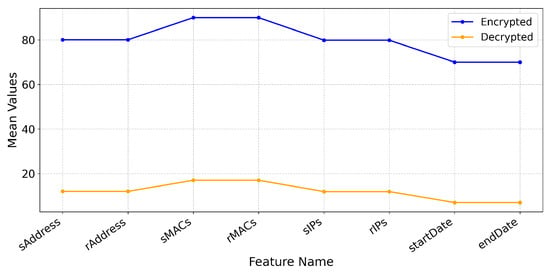
Figure 18.
Comparison of mean values between encrypted and decrypted data across features using AES-GCM with RSA.
In the Figure 14, the key takeaway is that for each of these columns, the match rate between the original and decrypted data is 100%. The encrypted data consistently displays longer string lengths when compared with the original data. The average string length was shown in Figure 19, where decrypted data that are same as those of the original data, suggesting that the decryption process effectively reverses the expansion introduced by encryption and recovers the data to a size comparable to its original form. This indicates a well-functioning encryption and decryption process of the data.
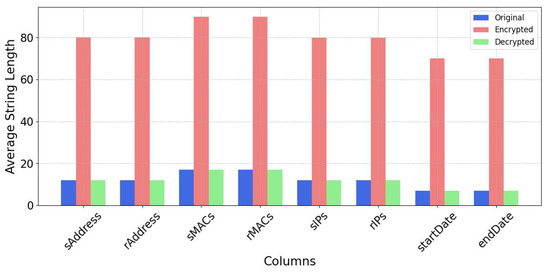
Figure 19.
Average string lengths before encryption, after AES-GCM with RSA encryption, and after decryption for different columns.
5.6.4. Security Test for Hybrid Encryption
Key Length
This encryption conforms to industry standards, ensuring resilience against brute-force assaults. The total key space for a 256-bit AES key K is . A brute-force attack necessitates comprehensive searching, showing a time complexity of . Although having processing capability of operations per second, the decryption of AES-256 would require around years, making attacks by brute force unfeasible.
Entropy Analysis
The entropy analysis graph shown in Figure 16 shows that the encrypted columns (sAddress, rAddress, sMACs, rMACs, sIPs, rIPs) show entropy values exceeding 15 bits per character, indicating robust randomness. This ensures that ciphertexts fail to disclose plaintext structures and remain resistant to frequency-based cryptanalysis. A drop in entropy may signify vulnerabilities, such as insufficient key management, nonce reuse, or deterministic encryption. Shannon entropy is evaluated to verify essential randomness, using Equation (31). Additionally, nonce (IV) generation sticks to a uniform distribution with an entropy of:
which guarantees non-deterministic encryption and mitigates statistical assaults.
Tampering Resistance and Built-In Integrity of AES-GCM
AES-GCM includes authentication via GMAC, thereby preventing ciphertext tampering. A valid ciphertext must correspond in the computed authentication tag as per Equation (37).
where represents the Galois subkey, A denotes the associated data, and C denotes the ciphertext. If tag verification fails, decryption is stopped. The likelihood of a successful tag production is small, hence ensuring integrity.
Nonce Reuse Vulnerability and Probabilistic Collision Analysis
AES-GCM requires unique nonces, as reusing them weakens the security. In a 96-bit nonce space, the possibility of a nonce collision after q encryptions follows to the principles of the Birthday Paradox as defined by the Equation (38)
For (4 billion encryptions), the chance of a collision is roughly , which is minimal yet non-negligible. Nonce reuse results in identical keystreams, revealing plaintext correlations as demonstrated in the Equation (39)
The entropy analysis graph indirectly confirms nonce uniqueness elevated entropy values confirm strong randomness. If nonce reuse occurred, entropy values would have reduced revealing structural weaknesses in the ciphertext.
Vulnerability Testing and Risk Quantification
This method obtained a vulnerability score of 0.25, indicating the effectiveness of nonce management.
Equation (40) indicates the exclusive ciphertext ratio. For properly managed nonces, bits and , leading to 0.25, which implies a minimum risk. Poor handling of nonces would lead to lower entropy, thus increasing vulnerability. The graph of entropy analysis supports this by showing uniformly high entropy values, which imply a very little possibility of structural leaks in the ciphertext. The security of AES-GCM encryption has been analyzed keeping in view various cryptanalytic attacks. Frequency analysis confirmed higher entropy, devoid of statistical biases or identifiable trends, attributable to authenticated encryption and distinct IVs. Evaluations of Known Plaintext Attacks (KPA) indicated slight correlations, as shown in Figure 20. Keystream extraction utilizing proved unsatisfactory due to unpredictable IVs. Chosen Plaintext Attack (CPA) evaluations utilizing structured plaintexts showed robust diffusion and obfuscation as seen in Figure 21, with uniform ciphertext distributions preventing statistical leakage. Brute-force attacks prove futile, in line with AES-256 security. No loopholes were shown through an n-gram analysis. Chosen Ciphertext Attack (CCA) tests confirmed resilience, where authentication failures hindered ciphertext modification. AES-GCM avoids Padding Oracle vulnerabilities, unlike AES-CBC. Security is also enhanced by unique nonces, constant-time decryption, and secure key management, thus enhancing AES-GCM’s resistance to cryptanalysis.
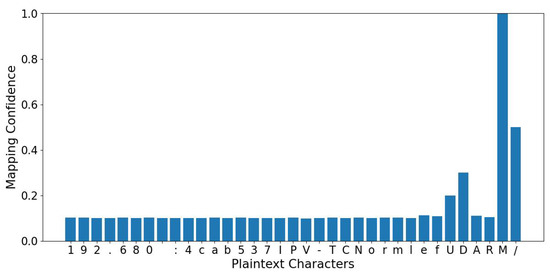
Figure 20.
Mapping confidence of encrypted values under Known Plaintext Attacks.

Figure 21.
Evaluation of encryption robustness using structured inputs in Chosen Plaintext Attacks.
5.7. Encryption Performance Evaluation and Scalability for ICS Security
We performed an exhaustive encryption performance validation on the ICS dataset (45,718 rows), concentrating on per-message latency, dataset-level processing time, throughput, key-generation time, and ciphertext expansion. The outcomes (Table 7) revealed that AES-GCM (256-bit key, 96-bit nonce, 128-bit tag) acquired an average encryption time of 0.018 ms (mean), with decryption averaging 0.033 ms. The total processing time for encrypting and decrypting the dataset was 6.63 s, with 5.7% ciphertext expansion. Additionally, AES-CBC + HMAC-SHA256 encryption has taken 0.040 ms (mean) for encryption and 0.004 ms for decryption, with a total time of 4.61 s and 9.8% ciphertext expansion. The RSA-2048 key generation averaged 412 ms (mean), and key wrap/unwrap for AES keys were 0.48 ms and 1.42 ms, respectively. These results indicate that per-message encryption/decryption times are well lower typical PLC scan cycles (5–10 ms), making the cryptographic overhead almost insignificant for real-time ICS workloads. The system’s performance was additionally evaluated for scalability, demonstrating that encrypting and decrypting the whole dataset was completed in seconds. The RSA key generation process, although slower, runs off the data path and can be pre-computed or provisioned, guaranteeing minimal impact on real-time operations. The AES-GCM method delivers a good balance between security and performance, while AES-CBC + HMAC presents higher overhead due to added integrity checks. With no observed nonce collisions and a manageable ciphertext expansion of 5.7% for AES-GCM and 9.8% for AES-CBC + HMAC, the encryption solutions are well-applicable for resource-constrained ICS devices, presenting a scalable, secure solution for extensive datasets and providing robust protection against cyber threats in industrial environments.

Table 7.
Encryption performance evaluation.
5.8. Adversary Indistinguishability Analysis
Adversary indistinguishability analysis is a concept from cryptography and security used to evaluate how well an encryption scheme or protocol hides information from an attacker. Implementing this analysis for AES-CBC and AES-GCM with RSA encryption methods.
5.8.1. For AES-CBC Encryption
AES-CBC encryption is assessed under the frameworks for Indistinguishability under Chosen Plaintext Attack (IND-CPA) and Indistinguishability under Chosen Ciphertext Attack (IND-CCA).
Indistinguishability Under Chosen Plaintext Attack (IND-CPA)
AES-CBC encryption protects against Chosen Plaintext Attacks (CPA) by rendering ciphertexts indistinguishable from random input. Let represent an encryption scheme in which generates a key K of length , encrypts a plaintext message m, and decrypts a ciphertext c. In the IND-CPA experiment, the challenger chooses at random a key , and the adversary delivers two messages of similar length. The challenger randomly selects and produces . In Equation (41), the adversary attempts to determine , and the encryption scheme is deemed IND-CPA safe if:
AES, operating as a pseudo-random permutation (PRP), produces ciphertexts that show statistical inconsistency, hence ensuring IND-CPA security.
Indistinguishability Under Chosen Ciphertext Attack (IND-CCA)
The robust security definition, IND-CCA, guarantees that an adversary capable of acquiring decryptions of all ciphertexts (except a challenge ciphertext) has no way to tell the difference between the encryptions of and . The IND-CCA experiment allows the adversary to query a decryption oracle for any ciphertext , and they succeed if they accurately predict b. If it is insignificant, the system is IND-CCA-secure. AES-CBC has weaknesses in IND-CCA security because of Padding Oracle Attacks, when attackers alter ciphertexts and deduce plaintext bytes via decryption error messages.
Proof of IND-CPA Security for AES-CBC
AES-CBC achieves IND-CPA security based on the premise that AES functions as a robust pseudo-random function (PRF). If an adversary can differentiate between the encryptions of and with a significant advantage , we develop a distinguisher for a pseudo-random function that undermines its pseudo-randomness. The AES-CBC encryption process is defined by Equations (42) and (43), where:
Here, represents the AES encryption function, and these equations describe how the ciphertexts are generated by encrypting the message blocks iteratively. Equation (42) demonstrates the encryption of the first block of plaintext with the Initialization Vector (IV), and Equation (43) shows how subsequent blocks are encrypted using the output of the previous ciphertext block, following the CBC mode.
If were replaced with a genuinely random function , each would be uniformly random conditioned on , resulting in identical ciphertexts. If can differentiate AES-CBC ciphertexts, it implies a statistical bias in , contradicting the pseudo-random function assumption. Thus, AES-CBC is secure from Indistinguishable Chosen Plaintext Attacks (IND-CPA). This proof demonstrates that AES-CBC’s pseudo-randomness ensures its resilience against Chosen Plaintext Attacks, making it a secure encryption method for confidentiality in the presence of adversaries.
Indistinguishability Breakdown Under IND-CCA Due to Padding Oracle Attacks
AES-CBC does not achieve IND-CCA security due to Padding Oracle Attacks, where a hacker modifies a ciphertext and monitors if the decryption returns valid padding. The probability of correctly predicting a valid last-byte padding using Equation (44) in a randomly modified ciphertext is:
By modifying while evaluating decryption results, an adversary can retrieve plaintext incrementally. This assault necessitates queries, rendering AES-CBC susceptible to adaptive Chosen Ciphertext Attacks.
5.8.2. For AES-GCM with RSA Encryption
AES-GCM encryption has been assessed under the frameworks of Indistinguishability under Chosen Plaintext Attack (IND-CPA) and Indistinguishability under Chosen Ciphertext Attack (IND-CCA). These experiments examine whether an adversary may distinguish between two selected plaintexts with a probability substantially above random chance. Below, we formally define and analyze the indistinguishability experiment for AES-GCM in various adversarial scenarios.
Indistinguishability Under Chosen Plaintext Attack (IND-CPA) for AES-GCM
An encryption scheme is IND-CPA secure if no polynomial-time adversary can distinguish between the encryptions of two chosen plaintexts. The process of the experiment is described as follows:
- The challenger generates a secret key .
- The adversary selects two plaintexts of equal length, such that .
- The challenger selects a uniform bit and encrypts .
- is given and outputs a guess .
- wins if .
The adversary’s advantage can be expressed in Equation (41), where the probability is calculated using the randomness of , , and . If is negligible, then possesses IND-CPA secure. AES-GCM achieves IND-CPA security through the premise that AES works as a pseudo-random function (PRF). Assume an adversary differentiates between the encryptions of and with a significant advantage . We develop a distinguisher for a PRF that disputes its pseudo-randomness hypothesis. The AES-GCM encryption method is executed by Equations (45) and (46).
where is the counter value, T is the authentication tag, and . If were replaced by a truly random function , each would be uniformly random given , making ciphertexts indistinguishable. If can distinguish AES-GCM ciphertexts, it implies a statistical bias in , contradicting the PRF assumption. Hence, AES-GCM is IND-CPA-secure.
Indistinguishability Under Chosen Ciphertext Attack (IND-CCA) for AES-GCM
For a stronger security notion under Chosen Ciphertext Attack (IND-CCA), the adversary is given additional power to decrypt arbitrary ciphertexts, except for the challenge ciphertext. The IND-CCA experiment is defined as follows: In the context of Chosen Ciphertext Attacks (IND-CCA), a more robust security definition permits the adversary to decrypt any arbitrary ciphertexts, with the exception of the challenge ciphertext. The IND-CCA experiment is delineated as follows:
- The adversary is given access to an encryption oracle and a decryption oracle .
- chooses and receives an encryption .
- is allowed to query the decryption oracle on any ciphertext .
- outputs a guess .
If is negligible, then the scheme is considered IND-CCA-secure. AES-GCM attains IND-CCA security through its authentication process. The decryption oracle gives plaintext P only if the authentication tag T is valid, given a ciphertext C. The likelihood of successfully creating a valid T without knowledge of K is at most , rendering it impractical. AES-GCM is resistant to adaptive selected ciphertext attacks.
5.9. Secure Communication
The secure technology for communication efficiently enabled encrypted file transfer between a client and server through SSH-based automation. Initially, file transfers were evaluated using Python 3.11 sockets; nevertheless, to improve security, Paramiko was added, employing Secure File Transfer Protocol (SFTP) over SSH. Two principal circumstances have been evaluated: (1) File sharing over a shared network using local IP addresses, and (2) File sharing across different networks using public IP addresses and port forwarding. The system was designed to be installed in SCADA (Supervisory Control and Data Acquisition) systems and industrial control systems (ICS) to facilitate secure remote access and file transfers. Introducing SSH key in place of passwords can be conducted for further security and ensuring strong authentication. In addition, it was recommended to change the common SSH port 22 to an uncommon port for minimizing the risk of brute-force attacks. The script was built in a way such that it will securely send the encrypted files from the client to the server. The safe transmission was accomplished by connecting to the receiver’s IP via SSH credentials and transferring the files to the specified distant locations. The terminal output confirmed the successful completion of the process, ensuring confidentiality and integrity in data transmission. The future improvements can focus on automating key exchange protocols, improving port forwarding, and incorporating two-factor authorization (2FA) for advanced security. This framework offers an extensive framework for secure communication, appropriate to industrial systems, cybersecurity-sensitive situations, and remote data transfers, ensuring rebellion against unwanted access and cyber attacks.
6. Conclusions
This paper provides an elaborate cybersecurity architecture for industrial control systems (ICS) communication networks, including machine learning (ML) for anomaly detection with strong cryptography methods. Using the ICS-Flow dataset, the proposed system exhibits outstanding performance: XGBoost obtains 99.96% accuracy in binary classification, while Decision Tree obtains 99.92% in multi-class scenarios. An autoencoder developed with LSTM effectively detects temporal anomalies by identifying 23 of 500 cases, while the ADWIN approach provides adaptation via real-time drift detection. AES-CBC with HMAC provides confidentiality and integrity, and the hybrid AES-GCM with RSA approach enhances security via secure key exchange as well as intrinsic authentication, verified by IND-CPA and IND-CCA compliance. The hardware implemented on a PYNQ-Zynq board which validates real-time feasibility, with a testing duration of 0.11 s.
The system identifies deficiencies in previous research by combining adaptive machine learning with post-quantum encryption and blockchain auditability, adapting various ICS protocols (e.g., Modbus, IEC, DNP3). Security assessments confirm robustness against brute-force attacks (requiring years for 256-bit keys), tampering, and cryptanalytic threats. Still, limitations comprise nonce management in AES-GCM and computational cost in resource-limited environments. This project enhances ICS cybersecurity by providing a scalable and secure solution for next-generation industrial networks. Future efforts should maximize efficiency and investigate FPGA accelerations to improve practical applicability.
Author Contributions
K.K. conceptualized the research framework and led the implementation of machine learning models; R.L.S. developed the LSTM-based autoencoder and conducted drift detection using ADWIN; R.D.A.R. supervised the cryptographic system design and performed formal security analyses; A.P. contributed to the literature review and dataset preprocessing; R.M.R.Y. handled the hardware deployment on the PYNQ-Zynq board and encryption entropy evaluation; C.N. and C.R. supervised the entire work throughout all its phases, with C.R. providing primary guidance and oversight, including the refinement of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable. This study did not involve humans or animals and therefore did not require ethical approval.
Informed Consent Statement
Not applicable. This study did not involve human participants.
Data Availability Statement
The dataset used in this study, ICS-Flow, is publicly available and can be accessed through the original source cited in the manuscript. No new data were generated in this study.
Acknowledgments
The authors thank their respective institutions for providing computational resources and infrastructure. No external administrative or technical support was involved.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| ICS | Industrial Control System |
| LSTM | Long Short-Term Memory |
| XG Boost | Extreme Gradient Boosting |
| ADWIN | Adaptive Windowing |
| AES-CBC | Advanced Encryption Standard-Cipher Block Chaining |
| HMAC | Hash-based Message Authentication Code |
| AES-GCM | Advanced Encryption Standard in Galois/Counter Mode |
| RSA | Rivest–Shamir–Adleman encryption |
| IND-CPA | Indistinguishability under Chosen Plaintext Attack |
| IND-CCA | Chosen Ciphertext Attack |
| It | Injection Timing |
| NST | Network Security Tools |
References
- Machaka, V.; Figueroa-Lorenzo, S.; Arrizabalaga, S.; Hernantes, J. Comparative analysis of the standalone and Hybrid SDN solutions for early detection of network channel attacks in Industrial Control Systems: A WWTP case study. Internet Things 2024, 28, 101413. [Google Scholar] [CrossRef]
- Priya, S.S.; Sanjana, P.S.; Yanamala, R.M.R.; Amar Raj, R.D.; Pallakonda, A.; Napoli, C.; Randieri, C. Flight-Safe Inference: SVD-Compressed LSTM Acceleration for Real-Time UAV Engine Monitoring Using Custom FPGA Hardware Architecture. Drones 2025, 9, 494. [Google Scholar] [CrossRef]
- Bahadoripour, S.; Karimipour, H.; Jahromi, A.N.; Islam, A. An explainable multi-modal model for advanced cyber-attack detection in industrial control systems. Internet Things 2024, 25, 101092. [Google Scholar] [CrossRef]
- Randieri, C.; Pollina, A.; Puglisi, A.; Napoli, C. Smart Glove: A Cost-Effective and Intuitive Interface for Advanced Drone Control. Drones 2025, 9, 109. [Google Scholar] [CrossRef]
- Mishra, N.; Islam, S.H.; Zeadally, S. A survey on security and cryptographic perspective of Industrial-Internet-of-Things. Internet Things 2024, 25, 101037. [Google Scholar] [CrossRef]
- Mrudula, P.S.; Raj, R.D.A.; Pallakonda, A.; Reddy, Y.R.M.; Prakasha, K.K.; Anandkumar, V. Smart Grid Intrusion Detection for IEC 60870-5-104 with Feature Optimization, Privacy Protection, and Honeypot-Firewall Integration. IEEE Access 2025, 13, 128938–128958. [Google Scholar] [CrossRef]
- Gómez, Á.L.P.; Maimó, L.F.; Celdrán, A.H.; Clemente, F.J.G.; Sarmiento, C.C.; Masa, C.J.D.C.; Nistal, R.M. On the generation of anomaly detection datasets in industrial control systems. IEEE Access 2019, 7, 177460–177473. [Google Scholar] [CrossRef]
- Iacobelli, E.; Randieri, C.; Roma, P.; Russo, S. Understanding Parental Characteristics of Child Adoption Candidates using MMPI-2 and Evolutionary Clustering. Ceur Workshop Proc. 2024, 3869, 69–77. [Google Scholar]
- Jiang, J.R.; Chen, Y.T. Industrial control system anomaly detection and classification based on network traffic. IEEE Access 2022, 10, 41874–41888. [Google Scholar] [CrossRef]
- Wang, W.; Wang, Z.; Zhou, Z.; Deng, H.; Zhao, W.; Wang, C.; Guo, Y. Anomaly detection of industrial control systems based on transfer learning. Tsinghua Sci. Technol. 2021, 26, 821–832. [Google Scholar] [CrossRef]
- Randieri, C.; Perrotta, A.; Puglisi, A.; Bocci, M.G.; Napoli, C. CNN-Based Framework for Classifying COVID-19, Pneumonia, and Normal Chest X-Rays. Big Data Cogn. Comput. 2025, 9, 186. [Google Scholar] [CrossRef]
- Abdelaty, M.; Doriguzzi-Corin, R.; Siracusa, D. DAICS: A deep learning solution for anomaly detection in industrial control systems. IEEE Trans. Emerg. Top. Comput. 2021, 10, 1117–1129. [Google Scholar] [CrossRef]
- Das, T.K.; Adepu, S.; Zhou, J. Anomaly detection in industrial control systems using logical analysis of data. Comput. Secur. 2020, 96, 101935. [Google Scholar] [CrossRef]
- Mokhtari, S.; Abbaspour, A.; Yen, K.K.; Sargolzaei, A. A machine learning approach for anomaly detection in industrial control systems based on measurement data. Electronics 2021, 10, 407. [Google Scholar] [CrossRef]
- Choi, W.H.; Kim, J. Unsupervised learning approach for anomaly detection in industrial control systems. Appl. Syst. Innov. 2024, 7, 18. [Google Scholar] [CrossRef]
- Jadidi, Z.; Pal, S.; Hussain, M.; Nguyen Thanh, K. Correlation-based anomaly detection in industrial control systems. Sensors 2023, 23, 1561. [Google Scholar] [CrossRef]
- Myers, D.; Suriadi, S.; Radke, K.; Foo, E. Anomaly detection for industrial control systems using process mining. Comput. Secur. 2018, 78, 103–125. [Google Scholar] [CrossRef]
- Dehlaghi-Ghadim, A.; Moghadam, M.H.; Balador, A.; Hansson, H. Anomaly detection dataset for industrial control systems. IEEE Access 2023, 11, 107982–107996. [Google Scholar] [CrossRef]
- Dell’Olmo, P.V.; Kuznetsov, O.; Frontoni, E.; Arnesano, M.; Napoli, C.; Randieri, C. Dataset Dependency in CNN-Based Copy-Move Forgery Detection: A Multi-Dataset Comparative Analysis. Mach. Learn. Knowl. Extr. 2025, 7, 54. [Google Scholar] [CrossRef]
- Gopinath, P.P.; Balasubramanian, K.; Amar Raj, R.D.; Pallakonda, A.; Yanamala, R.M.R.; Napoli, C.; Randieri, C. BESS-Enabled Smart Grid Environments: A Comprehensive Framework for Cyber Threat Classification, Cybersecurity, and Operational Resilience. Technologies 2025, 13, 423. [Google Scholar] [CrossRef]
- Peng, H.; Liu, F.; Cheng, D.; Chen, Y.; Hou, W.; Wang, H. Design of Cryptographic Application Scheme for Industrial Control System. In Proceedings of the 2024 2nd International Conference on Artificial Intelligence, Systems and Network Security, Mianyang, China, 20–22 December 2024; pp. 297–302. [Google Scholar]
- Shahzad, A.; Musa, S.; Aborujilah, A.; Irfan, M. Industrial control systems (ICSs) vulnerabilities analysis and SCADA security enhancement using testbed encryption. In Proceedings of the 8th International Conference on Ubiquitous Information Management and Communication, Siem Reap, Cambodia, 9–11 January 2014; pp. 1–6. [Google Scholar]
- Banerjee, S.; Khan, T.; Castellanos, J.H.; Russello, G. Selective encryption framework for securing communication in industrial control systems. In Proceedings of the ICC 2023-IEEE International Conference on Communications, Rome, Italy, 28 May–1 June 2023; pp. 4125–4130. [Google Scholar]
- Wang, L.; Wang, Z.H.; Guo, F.; Wu, C.K. A hybrid encryption transmission scheme for industrial control systems. In Proceedings of the 2022 7th International Conference on Intelligent Computing and Signal Processing (ICSP), Xi’an, China, 15–17 April 2022; pp. 1144–1147. [Google Scholar]
- Avanzato, R.; Randieri, C. Advances and Recent Applications of BlockChain Technologies: The Model of Blockchain Ecosystem in India. Ceur Workshop Proc. 2024, 3870, 80–85. [Google Scholar]
- Chen, Y.; Yin, F.; Hu, S.; Sun, L.; Li, Y.; Xing, B.; Chen, L.; Guo, B. ECC-based authenticated key agreement protocol for industrial control system. IEEE Internet Things J. 2022, 10, 4688–4697. [Google Scholar] [CrossRef]
- Li, W.; Wang, Y.; Xian, G.; Chen, G.; Han, L.; Zheng, C.; Tu, H. Design of Industrial Control Communication Encryption and Authentication System Based on Artificial Intelligence Algorithm. In Proceedings of the 2024 International Conference on Power, Electrical Engineering, Electronics and Control (PEEEC), Athens, Greece, 14–16 August 2024; pp. 429–433. [Google Scholar]
- Alonso, F.; Samaniego, B.; Farias, G.; Dormido-Canto, S. Analysis of cryptographic algorithms to improve cybersecurity in the industrial electrical sector. Appl. Sci. 2024, 14, 2964. [Google Scholar] [CrossRef]
- Kogiso, K.; Fujita, T. Cyber-security enhancement of networked control systems using homomorphic encryption. In Proceedings of the 2015 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 6836–6843. [Google Scholar]
- Song, Z.; Skuric, A.; Ji, K. A recursive watermark method for hard real-time industrial control system cyber-resilience enhancement. IEEE Trans. Autom. Sci. Eng. 2020, 17, 1030–1043. [Google Scholar] [CrossRef]
- Aftabi, N.; Li, D.; Sharkey, T.C. An integrated cyber-physical framework for worst-case attacks in industrial control systems. IISE Trans. 2025, 1–19. [Google Scholar] [CrossRef]
- Tanimu, J.A.; Abada, W. Addressing cybersecurity challenges in robotics: A comprehensive overview. Cyber Secur. Appl. 2025, 3, 100074. [Google Scholar] [CrossRef]
- Zhu, L.; Zhao, B.; Guo, J.; Ji, M.; Peng, J. A cutting-edge framework for industrial intrusion detection: Privacy-preserving, cost-friendly, and powered by federated learning. Appl. Intell. 2025, 55, 1–21. [Google Scholar] [CrossRef]
- Rahmati, M.; Pagano, A. Federated Learning-Driven Cybersecurity Framework for IoT Networks with Privacy Preserving and Real-Time Threat Detection Capabilities. Informatics 2025, 12, 62. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, C.; Chen, Z.; Feng, Z.; Gui, W. Digital Twin-Based Resilient Model Predictive Control for Industrial Cyber-Physical Systems. IEEE J. Emerg. Sel. Top. Ind. Electron. 2025. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, W.; Ding, J.; Lu, X.; Jing, Y. Leveraging digital twin technology for enhanced cybersecurity in Cyber–Physical production systems. Future Internet 2024, 16, 134. [Google Scholar] [CrossRef]
- Sahoo, B.; Panda, S.; Rout, P.K.; Bajaj, M.; Blazek, V. Digital twin enabled smart microgrid system for complete automation: An overview. Results Eng. 2025, 25, 104010. [Google Scholar] [CrossRef]
- Arora, P.; Kaur, B.; Teixeira, M.A. Evaluation of machine learning algorithms used on attacks detection in industrial control systems. J. Inst. Eng. (India) Ser. B 2021, 102, 605–616. [Google Scholar] [CrossRef]
- Chen, T.; He, T.; Benesty, M.; Khotilovich, V.; Tang, Y.; Cho, H.; Chen, K.; Mitchell, R.; Cano, I.; Zhou, T.; et al. Xgboost: Extreme Gradient Boosting. R Package Version 0.4-2. 2015. [Google Scholar]
- Mienye, I.D.; Jere, N. A survey of decision trees: Concepts, algorithms, and applications. IEEE Access 2024, 12, 86716–86727. [Google Scholar] [CrossRef]
- Lightweight spatial attention pyramid network-based image forgery detection optimized for real-time edge TPU deployment. Comput. Electr. Eng. 2025, 128, 110645. [CrossRef]
- Narmadha, S.; Balaji, N. Improved network anomaly detection system using optimized autoencoder–LSTM. Expert Syst. Appl. 2025, 273, 126854. [Google Scholar] [CrossRef]
- Kronberg, S. Concept Drift Detection in Document Classification: An Evaluation of ADWIN, KSWIN, and Page Hinkley Using Different Observation Variables. Master’s Thesis, Umea University, Umea, Sweden, 2024. [Google Scholar]
- Raj, R.D.A.; Naik, K.A. Optimal reconfiguration of PV array based on digital image encryption algorithm: A comprehensive simulation and experimental investigation. Energy Convers. Manag. 2022, 261, 115666. [Google Scholar] [CrossRef]
- Torad, M.A.; ElKassas, M.A.; Ashour, A.F.; Fouda, M.M.; El-Mokadem, E.S. Enhanced IoT Data Security with Robust AES-CBC Encryption Algorithm. In Proceedings of the 2024 2nd International Conference on Artificial Intelligence, Blockchain, and Internet of Things (AIBThings), Mt. Pleasant, MI, USA, 7–8 September 2024; pp. 1–6. [Google Scholar]
- Shrinivas, S.; Varun, G.; Priya, T. Integrating AES-GCM, ECC, and Steganography for Enhanced Confidential Communication. In Proceedings of the 2024 International Conference on Electrical Electronics and Computing Technologies (ICEECT), Greater Noida, India, 29–31 August 2024; pp. 1–7. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).