Abstract
The rise of wearable devices has enabled real-time processing of sensor data for critical health monitoring applications, such as human activity recognition (HAR) and cardiac disorder classification (CDC). However, the limited computational and memory resources of wearables necessitate lightweight yet accurate classification models. While deep neural networks (DNNs), including convolutional neural networks (CNNs) and long short-term memory networks, have shown high accuracy for HAR and CDC, their large parameter sizes hinder deployment on edge devices. On the other hand, various DNN compression techniques have been proposed, but exploiting the combination of various compression techniques with the aim of achieving memory efficient DNN models for HAR and CDC tasks remains under-investigated. This work studies the impact of CNN architecture parameters, focusing on the convolutional and dense layers, to identify configurations that balance accuracy and efficiency. We derive two versions of each model—lean and fat—based on their memory characteristics. Subsequently, we apply three complementary compression techniques: filter-based pruning, low-rank factorization, and dynamic range quantization. Experiments across three diverse DNNs demonstrate that this multi-faceted compression approach can significantly reduce memory and computational requirements while maintaining validation accuracy, leading to DNN models suitable for intelligent health monitoring on resource-constrained wearable devices.
1. Introduction
The remarkable advancements in deep neural network (DNN) models have greatly enhanced understanding and applications in health monitoring. This paper focuses on two prominent applications, human activity recognition (HAR) and cardiac disorder classification (CDC), as benchmarks to assess the impact of aggressively compressing the DNN models in the considered application domains. HAR has gained a lot of attention recently due to the widespread usage of wearable devices. These devices are an essential part of the Internet of Things (IoT), enabling seamless connectivity and intelligent data processing across various sectors. According to [1], more than 216 M people possess a smartwatch device and this number is expected to increase to more than 231 M in the next four years. The existence of embedded sensors in wearable devices (e.g., accelerometers and gyroscopes) has provided new opportunities in the development of HAR- and CDC-related use cases that are applicable in various market sectors, such as healthcare [2] and smart homes [3].
With the integration of the IoT, wearable devices can transmit real-time sensor data to cloud or edge computing platforms, enabling continuous health monitoring and early detection of anomalies. The target in HAR applications is to effectively combine and process the data captured by wearable sensors in order to predict specific human activities, such as standing, sitting, walking, or even abnormal activities [4]. This is an active research area that has received attention from many researchers and engineers mainly due to the recent advances in sensor technologies [5]. For example, FitBit Inspire 3 by Google [6] has a 3-axis accelerometer, a heart rate monitor sensor, sensors for blood oxygen monitoring, and an ambient light sensor that can be used to devise many healthcare-related applications. When combined with the IoT infrastructure, these sensors facilitate large-scale data collection, allowing researchers to develop more accurate and personalized HAR models. Cardiovascular diseases are a leading cause of mortality globally [7], necessitating effective and prompt diagnostic methods for improved patient outcomes. Various DNN architectures, such as convolutional neural networks (CNNs) and recurrent neural networks (RNNs), play crucial roles in CDC. State-of-the-art models employing these architectures demonstrate significant advancements in this field [8,9]. IoT-based wearable ECG monitoring systems allow continuous data collection, making CDC models more effective by enabling real-time anomaly detection and alerting systems.
On the other hand, the rapid increase in the computational capacity of graphics processing units (GPUs) and tensor processing units (TPUs) has enabled the training of deep learning (DL) models in reasonable time frames. This has been demonstrated in fields such as speech recognition [10] and pattern recognition [11]. Since HAR tasks are basically pattern recognition tasks, they are considered a good target for DL models since they overcome various limitations posed by conventional machine learning (ML) algorithms [12]. However, state-of-the-art DNN models consist of a vast number of parameters (hundreds of billions) and require trillions of computational operations, not only during the training but also at the inference phase [13]. If we consider that wearable devices (e.g., wristbands and smartwatches) are typically devices with limited memory and computing resources, the execution of DNN models in these devices is a challenging task [14]. This problem becomes more challenging when the target applications are associated with real-time constraints [15].
Generally speaking, the problem of executing DNN-based biomedical tasks in wearable devices can be addressed in two ways. First, by devising DNN models with meager computational and memory requirements. However, this might lead to limited model validation accuracy [16]. Second, by employing DNN compression methods that aim to reduce the required memory and computing operations without significantly impacting the model prediction performance [17]. Typical DNN compression techniques include low-rank factorization (LRF) [18,19], pruning (PR) [20], and quantization (QA) [21]. The effectiveness of these compression methods is particularly crucial in IoT-driven applications, where minimizing energy consumption and latency is essential for real-time decision making.
While the usage of DNNs for carrying out HAR and CDC tasks is a widely explored field, the compressibility potential of the resulting DNN models (lower their computing requirements at the same time) has not received particular attention. To the best of our knowledge, this is the first work that performs a thorough evaluation of the compressibility of DNN-based HAR and CDC models. Our analysis includes both CNN and LSTM models. However, since CNNs exhibit typically lower memory footprints than LSTMs [22], we concentrate on CNNs. Optimizing these models for IoT devices can significantly enhance their deployment feasibility, allowing real-time HAR and CDC execution directly on smart wearables and edge nodes.
As noted, our goal is to end up with CNN architectures of minimal size for both studied application domains. However, to this end, two different paths can be followed: (i) either start with a lean model (with a small memory footprint) and employ DNN compression techniques to operate in a moderate manner; or (ii) start with a more complex model (called a fat model hereafter) that is compressed in a more aggressive fashion. Our analysis combines three different compression techniques operating in a synergistic way: (i) LRF applied in the fully connected (FC) layers of the model; (ii) filter-based pruning (FBP) [23], targeting the convolution (conv.) layers; and (iii) dynamic range quantization (DRQ), targeting the removal of the complex floating-point operations of all layers. For the first two techniques, various compressibility levels are assumed. Of course, in all cases, the performance (accuracy) of the CNN model must not be significantly affected compared to that offered by the initial (uncompressed) DNN model. DRQ is selected due to existing limitations (significant accuracy loss) compared to full integer quantization schemes [24].
One of the challenging aspects of the compression process is pruning of models containing residual blocks [25]. In such cases, ensuring consistency between the inputs and outputs of the residual parts of the model necessitates a proper verification phase. Pruning different layers in the various “parallel” branches within the same block can lead to shape inconsistencies (e.g., a different number of output channels). To address this issue, a proper pruning methodology must take into account the residual connections and multi-branch blocks in the model to maintain their consistency. In particular, when pruning a layer within a residual block, appropriate adjustments are required in the dependent layers to accommodate the modified output and input dimensions.
This article is a revised and expanded version of a paper entitled Towards Highly Compressed CNN Models for Human Activity Recognition in Wearable Devices, which was presented at the Conference on Signal Processing: Algorithms, Architectures, Arrangements, and Applications, Poland, 2023 [26]. Exploiting the synergy of different compression techniques in HAR-based DNN models was investigated in [26]. Overall, this work presents a comprehensive re-evaluation of [26], incorporating a new application scenario (CDC) and investigating two additional DNN models (for ECG classification), including one with residual blocks, to explore their compressibility characteristics. In addition, compared to [26], this work includes more detailed evaluations with per-layer statistics and concludes with practical design guidelines for ML/DNN engineers that aim to deploy AI models on edge devices. The increasing relevance of the IoT in these domains highlights the need for optimized, resource-efficient models that can seamlessly operate within edge-based environments, further demonstrating the importance of this research.
The rest of this paper is organized as follows:Section 2 provides the background information and surveys the related approaches. Section 3 outlines the compression techniques utilized in this work. Section 4 describes our evaluation framework and presents the baseline models for the two target application domains. Section 5 includes an in-depth comparison of various configurations of the baseline CNN models, altering the size and/or the length (number) of their layers. Section 6 presents our experimental results and Section 7 concludes this work.
2. Background and Related Work
2.1. Biomedical Applications
The rapid advancements in the Internet of Things have significantly influenced biomedical applications, enabling seamless data collection, processing, and transmission through interconnected wearable devices and sensors. IoT-driven healthcare systems leverage these technologies to enhance remote patient monitoring, early disease detection, and real-time decision making, thus transforming traditional healthcare models into more efficient and accessible solutions. This section explores key biomedical applications, particularly in the domains of wearable technology, HAR, and ECG classification, where IoT plays a pivotal role in integrating smart sensing and deep learning techniques.
Biomedical applications encompass a broad spectrum of fields where technology intersects with healthcare targeting to enhance diagnosis, monitoring, and treatment. Wearable devices, equipped with sensors and advanced computing capabilities, have emerged as invaluable tools in biomedical applications, offering real-time, non-invasive monitoring of physiological parameters [27]. Moreover, wearable devices play a pivotal role in promoting preventive healthcare and personalized medicine by empowering individuals to track their health metrics and make informed lifestyle choices [28].
As a result, the integration of wearable technology into biomedical applications marked a new era of patient-centric healthcare delivery and disease management. HAR techniques are of great importance for biomedical applications. They can be divided into two main categories, vision-based and non-vision-based, depending on the type of sensors used to collect the physical actions of the target agents. The most widely used non-vision sensors for HAR detection are accelerometers (Accs.) and gyroscopes (Gyros.) or a combination of both (Figure 1) [29,30,31,32,33]. After the sensor data are captured, the next step is to perform the actual recognition task. The latter can be achieved either by devising hand-crafted features, or by classical ML- [12] or DNN-based methods [34].
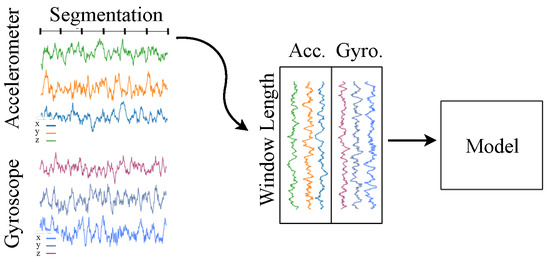
Figure 1.
Segmentation preprocessing of HAR input data [26].
The most common DNN types used to address the challenge of activity recognition are based on LSTM architectures [30], CNN architectures [29,33], or a combination of both [31]. Previous LSTM-based approaches show that this type of DNN is able to report satisfactory results in HAR classification. For example, the authors of [30] manage to achieve 95.78% accuracy using the WISDM dataset [35]. However, LSTMs are typically associated with high computational costs (both in terms of memory and FLOPs). As a result, many researchers turned their attention to CNN architectures in order to balance the computational time and the recognition accuracy. For example, ref. [36] achieves a classification accuracy of 93.32% on the WISDM dataset while significantly reducing the required computational operations.
Table 1 illustrates various representative approaches in the HAR area. As Table 1 indicates, Accs. and Gyros. are the most commonly used sensors. Also, a segmentation technique is utilized in the majority of the related approaches as a preprocessing step. Figure 1 illustrates the HAR procedure, where signal data are provided as input to the DNN model, and the classification results are produced as output. The central part of the figure highlights the segmentation technique used as a preprocessing step; by relying on a windows-based scheme, the input signals are segmented into smaller chunks before feeding them into the model. The rightmost column in Table 1 depicts the compression methods employed in previous approaches.

Table 1.
Approaches related to DNN-based HAR [26].
As noted, when a DNN is compressed, its computational operations can be significantly reduced. Given the fact that HAR classification is typically performed in wearable devices, ending up with a lightweight DNN model is of paramount importance. To the best of our knowledge, this is the first work that employs three compression techniques that operate in a synergistic manner; i.e., FBP is employed in the conv. layers, LRF in the FC layers, and DRQ in all layers in CNN-based HAR models.
With advancements in medical imaging technologies, such as magnetic resonance imaging (MRI) and computed tomography (CT) scans, along with the widespread use of ECGs and other monitoring techniques, healthcare professionals can accurately diagnose and classify a wide range of cardiac disorders [37]. In general, the categorization and identification of various heart-related conditions is based on clinical data, imaging studies, and physiological signals. ECG signals, in particular, are the dominant dataset attracting researchers’ interest. Table 2 illustrates several related approaches in the area. As the second column of Table 2 shows, different architectures have been utilized for CDC activities. Due to the modality of MRI images, most of the approaches that rely on MRI data are based on CNN architectures. However, given the wide usage of ECG data and the corresponding datasets, in this work we focus on ECG-based application scenarios.

Table 2.
Approaches related to DNN-based CDC.
Numerous studies in ECG classification have been carried out by the PhysioNet challenge group [43]. Figure 2 shows a high-level illustration of the ECG classification approach. To create ECG datasets, some sensors are placed on the patient’s body. Using the data collected from sensors attached to the body, specific subsets of data (referred to as leads) are extracted. The number and content of leads are dependent on the number and placement of the employed sensors. In general, a lead in an ECG is the voltage difference between two points on the body. The dataset used in this work includes 12 leads of data that are generated by 10 sensors. The locations of these sensors are shown in the left side of Figure 2. These 12 leads can be categorized into bipolar limb leads (I, II, III), augmented unipolar limb leads (aVR, aVL, aVF), and precordial (chest) leads (V1–V6) [44]. Figure 2 shows these groups of data. In the next step, the captured data are fed into the DNN model to classify disorders.
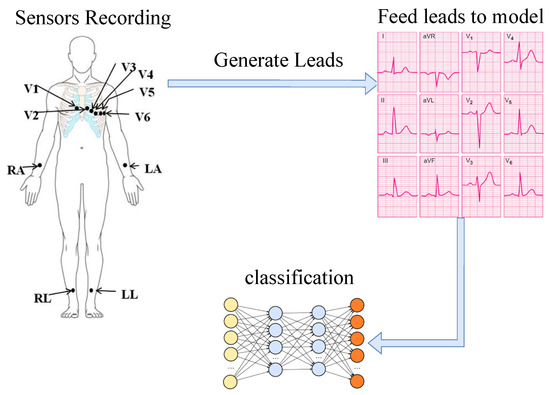
Figure 2.
ECG classification scheme [45].
2.2. Dataset and Preprocessing
The studied HAR use case relies on the WISDM dataset [35]. WISDM contains six HAR classes based on 51 subjects; namely, walking, typing, drinking, dribbling, writing, and clapping. The data have been collected from a smartwatch using 3-axis Acc. and 3-axis Gyro. sensors with a sampling rate of 20 Hz.
The ECG-based dataset provides a wealth of information that could lead to the discovery of new biomarkers, enhancement of personalized medicine, and improvement of patient monitoring systems. Typically, ECG-based datasets consist of recordings of the electrical activity of the heart for a specific time duration, capturing vital information about cardiac rhythms and abnormalities. A notable dataset is the PhysioNet/CinC Challenge database [43], offering a diverse range of ECG signals from different demographic groups and patients with different health conditions. The availability of these datasets facilitates the training and validation of ML or DNN models customized to various CDC application scenarios.
At the data preprocessing side of CDC, segmentation of the input data is also a commonly used approach. Another preprocessing method (as reported in Table 2) is to rely on Butterworth filters [40]. The Butterworth filter [40] is a type of signal processing filter designed to have a frequency response that is as flat as possible in the passband. However, in this work, in order to end up with a general approach, we decided to not rely on a specific preprocessing step for the CDC use cases.
3. CNN Compression Techniques
DNN compression methods can be classified into four main categories [17]: LRF, PR, QA, and knowledge distillation (KD). LRF decomposes the weight matrix/tensor of a layer into two or more thinner matrices/tensors, so the initial layer can be replaced by two or more lightweight layers in a factorized format, reducing both the number of parameters and computing operations [46]. PR reduces the DNN model size by removing connections and/or neurons that are unnecessary or redundant [20]. QA replaces the 32-bit FP numbers of the weights and/or activations of the DNN with lower-bit-width representations (e.g., int32 or int8) [47]. KD transfers knowledge from one or more pre-trained DNN models, namely, the teacher network, to a smaller, yet efficient, DNN model, namely, the student model [48]. In this work, we put forward an approach to combine LRF, PR, and QA to operate in a synergistic manner; therefore, more details about these three techniques are provided hereafter.
In LRF, there are different ways to decompose a tensor, e.g., Tucker decomposition [49], canonical polyadic decomposition (CPD) [50], and tensor train (TT) decomposition [51]. In this work, the LRF technique employed in the FC layers of the DNN relies on TT decomposition using the T3F library [52]. The T3F library decomposes an input 2D array of a weight matrix into a set of 4D tensors. To decompose the 2D array, the T3F library takes as input three parameters: (i) the 2D weight array, (ii) the max-rank that controls the compression rate (smaller values provide higher compression), and (iii) a set of tensor configuration parameters extracted from the dimensions of the input 2D array. The latter set of parameters is related to the shape of the output tensors into which the input 2D array is compressed; if these tensors are multiplied by each other, then the original 2D matrix can be approximated.
The main challenge for deploying LRF in a DNN model is to select an appropriate rank value [18]. This is due to the vast design space resulting from the multiple different configurations that a given layer of a model can be factorized to. In addition, if the target is to factorize more than one layer (typically more than two layers exist in a CNN model), then the design space will explode, including multiple millions of options. In the context of this work, we employ the design space exploration (DSE) methodology of [18] assuming different scenarios; i.e., extracting solutions that minimize the memory footprint or even solutions that result in an increase in the validation accuracy with respect to the initial model.
For the conv. layers of the studied DNN models, the pruning technique is employed. In general, there are two ways to apply pruning in DNN models: (i) unstructured pruning [53] and (ii) structured pruning [23]. Since how to speed up the inference phase is not straightforward in unstructured pruning [53], the structured pruning approach is followed in this work.
In particular, we implement an FBP technique that is a modified version of the channel-based pruning approach in [54]. More specifically, after the training phase, the L1-norm of each filter of a subset of the model’s conv. layers is calculated. As in LRF, multiple alternative options can be considered. As part of this work, the FBP technique is applied to the rightmost half of the conv. layers of the CNN model. Based on our experimental results, pruning the first (leftmost) layers causes a significant drop in accuracy and limits the achievable pruning rate. Therefore, we opted to not to prune the first 50% of the leftmost conv. layers. This approach allowed us to achieve a higher pruning rate and more aggressive model size reduction while maintaining accuracy close to the original.
In particular, our FBP scheme takes as input a predefined threshold (called N). Assuming an N value equal to 20% and a model with six conv. layers, then the FBP technique is enforced in the three rightmost conv. layers and removes 20% of the filters of each of these layers by starting with the filters with the lowest L1-norm. After removing the filters, the pruned model must undergo a calibration phase (re-training for three epochs in this paper) to retrieve the accuracy drop. Finally, it is important to mention that since LRF and FBP are applied in different parts/layers of the input models, the two selected compression techniques are orthogonal to each other.
Finally, as noted, during QA, the FP numbers of the weights/activations of the model are replaced by lower-bit-width representations. There are four different QA methods in the TFLite framework [55]: DRQ, integer QA, float16 QA, and integer QA with int16 activations. In this work, we rely on DRQ. DRQ quantizes the weights to 8-bit integer numbers. In the inference phase, the activations are quantized to 8-bit integers based on their ranges. Therefore, the actual arithmetic computations are performed in 8-bit integer. Since, the calculated results will be in 16-bit format, a subsequent de-quantization (de-QA) phase is required. To improve latency, QA and de-QA of the activation data is performed on the fly. This also allows the usage of quantized kernels for faster implementation and/or for mixing FP kernels with quantized kernels [24].
4. Evaluation Framework and Baseline Models
4.1. Evaluation Framework
Our implementations are based on TensorFlow 2.X. For the HAR models, the WISDM dataset is used [35]. As noted, WISDM contains six HAR classes based on 51 subjects; namely, walking, typing, drinking, dribbling, writing, and clapping. The data are collected from a smartwatch using 3-axis Acc. and 3-axis Gyro. sensors with a sampling rate of 20 Hz. A 70/30 split of the dataset is assumed among the training and testing sets, respectively. In addition, a window length of 100 samples is considered. For the training phase, the Adam optimizer is used [56], configured to a learning rate equal to 0.0001. Finally, the batch size and epochs are 32 and 10, respectively.
The selected ECG classification models [57] have been trained using the PTB-XL dataset [58]. As mentioned in [43], the PTB-XL ECG dataset is a large dataset of 21,799 clinical, 12-lead ECGs from 18,869 patients each covering a 10 s period. The waveform files are stored in WaveForm Database (WFDB) format with 16-bit precision at a resolution of 1 V/LSB (least significant bit) and a sampling frequency of 500 Hz. Similar to [57], a downsampled version of the waveform data at a sampling frequency of 100 Hz is used. Each ECG recording uses a binary MATLAB v4 file for the ECG signal data and a plain text file in WFDB header format for the recording and patient attributes, including the number of leads, sampling frequency, number of samples, the diagnosis (i.e., the labels for the recording), etc.
As mentioned in [32], CNNs can be effective in extracting the local features in time-series problems due to their ability to capture the spatial dependencies of the inputs. Since our target is to end up with lightweight models, we must find the best balance between computational time and validation accuracy. Figure 3 illustrates the baseline HAR model that we consider in this work. The model follows the typical structure of a CNN that consists of two main parts: the feature extraction part and the classification part. The former part includes six 2D conv. layers with a varying number of filters (8, 12, 16, 16, 16, and 24). The latter part includes two FC layers with 16 and 6 neurons, respectively. In the next section, the impact of the main parameters of the baseline architecture (number of layers and number of filters per layer) on the validation accuracy of the HAR model is explored.
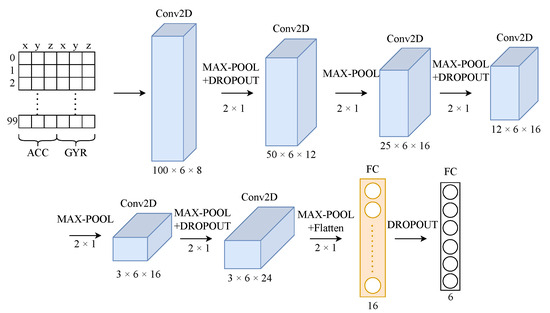
Figure 3.
Baseline CNN architecture of HAR model.
4.2. Baseline Models
Concerning the CDC applications, we selected two different model architectures, namely, ST-CNN-5 and ST-CNN-GAP-5 [57], for evaluation and testing. Figure 4 and Figure 5 show the architectures of the CDC models. ST-CNN-5 includes six 2D conv. layers followed by two FC layers. As can be seen from Figure 5, the architectures of the ST-CNN-5 and ST-CNN-GAP-5 models are almost identical (however, the shapes of the layers are different). In addition, both models use global average pooling (GAP) instead of max-pooling in the last conv. layer in order to drastically reduce the total number of trainable parameters. The main difference between the two models is the additional residual blocks included in ST-CNN-GAP-5 model.
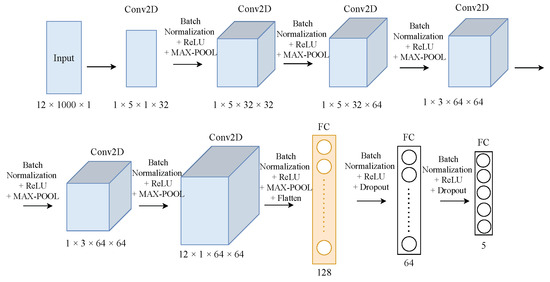
Figure 4.
Architecture of ST-CNN-5 model.
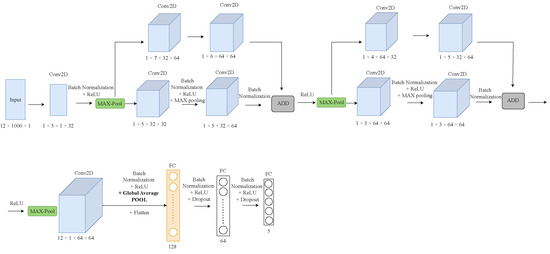
Figure 5.
Architecture of ST-CNN-GAP-5 model.
5. Investigating Alternative Model Architectures: Extracting the Lean and Fat Models
In this section, we evaluate alternative architectures of the selected models by changing the number and sizes of their layers. Our goal is to end up with two model versions (a lean and a fat model) for each case, with diverse characteristics in terms of memory footprint and validation accuracy. These two models will be used as a basis to study the compressibility potential of the baseline models by employing the FBP, LRF, and DRQ techniques.
5.1. HAR Models
In this section, we evaluate alternative configurations of the HAR baseline model. As mentioned, the target is to end up with two CNN models (a lean and a fat model) with diverse characteristics in terms of memory footprint and validation accuracy. These two models will be used as a basis to study the compressibility potential of HAR models by employing the FBP, LRF, and DRQ techniques. Our sensitivity analysis is performed in two directions by varying (i) the model length, i.e., the number of conv. layers; and (ii) the model width, i.e., the number of filters in each conv. layer and the number of units in the FC layers. While an arbitrary number of conv. layers can be considered, in this work, and in order to end up with a reasonable design space, the following numbers of conv. layers are studied: 2, 4, 6, 11, and 16 (Table 3).

Table 3.
Alternative architectures for HAR model.
Note that in all cases, the first (leftmost) conv. layer remains intact. For the width parameter, the following scaling factors are used: 0.25, 0.5, 1, 2, and 3 (normalized to the baseline HAR model). The latter scaling factors for the width parameter are configured to impact all conv. layers and one FC layer (marked in orange in Figure 3). The studied exploration space for the HAR model is depicted in Table 3 (21 configurations in total).
In addition, it is important to note that our approach also varies the parameters of the first FC layer (flatten layer in Figure 3), but in an implicit manner. Since we alter the width of the last (rightmost) conv. layer, the number of neurons in the first (leftmost) FC layer must change accordingly. For example, by keeping the length of the conv. layers equal to six (as in the baseline model) and by altering the width coefficient from 1 to 2, the number of model parameters increases from 9586 to 37,854. After defining the different CNN configurations (letters A to U in Table 3), the next step is to evaluate the validation accuracy of the extracted models. Figure 6 depicts the results of our sensitivity analysis for all the studied configurations. The left vertical axis (associated with the bars) shows the total number of parameters of each model, while the right vertical axis (lines) reports the accuracy of each configuration.
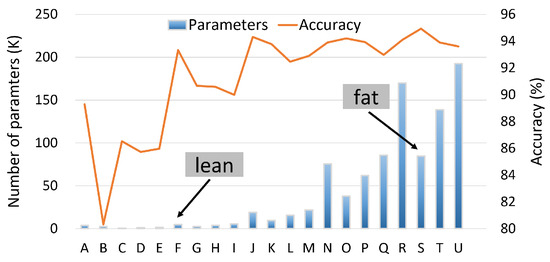
Figure 6.
Sensitivity analysis of HAR model [26].
As expected, by increasing the size of the model, the validation accuracy ramps up. As mentioned, our goal is to explore the compressibility potential of the CNN-based HAR models, but starting from two different design points: (i) a lightweight (lean) model with acceptable HAR recognition accuracy; and (ii) a model exhibiting the highest accuracy (at least among the studied models), but with significantly higher memory requirements (fat model). Based on the results presented in Figure 6, the S model is considered as the fat model (it exhibits the highest validation accuracy).
For the lean model, the F model is selected according to the following criterion: it is the model with the highest accuracy among the 10 models with the lowest memory footprints. It is worth mentioning that the accuracy of the fat model is comparable to the accuracy reported by previous works [30,36].
5.2. CDC Models
Moving to the second application scenario that we consider in this work, the corresponding lean and fat versions of the ST-CNN-5 model are extracted by altering only the number of FC units. Actually, we retain the original conv. layers and focus solely on FC layers. The motivation for this decision lies in the observation that, in the ST-CNN-5 model, the first (leftmost) FC layer constitutes 98.76% of the total model size (the target layer is annotated in orange in Figure 3).
In contrast, the HAR model exhibits a more balanced distribution, with FC layers accounting for 49.31% and conv. layers comprising 50.69% of the model size. Table 4 presents the scaling factors employed to reduce the size of the FC units in the ST-CNN-5 model. Similar to Table 3, the factors depicted in Table 4 are normalized to the corresponding size of the FC of the baseline model. As shown in Table 3, for the ST-CNN-5 model, all scaling factors result in reduced configurations of the original model. According to our initial experimental results (not included in the paper), increasing the size of the target FC layer beyond the original configuration did not yield any improvement in model performance (accuracy).

Table 4.
Alternative architectures for CDC models.
For the second CDC model (ST-CNN-GAP-5), a slightly different approach is adopted. While the two CDC models share many similarities, with ST-CNN-GAP-5 incorporating additional residual blocks, a key distinction between them significantly affects the size of the first (leftmost) FC layer, which largely determines the overall model size. Specifically, as illustrated in Figure 4 and Figure 5, the two models employ different pooling strategies to feed the target FC layer. In the ST-CNN-5 model, a max-pooling layer is used, whereas the ST-CNN-GAP-5 model utilizes a global average pooling mechanism. Unlike max-pooling, which operates over 2 × 1 windows with a stride of one, global average pooling outputs a single value per feature map. Consequently, the global average pooling layer in ST-CNN-GAP-5 leads to a substantially smaller (leftmost) FC layer compared to ST-CNN-5.
To further investigate the impact of the latter characteristic, the global average pooling layer in ST-CNN-GAP-5 is substituted by the max-pooling layer from ST-CNN-5. Obviously, this modification inflates the size of the target FC layer in ST-CNN-GAP-5, but also notably enhances its performance. The new version of ST-CNN-GAP-5 is used as the new baseline for generating the down-scaled configurations using the scaling factors presented in Table 3), as it demonstrates superior performance (as analyzed later in this section). For the sake of completeness and in order to enable a fair comparison, the original ST-CNN-GAP-5 architecture (the one featuring the global average pooling layer) is also evaluated for its compressibility potential using the FBP, LRF, and DRQ techniques (configuration F in Table 3). Figure 7 presents the results of our sensitivity analysis, illustrating the trade-off between memory requirements and accuracy for both CDC models across all the configurations listed in Table 3. Similar to the previous graph, the left vertical axis corresponds to the bars, indicating the total number of parameters for each evaluated configuration, while the right vertical axis corresponds to the lines, representing the recognition accuracy achieved by each configuration. The lean and fat CDC models are highlighted in Figure 7, extracted based on the following criteria. For each CDC model, the configuration yielding the highest accuracy is designated as the fat version, whereas the lean version is the configuration with the fewest parameters that maintains accuracy within 1% of the baseline model.
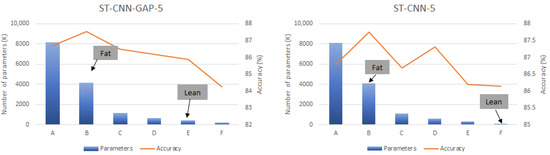
Figure 7.
Sensitivity analysis of CDC models.
6. Synergistic Compression of Lean and Fat Models
After the lean and fat models are defined for both the HAR and CDC models, the next step is to exploit the compressibility potential of these models. As mentioned, three different compression techniques (FBP, LRF, and DRQ) are employed in tandem. The LRF technique is formulated following the DSE methodology proposed in [18]. One obvious question is which compression to apply first. Given the fact that FBP is also employed in the last (rightmost) conv. layer (i.e., the one just before the flatten layer in Figure 3), the shape of the latter layer is affected by the FBP process. Therefore, first the FBP technique is employed, and then the input to LRF is an already-pruned model.
Figure 8 presents the results of applying FBP and LRF to the two selected HAR models. There are two graphs in Figure 8, corresponding to the lean (left) and fat (right) models. The blue bars/lines in the graphs depict the number of parameters and the resulting recognition accuracy, respectively, when the FBP process is employed. Similarly, the green bars/lines correspond to the statistics of the LRF compression process. More specifically, the results in Figure 8 are extracted assuming (i) the pruning ratios 30%, 40%, 50%, 55%, 60%, 65%, and 70% (annotated in the x-axis); and (ii) the LRF is configured to output the factorized FC with the lowest possible memory size with no accuracy drop with respect to the uncompressed (initial) model. Finally, the bar labeled with “0” corresponds to the initial model.
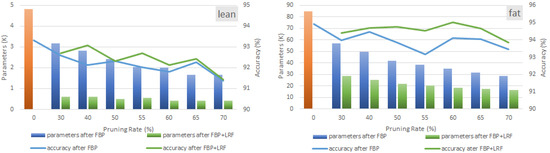
Figure 8.
Memory and validation accuracy after employing FBP and LRF on lean and fat versions of HAR model. LRF is configured to extract the solution with the lowest memory footprint with no accuracy drop.
As Figure 8 indicates, when the pruning rate of FBP technique increases, the number of parameters decreases (blue bars) in an almost linear fashion. Almost the same behavior can be observed in both models. However, a different situation can be seen when LRF is also employed. In the lean model, LRF manages to offer an extra reduction of the parameters from 74.44% (for the 70% pruning rate) up to 80.5% (30% pruning rate) over the parameter reduction reported by the standalone FBP. On the other hand, more moderate compression rates are observed in the fat model. The additional reduction achieved by LRF over FBP is from 42.98% (70% pruning rate) up to 49.79% (30% pruning rate). This is an expected result since the amounts of parameters occupied by FC layers are 85.16% and 49.3% in the lean and the fat model, respectively.
Overall, it is clear that the combination of FBP and LRF manages to significantly compress the studied models: 91.2% compression in the lean model and 79.42% in the fat model is reported for the 65% pruning rate. These are very promising results, showing that the use of compression techniques that operate in a synergistic manner can lead to significant reductions in the memory requirements of CNN-based HAR models. Most importantly, the reported compression ratios are accompanied by a meager drop in the recognition accuracy of the models. Focusing again on the 65% pruning rate, a 0.89% accuracy drop is seen in the lean model (from 93.33% in the uncompressed case to 92.44%) and a corresponding drop of 0.27% in the fat model (from 94.92% to 94.65%).
Considering the FLOP requirements (not shown in the graphs of Figure 8), the situation is different. For the 65% FBP case, the FBP-LRF combination offers a FLOP reduction of 45.14% and 28.41% in the lean and fat models, respectively. This is due to fact that the majority of FLOPs (typically more than 85%) in a typical CNN model come from the conv. (and not FC) layers [18]. Therefore, the calculated FLOP reductions follow the enforced FBP rate in an almost linear fashion.
Up to now, only one LRF configuration has been analyzed. The strength of the DSE methodology in [18] is that multiple LRF configurations can be extracted based on user-defined criteria; e.g., outputting all LRF configurations that exhibit less than 0.5% validation accuracy drop with respect to the initial model. Figure 9 depicts the final memory size and the associated HAR prediction accuracy for three different LRF configurations: (i) the configuration with the highest validation accuracy (leftmost blue bars); (ii) the one with the lowest memory size, but with no accuracy drop (blue bar in the middle); and (iii) the one with the lowest memory, but allowing 1% accuracy drop (rightmost blue bar). In all cases, an FBP rate of 65% is assumed. Finally, the green bars/lines show the corresponding results when DRQ is employed in each case.
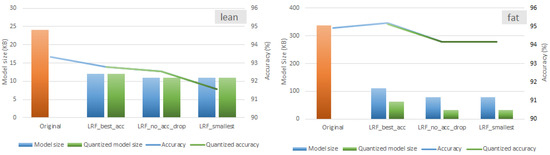
Figure 9.
Alternative LRF configurations (lowest memory footprint, no validation accuracy drop, highest validation accuracy) for a 65% pruning rate of HAR models when DRQ is employed.
As depicted in Figure 9, there is an average 52.8% memory reduction in the lean model, which results in HAR models of a size of almost 11 KB. In the fat model, the average memory reduction is 87.5%, resulting in model sizes up to 32 KB. Most importantly, these compression ratios are accompanied by a meager drop (up to 1.75%) in the accuracy of the models even when the DRQ is employed. Moreover, it is interesting to note that DRQ is more effective in the fat model (up to 59.9%), while almost no memory reduction is reported in the lean model.
In accordance with the DRQ methodology, the goal is to maximize the number of layers represented using int8 data types, while reverting to int32 or even float32 representations for the remaining layers to maintain model validation accuracy. This process follows an iterative approach to identify a suitable solution. Given that the fat model contains significantly more parameters than the lean model, it offers greater opportunities for DRQ. The DRQ algorithm effectively exploits these opportunities, achieving int8 quantization for up to 59.9% of the fat model’s parameters, as illustrated in Figure 9. Further investigating the internal workings of DRQ is beyond the scope of this work.
Moving now to the CDC models, it is important to note that both CDC models (ST-CNN-5, ST-CNN-GAP-5) rely on the same dataset for training and validation. In this way, a more direct and fair comparison (in terms of their compressibility characteristics) between the two models is ensured. The main difference between the two models lies in their underlying architecture: one employs a sequential structure, while the other adopts a residual approach (Figure 4 and Figure 5, respectively).
Figure 10 depicts the results of employing both FBP and LRF on the lean and fat ST-CNN-5 models. Unlike the results for the HAR model (Figure 8), the evaluation range of the FBP techniques for the ST-CNN-5 model (Figure 10) extends up to 90%. This extension is attributable to the greater tolerance of the ST-CNN-5 model’s accuracy compared to the HAR model. In the results, the blue bars and lines represent the LRF-related statistics, specifically parameter reduction and validation accuracy, respectively. Similarly, the green bars and lines indicate the outcomes when LRF is applied in tandem with FBP.
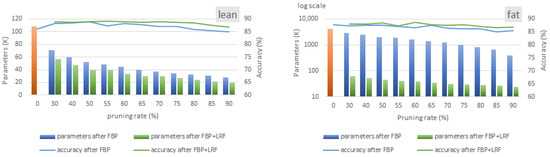
Figure 10.
Memory and validation accuracy after employing FBP and LRF in lean and fat versions of ST-CNN-5 model. LRF is configured to extract the solution with the lowest memory footprint with no accuracy drop.
As shown in Figure 10, both the lean and fat versions of the ST-CNN-5 model demonstrate notable tolerance to FBP. Specifically, at a 70% FBP rate, the lean model achieves a 65% reduction in parameters with no accuracy degradation. Furthermore, applying LRF yields an additional 8% compression. A comparison between the lean and fat models reveals that FBP achieves substantially higher compression ratios in the fat model than in the lean model. For instance, in the fat model (right part of Figure 10), a moderate compression of 70% is observed at a 70% FBP rate. Notably, the vertical axis for the fat model is presented on a logarithmic scale. By comparing lean and fat models with similar accuracy, we can infer that the fat model contains extra parameters that have negligible impact on accuracy and can be pruned. As a result, the fat model can tolerate higher pruning rates compared to the lean model. In this case, the application of LRF results in an additional 29% reduction in the number of model parameters.
A comparison of Figure 10 (ST-CNN-5 model) and Figure 11 (ST-CNN-GAP-5 model) shows that both models demonstrate almost similar behavior in terms of compressibility potential. At the 70% pruning rate, 64% and 70% parameter reductions are reported in the lean and fat models, respectively. Following the application of LRF, the compression ratios further increase by 18% and 28% for the lean and fat models, respectively. Notably, focusing on the fat versions of the ST-CNN-5 and ST-CNN-GAP-5 models (which are nearly identical in size), the accuracy of the ST-CNN-GAP-5 model, which incorporates residual connections, proves to be less robust as the FBP rate ramps up. Further investigating this issue is left for future work.
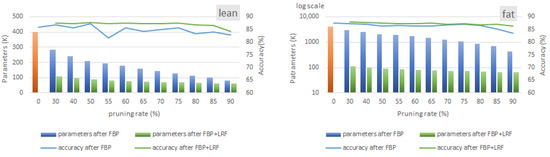
Figure 11.
Memory and validation accuracy after employing FBP and LRF in lean and fat versions of ST-CNN-GAP-5 model. LRF is configured to extract the solution with the lowest memory footprint with no accuracy drop.
Figure 12 and Figure 13 present the statistics for various LRF configurations. The blue bars/lines represent configurations with the highest validation accuracy, the lowest memory size, and the lowest memory size with no more than a 1% drop in accuracy. In contrast, the green bars/lines show the results when DRQ is applied. The results shown in Figure 12 and Figure 13 correspond to the following pruning rates: 90% for the lean version of ST-CNN-5 model, 80% for the fat version of ST-CNN-5, and 85% for both versions of the ST-CNN-GAP-5 model. The above pruning rates are the ones that offer a less than 1% accuracy drop in all cases.
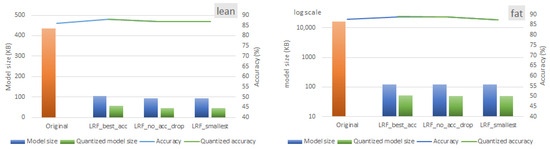
Figure 12.
Alternative LRF configurations for 90% and 80% pruning rates for lean and fat versions of ST-CNN-5 model when DRQ is employed.
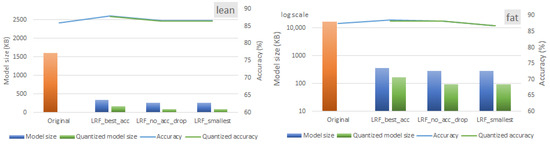
Figure 13.
Alternative LRF configurations for an 85% pruning rate for both lean and fat versions of the ST-CNN-GAP-5 models when DRQ is employed.
As the figures illustrate, the ST-CNN-GAP-5 model achieves an average memory reduction of 87.41% for the lean version and 99.27% for the fat version, with negligible validation accuracy loss. Similarly, the ST-CNN-5 model demonstrates parameter reductions of 87.96% (lean model) and 99.68% (fat model). These findings underscore the trade-off between memory optimization and model accuracy, highlighting the importance of balancing computational efficiency with performance metrics in deep learning models. When quantization is applied, the residual model (ST-CNN-GAP-5) achieves higher memory reductions. Specifically, as shown by the green bars in the rightmost groups in Figure 12 and Figure 13, DRQ reduces the memory size by 58% and 66% for the fat versions of the ST-CNN-5 and ST-CNN-GAP-5 models, respectively.
6.1. Layer-Level Analysis
This section presents a per-layer analysis of the compressed models. Figure 14 illustrates the results for the three studied models. The vertical axis presents the number of kilo-parameters, with the blue and green segments indicating the kilo-parameters for the FC and conv. layers, respectively. The three stacked bars correspond to the following scenarios: the original (uncompressed) model, the pruned model, and the final compressed model (FBP+LRF). All configurations are selected assuming an accuracy drop of less than 1%.
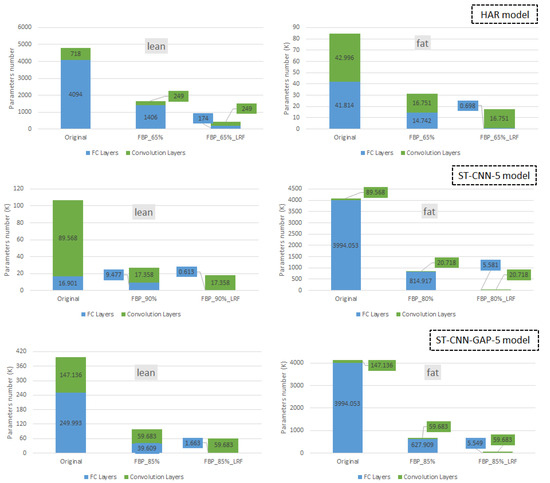
Figure 14.
Reduction in parameters categorized by layer type for the three studied models.
As discussed in Section 3, FBP is applied to the half (rightmost) conv. layers of each model, while the remaining (leftmost) conv. layers remain intact. Notably, FBP is proven effective not only in pruning filters within the conv. layers, but also in reducing the size of the first (leftmost) FC layer. This secondary effect is architecture-dependent. In models where the overall size is predominantly determined by the conv. layers (conv.-intensive models) and/or where the FC layers are relatively small, pruning the rightmost conv. layer has minimal impact on the size of the leftmost FC layer.
For instance, in the conv.-intensive lean variant of the ST-CNN-5 model (left graph in the middle of Figure 14), FBP achieves an 80.6% reduction in conv. parameters and a 43.9% reduction in FC parameters. Conversely, in the FC-intensive fat version of ST-CNN-5, applying FBP results in a 79.6% reduction in FC parameters and a 76.9% reduction in conv. parameters. When LRF is subsequently applied alongside FBP, further reductions in FC parameters are observed. For example, in the lean version of ST-CNN-5, LRF achieves an additional reduction of 37.9% in the FC parameters.
6.2. Discussion
The results presented in this study demonstrate the effectiveness of synergistic compression techniques (FBP, LRF, and DRQ) in significantly reducing the memory footprint and computational demands of CNN-based models, with minimal impact on accuracy. Both lean and fat versions of the HAR and CDC models exhibit varying degrees of compressibility, highlighting the critical role of architectural design and parameter distribution in the performance of these methods. The integration of FBP and LRF achieves substantial parameter reductions across all studied models. For example, the lean HAR model achieves a compression ratio of 91.2% at a 65% pruning rate, with only a 0.89% drop in accuracy. Similarly, the fat HAR model attains a compression ratio of 79.42%, with an even smaller accuracy loss of 0.27%. These findings demonstrate that the usage of FBP as an initial step to optimize input structures for LRF is particularly effective in reducing the size of FC layers.
In CDC models, the robustness of the proposed methodology is further evident. Both ST-CNN-5 and ST-CNN-GAP-5 demonstrate exceptional tolerance to pruning, achieving compression ratios exceeding 87% for lean models and 99% for fat models when FBP and LRF are applied in combination. However, the residual architecture of ST-CNN-GAP-5 shows reduced robustness to pruning, with lower accuracy observed at similar compression levels. While memory reduction is the primary objective of this work, the results reveal nuanced trade-offs between memory footprint and accuracy. For instance, in the HAR models, specific LRF configurations achieve substantial compression with negligible accuracy loss. The addition of DRQ further enhances memory reduction, particularly for fat models, by applying int8 quantization to parameter-rich layers while preserving critical layers in higher-precision formats. This approach achieves up to 59.9% quantization (to int8 formats) in the fat HAR model, demonstrating its potential for low-power applications.
A layer-level analysis provides further insights into the differential impact of compression techniques on conv. and FC layers. In conv.-intensive models such as the lean ST-CNN-5, FBP achieves a notable 80.6% reduction in conv. parameters. In contrast, in FC-intensive models like the fat ST-CNN-5, parameter reduction is more evenly distributed across layer types. These findings underscore the architecture-dependent nature of compression and the necessity of tailoring strategies to the specific parameter distribution of a model. In other words, this work emphasizes the importance of model architecture in determining compressibility. Models with a higher proportion of FC parameters show greater sensitivity to LRF, achieving significant memory savings with minimal accuracy degradation. Conversely, models with a higher proportion of conv. parameters exhibit greater tolerance to DRQ, enabling further optimization for resource-constrained devices.
Finally, the experimental findings highlight the potential of synergistic compression techniques for DNN-based real-world application scenarios. By achieving ultra-low-memory DNN models, such as 11 KB for lean HAR models and up to 32 KB for fat HAR models, these methods enable the deployment of high-performance CNNs on edge devices with stringent resource constraints. Moreover, the minimal accuracy degradation observed across all the studied cases confirms the feasibility of applying the approach presented in this work in mission-critical applications.
7. Conclusions
In this paper, we present a comprehensive analysis of CNN-based HAR and CDC classifiers designed for wearable devices. First, we examine the impact of convolutional and dense layers with varying configurations on the recognition accuracy of HAR and CDC models. Based on this analysis, we identify two distinct CNN models—lean and fat—for each application scenario, showing diverse characteristics in terms of memory usage, FLOPs, and model performance. Subsequently, we apply three model compression techniques, each representing different compression strategies. Interestingly, our experimental results reveal that more aggressive compression can be applied to the lean model (resulting in an average memory reduction of 77.5%). This level of compression is particularly beneficial for IoT-enabled wearable devices, where computational efficiency and energy conservation are crucial for real-world deployment.
As part of our future work, we aim to develop a framework for orchestrating the use of these compression techniques in a more systematic manner while exploring additional compression methods. Furthermore, we plan to investigate more complex scenarios, such as multi-input models, architectures featuring diverse layer types, and variations in layer sizes. Incorporating IoT-driven edge computing paradigms into this framework could enable adaptive processing strategies, optimizing workload distribution between local devices and cloud servers. Our tool will be designed to adapt dynamically to these different model scenarios. Finally, we intend to evaluate the models using alternative datasets, including those derived from 1-lead, 3-lead, and 6-lead ECG signals.
Author Contributions
Conceptualization, investigation, and validation: Z.K., D.G. and C.B.; methodology and software: M.K.; supervision and writing: G.K. and V.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research has been supported by a sponsored research agreement between Applied Materials, Inc. and Aristotle University of Thessaloniki, Greece (Grant Agreement 72714).
Data Availability Statement
This work relied on public datasets.
Conflicts of Interest
Author Charalampos Bournas was employed by the company Think Silicon. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Number of Users of Smartwatches Worldwide from 2020 to 2029. Available online: https://www.statista.com/forecasts/1314339/worldwide-users-of-smartwatches (accessed on 15 January 2023).
- Wang, Y.; Cang, S.; Yu, H. A Survey on Wearable Sensor Modality Centred Human Activity Recognition in Health Care. Expert Syst. Appl. 2019, 137, 167–190. [Google Scholar] [CrossRef]
- Jethanandani, M.; Sharma, A.; Perumal, T.; Chang, J.R. Multi-Label Classification based Ensemble Learning for Human Activity Recognition in Smart Home. J. Internet Things 2020, 12, 100324. [Google Scholar] [CrossRef]
- Lentzas, A.; Vrakas, D. Non-Intrusive Human Activity Recognition and Abnormal Behavior Detection on Elderly People: A Review. Artif. Intell. Rev. 2020, 53, 1975–2021. [Google Scholar] [CrossRef]
- Perez, A.J.; Zeadally, S. Recent Advances in Wearable Sensing Technologies. Sensors 2021, 21, 6828. [Google Scholar] [CrossRef]
- Fitbit.com Updates. Available online: https://www.fitbit.com/global/eu/products/trackers/inspire3 (accessed on 15 January 2023).
- Abderazzak, A.; Bouattane, O.; Youssfi, M. Automatic Cardiac Cine MRI Segmentation and Heart Disease Classification. J. Comput. Med. Imaging Graph. 2021, 88, 101864. [Google Scholar]
- Neha, G.; Rathore, M.; Suman, U. MHCNLS-HAR: Multi-Headed CNN-LSTM Based Human Activity Recognition Leveraging a Novel Wearable Edge Device for Elderly Health Care. IEEE Sens. J. 2024, 24, 35394–35405. [Google Scholar]
- Dua, N.; Singh, S.N.; Semwal, V.B.; Challa, S.K. Inception Inspired CNN-GRU Hybrid Network for Human Activity Recognition. J. Multimed. Tools Appl. 2023, 82, 5369–5403. [Google Scholar] [CrossRef]
- Davide, M.; Campobello, G.; Gugliandolo, G.; Celesti, A.; Villari, M.; Donato, N. Comparison of Noise Reduction Techniques for Dysarthric Speech Recognition. In Proceedings of the 2022 IEEE International Symposium on Medical Measurements and Applications (MeMeA), Messina, Italy, 22–24 June 2022. [Google Scholar]
- Yu, J.; Zheng, X.; Wang, S. A Deep Autoencoder Feature Learning Method for Process Pattern Recognition. J. Process Control 2019, 79, 1–15. [Google Scholar] [CrossRef]
- Dargan, S.; Kumar, M.; Ayyagari, M.R.; Kumar, G. A Survey of Deep Learning and its Applications: A New Paradigm to Machine Learning. Arch. Comput. Methods Eng. 2020, 27, 1071–1092. [Google Scholar] [CrossRef]
- Hu, Z.; Zou, X.; Xia, W.; Zhao, Y.; Zhang, W.; Wu, D. Smart-DNN: Efficiently Reducing the Memory Requirements of Running Deep Neural Networks on Resource-Constrained Platforms. In Proceedings of the 2021 IEEE 39th International Conference on Computer Design (ICCD), Storrs, CT, USA, 24-27 October 2021. [Google Scholar]
- Hossain, S.M.; Islam, S.K.; Cheng, J.; Morshed, B.I. Efficient Acceleration of Deep Learning Inference on Resource-Constrained Edge Devices: A Review. Proc. IEEE 2023, 111, 42–91. [Google Scholar]
- Muck, T.; Donyanavard, B.; Moazzemi, K.; Rahmani, A.M.; Jantsch, A.; Dutt, N. Design Methodology for Responsive and Robust MIMO Control of Heterogeneous Multicores. Trans.-Multi-Scale Comput. Syst. 2018, 4, 944–951. [Google Scholar] [CrossRef]
- Suwannarat, K.; Kurdthongmee, W. Optimization of Deep Neural Network-based Human Activity Recognition for a Wearable Device. Heliyon 2021, 7, e07797. [Google Scholar] [CrossRef] [PubMed]
- Marino, G.C.; Petrini, A.; Malchiodi, D.; Frasca, M. Deep Neural Networks Compression: A Comparative Survey and Choice Recommendations. J. Neurocomput. 2023, 520, 152–170. [Google Scholar] [CrossRef]
- Kokhazadeh, M.; Keramidas, G.; Kelefouras, V.; Stamoulis, I. A Design Space Exploration Methodology for Enabling Tensor Train Decomposition in Edge Devices. In Conference in Embedded Computer Systems: Architectures, Modeling, and Simulation; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Kokhazadeh, M.; Keramidas, G.; Kelefouras, V.; Stamoulis, I. Denseflex: A Low Rank Factorization Methodology for Adaptable Dense Layers in DNNs. In Proceedings of the CF ’24: 21st ACM International Conference on Computing Frontiers, Ischia, Italy, 7–9 May 2024. [Google Scholar]
- Niu, W.; Zhao, P.; Zhan, Z.; Lin, X.; Wang, Y.; Ren, B. Towards Real-Time DNN Inference on Mobile Platforms with Model Pruning and Compiler Optimization. arXiv 2020, arXiv:2004.11250. [Google Scholar]
- Gong, C.; Chen, Y.; Lu, Y.; Li, T.; Hao, C.; Chen, D. VecQ: Minimal Loss DNN Model Compression with Vectorized Weight Quantization. IEEE Trans. Comput. 2020, 70, 696–710. [Google Scholar] [CrossRef]
- Bai, S.; Kolter, J.Z.; Koltun, V. An Empirical Evaluation of Generic Convolutional and Recurrent Networks for Sequence Modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Luo, J.H.; Zhang, H.; Zhou, H.Y.; Xie, C.W.; Wu, J.; Lin, W. Thinet: Pruning CNN Filters for a Thinner Net. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 41, 2525–2538. [Google Scholar] [CrossRef]
- Shan, L.; Zhang, M.; Deng, L.; Gong, G. A Dynamic Multi-Precision Fixed-Point Data Quantization Strategy for Convolutional Neural Network. In Communications in Computer and Information Science; Springer: Singapore, 2016. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2024. [Google Scholar]
- Gkountelos, D.; Kokhazadeh, M.; Bournas, C.; Keramidas, G.; Kelefouras, V. Towards Highly Compressed CNN Models for Human Activity Recognition in Wearable Devices. In Proceedings of the 2023 Signal Processing: Algorithms, Architectures, Arrangements, and Applications (SPA), Poznan, Poland, 20–22 September 2023. [Google Scholar]
- Jegan, R.; Nimi, W.S. On the Development of Low Power Wearable Devices for Assessment of Physiological Vital Parameters: A Systematic Review. J. Public Health 2023, 32, 1093–1108. [Google Scholar] [CrossRef]
- Guk, K.; Han, G.; Lim, J.; Jeong, K.; Kang, T.; Lim, E.K.; Jung, J. Evolution of Wearable Devices with Real-Time Disease Monitoring For Personalized Healthcare. J. Nanomater. 2019, 9, 813. [Google Scholar] [CrossRef]
- Laput, G.; Harrison, C. Sensing Fine-Grained Hand Activity with Smartwatches. In Proceedings of the CHI ’19: CHI Conference on Human Factors in Computing Systems, Glasgow Scotland, UK, 4–9 May 2019. [Google Scholar]
- Agarwal, P.; Alam, M. A Lightweight Deep Learning Model for Human Activity Recognition on Edge Devices. Conf. Comput. Sci. 2020, 167, 2364–2373. [Google Scholar] [CrossRef]
- Mekruksavanich, S.; Jitpattanakul, A.; Youplao, P.; Yupapin, P. Enhanced Hand-Oriented Activity Recognition based on Smartwatch Sensor Data using LSTMs. Symmetry 2020, 12, 1570. [Google Scholar] [CrossRef]
- Coelho, Y.L.; Santos, F.D.A.S.d.; Frizera-Neto, A.; Bastos-Filho, T.F. A Lightweight Framework for Human Activity Recognition on Wearable Devices. IEEE Sens. J. 2021, 21, 24471–24481. [Google Scholar] [CrossRef]
- Zebin, T.; Scully, P.J.; Peek, N.; Casson, A.J.; Ozanyan, K.B. Design and Implementation of a Convolutional Neural Network on an Edge Computing Smartphone for Human Activity Recognition. IEEE Access 2019, 7, 133509–133520. [Google Scholar] [CrossRef]
- Zhu, Y.; Mo, L. A Review of Wearable Sensor-based Human Activity Recognition using Deep Learning. In Proceedings of the 2022 International Conference on Sensing, Measurement & Data Analytics in the era of Artificial Intelligence (ICSMD), Harbin, China, 30 November–2 December 2022. [Google Scholar]
- Weiss, G.M.; Yoneda, K.; Hayajneh, T. Smartphone and Smartwatch-Based Biometrics Using Activities of Daily Living. IEEE Access 2019, 7, 133190–133202. [Google Scholar] [CrossRef]
- Ignatov, A. Real-Time Human Activity Recognition from Accelerometer Data using Convolutional Neural Networks. J. Appl. Soft Comput. 2018, 62, 915–922. [Google Scholar] [CrossRef]
- Shah, H.; Mubeen, I.; Ullah, N.; Shah, S.S.U.D.; Khan, B.A.; Zahoor, M.; Ullah, R.; Khan, F.A.; Sultan, M.A. Modern Diagnostic Imaging Technique Applications and Risk Factors in the Medical Field: A Review. BioMed Res. Int. 2022, 2022, 5164970. [Google Scholar]
- Iqbal, T.; Aaleen, K.; Ihsan, U. Explaining Decisions of a Light-Weight Deep Neural Network for Real-Time Coronary Artery Disease Classification in Magnetic Resonance Imaging. J. Real-Time Image Process. 2024, 21, 31. [Google Scholar] [CrossRef]
- Alamatsaz, N.; Tabatabaei, L.; Yazdchi, M.; Payan, H.; Alamatsaz, N.; Nasimi, F. A Lightweight Hybrid CNN-LSTM Explainable Model for ECG-based Arrhythmia Detection. J. Biomed. Signal Process. Control 2024, 90, 105884. [Google Scholar] [CrossRef]
- Mostayed, A.; Luo, J.; Shu, X.; Wee, W. Classification of 12-lead ECG signals with bi-directional LSTM network. arXiv 2018, arXiv:1811.02090. [Google Scholar]
- Moura, V.; Almeida, V.; Santos, D.B.S.; Costa, N.; Sousa, L.L.; Pimentel, P.C. Mobile Device ECG Classification using Quantized Neural Networks. J. Comput. Biol. Med. 2022. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, J.; Tian, Y.; Jin, Y.; Li, Z.; Zhao, L.; Liu, C. Pruned Lightweight Neural Networks for Arrhythmia Classification with Clinical 12-Lead ECGs. J. Appl. Soft Comput. 2024, 154, 111340. [Google Scholar] [CrossRef]
- PhysioNet. Available online: https://physionet.org/ (accessed on 15 March 2023).
- The ECG Leads: Electrodes, Limb Leads, Chest (Precordial) Leads and the 12-Lead ECG. Available online: https://ecgwaves.com/topic/ekg-ecg-leads-electrodes-systems-limb-chest-precordial/ (accessed on 15 March 2023).
- Kumar, S.S.; Gupta, R. Artificial Intelligence Methods for Analysis of Electrocardiogram Signals for Cardiac Abnormalities: State-of-the-Art and Future Challenges. Artif. Intell. Rev. 2022, 55, 1519–1565. [Google Scholar]
- Sobolev, K.; Ermilov, D.; Phan, A.H.; Cickocki, A. PARS: Proxy-Based Automatic Rank Selection for Neural Network Compression via Low-Rank Weight Approximation. Mathematics 2022, 10, 3801. [Google Scholar] [CrossRef]
- Jin, H.; Wu, D.; Zhang, S.; Zou, X.; Jin, S.; Tao, D.; Liao, Q.; Xia, W. Design of a Quantization-based DNN Delta Compression Framework for Model Snapshots and Federated Learning. IEEE Trans. Parallel Distrib. Syst. 2023, 34, 923–937. [Google Scholar] [CrossRef]
- Karimzadeh, F.; Raychowdhury, A. Towards Energy Efficient DNN Accelerator via Sparsified Gradual Knowledge Distillation. In Proceedings of the 2022 IFIP/IEEE 30th International Conference on Very Large Scale Integration (VLSI-SoC), Patras, Greece, 3–5 October 2022. [Google Scholar]
- Li, D.; Wang, X.; Kong, D. Deeprebirth: Accelerating Deep Neural Network Execution on Mobile Devices. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence (AAAI-18), New Orleans, LA, USA, 2–7 February 2018. [Google Scholar]
- Frusque, G.; Michau, G.; Fink, O. Canonical Polyadic Decomposition and Deep Learning for Machine Fault Detection. arXiv 2021, arXiv:2107.09519. [Google Scholar] [CrossRef]
- Oseledets, I.V. Tensor-Train Decomposition. SIAM J. Sci. Comput. 2011, 33, 2295–2317. [Google Scholar] [CrossRef]
- Novikov, A.; Izmailov, P.; Khrulkov, V.; Figurnov, M.; Oseledets, I. Tensor Train Decomposition on Tensorflow (T3F). J. Mach. Learn. Res. 2020, 21, 1–7. [Google Scholar]
- Ozen, E.; Orailoglu, A. Squeezing Correlated Neurons for Resource-Efficient Deep Neural Networks. In Machine Learning and Knowledge Discovery in Databases; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Liu, Z.; Li, J.; Shen, Z.; Huang, G.; Yan, S.; Zhang, C. Learning Efficient Convolutional Networks Through Network Slimming. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017. [Google Scholar]
- TensorFlow, Post-Training Quantization. Available online: https://www.tensorflow.org/lite/performance/post_training_quantization (accessed on 1 December 2024).
- Kingma, D.P.; Adam, J.B. A Method for Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- An, A.; Kadian, T.; Shetty, M.K.; Gupta, A. Explainable AI decision model for ECG data of cardiac disorders. Biomed. Signal Process. Control 2022, 75, 103584. [Google Scholar]
- Patrick, W.; Strodthoff, N.; Bousseljot, R.D.; Kreiseler, D.; Lunze, F.I.; Samek, W.; Schaeffter, T. PTB-XL, a Large Publicly Available Electrocardiography Dataset. Sci. Data 2020, 7, 154. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).