Designing a Block Cipher in Galois Extension Fields for IoT Security

Abstract

This paper focuses on a block cipher adaptation of the Galois Extension Fields (GEF) combination technique for PRNGs and targets application in the Internet of Things (IoT) space, an area where the combination technique was concluded as a quality stream cipher. Electronic Codebook (ECB) and Cipher Feedback (CFB) variations of the cryptographic algorithm are discussed. Both modes offer computationally efficient, scalable cryptographic algorithms for use over a simple combination technique like XOR. The cryptographic algorithm relies on the use of quality PRNGs, but adds an additional layer of security while preserving maximal entropy and near-uniform distributions. The use of matrices with entries drawn from a Galois field extends this technique to block size chunks of plaintext, increasing diffusion, while only requiring linear operations that are quick to perform. The process of calculating the inverse differs only in using the modular inverse of the determinant, but this can be expedited by a look-up table. We validate this GEF block cipher with the NIST test suite. Additional statistical tests indicate the condensed plaintext results in a near-uniform distributed ciphertext across the entire field. The block cipher implemented on an MSP430 offers a faster, more power-efficient alternative to the Advanced Encryption Standard (AES) system. This cryptosystem is a secure, scalable option for IoT devices that must be mindful of time and power consumption.

1. Introduction

The use of Internet-of-Things (IoT) devices became increasingly popular due to their cheap mass-manufacturing costs and ease of use. Generally, this classification describes any single-purpose computer that wirelessly communicates to a network of similar devices [1]. Some common examples in the consume space include home-automation devices such as smart lights, plugs, and motion sensors. However, they are being applied in more fields than home automation, such as the industrial [2] and medical spaces [3]. Due to the diverse network of devices and broad application space, the standardization of IoT protocols and hardware is limited [4,5]. Low size, weight, power, cost (SWaP-C), and time-to-market are the fundamental drivers of no/low security in IoT. These challenges lead to little security or use of custom protocols that are not widely accepted and validated. Since IoT devices are single-purpose sensors or actuators in many cases, they are manufactured with cheap, slow processors. Any security system implemented towards protecting IoT communication must fit these constraints. This paper aims to provide a cryptosystem that is more suitable for these constraints than AES.

Pseudorandom number generators (PRNGs) offer a cheap, efficient method at generating a seemingly random string of bits for use in cryptography. Some examples include linear feedback shift registers (LFSR) [6,7], one-time pads [8,9,10], sequence precession [11], residue number systems [12], and chaotic maps [13]. An analysis into Arnold Cat maps, represented by matrices, determined that no matter the period of the Cat map the cycle distribution could be derived [14]. The techniques described in by the author’s can be extended to other chaotic maps to determine their distribution. While not as strong as cryptographic systems like AES, they can be used in concert with other techniques on devices that need to prioritize speed and efficiency while maintaining reasonable levels of security for any data communication. IoT devices fall into this category, as many are single-purpose, and in some cases, run off battery power. Using stronger cryptographic protections is always preferred, but additional cheap techniques can be used in addition to ensure extracting the plaintext without the key is computationally infeasible. One assumption made here is that the attacker will understand everything about the cryptosystem except for the key, enforcing Kerckhoff’s Principle [15]: obscurity should not be used for security.

Traditionally, PRNGs are used in a stream cipher, which is a classification of cryptosystem that acts on a single word of plaintext at a time. On the other hand, a block cipher such as AES takes in a large block of plaintext and outputs an equally sized block of ciphertext. Traditional block cipher encryption algorithms employ methods of confusion and diffusion so minimal changes to the plaintext propagate throughout the ciphertext. Both categories of cryptographic systems offer generic, accepted techniques to strengthen the security, such as AES Cipher Feedback Mode (CFB), which treats previous ciphertext as a variable in the next iteration of the encryption algorithm [16,17]. For stream ciphers, additional strategies were developed to strengthen them, such as using a GEF approach to sequence combination rather than XOR [18]. Another method uses the properties of matrices as an extension on stream ciphers or public key cryptosystems to strengthen the protocol while maintaining invertibility and providing third-party auditability [19,20,21,22].

This paper describes a custom cryptosystem that takes in any input stream of variable size and combines the data with any PRNG’s outputs in a block cipher format, which returns ciphertext of the same size. Decryption utilizes the inverse property of matrices when entries are taken from a Galois Field. The block cipher discussed expands on the work done on Galois Extension Fields as a stream cipher combination technique and provides a block cipher framework to strengthen the security, while maintaining speed and efficiency for IoT applications.

The rest of the paper is organized as follows. Section 2 discusses the mathematical theory behind the constructions used in the cryptosystem. Matrix inverses are reintroduced and the requirements for invertibility are discussed. Following, the section explains how some of the basic matrix arithmetic changes when the elements are from a finite field and the requirements for invertibility differ. A brief background on and discussion on the importance of Galois Extension Fields [18] are discussed. Section 3 discusses the structure of the cryptosystem, including initial assumptions and variables, a high-level system view of both ECB and CFB modes. The section also contains pseudocode for computing the matrix inverse under a finite field. A basic numeric example is provided to make the system more accessible for readers. Section 4 discusses results based on a series of measurements used to judge the strength of the cryptosystem, and compares these results to the stream cipher variation [23] and AES. The results of the NIST statistical test suite are compiled and displayed for each mode of this crytographic algorithm. Further analysis into diffusion and the Law of Iterated Logarithm [24] tests are provided. Section 4 also discusses a hardware validation of the system. Section 5 contains conclusions and extensions planned for future work.

2. Mathematical Background and Tools

This section introduces the mathematical constructions used in this cryptosystem and gives a brief background.

2.1. Matrix and Finite Field Math

Given a square matrix A in ${\mathbb{R}}^{n\times n}$, where ${\mathbb{R}}^n$ is the collection of real numbers and n is a positive integer, the matrix is considered invertible if there exists an equally sized matrix B in ${\mathbb{R}}^{n\times n}$ that satisfies the following, $AB=BA=I$ [25]. The invertible matrix will further on be denoted as B. However, not all square matrices are invertible. The invertible matrix theorem describes a list of properties that a square matrix must meet to have an inverse, but this theorem can be condensed down to $\left|A\right|\ne 0$, where $\left|A\right|$ is the determinant of matrix A.

In the context of this paper, the entries of the matrix A are from a finite field ${\mathbb{Z}}_m$, where m can be any positive integer. The invertible matrix theorem does not hold under this circumstance as all matrix operations are performed modulo m. While the process of calculating the inverse is the same, the matrix A in ${\mathbb{Z}}_m^{n\times n}$ must have a determinant that satisfies $gcd\left(\right|A|,m)=1$, where $gcd$ is the greatest common divisor function.

In the case of m being a prime, a matrix is invertible as long as the determinant is not equal to zero modulo m. The inverse in this case exists as long as the entries in the diagonal are not equal to zero modulo m [19,20]. Matrices used for encryption and decryption operations in the block cipher are in a field where p is not necessarily prime. In this case, the set of invertible matrices in ${\mathbb{Z}}_m^{n\times n}$ is much smaller. Examples shown later in this paper represent fields GF($2^k$) as the data encrypted are usually ASCII text, which has a word size of $2^8$. For the determinant to be relatively prime to an even m, it must be odd. Constructing an invertible matrix with entries from an odd, nonprime field is less common, as all computer operations are binary. However, an invertible matrix is possible and would be useful in the p-adic space, given a computer system that operates in non-binary operations. To be invertible, the determinant of the constructed matrix must be odd. Once an invertible matrix is constructed, the algorithm varies slightly to account for the finite field. The determinant is calculated modulo m and is then used in the Extended Euclidean Algorithm [26] to find the inverse within the field. The adjoint matrix (transpose of the cofactor matrix [25]) is multiplied by this value modulo m, producing B.

2.2. GEF

Galois Extension Fields [27] are used as a combination technique that guarantees an invertible mapping to a higher finite field. Similar techniques, which map operations on GF($p^k$) to a closed subset on GF($p^{k+1}$), were demonstrated in [18] to have substantially better diffusion and forward secrecy properties than other stream cipher and sequence combination techniques. By extending the elements to a higher field, GF($2^k$) → GF($2^{k+1}$), they have provided an invertible mapping to only odd elements in the higher field where the issue of nonuniformity was solved. However, in this higher field addition and subtraction are no longer closed operations as even numbers are not invertible in GF($2^k+1$). The combination function is represented by $z_n=\frac{((2\ast x_n+1)\ast (2\ast y_n+1)mod{2}^{k+1})-1}{2}$. Specifically, the function is used when working with binary data, where $z_n$ is the ciphertext, $x_n$ is the plaintext, and $y_n$ is a discrete-time PRNG output.

Galois Extension Fields were used as a stream cipher combination technique in the previous paper as an alternative to traditional methods like XOR. Additionally, they were proven to be an effective technique for fast, power-efficient stream cipher encryption in IoT devices [23]. This paper extends this technique to be usable as a block cipher by constructing an upper-right triangular matrix with outputs from a PRNG in GF($2^k$). When working in a Galois field space of order $2^k$, the matrix determinant needs to be odd for it to be invertible. The constructed matrix is upper-right triangular as this makes the determinant only a product of the diagonal elements, meaning all elements in the diagonal need to be odd themselves. Since the elements of the matrix are being filled by a uniform PRNG, the probability of every element in the diagonal being odd and non-zero is ${\left(\frac{p-1}{p}\right)}^n$. For a realistically sized matrix, $n=$ 16 or 32, the probability is very small, and GEF transformations are used to guarantee invertibility. Rather than discarding every constructed matrix that does not meet these requirements, the elements within the matrix can be mapped to odd elements in a higher field, which forms a closed subset on GF($p^{k+1}$). In the case of p = 2, this extension field mapping ensures all elements are bijectively mapped to the odd subset of GF($2^{k+1}$). Not all elements within the matrix are extended since the triangular matrix needs to be preserved. For example, the mapping of a 2 × 2 matrix, $\left(\begin{array}{cc}2& 0\\ 0& 7\end{array}\right)$, from GF($2^3$) to GF($2^4$) results in $\left(\begin{array}{cc}5& 1\\ 0& 15\end{array}\right)$.

2.3. Single-Stage RNS PRNG

The PRNG used to generate the elements of the matrices in this cryptosystem is a single-stage residue number system (RNS) based PRNG [12]. The choice of PRNG to generate the matrix is arbitrary as long as the output generated is sufficiently strong. The RNS system was chosen because of prior work in analyzing the strength of this PRNG and its suitability in IoT use cases.

2.4. Validation Tools

The NIST statistical test suite (STS) is a standardized method for testing the strength of randomness in a cryptosystem’s output [28]. For the purpose of this paper, the NIST test suites is used to validate the randomness in the binary output of this system following sequence combination between the plaintext and matrices generated from the RNS PRNG. The strength of the single-stage RNS PRNG was validated using these test suites as well. Additionally, an implementation on a Texas Instruments (TI) MSP430 microcontroller is discussed in Section 5.

3. Materials and Methods

This section discusses the setup of the cryptosystem that uses the tools described in the previous sections, including any assumptions made and variables the user defines. A high-level view is provided to show the interconnection of components in both ECB and CFB mode, along with a more thorough discussion of pieces that were developed for this paper. A toy example follows to show the encryption and decryption operations with real numbers.

3.1. Assumptions and Variables

There are a few assumptions that are made when using this system. The first is the most important: the PRNG used for key generation must be of reasonably high quality as a potential attacker will be assumed to have complete knowledge of generation parameters except for initial conditions. Other defense strategies can be used to strengthen these PRNGs, but that is not the focus of this paper. A single-stage RNS PRNG is chosen for key generation in this system because the quality of this PRNG was validated in previous work [12]. Since this cryptosystem is being used in IoT-caliber devices where speed and efficiency are necessary requirements, the PRNG chosen must meet these requirements. Moreover, as a symmetric cryptosystem, both sender and receiver must maintain this structure, so computational burden must be low.

The user is able to define the order of the Galois Field, but this is assumed to be of order $2^k$ as the majority of data encrypted will be represented in binary. Examples provided in later subsections encrypt ASCII text in GF($2^8$). The PRNG used should output values that are in similar fields. The plaintext can be partitioned if necessary to fit smaller or larger fields. As mentioned in Section 2, in the case of a p-adic system, the field size can be chosen to fit this space.

The block size is dependent on the order of the square matrix, n. Larger n values increase complexity by a quadratic factor, but have a trade-off with computation time when encrypting and decrypting. The relationship between block size and computation time will be discussed more in Section 4. Recommendations will be given on how to define these variables to provide strong, efficient security. Padding is used in the case that there is not enough data to fill a vector when encrypting, but is never used in the case of matrix generation as the key needs to be random. Padding can be composed of any chosen value as long as the choice remains consistent for the entire session.

3.2. High-Level System View

At the start, both transmit and receive devices must setup a synchronized PRNG that will be used for symmetric encryption and decryption processes. What type of PRNG used is a choice that will vary based on available computing resources such as memory usage and processing speed: a trade-off discussed more in Section 4. The outputs of the PRNG are formed into an empty matrix in an upper-right triangular format, row by row. The GEF technique is applied to the upper-right triangular matrix to map all elements to an odd value in the higher-order field. The plaintext vector’s elements are also mapped to the higher-order field. Once both key and plaintext are extended to a higher field, they are combined using matrix multiplication modulo $2^{k+1}$ to produce a vector of ciphertext in the higher-order field. In stream cipher combinations, the combination always produces an odd number, which can be reduced to the field $2^k$ through an inverse of the extension operation. However, in this block cipher application, the multiplication yields even numbers in the higher field, which is not in the closed subset in GF($2^{k+1}$). The operation used to combine the plaintext and key can be reduced to a series of element-wise addition operations. However, addition and subtraction are not closed operations when using a GEF combination technique. Following the field reduction of the ciphertext vector, a ceiling operation is applied to bijectively map all elements to a closed subset in GF($2^k$). Figure 1 depicts the encryption process when operating in Electronic Codebook (ECB) mode. ECB is the standard operation of block ciphers where each block of plaintext is encrypted independently from the rest.

The decryption process is almost the reverse of the encryption process with the addition of the matrix inverse calculation. The receiving device maintains a generates the same key matrix, but must calculate the inverse to decrypt the ciphertext (see Section 2.3). Once extended to the higher order field, a floor operation is applied to the ciphertext to reverse the mapping peformed during encryption. Following, the inverse matrix and ciphertext vector are combined with a matrix multiplication modulo $2^{k+1}$. The resulting vector is reduced to GF($2^k$) to retrieve the original plaintext.

Modes of operation in stream/block ciphers allow for additional flexibility, increasing diffusion and confusion of the resulting ciphertext. In systems that implement Cipher Feedback Mode (CFB) or Cipher Block Chain (CBC), ciphertext from a previous iteration is filtered back into the next encryption operation with the plaintext. Feeding ciphertext back into the encryption operations results in additional computation and slower encryption, but generates a more secure ciphertext. The cryptosystem discussed in this paper can operate in CFB mode as well as CBC mode. Following each encryption operation, the next plaintext vector is assigned the previous ciphertext vector shifted up one element, with one additional plaintext word appended. An illustration of CFB mode encryption and decryption is depicted in Figure 2. Each decryption operation only retrieves a single word of plaintext. The standard mode can be parallelized in both encryption and decryption processes to increase speed, whereas CFB mode can not.

3.3. Implementation of Galois Extension Fields in a Block Cipher

Matrices are used in this system as a block cipher combination technique on data and the outputs of a PRNG. Decrypting this requires calculating the inverse of the matrix constructed from the PRNG. Since these values are from a Galois field, the process of calculating the inverse is different (Section 2.1). Galois Extension Fields are implemented to satisfy the requirements for invertibility. The process of building an invertible matrix and calculating the corresponding inverse is shown in Algorithm 1. Note that this algorithm is specifically for data that are represented in a binary space.

The user inputs a size for the square matrix, the exponent for the order of the Galois field of the plaintext and PRNG values, and a sequence generator object for a selected PRNG. A is initialized to an $n\times n$ matrix of zeros. A nested loop then iterates through all entries in the upper-right of the matrix, storing an output from the PRNG in a temporary variable. The inverse is then computed by multiplying the inverse of the determinant in GF($2^{k+1}$) by the adjoint of A modulo $2^{k+1}$. Rather than running the Extended Euclidean Algorithm every time to compute the inverse of the determinant, these values can be stored in a lookup table when working with reasonably sized k values ($k\le$ 16). The key matrix is then mapped from GF($2^{k+1}$) to GF($2^k$). The plaintext vector is also extended to GF($2^{k+1}$), but this calculation is simple and is discussed in Section 2.2. As mentioned above, not all resulting ciphertext values are part of the odd subset in GF($2^{k+1}$). While this can also be solved by operating in a prime field, performing a mixed radix translation of binary data into prime field characteristics is an unnecessary computational expense. Therefore, a closed ceiling operation is applied following field reduction of the ciphertext. The bijective mapping does not affect the randomness of the ciphertext in any way, as discussed more in Section 4.

Algorithm 1: InvertibleMatrixGF(n, k, seq)—algorithm for generating an invertible matrix under a Galois Field

3.4. Toy Example

This section works out a toy example to show the encryption/decryption processes in ECB mode with sample data represented in decimal for ease in following along.

3.4.1. Encryption

Consider a small example in GF($2^4$) with a key matrix sized 3 × 3, where PRNG used to generate key

$$\left(\begin{array}{ccc}13& 11& 2\\ 0& 3& 14\\ 0& 0& 14\end{array}\right)$$

is a single-stage RNS, refer to [12] for setup. The plaintext vector

$$\left(\begin{array}{c}8\\ 0\\ 8\end{array}\right)$$

is sized 3 × 1 to satisfy dimension requirements when utilizing a dot product operation for encryption. The data encrypted are ASCII that is partitioned into nibbles to fit in GF($2^4$). Galois Extension Fields are then applied to the plaintext vector

$$\left(\begin{array}{c}8\\ 0\\ 8\end{array}\right)\to \left(\begin{array}{c}17\\ 1\\ 17\end{array}\right)$$

to map the plaintext to GF($2^5$). Galois Extension Fields are applied to every entry in the upper-right of the matrix to satisfy the requirements for invertibility.

$$\left(\begin{array}{ccc}13& 11& 2\\ 0& 3& 14\\ 0& 0& 14\end{array}\right)\to \left(\begin{array}{ccc}27& 23& 5\\ 0& 7& 29\\ 0& 0& 29\end{array}\right)$$

Following, the plaintext is encrypted using a dot product operation with the key matrix.

$$\left(\begin{array}{ccc}13& 11& 2\\ 0& 3& 14\\ 0& 0& 14\end{array}\right)·\left(\begin{array}{c}17\\ 1\\ 17\end{array}\right)(mod{2}^5)=\left(\begin{array}{c}23\\ 20\\ 13\end{array}\right)$$

When reducing the ciphertext to the original field, a ceiling operation is applied to bijectively map all outputs to a closed subset in GF($2^4$).

$$\left(\begin{array}{c}23\\ 20\\ 13\end{array}\right)\to \left(\begin{array}{c}11\\ 10\\ 6\end{array}\right)$$

3.4.2. Decryption

This subsection details the decryption process used to retrieve the plaintext from ciphertext generated in the previous subsection. Firstly, an inverse mapping operation is applied to the ciphertext vector’s elements, and then it is extended to GF($2^5$).

$$\left(\begin{array}{c}11\\ 10\\ 6\end{array}\right)\to \left(\begin{array}{c}23\\ 20\\ 13\end{array}\right)$$

Following an extension of the key matrix to GF($2^5$), the determinant of the key matrix is computed modulo $2^5$. The inverse of the determinant in GF($2^5$) can then be found using the Extended Euclidean algorithm, or for efficiency, retrieved from a look-up table. To generate the inverse matrix, the determinant inverse is multiplied by the adjoint matrix modulo $2^5$.

$$25\times \left(\begin{array}{ccc}11& 5& 24\\ 0& 15& 17\\ 0& 0& 29\end{array}\right)(mod{2}^5)=\left(\begin{array}{ccc}19& 29& 24\\ 0& 23& 9\\ 0& 0& 21\end{array}\right)$$

Finally, the inverse matrix and ciphertext vector are combined using a dot product and reduced to the original field to retrieve the original plaintext.

$$\left(\begin{array}{ccc}19& 29& 24\\ 0& 23& 9\\ 0& 0& 21\end{array}\right)·\left(\begin{array}{c}23\\ 20\\ 13\end{array}\right)(mod{2}^5)=\left(\begin{array}{c}17\\ 1\\ 17\end{array}\right)\to \left(\begin{array}{c}8\\ 0\\ 8\end{array}\right)$$

3.5. Use Cases

An upper-right triangular matrix is used as the key in this cryptographic algorithm and requires $\frac{n\ast (n+1)}{2}$ outputs from PRNG to encrypt a block of n plaintext words. The system designer could draw these values from multiple PRNGs if they had enough computational power to maintain all these algorithms. Given two PRNGs, the algorithm could be modified to alternate drawing values from them to construct the key matrix. Every individual entry within the matrix could be generated by a PRNG, and they need not be the same type of PRNG as long as they produce values within GF($2^k$). Maintaining a PRNG for each entry of the key structure would serve as an additional layer of security since a potential attacker would need to break, or discover the key for all those individual PRNGs. However, gaining access to any of the PRNGs does detract from overall security as remaining key values can be filled in with a brute force attack. Computing a single value in this manner would require at most $\frac{2^k}{2}$ guesses. Given only a single unknown, this would be trivial on modern computers, but based on transmission rates, reliance on brute force attacks would contribute significant latency if this was necessary to perform for every block of decryption by the attacker. Based on the PRNG used to generate this entry, an attacker could choose an intelligent attack to reverse engineer the key, such as Berlekamp–Massey for an LFSR [29].

One application of this combination technique is for use in a multiparty cryptographic system, where entries in the key matrices are generated by different parties. To encrypt, every party would need to provide their own portion of the key and could not uncover any information about the plaintext without a full key. As before, each value for the key could be an independent cryptographic algorithm that outputs values in GF($2^k$). Unlike [23], the encryption/decryption processes are not independent and require coordinated party effort.

Aside from the matrix generation, this cryptographic algorithm can be modified to be more efficient in decryption operations for edge nodes in an IoT network. In many cases, these nodes are battery-powered sensors or actuators that communicate with a central system with substantially more computational power. The decryption operation requires an additional step: to calculate the inverse of the key matrix. While relatively inexpensive, this requires additional energy, storage, and time. The base station could instead calculate this inverse and encrypt the plaintext with this matrix instead. The edge node would still need to maintain a synchronized PRNG, but could just build the key matrix and use this as the decryption key since the matrix inverse is commutative. Encrypting with the matrix inverse results in a small decrease in entropy of the resulting ciphertext. This computationally asymmetric modification to the cryptosystem, as shown in Figure 3, is more suitable for edge computing cases.

4. Results

This section discusses the results of encrypting ASCII data with the proposed block cipher in both ECB and CFB modes. Randomness of the resulting ciphertext is measured through the use of statistical tools discussed in Section 2.4, as well as Shannon entropy and Law of Iterated Logarithm calculations. A detailed discussion into diffusion follows, including measurements of decay and security concerns with repeated plaintext. Lastly, a comparison of memory and computational requirements between the cryptosystem modes and AES is made to illustrate the point that the proposed block cipher in this paper is a better option for IoT devices. All comparisons include metrics on the GEF stream cipher variation [23] as an additional baseline. Confusion and other cryptographic properties generally offered in block ciphers are not included in this analysis because the proposed cryptographic algorithm does not include techniques to introduce them. The tools used to validate the results in this section do not guarantee security to intelligent attacks. They offer a baseline measurement of strength against generic statistical attacks like frequency analysis.

4.1. Entropy Analysis

A sample of 1,000,000 characters were used as the plaintext in a MATLAB implementation of this cryptographic algorithm. All punctuation was removed except spaces and was raised to upper case. The frequency of characters is displayed in a histogram in Figure 4.

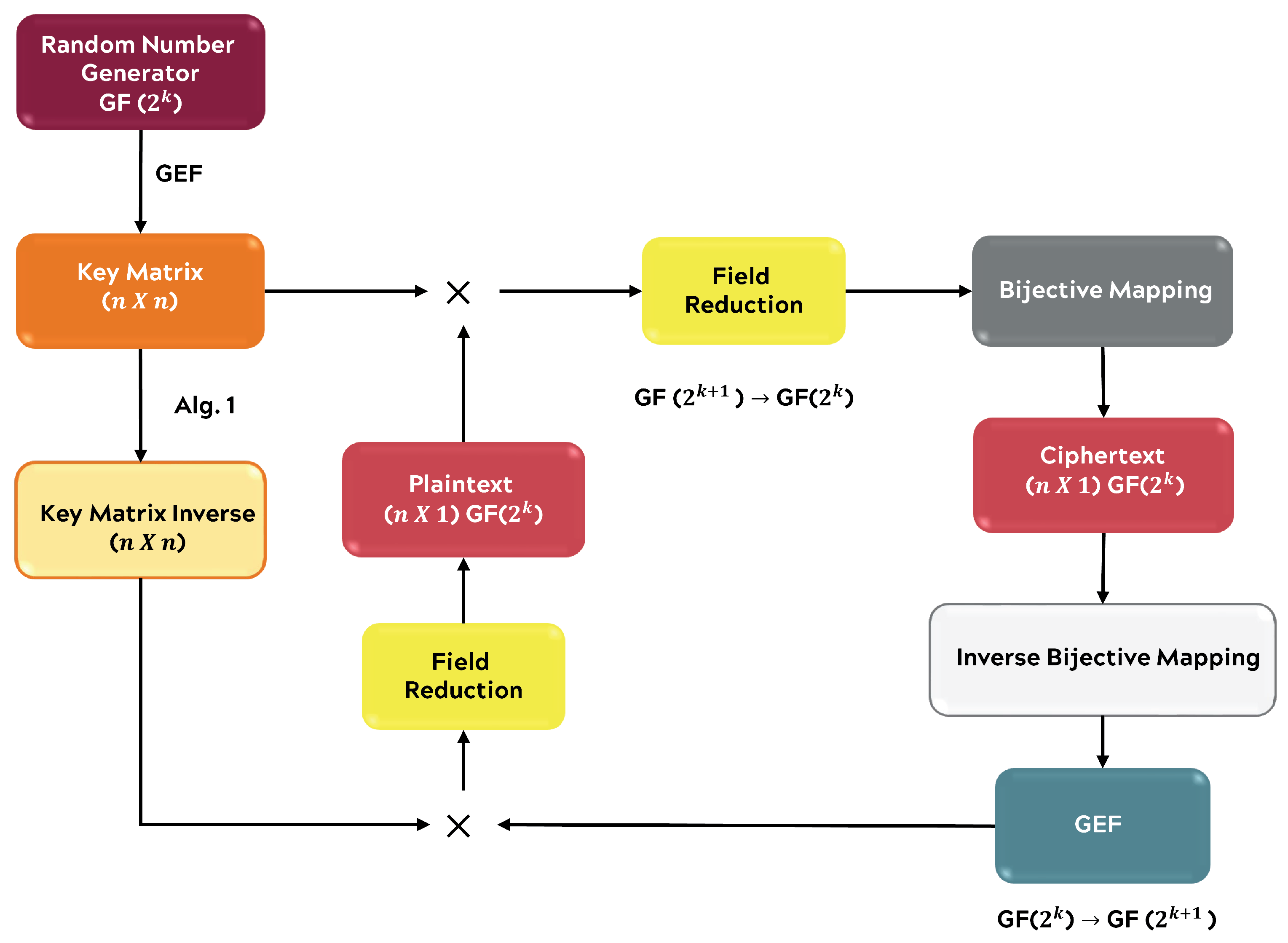
A single-stage RNS PRNG was used for matrix construction, generating values in GF($2^8$). The matrix was sized $16\times 16$. The distribution of the ciphertext from ECB mode is shown in Figure 5. The mean of the histogram of ciphertext is 3906.25, with one standard deviation of 62.56. The expected mean of the ciphertext in GF($2^8$) is 3906.25, indicating the resulting ciphertext is uniformly distributed. The Shannon entropy is 7.9998 bits, where the maximum entropy for this system is 8, meaning the ciphertext is almost uniformly distributed.

Table 1. NIST STS results of 1000 1000-bit samples.

	ECB Mode	CFB Mode	Stream Mode
Frequency	99.6%	99.1%	99.1%
Block Frequency	99.5%	98.6%	98.9%
Cumulative Sums	99.4%	99.3%	99.2%
Runs	99.5%	98.8%	99.0%
Longest Run	99.3%	99.2%	99.0%
FFT	98.1%	98.6%	98.0%
Approx. Entropy	100%	100%	100%
Serial	98.6%	99.2%	98.2%

displays the results of the NIST STS after analyzing the generated ciphertext from this implementation. The test suite was provided 1,000,000 characters, where 1000 bitstreams 1000 bits long were chosen randomly from the pool of provided ciphertext. With $\alpha$ (significance) set to 0.001, 980 sequences needed to pass a specific test for the ciphertext to be considered seemingly random. Each test relevant to the cryptosystem is displayed in the table, and indicates an overall success. For more information regarding what the individual tests examine, refer to the documentation on NIST’s website [28].

The same exact setup was run, but using CFB mode when encrypting. The distribution of the resulting ciphertext is displayed in Figure 6. The Shannon entropy is 7.99$\overline{9}$ bits, which is essentially equivalent to the maximal entropy. The mean of the histogram in GF($2^8$) for the ciphertext is 625,000 since CFB mode produces n times more ciphertext than ECB mode, and the standard deviation is 128.65. Interpreting these values, the cryptographic algorithm run in CFB mode is nearly uniformly distributed. The ciphertext was analyzed using NIST’s test suite with the same parameters as the standard mode. The results are also displayed in Table 1.

The stream cipher variation of the GEF cryptosystem from [23] was also implemented in MATLAB and used to encrypt the same plaintext as ECB mode and CBC mode, resulting in a Shannon entropy of 7.9998 bits. The distribution, shown in Figure 7, indicates a mean of 3906.25 and standard deviation of 63.56.

As expected, the stream and ECB modes of the cryptographic algorithm were nearly equivalent in their distribution. However, CFB mode’s results indicated a more secure option due to the higher entropy and lower standard deviation for a substantially larger mean. Based on the results of the NIST test suite, all three variations of the algorithm appear seemingly random since each test passed the threshold of 98%. ECB mode outperformed the other two modes in the context of these tests.

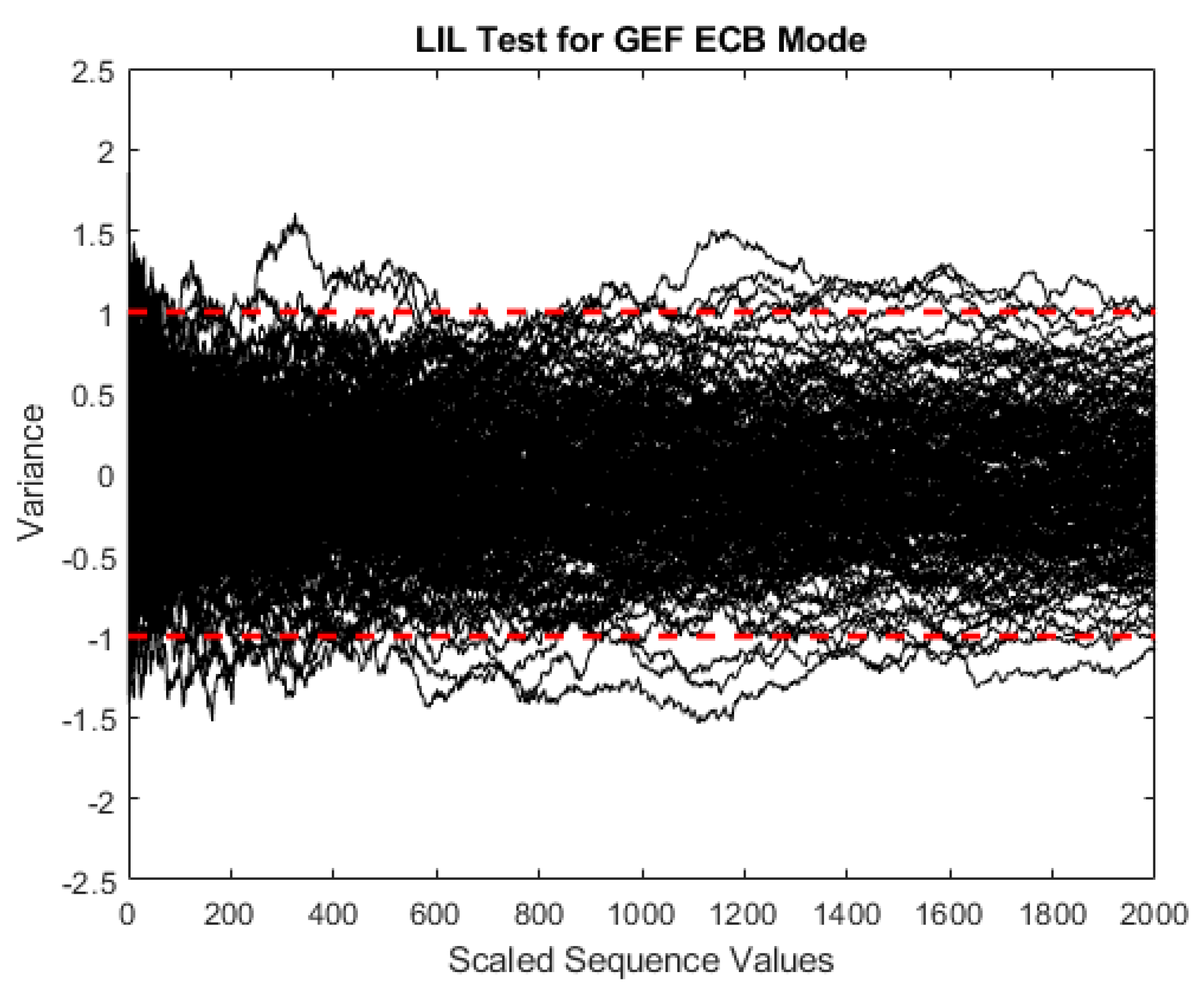
4.2. The Law of the Iterated Logarithm

While the NIST test suite validates the randomness of a cryptosystem’s output, the Law of the Iterated Logarithm (LIL) provides another level of confidence in the randomness of the ciphertext. Previous research indicates that some cryptographically weak systems have passed the NIST test suite, but did not pass the LIL test [24,30]. The test analyzes the variance of a pseudorandom string by looking at the reduced number of 1s after a large output capture. Generally, the provided data is on the order of $2^{26}$ to $2^{34}$ captured outputs. Summarizing what merits a success in the LIL test, the variance must converge to the bounds [−1, 1], but still maintain a large distribution within those bounds. The tool referenced in [30] requires a sample ciphertext size of at least 62.5 Megabytes to accurately measure the variance. The output stream is randomly broken into smaller samples upon which three statistical metrics of distance are calculated: total variation, Hellinger, and root-mean-square deviation. If the distance values calculated from the sample ciphertext are less than accepted thresholds dependent on the sample size, the test is considered a success. Figure 8 shows the results of the LIL test on the ECB mode and Figure 9 displays the results of the CFB mode. Both of the modes pass all three distance metrics while staying within the bounds [−1, 1] with few deviations outside. As shown in the figures, a wide distribution of variance is maintained within the bounds indicated by the dashed red line.

4.3. Diffusion Analysis

Two properties used in the operation of a symmetric cryptosystem are diffusion and confusion. When employed correctly, these work together to prevent statistical tests and other analysis methods from finding meaningful information in ciphertext. Diffusion means that a change in plaintext should propagate throughout the resulting ciphertext. In an ideal cryptosystem, a change in a single bit of plaintext should result in at least 50% of the ciphertext changing. Confusion means each bit of ciphertext should depend on multiple bits of plaintext. These properties are most commonly achieved through permutation and substitution operations respectively. The block cipher described in this paper only employs methods of diffusion.

In the stream cipher version of the GEF cryptosystem, when a bit change occurs in a plaintext word or key generated by a PRNG, the resulting diffusion is isolated to the corresponding ciphertext word, as shown in Figure 10. Given a repeated plaintext word, the probability that a uniformly distributed PRNG, operating in GF($2^k$), will generate the same key for encryption is $\frac{1}{2^k}$. While the probability is relatively small, given a large sample of plaintext, identical ciphertext words can occur. Intelligent attacks can then use repeated ciphertext as a clue on how to retrieve the ciphertext. To solve this problem, the stream cipher can operate in a different mode of operation that uses previous ciphertext as an encryption parameter, such as Counter (CTR) or Output Feedback (OFB) mode. In this case, diffusion would propagate throughout the remaining ciphertext. Bit errors also need to be considered when making the decision of which mode to operate in. In the standard stream cipher mode, a bit error would only result in a single ciphertext word changing, whereas an error in CTR or OFB mode would propagate through the remaining ciphertext.

Diffusion in block ciphers is different as a change in the plaintext or key results in a change in the entire block. Within the ECB mode, if a bit change in a plaintext word at index i occurs, diffusion only occurs within the corresponding ciphertext words from index i up to 0 since the combination technique utilizes a dot product with a triangular matrix. Figure 10 shows an example of the diffusion propagation. Any change in the first n plaintext words will only result in propagation throughout the first block of ciphertext. The change does not propagate between blocks. In traditional block ciphers such as AES or 3DES, no propagation between blocks introduces security issues as a repeated message generates the same output [31]. However, in the proposed system, the use of a PRNG with sufficiently large k (k >= 8) to generate the key matrix mitigates concern as two identical blocks will not be encrypted with the same key. If, for some reason, a prime p is chosen for the field order, the key matrix need not be triangular so long as the determinant is relatively prime to p. In this case, a single bit change between two exact plaintext words with identical key matrices will hopefully result in a substantially changed ciphertext block. On the other hand, a low rate of diffusion between plaintext blocks means bit transmission errors only propagate as far as the corresponding ciphertext block.

Table 2. Shannon diffusion rates for different values of n in ECB mode.

	i	1	$\mathit{n}/2$	n
n
4		13.94%	28.02%	55.68%
8		7.08%	28.12%	55.78%
16		3.54%	28.12%	56.09%

displays the Shannon diffusion averaged from 1000 samples for different block sizes. The row indicates the block size n and the column marks the index i of the plaintext word that was changed. As mentioned earlier, using an upper-right triangular matrix results in a lower rate of diffusion when a change occurs in a lower index. As the block size increases, the overall diffusion decreases with a change in index 1 since this does not propagate throughout blocks 2 through n. However, diffusion reaches the targeted $50\%$ in every scenario when the change occurs at index n. Given smaller block sizes, n = 4, a system can still meet an acceptable rate of diffusion.

Since the CFB mode reuses the ciphertext as a variable in the next iteration of encryption with only a single new plaintext value, diffusion propagates from the current block to further blocks before eventually decaying out. How far the change propagates depends on which word in the plaintext vector is modified, as the lower down it is the farther this change propagates. A small change propagating is great for diffusion when identical blocks with a single bit change are encrypted. The plaintext word would be encrypted through n blocks and contribute to increased diffusion in following blocks. However, an increase in diffusion indicates a larger impact when errors occur. A single bit error would result in incorrect plaintext, following decryption, in each block after the location of the error. Since the ciphertext vector shifts out a word with each iteration of encryption, the diffusion eventually decays. An example of this can be seen in Figure 10. The change made in plaintext word one does not propagate to the second ciphertext block, the change made in plaintext word two only propagates to ciphertext blocks one and two, and so forth.

Further research on triangular matrices as a key proved that the inverse of a lower-left triangular matrix with entries from a finite field can be computed using Algorithm 1. The direction of diffusion in the ciphertext vector is completely dependent upon the type of triangular matrix used as a key since the operator used for encryption is a dot product. 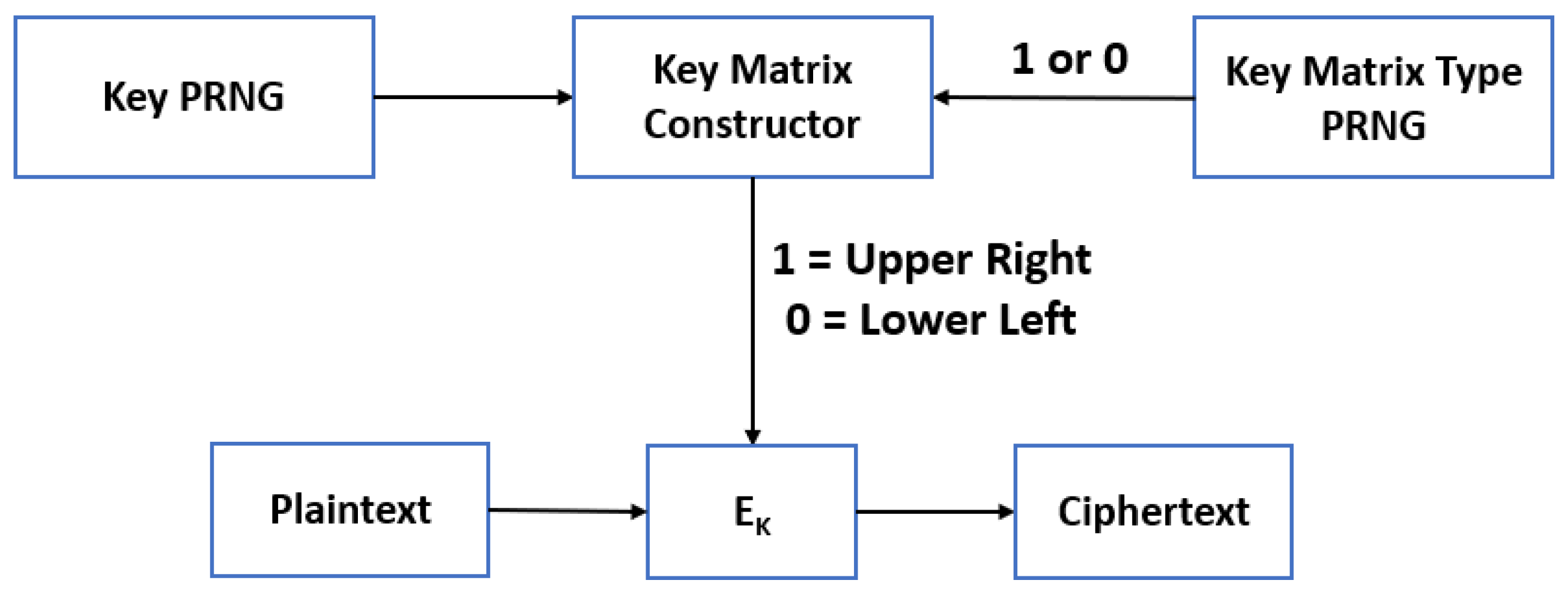In an upper-right triangular matrix, ciphertext words at index i are a result of $n-i$ plaintext combinations; in a lower-left matrix, ciphertext words at index i are a result of i plaintext combinations. Diffusion propagates to lower index words in an upper-right matrix and the opposite with a lower-left matrix. To achieve a constant rate of diffusion while maximizing entropy, a system designer could alternate key construction between an upper-right and lower-left triangle. Alternatively, a synchronized PRNG between the sending and receiving devices could make this decision, as shown in Figure 11. By alternating, diffusion need not be restricted to one direction when propagating throughout the resulting ciphertext. Implementing this process does require maintenance of another synchronized PRNG between the transmit and receive devices.

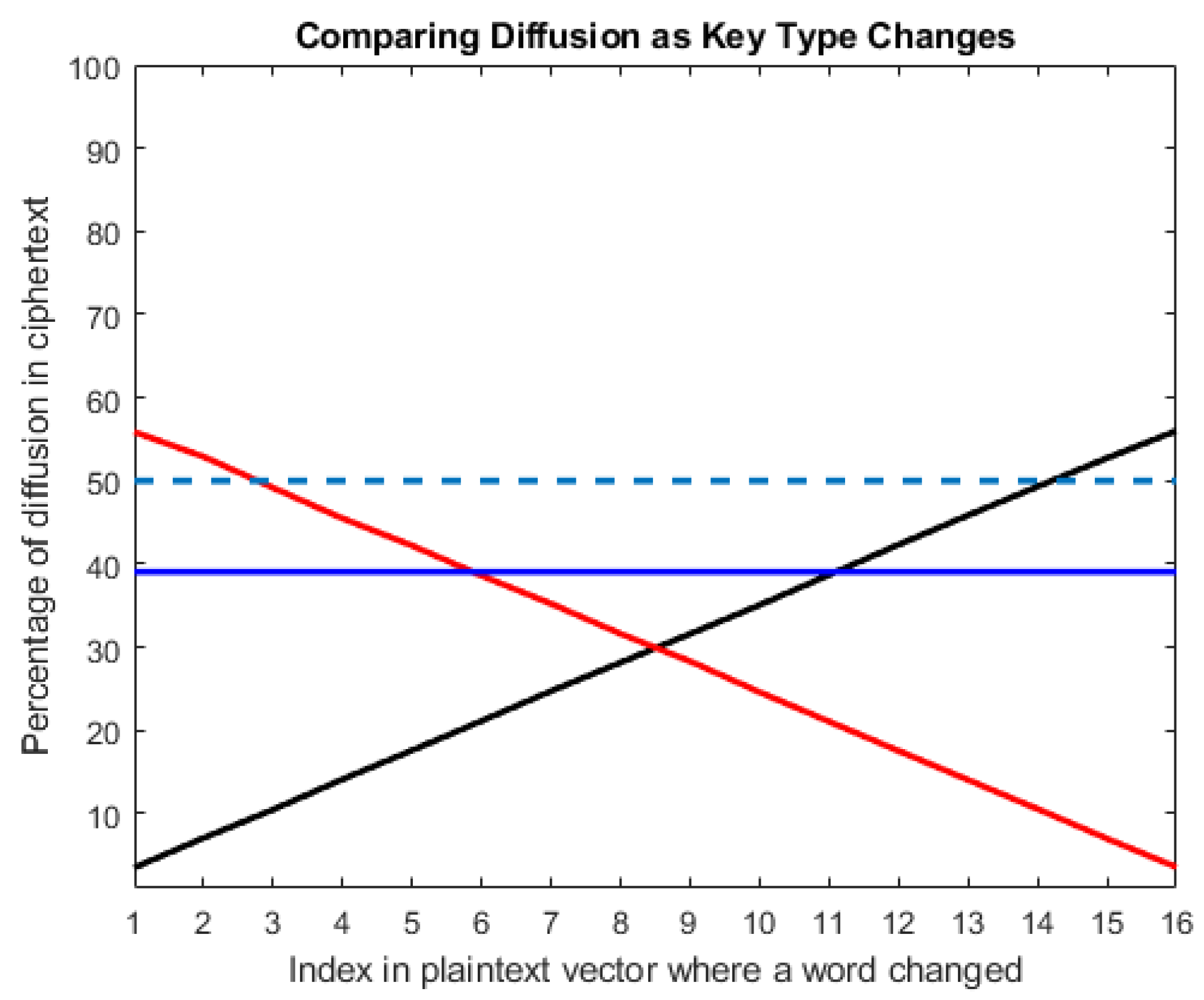
Figure 12 shows a comparison of diffusion rate when encrypting with different types of keys. The black line represents diffusion rate when encrypting with upper-right triangular keys, the red line represents lower-left triangular keys, and the blue line is when the key structure alternates. The dashed line indicates the targeted diffusion rate of 50%. The displayed percentages are averaged over 1000 samples where the x-axis indicates the index of the plaintext word modified by a single bit in each block. As expected, upper-right triangular keys result in higher diffusion at greater indices, whereas using lower-left triangular keys results in the inverse. Alternating between the two every other encryption operation results in a constant rate of diffusion. Note that these are measurements based off a single bit change per block. To achieve a targeted Shannon diffusion rate of 50%, more changes can be induced in the plaintext.

4.4. Memory and Computation Requirements

In this subsection, we attempt to analyze the memory and computation requirements for the ECB, CFB, and stream modes. Scalability is considered, and parameters for real-world applications are recommended. The use of the PRNG is relevant as maintaining this structure contributes to the overall memory space used and computation time.

Memory and computation requirements for ECB mode of the cryptosystem are substantially less than CFB. For a matrix sized $n\times n$, the total memory necessary to construct all key matrices in GF($2^k$) is given by $\frac{\mathrm{plaintext}\_\mathrm{length}\ast (n+1)\ast k}{2}\mathrm{bits}$ where $\mathrm{plaintext}\_\mathrm{length}=\frac{\#\mathrm{of\; bits\; in\; plaintext}}{k}$. Each plaintext word is encrypted exactly once in ECB mode. Overall, the mode requires only $\frac{\# \mathrm{of\; plaintext/ciphertext\; words}}{n}$ encryption or decryption operations to build the ciphertext or retrieve the plaintext.

In CFB mode, the option for an initialization vector (IV) is provided and can be generated by the key PRNG. Without using one, every plaintext word in the first block from index, i, 1 to $n-1$ is encrypted an i number of times. Every subsequent plaintext word is encrypted n times. The use of an initialization vector ensures every value of plaintext is encrypted n times. With the inclusion of an IV, the number of PRNG outputs needed to construct sufficient key matrices is given by $\frac{\mathrm{plaintext}\_\mathrm{length}\ast n\ast (n+1)}{2}$. The amount of ciphertext generated is given by $\mathrm{plaintext}\_\mathrm{length}\ast n\mathrm{bits}$. The total ciphertext generated is n times more than in the standard mode, but a very small increase in entropy and a more uniformly distributed output, as seen in Section 4.1.

While in ECB or stream mode, the amount of memory generated by the encryption process is equivalent to the amount of plaintext. However, the stream cipher requires only as many PRNG outputs as there are plaintext words. The trade-off here is between diffusion rate and PRNG maintenance. CFB mode generates substantially larger amounts of ciphertext than the given plaintext. A maximum practical size for an IoT caliber platform is likely on the order of GF($2^8$) with n = 16 or 32. Keep in mind that during the encryption and decryption operations, all values are extended to a higher field, requiring additional space to temporarily store these values. The PRNG outputs used to construct the matrices can be recycled as soon as they are used, but the computational requirements of this cryptosystem need to be considered.

4.5. Hardware Validation

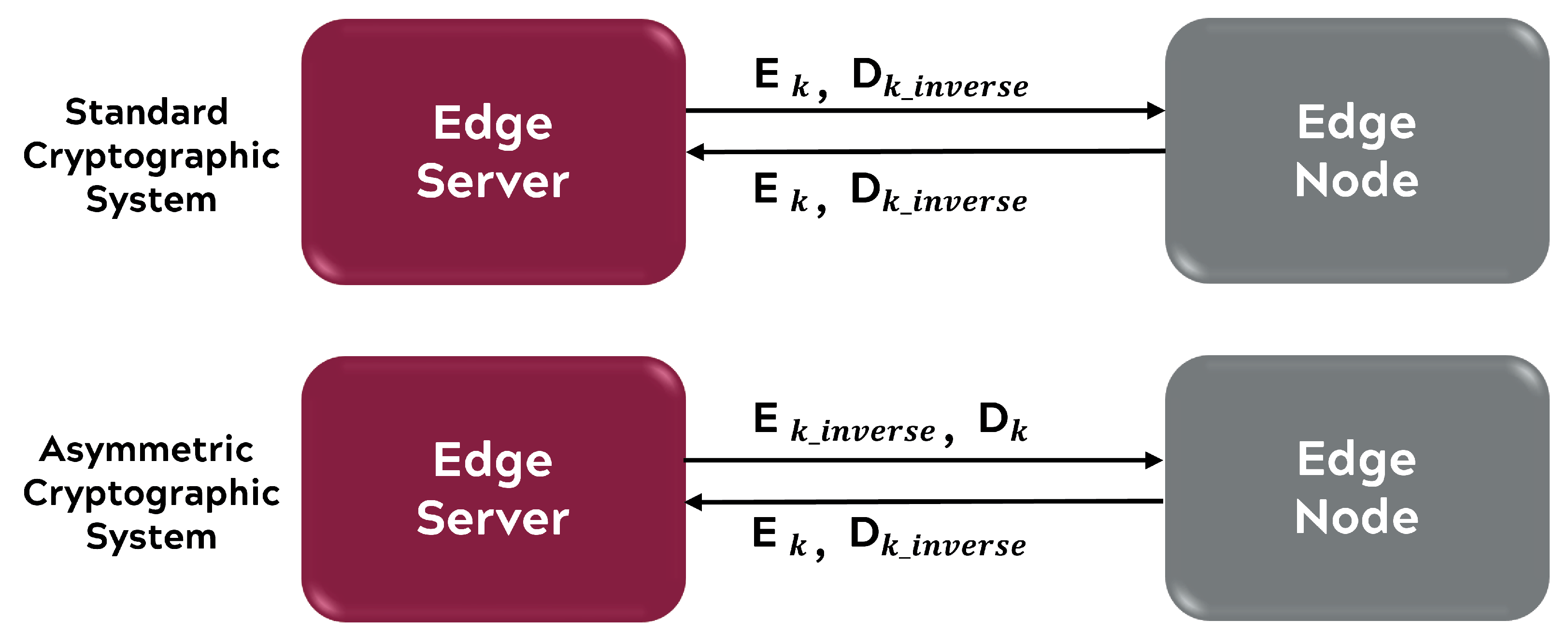
To measure the speed and energy efficiency of this cryptosystem, an implementation was built on a TI MSP430FR5994. The microcontroller chosen to implement the proposed system represents many modern IoT devices, as the device only has 256 KB of FRAM, 8 KB of RAM, and a 16 MHz processor. The microcontroller was chosen to remain consistent with the device used in the stream cipher implementation [23]. The program required 3% of the device’s RAM and 9% of the available FRAM when fully optimized by the compiler. To measure scalability, the cryptosystem was set up to encrypt ASCII text, GF($2^8$), with parameter n = 4. The key matrix was generated by the same single-stage RNS PRNG used in CPU implementation with a period of $M=$14,429,764,351.

The TI microcontroller has internal software called EnergyTrace that can be used to provide time and energy measurements of a section of code. Using EnergyTrace, time and energy usage during encryption and decryption operations were recorded and averaged from 1000 samples in both ECB and CFB modes, as well as AES. These results are compiled in

Table 3. Computation time and energy consumption for encryption and decryption operations on TI MSP430FR5994.

	Stream	ECB	CFB	AES
E${}_K$ Time (mS)	1.167	0.981	3.43	6.379
E${}_K$ Energy ($\mathsf{\mu }$J/byte)	0.155	0.458	2.344	0.884
D${}_K$ Time (mS)	N/A	7.84	77.9	8.12
D${}_K$ Energy ($\mathsf{\mu }$J/byte)	N/A	3.52	33.42	1.125

. The measured results for the stream cipher’s encryption is gathered from previous work [23]. Details on the decryption operation were not provided and are not displayed in the table, but the time and energy required would be about the same. The use of the EnergyTrace program slightly increases the recorded speed and energy consumption due to the capturing process running in the background.

ECB mode required substantially less time and energy for both encryption and decryption than AES, but encrypted a smaller block size. The CFB mode implementation started with a randomly generated initialization vector and encrypted the same plaintext as the ECB experiment. Encrypting all the plaintext required n more operations, contributing to larger time and energy requirements. Decryption operations involve calculating the adjoint of a matrix. The algorithm to do so is almost equivalent to calculating the inverse of a matrix, which has a complexity of $O\left(n^3\right)$. As a result, decrypting the ciphertext in both ECB and CFB modes takes much longer and requires more energy. The system does not scale well on IoT devices when considering values of n and k that would encrypt equivalent amounts of data per block compared to AES. However, the system can encrypt and decrypt more efficiently when operation on smaller block sizes, $n\le$ 4.

5. Conclusions

This paper modified the Galois Extension Field combination technique to work as a block cipher in both ECB and CFB modes. Results displayed in Section 4 validated randomness and uniformity of the resulting ciphertext using the NIST statistical test suite as well as the Law of the Iterated Logarithm. The proposed system relied on the use triangular matrices and PRNGs for both encryption and decryption operations, resulting in easy construction of keys and operation when generating ciphertext or retrieving plaintext. The orientation of the key structure was flexible and could be operated in both upper-right or lower-left triangular format to maximize diffusion and entropy. An implementation of the cryptosystem on a Texas Instruments MSP430FR5994 indicated the system offers a fast, power-efficient alternative to AES on an IoT caliber device. Measurements of energy usage and speed for both encryption and decryption operations show the system was scalable for relatively small values of n. Encryption takes substantially less time since decryption required computing the inverse of the key matrix. While the block size in realistic applications was smaller than AES, the resulting ciphertext maintains strong cryptographic properties, such as a high rate of Shannon diffusion. Optionally, the cryptographic algorithm could be run asymmetrically to support edge computing scenarios, placing the higher load of the cryptosystem on a more powerful device.

Future work on the system would look at implementing a time-varying S-box to include a method of confusion. Research into matrix inverses in finite fields for this paper suggests that nonsquare matrices could tie into a cheap hashing system, checksum, or signature process for the plaintext. More work can be done on the optimization of the hardware implementation to improve performance for larger block sizes.