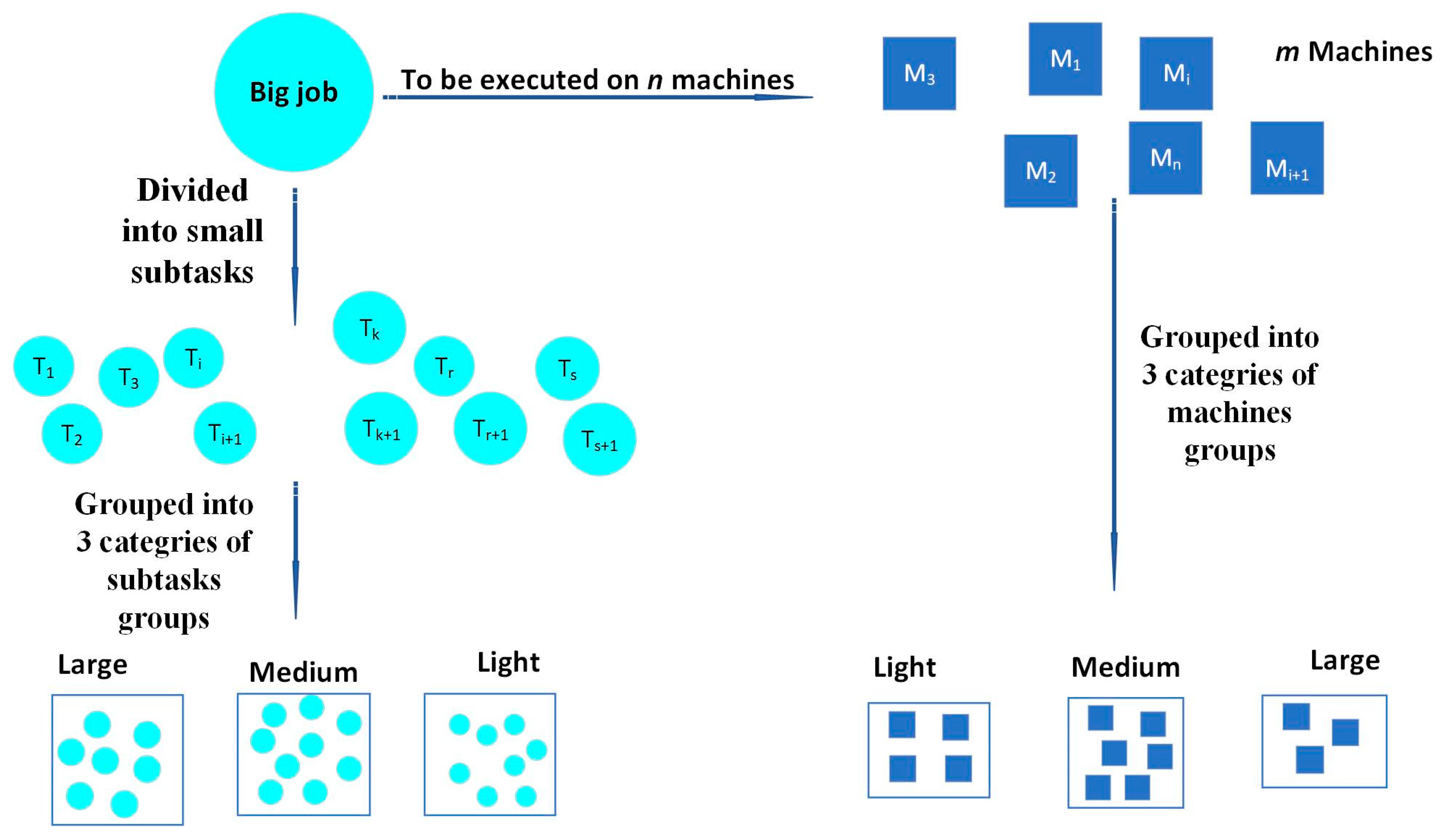
1. Introduction
Continual and accelerated innovation in communications and information technologies has led to an expansion of the modern Internet and its applications and extensions, such as the Internet of things (IoT). The IoT continues to grow rapidly. It has become the basis for the so-called Fourth Industrial Revolution and the digital transformation of business and society [
1]. It is an emerging paradigm aimed at providing appropriate and smart systems of objects [
2]. Making objects smart may be interpreted in two ways. The first interpretation is about entrusting computing power to an object, making it autonomous by allowing it to make its own choices. The second interpretation, for its part, consists of allowing objects to communicate with the outside world and, if necessary, to communicate with machines that can calculate and make decisions. These machines can be located in cloud centers to limit their economic impact [
3]. However, the proliferation of connected objects generates a huge amount of data that is difficult for resource-limited IoT objects to manage. In addition, the exchange and security of this data is a challenge when it is loaded and uploaded between peripheral devices and cloud server centers. In this regard, artificial intelligence (AI) can make a significant contribution to solving this problem, where it can become, along with the IoT, an important achievement [
4].
The IoT supports a wide range of distributed systems that are interconnected with various devices such as servers, database centers, and computers. This is in addition to more powerful and compact portable devices such as smart cell phones and personal digital assistants (PDA) [
5]. It is obvious to researchers and specialists that the demand for these devices has increased steadily. Unfortunately, technological progress has not always followed this tendency. Therefore, scheduling and load balancing techniques [
6,
7,
8,
9] have been developed to close this technological gap.
The scheduling process is concerned with the allocation of tasks to devices over time, whatever the environment may be (deterministic, stochastic, or online), with respect to a given criterion. For the sake of clarity, let us recall the definitions of these environments [
10]:
Deterministic scheduling: the data defining the problem are known in advance;
Stochastic scheduling: all or most of the parameters that describe the problem are random variables over known distributions;
Online scheduling: all or some of the parameters describing the model are known only at the time the decision has been made.
Improving the scheduling process requires a better understanding of the environment under study and depends on whether it is static (fixed and non-modifiable scheduling) or dynamic (re-evaluated online to respond to changes). Likewise, the environment treatment criteria on a local or distributed level can be classified into different types: (1) hard constraints (the constraints must be strictly respected), (2) soft constraints (there is a flexibility with respect to the constraints), (3) preemptive (tasks may be interrupted before completion), or (4) non-preemptive (tasks are executed without interruption until completion) [
11,
12,
13].
Scheduling problems occur in various real-world applications, such as industrial production, hoist scheduling, airport control towers, assignment of processes on processors, and data transfer services. Scheduling problems were originally studied in the industrial sector, such as the manufacture and assembly of large generators, and this led to the introduction of critical path analysis (CPA) and the critical path method (CPM) [
14,
15]. Recently, scheduling problems has emerged as an active field of research in the IoT community [
16] and in mobile collaborative computing models via architectural models of cloud, fog, and edge computing [
6,
17]. As these emerging architectural models of computing are distributed systems, we focused our study on scheduling parallel machine models.
The development of mobile devices and communication technologies has contributed to their growing utilization in collaborative applications that are complex and resource-intensive [
18,
19,
20]. This has led to innovative designs in mobile collaborative computing and interaction techniques between devices. Among the most important closely related techniques are those for the scheduling and load balancing of tasks. Indeed, the scheduling problem consists of organizing the task execution order on ready devices, while load balancing aims to balance the tasks between devices [
11]. As pointed out in Mishra et al. [
21], the load balancing task determines where certain applications should be executed; it is used for distributing workloads across computing resources.
In this paper, we focus on establishing collaborative mobile systems based on modern technologies such as Pycom’s LOPY4 and direct radio communication by devices to maintain wireless connectivity in different environments, even in the harshest ones [
22,
23]. In the present study, we develop a new scheduling algorithm based on a greedy approach, which is well suited to these environments in terms of speed, quality, and ease of decision-making at every step [
24,
25,
26]. This approach enables small mobile devices to process tasks that match their capabilities where they have resource constraints in the IoT paradigm. Therefore, we adopted a strategy that consists of dividing the task and device groups into corresponding subgroups in terms of task size and device capacity. This algorithm aims to ensure load balancing through a technique that chooses among these corresponding subgroups the devices with the longest execution time first to allocate them to the appropriate tasks.
We conducted an experimental study (simulation) to compare, with respect to criteria based on the overall completion times, three existing solutions with our approach to improve the scheduling and load balancing techniques on the available devices of these systems. Let us note that the choice of these three algorithms was mainly based on the simplicity, efficiency, and speed, as well as the mechanism for allocating devices to tasks [
27,
28]. We believe that the present study provides a path to further research on the development and efficient use of mobile and pervasive computing devices in crucial and urgent situations, such as highly intensive communications that require high bandwidth, smart healthcare, smart cities, harsh cases, and smart cars.
This paper is organized as follows.
Section 2 presents the related works.
Section 3 introduces greedy algorithms as a solution in our approach.
Section 4 describes our contribution to scheduling and load balancing in peripheral autonomous mobile systems. Through an intensive experimental study,
Section 5 validates our approach, then analyzes and undertakes a comparison between our solution and three other algorithms. Finally,
Section 6 presents our concluding remarks and perspectives.
2. Related Works
In this section, we present a review of the literature on scheduling techniques applied in the IoT field. The algorithms presented in [
11] show that the tendencies in this area are evolving more toward approximate (near-optimal) solutions that are generated within a reasonable time. The main reason for these trends is that most scheduling problems are difficult to solve from the computational point of view [
29].
Le et al. [
30] pointed out that source code optimization is an emerging technique used to reduce energy consumption in parallel with increasing the storage and power capacity of mobile devices. This improvement may be achieved by partitioning tasks into smaller tasks.
The classification of task scheduling algorithms differs depending on the viewpoints of the authors. The algorithms fall into six categories [
31], which are presented in
Table 1.
In cloud computing, there are three levels suitable for the task scheduling system [
31]:
The first level is the set of tasks (cloudlets) to be executed;
The second level is the process of appropriately allocating resources to tasks to optimize the use of these resources with respect to the makespan or overall completion times;
The third level is the use of a set of virtual machines (VMs) to perform tasks.
In Sharma et al. [
32], it is stated that there are several task scheduling techniques available for scheduling tasks in a cloud environment under the following categories:
Heuristic techniques can be divided into two subcategories. The first one is a traditional technique for scheduling various tasks, such as FCFS, round robin (RR), and SJF. This approach is simple and imperative, but it always approaches the local optima [
33]. The second category uses a random sample to find the optimal or near-optimal solution. Some of its techniques are Min-Min, Max-Min, improved Max-Min [
34], and Min-Min based on priorities. These techniques generate better results than traditional approaches [
35];
Metaheuristic algorithms generally have functionalities that are like aspects of biological science. They are classified into three categories: (1) metaheuristics, such as genetic and transgenic algorithms, based on gene transfer; (2) metaheuristics based on insect behaviors and their interactions, such as ant colony optimization, the firefly algorithm, bee marriage optimization algorithm, and bee colony algorithm; and (3) metaheuristics based on aspects of biological life, such as the tabu search algorithm, simulated annealing algorithm, optimization algorithm for particle swarms, and artificial immune system [
36].
The main difference between heuristic and metaheuristic is that the former is problem-specific and generates, step by step, only one solution, while the latter is problem-independent and generates several solutions [
32].
Recently, improvements made to scheduling algorithms in cloud computing were discussed and investigated extensively in the literature (see, for example, Sharma et al. [
32]). The analysis of scheduling algorithms is summarized in
Scheme 1.
The need for the fair sharing of resources in wireless networks increases with both the increased demand for their use and the cost of their equipment as it becomes difficult to install more devices (Sherin et al. [
47]). Therefore, the scheduling process becomes the most important factor for improving wireless resource management. Multiple users of the system can access their shared resources efficiently by this scheduling process. These resources are mostly limited when compared with the increasing number of users. Scheduling algorithms offer equitable user access and are essential for ensuring the provision of quality of service (QoS). Let us observe that researchers and practitioners are becoming more concerned with packet scheduling algorithms, which are highly essential for QoS. The design of scheduling algorithms has become more complex due to several factors, including the dynamism of mobile ad hoc networks (MANETs) and vehicular ad hoc networks (VANETs) with frequent topology changes and breakdowns in connectivity. A MANET has many applications, including disaster management, emergency relief, vehicular ad hoc network services (VANETs), war field communications, mobile teleconferencing, and electronic payments. QoS is essential in these real-time applications due to the limited resources and dynamic topology. QoS indicates the service performance level provided by the network to the end user. Depending on the application, it can be based on bandwidth, delay, packet loss, throughput, overhead, jitter, and so on.
One of the key features of ad hoc networks is their capability of operating without a standard infrastructure, and they can be deployed easily for various applications. However, it is difficult to provide QoS for all packets because of the dynamic nature of nodes [
48]. Generally, scheduling algorithms manage changes in queuing dynamics and indicate the packets to be submitted from the queue. To ensure the QoS parameters, these algorithms are determined based on network requirements [
49]. There are two major problems in multi-hop wireless networks: the packet (or package of information, as it is known in the jargon of computer networks [
48]) and the channel scheduling. In this area, scheduling algorithms, generally considered to be non-preemptive, are based on analysis of the QoS parameters, such as the throughput rate, fairness in the network, bounded delay, and jitter. The traditional scheduling approach, which takes advantage of the priority lists, is mainly used in mobile ad hoc networks.
Wireless scheduling algorithms in mobile ad hoc networks are classified according to their application domains into two general classes: packet scheduling and channel-aware scheduling [
47], as presented in
Table 2 and
Table 3 and
Scheme 2.
3. Greedy Approach
Greedy algorithms are a problem-solving paradigm in which local optimal choices are made at every step, and they are expected to yield an optimal overall solution. However, in many problems, they only produce near-optimal solutions [
50]. Let us recall that the greedy approach is well justified for NP-hard problems and it is suited as a solving approach for real problems. However, it is worth noting that for problems with an optimal substructure, greedy algorithms are able to find globally optimal solutions [
51].
For the objective of minimizing an unloading cost function, Mazouzi et al. [
52] studied discharging policies to choose the tasks that must be discharged before selecting the assigned cloudlet, depending on the network and system resources. The unloading cost is declared to be a combination of task execution time and energy consumption. This problem is represented with mixed binary programming. As this problem is NP-hard, a distributed linear relaxation-based heuristic approach is proposed. Likewise, a greedy heuristic algorithm is proposed to solve the subproblems, and it calculates the best cloudlet selection and bandwidth allocation based on the task unloading costs.
Ayanzadeh et al. [
51] proposed a novel hybrid approach, the quantum-assisted greedy algorithm (QAGA), to improve the performance of physical quantum annealers in the process of finding the global minimum in an Ising Hamiltonian model. Ising models are widely used in many areas of science.They routinely apply a Hamiltonian equation to, among other subjects, alloy thermodynamics and the thermal properties of solids [
53]. The QAGA algorithm leverages the quantum annealers to better select candidates at each stage of the greedy algorithm. In fact, it consists of using a quantum annealer at each step to give rise to samples of the ground state of the problem. These samples are used to estimate the probability distribution of the problem variables. Then, it fixes these variables with insignificant uncertainties to move to the next step, where quantum annealing will solve a smaller problem using scattered couplings [
51]. In their experimental study, the authors used a D-Wave 2000Q quantum computer with 2000 qubits and new control features to solve larger problems. The results showed that the QAGA approach could find samples with remarkably lower energy values compared to the better-known improvements in the field of quantum annealing.
In their study, Durmus et al. [
54] aimed to support the assumption that the classic algorithms generate optimal solutions while the greedy heuristic algorithms generate proximate solutions. They argued that not only do the dimensions of problems increase, but the dimensions and number of constraints in packet programs are also limited, so it is difficult for the classic algorithms to provide the appropriate results. However, regardless of the dimensions or the number of constraints, the greedy approach generates appropriate results. As shown in the literature, both the former and the newer versions, such as the ones proposed by Akçay et al. [
55] and Zhou et al. [
56], work efficiently. Indeed, greedy algorithms are more efficient in comparison with other complex algorithms; they produce solutions to everyday problems within a reasonable time. Durmus et al. [
54] applied greedy and some classical algorithms to the problems of integer linear programming and then compared the differences and similarities of the obtained results. Throughout this work, they classified the most-used algorithms in the literature, as displayed in
Table 4, to which we added other greedy approaches and algorithms [
51,
57].
5. Simulation
We present in this section the results of a simulation study we conducted to compare the performance of Algorithm 4, as described above, with LCFP, SCFP, and Min-Min. In these algorithms, a variety of factors and their proper values are considered, such as the processing time, bandwidth, number of tasks, number of devices, sending and receiving tasks, waiting times in the queues of the devices, and capacity of each device.
Note that the simulation did not consider some factors in mobile systems such as device communication, bandwidth, the sending and receiving of tasks through networks, and their waiting time in the queues of the devices.
Even though we used a single computer in this experimental study instead of several devices to process all the tasks, we accurately calculated the values of the estimated factors of algorithm performance. We compared and analyzed the four algorithms based on the following criteria:
The overall completion time, known as the makespan M (, where denotes the completion time of device ;
The standard deviation SD (SD = );
The absolute difference AD between the maximum completion time M () and the minimum completion time L () (i.e., AD = |M-L|).
We then computed the percentage for the number of times that each algorithm produced the minimum values of these factors (makespan, SD, and AD). The value of the makespan indicates the time at which the entire set of tasks is completed, thus representing how efficiently the devices are used. The value AD represents the range of the completion times of the devices, thus representing how well-balanced the generated solution is. The standard deviation expresses the dispersion of the completion times of the devices around the makespan. A low value of standard deviation indicates that the completion times tend to be close to the value of the makespan, which is to say that the schedule is well-balanced.
The experimental study we conducted used the WampServer web platform, an SQL server, and the PHP programming language to implement and validate the proposed algorithms. It was implemented on a laptop with the following characteristics: Intel
® Core™ i7 processor, x64-based processor, Windows 10 Pro 64-bit OS, 2.3 GHz CPU, and 16 GB of RAM.
Figure 4 presents the graphical interface for the simulation.
To ensure the reliability of our method, it is necessary to mention the external factors that might have affected the tested algorithms. Among those factors, we may mention the computer self-configuration resources in execution times. Thus, they influenced the operating system in terms of scheduling their execution in conjunction with these algorithms. As these factors operate automatically while the algorithms are executed, they affect the length of the processing time. Therefore, considering these factors, in terms of the impacts they may have had on the implementation of the algorithms, enabled us to verify and confirm the credence of the results.
For each group of m devices (
m = 60, 40, 30, 20, 10, 5), we randomly generated from [
11,
24] the estimated available time values for each device. Then, for each group of tasks (
n = 200, 100, 80, 60, 40, 20, 10), we generated 100 instances, for which the processing times were randomly drawn from [
11,
53] and on which the four algorithms were executed.
For each instance, we compared the makespan values of the four algorithms. We increased by one the score of the algorithm with the minimum makespan. If two algorithms had the same minimum makespan, we compared their standard deviations and increased by one the score of the algorithm with the minimum standard deviation. If they again produced the same minimum standard deviations, we compared their absolute difference and increased by one the score of the algorithm with the minimum value. If they still had the same absolute difference, we increased by one the score of the algorithm with the minimum score. The best algorithm was the one that had the highest score over the 100 instances.
In the following, we first present a comparison of the minimum makespan, the standard deviation, and the absolute difference with respect to the completion times of the four algorithms (LCFP, SCFP, Min-Min, and Algorithm 4). Next, we also present, for the same instances, the results with respect to the running times of these algorithms.
Displayed in
Figure 5 are the different tables that summarize the results of the experimental study which satisfied the criteria (completion time M, standard deviation SD, and absolute difference AD).
Figure 5 illustrates the performance of the four algorithms for various number of devices and tasks. Whereas,
Figure 6 summarizes the average running times of these four algorithms.
Regarding the scheduling solution, our algorithm succeeded in reducing the completion time of the tasks. At the same time, it improved the device load balancing by preparing devices with larger execution times to be chosen first by the algorithm and accomplish the appropriate tasks.
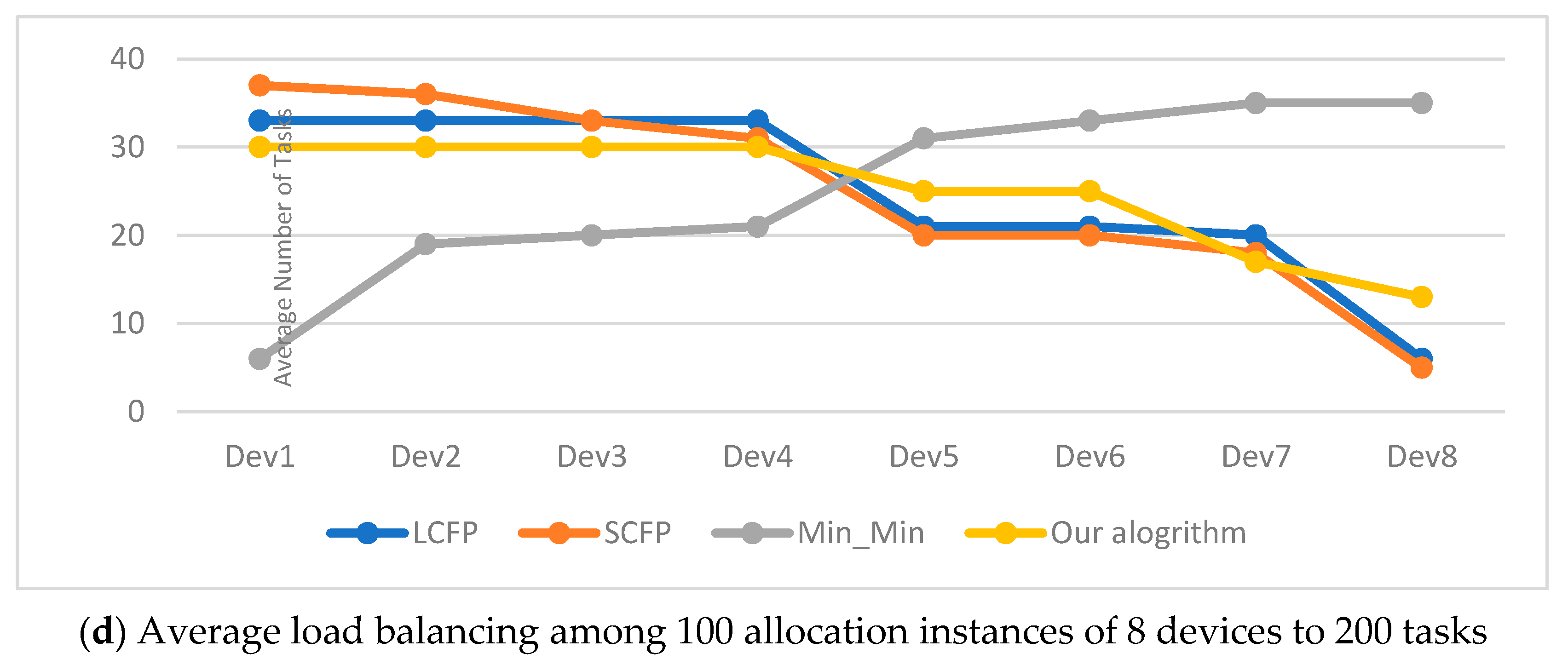
Figure 7 shows our algorithm performance compared with the other algorithms for load balancing in the experimental results, with respect to 10 devices and 20, 70, 100, and 200 tasks. For the correct interpretation of these graphic lines in
Figure 7, we proceeded from the fact that the ideal line representing the best performance is the horizontal line crossing them in the middle. Therefore, the best algorithm is the one with the closest graphic line to that ideal line, illustrated by our algorithm for most of the cases.
The results in these above tables clearly show the superiority of our algorithm. Indeed, our algorithm became more advantageous whenever the difference between the number of tasks and the number of devices became larger (i.e., in cases where the number of tasks is greater than the number of devices). This advantage is directly proportional to the increase in this difference in favor of tasks. Whenever this difference is large, the results generated by our algorithm are the best. The main reason for this is that the device and task groups were partitioned into three similar and relatively small subgroups. This reduced the time it took to navigate through them and find the appropriate devices to execute the tasks. The performance of the remaining algorithms, in decreasing order, is as follows: LCFP, Min-Min, and SCFP. From the above tables, it is easy to observe that our algorithm outperformed the other three algorithms with respect to three criteria: makespan, standard deviation, and the maximum of the absolute difference in completion times, whatever the number of devices or the number of tasks.
To summarize the results, our contribution is made through a dedicated approach adapted to the ubiquitous devices widely used in the IoT paradigm, particularly at the periphery of their communication networks. The goal was to build a new heuristic algorithm and compare it with the other scheduling heuristic algorithmsmostly used in the literature. The main advantages of this approach are brought up through the reduction of the size of the tasks to be performed and breaking them into smaller subtasks. In addition, the process of dividing the groups of subtasks and devices into smaller sub-groups makes it possible for a parallel search to get the desired solution. Proceeding as such makes our algorithm faster and the quality of the generated solutions much better. Consequently, our approach saves a lot of energy, in addition to improving the efficiency of these devices.
6. Conclusions and Future Works
The effectiveness of any scheduling algorithm depends, among other things, upon the overall completion time. Partitioning large tasks into smaller tasks plays an important role in getting these tasks done with shorter completion times. Greedy scheduling algorithms are a popular and widely used approach that produces a balanced, near-optimal solution for scheduling problems. Based on this idea, we proposed a new greedy scheduling algorithm for autonomous smart mobile systems, especially those found at the network’s periphery. It takes advantage of the ability of these devices to maintain connectivity through a D2D radio connection. This feature allows devices to continue to communicate and therefore to work with each other, even in the event of wireless failures or communication flooding on the network. Thus, they can always perform the necessary tasks at any time and in any situation. This algorithm is based on the idea of dividing large tasks into smaller tasks to facilitate and speed up the scheduling process and thus their rapid completion. It creates similar subgroups in terms of the size of the tasks and devices. Then, it allocates tasks to devices between similar subgroups and, if necessary, to the larger device subgroups. We have shown through a preliminary study that this algorithm is compatible with mobile systems having resource constraints. Due to the limited capacity of devices, they do not tolerate the long process of computing. Therefore, they are not able to adopt a complex scheduling method. Instead, they require a series of simple scheduling strategies. The preliminary study we conducted showed that our algorithm had a clear advantage over the LCFP, SCFP, and Min-Min algorithms. On the one hand, our algorithm generated small average times for allocating devices to tasks. On the other hand, our algorithm outperformed the three comparison algorithms we presented with respect to the makespan, standard deviation, and range of completion times criteria. Likewise, significant improvements in load balancing could also be added to these advantages.
Current research provides reliability in reducing the completion time for urgent requests and thus in speeding up their completion, especially in harsh environments. For future work, we aim to apply our algorithm to more scenarios and situations. In particular, we aim to use it with more autonomous intelligent mobile systems having a large number of tasks to be performed on multiple devices. These advantages of the proposed method could be added to other functionalities, such as maintaining connectivity and processing via parallelism.