A Binary Trust Game for the Internet of Things

Abstract

The IoT is transforming the ordinary physical objects around us into an ecosystem of information that will enrich our lives. The key to this ecosystem is the cooperation among the devices, where things look for other things to provide composite services for the benefit of human beings. However, cooperation among nodes can only arise when nodes trust the information received by any other peer in the system. Previous efforts on trust were concentrated on proposing models and algorithms to manage the level of trustworthiness. In this paper, we focus on modelling the interaction between trustor and trustee in the IoT and on proposing guidelines to efficiently design trust management models. Simulations show the impacts of the proposed guidelines on a simple trust model.

1. Introduction

The Internet of Things (IoT) has become one of the most important realities of our century, able to connect billions of devices. This paradigm allows us to connect everyday objects seamlessly to the Internet, in any place and at any time [1]. The massive amount of data flowing through the IoT has pushed forward the development of new applications in several domains, such as the management of industrial production plants, logistics and the transport supply chain, e-health and smart buildings, just to cite a few.

The IoT is transforming the ordinary physical objects around us into an ecosystem of information that will enrich our lives. The key to this ecosystem is the cooperation among the devices, where things look for other things to provide composite services for the benefit of human beings. Thanks to the interactions between objects, IoT applications can be designed so that each device can play the role of a service provider or a service requester, or both. In this scenario of object-object interactions, it is essential to understand how the information provided by each object can be processed automatically by any other peer in the system. This cannot clearly disregard the level of trustworthiness of the object providing information and services, which should take into account the profile and history of it. Trust management is a crucial aspect of the IoT that ensures the exchange of information by the nodes, reducing the risk of untrustworthy data [2]. Trust can concern many fields in everyday life, and it has many definitions; however, the IoT literature on trust is quite confusing. In this paper, we adopt a specific definition of trust:

Trust is the subjective probability by which an individual, the trustor, expects that another individual, the trustee, performs a given action on which its welfare depends [3].

In the IoT, the requester represents the trustor, the object that looks for services, while the trustee provides the needed information and is depicted by the provider. The trustworthiness management model has to identify which provider is trustworthy, select it as the requester and check if the interaction is reliable. However, malicious devices can perform attacks providing scarce services for their own gain. Trust models are designed in order to detect and discard these nodes and to increase the trust of the network.

In the state-of-the-art, many researchers have proposed different models that encourage collaboration in IoT networks and try to detect malicious behaviours. Nevertheless, these works consider only a subset of attacks and are strongly tied to their reference scenario. Indeed, collaboration among nodes can only be achieved when trust is built between all involved parties, since without effective trust management foundations, attacks and malfunctions in the IoT will outweigh any of its benefits. As shown in Figure 1, the concept of trust is tied to the perception of a trustor to evaluate a trustee’s trustworthiness under external conditions, such as the misbehaviour of devices or errors on data process and analysis. Therefore, it is important to understand the general problem of trust in a generic IoT network and which behaviours all the nodes can assume. Therefore, we propose the guidelines to design a suitable trust model in order to address it and to guarantee the proper functioning of the IoT network. To this, game theory can represent a useful tool to analyse the interactions between requesters and providers. In this paper, we illustrate the game dilemma that describes the behaviour adopted by the nodes, both benevolent and malicious. To the best of our knowledge, this is the first work that derives the guidelines needed to design a trust management model for the IoT so that it is able to cope with the most common attacks.

To summarize, the major contributions of the paper are:

• Modelling the interaction process between requesters and providers through a binary trust game, which defines the node’s behaviours, i.e., the possible strategies, and the possible payoffs.
• Proposing guidelines to design a suitable trust management model in two different scenarios: an errorless scenario, where cooperative nodes are always able to deliver the requested service, and a realistic environment, where cooperative devices can show poor performance, because of errors, poor accuracy, or technical problems in general.
• Analysing the performance of the proposed model to evaluate the efficiency of the proposed guidelines.

The rest of the paper is organized as follows: Section 2 presents a brief survey on the importance of trust in the IoT, attacks on services and the game dilemma used to design a trust model. In Section 3, we define the scenario and the game definition; moreover, we expose the mathematical model for all the behaviours and the rules to design a suitable trust model. Section 4 presents the performance and the experiment simulations, while Section 5 draws final remarks and a discussion about the guidelines’ usability for the community.

2. Background

2.1. Importance of Trust in the Internet of Things

Trust has been recognized as a critical factor for the Internet of Things. Trust management allows multiple objects to share opinions about the trustworthiness of other devices. Trust as an abstract concept can provide a uniform decision for heterogeneity and multiple domains in the IoT [4].

Trust is the critical factor in almost every aspect of the IoT and in network applications. Figure 2 provides a simple example of a generic network, with each node capable of providing one or more services, as highlighted in the grey clouds; Node 1 is the node that is requesting the service $S_7$, as highlighted in the white cloud; in this example, we consider that Nodes 5 and 6 can provide the requested service, and then, they represent the providers. For each of the possible providers, the requester computes the trustworthiness level ($T_{15}$ and $T_{16}$) and then chooses the provider with the highest value, which is number 5 in our example. Therefore, the goal of the paper is to provide the guidelines to design a trust management model in order to provide suitable services to the IoT nodes, discarding all the malicious behaviours.

Over the last few years, many researchers have taken into account this problem, so the literature presents trust models that implement different techniques and metrics. However, the extensive research on the topic has created confusion about the effectiveness of some trust parameters and how these can be used effectively to create a trustworthy environment. Moreover, there is confusion around the concept of trust, which sometimes gets even misunderstood with the security issue.

This subsection provides a brief overview of the main concepts used in trust models that are well known by the research community. Accordingly, we analyse the trust models and their parameters.

Trustworthiness is an important element in many IoT scenarios. For example, recently, the medical industry tried to combine IoT technology with medical instruments: the reliability of the information exchanged by IoT devices is of paramount importance for the safety of people. In this regard, in [5], the authors proposed a trust management approach based on Bayesian inference to detect malicious devices. The authors proposed a trust protocol that uses information sharing among IoT devices in a centralized architecture. They defined the nodes’ trust in an interval $[0, 1]$ as the probability that the packets are normal and not bad, using 0 for a bad provider and 1 for trustworthy nodes. All the nodes have the competency to perfectly evaluate the received service, and they start with a trust value equal to 0.5. The threshold used to consider the node as benevolent is set according to a particular scenario, and it can be modified by the network’s owner.

Two other approaches developed for a generic scenario were described in [6,7]. In the first work, the authors proposed a trust management model for mobile networks that support both direct and indirect trust opinions in a weighted sum equation. Each requester node calculates for each interaction the providers’ trust by taking into consideration several parameters, such as the number of packets properly forwarded and the recommendations provided by other nodes. In their model, a value of zero was used for untrustworthy nodes, while one was used for completely trustworthy objects; the decision threshold was computed according to the network deployment scenarios, and the initial trust for recommendations was set to 0.5. In [7], the authors illustrated a centralized trust mechanism in order to detect attacks on recommendations. The system assigned to each node a trust value in $[0, 1]$, which was computed based on its past interactions, QoS metrics and recommendations from other objects, while the trust threshold was set to 0.5. Similar to the previous work, no decrement/increment of trust was evaluated, but the model computed the trust of the provider anew during each interaction.

In recent years, many researchers have tried to improve the reliability of trust models, in terms of the ability to detect malicious behaviours, e.g., by making use of blockchain approaches. However, several of these works aimed to increase trustworthiness through security mechanisms. Among them, in [8], the authors proposed a blockchain-based trust system for IoT access control. Each node calculates the trust in an interval of $[0, 1]$ for each provider starting from an initial value of zero according to the previous interactions, while the blockchain network takes care of the global recommendations from other objects. The decision takes care of two thresholds for the internal trust and the global reputation set by the owner. Moreover, a recent work based on the blockchain was described in [9]. The model guarantees the nodes’ authentication thanks to the blockchain. The trustworthiness is measured according to a voting mechanism and the reputation received from the other nodes in the network. A different interval for trust was used by the authors; in this case, they set $[0, 2]$, where values of zero or two were assigned to completely trustworthy nodes and zero to objects that only received bad recommendations. Any initial value was used, and the trust was calculated for each interaction from scratch.

To sum up,

Table 1. Trust models’ parameters’ comparison of the most recent studies.

Ref.	Architecture	Trust Interval	Initial Trust	Trust Threshold
[5]	Centralized	$[0,1]$	0.5	Based on the scenario
[6]	Distributed	$[0,1]$	0.5	Based on the scenario
[7]	Centralized	$[0,1]$	0.5	0.5
[8]	Distributed	$[0,1]$	0	Set by the owner
[9]	Centralized	$[0,2]$	No initial trust	Set by the owner

shows a comparison of the analysed models and their parameters. The analysed works designed trust algorithms with different levels of performance.

However, all the works presented confusion in some important parameters, and these were set as a consequence of simulations and not on the basis of theoretical analysis. Trust models showed the highest dissimilarities, especially in the choice of the initial trust for the nodes and of the threshold used to identify the malicious objects. Therefore, it is important to understand how these values must be set and how they are essential in order to design a suitable trust management model.

2.2. Trustworthiness Attacks

In an IoT network, two different behaviours can be considered: one is always benevolent, trustworthy and honest, while the other one is malicious and cheats whenever it is advantageous for it to do so. It is then important to evaluate the consequences that may occur to a network due to the presence of malicious nodes [10]. The goal of a malicious device is to maintain its own resources intact by providing false or poor quality services. At the same time, a malicious node wants to maintain a high level of trust in order to not be discarded from the network. This strategy, even if successful for a single node, at first sight, involves a huge risk for the network because trusting the information from malicious devices could lead to serious compromises within the network, and this has a direct impact on the applications that can be delivered to users [11]. In this paper, we are concerned with trust-related attacks, and in particular, we consider malicious devices that can perform the following attacks on services:

Malicious with Everyone (ME): This is the simplest attack. The malicious node provides only false services to everyone [12]. It is the first malicious behaviour considered by a generic trust management model and is often used as a reference attack.

On-Off Attack (OOA): This is a dynamic attack in which the malicious object periodically changes its behaviour from an ON to an OFF state, and vice versa [13]. In the OFF state, the node acts maliciously and provides bad services, while during the ON condition, the node behaves benevolently to build up its trust value.

Whitewashing Attack (WA): A malicious node with a low value of trust leaves the network and then re-joins using a new identity [14]. Therefore, the object returns to its default reputation value and can start to provide bad services again.

Opportunistic Service Attack (OSA): A malicious node provides opportunistically good services to attract service requesters [15]. When it has a high reputation level, it starts to act maliciously. The node tries to maintain its trust at an adequate value.

2.3. Binary Trust Games

In many situations, from social to economic, the interactions among peers presuppose trust. These interactions have been formalized and described as games with two players and two periods of play, and the resulting games have been referred to as trust games [16]. A trust game can be considered as a one-sided prisoner’s dilemma game.

Each device acts as a player that chooses its own strategy based on the information it has in order to maximize its payoff [17]. This way, the game can be used to study the dynamics between untrustworthy and trustworthy nodes. An analysis of the two-player game (requester versus provider) can provide the tools to design a suitable trust model. This study is supported by decision-making theorems that help to analyse the strategies of the player: one of them is the Nash equilibrium. According to it, the dominant strategy for each player exists if no one changes its behaviour, and each player’s payoff is optimal when considering the decisions of other players. This study helps us to identify the nodes’ behaviour in the IoT and how the network owner can improve the trust for all the interactions.

In the IoT, both the requester and the provider face a binary choice, not a continuous one: the trustor has the binary choice to trust the trustee or not, and in case the trustor decides to trust, the trustee faces a binary choice to either honour it or abuse the demonstrated trust. The binary trust game was formalized in [18]. Figure 3 illustrates the original game proposed in the state-of-the-art [18]. We add a brief description of it for the sake of clarity, but we refer to the cited paper for a more detailed description. In the game, a player, the trustor, is endowed with an amount of €10, and it has to decide to keep the whole amount for itself or to transfer the sum to a second player, the trustee. In the first case, the game ends with an amount of €0 for the second player, so the trustee is not trustful. Otherwise, if the trustor provides the sum to the trustee, the €10 is quadrupled, and consequently, the trustee receives €40. Now, it has to decide between two behaviours: it can be a trustworthy player giving €22 to the first player while keeping €18 for itself or it can act maliciously by keeping €40 for itself and leaving the trustor with an amount of €0.

For many years, researchers have studied the binary trust game in order to analyse the mutual benefit originated from a form of reciprocity. In [19], the authors illustrated the impact of a set of different motives of choices in the dual-role game. They employed data from a large experiment in which all the participants made a decision from both of the roles. At the end of the experiments, they identified four types of players: trustful and trustworthy, non-trustful and non-trustworthy, trustful and non-trustworthy and non-trustful and trustworthy. Most results from the analysis illustrated how especially strategic considerations rule the behaviours, and not altruism or spitefulness. Furthermore, in [20], the authors used the game in order to study the evolution of trust and trustworthiness in different populations. They showed how the network structure has little effect on the evolution of trust and trustworthiness and how other parameters rule the players’ decisions, e.g., rewards or individual differences among participants.

Moreover, the binary trust game is employed in other scenarios. Among these works, in [21], the authors conducted experiments based on the mentioned game in order to analyse the form of behaviours in many important economic decisions. The cooperation regarding economic psychology was also illustrated in [22]. The authors showed how cooperation is affected by many parameters. People try to mitigate the risk of decisions according to details from other encounters, while if they are strangers, they have to rely on their intuitions in order to predict the behaviour of the other player. Another work was presented in [23] for a physiological human scenario. The authors used the game in order to study human behaviour concerning cooperation and to describe the personality characteristic that would play this significant role. On the other hand, the game was employed also to describe the highly uninhibited and impulsive personality that refuses game cooperation, acting maliciously.

All these works tried to explain the different behaviours in a two-player game that requires trust. This paper aims to provide the essential elements needed to design trustworthiness management algorithms in an IoT scenario. We address this goal by applying a binary trust game to the IoT scenario in order to capture the potential insights from the evolution of trust and trustworthiness due to the objects’ interactions.

3. The Trustworthiness Model

In this section, we model the trust game between the generic requester and the generic provider, and we provide the guidelines to build a trust management algorithm able to detect malicious behaviours.

3.1. Scenario

The IoT is composed of billions of intelligent nodes that are uniquely addressable, where each node can provide a combination of sensing, actuation and computational services. Things are then able to look autonomously for other things to request their services to compose them for the benefit of human beings. In order to deliver trustworthy applications back to the users, nodes have to understand which, among the nodes in the network, are trustworthy and can then lead to successful collaborations.

In such a scenario, the requester has the role of the trustor and has to trust that the provider, which is then the trustee, will provide the required service. For every service request, both the requester and provider have costs and benefits associated with them, so each node needs to find a trade-off between the cost and the benefit related to a request. From the point of view of the requester, it has a cost $c_r$ associated with its request, which can be related for example to the delay in providing the service back to the user, but it has an obvious benefit $b_r$ related to obtaining the desired service. The provider, instead, has to consider the cost $c_p$ to solve the request, which can be tied for example to the energy consumption to make a sensing measurement, and a benefit $b_p$ for its reputation, which can be increased or decreased according to its behaviour.

In our scenario, the requester has to select one of the providers based on their level of trust: the higher the level of trust, the higher the probability to receive the desired service, and thus to maximize the payoff. The trust level is computed according to the trustworthiness management model implemented, which has the fundamental role of identifying malicious nodes. The goal of this paper is to study the trust game between the requester and the provider as a framework and to propose guidelines to design suitable trust models.

3.2. Game’s and Payoffs’ Definitions

The proposed trust game consists of a finite set of devices acting as players, where a link between two devices denotes the possibility of interactions or transactions between them. The game is based on pairwise interactions, i.e., every device interacts or transacts with other directly connected devices in pairs. Pairwise interactions proceed in two phases. A requester needs a service and can choose whether to select a provider, the trustee, to retrieve it (i.e., being trustful) or to do nothing (i.e., being not trustful). In the latter case, the game ends, and both players get a zero payoff: the trustor has not received the service, and the trustee did not have any chance to take part in the game. In the former case, the trustor needs to consume some of its resources in order to send the request to the provider, which in return has to decide to defect or collaborate. If it collaborates, both players receive a reward, respectively $R_r$ for the requester and $R_p$ for the provider. However, if the provider defects, i.e., it behaves maliciously, it receives a greater reward, equal to T (temptation), while the requester receives a negative payoff S. The negative payoff is due to the false service received by the requester that must be discarded, while the malicious provider safeguards its resources and obtains a greater reward. During a single interaction, for the provider, defection always results in a better payoff than cooperation, since the requester cannot punish it, and so, it represents a dominant strategy. The best strategy for the requester is then to be not cooperative and not to ask for services. Mutual defection is the only strong Nash equilibrium in the game, so this results in a network where nodes do not interact with each other.

Figure 4 illustrates the decision tree for the evaluated trust game.

However, two IoT nodes can interact more than once in succession, and they can remember the previous actions of their opponents and change their strategy accordingly. Under these conditions, the game becomes iterated; nevertheless, if the game is played exactly N times and both players know the number of transactions, then it is still optimal to defect in all rounds, and the Nash equilibrium is to always defect. The proof is inductive: the provider could defect on the last transaction since the requester will not have a chance to change its strategy later. Therefore, both will defect on the last transaction. Thus, the provider might as well defect on the second-to-last interaction, since the requester will defect on the last no matter the provider’s behaviour, and so on.

For these reasons, we consider an iterated trust game with an unknown number of transactions, where the complete payoff is determined according to the strategy adopted in each game. The incentive to behave maliciously in the short term is compensated by the possibility for the requester to punish the provider after the abuse of trust. For cooperation to emerge between rational game players, the total number of rounds must be unknown to the players. In this case, “always defect” may no longer be a strictly dominant strategy, but it remains a suboptimal Nash equilibrium. Based on the previous considerations about the cost and benefit for the two players, the payoffs are determined as follows:

$$\left\{\begin{array}{c}S=-b_r-c_r\hfill \\ T=b_p\hfill \\ R_r=b_r-c_r\hfill \\ R_p=b_p-c_p\hfill \end{array}\right.$$

(1)

The punishment S reflects the request’s cost $c_r$ and the false benefit received, specified by $-b_r$. Moreover, the temptation T is related to the benefit of the malicious behaviour $b_p$, without any cost. In addition, the payoffs $R_r$ and $R_p$ are the results of the collaboration between the players: the first depends on the request’s cost $c_r$ and on the benefit of the received service $b_r$, whereas the second payoff concerns the provider with the cost to provide the service $c_p$ and the benefit in terms of its reputation $b_p$. From this, we model the payoffs’ constraints as follows:

$$\begin{array}{cc}\hfill & Requester:R_r>0>S\hfill \\ \hfill & Provider:T>R_p>0\hfill \end{array}$$

(2)

The punishment S is the worst payoff for a requester: this is due to the resources used for the request and to the false service received. Regarding the provider, the temptation T is greater than the payoff resulting from collaboration and the related reward. Moreover, the requester and provider payoffs are related by the following:

$$R_r>T$$

(3)

This relation shows how the requester obtains a greater payoff than the provider since the requester receives the desired service, while the requester increases its reputation.

The relations in terms of benefit and cost are shown below:

$$b_r-c_r>b_p$$

(4)

where it is remarked how the requester has a benefit/cost greater than the provider; this is due to the requester being more interested in the communication to receive the needed service.

3.3. Strategies and Attacks

In order to provide general guidelines for the development of trust algorithms, we consider a generic trust model. Due to the iterated nature of the considered trust game, the nodes’ strategies must reflect their past interactions. For each interaction k, the generic trust value assigned to the provider can be expressed as:

$$T\left(k\right)=T(k-1)+\Delta$$

(5)

where $T(k-1)$ represents the trust value during the previous transaction, while $\Delta$ indicates the trust variation based on the provider’s behaviour in the last round:

$$\Delta =\left\{\begin{array}{cc}-{\Delta }^{-},\hfill & \mathrm{malicious} \mathrm{behaviour}\hfill \\ {\Delta }^{+},\hfill & \mathrm{benevolent} \mathrm{behaviour}\hfill \end{array}\right.$$

(6)

When there is no previous information, i.e., during the first interaction, an initial trust value is assigned to each provider, so that $T\left(0\right)=T_{init}$.

The requester changes its behaviour based on the computed trust value and chooses a strategy in the iterated games in order to increase its total payoff. To simplify the analysis, all the parameters are in the range $[0, 1]$, so that, e.g., a trust value of zero indicates untrustworthy nodes, while a trust value of one is used for completely trustworthy nodes. Moreover, whenever the trust value of a device is lower than a given threshold $T_{th}$, the node is immediately labelled as malicious.

The evolution of trust depends on the strategy adopted by the provider in the previous interaction, which has a direct impact on the trust variation $\Delta$. Two different behaviours can be considered in a network: one is always benevolent (or cooperative) and provides only good services; therefore, its trust is always increased after a transaction, and $\Delta ={\Delta }^{+}$. The other behaviour is a strategic one corresponding to an opportunistic participant who cheats whenever it is advantageous for it to do so. A node that performs maliciously usually provides false or scarce services in order to save its resources. Below, we model the most studied attacks on trust in the literature and study the strategies that can be used to develop a suitable trust model.

A node performing the Malicious with Everyone (ME) strategy acts maliciously with everyone. Regardless of the interaction, the node sends only false services, and its trust value is then always reduced ($\Delta =-{\Delta }^{-}$). We can then model its trust evolution as follows:

$$T\left(k\right)=T(k-1)-{\Delta }^{-}$$

(7)

Another malicious attack is the Whitewashing Attack (WA), which shows a very simple dynamic behaviour. This behaviour is similar to the ME, which provides only bad services, with the difference that a node performing this attack can re-join the network and then re-initialize its trust value. Similar to the previous case, $\Delta =-{\Delta }^{-}$, and the trust evolution is the same as Equation (7).

A more complex dynamic attack is the On-Off Attack (OOA), where the malicious node changes its behaviour from benevolent to malicious, and vice versa, every M interactions. In this case, we can model the trust variation $\Delta$ based on the first behaviour adopted by the provider. If the node starts with malicious behaviour, $\Delta$ can be expressed as:

$$\Delta =\left\{\begin{array}{cc}-{\Delta }^{-},\hfill & \mathrm{if}2nM<k\le (2n+1)M\hfill \\ {\Delta }^{+},\hfill & \mathrm{if}(2n+1)M<k\le (2n+2)M\hfill \end{array}\right.$$

(8)

Otherwise, if the node initially acts as a benevolent node, $\Delta$ can be computed as:

$$\Delta =\left\{\begin{array}{cc}{\Delta }^{+},\hfill & \mathrm{if}2nM<k\le (2n+1)M\hfill \\ -{\Delta }^{-},\hfill & \mathrm{if}(2n+1)M<k\le (2n+2)M\hfill \end{array}\right.$$

(9)

with $n\in \mathcal{N}$. The two Equations (8) and (9) illustrate the oscillatory behaviour of this attack.

The last strategy is represented by the Opportunistic Service Attack (OSA). A node performing this attack provides bad service only when its trust is at an acceptable level. It represents a rational player that performs attacks with the aim to maximize its own payoff. The node adapts its strategy in order to not be detected: to do this, it defines its own trust limit $T_{OSA}$ and behaves so that its trust value is always higher than this limit. Indeed, this limit must be greater than the threshold $T_{th}$ in order for the node to be considered as benevolent ($T_{OSA}\ge T_{th}$). The trust variation can then be described as:

$$\Delta =\left\{\begin{array}{cc}{\Delta }^{+},\hfill & \mathrm{if}T(k-1)-{\Delta }^{-}<T_{OSA}\hfill \\ -{\Delta }^{-},\hfill & \mathrm{if}T(k-1)-{\Delta }^{-}\ge T_{OSA}\hfill \end{array}\right.$$

(10)

When the node senses that its trust is dropping below the trust limit, it sends good services, and then, $\Delta ={\Delta }^{+}$. Otherwise, the node continues to provide bad services ($\Delta =-{\Delta }^{-}$).

Table 2. Trust model parameters. WA, Whitewashing Attack; OOA, On-Off Attack; OSA, Opportunistic Service Attack.

Parameter	Description
k	Generic interaction between a requester and a provider
K	Total number of interactions between the two players
$Tinit$	Initial trust value for a provider node
$T_{th}$	Threshold to consider a node as “benevolent”
$\Delta =\left\{\begin{array}{c}{\Delta }^{-}\hfill \\ {\Delta }^{+}\hfill \end{array}\right.$	Decrement/increment of the trust value based on the provider’s behaviour
$k^{\prime }$	Re-join interaction for a WA node in which the trust is re-initialized
M	Number of interactions after an OOA node changes its behaviour
$T_{OSA}$	The lowest trust value accepted for an OSA node for itself

shows all the parameters used in the proposed investigation.

3.4. Trust Management Model Guidelines

The goal of a trust model is to detect malicious nodes without discarding the cooperative nodes. With ideal conditions, a cooperative node will always provide good services, and thus, it will receive a positive trust variation (i.e., $\Delta ={\Delta }^{+}$, which as described before can have a value in the range $[0,1]$). For this reason, the only condition to not discard any cooperative node is trivial:

$$T_{init}\ge T_{th}$$

(11)

The initial trust represents a crucial parameter for a trust model: it establishes the number of interactions that a malicious node can take advantage of in order to act maliciously. A high value confers the best trust to the nodes, while a low value makes the model suspicious. In the community, many works take on the choice of the initial value using the static characteristics of the nodes, e.g., the computation capabilities of the nodes [24] or social relationships between the objects’ owners [25].

However, due to the presence of malicious behaviours, stricter conditions are necessary. Indeed, the goal of any trustworthiness management model consists of maximizing the payoff for the cooperative nodes and thus isolating malicious objects as quickly as possible, i.e., with the lowest number of transactions, so that they are not selected as providers. Since a requester will discard a provider if its trust value drops below a certain threshold $T_{th}$, we can express the goal of a trust algorithm as:

$$max{\left\{payoff\right\}}^{req}\to min\left(k\right):T^{prov}\left(k\right)<T_{th}$$

(12)

Ideally, the highest payoff for the requester is achieved if the model is able to detect a malicious node at the first malicious transaction. Starting from Equation (12), we derive the most suitable configurations for the trust model parameters: the initial value of trust $T_{init}$, the trust variation ${\Delta }^{+}$ and ${\Delta }^{-}$ and the threshold $T_{th}$.

In order to detect an ME attack after the first malicious transaction, the following relation must be true:

$$T\left(1\right)=T_{init}-{\Delta }^{-}<T_{th}$$

(13)

where the reader should remember that $T\left(0\right)=T_{init}$. From Equation (13), we have three parameters, so we need to set two of them and calculate the last. Three conditions can then be set as follows:

$$\begin{array}{cc}\hfill & T_{th}>T_{init}-{\Delta }^{-}\hfill \\ \hfill & T_{init}<T_{th}+{\Delta }^{-}\hfill \\ \hfill & {\Delta }^{-}>T_{init}-T_{th}\hfill \end{array}$$

(14)

Similar considerations can be derived for a node implementing a WA. However, a node performing this attack re-initializes its trust value every $k^{\prime }$ transactions, so the conditions to maximize the payoff of the requester have to be generalized as follows:

$$min\left\{k\right\}\to k=k^{\prime }+1$$

(15)

$$\forall \left(entry\right):(T_{init}-{\Delta }^{-})<T_{th}$$

(16)

where $T\left(k^{\prime }\right)=T_{init}$, and for each re-initialization, the malicious node performing WA is identified at transaction $k^{\prime }+1$. The conditions found in Equation (14), calculated for an ME attack, are still valid also for the WA.

Other conditions can be obtained considering other attacks. As described before, a node performing an OOA has two distinct behaviours: the node starts with M malicious interactions or with M cooperative interactions. The first behaviour is similar to the ME attack: a trust algorithm can maximize the payoff of the requester by detecting the malicious node during the first (malicious) transaction, and thus, we obtain again the same conditions as Equation (14). However, if the malicious node starts with M cooperative transactions, the first malicious interaction is the $k=(M+1)$-th. In order to identify malicious behaviour, the trust model’s parameters should be set in order to satisfy the following:

$$T(M+1)=T_{init}+M{\Delta }^{+}-{\Delta }^{-}<T_{th}$$

(17)

which takes into account that the first M positive interactions have increased the trust of the node. However, M is a typical parameter of the OOA, so in order to avoid leaving any degree of freedom to the malicious node, it is important to set a condition that is independent of M and that can be obtained with:

$${\Delta }^{+}=0$$

(18)

With this condition, both malicious and cooperative nodes are never rewarded when providing good services, but they are still punished when delivering bad ones. Applying this condition to (17), it is possible to obtain the same relation as in (13), which can be solve applying the conditions in (14).

Another condition can be obtained by analysing nodes performing the OSA. As mentioned earlier, in the OSA, the malicious nodes set a trust limit $T_{OSA}$ higher than the threshold $T_{th}$ and use this limit to decide its behaviour. From this, we can set an ideal value for $T_{th}$: a value lower than one allows the node to act maliciously, while with a value equal to one, regardless of the trust limit $T_{OSA}$ set by the malicious node, the node performing OSA is forced to provide only good services and is unable to assume malicious behaviour.

Table 3. Adequate value for the trust model to detect the malicious behaviours.

Parameter	Value
$T_{th}$	1
$T_{init}$	1
${\Delta }^{+}$	0
${\Delta }^{-}$	$x\in (0,1]$

summarizes the evaluated parameters. In order to prevent OSAs, we must have the threshold $T_{th}$ set to one. As a consequence of Equation (11), the initial value of trust must be set to $T_{init}=1$. Moreover, from the considerations on the OOA, ${\Delta }^{+}$ is set to zero, while, from the third condition in (14), ${\Delta }^{-}$ has to assume any value greater than zero in order to immediately detect any malicious behaviours.

3.5. Probability of Error

The conditions obtained in the previous section represent an ideal scenario where the benevolent node will always cooperate. However, in a real IoT system, a cooperative device can be discarded from a network due to errors related to several reasons: well-behaving devices can show poor performance, due to errors, poor accuracy, or technical problems in general. This problem is usually overlooked by trust algorithm models, while it should be fundamental for them to be able to discern a malicious node from a poorly-behaving one. A trust model should be designed to take into account the errors of cooperative nodes, according to some admissible error rate for the model. If we consider that a benevolent node has a probability p to provide an unintentional bad service, then we can express the trust value calculated by the generic trust model as:

$$T\left(k\right)=T(k-1)+(1-p){\Delta }^{+}-p{\Delta }^{-}$$

(19)

In order to not isolate any benevolent node, a trust model should always be sure that $T\left(k\right)\ge T_{th}$. To this end, the following conditions must be met:

$$\begin{array}{c}(1-p){\Delta }^{+}-p{\Delta }^{-}\ge 0\\ {\Delta }^{+}\ge \frac{p}{(1-p)}{\Delta }^{-}\end{array}$$

(20)

and since ${\Delta }^{-}\in (0,1]$, it is possible to observe a first difference w.r.t. the errorless scenario: ${\Delta }^{+}$ cannot be equal to zero, in order for a trust model to balance any error from cooperative nodes.

However, Condition 19 can still be violated, and some cooperative nodes can be discarded: in the worst-case scenario, the first $\overline{k}$ interactions are all affected by errors. Considering consecutive transactions among nodes as independent, we can compute the probability of such a scenario as $p^{\overline{k}}$. It is then possible to set a maximum admissible error $A_{max}$ for the trust model as:

$$A_{max}=p^{\overline{k}+1}$$

(21)

so that, by knowing the admissible model error $A_{max}$ and the probability of error on the single transaction p, we can compute how many consecutive transactions $\overline{k}$ can be tolerated by the trust model as:

$$\overline{k}={log}_p{A}_{max}-1$$

(22)

This value determines that any node should not be discarded before $\overline{k}$ transactions, even if they are all malicious/have errors. This condition can be expressed as:

$$T\left(\overline{k}\right)=T_{init}-\overline{k}{\Delta }^{-}\ge T_{th}$$

(23)

The goal of the trust model is still to isolate the malicious nodes; similar to what we have done in the previous section, we aim to find the conditions that allow the trust model to isolate the malicious nodes as soon as possible. For nodes performing ME attacks and WAs, the first useful transaction to detect the malicious nodes is the $(\overline{k}+1)$-th transaction, and then, the following condition must be true:

$$T(\overline{k}+1)=T_{init}-(\overline{k}+1){\Delta }^{-}<T_{th}$$

(24)

so that the first $\overline{k}$ transactions allow errors to occur, while the system recognizes a malicious behaviour afterwards. Similar to (14), three conditions can be set as follows:

$$\begin{array}{cc}\hfill & T_{th}>T_{init}-(\overline{k}+1){\Delta }^{-}\hfill \\ \hfill & T_{init}<T_{th}+(\overline{k}+1){\Delta }^{-}\hfill \\ \hfill & {\Delta }^{-}>\frac{T_{init}-T_{th}}{\overline{k}+1}\hfill \end{array}$$

(25)

where each parameter is described based on the other two and ${\Delta }^{-}\in (0,\frac{1}{\overline{k}+1})$.

Another condition can be obtained by analysing the OOA. If the node implementing OOA starts with a malicious behaviour performing M malicious transactions, it is possible to devise the same condition as Equation (25). However, if the malicious node starts with M benevolent transactions, the trust model can identify the malicious node at the $k=(M+\overline{k}+1)$-th transaction, if the following condition is satisfied:

$$(T_{init}+M{\Delta }^{+}-(\overline{k}+1){\Delta }^{-})-T_{th}<0$$

(26)

In order to minimize the impact of M and the number of transactions needed to detect the OOA, ${\Delta }^{+}$ should be set at the minimum admissible value, which can be derived from Equation (20) as:

$${\Delta }^{+}=\frac{p}{(1-p)}{\Delta }^{-}$$

(27)

which allows cooperative nodes to avoid being discarded due to errors, but at the same time, enables the trust model to quickly identify the OOA.

Finally, it is not possible to devise any further conditions by analysing OSA attack. In order to satisfy Equation (25), it is not possible to set $T_{th}$ equal to one, as in the errorless scenario. This allows a node implementing the OSA to perform malicious transactions with a rate equal to the error probability p, since performing a higher number of malicious transactions would cause the node to be detected. In this way, the value for $T_{th}$ must follow Equation (25) correlated to the probability of error p, while $T_{init}$ is set equal to one in order to overcome the scenario without error as well.

Table 4. Final parameters’ value for the trust model to detect the malicious behaviours in the scenario with errors.

Parameter	Value
$T_{th}$	$T_{th}>T_{init}-(\overline{k}+1){\Delta }^{-}$
$T_{init}$	1
${\Delta }^{+}$	$\frac{p}{(1-p)}{\Delta }^{-}$
${\Delta }^{-}$	$x\in (0,\frac{1}{\overline{k}+1})$

shows the adequate parameters’ values in order to design a suitable trust management model, both without or with an error probability for cooperative nodes.

Table 5. Trust model parameters considering an error probability.

Parameter	Description
p	Probability of error in a generic interaction
$A_{th}$	Maximum tolerable error for the trustworthiness management model
$A_{max}$	Maximum error for a trust model
$\overline{k}$	Number of consecutive malicious behaviours permitted by the trust model

shows all the parameters used to study the trust management models with an error probability on cooperative nodes.

4. Experiments and Results

4.1. Experimental Setup

In order to test the effectiveness of the guidelines for a trustworthiness model examined in the previous section, we need to simulate the binary game and all the possible behaviours. To this end, we make use of a full mesh network of $N=100$ devices, where each device interacts K times, not known beforehand by the devices, with each other device, alternating the roles of provider and requester. This way, all nodes can play all the possible strategies in the game. For each pairwise interaction, two players, one acting as a requester and the other as a provider, play the game and change their strategies according to their behaviour in the previous rounds and according to the adopted trust model.

According to Equation (4), we can set the values of all the payoffs. Different values might be assigned to the parameters; however, if they respect the exposed relations, the final game would be the same. In this case, the greatest value is assigned to the requester’s benefit since it receives the required service, while the provider has a minor benefit related to its reputation. Taking into account the cost, the provider needs to use its own resources in order to solve the request, and then, the cost is higher w.r.t. the requester, where the cost is associated with the time spent to obtain the service and with the resources needed to send the request. For each game, the payoff for the two nodes, requester and provider, is computed according to the payoffs’ values, and the total payoff for a node is the sum of all the games.

The interactions follow the trust model based on the guidelines exposed in Section 3 in order to detect the malicious behaviours and guarantee a high payoff for the benevolence. To do this, we set ${\Delta }^{-}$ equal to 0.1 in order to satisfy the condition ${\Delta }^{-}>0$ and $T_{init}=1$ to grant the highest possible initial trustworthiness to all the nodes, while ${\Delta }^{+}$ and $T_{th}$ are consequently evaluated for the specific set of simulations. The maximum admissible error for the algorithm is set to $A_{max}={10}^{-3}$ in order to reach a compromise between the errors due to the cooperative nodes and the bad services provided by malicious nodes: considering an error probability equal to $p=0.2$, $\overline{k}=3.29$ that allows a number of consecutive errors starting from $T_{init}$ equal to 3.

Moreover, malicious nodes are designed according to the description supplied in Section 2.2. All the behaviours, both benevolent and malicious, are used to measure the effectiveness of the guidelines for the trust management model. The ME behaviour always provides bad services and defects in all transactions. Similarly, a node implementing the WA acts maliciously with everyone, but after a fixed number of transactions, 25 for our simulations, it resets its trust value by leaving and re-entering the network. Nodes performing the OOA change their state from ON to OFF, and vice versa, every $M=5$ interactions, starting from the cooperative behaviour, which is harder to detect. Finally, the OSA node represents a smart attacker that modifies its $T_{OSA}$ threshold, which is used in order to choose a behaviour. In the first set of simulations, the OOA node sets $T_{OSA}=T_{th}$ so as to have more possibilities to act malicious and to increase its payoff.

Table 6. Simulation parameters.

Parameter	Description	Value
N	Number of nodes	100
K	Number of interactions between two players	100
$b_r$	Benefit value for the requester	0.5
$b_p$	Benefit value for the provider	0.3
$c_r$	Cost value for the requester	0.1
$c_p$	Cost value for the provider	0.2
${\Delta }^{-}$	Decrement of the trust value	0.1
$T_{init}$	Initial trust value	1
$A_{max}$	Maximum tolerable error for the model	0.001
p	Probability of error	0.2
$\overline{k}$	Consecutive malicious behaviours permitted	3
${\Delta }^{+}$	Increment of the trust value	0.025
$T_{th}$	Decision threshold	0.625

shows all the configuration parameters for the proposed simulations, the different payoffs used for the game and the trust model details.

4.2. Experimental Results

We evaluate the performance of the proposed guidelines by analysing the binary trust game in the simulated IoT network. Each device is alternately a requester or a provider and has interactions with all the other nodes.

We first examine a scenario with a population composed of only cooperative nodes and no trust management model: the goal is to understand which is the payoff that can be achieved in an ideal network. Each requester trusts all the providers, while providers have benevolent behaviour and collaborate in all interactions. The payoff average value for a single node is 24.75. This value consists of the maximum payoff achievable in a game of 100 interactions by a cooperative node. The node is not interested in preserving its own resources and then collaborates in each game.

Starting from the case with only cooperative nodes, we add malicious nodes to the network to illustrate how the attackers can obtain a greater payoff. Out of the total number of nodes in the network, we replace 5% of the nodes for each type of attack’s behaviour, so that the final network is composed of 80 cooperative nodes and 20 malicious nodes, evenly distributed among the four types of attacks. No trust algorithm is implemented, so the requesters will always choose to play the game, while malicious providers will behave according to the implemented attack.

Table 7. Average payoffs of nodes without any trust model. ME, Malicious with Everyone.

	Benevolent	ME	WA	OOA	OSA
Average Payoff	16.00	26.40	26.40	21.20	26.40

illustrates the resulting average payoffs for all the behaviours: the results show how cooperative nodes achieve the minimum payoff, which is lower than the previous scenario due to the negative payoff S. Indeed, a requester interacting with a malicious provider will not receive any service, so its average payoff decreases from 24.75 to 16.00. On the other hand, malicious nodes receive the best payoff by acting maliciously: this payoff is higher w.r.t. the case with only cooperative nodes, because malicious nodes do not have to use their resource to produce the service (sense the environment or act on something). ME, WA and OSA can always defect without being detected due to the absence of the trustworthiness management model. The OOA behaviour presents a slightly lower payoff due to a certain number of transactions during the ON state, where the node performs benevolently; anyway, the malicious interactions allow them to receive a greater payoff w.r.t. the cooperative nodes.

The employment of a suitable trust model is essential in order to detect the malicious nodes and increase the payoff of the cooperative nodes. To this end, the next set of experiments examines the same network used in the previous scenario, i.e., with both cooperative and malicious nodes, but adopting a trust management model. Starting with the scenario where cooperative nodes always deliver the right service, i.e., they are not subject to errors, we design the trust model according to Section 4.1: $T_{init}=1$ and ${\Delta }^{-}=0.1$ in order to trust all nodes at start and to detect as fast as possible the malicious behaviours. Moreover, $T_{th}$ and ${\Delta }^{+}$ are set based on Table 3: for the case without errors for cooperative nodes, $T_{th}=T_{init}=1$ to detect the attackers at their first malicious transactions and ${\Delta }^{+}=0$ to never increase the trust for intelligent malicious nodes, such as the OSA.

Table 8. Average payoffs of nodes in a no error scenario with a trust model.

	Benevolent	ME	WA	OOA	OSA
Average Payoff	21.73	17.28	17.57	17.76	21.73

illustrates the average payoffs of the nodes using the trust model previously described. The trust model is able to detect the ME, WA and OOA behaviours, thus reducing their average payoff with an advantage for the cooperative nodes. Even with a very low value of ${\Delta }^{-}$, the model discards these malicious nodes after the first malicious transaction. The result is that when a malicious node acts as a provider, it will not be trusted, and then, it will not receive a payoff from any of the benevolent requesters: it will only be able to accumulate payoff when it acts as a requester and trusts other nodes. The WA behaviour resets its trust reputation after 25 interactions, then it has a slightly higher payoff than the ME attack, but nevertheless, it is detected immediately after the first malicious interaction. The OOA behaviour can achieve an even higher payoff compared to the other two behaviours by acting as a benevolent node and providing good services in its ON state (the first M transactions); however, when the node switches to the OFF state, it is immediately detected at the first malicious interaction. Finally, the OSA behaviour exhibits the highest payoff equal to the cooperative nodes. The node performing the OSA changes its behaviour in order to be chosen as the provider and to not be discarded. However, since the model can detect a malicious node at its first interaction, the malicious node must always perform benevolently and thus achieve the same payoff as the cooperative nodes. Finally, we can observe how the average payoff of a cooperative node in this scenario is equal to 21.73, which is lower when compared to the payoff of 24.75 of the benevolent node in a completely cooperative network. This is tied to the presence of malicious nodes that decreases the average payoff for cooperative nodes even though the trust model detects them at the first interaction.

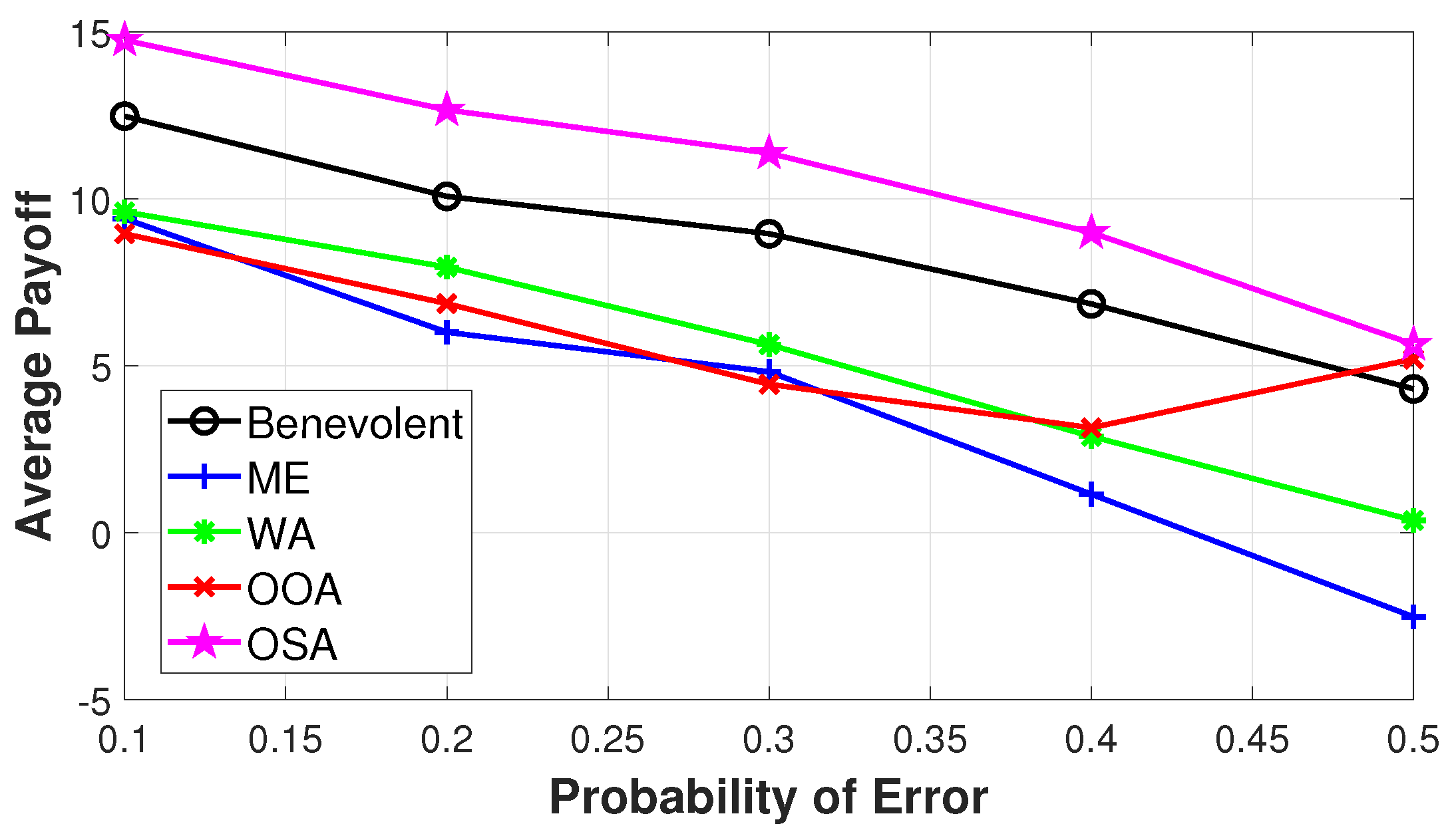
We now want to analyse the results when cooperative nodes can send bad services to the requester due to unintentional errors. The focus of the next test of simulations is to test how the trust model can be designed in order to take into account an error probability. Figure 5 shows the average payoffs for different values of the error probability p. For each value and considering $T_{init}=1$, the model can set $T_{th}$ according to Equation (24). The figure shows the average payoff for all the possible behaviours. The ME and WA behaviours show a lower payoff w.r.t. cooperative nodes, thus indicating how they are always detected: while the cooperative nodes make errors with a certain probability, ME and WA always send scarce services, and the model can easily detect them. Similarly, the OOA is discarded until an error probability of 0.5, because this behaviour is similar to a condition of a percentage of error equal to 50%. This results in a greater payoff of the OOA nodes with an error probability greater than 0.5. Furthermore, the OSA is able to reach the best payoff in all the simulations sending scarce services in a percentage equal to the probability of error (e.g., for a probability of error equal to 0.2, the OSA is able to act maliciously for 20% of its interactions). Moreover, OSA takes advantage of the admissible error set by the model sending for each requester a number of $\overline{k}$ bad services in the first interactions.

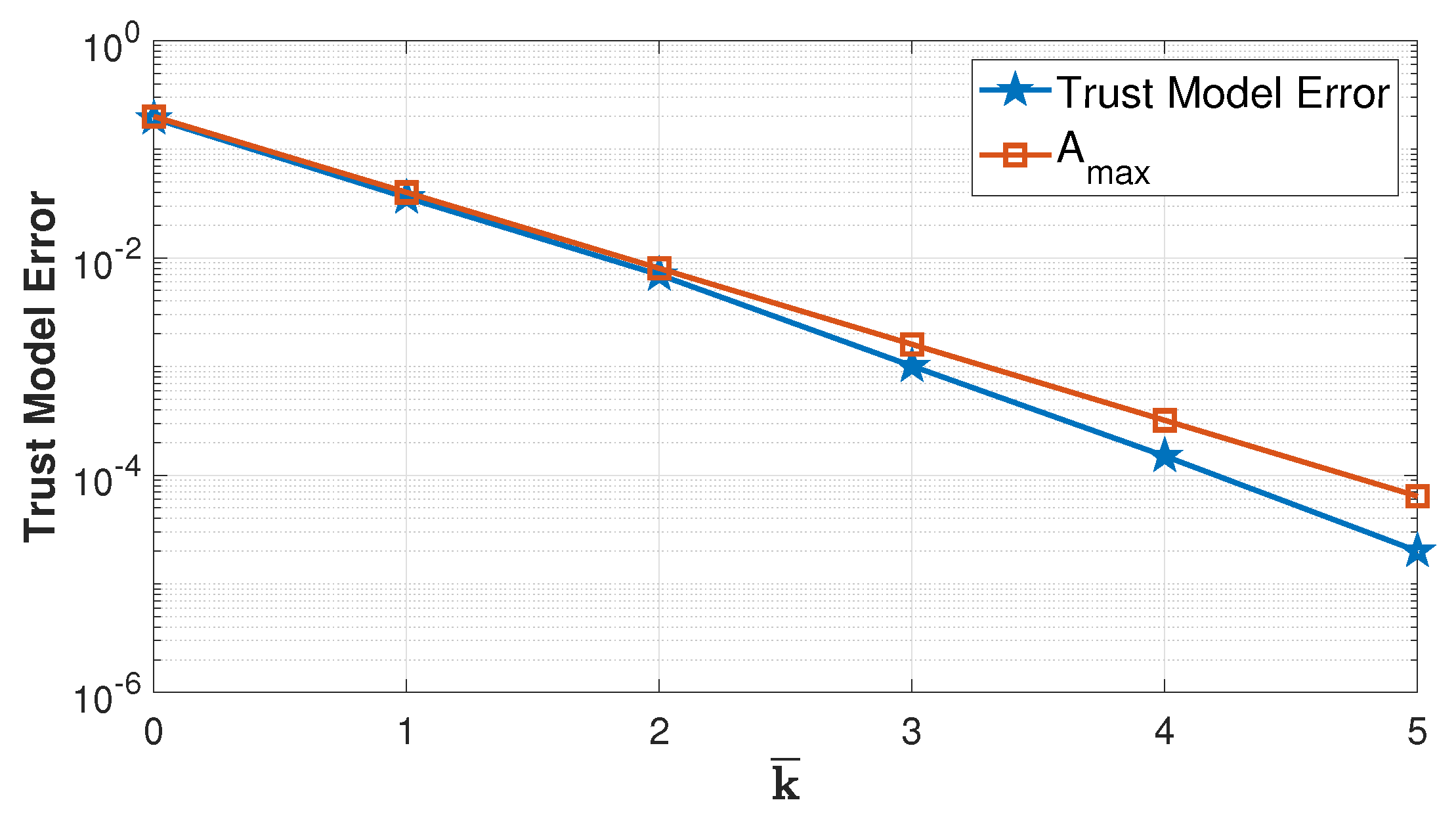
Figure 6 shows the trust model error in discarding cooperative nodes, considering a scenario with $N={10}^5$ cooperative nodes and a probability of error equal to $0.2$. The orange line shows the computed value for the maximum admissible error $A_{max}$ as referenced. The Figure shows how the value of $\overline{k}$ is essential to overcome the probability of error of the cooperative nodes and obtain an acceptable error of the trust algorithms. By increasing the value of $\overline{k}$, the model can decrease the number of discarded cooperative nodes, i.e., the trust model error, at the cost of increasing the vulnerability to attacks.

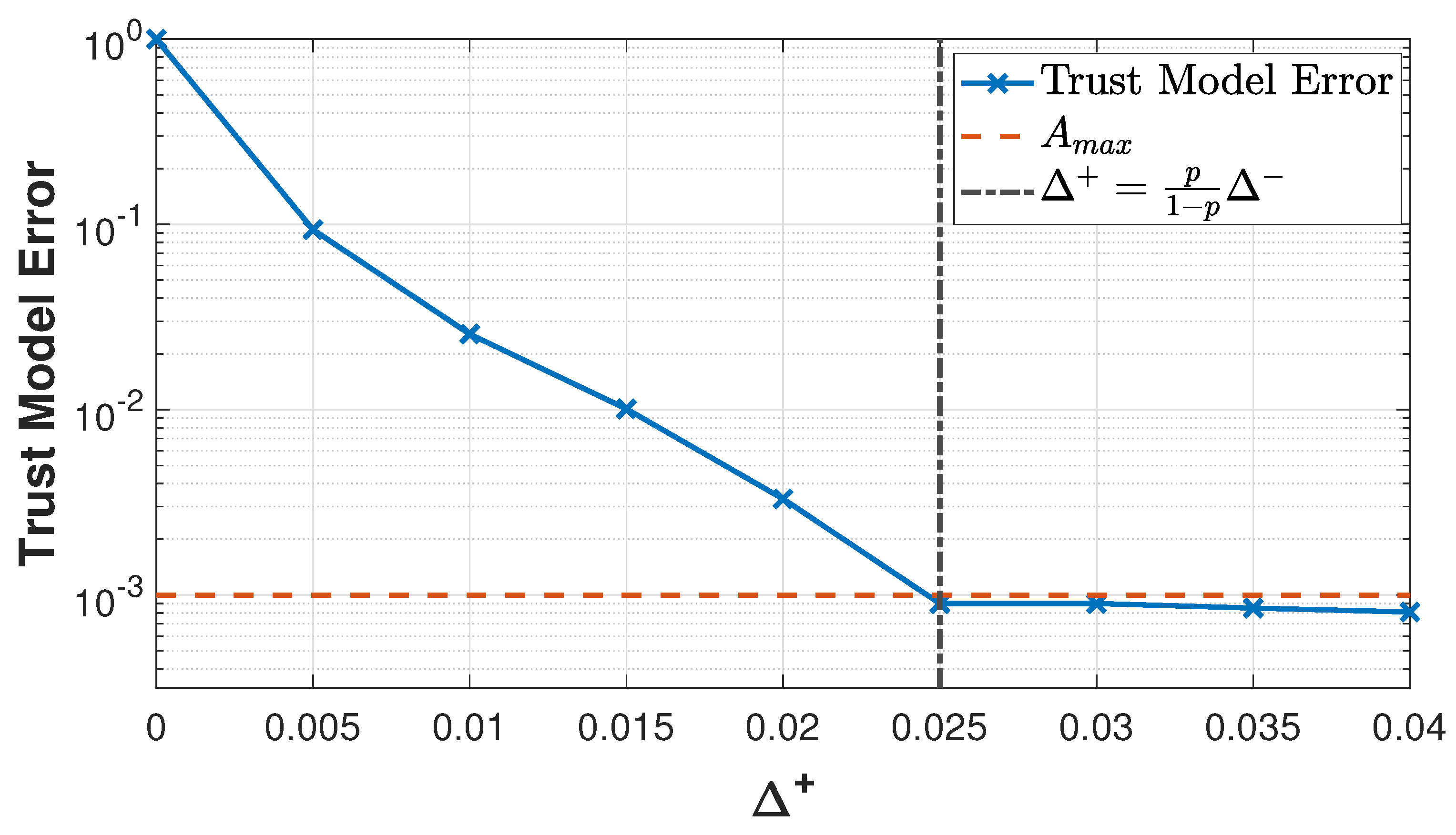
Furthermore, the importance of the parameter ${\Delta }^{+}$ is illustrated in Figure 7. At the end of the simulation, i.e., after 100 transactions, the figure shows how the worst error is when ${\Delta }^{+}=0$ since the cooperative nodes are all discarded and no errors are allowed. The minimum value that allows a maximum admissible error $A_{max}$ equal to 0.001 is ${\Delta }^{+}=\frac{p}{1-p}{\Delta }^{-}$: this value allows cooperative nodes to avoid being discarded due to errors and, at the same time, enables the trust model to quickly identify the attacks.

Finally, the last two sets of simulations are aimed at understanding how malicious nodes can change their parameters in order to overcome the trust model. According to the previous simulations, the probability of error p is set equal to 0.2, and the simulations focus on an individual malicious node. Each malicious node tries to bypass the trust model in order to increase its own payoff at the expense of the cooperative nodes. The ME attack has no way to modify its behaviour, and with a probability of error $p<1$, it is always detected during the first transaction by the trust model. Concerning the WA, a node can change how often it re-enters the network, but since its behaviour is similar to the ME attack, the node is always detected at the first malicious transaction. The worst-case scenario is when a node implementing the WA re-enters the network after each malicious interaction, and the WA can never be detected. However, the high cost of leaving and re-entering the network with a different identity limits this behaviour.

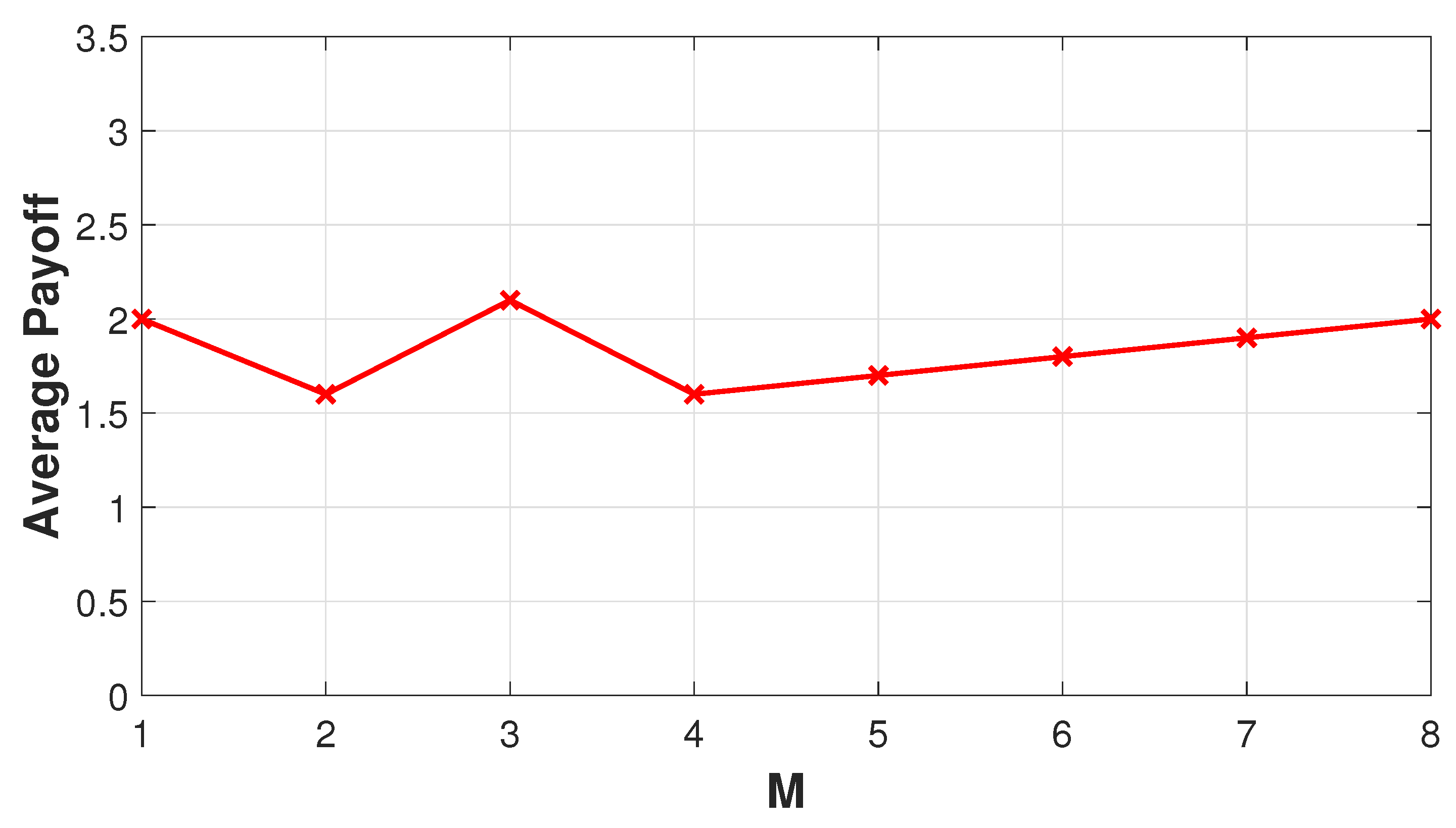
Analysing the OOA behaviour, a node has two choices available: which state is used for the first transactions and the duration of each state, i.e., the value of M. As stated in the previous section, the best choice for a node is to start with a benevolent behaviour in order to increase its trust value. Figure 8 illustrates then the average payoff of a node implementing the OOA with different values of M. With an error probability equal to 0.2 and $A_{max}$ set to 0.001, the model can allow a number of $\overline{k}=3$ consecutive errors starting from the first interaction. This means that a node performing the OOA will be detected as malicious after four malicious interactions. The average payoff is then tied to the number of benevolent interactions the node performs when it is in the ON state, so that the average payoff increases for $M>\overline{k}$. Before this condition, the average payoff shows an oscillatory behaviour due to the variation in the number of cooperative transactions.

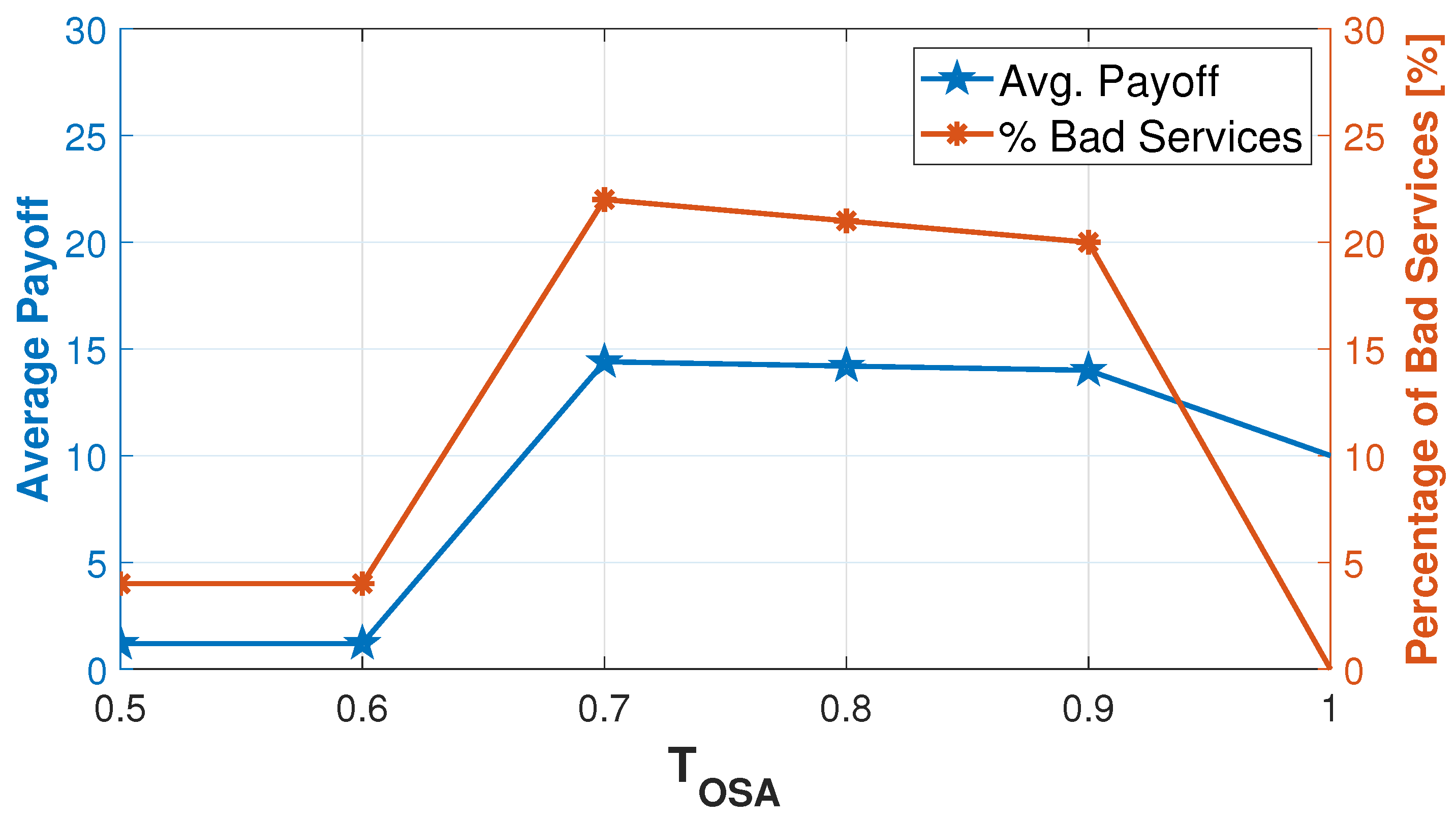
Finally, the behaviour of the OSA node is described in Figure 9. The model threshold $T_{th}$ is set according to Equation (24) with a value near $0.7$, because ${\Delta }^{-}=0.1$. The figure shows how the best value for $T_{OSA}$ is equal to $T_{th}$, where the node can perform the highest number of bad services, and thus, its average payoff is maximum. We can also note how the percentage of bad services the OSA behaviour is able to deliver is higher than the error probability of a node ($p=0.2$): this is due to the ability of the OSA to exploit the tolerance margin due to the maximum admissible error by the algorithm, $A_{max}$. With $T_{OSA}<T_{th}$, the node is immediately detected, and its payoff is lower; while with $T_{OSA}>T_{th}$, the node does not fully exploit malicious opportunities, and then, it cannot achieve the maximum payoff.

5. Discussion and Conclusions

In this paper, we modelled the interactions among nodes in the IoT following a binary trust game to study how trust can arise between them. In particular, we analysed the interactions between a service requester, which acts as the trustor, and a service provider, the trustee. Based on this model, we proposed guidelines that can be used to design trust management algorithms.

Even if a network composed of only cooperative nodes can achieve on average the highest payoff, malicious behaviours are still implemented since they are able to take advantage of cooperative nodes in the short term. The proposed guidelines help trust models to quickly identify the most common attacks, such as the whitewashing attack, the on-off attack and even the opportunistic service attack by setting suitable values for the initial trust, the trust variation or the trust threshold. Moreover, we analysed two different scenarios: an errorless scenario, where cooperative nodes are always able to deliver the requested service without errors, and a scenario where well-behaving devices can show poor performance, due to errors, poor accuracy or technical problems in general, and can then be labelled erroneously as malicious.

Unexpectedly, we discovered that the rewards of the cooperative nodes are not useful unless they are prone to errors, and therefore, it is necessary to reward them to balance the trust lost due to errors. Nevertheless, it is not possible for a trust algorithm to never discard a cooperative node due to errors: to this end, trust algorithms should always declare their maximum acceptable error.

In the future, we aim to extend this model in order to take into account recommendations from other nodes and the possible attacks related to this. Moreover, we plan to improve the evaluation of the costs and benefits for the nodes: we want to consider the cost associated with the implementation of a particular malicious behaviour and the differences in terms of costs and benefits based on the service requested. Finally, we also want to introduce in the model the ability of a requester to identify a malicious attack and how this impacts the setting of trust parameters.