Estimators for Time Synchronization—Survey, Analysis, and Outlook
Abstract
1. Introduction
1.1. Motivation
1.2. Problem Definition and Objectives of the Survey Paper
- Accuracy: The remaining time difference between master and slave, which cannot be compensated by synchronization, should be as small as possible. In this context, there are two parameters defined. The offset is the time difference between master and slave. Compensating the offset is referred to as synchronization. The skew is the frequency difference between both. Compensating the skew is referred to as syntonization.
- Scalability and bandwidth efficiency: Synchronization messages always generate an overhead. If less bandwidth is used for synchronization, more bandwidth is available for the actual tasks of the distributed system (control, data acquisition, data exchange, etc.). This is crucial for the scalability of an synchronization approach, as the synchronization of all devices might be impossible at some point due to limited bandwidth and thousands of devices to be synchronized. Additionally, reducing the number of messages also reduces the energy consumption. This is especially important in wireless scenarios with battery-powered devices (note that communication typically requires a lot more energy than computing [15]).
- Computational efficiency: The time synchronization requires additional computing power on devices. The less additional computing power is required for synchronization, the more is available for the actual tasks of the devices.
- Hardware (HW) requirements: The HW requirements are also decisive. This applies to both the end devices (e.g., networks interface cards) and the network infrastructure (e.g., switches). Lower HW requirements lead to lower installation costs and greater future-proofness.
- Robustness: Depending on the use case, it might be important that an approach is especially robust. Robustness is very relevant in highly dynamic IoT scenarios (high node churn and frequent topology changes). In IIoT scenarios, robustness against failing nodes and links is important in order to achieve high availability of the system.
- Security: One major concern in modern networks is security. Consequently, it is also relevant for synchronization. Especially, in IIoT scenarios, it is crucial that secure time synchronization protocols are safe against malicious nodes and attacks, as a failing synchronization can lead to failure of the entire system.
1.3. Structure of This Article
2. Classification of the Research Area
2.1. Time Synchronization in Computer Networks
2.2. Synchronization in Complex Networks
2.3. Alternatives to Synchronization
3. Comparison with and Differentiation from Other Surveys
3.1. Non-WSNs
3.2. WSNs
3.3. Summary of Comparison with Other Surveys
4. Methodology for Evaluating the Approaches
4.1. Quantitative: Which Synchronization Accuracy Was Achieved?
4.2. Qualitative: Is the Approach Compliant with a Standard?
4.3. Qualitative: Which Estimation Method Was Used?
4.4. Qualitative: What Conditions and Restrictions Are There?
4.5. Restriction
5. Time Synchronization Protocols
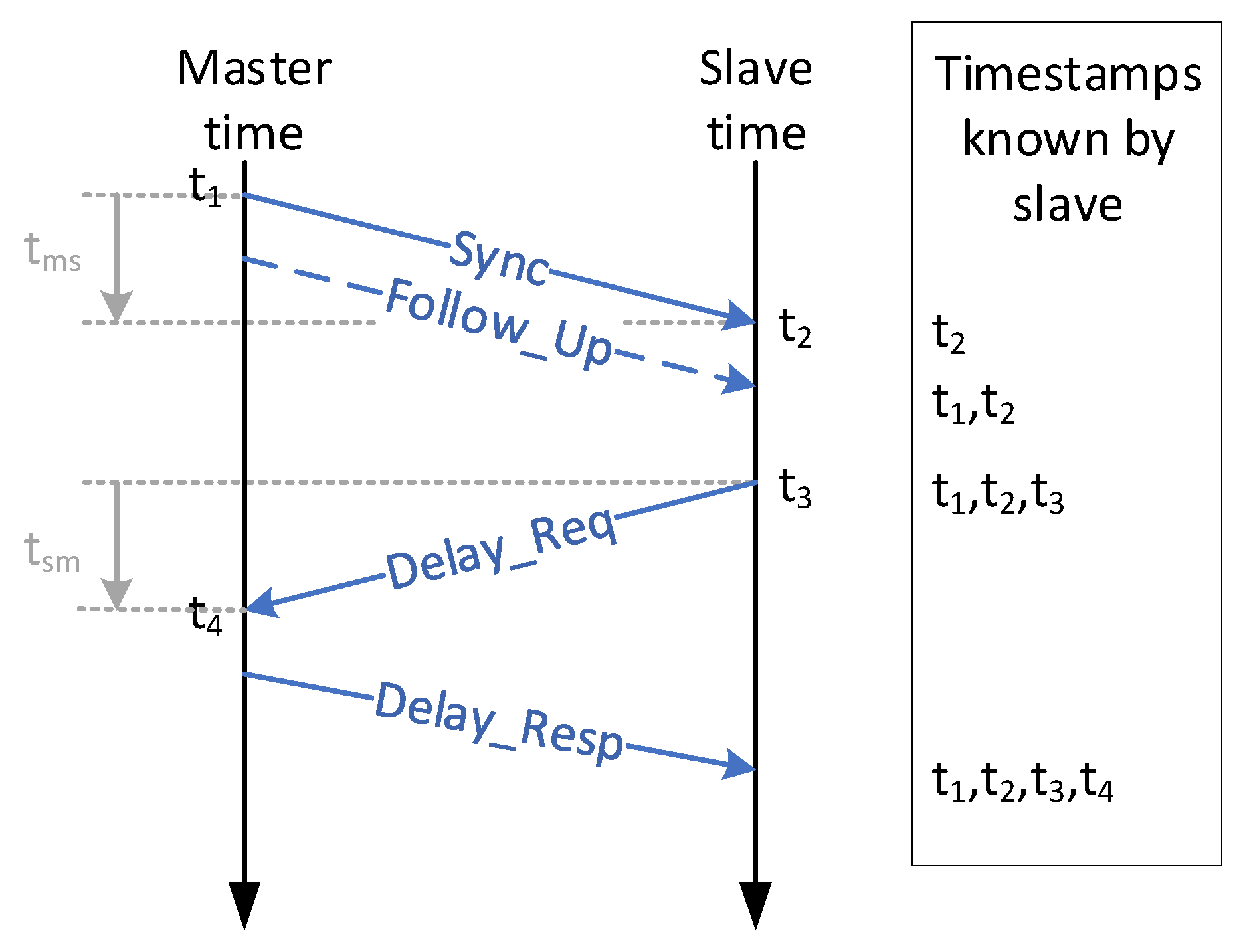
5.1. NTP
5.2. PTP
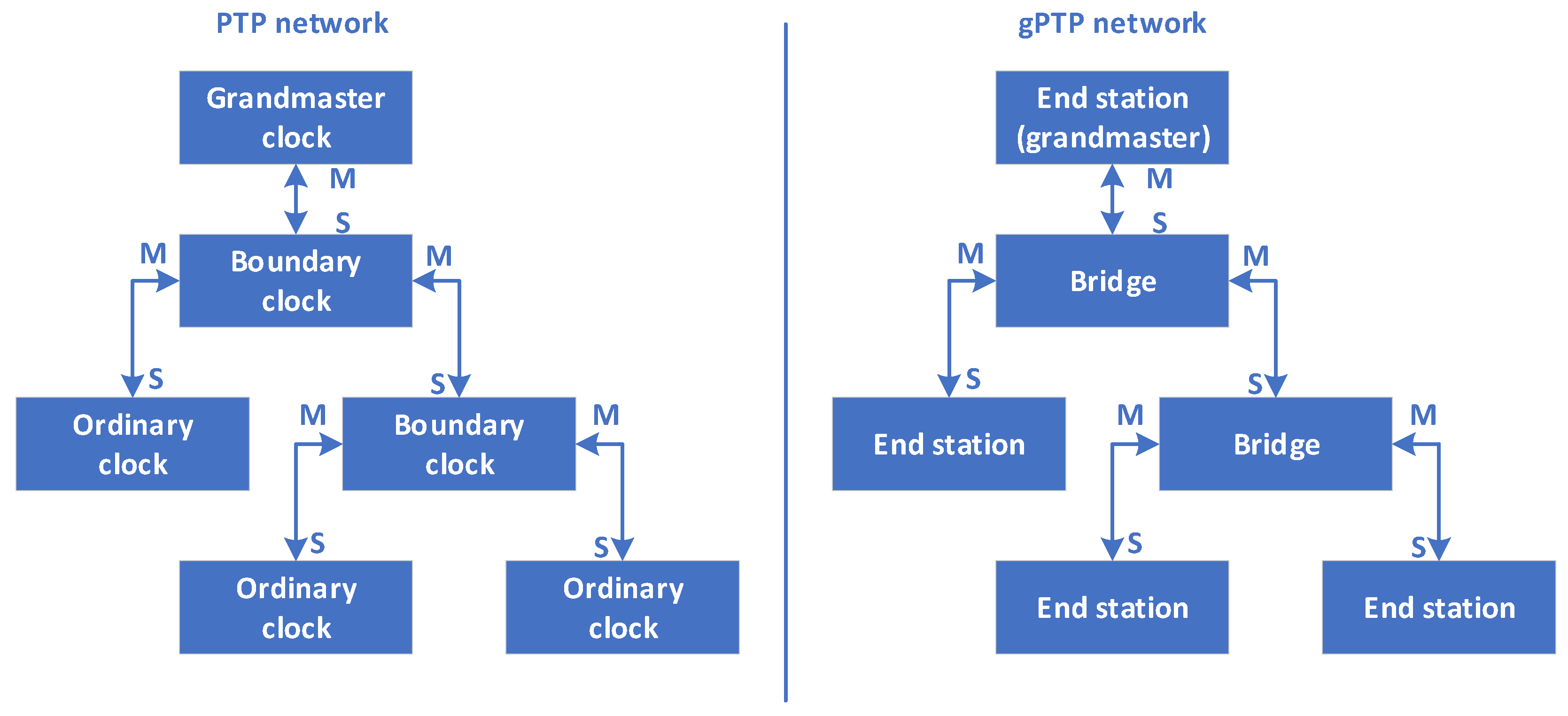
5.3. gPTP
5.4. PTCP
5.5. SyncE
5.6. Summary of Existing Time Synchronization Protocols
6. Research Approaches to Time Synchronization
6.1. PTP/gPTP Modifications
6.1.1. PTP/gPTP Modifications Using RTT-Based Estimation
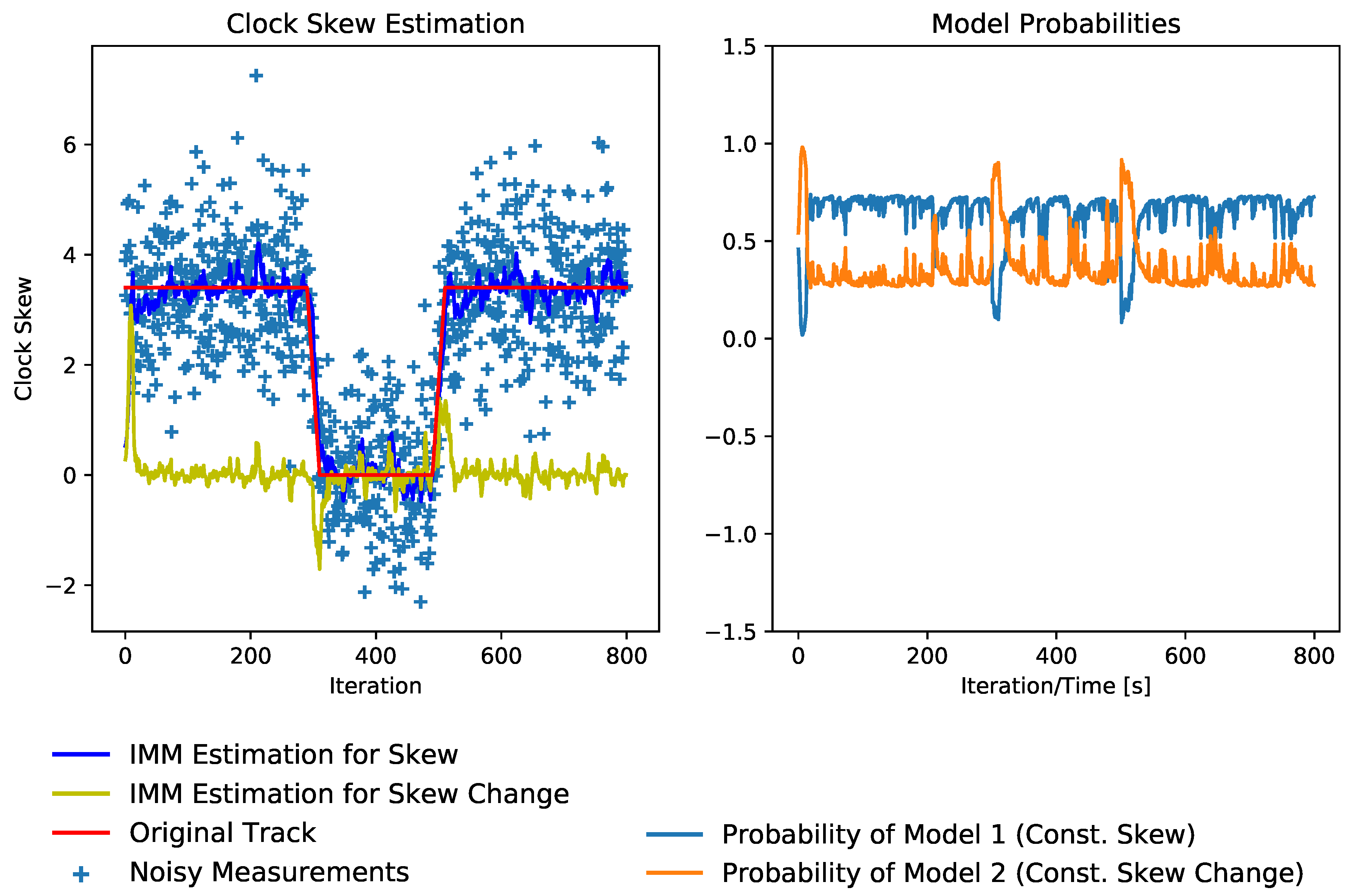
6.1.2. PTP/gPTP Modifications Using KF-Based Estimation
6.1.3. PTP/gPTP Modifications Using PI-Based Estimation
6.1.4. PTP/gPTP Modifications Using Expectation Maximization (EM)-Based Estimation
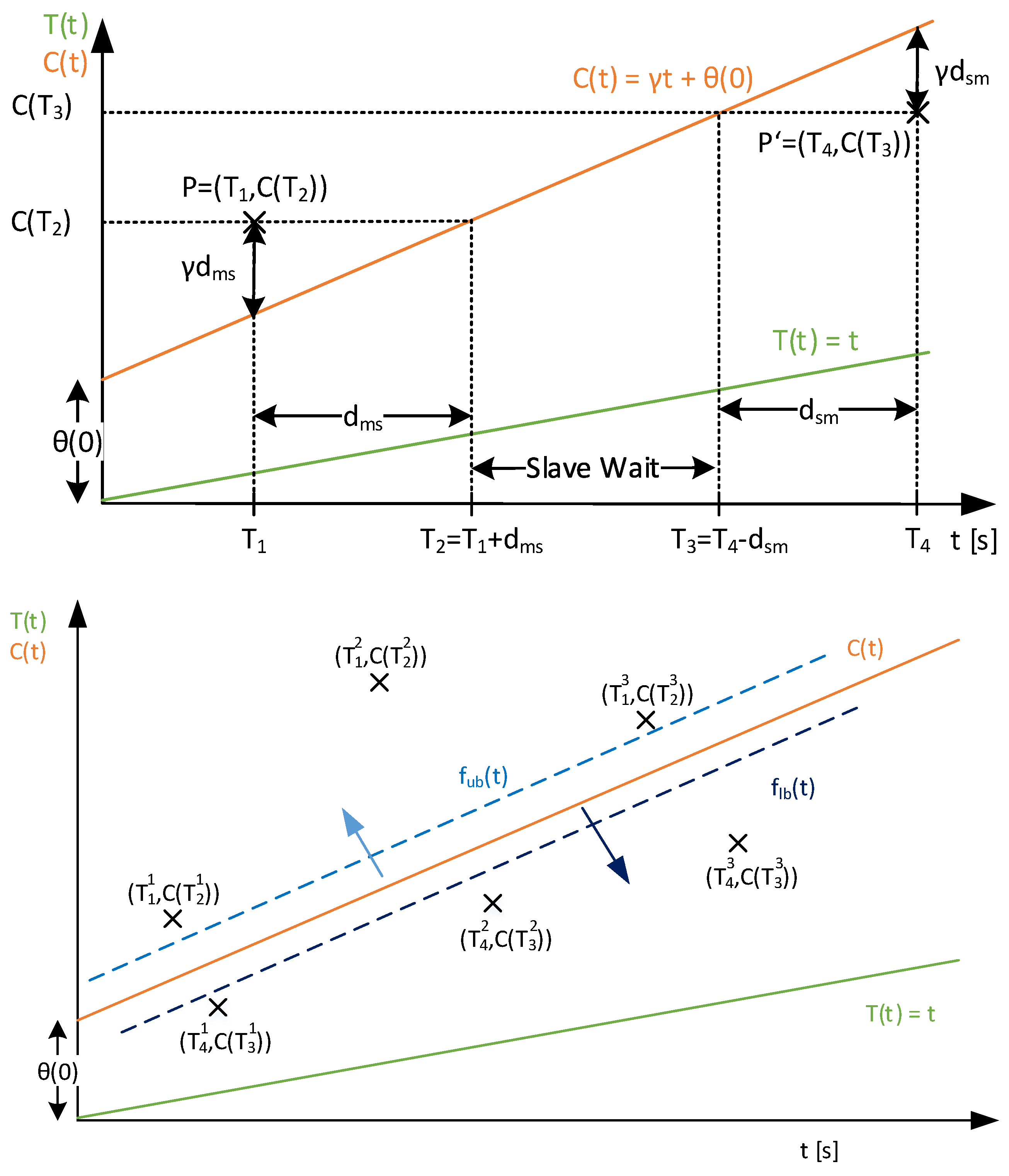
6.1.5. PTP/gPTP Modifications Using LP-Based Estimation
6.1.6. Summary of PTP/gPTP Modifications
6.2. Wired Approaches
6.2.1. Wired Approaches Using RTT-Based Estimation
6.2.2. Wired Approaches Using EF-Based Estimation
6.2.3. Wired Approaches Using KF-Based Estimation
6.2.4. Wired Approaches Using PI-Based Estimation
6.2.5. Wired Approaches Using Convex Hull (CH)-Based Estimation
6.2.6. Wired Approaches Using LP-Based Estimation
6.2.7. Wired Approaches Using Other Estimators
6.2.8. Summary of Research Approaches Addressing Wired Scenarios
6.3. Wireless Approaches
6.3.1. Wireless Approaches without (Delay) Estimation
6.3.2. Wireless Approaches Using RTT-Based Estimation
6.3.3. Wireless Approaches Using CA-Based Estimation
6.3.4. Wireless Approaches Using KF-Based Estimation
6.3.5. Wireless Approaches Using LR-Based Estimation
6.3.6. Wireless Approaches Using Other Estimators
6.3.7. Summary of Existing Wireless Time Synchronization Approaches
7. Conclusion and Future Research Directions
- Achieving high synchronization accuracies (<1 s) without the use of a specialized HW remains an open research question.
- In the wireless domain, many broadcast-based approaches have been proposed to improve scalability. Broadcasts could also be beneficial for wired networks. Scalability is particularly important for IoT and IIoT scenarios due to the large number of devices to be networked.
- In order to place as few requirements as possible on the platform, an approach should be implemented in SW (if possible). This reduces costs and improves future-proofness. Some approaches, however, use HW timestamps if they are available to increase the synchronization accuracy. It is worth emphasizing that this only places a requirement on the end nodes but not on the switches.
- In the best case scenario, an approach does not place any special requirements on the switches and compensates for the delays that arise in the network using powerful estimators on the end nodes. Consequently, this survey paper focuses on delay estimators and their achievable synchronization accuracy.
- As such, an estimator, LP in particular, achieves very good results. Instead, LR is in particular used in WSNs. Compared to LP, LR has an even lower computational complexity while slightly sacrificing accuracy. LR was already extensively examined in the wireless domain but could be interesting for further consideration in the wired domain.
- One EM-based approach was presented as a PTP extension. EM could also be generally interesting for wired and wireless synchronization.
- A few works consider CHs in wired networks. From our point of view, CHs are an interesting approach and need further investigation.
- One work proposes SVMs for wired synchronization. From our point of view, SVMs might be interesting for both wireless scenarios and as extension to existing protocols.
- With regard to clock stabilization, it should be noted that the temperature is the main factor for clock frequency instabilities. However, this influence can be compensated, as some works show impressively.
- Although there are several approaches for secure time synchronization, secure time synchronization protocols in general remain an open research question [6].
Funding
Conflicts of Interest
Abbreviations
| AP | Access Point |
| ATD | Averaged Time Differences |
| AVB | Audio/Video Bridging |
| BMCA | Best Master Clock Algorithm |
| CA | Consensus Algorithm |
| CCS | Consensus Clock Synchronisation |
| CCT | Coordinated Cluster Time |
| CERN | European Organization for Nuclear Research |
| CESP | Coefficient Exchange Synchronization Protocol |
| CH | Convex Hulls |
| CKF | Custom Kalman Filter |
| CMA | Cumulative Moving Average |
| CPU | Central Processing Unit |
| CWA | Confidence Weighted Average |
| DC | Distributed Clock Synchronization |
| DS | De Facto Standard |
| DSR | Direct Skew Removal |
| DSR | Direct Skew Removal (Technique) |
| DTP | Datacenter Time Protocol |
| EACS | Environment-Aware Clock Synchronization |
| EF | Exponential Filtering |
| EKF | Extended Kalman Filter |
| EM | Expectation Maximization Algorithm |
| FTM | Fault-Tolerant Midpoint |
| FTSP | Flooding Time Synchronization Protocol |
| FWA | Forwards Weighted Average |
| gPTP | Generalized Precision Time Protocol |
| GD | Gradient Descent |
| GT | Gaussian Traffic |
| GTSP | Gradient Time Synchronization Protocol |
| HW | Hardware |
| HW-TS | Hardware Timestamps |
| IIoT | Industrial Internet of Things |
| IMM | Interacting Multiple Model (Kalman filter) |
| ISR | Interrupt Service Routine |
| ITU-T | Telecommunication Standardization Sector |
| KF | Kalman filter |
| LCM | Least Common Multiple |
| LP | Linear Programming |
| LR | Linear Regression |
| MA | Moving Average |
| MAC Layer | Medium Access Control Layer |
| MII | Media Independent Interface |
| ML | Machine Learning |
| MSR | Mean Subsequence Reduced |
| MV | Mean Value |
| NTP | Network Time Protocol |
| P2P | Peer-to-Peer |
| PHY Layer | Physical Layer |
| PI | Proportional Integral (Controller) |
| PLL | Phase-Locked Loop |
| PTCP | Precision Transparent Clock Protocol |
| RBIS | Reference Broadcast Infrastructure Synchronization |
| RBS | Reference-Broadcast Synchronization |
| RMSE | Root Mean Square Error |
| RSS | Received Signal Strength |
| RTSP | Recursive Time Synchronization Protocol |
| RTT | Round-Trip Time |
| SAGE | Space Altering Generalized Expectation-Maximization |
| SDN | Software-Defined Networking |
| SLE | System of Linear Equations |
| SPiRT | Synchronization through Piggybacked Reference Timestamps |
| ST | Self-Similar Traffic |
| SVM | Support Vector Machine |
| SW | Software |
| SW | Sliding Window |
| SyncE | Synchronous Ethernet |
| TACSC | Temperature-Assisted Clock Self-Calibration |
| TCTS | Temperature Compensated Time Synchronization |
| TCXO | Temperature Compensated Oscillator |
| TDMA | Time Division Multiple Access |
| TKDS | Temperature-compensated Kalman-based Distributed Synchronization |
| TPSN | Timing-sync Protocol for Sensor Networks |
| TSC | Time Stamp Counter |
| TSCH | Time Slotted Channel Hopping Networks |
| TSN | Time-Sensitive Networking |
| TTE | Trigger-Time-Event System |
| VANETs | Vehicular Ad-Hoc Networks |
| VCO | Voltage Controlled Oscillator |
| W7-X | Wendelstein 7-X |
| WLAN | Wireless Local Area Network (IEEE 80211) |
| WSN | Wireless Sensor Network |
References
- Scheiterer, R.L.; Na, C.; Obradovic, D.; Steindl, G. Synchronization Performance of the Precision Time Protocol in Industrial Automation Networks. IEEE Trans. Instrum. Meas. 2009, 58, 1849–1857. [Google Scholar] [CrossRef]
- Chen, B.; Chen, Y.P.; Xie, J.M.; Zhou, Z.D.; Sa, J.M. Control methodologies in networked motion control systems. In Proceedings of the 2005 International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2005; IEEE Operations Center: Piscataway, NJ, USA, 2005; Volume 2, pp. 1088–1093. [Google Scholar] [CrossRef]
- Felser, M. Real-Time Ethernet—Industry Prospective. Proc. IEEE 2005, 93, 1118–1129. [Google Scholar] [CrossRef]
- Steinhauser, F.; Riesch, C.; Rudigier, M. IEEE 1588 for time synchronization of devices in the electric power industry. In Proceedings of the International IEEE Symposium on Precision Clock Synchronization for Measurement, Control and Communication (ISPCS), Portsmouth, NH, USA, 27 September–1 October 2010; pp. 1–6. [Google Scholar] [CrossRef]
- Geng, Y.; Liu, S.; Yin, Z.; Naik, A.; Prabhakar, B.; Rosenblum, M.; Vahdat, A. Exploiting a natural network effect for scalable, fine-grained clock synchronization. In Proceedings of the USENIX Conference on Networked Systems Design and Implementation (NSDI) 2018, Renton, WA, USA, 9–11 April 2018. [Google Scholar]
- Mahmood, A.; Exel, R.; Trsek, H.; Sauter, T. Clock synchronization over IEEE 802.11—A survey of methodologies and protocols. IEEE Trans. Ind. Inform. 2017, 13, 907–922. [Google Scholar] [CrossRef]
- Akhlaq, M.; Sheltami, T.R. RTSP: An Accurate and Energy-Efficient Protocol for Clock Synchronization in WSNs. IEEE Trans. Instrum. Meas. 2013, 62, 578–589. [Google Scholar] [CrossRef]
- Wu, Y.C.; Chaudhari, Q.; Serpedin, E. Clock Synchronization of Wireless Sensor Networks. IEEE Signal Process. Mag. 2011, 28, 124–138. [Google Scholar] [CrossRef]
- Schacht, J.; Laqua, H.; Niedermeyer, H. Synchronization of Processes in a Distributed Real Time System Exemplified by the Control System of the Fusion Experiment WENDELSTEIN 7-X. IEEE Trans. Nucl. Sci. 2006, 53, 2187–2194. [Google Scholar] [CrossRef]
- Wolf, R.C.; Ali, A.; Alonso, A.; Baldzuhn, J.; Beidler, C.; Beurskens, M.; Biedermann, C.; Bosch, H.S.; Bozhenkov, S.; Brakel, R.; et al. Major results from the first plasma campaign of the Wendelstein 7-X stellarator. Nucl. Fusion 2017, 57, 102020–102033. [Google Scholar] [CrossRef]
- Lipinski, M.; Wlostowski, T.; Serrano, J.; Alvarez, P. White rabbit: A PTP application for robust sub-nanosecond synchronization. In Proceedings of the 2011 IEEE International Symposium on Precision Clock Synchronization for Measurement, Control and Communication, Munich, Germany, 9–12 September 2011; pp. 25–30. [Google Scholar] [CrossRef]
- Akiyama, K.; Alberdi, A.; Alef, W.; Asada, K.; Azulay, R.; Baczko, A.K.; Ball, D.; Baloković, M.; Barrett, J.; Bintley, D.; et al. First M87 event horizon telescope results. IV. Imaging the central supermassive black hole. Astrophys. J. Lett. 2019, 875, L4. [Google Scholar]
- Noel, A.B.; Abdaoui, A.; Elfouly, T.; Ahmed, M.H.; Badawy, A.; Shehata, M.S. Structural Health Monitoring Using Wireless Sensor Networks: A Comprehensive Survey. IEEE Commun. Surv. Tutor. 2017, 19, 1403–1423. [Google Scholar] [CrossRef]
- Yang, Z.; Cai, L.; Liu, Y.; Pan, J. Environment-aware clock skew estimation and synchronization for wireless sensor networks. In Proceedings of the IEEE INFOCOM, Orlando, FL, USA, 25–30 March 2012. [Google Scholar] [CrossRef]
- Pottie, G.J.; Kaiser, W.J. Wireless integrated network sensors. Commun. ACM 2000, 43, 51–58. [Google Scholar] [CrossRef]
- Freris, N.M.; Graham, S.R.; Kumar, P.R. Fundamental Limits on Synchronizing Clocks Over Networks. IEEE Trans. Autom. Control 2011, 56, 1352–1364. [Google Scholar] [CrossRef]
- Zucca, C.; Tavella, P. The clock model and its relationship with the Allan and related variances. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52, 289–296. [Google Scholar] [CrossRef]
- Allan, D.W. Time and frequency (time-domain) characterization, estimation, and prediction of precision clocks and oscillators. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 1987, 34, 647–654. [Google Scholar] [CrossRef] [PubMed]
- Wu, D.; Zhu, H.; Zhu, Y.; Chang, V.; He, C.; Hsu, C.H.; Wang, H.; Feng, S.; Tian, L.; Huang, Z. Anomaly Detection Based on RBM-LSTM Neural Network for CPS in Advanced Driver Assistance System. ACM Trans. Cyber-Phys. Syst. 2020, 4, 1–17. [Google Scholar] [CrossRef]
- Sohal, A.S.; Sandhu, R.; Sood, S.K.; Chang, V. A cybersecurity framework to identify malicious edge device in fog computing and cloud-of-things environments. Comput. Secur. 2018, 74, 340–354. [Google Scholar] [CrossRef]
- Jafarpour, S.; Bullo, F. Synchronization of Kuramoto Oscillators via Cutset Projections. IEEE Trans. Autom. Control 2019, 64, 2830–2844. [Google Scholar] [CrossRef]
- Ha, S.Y.; Ko, D.; Park, J.; Zhang, X. Collective synchronization of classical and quantum oscillators. EMS Surv. Math. Sci. 2016, 3, 209–267. [Google Scholar] [CrossRef]
- Schaub, M.T.; O’Clery, N.; Billeh, Y.N.; Delvenne, J.C.; Lambiotte, R.; Barahona, M. Graph partitions and cluster synchronization in networks of oscillators. Chaos 2016, 26, 094821. [Google Scholar] [CrossRef]
- Dörfler, F.; Bullo, F. Synchronization in complex networks of phase oscillators: A survey. Automatica 2014, 50, 1539–1564. [Google Scholar] [CrossRef]
- Tang, Y.; Qian, F.; Gao, H.; Kurths, J. Synchronization in complex networks and its application–A survey of recent advances and challenges. Annu. Rev. Control 2014, 38, 184–198. [Google Scholar] [CrossRef]
- Dörfler, F.; Chertkov, M.; Bullo, F. Synchronization in complex oscillator networks and smart grids. Proc. Natl. Acad. Sci. USA 2013, 110, 2005–2010. [Google Scholar] [CrossRef] [PubMed]
- Gómez-Gardeñes, J.; Gómez, S.; Arenas, A.; Moreno, Y. Explosive synchronization transitions in scale-free networks. Phys. Rev. Lett. 2011, 106, 128701. [Google Scholar] [CrossRef]
- Chung, S.J.; Paranjape, A.A.; Dames, P.; Shen, S.; Kumar, V. A Survey on Aerial Swarm Robotics. IEEE Trans. Robot. 2018, 34, 837–855. [Google Scholar] [CrossRef]
- Cao, J.; Li, R. Fixed-time synchronization of delayed memristor-based recurrent neural networks. Sci. China Inf. Sci. 2017, 60. [Google Scholar] [CrossRef]
- Zhang, W.; Yang, X.; Xu, C.; Feng, J.; Li, C. Finite-Time Synchronization of Discontinuous Neural Networks With Delays and Mismatched Parameters. IEEE Trans. Neural Netw. Learn. Syst. 2018, 29, 3761–3771. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Ho, D.W.C.; Song, Q.; Xu, W. Finite/Fixed-Time Pinning Synchronization of Complex Networks With Stochastic Disturbances. IEEE Trans. Cybern. 2019, 49, 2398–2403. [Google Scholar] [CrossRef] [PubMed]
- Wei, B.; Xiao, F.; Shi, Y. Synchronization in Kuramoto Oscillator Networks With Sampled-Data Updating Law. IEEE Trans. Cybern. 2020, 50, 2380–2388. [Google Scholar] [CrossRef]
- Bojic, I.; Nymoen, K. Survey on synchronization mechanisms in machine-to-machine systems. Eng. Appl. Artif. Intell. 2015, 45, 361–375. [Google Scholar] [CrossRef]
- Wang, Y.; Doyle, F.J. Exponential synchronization rate of Kuramoto oscillators in the presence of a pacemaker. IEEE Trans. Autom. Control 2012, 58. [Google Scholar] [CrossRef]
- Zhou, Z.; Berger, M.S.; Ruepp, S.R.; Yan, Y. Insight into the IEEE 802.1 Qcr asynchronous traffic shaping in time sensitive network. Adv. Sci. Technol. Eng. Syst. J. 2019, 4, 292–301. [Google Scholar] [CrossRef]
- Zhou, Z.; Yan, Y.; Berger, M.; Ruepp, S. Analysis and modeling of asynchronous traffic shaping in time sensitive networks. In Proceedings of the WFCS 2018, Piscataway, NJ, USA, 13–15 June 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Hasan, K.F.; Wang, C.; Feng, Y.; Tian, Y.C. Time synchronization in vehicular ad-hoc networks: A survey on theory and practice. Veh. Commun. 2018, 14, 39–51. [Google Scholar] [CrossRef]
- Levesque, M.; Tipper, D. A Survey of Clock Synchronization Over Packet-Switched Networks. IEEE Commun. Surv. Tutor. 2016, 18, 2926–2947. [Google Scholar] [CrossRef]
- Praveen Kumar, D.; Amgoth, T.; Annavarapu, C.S.R. Machine learning algorithms for wireless sensor networks: A survey. Inf. Fusion 2019, 49, 1–25. [Google Scholar] [CrossRef]
- Swain, A.R.; Hansdah, R.C. A model for the classification and survey of clock synchronization protocols in WSNs. Ad Hoc Netw. 2015, 27, 219–241. [Google Scholar] [CrossRef]
- Lasassmeh, S.M.; Conrad, J.M. Time synchronization in wireless sensor networks: A survey. In Proceedings of the IEEE SoutheastCon 2010, Charlotte-Concord, CA, USA, 18–21 March 2010; pp. 242–245. [Google Scholar] [CrossRef]
- Ranganathan, P.; Nygard, K. Time synchronization in wireless sensor networks: A survey. Int. J. Ubicomp 2010, 1, 92–102. [Google Scholar] [CrossRef]
- Sundararaman, B.; Buy, U.; Kshemkalyani, A.D. Clock synchronization for wireless sensor networks: A survey. Ad. Hoc. Netw. 2005, 3, 281–323. [Google Scholar] [CrossRef]
- Sivrikaya, F.; Yener, B. Time synchronization in sensor networks: A survey. IEEE Netw. 2004, 18, 45–50. [Google Scholar] [CrossRef]
- Giorgi, G.; Narduzzi, C. Performance Analysis of Kalman-Filter-Based Clock Synchronization in IEEE 1588 Networks. IEEE Trans. Instrum. Meas. 2011, 60. [Google Scholar] [CrossRef]
- Bletsas, A. Evaluation of Kalman filtering for network time keeping. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52. [Google Scholar] [CrossRef]
- Mills, D.; Martin, J.; Burbank, J.; Kasch, W. Network Time Protocol Version 4: Protocol and Algorithms Specification, Internet Engineering Task Force (IETF) Request for Comments (RFC) 5905, June 2020.
- IEEE 1588-2008 Standard for a Precision Clock Synchronization Protocol for Networked Measurement and Control Systems, 24 July 2008. Available online: https://ieeexplore.ieee.org/document/4579760 (accessed on 10 November 2020). [CrossRef]
- IEEE 802.1AS-2011 Standard for Local and Metropolitan Area Networks—Timing and Synchronization for Time-Sensitive Applications in Bridged Local Area Networks, 30 March 2011. Available online: https://ieeexplore.ieee.org/document/5741898 (accessed on 10 November 2020). [CrossRef]
- IEC 61784-2. Digital Data Communications for Measurement and Control-Part 2: Additional Profiles for ISO/IEC 8802-3 Based Communication Networks in Real-Time Applications; German Institute for Standardisation (Deutsches Institut für Normung): Berlin, Germany, 2005. [Google Scholar]
- Pigan, R.; Metter, M. Automating with PROFINET: Industrial Communication Based on Industrial Ethernet; Publicis MCD Werbeagentur GmbH: Somerset, UK, 2015. [Google Scholar]
- Fontanelli, D.; Macii, D.; Rinaldi, S.; Ferrari, P.; Flammini, A. Performance analysis of a clock state estimator for PROFINET IO IRT synchronization. In Proceedings of the 2013 IEEE International Instrumentation and Measurement Technology Conference, Minneapolis, MN, USA, 6–9 May 2013; Staff, I., Ed.; pp. 1828–1833. [Google Scholar] [CrossRef]
- International Telecommunication Union. ITU-I G.8262: Timing Characteristics of a Synchronous Equipment Slave Clock, 29 November 2018. Available online: https://www.itu.int/rec/T-REC-G.8262 (accessed on 10 November 2020).
- Hann, K.; Jobert, S.; Rodrigues, S. Synchronous ethernet to transport frequency and phase/time. IEEE Commun. Mag. 2012, 50, 152–160. [Google Scholar] [CrossRef]
- IEEE 1588-2019 Standard for a Precision Clock Synchronization Protocol for Networked Measurement and Control Systems, 16 June 2020. Available online: https://ieeexplore.ieee.org/document/9120376 (accessed on 10 November 2020). [CrossRef]
- IEEE 1588-2002 Standard for a Precision Clock Synchronization Protocol for Networked Measurement and Control Systems, 31 October 2002. Available online: https://ieeexplore.ieee.org/document/1048550 (accessed on 10 November 2020). [CrossRef]
- Lee, K.S.; Wang, H.; Shrivastav, V.; Weatherspoon, H. Globally Synchronized Time via Datacenter Networks. In Proceedings of the 2016 ACM SIGCOMM Conference, Florianopolis, Brazil, 22–26 August 2016; Barcellos, M., Ed.; Association for Computing Machinery: New York, NY, USA, 2016; pp. 454–467. [Google Scholar] [CrossRef]
- Watt, S.T.; Achanta, S.; Abubakari, H.; Sagen, E.; Korkmaz, Z.; Ahmed, H. Understanding and applying precision time protocol. In Proceedings of the 2015 Saudi Arabia smart grid (SASG), Jeddah, Saudi Arabia, 7–9 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–7. [Google Scholar] [CrossRef]
- Puttnies, H.; Danielis, P.; Timmermann, D. PTP-LP: Using Linear Programming to Increase the Delay Robustness of IEEE 1588 PTP. In Proceedings of the IEEE GLOBECOM 2018, Abu Dhabi, UAE, 9–13 December 2018. [Google Scholar]
- Correll, K.; Barendt, N.; Branicky, M. Design considerations for software only implementations of the IEEE 1588 precision time protocol. In Proceedings of the Conference on IEEE 1588, Zurich, Switzerland, 10–12 October 2005; pp. 11–15. [Google Scholar]
- IEEE 802.1AS-2020 Standard for Local and Metropolitan Area Networks–Timing and Synchronization for Time-Sensitive Applications, 19 June 2020. Available online: https://ieeexplore.ieee.org/document/9121845 (accessed on 10 November 2020). [CrossRef]
- Johas Teener, M.D.; Garner, G.M. Overview and timing performance of IEEE 802.1AS. In Proceedings of the 2008 IEEE International Symposium on Precision Clock Synchronization for Measurement, Control and Communication (ISPCS), Ann Arbor, MI, USA, 22–26 September 2008; pp. 49–53. [Google Scholar] [CrossRef]
- Garner, G.; Ryu, H. Synchronization of audio/video bridging networks using IEEE 802.1AS. IEEE Commun. Mag. 2011, 49, 140–147. [Google Scholar] [CrossRef]
- Gutierrez, M.; Steiner, W.; Dobrin, R.; Punnekkat, S. Synchronization Quality of IEEE 802.1AS in Large-Scale Industrial Automation Networks. In Proceedings of the 2017 IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS), Pittsburgh, PA, USA, 18–21 April 2017; pp. 273–282. [Google Scholar] [CrossRef]
- Steinbach, T.; Lim, H.T.; Korf, F.; Schmidt, T.C.; Herrscher, D.; Wolisz, A. Tomorrow’s In-Car Interconnect? A Competitive Evaluation of IEEE 802.1 AVB and Time-Triggered Ethernet (AS6802). In Proceedings of the 2012 IEEE Vehicular Technology Conference (VTC Fall), Quebec City, QC, Canada, 3–6 September 2012; pp. 1–5. [Google Scholar] [CrossRef]
- Yang, Z.; Pan, J.; Cai, L. Adaptive Clock Skew Estimation with Interactive Multi-Model Kalman Filters for Sensor Networks. In Proceedings of the IEEE ICC, Cape Town, South Africa, 23–27 May 2010. [Google Scholar] [CrossRef]
- Exel, R. Mitigation of Asymmetric Link Delays in IEEE 1588 Clock Synchronization Systems. IEEE Commun. Lett. 2014, 18, 507–510. [Google Scholar] [CrossRef]
- Diarra, A.; Hogenmueller, T.; Zimmermann, A.; Grzemba, A.; Khan, U.A. Improved clock synchronization start-up time for Ethernet AVB-based in-vehicle networks. In Proceedings of the 2015 IEEE 20th Conference on Emerging Technologies & Factory Automation (ETFA), Luxembourg, 8–11 September 2015; pp. 1–8. [Google Scholar] [CrossRef]
- Serrano, J.; Lipinski, M.; Wlostowski, T.; Gousiou, E.; van der Bij, E.; Cattin, M.; Daniluk, G. The white rabbit project. In Proceedings of the 2nd International Beam Instrumentation Conference, Oxford, UK, 16–19 September 2013. [Google Scholar]
- Moreira, P.; Serrano, J.; Wlostowski, T.; Loschmidt, P.; Gaderer, G. White rabbit: Sub-nanosecond timing distribution over ethernet. In Proceedings of the 2009 International Symposium on Precision Clock Synchronization for Measurement, Control and Communication (ISPCS), Brescia, Italy, 12–16 October 2009; pp. 1–5. [Google Scholar] [CrossRef]
- Mizrahi, T.; Moses, Y. ReversePTP: A clock synchronization scheme for software-defined networks. Int. J. Netw. Manag. 2016, 26, 355–372. [Google Scholar] [CrossRef]
- Mizrahi, T.; Moses, Y. Using ReversePTP to distribute time in Software Defined Networks. In Proceedings of the 2014 IEEE International Symposium on Precision Clock Synchronization for Measurement, Control and Communication (ISPCS), Austin, TX, USA, 22–26 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 112–117. [Google Scholar] [CrossRef]
- Mizrahi, T.; Moses, Y. ReversePTP: A software defined networking approach to clock synchronization. In Proceedings of the ACM HotSDN ’14: Proceedings of the third workshop on Hot Topics in Software Defined Networking, Chicago, IL, USA, 22 August 2014; Association for Computing Machinery: New York, NY, USA; pp. 203–204. [Google Scholar] [CrossRef]
- Kero, N.; Puhm, A.; Kernen, T.; Mroczkowski, A. Performance and Reliability Aspects of Clock Synchronization Techniques for Industrial Automation. Proc. IEEE 2019, 107, 1011–1026. [Google Scholar] [CrossRef]
- Fontanelli, D.; Macii, D. Accurate time synchronization in PTP-based industrial networks with long linear paths. In Proceedings of the 2010 IEEE International Symposium on Precision Clock Synchronization for Measurement, Control and Communication (ISPCS), Portsmouth, NH, USA, 27 September–1 October 2010; pp. 97–102. [Google Scholar] [CrossRef]
- Abubakari, H.; Sastry, S. IEEE 1588 style synchronization over wireless link. In Proceedings of the 2008 IEEE International Symposium on Precision Clock Synchronization for Measurement, Control and Communication, Ann Arbor, MI, USA, 22–26 September 2008; pp. 127–130. [Google Scholar] [CrossRef]
- Mahmood, A.; Exel, R. Servo design for improved performance in software timestamping-assisted WLAN synchronization using IEEE 1588. In Proceedings of the IEEE 18th Conference on Emerging Technologies & Factory Automation (ETFA), Cagliari, Italy, 10–13 September 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–8. [Google Scholar] [CrossRef]
- Karthik, A.K.; Blum, R.S. Robust Clock Skew and Offset Estimation for IEEE 1588 in the Presence of Unexpected Deterministic Path Delay Asymmetries. IEEE Trans. Commun. 2020, 8, 5102–5119. [Google Scholar] [CrossRef]
- IEEE 802.1Q-2011 Standard for Local and Metropolitan Area Networks–Media Access Control (MAC) Bridges and Virtual Bridged Local Area, 31 August 2011. Available online: https://ieeexplore.ieee.org/document/6009146 (accessed on 10 November 2020). [CrossRef]
- Benson, T.; Akella, A.; Maltz, D.A. Network Traffic Characteristics of Data Centers in the Wild. In Proceedings of the ACM SIGCOMM, Melbourne, Australia, November 2010. [Google Scholar] [CrossRef]
- Schmid, T.; Dutta, P.; Srivastava, M.B. High-resolution, low-power time synchronization an oxymoron no more. In Proceedings of the ACM/IEEE International Conference on Information Processing in Sensor Networks, Stockholm, Sweden, April 2010. [Google Scholar] [CrossRef]
- Wu, Q.; Yang, L.; Chen, J. Enhancement for Real-Time Ethernet Clock Synchronization by Internal Processing Delay Measurement. IEEE Commun. Lett. 2019, 23, 2063–2067. [Google Scholar] [CrossRef]
- Ahmed, T.; Rahman, S.; Tornatore, M.; Kim, K.; Mukherjee, B. A survey on high-precision time synchronization techniques for optical datacenter networks and a zero-overhead microsecond-accuracy solution. Photonic Netw. Commun. 2018, 36, 56–67. [Google Scholar] [CrossRef]
- Schacht, J.; Laqua, H.; Muller, I.; Puttnies, H.; Skodzik, J. The Trigger-Time-Event System for Wendelstein 7-X: Overview and First Operational Experiences. IEEE Trans. Nucl. Sci. 2019, 66, 969–973. [Google Scholar] [CrossRef]
- Schacht, J.; Skodzik, J. Multifunction-Timing Card lTTEV2 for CoDaC Systems of Wendelstein 7-X. IEEE Trans. Nucl. Sci. 2015, 62, 1187–1194. [Google Scholar] [CrossRef]
- Puttnies, H.; Timmermann, D.; Danielis, P. An approach for precise, scalable, and platform independent clock synchronization. In Proceedings of the 2017 14th IEEE Annual Consumer Communications Networking Conference (CCNC), Las Vegas, NV, USA, 8–11 January 2017; pp. 461–466. [Google Scholar] [CrossRef]
- Mallada, E.; Meng, X.; Hack, M.; Zhang, L.; Tang, A. Skewless Network Clock Synchronization Without Discontinuity: Convergence and Performance. IEEE/ACM Trans. Netw. 2015, 23, 1619–1633. [Google Scholar] [CrossRef]
- Veitch, D.; Ridoux, J.; Korada, S.B. Robust Synchronization of Absolute and Difference Clocks Over Networks. IEEE/ACM Trans. Netw. 2009, 17, 417–430. [Google Scholar] [CrossRef]
- Davis, M.; Villain, B.; Ridoux, J.; Orgerie, A.C.; Veitch, D. An IEEE-1588 compatible RADclock. In Proceedings of the 2012 International IEEE Symposium on Precision Clock Synchronization for Measurement, Control and Communication (ISPCS), San Francisco, CA, USA, 24–28 September 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 1–6. [Google Scholar] [CrossRef]
- Auler, L.F.; d’Amore, R. Adaptive Kalman Filter for Time Synchronization over Packet-Switched Networks: An Heuristic Approach. In Proceedings of the 2nd International Conference on Communication Systems Software and Middleware, Bangalore, India, 7–12 January 2007; IEEE Service Center: Piscataway, NJ, USA, 2007; pp. 1–7. [Google Scholar] [CrossRef]
- Giorgi, G. An Event-Based Kalman Filter for Clock Synchronization. IEEE Trans. Instrum. Meas. 2015, 64, 449–457. [Google Scholar] [CrossRef]
- Giorgi, G.; Narduzzi, C. Kalman filtering for multi-path network synchronization. In Proceedings of the 2014 IEEE International Symposium on Precision Clock Synchronization for Measurement, Control and Communication (ISPCS), Austin, TX, USA, 22–26 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 65–70. [Google Scholar] [CrossRef]
- Giorgi, G.; Narduzzi, C. A resilient Kalman filter based servo clock. In Proceedings of the 2013 IEEE International Symposium on Precision Clock Synchronization for Measurement, Control and Communication (ISPCS) Proceedings, Lemgo, Germany, 22–27 September 2013; pp. 59–64. [Google Scholar] [CrossRef]
- Fontanelli, D.; Macii, D.; Wolfrum, P.; Obradovic, D.; Steindl, G. A clock state estimator for PTP time synchronization in harsh environmental conditions. In Proceedings of the 2011 IEEE International Symposium on Precision Clock Synchronization for Measurement, Control and Communication, Munich, Germany, 12–16 September 2011; pp. 99–104. [Google Scholar] [CrossRef]
- Exel, R.; Ring, F. Improved clock synchronization accuracy through optimized servo parametrization. In Proceedings of the 2013 IEEE International Symposium on Precision Clock Synchronization for Measurement, Control and Communication (ISPCS) Proceedings, Lemgo, Germany, 22–27 September 2013; pp. 65–70. [Google Scholar] [CrossRef]
- Xu, X.; Xiong, Z.; Sheng, X.; Wu, J.; Zhu, X. A New Time Synchronization Method for Reducing Quantization Error Accumulation Over Real-Time Networks: Theory and Experiments. IEEE Trans. Ind. Inform. 2013, 9, 1659–1669. [Google Scholar] [CrossRef]
- Zhang, L.; Liu, Z.; Honghui Xia, C. Clock synchronization algorithms for network measurements. In IEEE INFOCOM 2002; Kermani, P., Ed.; IEEE: Piscataway, NJ, USA, 2002; pp. 160–169. [Google Scholar] [CrossRef]
- Khlifi, H.; Gregoire, J.C. Estimation and removal of clock skew from delay measures. In LCN 2004; IEEE Computer Society: Los Alamitos, CA, USA, 2004; pp. 144–151. [Google Scholar] [CrossRef]
- Moon, S.B.; Skelly, P.; Towsley, D. Estimation and removal of clock skew from network delay measurements. IEEE INFOCOM 1999, 1, 227–234. [Google Scholar] [CrossRef]
- Lemmon, M.D.; Ganguly, J.; Xia, L. Model-based clock synchronization in networks with drifting clocks. Dependable Computing, 2000. In Proceedings of the 2000 Pacific Rim International Symposium on, Los Angeles, CA, USA, USA, 20 December 2000; pp. 177–184. [Google Scholar]
- Puttnies, H.; Schweissguth, E.; Timmermann, D.; Schacht, J. Clock Synchronization Using Linear Programming, Multicasts, and Temperature Compensation. In Proceedings of the 2019 IEEE Global Communications Conference (GLOBECOM), Waikoloa, HI, USA, 9–13 December 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zaidi, S.; Boutekkouk, F. Agent based simulator of the Flexray protocol: A case study of the clock synchronization and media access control services. In Proceedings of the 6th Seminar on Detection Systems Architecture and Technology (DAT), Algiers, Algeria, 17–19 February 2014. [Google Scholar]
- Froehlich, S.; Hack, M.; Meng, X.; Zhang, L. Achieving precise coordinated cluster time in a cluster environment. In Proceedings of the IEEE International Symposium on Precision Clock Synchronization for Measurement, Control and Communication, Ann Arbor, MI, USA, 22–26 September 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 54–58. [Google Scholar] [CrossRef]
- Schmid, T.; Charbiwala, Z.; Shea, R.; Srivastava, M.B. Temperature Compensated Time Synchronization. IEEE Embed. Syst. Lett. 2009, 1, 37–41. [Google Scholar] [CrossRef]
- Li, Z.; Chen, W.; Li, C.; Li, M.; Li, X.Y.; Liu, Y. FLIGHT: Clock calibration using fluorescent lighting. In Proceedings of the 18th Annual International Conference on Mobile Computing and Networking, Istanbul, Turkey, August 2012; Akan, O.B., Ed.; ACM: New York, NY, USA, 2013; p. 329. [Google Scholar] [CrossRef]
- Skiadopoulos, K.; Tsipis, A.; Giannakis, K.; Koufoudakis, G.; Christopoulou, E.; Oikonomou, K.; Kormentzas, G.; Stavrakakis, I. Synchronization of data measurements in wireless sensor networks for IoT applications. Ad. Hoc. Netw. 2019, 89, 47–57. [Google Scholar] [CrossRef]
- Cena, G.; Scanzio, S.; Valenzano, A.; Zunino, C. Implementation and Evaluation of the Reference Broadcast Infrastructure Synchronization Protocol. IEEE Trans. Ind. Inform. 2015, 11, 801–811. [Google Scholar] [CrossRef]
- Guo, F.; Zhou, B.; Vuran, M.C. CFOSynt: Carrier frequency offset assisted clock syntonization for wireless sensor networks. In Proceedings of the IEEE INFOCOM, Atlanta, GA, USA, 1–4 May 2017. [Google Scholar]
- Dongare, A.; Lazik, P.; Rajagopal, N.; Rowe, A. Pulsar: A Wireless Propagation-Aware Clock Synchronization Platform. In Proceedings of the 2017 IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS), Pittsburgh, PA, USA, 18–21 April 2017; pp. 283–292. [Google Scholar] [CrossRef]
- Ganeriwal, S.; Kumar, R.; Srivastava, M.B. Timing-sync protocol for sensor networks. In Proceedings of the 1st International Conference on Embedded Networked Sensor Systems, Los Angeles, CA, USA, November 2003; Akyildiz, I., Ed.; ACM: New York, NY, USA, 2003; p. 138. [Google Scholar] [CrossRef]
- Sommer, P.; Wattenhofer, R. Gradient clock synchronization in wireless sensor networks. In Proceedings of the 2009 International Conference on Information Processing in Sensor Networks, San Francisco, CA, USA, 13–16 April 2009; pp. 37–48. [Google Scholar]
- Chang, T.; Watteyne, T.; Pister, K.; Wang, Q. Adaptive synchronization in multi-hop TSCH networks. Comput. Networks 2015, 76, 165–176. [Google Scholar] [CrossRef]
- Qiu, T.; Zhang, Y.; Qiao, D.; Zhang, X.; Wymore, M.L.; Sangaiah, A.K. A Robust Time Synchronization Scheme for Industrial Internet of Things. IEEE Trans. Ind. Inform. 2017, 14, 1. [Google Scholar] [CrossRef]
- Kikuya, Y.; Dibaji, S.M.; Ishii, H. Fault-Tolerant Clock Synchronization Over Unreliable Channels in Wireless Sensor Networks. IEEE Trans. Control Netw. Syst. 2018, 5, 1551–1562. [Google Scholar] [CrossRef]
- Xie, K.; Cai, Q.; Fu, M. A fast clock synchronization algorithm for wireless sensor networks. Automatica 2018, 92, 133–142. [Google Scholar] [CrossRef]
- Kadowaki, Y.; Ishii, H. Event-Based Distributed Clock Synchronization for Wireless Sensor Networks. IEEE Trans. Autom. Control 2015, 60, 2266–2271. [Google Scholar] [CrossRef]
- Carli, R.; Zampieri, S. Network Clock Synchronization Based on the Second-Order Linear Consensus Algorithm. IEEE Trans. Autom. Control 2014, 59, 409–422. [Google Scholar] [CrossRef]
- Maggs, M.K.; O’Keefe, S.G.; Thiel, D.V. Consensus Clock Synchronization for Wireless Sensor Networks. IEEE Sens. J. 2012, 12, 2269–2277. [Google Scholar] [CrossRef]
- Gong, F.; Sichitiu, M.L. Temperature compensated Kalman distributed clock synchronization. Ad. Hoc. Netw. 2017, 62, 88–100. [Google Scholar] [CrossRef]
- Koivisto, M.; Costa, M.; Werner, J.; Heiska, K.; Talvitie, J.; Leppänen, K.; Koivunen, V.; Valkama, M. Joint device positioning and clock synchronization in 5G ultra-dense networks. IEEE Trans. Wirel. Commun. 2017, 16, 2866–2881. [Google Scholar] [CrossRef]
- Nilsson, J.O.; Händel, P. Robust recursive network clock synchronization. In Proceedings of the 2014 IEEE International Conference on Electronics, Computing and Communication Technologies (CONECCT), Bangalore, India, 6–7 January 2014; pp. 1–5. [Google Scholar] [CrossRef]
- Masood, W.; Schmidt, J.F.; Brandner, G.; Bettstetter, C. Disty: Dynamic stochastic time synchronization for wireless sensor networks. IEEE Trans. Ind. Inform. 2016, 13, 1421–1429. [Google Scholar] [CrossRef]
- Lenzen, C.; Sommer, P.; Wattenhofer, R. PulseSync: An Efficient and Scalable Clock Synchronization Protocol. IEEE/ACM Trans. Netw. 2015, 23, 717–727. [Google Scholar] [CrossRef]
- Lenzen, C.; Sommer, P.; Wattenhofer, R. Optimal clock synchronization in networks. In Proceedings of the Proceedings of the 7th ACM Conference on Embedded Networked Sensor Systems (SenSys), Berkeley, CA, USA, November 2009; p. 225. [Google Scholar] [CrossRef]
- Maróti, M.; Kusy, B.; Simon, G.; Lédeczi, Á. The flooding time synchronization protocol. In Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems, Baltimore, MD, USA, November 2004; Stankovic, J.A., Ed.; ACM: New York, NY, USA, 2004; p. 39. [Google Scholar] [CrossRef]
- Elson, J.; Girod, L.; Estrin, D. Fine-grained network time synchronization using reference broadcasts. ACM SIGOPS Oper. Syst. Rev. 2002, 36, 147–163. [Google Scholar] [CrossRef]
- Jin, M.; Xing, T.; Chen, X.; Meng, X.; Fang, D.; He, Y. DualSync: Taming clock skew variation for synchronization in low-power wireless networks. In Proceedings of the IEEE INFOCOM, San Francisco, CA, USA, 10–14 April 2016. [Google Scholar] [CrossRef]
- Gong, F.; Sichitiu, M.L. CESP: A Low-Power High-Accuracy Time Synchronization Protocol. IEEE Trans. Veh. Technol. 2016, 65, 2387–2396. [Google Scholar] [CrossRef]
- Benzaïd, C.; Bagaa, M.; Younis, M. Efficient clock synchronization for clustered wireless sensor networks. Ad. Hoc. Netw. 2017, 56, 13–27. [Google Scholar] [CrossRef]
- Hao, T.; Zhou, R.; Xing, G.; Mutka, M.W.; Chen, J. WizSync: Exploiting Wi-Fi Infrastructure for Clock Synchronization in Wireless Sensor Networks. IEEE Trans. Mob. Comput. 2014, 13, 1379–1392. [Google Scholar] [CrossRef]
- Yang, Z.; He, L.; Cai, L.; Pan, J. Temperature-Assisted Clock Synchronization and Self-Calibration for Sensor Networks. IEEE Trans. Wirel. Commun. 2014, 13, 3419–3429. [Google Scholar] [CrossRef]
- Lasoi, W.; Pornpromlikit, S. Temperature-aware Time Synchronization with an Accuracy-efficiency Trade-off in Wireless Sensor Networks. Procedia Eng. 2016, 168, 1706–1709. [Google Scholar] [CrossRef]
- Yıldırım, K.S.; Carli, R.; Schenato, L. Adaptive control-based clock synchronization in wireless sensor networks. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 2806–2811. [Google Scholar]
- Yıldırım, K.S. Gradient descent algorithm inspired adaptive time synchronization in wireless sensor networks. IEEE Sens. J. 2016, 16, 5463–5470. [Google Scholar] [CrossRef]
- Chang, T.; Wang, Q. Adaptive Compensation for Time-Slotted Synchronization in Wireless Sensor Network. Int. J. Distrib. Sens. Netw. 2014, 10, 540397. [Google Scholar] [CrossRef]
- Qiu, T.; Chi, L.; Guo, W.; Zhang, Y. STETS: A novel energy-efficient time synchronization scheme based on embedded networking devices. Microprocess. Microsyst. 2015, 39, 1285–1295. [Google Scholar] [CrossRef]
- Sun, G.; Song, L.; Yu, H.; Chang, V.; Du, X.; Guizani, M. V2V routing in a VANET based on the autoregressive integrated moving average model. IEEE Trans. Veh. Technol. 2018, 68, 908–922. [Google Scholar] [CrossRef]

| Approach | SC | Estimator | Accuracy | Cond./restr. |
|---|---|---|---|---|
| NTP [47] | Yes | RTT | 1ms | None |
| PTP [48] | Yes | RTT | <1s | Custom HW |
| gPTP [49] | Yes | RTT | <1s | Custom HW |
| PTCP [50,51] | Yes | RTT | <1s | Custom HW |
| PTCP-KF [52] | Yes | KF | 20–200 ns | Eval. with Matlab |
| SyncE [53] | Yes | Offset: MV Freq.: PLL | Freq.: 4 ppm | Custom HW |
| c SyncE + Offset [54] | No | Offset: MV Freq.: PLL | NI Freq.: 4 ppm | Custom HW |
| Approach | SC | Estimator | Accuracy | Cond./restr. |
|---|---|---|---|---|
| [67] | Yes (PTP) | RTT (ISR) | 10–100 ns | Testbed |
| [4] | Yes (PTP) | RTT | SW:20 s HW:10 ns–1 s | Analytically |
| [68] | No | RTT | <1 ns | Analytically + Sim. |
| White Rabbit [11,69,70] | Yes (PTP, IEEE 802.1Q, IEEE 802.3) | Offset:RTT Freq.: PLL | 200 ps | Testbed Custom HW |
| ReversePTP [71,72,73] | Yes | RTT | aprox. 8 ms (SW) | Testbed |
| [45] | Yes (PTP) | KF | NI | Sim. |
| [74] | Yes | KF | 100 ns–1 s | Analytically + Sim. |
| [75] | Yes (PTP) | KF | approximately 30 ns | Sim. |
| [76] | NI | KF + PI | 25 μs | Testbed |
| [77] | No | PI | 40–350 ns | Sim. + Testbed |
| [78] | NA | SAGE | NI | Sim. |
| PTP-LP [59] | Yes | LP/LR | approximately 100 ns | Sim. |
| Approach | SC | Estimator | Accuracy | Cond./Restr. |
|---|---|---|---|---|
| [35,36] | Yes (802.1Qcr) | None | None | Sim. |
| [82] | No | RTT | 11 ns | Testbed (Custom HW) |
| [83] | No | RTT | <7 s | Sim. (Custom HW) |
| DTP [57] | No | RTT | approximately 25 ns | (Custom HW) |
| TTE | ||||
| [84,85] | No | RTT | 10 ns–100 ns | Testbed (Custom HW) |
| PSPI-Sync [86] | No | RTT + SLE | approximately 100 s | Testbed |
| [87] | No | EF | 5–20 s | Analytically + Testbed |
| RADclock [88,89] | Almost (PTP) | EF | approximately 10 s | Testbed |
| [90] | No | KF | approximately 100 s | Testbed |
| [46] | Yes (NTP) | KF/LP/ATD | <30 ms (GT) <0.5 s (ST, LP) <0.75 s (ST, KF) <1.2 s (ST, ATD) | Sim. + Testbed |
| [91] | No | KF | <0.5 s | Sim. |
| [92] | No | KF | <1 s | Sim. |
| [93] | NI | KF | ca. 0.1 s | Sim. |
| [94] | No | KF | <100 s (RMSE) | Sim. |
| [95] | No | PI | 6.4 ns (RMSE) | Sim. |
| [96] | No | KF + PI | <18 ns | Testbed |
| [97] | No | CH | 1–1.6 ms | Sim. |
| [98] | NI | MW/DSR/SWI/CH | NI | Sim. |
| [99] | NI | LP | NI | Sim. |
| [100] | No | LP | NI | Analytically |
| SLMT [101] | No | LP + IMM | approximately 100 ns | Sim. |
| HYGENS [5] | Almost | |||
| (entirely SW) | SVM | approximately 100 ns | Testbed | |
| (HW-TS) | ||||
| [102] | Yes (FlexRay) | FTM | NI | Testbed |
| Approach | SC | Estimator | Accuracy | Cond./Restr. |
|---|---|---|---|---|
| FLIGHT [105] | No | None | approximately s | Testbed |
| [106] | No | Difference | <1 ms | Analytically + Sim. |
| RBIS [107] | Yes (802.11) | Difference | 0.2–3 s | Testbed |
| [108] | No | CFO + ECT | approximately 12–5 kHz (RMSE) | Sim. + Testbed |
| Pulsar [109] | NI | RTT | <5 ns | Testbed |
| TPSN [110] | NI | RTT | 16.9 s | Sim. + Testbed |
| GTSP [111] | Almost (entirely SW) | MW | 4–14 s | Sim. + Testbed (HW-TS + ISR) |
| [112] | NI | Sum | 76 s | Sim. + Testbed |
| R-Sync [113] | No | RTT | approximately 50 s | Sim. + Testbed |
| TCTS [104] | No | MW | 100–200 s | Sim. |
| [114] | No | CA+MSR | <100 ms | Sim. |
| [115] | NI | CA | NI | Analytically |
| [116] | Yes | CA | 100–1 ms | Analytically + Sim. |
| [117] | Yes | CA | approximately 1 s | Analytically + Sim. |
| CCS [118] | Yes | CA | NI | Sim. |
| TKDS [119] | NI | KF | NI | Sim. |
| [120] | NI | EKF | 0.5–34 ns | Sim. |
| [121] | NI | CKF | NI | Testbed |
| [66] | No | IMM-KF | <1 s (RMSE) | Sim. |
| EACS [14] | No | IMM-KF | 1 s–1 ms | Sim. + Testbed |
| DISTY [122] | Yes | KF | approximately 8 s | Analytically + Testbed |
| PulseSync [123,124] | NI | LR | approximately 2 s | Sim. + Testbed |
| FTSP [125] | Yes (DS) | LR | 1.48 s | Testbed |
| RBS [126] | Yes (DS, 802.11) | LR | 6.29 s | Sim. + Testbed |
| DualSync [127] | No | LR | <100 s | Sim. + Testbed |
| CESP [128] | Yes | LR/MA | approximately 2–3 s (MAC-TS) approximately 10 s (APP-TS) | Testbed |
| RTSP [7] | No | LR | approximately 0.2–0.3 s | Sim. |
| SPiRT [129] | NI | LCM | NI | Sim. + Testbed |
| WizSync [130] | NI | Convolution | approximately 0.12ms | Testbed |
| TACSC [131] | No | DSC | External: 15 s Internal: 160 s | Analytically + Sim. + Testbed |
| [132] | No | NI | 0.2 ms | Testbed |
| PISync [133] | Yes | PI | 20 s | Analytically + Testbed |
| GraDeS [134] | Yes | GD | <20 s | Analytically + Testbed |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Puttnies, H.; Danielis, P.; Sharif, A.R.; Timmermann, D. Estimators for Time Synchronization—Survey, Analysis, and Outlook. IoT 2020, 1, 398-435. https://doi.org/10.3390/iot1020023
Puttnies H, Danielis P, Sharif AR, Timmermann D. Estimators for Time Synchronization—Survey, Analysis, and Outlook. IoT. 2020; 1(2):398-435. https://doi.org/10.3390/iot1020023
Chicago/Turabian StylePuttnies, Henning, Peter Danielis, Ali Rehan Sharif, and Dirk Timmermann. 2020. "Estimators for Time Synchronization—Survey, Analysis, and Outlook" IoT 1, no. 2: 398-435. https://doi.org/10.3390/iot1020023
APA StylePuttnies, H., Danielis, P., Sharif, A. R., & Timmermann, D. (2020). Estimators for Time Synchronization—Survey, Analysis, and Outlook. IoT, 1(2), 398-435. https://doi.org/10.3390/iot1020023







