Gravity Data-Driven Machine Learning: A Novel Approach for Predicting Volcanic Vent Locations in Geohazard Investigation
Abstract
1. Introduction
2. Materials and Methods
2.1. Implementation Framework
- (a)
- Data Acquisition and Preparation: Gravity datasets incorporated longitude, latitude, and gravitational anomaly measurements from documented volcanic vent sites. Non-vent location data was integrated to establish contrasting patterns for model differentiation between volcanic and non-volcanic zones. Preprocessing addressed missing data points, normalized feature scales, and structured datasets for algorithm training.
- (b)
- The machine learning target parameter was established as binary classification indicating volcanic vent presence or absence at designated geographic positions.
- (c)
- Feature Development: The gravity data served as the features for the model.
- (d)
- Model Training: Training employed confirmed volcanic vent coordinates as positive instances (class 1) and non-volcanic locations as negative instances (class 0).
- (e)
- Model evaluation (accuracy, precision, recall, F1 score).
- (f)
- Prediction: The trained algorithm produced probability assessments for potential volcanic vent locations at untested coordinates using corresponding gravity anomaly features.
- 1.
- Random Forest Algorithm
- 2.
- Support Vector Machines (SVM)
- 3.
- Logistic Regression
- 4.
- Gradient Boosting Machines (GBM)
- 5.
- Decision Trees
- Performance Assessment Metrics
2.2. Training Dataset Provenance and Partitioning Strategy
- Dataset sources and labeling
- Labeling process
- Data partitioning and sample sizes
- (a)
- Training set: 80% of total samples
- (b)
- Validation set: 10% of total samples
- (c)
- Testing set: 10% of total samples
- Geospatial distribution maps
2.3. Possible Limitations of the Dataset
- (a)
- Incomplete surface representation: Some vents may remain undetected due to burial beneath younger lava flows, pyroclastic deposits, or erosion, potentially leading to underrepresentation of the positive class.
- (b)
- Resolution constraints: The gravity station spacing limits the ability to resolve very small or subtle density anomalies.
- (c)
- Single dataset dependency: Additional datasets (from other methods) could improve predictive robustness.
- (d)
- Field validation—No direct field verification of predicted vent locations was conducted due to logistical constraints; this remains a recommended step for future work.
3. Results
4. Interpretation of Results
4.1. Comparative Performance of Machine Learning Algorithms
4.2. Feature Importance and Geophysical Interpretation
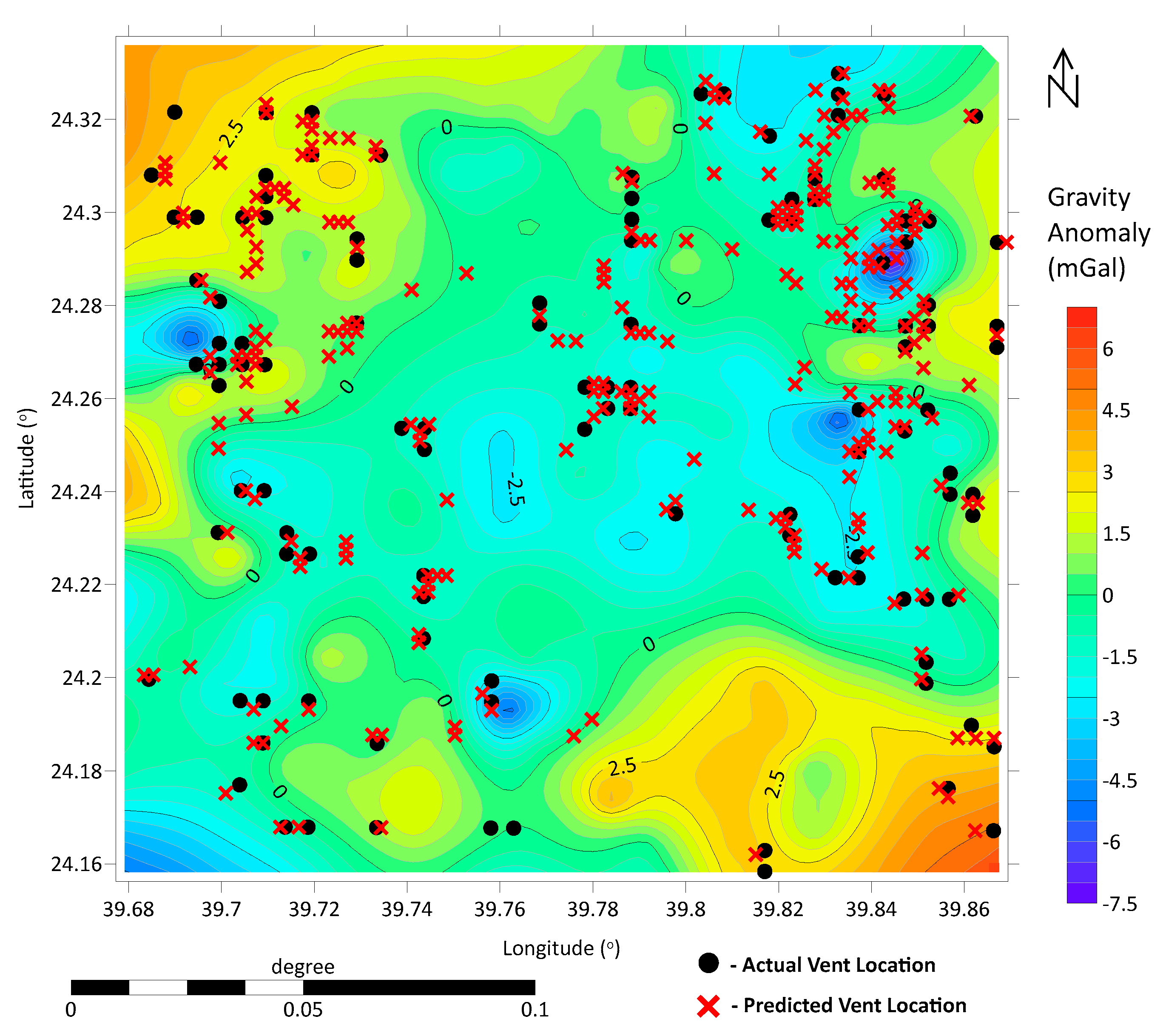
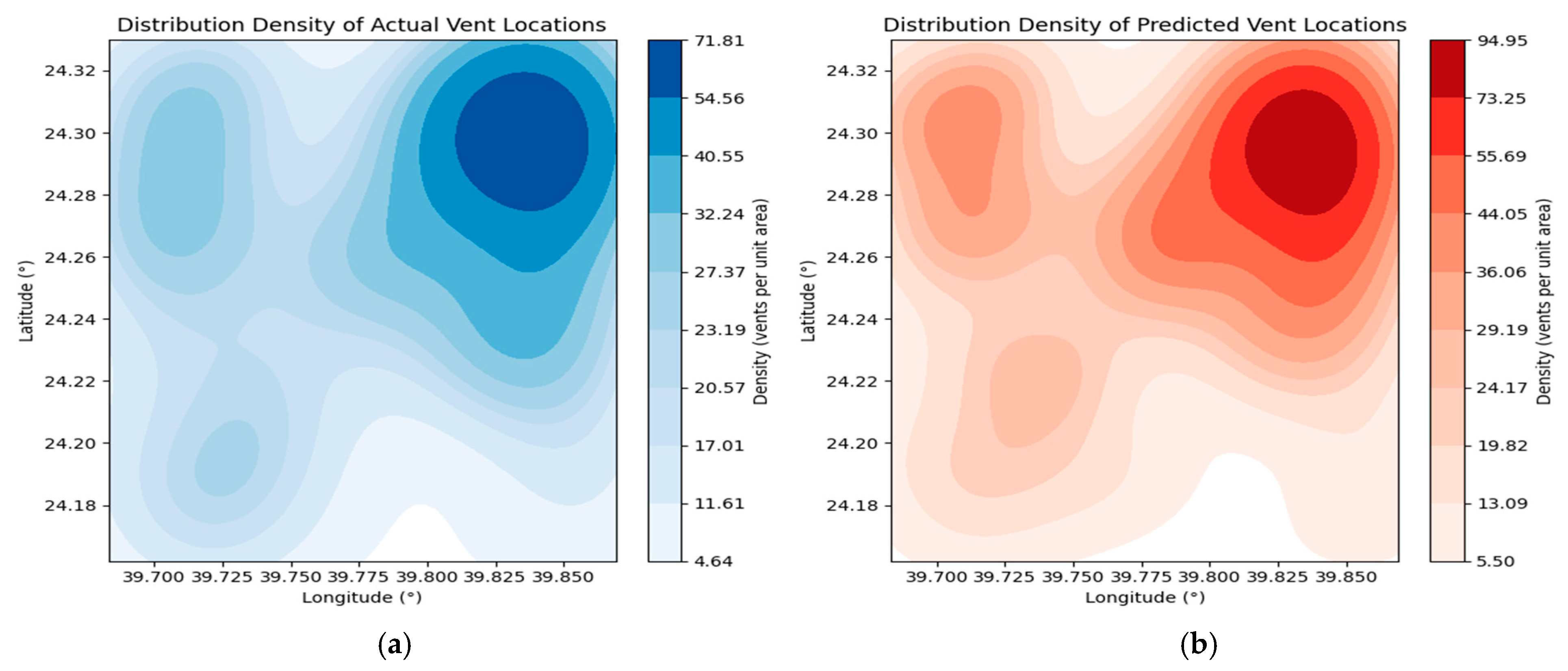
4.3. Spatial Patterns of Predicted Vents
4.4. Agreement Between Predicted and Actual Vents
4.5. Regional Sensitivity Variations
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| AUC-ROC | Area Under the Curve of the Receiver Operating Characteristic Curve |
| ASM | Attribute Selection Measure |
| DC | degree of certainty |
| GBM | Gradient Boosting Machine |
| SVM | Support Vector Machine |
References
- Marjoribanks, R. Geological Methods in Mineral Exploration and Mining; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Giavarini, C.; Hester, K. Gas Hydrates: Immense Energy Potential and Environmental Challenges; Springer: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Herz, N.; Garrison, E.G. Geological Methods for Archaeology; Oxford University Press: Oxford, UK, 1998; ISBN 9780195090246. [Google Scholar]
- Gravenstein, J.S.; Jaffe, J.A.; Paulus, R.A. Gas Monitoring and Pulse Oximetry; Springer: New York, NY, USA, 1986; Available online: https://www.sciencedirect.com/book/9780409902617/gas-monitoring-and-pulse-oximetry (accessed on 22 March 2023).
- Abdulfarraj, M.; Abraham, E.; Alqahtani, F.; Aboud, E. Advancements in Geohazard Investigations: Developing a Machine Learning Framework for the Prediction of Vents at Volcanic Fields Using Magnetic Data. Geosciences 2024, 14, 328. [Google Scholar] [CrossRef]
- Abraham, E.M.; Usman, A.O.; Amano, I. Machine Learning-Based Classification of Geological Structures from Magnetic Anomaly Data: Case study of Northern Nigeria Basement Complex. Mach. Learn. Appl. 2025, 20, 100678. [Google Scholar] [CrossRef]
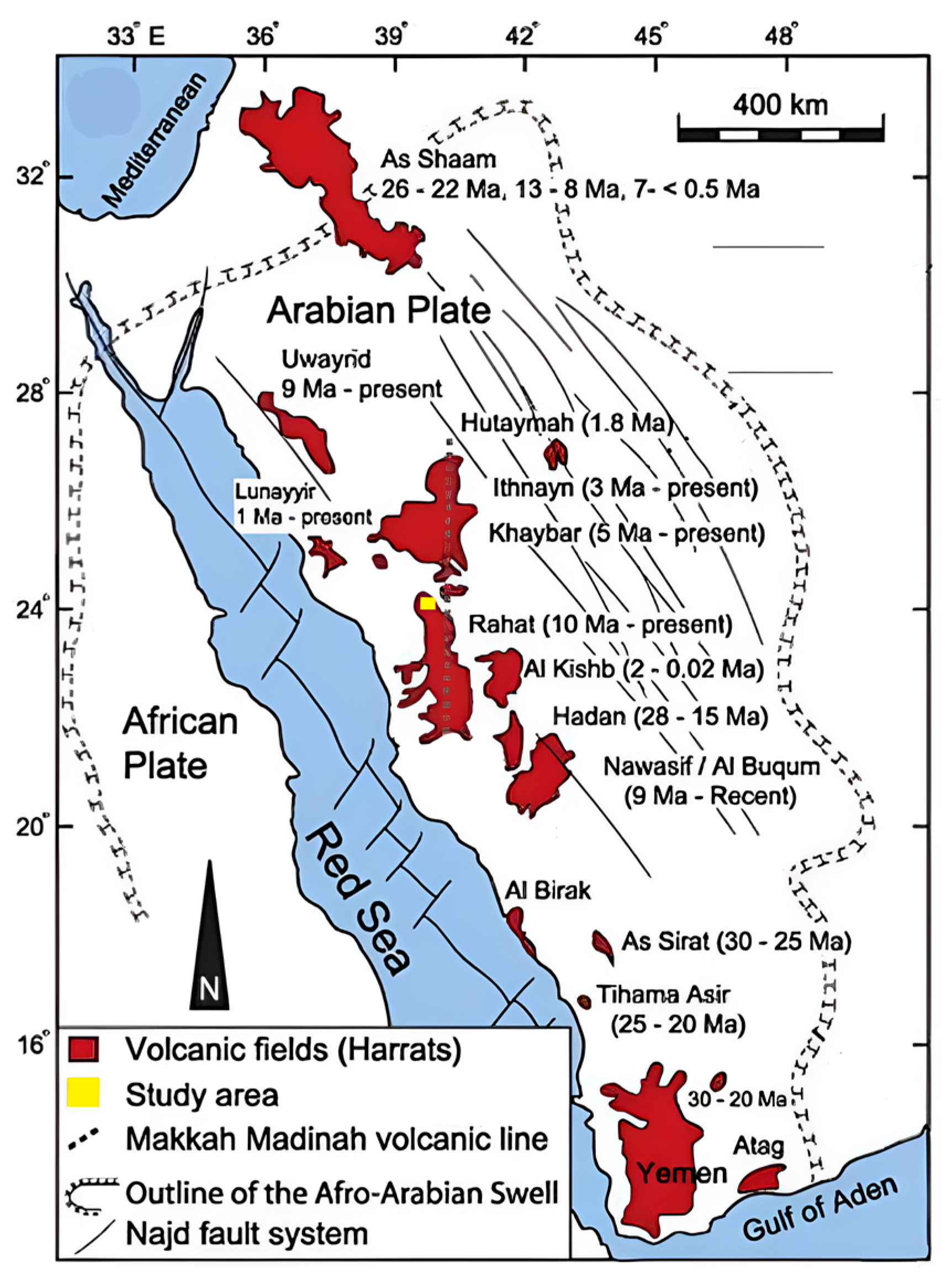
- Aboud, E.; Abraham, E.; Alqahtani, F.; Abdulfarraj, M. High potential geothermal areas within the Rahat volcanic field, Saudi Arabia, from gravity data and 3D geological modeling. Acta Geophys. 2023, 72, 1713–1729. [Google Scholar] [CrossRef]
- Alqahtani, F.; Abraham, E.M.; Aboud, E.; Rajab, M. Two-dimensional gravity inversion of basement relief for geothermal energy potentials at the Harrat Rahat volcanic field, Saudi Arabia, using particle swarm optimization. Energies 2022, 15, 2887. [Google Scholar] [CrossRef]
- Battaglia, M.; Gottsmann, J.; Carbone, D.; Fernández, J. 4D volcano gravimetry. Geophysics 2008, 73, WA3–WA18. [Google Scholar] [CrossRef]
- Tilling, R.I.; Lipman, P.W. Lessons in reducing volcano risk. Nature 1993, 364, 277–280. [Google Scholar] [CrossRef]
- Rymer, H.; Brown, G.C. Gravity fields and the interpretation of volcanic structures: Geological discrimination of volcanic structures in Central America. J. Volcanol. Geotherm. Res. 1986, 27, 225–240. [Google Scholar] [CrossRef]
- Robinson, J.E.; Downs, D.T. Chapter R: Overview of the Cenozoic geology of the northern Harrat Rahat volcanic field, Kingdom of Saudi Arabia. In Active Volcanism on the Arabian Shield-Geology, Volcanology, and Geophysics of Northern Harrat Rahat and Vicinity, Kingdom of Saudi Arabia; Sisson, T.W., Calvert, A.T., Mooney, W.D., Eds.; U.S. Geological Survey Professional Paper 1862 [Also Released as Saudi Geological Survey Special Report SGS-SP-2021-1]; U.S. Geological Survey: Reston, VA, USA, 2023; 20p. [Google Scholar] [CrossRef]
- Downs, D.T.; Stelten, M.E.; Champion, D.E.; Dietterich, H.R.; Nawab, Z.; Zahran, H.; Hassan, K.; Shawali, J. Volcanic history of the northernmost part of the Harrat Rahat volcanic field, Saudi Arabia. Geosphere 2018, 14, 1253–1282. [Google Scholar] [CrossRef]
- Moufti, M.R.; Moghazi, A.M.; Ali, K.A. 40 Ar/39 Ar geochronology of the Neogene-Quaternary Harrat Al-Madinah intercontinental volcanic field, Saudi Arabia: Implications for duration and migration of volcanic activity. J. Asian Earth Sci. 2013, 62, 253–268. [Google Scholar] [CrossRef]
- Aboud, E.; Alqahtani, F.; Elmasry, N.; Abdulfarraj, M.; Osman, H. Geothermal anomaly detection using potential field geophysical Data in Rahat volcanic field, Madinah, Saudi Arabia. J. Geol. Geophys. 2022, 11, 1026. [Google Scholar]
- Runge, M.G.; Bebbington, M.S.; Cronin, S.J.; Lindsay, J.M.; Kenedi, C.L.; Moufti, M.R.H. Vents to events: Determining an eruption event record from volcanic vent structures for the Harrat Rahat, Saudi Arabia. Bull. Volcanol. 2014, 76, 804. [Google Scholar] [CrossRef]
- Alohali, A.; Bertin, D.; de Silva, D.; Cronin, S.; Duncan, R.; Qaysi, S.; Moufti, M.R. Spatio-temporal forecasting of future volcanism at Harrat Khaybar, Saudi Arabia. J. Appl. Volcanol. 2022, 11, 12. [Google Scholar] [CrossRef]
- Alshehri, F.; Abdelrahman, K. Groundwater aquifer detection using the time-domain electromagnetic method: A case study in Harrat Ithnayn, northwestern Saudi Arabia. J. King Saud Univ.-Sci. 2022, 34, 101684. [Google Scholar] [CrossRef]
- Abdelfattah, A.K.; Al-amri, A.; Alzahrani, H.; Abuamarah, B.A. Ambient noise tomography in the upper crust of North Harrat Rahat, Saudi Arabia. J. King Saud Univ.-Sci. 2022, 35, 102523. [Google Scholar] [CrossRef]
- Metwaly, M.; Abdalla, F.; Taha, A.I. Hydrogeophysical Study of Sub-Basaltic Alluvial Aquifer in the Southern Part of Al-Madinah Al-Munawarah, Saudi Arabia. Sustainability 2021, 13, 9841. [Google Scholar] [CrossRef]
- Powers, D.M.W. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. Int. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]
- Yilmaz, I. Landslide susceptibility mapping using frequency ratio, logistic regression, artificial neural networks and their comparison: A case study from Kat landslides (Tokat-Turkey). Comput. Geosci. 2009, 35, 1125–1138. [Google Scholar] [CrossRef]
- Caruana, R.; Niculescu-Mizil, A. An Empirical Comparison of Supervised Learning Algorithms. In Proceedings of the 23rd International Conference on Machine Learning, Pittsburgh, PA, USA, 25–29 June 2006. [Google Scholar] [CrossRef]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Thottoth, S.R.; Das, P.P.; Khatri, V.N. Prediction of compression capacity of under-reamed piles in sand and clay. Multiscale and Multidiscip. Model. Exp. Des. 2024, 7, 2289–2305. [Google Scholar] [CrossRef]
- Menon, V.; Kolathayar, S. Optimizing nailing parameters for hybrid retaining systems using supervised learning regression models. Multiscale Multidiscip. Model. Exp. Des. 2024, 7, 4683–4698. [Google Scholar] [CrossRef]
- Li, Y.; Rahardjo, H.; Satyanaga, A.; Rangarajan, S.; Lee, D.T. Soil database development with the application of machine learning methods in soil properties prediction. Eng. Geol. 2022, 306, 106769. [Google Scholar] [CrossRef]
- Abraham, M.T.; Satyam, N.; Lokesh, R.; Pradhan, B.; Alamri, A. Factors Affecting Landslide Susceptibility Mapping: Assessing the Influence of Different Machine Learning Approaches, Sampling Strategies and Data Splitting. Land 2021, 10, 989. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, C.; Zhong, H.; Li, Y.; Wang, L. Prediction of undrained shear strength using extreme gradient boosting and random forest based on Bayesian optimization. Geosci. Front. 2021, 12, 469–477. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Cox, D.R. The regression analysis of binary sequences. J. R. Stat. Soc. Ser. B 1958, 20, 215–242. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Lang, N. What Is Model Evaluation? Machine Learning. Data Base Camp. 2023. Available online: https://databasecamp.de/en/ml/model-evaluation-en (accessed on 12 February 2024).
- Manning, C.D.; Raghavan, P.; Schütze, H. Introduction to Information Retrieval; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar] [CrossRef]
- Sasaki, Y. The Truth of the F-Measure; RIKEN Brain Science Institute Technical Report. 2007. Available online: https://www.researchgate.net/publication/268185911_The_truth_of_the_F-measure (accessed on 16 December 2024).
- Berthier, F.; Demange, J.; Iundt, F. Geothermal Resources of Harrat Khaybar and Harrat Rahat Progress Report 1400–1401 the Kingdom of Saudi Arabia; Saudi Arabian Deputy Ministry for Mineral Resources Open-File Report BRGM-OF-02-44; Ministry of Petroleum and Mineral Resources: Jiddah, Saudi Arabia, 1982; p. 116.


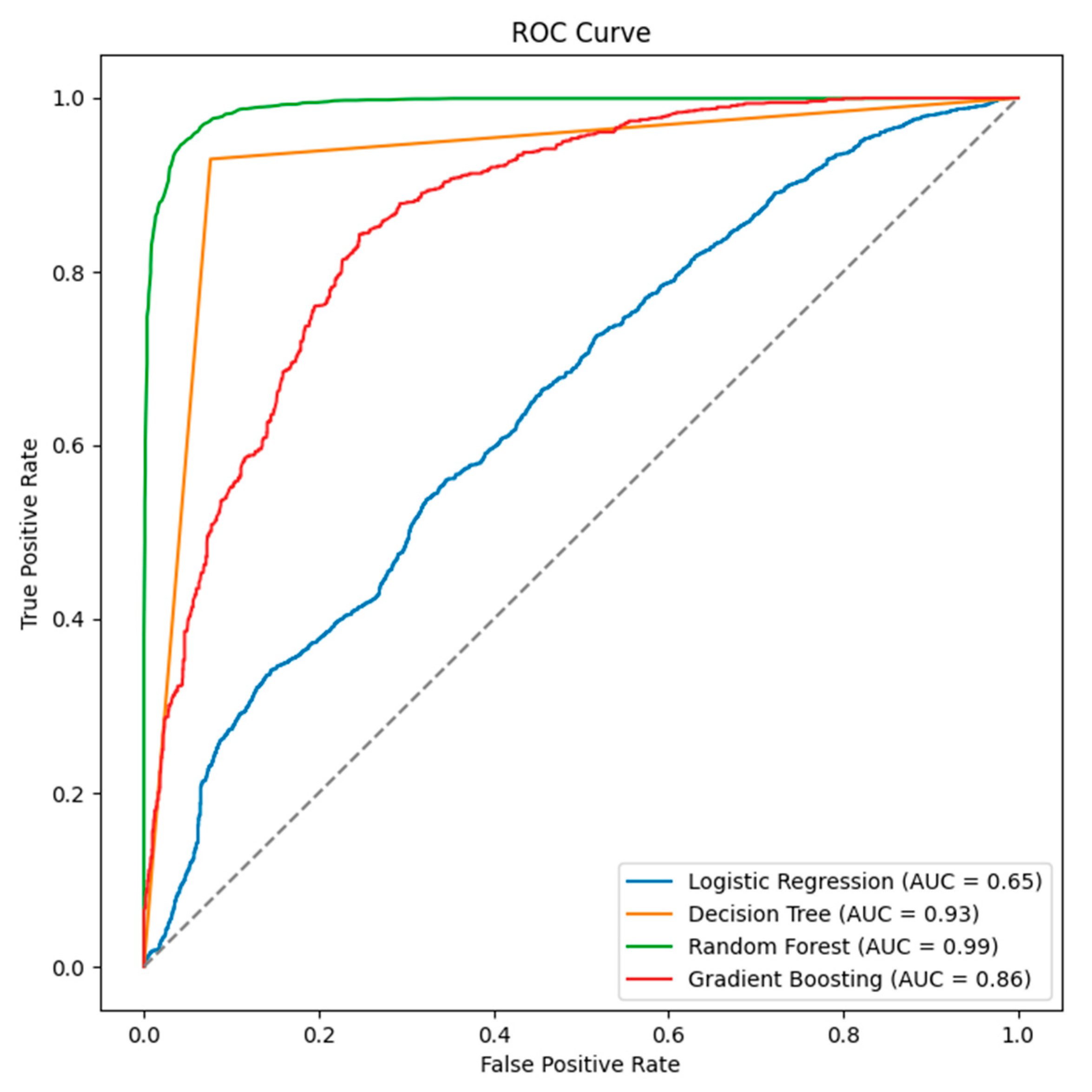
| Model | Accuracy | Precision | Recall | F1-Score | Execution Time (mins) | |
|---|---|---|---|---|---|---|
| 1 | Logistic Regression | 0.600 | 0.592 | 0.627 | 0.609 | 0.080 |
| 2 | Decision Tree | 0.927 | 0.924 | 0.930 | 0.927 | 0.119 |
| 3 | Random Forest | 0.950 | 0.946 | 0.955 | 0.950 | 2.844 |
| 4 | Gradient Boosting | 0.796 | 0.768 | 0.844 | 0.805 | 2.436 |
| 5 | Support Vector Machine | 0.559 | 0.544 | 0.702 | 0.613 | 13.459 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdulfarraj, M.; Abraham, E.; Alqahtani, F.; Aboud, E. Gravity Data-Driven Machine Learning: A Novel Approach for Predicting Volcanic Vent Locations in Geohazard Investigation. GeoHazards 2025, 6, 49. https://doi.org/10.3390/geohazards6030049
Abdulfarraj M, Abraham E, Alqahtani F, Aboud E. Gravity Data-Driven Machine Learning: A Novel Approach for Predicting Volcanic Vent Locations in Geohazard Investigation. GeoHazards. 2025; 6(3):49. https://doi.org/10.3390/geohazards6030049
Chicago/Turabian StyleAbdulfarraj, Murad, Ema Abraham, Faisal Alqahtani, and Essam Aboud. 2025. "Gravity Data-Driven Machine Learning: A Novel Approach for Predicting Volcanic Vent Locations in Geohazard Investigation" GeoHazards 6, no. 3: 49. https://doi.org/10.3390/geohazards6030049
APA StyleAbdulfarraj, M., Abraham, E., Alqahtani, F., & Aboud, E. (2025). Gravity Data-Driven Machine Learning: A Novel Approach for Predicting Volcanic Vent Locations in Geohazard Investigation. GeoHazards, 6(3), 49. https://doi.org/10.3390/geohazards6030049











