Landslide Susceptibility Assessment Based on a Quantitative Continuous Model: A Case Study of Wanzhou
Abstract
1. Introduction
2. Materials
2.1. Study Area
2.2. Data Source
2.3. Data Preprocessing
3. Methods
3.1. Landslide Susceptibility Evaluation Models
3.1.1. Information Value (IV)
3.1.2. Frequency Ratio (FR)
3.1.3. Certainty Factor (CF)
3.1.4. Cosine Amplitude (CA)
3.1.5. Bias-Standardized Information Value (BSIV)
3.1.6. Support Vector Machine (SVM)
3.1.7. Random Forest (RF)
3.1.8. Gradient Boosting Decision Tree (GBDT)
3.2. Quantitative Continuum Model
- (1)
- Normalized factor value
- (2)
- Precision Set
- (3)
- Generation LS Layer
3.3. Accuracy of Models
4. Results
4.1. Factor Selection
4.2. Landslide Susceptibility Results
4.2.1. Characteristics of the Spatial Distribution of LS
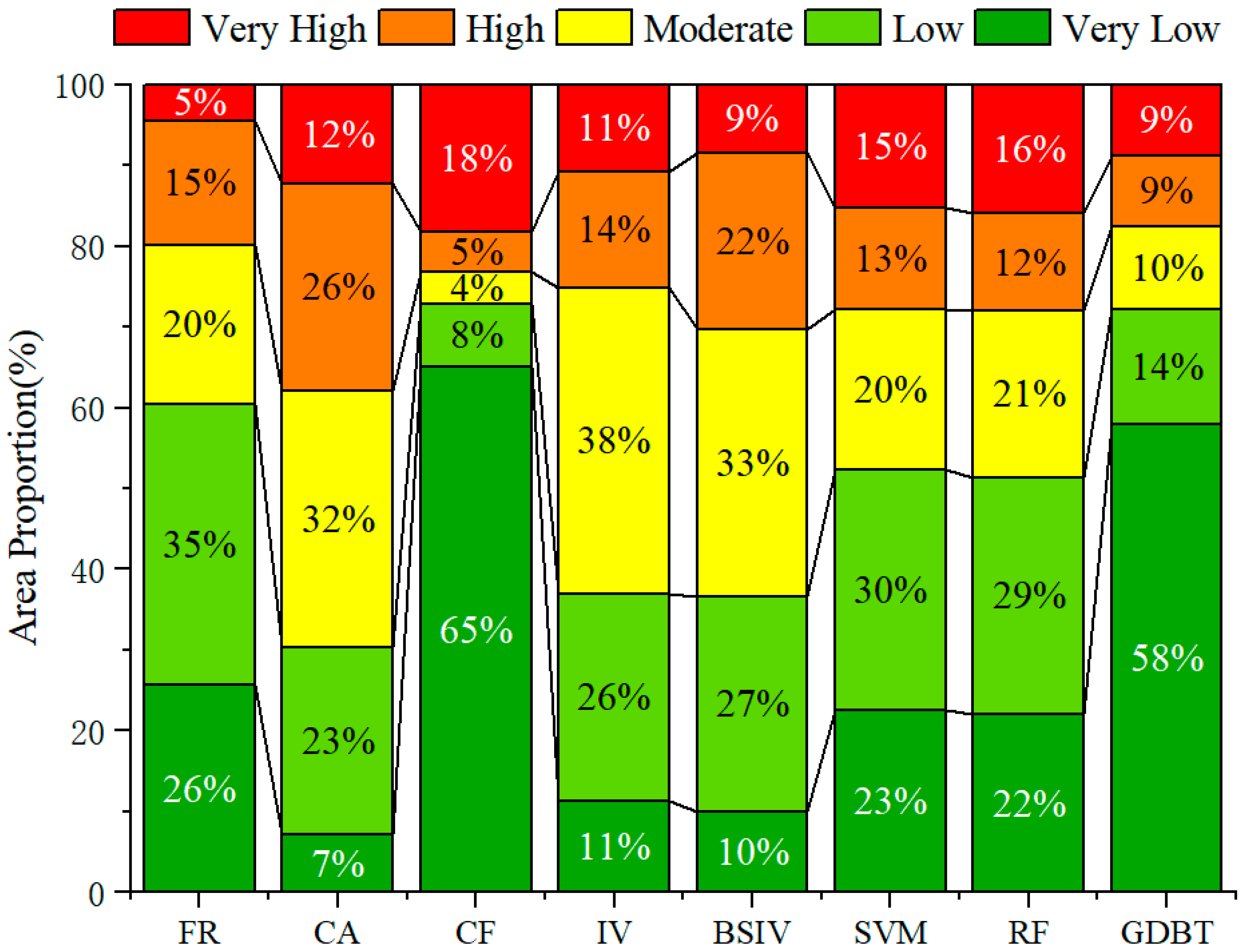
4.2.2. Percentage of Area in Different LS Classes
4.3. Evaluation of Model Accuracy
4.3.1. The Statistical Table of Grids
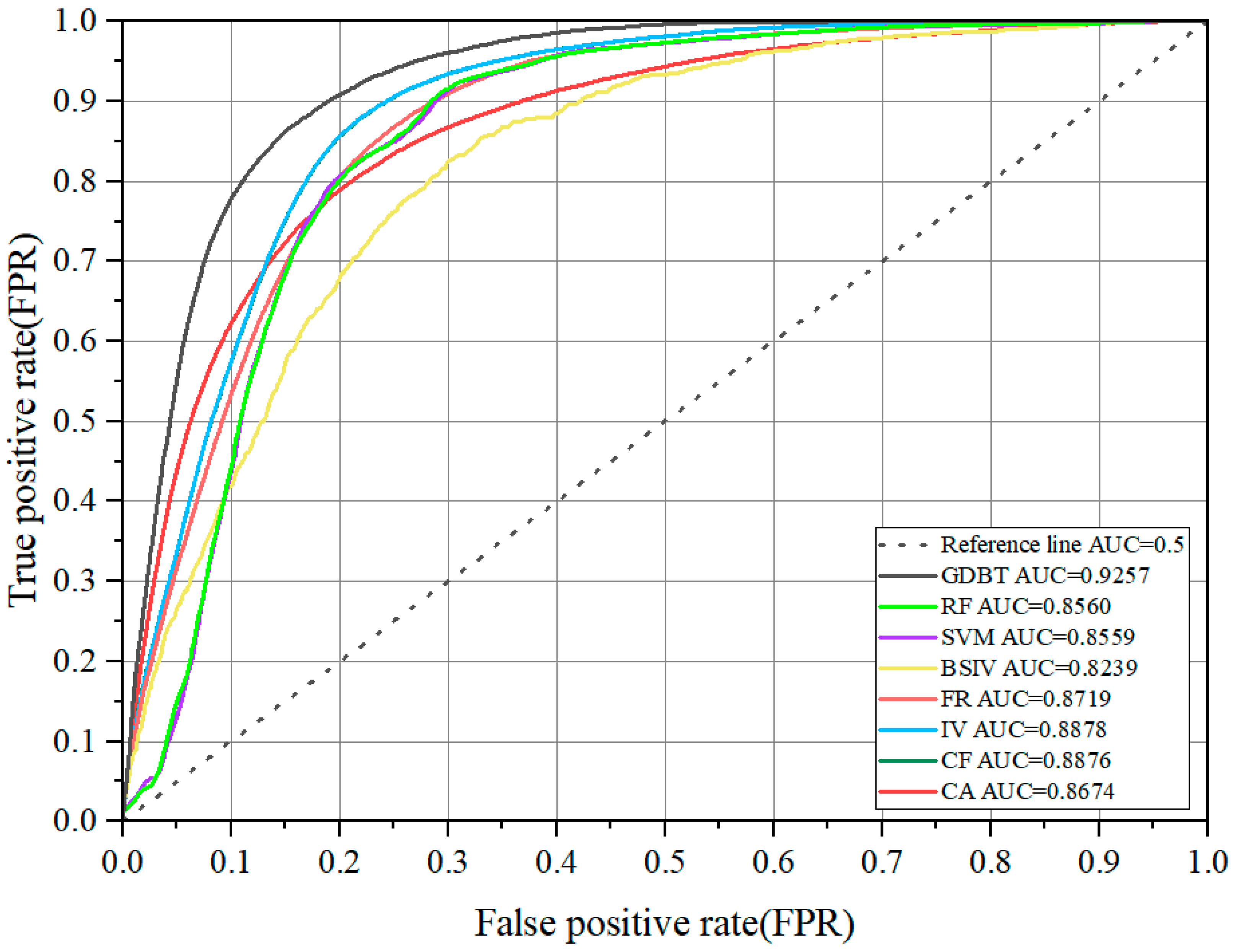
4.3.2. ROC Curves
4.3.3. Summary and Comparison of the LS Models
5. Discussion
5.1. Quantitative Validation of Spatial Patterns
5.2. Enhanced Interpretability Through Quantitative Continuous Models
5.3. Model Limitations and Future Research Directions
6. Conclusions
- (1)
- The susceptibility zoning shows that the extremely high-risk zones are concentrated along the main stream of the Yangtze River and the built-up areas of cities and towns, which is more consistent with the spatial distribution of historical landslides, and this distribution pattern confirms the synergistic mechanism of the reservoir level fluctuation and engineering activities.
- (2)
- The susceptibility maps generated by the continuous model are less patchy, and the spatial continuity is significantly improved. Compared with the traditional BSIV model, the AUC value is increased to 0.8878, which is close to the machine learning model accuracy.
- (3)
- The continuous model processing technique effectively solves the subjectivity problem of factor grading in the traditional statistical method. It achieves continuous quantification of the sensitivity of disaster-causing factors through the dynamic window sliding calculation, which can successfully capture the nonlinear response characteristics of factors such as slope and earthquake magnitude.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kalantar, B.; Ueda, N.; Saeidi, V.; Ahmadi, K.; Halin, A.A.; Shabani, F. Landslide Susceptibility Mapping: Machine and ensemble learning based on remote sensing big data. Remote Sens. 2020, 12, 1737. [Google Scholar] [CrossRef]
- Karagianni, A.; Lazos, I.; Chatzipetros, A. Remote sensing techniques in disaster management: Amynteon Mine Landslides, Greece. In Intelligent Systems for Crisis Management; Lecture notes in geoinformation and cartography; Springer: Cham, Switzerland, 2019; pp. 209–235. [Google Scholar] [CrossRef]
- Liu, P.; Wei, Y.; Wang, Q.; Chen, Y.; Xie, J. Research on Post-Earthquake Landslide extraction algorithm based on improved U-Net model. Remote Sens. 2020, 12, 894. [Google Scholar] [CrossRef]
- Xu, S.; Song, Y.; Lu, P.; Mu, G.; Yang, K.; Wang, S. An optimized non-landslide sampling method for Landslide susceptibility evaluation using machine learning models. Nat. Hazards 2024, 121, 5873–5900. [Google Scholar] [CrossRef]
- Zhou, C.; Yin, K.; Cao, Y.; Ahmed, B.; Li, Y.; Catani, F.; Pourghasemi, H.R. Landslide susceptibility modeling applying machine learning methods: A case study from Longju in the Three Gorges Reservoir area, China. Comput. Geosci. 2017, 112, 23–37. [Google Scholar] [CrossRef]
- Frattini, P.; Crosta, G.; Carrara, A. Techniques for evaluating the performance of landslide susceptibility models. Eng. Geol. 2009, 111, 62–72. [Google Scholar] [CrossRef]
- Aleotti, P.; Chowdhury, R. Landslide hazard assessment: Summary review and new perspectives. Bull. Eng. Geol. Environ. 1999, 58, 21–44. [Google Scholar] [CrossRef]
- Casagli, N.; Intrieri, E.; Tofani, V.; Gigli, G.; Raspini, F. Landslide detection, monitoring and prediction with remote-sensing techniques. Nat. Rev. Earth Environ. 2023, 4, 51–64. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, T.; Hei, L.; Wang, Y. Study on rainfall threshold of geological disasters based on effective rainfall model in Wenzhou City. East China Geol. 2025, 46, 252–267. (In Chinese) [Google Scholar] [CrossRef]
- Clerici, A.; Perego, S.; Tellini, C.; Vescovi, P. A GIS-based automated procedure for landslide susceptibility mapping by the Conditional Analysis method: The Baganza valley case study (Italian Northern Apennines). Environ. Geol. 2006, 50, 941–961. [Google Scholar] [CrossRef]
- Abeysiriwardana, H.D.; Gomes, P.I.A. Integrating vegetation indices and geo-environmental factors in GIS-based landslide-susceptibility mapping: Using logistic regression. J. Mt. Sci. 2022, 19, 477–492. [Google Scholar] [CrossRef]
- Gameiro, S.; Riffel, E.S.; De Oliveira, G.G.; Guasselli, L.A. Artificial neural networks applied to landslide susceptibility: The effect of sampling areas on model capacity for generalization and extrapolation. Appl. Geogr. 2021, 137, 102598. [Google Scholar] [CrossRef]
- Ikram, N.; Basharat, M.; Ali, A.; Usmani, N.A.; Gardezi, S.A.H.; Hussain, M.L.; Riaz, M.T. Comparison of landslide susceptibility models and their robustness analysis: A case study from the NW Himalayas, Pakistan. Geocarto Int. 2021, 37, 9204–9241. [Google Scholar] [CrossRef]
- Chang, L.; Xing, G.; Yin, H.; Fan, L.; Zhang, R.; Zhao, N.; Huang, F.; Ma, J. Landslide susceptibility evaluation and interpretability analysis of typical loess areas based on deep learning. Nat. Hazards Res. 2023, 3, 155–169. [Google Scholar] [CrossRef]
- Chang, Z.; Catani, F.; Huang, F.; Liu, G.; Meena, S.R.; Huang, J.; Zhou, C. Landslide susceptibility prediction using slope unit-based machine learning models considering the heterogeneity of conditioning factors. J. Rock Mech. Geotech. Eng. 2022, 15, 1127–1143. [Google Scholar] [CrossRef]
- Li, L.; Lan, H. Bivariate landslide susceptibility Analysis: Clarification, optimization, open software, and preliminary comparison. Remote Sens. 2023, 15, 1418. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Yansari, Z.T.; Panagos, P.; Pradhan, B. Analysis and evaluation of landslide susceptibility: A review on articles published during 2005–2016 (periods of 2005–2012 and 2013–2016). Arab. J. Geosci. 2018, 11, 193. [Google Scholar] [CrossRef]
- Yin, K.; Zhu, L. Landslide hazard zonation and application of GIS. Earth Sci. Front. 2001, 8, 279–284. (In Chinese) [Google Scholar]
- Li, L.; Lan, H.; Guo, C.; Zhang, Y.; Li, Q.; Wu, Y. A modified frequency ratio method for landslide susceptibility assessment. Landslides 2016, 14, 727–741. [Google Scholar] [CrossRef]
- Van Westen, C. Application of Geographic Information Systems to Landslide Hazard Zonation. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 1993. Available online: http://repository.tudelft.nl/islandora/object/uuid%3Aa59d2eca-ab58-41e6-91c9-01e4e090cf81/datastream/OBJ/view (accessed on 5 May 2024).
- Dam, N.D.; Amiri, M.; Al-Ansari, N.; Prakash, I.; Van Le, H.; Nguyen, H.B.T.; Pham, B.T. Evaluation of Shannon Entropy and Weights of evidence models in landslide susceptibility mapping for the Pithoragarh district of Uttarakhand State, India. Adv. Civ. Eng. 2022, 2022, 6645007. [Google Scholar] [CrossRef]
- Zhou, C.; Gan, L.; Cao, Y.; Wang, Y.; Segoni, S.; Shi, X.; Motagh, M.; Singh, R.P. Landslide susceptibility assessment of the Wanzhou district: Merging landslide susceptibility modelling (LSM) with InSAR-derived ground deformation map. Int. J. Appl. Earth Obs. Geoinf. 2025, 136, 104365. [Google Scholar] [CrossRef]
- Song, Y.; Niu, R.; Xu, S.; Ye, R.; Peng, L.; Guo, T.; Li, S.; Chen, T. Landslide susceptibility mapping based on weighted gradient boosting decision tree in Wanzhou section of the Three Gorges Reservoir area (China). ISPRS Int. J. Geo-Inf. 2018, 8, 4. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, L.; Zhang, J.; Zhu, Y. Deformation characteristics and failure mechanisms of a rainfall-induced complex landslide in Wanzhou County, Three Gorges Reservoir, China. Landslides 2019, 17, 419–431. [Google Scholar] [CrossRef]
- De Reu, J.; Bourgeois, J.; Bats, M.; Zwertvaegher, A.; Gelorini, V.; De Smedt, P.; Chu, W.; Antrop, M.; De Maeyer, P.; Finke, P.; et al. Application of the topographic position index to heterogeneous landscapes. Geomorphology 2012, 186, 39–49. [Google Scholar] [CrossRef]
- Mieza, M.S.; Cravero, W.R.; Kovac, F.D.; Bargiano, P.G. Delineation of site-specific management units for operational applications using the topographic position index in La Pampa, Argentina. Comput. Electron. Agric. 2016, 127, 158–167. [Google Scholar] [CrossRef]
- Couteron, P.; Barbier, N.; Gautier, D. Textural ordination based on Fourier Spectral decomposition: A method to analyze and compare landscape patterns. Landsc. Ecol. 2006, 21, 555–567. [Google Scholar] [CrossRef]
- Bugnicourt, P.; Guitet, S.; Santos, V.F.; Blanc, L.; Sotta, E.D.; Barbier, N.; Couteron, P. Using textural analysis for regional landform and landscape mapping, Eastern Guiana Shield. Geomorphology 2018, 317, 23–44. [Google Scholar] [CrossRef]
- Berti, M.; Corsini, A.; Daehne, A. Comparative analysis of surface roughness algorithms for the identification of active landslides. Geomorphology 2012, 182, 1–18. [Google Scholar] [CrossRef]
- Mhiret, D.A.; Dagnew, D.C.; Assefa, T.T.; Tilahun, S.A.; Zaitchik, B.F.; Steenhuis, T.S. Erosion hotspot identification in the sub-humid Ethiopian highlands. Ecohydrol. Hydrobiol. 2018, 19, 146–154. [Google Scholar] [CrossRef]
- Mohseni, N.; Salar, Y.S. Terrain indices control the quality of soil total carbon stock within water erosion-prone environments. Ecohydrol. Hydrobiol. 2020, 21, 46–54. [Google Scholar] [CrossRef]
- Li, D.; Huang, F.; Yan, L.; Cao, Z.; Chen, J.; Ye, Z. Landslide Susceptibility Prediction Using Particle-Swarm-Optimized Multilayer Perceptron: Comparisons with Multilayer-Perceptron-Only, BP Neural Network, and Information Value Models. Appl. Sci. 2019, 9, 3664. [Google Scholar] [CrossRef]
- Lan, H.; Zhou, C.; Wang, L.; Zhang, H.; Li, R. Landslide hazard spatial analysis and prediction using GIS in the Xiaojiang watershed, Yunnan, China. Eng. Geol. 2004, 76, 109–128. [Google Scholar] [CrossRef]
- Shortliffe, E.H.; Buchanan, B.G. A model of inexact reasoning in medicine. Math. Biosci. 1975, 23, 351–379. [Google Scholar] [CrossRef]
- Heckerman, D. Probabilistic Interpretations for Mycin’s Certainty Factors*. In Machine Intelligence and Pattern Recognition; *This work was supported in part by the Josiah Macy, Jr. Foundation, the Henry J. Kaiser Family Foundation, and the Ford Aerospace Corporation. Computing facilities were provided by the SUMEX-AIM resource under NIH grant RR-00785; Elsevier B.V.: Amsterdam, The Netherlands, 1986; pp. 167–196. [Google Scholar] [CrossRef]
- Ross, T.J. Fuzzy Logic with Engineering Applications. 2010. Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/9781119994374 (accessed on 1 March 2025).
- Kanungo, D.; Arora, M.; Sarkar, S.; Gupta, R. A comparative study of conventional, ANN black box, fuzzy and combined neural and fuzzy weighting procedures for landslide susceptibility zonation in Darjeeling Himalayas. Eng. Geol. 2006, 85, 347–366. [Google Scholar] [CrossRef]
- Zhou, W.; Fang, J. Assessment of landslide susceptibility based on information quantity model and data normalization. J. Geo-Inf. Sci. 2018, 20, 674–683. (In Chinese) [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Pandey, V.K.; Pourghasemi, H.R.; Sharma, M.C. Landslide susceptibility mapping using maximum entropy and support vector machine models along the highway corridor, Garhwal Himalaya. Geocarto Int. 2018, 35, 168–187. [Google Scholar] [CrossRef]
- Han, Z.; Fang, Z.; Li, Y.; Fu, B. A novel Dynahead-Yolo neural network for the detection of landslides with variable proportions using remote sensing images. Front. Earth Sci. 2023, 10, 1077153. [Google Scholar] [CrossRef]
- Hong, H.; Miao, Y.; Liu, J.; Zhu, A. Exploring the effects of the design and quantity of absence data on the performance of random forest-based landslide susceptibility mapping. CATENA 2019, 176, 45–64. [Google Scholar] [CrossRef]
- Merghadi, A.; Yunus, A.P.; Dou, J.; Whiteley, J.; ThaiPham, B.; Bui, D.T.; Avtar, R.; Abderrahmane, B. Machine learning methods for landslide susceptibility studies: A comparative overview of algorithm performance. Earth-Sci. Rev. 2020, 207, 103225. [Google Scholar] [CrossRef]
- Zhang, Y.; Lan, H.; Li, L.; Wu, Y.; Chen, J.; Tian, N. Optimizing the frequency ratio method for landslide susceptibility assessment: A case study of the Caiyuan Basin in the southeast mountainous area of China. J. Mt. Sci. 2020, 17, 340–357. [Google Scholar] [CrossRef]
- Pourghasemi, H.R.; Jirandeh, A.G.; Pradhan, B.; Xu, C.; Gokceoglu, C. Landslide susceptibility mapping using support vector machine and GIS at the Golestan Province, Iran. J. Earth Syst. Sci. 2013, 122, 349–369. [Google Scholar] [CrossRef]
- Bui, D.T.; Pradhan, B.; Lofman, O.; Revhaug, I.; Dick, Ø.B. Regional prediction of landslide hazard using probability analysis of intense rainfall in the Hoa Binh province, Vietnam. Nat. Hazards 2012, 66, 707–730. [Google Scholar] [CrossRef]
- Yang, K.; Niu, R.; Song, Y.; Dong, J.; Zhang, H.; Chen, J. Dynamic Hazard Assessment of Rainfall-Induced Landslides Using Gradient Boosting Decision Tree with Google Earth Engine in Three Gorges Reservoir Area, China. Water 2024, 16, 1638. [Google Scholar] [CrossRef]
- Murillo-García, F.G.; Steger, S.; Alcántara-Ayala, I. Landslide susceptibility: A statistically-based assessment on a depositional pyroclastic ramp. J. Mt. Sci. 2019, 16, 561–580. [Google Scholar] [CrossRef]
- Sun, L.; Zhang, H.; Qiu, C.; Yang, Z.; Zhang, C.; Zhang, B.; Zhang, T. Temporal variability of influence factors weights and rainfall thresholds of geological hazards in Ningbo City. East China Geol. 2024, 45, 218–227. (In Chinese) [Google Scholar] [CrossRef]
- Bukhari, M.H.; Da Silva, P.F.; Pilz, J.; Istanbulluoglu, E.; Görüm, T.; Lee, J.; Karamehic-Muratovic, A.; Urmi, T.; Soltani, A.; Wilopo, W.; et al. Community perceptions of landslide risk and susceptibility: A multi-country study. Landslides 2023, 20, 1321–1334. [Google Scholar] [CrossRef]
- Liu, L.; Wang, P.; Su, L.; Li, F. Landslide data sample augmentation and landslide susceptibility analysis in Nyingchi City based on the MCMC model. Sci. Rep. 2025, 15, 25624. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Lee, C. Assessment of landslide susceptibility using Statistical- and Artificial Intelligence-Based FR–RF integrated model and multiresolution DEMs. Remote Sens. 2019, 11, 999. [Google Scholar] [CrossRef]
- Wang, P.; Deng, H.; Li, Y.; Pan, Z.; Peng, T. Enhancing landslide susceptibility modelling through predicted InSAR deformation rates. Environ. Earth Sci. 2025, 84, 347. [Google Scholar] [CrossRef]


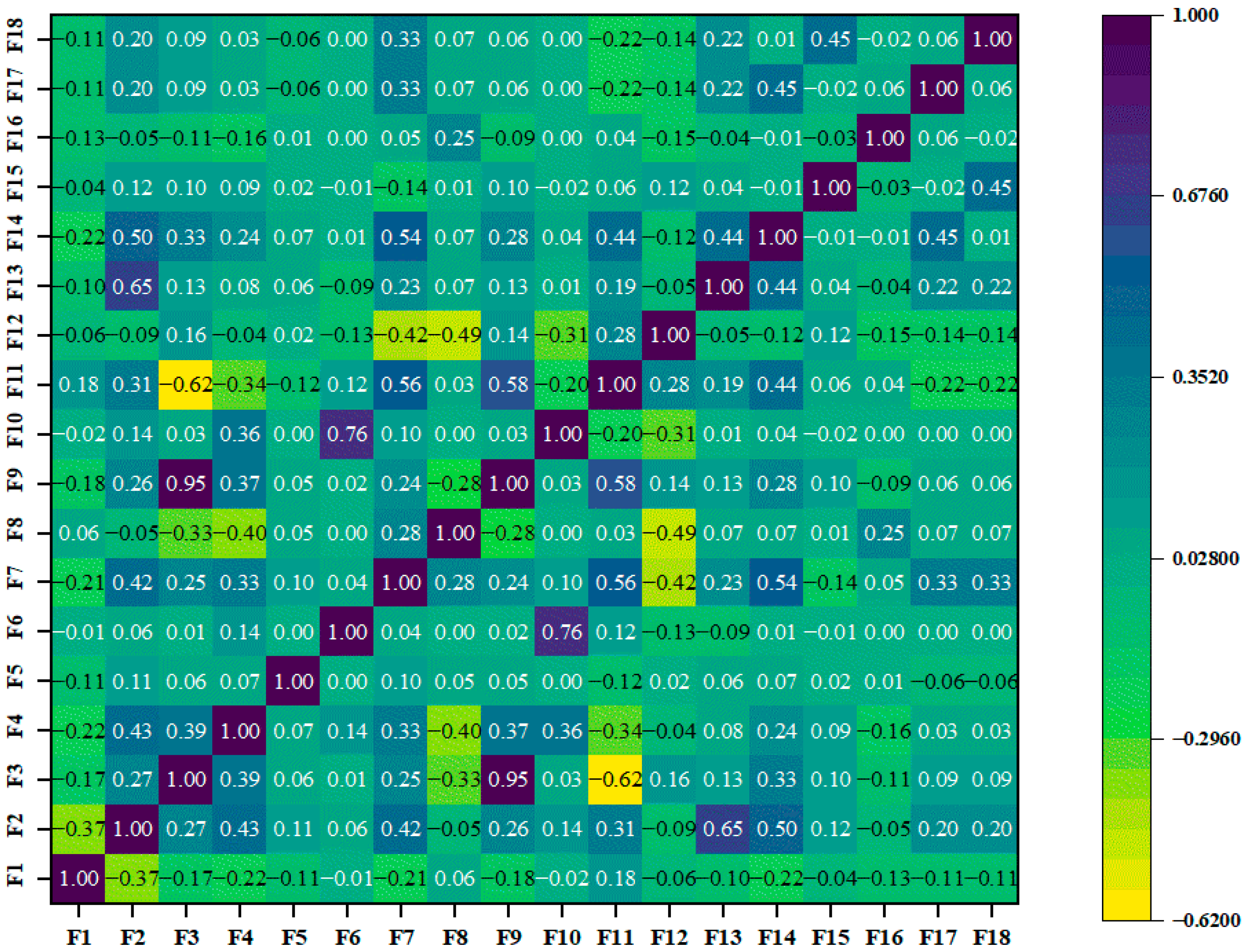


| Category | Factor | Data Source | Data Extraction Methods | Factor ID |
|---|---|---|---|---|
| Geological | Engineered Rock Group | National Geological Data Museum | From the 1:50,000 geological map, the factor is classified into four categories based on its engineering mechanical properties: Carbonate Formation (I), Thick Hard Sandstone Formation (II), Soft and Hard Interbedded Sandstone and Mudstone Formation (III), and Thinly Layered Weak Claystone Formation (IV), as shown in Figure 2a. | F1 |
| Topographical | Elevation | Geospatial Data Cloud Platform | DEM data, Figure 2b | F2 |
| Slope | Use the slope module in ArcGIS, Figure 2c | F3 | ||
| Slope height | Use the focal statistics module in ArcGIS, Figure 2d | F4 | ||
| Aspect | Use the aspect module in ArcGIS, Figure 2e | F5 | ||
| Profile curvature | Use the curvature module in ArcGIS, Figure 2f | F6 | ||
| Plain curvature | Use the curvature module in ArcGIS, Figure 2g | F7 | ||
| TST | Use raster analysis tools in QGIS, Figure 2h [25,26] | F8 | ||
| TRI | TRI = 1/Cos(‘Slope’ × 3.14/180), Figure 2i [27] | F9 | ||
| TPI | Use the map algebra tool in ArcGIS, Figure 2j [28,29] | F10 | ||
| Hydrological | TWI | Geospatial Data Cloud Platform | Use hydrology and map algebra tools in ArcGIS, Figure 2k [30,31] | F11 |
| Valley depth | Use the Valley Depth module in SAGA, Figure 2l | F12 | ||
| Distance to river | National Geological Data Museum | Use the Euclidean distance module in ArcGIS, Figure 2m | F13 | |
| Environmental | Rainfall | China Meteorological Data Network | Use the Inverse Distance Weighting (IDW) module in ArcGIS, based on annual precipitation at meteorological stations from 2010 to 2020, Figure 2n | F14 |
| NDVI | Landsat-8 imagery, Geographic Information Cloud Platform | Use the NDVI module in ENVI, based on Landsat-8 imagery (8 December 2013, row/column number 152/39), Figure 2o | F15 | |
| NDWI | Use the Band Math in ENVI, based on Landsat-8 imagery (8 December 2013, path/row 152/39), Figure 2p | F16 | ||
| Magnitude of earthquake | China Earthquake Networks Centre | Use the Kriging Interpolation module in ArcGIS, based on historical earthquakes from 1970 to 2020, Figure 2q | F17 | |
| Land use | Esri Land Cover | Five categories: water, built area, forest, agriculture, grassland, Figure 2r | F18 |
| Model | Key Advantage | Key Limitation | AUC Value | Landslides over High LS/ Total Number of Landslides |
|---|---|---|---|---|
| IV | High interpretability, captures continuous factor responses, and reduces subjectivity [32] | Slightly lower AUC than top ML models | 0.8878 | 0.8954 |
| FR | Simple principle, easy to implement and understand [20] | May slightly underestimate susceptibility | 0.8719 | 0.7769 |
| CF | Handles uncertainty in data, combines evidence effectively [33] | Calculation is more complex than FR/IV | 0.8876 | 0.8761 |
| CA | Measures similarity based on vector angles | Interpretation can be less intuitive than probability-based methods [36] | 0.8674 | 0.9020 |
| BSIV | Standardizes information values across factors [4] | Subjective grading misses continuous variations | 0.8239 | 0.7529 |
| SVM | Effective in high-dimensional spaces, good for non-linear problems [40] | “Black-box” nature, poor interpretability, sensitive to parameters | 0.8399 | 0.8639 |
| RF | High accuracy, handles non-linearity well, reduces overfitting [41] | “Black-box” nature, poor interpretability | 0.8569 | 0.8693 |
| GBDT | Highest accuracy, often superior performance [43] | “Black-box” nature, most complex, computationally intensive | 0.9257 | 0.8771 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Niu, X.; Xiao, S.; Sun, Y.; Zong, L.; Liu, J.; Zhang, M. Landslide Susceptibility Assessment Based on a Quantitative Continuous Model: A Case Study of Wanzhou. GeoHazards 2025, 6, 48. https://doi.org/10.3390/geohazards6030048
Wang S, Niu X, Xiao S, Sun Y, Zong L, Liu J, Zhang M. Landslide Susceptibility Assessment Based on a Quantitative Continuous Model: A Case Study of Wanzhou. GeoHazards. 2025; 6(3):48. https://doi.org/10.3390/geohazards6030048
Chicago/Turabian StyleWang, Shangxiao, Xiaonan Niu, Shengjun Xiao, Yanwei Sun, Leli Zong, Jian Liu, and Ming Zhang. 2025. "Landslide Susceptibility Assessment Based on a Quantitative Continuous Model: A Case Study of Wanzhou" GeoHazards 6, no. 3: 48. https://doi.org/10.3390/geohazards6030048
APA StyleWang, S., Niu, X., Xiao, S., Sun, Y., Zong, L., Liu, J., & Zhang, M. (2025). Landslide Susceptibility Assessment Based on a Quantitative Continuous Model: A Case Study of Wanzhou. GeoHazards, 6(3), 48. https://doi.org/10.3390/geohazards6030048






