Abstract
We developed a rainfall threshold model with the objective of limiting the effects of uncertainties typically associated with them, such as a lack of robust landslide database, the selection of the contributing rain gauge, seasonal variations in rainfall patterns, and the effect of extreme rainfall conditions. With the aid of gauge-corrected satellite precipitation data and a landslide database compiled from various sources, separate rainfall thresholds were developed for two waves of the monsoon season in the Western Ghats, India. The daily vs. antecedent rainfall distributions for different scenarios of antecedent rainfall were analyzed for landslide occurrence. The different scenarios considered included 1, 2, 3, 5, 10-, 20-, 30- and 40-day antecedent rainfalls along with the monsoon antecedent defined as the cumulative rainfall from the start of the monsoon to the day prior to landslide occurrence, and the event antecedent defined as the cumulative rainfall from the start of a rainfall event to the day prior to landslide occurrence. A statistically defined critical value was used to define the thresholds for extreme rainfall conditions, while ordinary least squares and quantile regression models were compared to identify the best-fit model for the non-extreme rainfall threshold. Receiver Operating Characteristic (ROC) analysis was performed on all these models and the best model was chosen based on the efficiency values. The daily vs. monsoon antecedent threshold was the best model for the first monsoon wave, and the daily vs. event antecedent model was the best model for the second monsoon wave. A separate rainfall threshold was defined for the entire monsoon without subdivision into separate waves, and corresponding ROC statistics were compared with the former approach to analyze the efficacy of intra-seasonal variations in rainfall threshold development. The results suggest that cumulative rainfall makes a significant contribution towards landslide initiation and that intra-seasonal variations should be necessarily considered in rainfall threshold modeling.
1. Introduction
Landslides are one of the most potent geohazards, with frequent incidences that cause considerable damage to life and infrastructure. Landslides can be triggered by many factors, including rainfall, earthquakes, and snowmelt [1], with orographic regions more susceptible to rainfall-induced landslides. Developing countries in the tropics are one of the major regions subjected to heavy losses in rainfall-triggered landslides, with an annual average of 500 casualties and financial loss of about 3 billion US dollars [2]. The Western Ghats of India, a mountainous region that is historically a hotspot for landslides, has seen an increase in frequency and intensity over the past few years [3,4,5]. The past few years have also seen exceptionally disastrous landslides in this region that claimed hundreds of lives [6,7]. Thus, developing a rainfall threshold for landslides is a topic of extensive research [8,9,10,11,12,13,14,15,16]. Rainfall thresholds are usually defined as the minimum amount of rainfall required to trigger a landslide, represented as a curve, defined by rainfall amounts, which separates the failure zone from the stable zone [17]. The pioneering research in this field was conducted by Caine [18], who established a global empirical rainfall threshold model by developing a relationship between rainfall intensity and duration.
Rainfall threshold methods are usually classified into physical and empirical, where physical methods consider the mechanical processes, especially the shear strength response of slopes toward rainwater infiltration in the initiation of landslides [19,20,21], while empirical methods rely on the statistical analysis of landslide-triggering rainfall amounts [22]. Such methods require rainfall data from contributing rain gauges and a well-defined database of historical landslides [23,24], while requiring lesser fieldwork than physical methods. Empirical methods are advantageous especially when the required output is a large-scale estimation of the temporal probability of landslide occurrence.
Empirical rainfall threshold approaches are further classified into duration-based approaches and antecedent rainfall-based approaches. Duration-based thresholds are computed as the minimum amount of rainfall required in a particular duration to initiate a landslide. The most popular duration-based approach is intensity–duration (ID), which defines a power law curve [25,26,27] of the rainfall intensity over the duration. Another duration-based approach is the Event-Duration (E-D) threshold [28,29,30,31,32,33], which is defined by a power law curve between the cumulative rainfall in an event and the corresponding event duration. A rainfall event is often defined using a period of separation between stretches of continuous rainfall. While duration thresholds rely on immediate events triggering the landslides, antecedent rainfall-based thresholds have the advantage of considering the variation in soil water levels over a continuous period before rainfall incidence [34,35,36,37,38,39,40,41,42]. Furthermore, antecedent rainfall-based threshold approaches can be advantageous in areas of sparse rainfall data and poor data records as they alleviate the need for hourly rainfall data and records of the exact time of the occurrence of the landslide.
Rainfall threshold calculations are marred by uncertainties such as those associated with the selection of contributing rain gauges [43,44], the availability of a robust landslide database, and variations in rainfall patterns. In this study, we propose the use of satellite rainfall datasets (Global Precipitation Mission Integrated MultiSatellite Retrievals for GPM (GPM IMERG)) to counter the uncertainties related to rain gauges. The use of continuous gridded data can considerably reduce the uncertainty in the selection of a contributing rain gauge [45], despite the thresholds developed by such data being lower than the actual thresholds, owing to their inherent underestimation of actual rainfall. However, this disadvantage can be overcome using bias-correction techniques like conditional merging [46,47,48], and error models that use gauge-to-satellite rainfall ratios [49]. An often-overlooked aspect in rainfall threshold development and a major uncertainty is the intra-seasonal variations in rainfall and their differential contribution towards landslide initiation. A relevant solution to this is to derive separate rainfall thresholds for different rainfall patterns as in Rossi et al. [50], who used both rain gauges and satellite rainfall to derive separate thresholds using three different methods: least squares, quantile regression, and non-linear least squares. In another instance, Chikalamo et al. [51] used satellite precipitation for rainfall threshold calculations with different thresholds calculated for different time periods within the monsoon season to account for the variation in rainfall patterns. In this research, we developed separate thresholds for the two waves of monsoon and also for extreme and non-extreme rainfall conditions to account for the seasonal variations. Another important uncertainty is the availability of a robust landslide database with accurate records of the date and time of the occurrence of landslides. These data are often the most difficult to obtain. Our study area, Idukki, a mountainous and landslide-marred district in the Western Ghats, India, also suffers from a lack of a proper landslide database. Hao et al. [52] published an exhaustive landslide database with 2223 landslides in Idukki for a single year (2018). However, this database lacked information about the date and time of the occurrence of landslides. To counter this, we prepared a database from various reports and news articles that mentioned the date of the occurrence of landslides. Furthermore, we used the antecedent rainfall to develop rainfall thresholds instead of rainfall intensity–duration curves so that the need for the exact time of the occurrence of landslides was alleviated. With climate change being a major factor, the frequency and intensity of landslides are expected to rise [53,54]. With rainfall being the most prominent landslide-triggering factor [55], continued research in this field is required with focus on reducing the uncertainties and adapting rainfall thresholds to locally specific climatic conditions and data constraints [56]. To that end, this paper focuses on addressing the uncertainties associated with rainfall threshold development, specifically regarding rain gauge selection, rainfall parameter selection, landslide database availability, and intra-seasonal variations in a local setting with sparse datasets.
2. Materials and Methods
2.1. Study Area
Idukki experiences a tropical climate with a preponderance of monsoon rainfall and plentitude of landslides and lacks appropriate rain gauges, even though this area receives a mean annual precipitation (MAP) of about 4100 mm. Hence, we believe that this area could be an ideal candidate to develop a rainfall threshold. The rainfall in this region is predominantly received during the monsoon season from June to December. Figure 1a shows the location map of Idukki. Historically, the Western Ghats are subject to landslide activity, predominantly shallow landslides, during these months. Physiographically, the area is divided into highlands (amsl > 75 m) and midlands (7.5–75 m amsl). The topography consists of elevations as high as 2692 m and slopes as steep as 80°. The regolith thickness ranges from 0.5 to 5 m, thereby restricting most landslides to shallow translational slides or debris flows. The primary geologic setting consists of charnockite, khondalite, and migmatite, with clay-rich top soils.
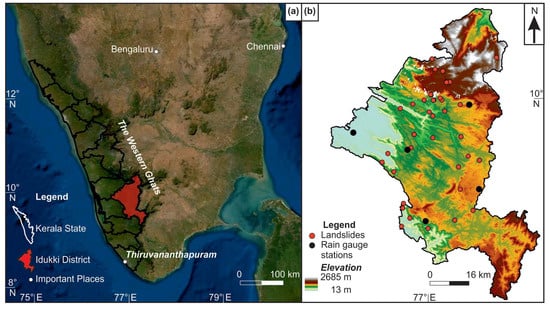
Figure 1.
(a) Geographic setting of the study area; (b) unique landslide events in Idukki during the study period.
The region is subject to high levels of chemical weathering leading to landslides with a combination of saprock, saprolite, and soil [57]. Although a historically landslide-affected area, the frequency and intensity of these landslides have risen in the past few years, especially since 2018. This increase in landslide activity is coupled with a change in the local climate [58] that has brought about more Mesoscale Cloud Burst (MCB) incidents. With this climatic change, more frequent and intense landslides are expected in the future. Coupled with high population statistics (1.11 million in an area of 4366 sq.km at an average density of about 250 per sq.km), the highlands of Idukki are becoming more vulnerable to slope instabilities [59]. Human influences on vulnerable slopes, like land clearance and slope modifications for agricultural and construction purposes, accentuate such instabilities. Historically prevailing deforestation rates also contribute to changing slope dynamics. The changing climate and increasing slope deterioration call for developing a landslide early-warning model that utilizes rainfall measurements and slope stability analysis to forecast future landslides and issue alerts. Thus, in our research, we considered the landslide activity in Idukki from 2018 and beyond to develop a rainfall threshold in changing climatic and anthropogenic conditions.
2.2. Data
Two important datasets are required for any rainfall-triggered landslide model: a landslide database and corresponding rainfall observations. An extensive study on the landslides of Idukki was conducted by Hao et al. [60]. However, only location information for these landslides was available. For rainfall threshold studies, the time or date of the occurrence of landslides is necessary. Various sources, including reports from organizations like the Geological Survey of India (GSI) and National Remote Sensing Center (NRSC), and newspaper articles were utilized and a landslide database of 250 landslide events was identified for the study period of 2018 to 2021. Though the exact time of the occurrence of these landslides could not be identified, the day of occurrence was recorded for all of them.
The rainfall data were procured from two sources: (i) rain gauge observations from the India Meteorological Department (IMD); and (ii) satellite rainfall measurements in the form of GPM IMERG-L. GPM is a successor mission to the TRMM and has been operational since 2010. It is a constellation of active radar, passive microwave, and infrared imaging on a global scale [61]. This study utilized the level 4 IMERG-L precipitation product. However, satellite rainfall data are found to underestimate rainfall, and thus, have a lower accuracy than rain gauges albeit having a better spatial variability. To avoid this inherent disadvantage, the IMERG-L was merged with the rain gauge data using a process called conditional merging. The following steps explain the conditional merging process:
- (i)
- The rain gauge observations are interpolated to create a continuous gridded rainfall product that provides the best linear unbiased rainfall estimate (Irg). Here, the resolution of the interpolated product is kept the same as that of the satellite product (GPM IMERG-L, 0.1 degrees);
- (ii)
- The satellite pixel values corresponding to the rain gauge locations are interpolated to create a continuous gridded rainfall product (Srg);
- (iii)
- The continuous rainfall product thus obtained (Srg) is subtracted from the original satellite product (S). This difference (S − Srg) gives a gridded error product;
- (iv)
- The error product obtained in step (iii) is added to the rainfall product obtained in step (i) (Irg). The result is a rainfall-gridded product that follows the mean field of the rain gauge interpolation while preserving the rainfall pattern of the satellite product.
The resulting conditionally merged product can be represented as:
where
CM = Irg + S − Srg
- CM is the conditionally merged rainfall at each grid;
- Irg is the interpolation product of the rain gauge observations;
- S is the satellite (gridded) product;
- Srg is the interpolation product of the satellite estimations in the location of rain gauges.
This conditionally merged rainfall product has better coverage than the sparse rain gauge network over the study area and a comparable accuracy. Moreover, a continuous gridded product reduces the uncertainties associated with the choice of the contributing rain gauge. This calibration procedure also eliminates the effect of rain gauges falling in different elevations. The error field in the conditional merging process is representative of the spatial variability of rainfall, which is derived entirely from the satellite precipitation. Thus, by adding the error field to the rain gauge interpolated product, the trend of the spatial variability of rainfall is held true irrespective of any elevation differences.
Any landslide falling within a particular conditionally merged GPM IMERG-L grid is attributed to a rainfall measurement corresponding to the pixel value of that grid. This means that all landslide events from the same date falling within the same grid have identical rainfall values. All such landslide events were considered as a single event for threshold calculation purposes. Thus, from a database of 250 landslides, 41 such unique events were available for the study area from 2018 to 2021 and these events were used to model the rainfall threshold. These unique landslide points are shown in Figure 1b.
2.3. Methods
2.3.1. Rainfall Threshold Development
The landslide activity in the study period (2018–2021) was found to be spread over the months of June to November. The rainfall distribution corresponding to the initiation of landslides was analyzed to check for any intra-monsoon change in rainfall pattern using box plots and a Mann–Whitney U-Test. A Mann–Whitney U-Test is used to test two or more non-normal datasets of significant difference [62]. It was found that there was a significant difference in the rainfall distribution between the periods from June to August and September to November. To include this significant difference in rainfall distribution, the entire monsoon was divided into 1st (June–August) and 2nd (September–November) waves, and separate rainfall thresholds were computed for each wave.
The cumulative antecedent rainfall was computed for each landslide event and scatter plots of daily vs. antecedent rainfall were developed. Apart from the typical antecedent variables considered by the previous researchers [63,64] in the study area, like 1-, 2-, 3-, 5-, 10-, 20-, 30-, and 40-day antecedent rainfall, four other antecedent rainfall variables were also calculated, which are defined below:
- (i)
- Monsoon antecedent (MA): for every landslide event, the cumulative rainfall from the beginning of the monsoon season to the day prior to the date of the landslide was calculated;
- (ii)
- Event antecedent (EA): for every landslide event, the cumulative rainfall from the first day of the event to the day prior to the date of the landslide was calculated;
- (iii)
- Monsoon antecedent average (MAA): the average monsoon antecedent rainfall was computed for every landslide event by dividing the monsoon antecedent by the number of days from the beginning of the monsoon to the day prior to the date of the landslide;
- (iv)
- Event antecedent average (EAA): the average event antecedent rainfall was computed for every landslide event by dividing the event antecedent by the number of days from the beginning of the event to the day prior to the date of the landslide.
The above four antecedents were calculated to reflect the continuing effect of monsoon rainfall on the initiation of landslides. For the event-based thresholds, the beginning of each individual event was defined as the first day of rainfall after a period of separation in continuous precipitation. For this study, a period of separation was considered to occur when there was at least one day with less than 1 mm of rainfall in between continuous rainfall.
Once the antecedent rainfalls were computed, scatter plots for daily vs. antecedent rainfalls were generated. Then, two stages of rainfall threshold were developed:
- (i)
- A critical value for extreme daily and antecedent rainfall was defined with an assumption that exceeding this critical value always causes a landslide;
- (ii)
- A threshold for the non-extreme daily and antecedent rainfall was defined using a best-fit line that represents the trend of these data.
The 3rd quartile of the daily and antecedent rainfall distribution corresponding to landslide initiation was chosen as the critical value to separate extreme events from non-extreme events. This value was also in accordance with previous research in the study area that defined extreme precipitation under local climatic conditions (KSCSTE, 2019). Thus, whenever the daily or antecedent rainfall crosses this critical value, the rainfall is considered an extreme event, and a landslide is assumed to occur. Such a threshold definition will segregate both possible cases of extreme rainfall:
- (i)
- When continuous rainfall occurs over several days;
- (ii)
- A sudden rainfall of a large quantity occurs over a day.
The condition for landslide occurrence due to extreme precipitation is thus given as:
where
If (D > Dt OR A > At): landslide, else: no landslide
- D is the rainfall on any day;
- Dt is the critical value for extreme daily rainfall;
- A is the nth antecedent rainfall, where n corresponds to the number of days of antecedent rainfall;
- At is the critical value for extreme antecedent rainfall.
Such a definition of rainfall threshold divides the daily vs. antecedent rainfall scatter plot into four quadrants. Quadrant 1 represents the condition where the antecedent critical value for extreme rainfall is exceeded, quadrant 2 where both the daily and antecedent critical values for extreme rainfall are exceeded, quadrant 3 where the critical value for daily extreme rainfall is exceeded, and quadrant 4 where neither the daily nor the antecedent critical value for extreme rainfall is exceeded. Quadrants 1, 2, and 3 all correspond to extreme rainfall events where a landslide is always considered to occur. Quadrant 4, which is below both the daily and antecedent critical values, was separated from the remaining data and regression modeling was performed to find a best-fit line to define the rainfall threshold that represents the trend of the distribution. Figure 2 shows an example of the division of a scatter plot of daily vs. 10-day antecedent rainfall.
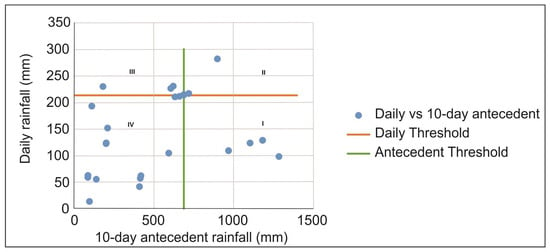
Figure 2.
Representation of the 4 quadrants that separate extreme rainfall from non-extreme rainfall.
2.3.2. Regression Modeling
Regression modeling is a commonly applied technique to find a best-fit estimate between two or more related parameters. Its simplicity and effectiveness have led to wide-spread application in rainfall threshold modeling problems [65,66,67]. In this study, in the 4th quadrant, regression modeling was used to predict the daily rainfall required to initiate a landslide, given the rainfall over n-antecedent days. The linear model has the following form:
where
y = mx + c
- y is the daily rainfall;
- x is the expected antecedent rainfall;
- m is the slope;
- c is the y-axis intercept.
Two kinds of regression modeling were attempted for the data separated out in the 4th quadrant:
- (i)
- Ordinary least square regression (OLS);
- (ii)
- Quantile regression (QR).
OLS minimizes the sum of the squared residuals to estimate the conditional mean [68], whereas QR asymmetrically minimizes the weighted absolute residuals, thereby estimating the conditional median and other quantiles [69]. We computed the Least Absolute Deviation (LAD) or 50th quantile (median), 5th quantile, and 95th quantile for the data in the 4th quadrant. The 5th and 95th quantiles represent the 5% and 95% non-exceedance thresholds, respectively. The best model between OLS and QR was chosen using ROC analysis and was used to derive the threshold for daily rainfall required to initiate landslides under non-extreme rainfall conditions.
At the end of the regression model, three sets of threshold equations were developed for each wave of monsoon rainfall:
- (i)
- The critical daily rainfall above which a landslide always occurs, represented in the form y = x;
- (ii)
- The critical antecedent rainfall above which a landslide always occurs, represented in the form x = y;
- (iii)
- The model for predicting landslide initiation in cases of non-extreme daily and antecedent rainfall, represented in the form y = mx +c.
Based on these thresholds, three scenarios for issuing landslide warnings are possible:
- (i)
- The forecasted daily rainfall on a particular day is above the daily critical rainfall;
- (ii)
- The forecasted antecedent rainfall for a particular day is above the antecedent critical rainfall;
- (iii)
- Both daily and antecedent rainfall forecasts for a particular day are below the corresponding critical rainfalls, but the forecasted daily rainfall is above the daily rainfall value predicted by the regression model developed from the 4th quadrant.
2.3.3. Validation
Validation of the computed models was carried out with the help of ROC analysis. Six days of rainfall were considered as validation samples for each landslide. These included the rainfall on the day of the landslide and from 5 days prior to the landslide. A confusion matrix was developed to represent four possible outcomes of prediction by comparing the predicted daily rainfall with the actual rainfall. If an actual landslide occurred on the day of a landslide prediction, then it was recorded as a true positive (TP). If no landslide occurred on a day of no landslide prediction, it was recorded as a true negative (TN). If for a particular day, a landslide was predicted to occur, but no landslide occurred, then it was a false positive (FP). If for a particular day, no landslide occurrence was predicted, but a landslide occurred, then it was a false negative (FN). Based on the ROC analysis, the model sensitivity, specificity, efficiency, and false positive rates were computed.
- Sensitivity is defined as (TP)/(TP + FN);
- Specificity is defined as (TN)/(TN + FP);
- Efficiency is defined as (TP + TN)/(TP + FP + FN + TN);
- False positive rate is defined as (FP)/(FP + TN).
Separate ROC analyses were performed for extreme and non-extreme events and later the statistics were combined to assess the total performance of each type of antecedent rainfall. A scenario where the entire monsoon was considered without subdivision into two waves was also considered for threshold development. Here, the same approach of computing different thresholds for extreme and non-extreme rainfalls was followed. The ROC analysis for this approach was compared with that of the thresholds for the separate waves to assess the significance of intra-seasonal variations of rainfall patterns in threshold definition.
3. Results
3.1. Understanding the Variations in Intra-Seasonal Rainfall
The Mann–Whitney U-Test was performed to assess the statistical difference between the two monsoon waves. For the Mann–Whitney U-Test, the null and alternate hypotheses were defined as follows: H0—the median difference for rainfall between the two waves of monsoon is zero; H1—the median difference for rainfall between the two waves of monsoon is not zero. If the p-value for the test is less than 0.05, the null hypothesis will be rejected. Here, a p-value of 2.294 × 10−7 was obtained, thereby rejecting the null hypothesis. Thus, a significant difference in landslide-triggering rainfall was observed between the two waves of monsoon. While the median rainfall for the 1st wave of rainfall was 123.59 mm, the 2nd wave had a value of just 4.08 mm. Figure 3 shows the box plot of the rainfall distribution in the two monsoon waves.
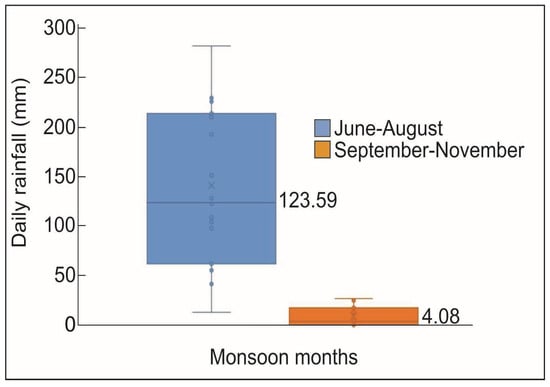
Figure 3.
Box plot showing the difference in rainfall distribution between the two waves of monsoon. Blue filled circles are outliers.
3.2. Rainfall Threshold Calculation for the First Wave of Monsoon
Out of the 41 distinct landslide events considered, 25 belonged to the 1st wave of monsoon and 16 to the 2nd wave. The critical values for daily and antecedent extreme rainfall separated these landslides into four quadrants, out of which the 1st, 2nd, and 3rd quadrants represent the landslides occurring due to extreme events and the 4th quadrant represents the landslides occurring due to non-extreme events. Table 1 shows the confusion matrix of the various threshold models for quadrants 1, 2, and 3 of the 1st waves of monsoon. Moreover, 10–12 out of these 25 landslide events had daily and antecedent rainfall values above the corresponding critical rainfall value. This means that about 40–48% of the total landslides that occurred in the 1st wave of monsoon were associated with extreme precipitation. Also, such landslides were predicted with sensitivity values of 1 in all models. Out of the 12 threshold models considered, the daily vs. monsoon antecedent performed the best, with an efficiency of 0.88 and a false positive rate of just 0.15. Even though none of the models were perfect as all of them reported false positives in varying frequencies, MA had an acceptable specificity of 0.84, which can be considered the best model for the 1st monsoon wave.

Table 1.
Confusion matrix for quadrants 1, 2, and 3 for the first monsoon wave.
Since MA was the best-performing model, the 4th quadrant of the daily vs. MA plot was subjected to regression modeling. Figure 4 shows the model fitting in the 4th quadrant. Both OLS and LAD had a similar efficiency. While OLS had a higher specificity rate, it came at the price of capturing very few landslide points. The 50th quantile (median) captured more landslides than OLS without adding many more false positives. The lower quantile captured all the landslides, but since rainfall values of less than 10 mm were associated with landslide initiation, 100% landslide detection led to overfitting with unacceptable numbers of false positives. Thus, in the case of 1st wave of monsoon, the quantile regression model provided a better prediction of landslides. However, the accuracy of prediction in the 4th quadrant was less than that in the other three quadrants and can be attributed to the landslides triggered by lower rainfall values. Table 2 shows the confusion matrix of the 4th quadrant of daily vs. MA rainfall for various regression fits.
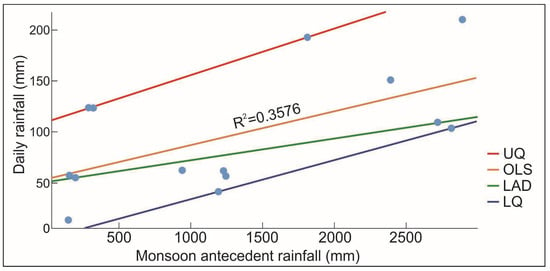
Figure 4.
Model fitting in the 4th quadrant for the first wave of monsoon for the monsoon antecedent rainfall and daily rainfall.

Table 2.
Confusion matrix of thresholds for the regression models in the fourth quadrant of the 1st wave for the daily vs. MA rainfall. The table also shows the combined statistics of all four quadrants of MA in the final row.
Combining the extreme and non-extreme events, the following criteria for landslide prediction were developed for the 1st monsoon wave:
- (i)
- The critical values for extreme daily and extreme monsoon antecedent rainfall are 213 mm and 2921 mm, respectively, and whenever the daily or antecedent rainfall forecast is above these values, a landslide is predicted to occur;
- (ii)
- For non-extreme rainfall, a landslide is predicted if the daily rainfall forecast is above the value given by the model:wherey = 0.0212x + 51.0556
- y is the predicted daily rainfall;
- x is the corresponding monsoon antecedent rainfall.
Combining the results of all four quadrants gives a model that captures 76% of the total landslide occurrences, with a low false positive rate of 0.17 and a high efficiency of 0.82. The confusion matrix for this combined result is shown in the last row of Table 2.
3.3. Rainfall Threshold Calculation for the Second Wave of Monsoon
For the 2nd wave of monsoon, the landslides were initiated by far smaller quantities of rainfall. In total, 16 of the 41 distinct landslide events occurred in the 2nd wave. The same method adopted for the 1st wave was followed for modeling landslides in this wave as well. Using the critical values for daily and antecedent rainfall, the scatter plots were divided into four quadrants. Table 3 shows the results of the corresponding ROC analysis. Here, 7–10 out of 16 landslide events fell above the critical rainfall value for extreme rainfall. However, the false positive rate was higher for all thresholds when compared with those of the 1st wave. This indicates the highly erratic nature of the 2nd monsoon waves and indicates the compounding effect of the 1st wave of monsoon on the soil moisture content. The event antecedent (EA) threshold had the best efficiency rate out of all the models considered for the 2nd monsoon wave.

Table 3.
Confusion matrix for quadrants 1, 2, and 3 for the second monsoon wave.
We performed OLS and QR on the 4th quadrant of the daily vs. EA threshold since it had the best efficiency among all the threshold types. Figure 5 shows the best-fit regression lines in the 4th quadrant. Only three models are shown in Figure 5, as the 5th quantile is the line almost parallel to the x-axis with a slope and intercept value of almost 0. This is owing to the record of landslides on days with little to no recorded rainfall (less than 1 mm). However, all such landslides were preceded with heavy rainfall until a day before, and this wetting of the soil is the reason for their eventual failure. Also, the 50th quantile shows no further improvement in capturing landslides than OLS, while its placement far below the latter contributed to the prediction of more false positives. Table 4 shows the confusion matrix of the 4th quadrant.
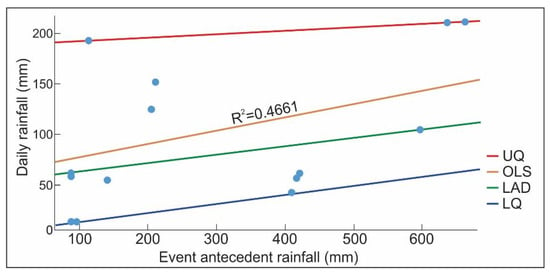
Figure 5.
Model fitting in the 4th quadrant for the second wave of monsoon for the event antecedent rainfall and daily rainfall.

Table 4.
Confusion matrix of thresholds for the regression models in the fourth quadrant of the 2nd wave for the daily vs. EA rainfall. The table also shows the combined statistics of all four quadrants of EA in the final row.
The best-fit lines in the 4th quadrant of the 2nd wave have a negative slope, meaning that, with the increase in antecedent rainfall, the amount of daily rainfall required to trigger landslides decreased. However, this is not the case in the 1st wave (see Figure 4) where all the models follow a positive slope. This further points to the cumulative effect of the 1st wave on the 2nd wave. It can be reasonably argued that the soil was left adequately wet during the 1st monsoon wave thereby increasing the chance of the occurrence of landslides in the 2nd wave. The lesser rainfall values required to initiate landslides in the 2nd wave may also be the result of this cumulative effect. This points to the need for considering seasonal variations in rainfall patterns while developing rainfall thresholds.
However, the larger number of false positives made landslide prediction in the 2nd wave of monsoon difficult. The last row of Table 4 shows the confusion matrix of all four quadrants combined for the daily vs. event antecedent threshold. The efficiency of the model was under 0.5, thereby contributing to half of all predictions being wrong, with a higher chance of false positives. From the study period, the critical values for daily and the event antecedent rainfalls for the 2nd wave were identified as 17 mm and 365 mm, respectively. OLS in the 4th quadrant is given by Equation (5):
where
y = −0.00237x + 1.7648
- y is the daily rainfall threshold required to trigger a landslide;
- x is the corresponding monsoon antecedent rainfall.
In the case of the 2nd wave of monsoon, the threshold models returned too many false positives. However, in both waves, the number of false negatives was less and, thus, points to the overall conservative nature of the models developed. In summary, the approach chosen in this study proved efficient in the case of the 1st monsoon wave, while in the case of the 2nd monsoon wave, factors other than the immediate rainfall affected the initiation of landslides. An analysis of complementary parameters like runoff and soil moisture will be required to improve the landslide prediction in the 2nd wave of monsoon. Still, the landslides affected by extreme rainfall could be predicted with an efficiency of ~0.6. Moreover, rainfall thresholds should be considered as representations for issuing warnings for chances of the occurrence of landslides rather than absolute measures above which there is a 100% chance of landslide initiation. Also, considering previous studies [61], the predictability rate of 57% for the 2nd wave is an acceptable ratio in rainfall threshold-based landslide modeling.
3.4. Rainfall Threshold without Considering Intra-Seasonal Variation
To further explore the significance of the approach followed in this study, we developed a rainfall threshold for the entire rainfall season without considering the intra-seasonal variability. Table 5 shows the ROC analysis performed on the daily vs. antecedent thresholds for the entire monsoon season irrespective of subdivision into two waves. Here, both the daily vs. 10-day and daily vs. 40-day antecedent thresholds performed the best with a very high efficiency of 0.89 and a specificity of 0.87. The ROC analysis of the regression modeling on the 4th quadrant of this distribution is shown in Table 6. In both cases, the OLS model provided better statistics. Out of the two thresholds, the daily vs. 40-day antecedent showed a slightly better performance and was, hence, chosen as the overall best threshold and the combined statistics for all the four quadrants were computed. This model was then compared with the best models for the separate 1st and 2nd wave threshold approach in Figure 6.

Table 5.
Confusion matrix of quadrants 1, 2, and 4 for the threshold models for the entire monsoon without subdivision into 1st and 2nd waves.

Table 6.
Confusion matrix of the regression modeling in the 4th quadrant of the best threshold models for the entire monsoon without subdivision into 1st and 2nd waves.
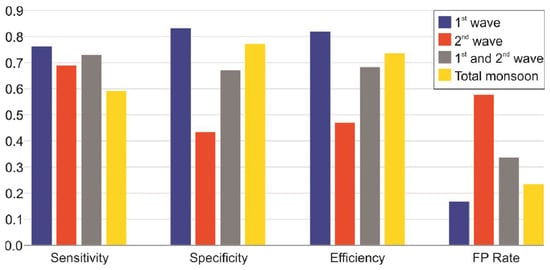
Figure 6.
Comparison of ROC statistics for different scenarios of monsoon rainfall.
Out of the three rainfall thresholds compared, the one for the 1st wave of monsoon was the best-performing, with an efficiency of 0.82 and an FP rate of 0.17. The worst performance was with the threshold model for the 2nd wave of monsoon, with an efficiency of 0.47 and a high FP rate of 0.58. While combining the two models, the overall efficiency for landslide prediction was 0.68 with an FP rate of 0.33. It is evident that the higher number of false positives was a contribution of the 2nd wave and was instrumental in reducing the overall efficiency of the threshold model developed for the entire monsoon season without considering the intra-seasonal variations. The threshold developed for the entire monsoon had an efficiency of 0.74 with an FP rate of 0.23, which is applicable for both waves combined. Thus, analyzing seasonal variations and developing separate rainfall thresholds accordingly should be the preferred approach in rainfall threshold modeling. Moreover, dividing the rainfall threshold based on intra-seasonal variations and the presence of extreme rainfall events should be an essential strategy in developing a landslide early-warning system for the area. This study also showcases the importance of validation, especially considering the number of false positives in any proposed model, before adopting it for early-warning purposes. Thus, based on the results of this research, the authors propose developing four different thresholds for early-warning purposes in Idukki as follows:
- (i)
- A rainfall threshold for extreme precipitation for the 1st wave of monsoon;
- (ii)
- A rainfall threshold for non-extreme precipitation for the 1st wave of monsoon;
- (iii)
- A rainfall threshold for extreme precipitation for the 2nd wave of monsoon;
- (iv)
- A rainfall threshold for non-extreme precipitation for the 2nd wave of monsoon.
3.5. Limitations of the Study
Though this study tries to overcome specific uncertainties with rainfall threshold models, there are certain limitations, addressing which would further improve the model. Firstly, though landslide activity in Idukki is frequent, due to the lack of temporal information in the database, the authors were forced to construct a new database that included landslide temporal information, which contained only 250 landslides. The actual modeling was further limited to 41 unique events since multiple landslides fell on the same rainfall grid on the same day.
Furthermore, the authors worked with calibrated satellite precipitation owing to the scarcity of rain gauges in the area. Though the conditional merging methodology used for calibrating the satellite precipitation improved their accuracy, the calibration technique itself is dependent on the number of rain gauges in the area. An increased number of rain gauges could improve the performance of conditional merging and of the threshold development model overall.
Though considering the antecedent rainfall reduced uncertainties surrounding the lack of the time of the occurrence of landslides, this would be welcome information, as the cumulative rainfall from the start of the monsoon, or from the start of an event, to the moment immediately preceding a landslide could certainly improve the threshold model. However, these limitations are for future studies to address and would need infrastructural improvements like the expansion of rain gauge networks.
4. Discussion
This study aimed to overcome specific uncertainties related to rainfall threshold models, especially in data-sparse regions. The first uncertainty is the selection of contributing rain gauges. Studies like that of Abraham et al. [44] used Thiessen polygons and elevation considerations to divide the area into zones of influence under each rain gauge. While this is a valuable method to ascertain rainfall quantities corresponding to landslides, the granularity of these data is be coarser than ideal, especially when dealing with smaller landslide databases. The total area of Idukki is approximately 4600 sq.km, which would mean the average area under each of the rain gauges is roughly 900 sq.km. On the other hand, one pixel of a GPM IMERG is roughly 100 sq.km, thereby providing roughly 46 pixels or 46 different rainfall values for the study area in place of the five rain gauge observations. This higher resolution of rainfall data provides a much better understanding of the geographic variability of rainfall within the study area.
The second uncertainty was the choice of threshold parameter. While both rainfall intensity–duration and antecedent rainfall are commonly considered rainfall threshold parameters, in this study, we chose the antecedent rainfall as the threshold-defining parameter owing to the unavailability of hourly rainfall from the rain gauge stations and the difficulty in ascertaining the exact time of the occurrence of the landslides. However, the results of this study show that, in Idukki, the compounding effects of cumulative rainfall have a major role to play in triggering landslides, in which case, the antecedent rainfall is a much better option than intensity–duration thresholds.
The third uncertainty is the intra-seasonal variations in rainfall patterns. To the best of our knowledge, no studies in a similar geographic extent [44,64] have considered the intra-seasonal variations in rainfall patterns. As shown in Figure 3, there was a large difference between the rainfall values associated with landslides in the first and second monsoon waves. This is a matter that was overlooked by all of the above studies and further consolidates the fact that rainfall threshold definitions are complex problems that require more granularity, not only in the spatial domain, but also in the temporal domain. The remarkable variation in the rainfall patterns between the first and second monsoon waves warrant the development of separate thresholds for different parts of the year.
5. Conclusions
The rainfall–landslide distribution for Idukki was analyzed with a landslide database comprising 250 landslides for the period 2018–2021 from various sources of data. Satellite rainfall data in the form of GPM IMERG-L were calibrated using rain gauge observations using a process called conditional merging and this improved rainfall product was used as rainfall data. Distinct intra-seasonal patterns were observed in landslide-inducing rainfall, and thus, separate thresholds were developed for each of these separate monsoon waves. The monsoon antecedent was identified as the best threshold parameter for the first wave of monsoon, while the event antecedent was identified as the best threshold parameter for the second wave of monsoon. Moreover, to account for the erratic nature of monsoons in the study area, separate thresholds were developed for extreme and non-extreme rainfall. Regression models were used to develop thresholds for non-extreme rainfall, while critical values developed from the statistical distribution of rainfall were used to separate extreme rainfalls from non-extreme ones.
Overall, this study aimed to address the following uncertainties in rainfall threshold modeling: the lack of a robust landslide database with temporal information, the choice of contributing rain gauges, and the temporal variations in rainfall. They were addressed by developing a landslide database with accurate information on the date of the occurrence of landslides, using antecedent rainfall instead of duration-based threshold parameters, by considering calibrated satellite precipitation instead of rain gauges, and by developing separate thresholds for distinct intra-seasonal variations.
Three different scenarios of landslide warning are proposed from the developed rainfall thresholds: (a) when the daily rainfall is above extreme levels; (b) when the antecedent rainfall is above the extreme levels; and (c) when the daily rainfall is above the threshold for non-extreme rainfall. Such a proposition warrants the continuous monitoring of rainfall as cumulative rainfall was found to have a major contribution towards landslide initiation. This points towards the development of a landslide early-warning system that continuously monitors the rainfall levels in the study area using satellite rainfall observations. The future directions of this study points towards this end.
Author Contributions
Conceptualization, C.L.V. and T.O.; methodology, C.L.V.; validation, C.L.V., T.O., S.C. and K.S.S.; formal analysis, C.L.V.; investigation C.L.V.; resources, C.L.V.; data curation, C.L.V.; writing—original draft preparation, C.L.V.; writing—review and editing, C.L.V., T.O., K.S.S. and S.C.; visualization, K.S.S.; supervision, T.O.; project administration, T.O.; funding acquisition, T.O. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Society of Exploration Geophysicists (SEG) Geoscientists Without Borders (GWB) (Grant number: SEG GWB #201907008).
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kazmi, D.; Qasim, S.; Harahap, I.S.H.; Baharom, S.; Imran, M.; Moin, S. A study on the contributing factors of major landslides in Malaysia. Civ. Eng. J. 2016, 2, 669–678. [Google Scholar] [CrossRef]
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef]
- Kuriakose, S.L.; Sankar, G.; Muraleedharan, C. History of landslide susceptibility and a chorology of landslide-prone areas in the Western Ghats of Kerala, India. Environ. Geol. 2009, 57, 1553–1568. [Google Scholar] [CrossRef]
- Jain, N.; Martha, T.R.; Khanna, K.; Roy, P.; Kumar, K.V. Major landslides in Kerala, India, during 2018–2020 period: An analysis using rainfall data and debris flow model. Landslides 2021, 18, 3629–3645. [Google Scholar] [CrossRef]
- Ramasamy, S.M.; Gunasekaran, S.; Saravanavel, J.; Joshua, R.M.; Rajaperumal, R.; Kathiravan, R.; Muthukumar, M. Geomorphology and landslide proneness of Kerala, India A geospatial study. Landslides 2021, 18, 1245–1258. [Google Scholar] [CrossRef]
- Achu, A.L.; Joseph, S.; Aju, C.D.; Mathai, J. Preliminary analysis of a catastrophic landslide event on 6 August 2020 at Pettimudi, Kerala State, India. Landslides 2021, 18, 1459–1463. [Google Scholar] [CrossRef]
- Ajin, R.S.; Nandakumar, D.; Rajaneesh, A.; Oommen, T.; Ali, Y.P.; Sajinkumar, K.S. The tale of three landslides in the Western Ghats, India: Lessons to be learnt. Geoenvironmental Disasters 2022, 9, 16. [Google Scholar] [CrossRef]
- Zhai, X.; Guo, L.; Liu, R.; Zhang, Y. Rainfall threshold determination for flash flood warning in mountainous catchments with consideration of antecedent soil moisture and rainfall pattern. Nat. Hazards 2018, 94, 605–625. [Google Scholar] [CrossRef]
- Monsieurs, E.; Dewitte, O.; Demoulin, A. A susceptibility-based rainfall threshold approach for landslide occurrence. Nat. Hazards Earth Syst. Sci. 2019, 19, 775–789. [Google Scholar] [CrossRef]
- Pradhan, A.M.S.; Lee, S.R.; Kim, Y.T. A shallow slide prediction model combining rainfall threshold warnings and shallow slide susceptibility in Busan, Korea. Landslides 2019, 16, 647–659. [Google Scholar] [CrossRef]
- Zhao, B.; Dai, Q.; Han, D.; Dai, H.; Mao, J.; Zhuo, L. Probabilistic thresholds for landslides warning by integrating soil moisture conditions with rainfall thresholds. J. Hydrol. 2019, 574, 276–287. [Google Scholar] [CrossRef]
- Dikshit, A.; Satyam, N.; Pradhan, B.; Kushal, S. Estimating rainfall threshold and temporal probability for landslide occurrences in Darjeeling Himalayas. Geosci. J. 2020, 24, 225–233. [Google Scholar] [CrossRef]
- Maturidi, A.M.A.M.; Kasim, N.; Taib, K.A.; Azahar, W.N.A.W.; Tajuddin, H.B.A. Empirically Based Rainfall Threshold for Landslides Occurrence in Peninsular Malaysia. KSCE J. Civ. Eng. 2021, 25, 4552–4566. [Google Scholar] [CrossRef]
- Vessia, G.; Parise, M.; Brunetti, M.T.; Peruccacci, S.; Rossi, M.; Vennari, C.; Guzzetti, F. Automated reconstruction of rainfall events responsible for shallow landslides. Nat. Hazards Earth Syst. Sci. 2014, 14, 2399–2408. [Google Scholar] [CrossRef]
- He, J.; Qiu, H.; Qu, F.; Hu, S.; Yang, D.; Shen, Y.; Cao, M. Prediction of spatiotemporal stability and rainfall threshold of shallow landslides using the TRIGRS and Scoops3D models. Catena 2021, 197, 104999. [Google Scholar] [CrossRef]
- Conte, E.; Pugliese, L.; Troncone, A. A Simple Method for Predicting Rainfall-Induced Shallow Landslides. J. Geotech. Geoenvironmental Eng. 2022, 148, 04022079. [Google Scholar] [CrossRef]
- Crozier, M.J. The climate-landslide couple: A southern hemisphere perspective. In Rapid Mass Movement as a Source of Climatic Evidence for the Holocene; Georg Fischer: Schaffhausen, Switzerland, 1997; pp. 333–354. [Google Scholar]
- Caine, N. The rainfall intensity-duration control of shallow landslides and debris flows. Geogr. Ann. Ser. A Phys. Geogr. 1980, 62, 23–27. [Google Scholar]
- Crosta, G.B.; Frattini, P. Rainfall thresholds for triggering soil slips and debris flow. In Proceeding of the 2nd EGS Plinius Conference on Mediterranean Storms, Siena, Italy, 1–3 October 2001; Volume 1, pp. 463–487. [Google Scholar]
- Gariano, S.L.; Brunetti, M.T.; Iovine, G.; Melillo, M.; Peruccacci, S.; Terranova, O.; Guzzetti, F. Calibration and validation of rainfall thresholds for shallow landslide forecasting in Sicily, southern Italy. Geomorphology 2015, 228, 653–665. [Google Scholar] [CrossRef]
- Fusco, F.; Bordoni, M.; Tufano, R.; Vivaldi, V.; Meisina, C.; Valentino, R.; De Vita, P. Hydrological regimes in different slope environments and implications on rainfall thresholds triggering shallow landslides. Nat. Hazards 2022, 114, 907–939. [Google Scholar] [CrossRef]
- Bordoni, M.; Corradini, B.; Lucchelli, L.; Valentino, R.; Bittelli, M.; Vivaldi, V.; Meisina, C. Empirical and physically based thresholds for the occurrence of shallow landslides in a prone area of Northern Italian Apennines. Water 2019, 11, 2653. [Google Scholar] [CrossRef]
- Peres, D.J.; Cancelliere, A.; Greco, R.; Bogaard, T.A. Influence of uncertain identification of triggering rainfall on the assessment of landslide early warning thresholds. Nat. Hazards Earth Syst. Sci. 2018, 18, 633–646. [Google Scholar] [CrossRef]
- Segoni, S.; Rossi, G.; Rosi, A.; Catani, F. Landslides triggered by rainfall: A semi-automated procedure to define consistent intensity–duration thresholds. Comput. Geosci. 2014, 63, 123–131. [Google Scholar] [CrossRef]
- Innes, J.L. Debris flows. Prog. Phys. Geogr. 1983, 7, 469–501. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity–duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Napolitano, E.; Fusco, F.; Baum, R.L.; Godt, J.W.; De Vita, P. Effect of antecedent-hydrological conditions on rainfall triggering of debris flows in ash-fall pyroclastic mantled slopes of Campania (southern Italy). Landslides 2016, 13, 967–983. [Google Scholar] [CrossRef]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. Rainfall thresholds for the initiation of landslides in central and southern Europe. Meteorol. Atmos. Phys. 2007, 98, 239–267. [Google Scholar] [CrossRef]
- Floris, M.; Bozzano, F. Evaluation of landslide reactivation: A modified rainfall threshold model based on historical records of rainfall and landslides. Geomorphology 2008, 94, 40–57. [Google Scholar] [CrossRef]
- Li, C.; Ma, T.; Zhu, X.; Li, W. The power–law relationship between landslide occurrence and rainfall level. Geomorphology 2011, 130, 221–229. [Google Scholar] [CrossRef]
- Peruccacci, S.; Brunetti, M.T.; Luciani, S.; Vennari, C.; Guzzetti, F. Lithological and seasonal control on rainfall thresholds for the possible initiation of landslides in central Italy. Geomorphology 2012, 139, 79–90. [Google Scholar] [CrossRef]
- Lainas, S.; Sabatakakis, N.; Koukis, G. Rainfall thresholds for possible landslide initiation in wildfire-affected areas of western Greece. Bull. Eng. Geol. Environ. 2016, 75, 883–896. [Google Scholar] [CrossRef]
- He, S.; Wang, J.; Liu, S. Rainfall event–duration thresholds for landslide occurrences in China. Water 2020, 12, 494. [Google Scholar] [CrossRef]
- Crozier, M.J. Prediction of rainfall-triggered landslides: A test of the antecedent water status model. Earth Surf. Process. Landf. J. Br. Geomorphol. Res. Group 1999, 24, 825–833. [Google Scholar] [CrossRef]
- Glade, T.; Crozier, M.; Smith, P. Applying probability determination to refine landslide-triggering rainfall thresholds using an empirical “Antecedent Daily Rainfall Model”. Pure Appl. 2000, 157, 1059–1079. [Google Scholar] [CrossRef]
- Aleotti, P. A warning system for rainfall-induced shallow failures. Eng. Geol. 2004, 73, 247–265. [Google Scholar] [CrossRef]
- Dahal, R.K.; Hasegawa, S. Representative rainfall thresholds for landslides in the Nepal Himalaya. Geomorphology 2008, 100, 429–443. [Google Scholar] [CrossRef]
- Kanungo, D.P.; Sharma, S. Rainfall thresholds for prediction of shallow landslides around Chamoli-Joshimath region, Garhwal Himalayas, India. Landslides 2014, 11, 629–638. [Google Scholar] [CrossRef]
- Leonarduzzi, E.; Molnar, P. Deriving rainfall thresholds for landsliding at the regional scale: Daily and hourly resolutions, normalization, and antecedent rainfall. Nat. Hazards Earth Syst. Sci. 2020, 20, 2905–2919. [Google Scholar] [CrossRef]
- Abraham, M.T.; Satyam, N.; Rosi, A.; Pradhan, B.; Segoni, S. Usage of antecedent soil moisture for improving the performance of rainfall thresholds for landslide early warning. Catena 2021, 200, 105147. [Google Scholar] [CrossRef]
- Kim, S.W.; Chun, K.W.; Kim, M.; Catani, F.; Choi, B.; Seo, J.I. Effect of antecedent rainfall conditions and their variations on shallow landslide-triggering rainfall thresholds in South Korea. Landslides 2021, 18, 569–582. [Google Scholar] [CrossRef]
- Yin, Z.; Qin, G.; Guo, L.; Tang, X.; Wang, J.; Li, H. Coupling antecedent rainfall for improving the performance of rainfall thresholds for suspended sediment simulation of semiarid catchments. Sci. Rep. 2022, 12, 4816. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Peruccacci, S.; Rossi, M.; Luciani, S.; Valigi, D.; Guzzetti, F. Rainfall thresholds for the possible occurrence of landslides in Italy. Nat. Hazards Earth Syst. Sci. 2010, 10, 447–458. [Google Scholar] [CrossRef]
- Abraham, M.T.; Satyam, N.; Rosi, A.; Pradhan, B.; Segoni, S. The selection of rain gauges and rainfall parameters in estimating intensity-duration thresholds for landslide occurrence: Case study from Wayanad (India). Water 2020, 12, 1000. [Google Scholar] [CrossRef]
- Brunetti, M.T.; Melillo, M.; Peruccacci, S.; Ciabatta, L.; Brocca, L. How far are we from the use of satellite rainfall products in landslide forecasting? Remote Sens. Environ. 2018, 210, 65–75. [Google Scholar] [CrossRef]
- Sinclair, S.; Pegram, G. Combining radar and rain gauge rainfall estimates using conditional merging. Atmos. Sci. Lett. 2005, 6, 19–22. [Google Scholar] [CrossRef]
- Kim, T.J.; Lee, D.R.; Kwon, H.H. Assessment of merging weather radar precipitation data and ground precipitation data according to various interpolation methods. J. Korea Water Resour. Assoc. 2017, 50, 849–862. [Google Scholar]
- Vishnu, C.L.; Oommen, T.; Chatterjee, S.; Sajinkumar, K.S. Challenges of modeling rainfall triggered landslides in a data-sparse region: A case study from the Western Ghats, India. Geosystems Geoenvironment 2022, 1, 100060. [Google Scholar] [CrossRef]
- Zhao, B.; Dai, Q.; Zhuo, L.; Mao, J.; Zhu, S.; Han, D. Accounting for satellite rainfall uncertainty in rainfall-triggered landslide forecasting. Geomorphology 2022, 398, 108051. [Google Scholar] [CrossRef]
- Rossi, M.; Luciani, S.; Valigi, D.; Kirschbaum, D.; Brunetti, M.T.; Peruccacci, S.; Guzzetti, F. Statistical approaches for the definition of landslide rainfall thresholds and their uncertainty using rain gauge and satellite data. Geomorphology 2017, 285, 16–27. [Google Scholar] [CrossRef]
- Chikalamo, E.E.; Mavrouli, O.C.; Ettema, J.; van Westen, C.J.; Muntohar, A.S.; Mustofa, A. Satellite-derived rainfall thresholds for landslide early warning in Bogowonto Catchment, Central Java, Indonesia. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102093. [Google Scholar] [CrossRef]
- Hao, L.; Rajaneesh, A.; Van Westen, C.; Sajinkumar, K.S.; Martha, T.R.; Jaiswal, P.; McAdoo, B.G. Constructing a complete landslide inventory dataset for the 2018 monsoon disaster in Kerala, India, for land use change analysis. Earth Syst. Sci. Data 2020, 12, 2899–2918. [Google Scholar] [CrossRef]
- Neumayer, E.; Barthel, F. Normalizing economic loss from natural disasters: A global analysis. Glob. Environ. Change 2011, 21, 13–24. [Google Scholar] [CrossRef]
- De Falco, M.; Forte, G.; Marino, E.; Massaro, L.; Santo, A. UAV and field survey observations on the 26 November 2022 Celario flow-slide, Ischia(Southern Italy). J. Maps 2023, 19. [Google Scholar] [CrossRef]
- Crosta, G.B.; Frattini, P. Rainfall-induced landslides and debris flows. Hydrol. Process. Int. J. 2008, 22, 473–477. [Google Scholar] [CrossRef]
- Lee, M.L.; Ng, K.Y.; Huang, Y.F.; Li, W.C. Rainfall-induced landslides in Hulu Kelang area, Malaysia. Nat. Hazards 2014, 70, 353–375. [Google Scholar] [CrossRef]
- Sajinkumar, K.S.; Anbazhagan, S.; Pradeepkumar, A.P.; Rani, V.R. Weathering and landslide occurrences in parts of Western Ghats, Kerala. J. Geol. Soc. India 2011, 78, 249–257. [Google Scholar] [CrossRef]
- Vijaykumar, P.; Abhilash, S.; Sreenath, A.V.; Athira, U.N.; Mohanakumar, K.; Mapes, B.E.; Sreejith, O.P. Kerala floods in consecutive years-Its association with mesoscale cloudburst and structural changes in monsoon clouds over the west coast of India. Weather. Clim. Extrem. 2021, 33, 100339. [Google Scholar] [CrossRef]
- Jones, S.; Kasthurba, A.K.; Bhagyanathan, A.; Binoy, B.V. Landslide susceptibility investigation for Idukki district of Kerala using regression analysis and machine learning. Arab. J. Geosci. 2021, 14, 838. [Google Scholar] [CrossRef]
- Hao, L.; van Westen, C.; Rajaneesh, A.; Sajinkumar, K.S.; Martha, T.R.; Jaiswal, P. Evaluating the relation between land use changes and the 2018 landslide disaster in Kerala, India. Catena 2022, 216, 106363. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Iguchi, T. The global precipitation measurement mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- MacFarland, T.W.; Yates, J.M. Mann–Whitney U Test. In Introduction to Nonparametric Statistics for the Biological Sciences Using R; Springer: Cham, Switzerland, 2016. [Google Scholar]
- Abraham, M.T.; Pothuraju, D.; Satyam, N. Rainfall thresholds for prediction of landslides in Idukki, India: An empirical approach. Water 2019, 11, 2113. [Google Scholar] [CrossRef]
- Naidu, S.; Sajinkumar, K.S.; Oommen, T.; Anuja, V.J.; Samuel, R.A.; Muraleedharan, C. Early warning system for shallow landslides using rainfall threshold and slope stability analysis. Geosci. Front. 2018, 9, 1871–1882. [Google Scholar] [CrossRef]
- Beguería, S.; Vicente-Serrano, S.M. Mapping the hazard of extreme rainfall by peaks over threshold extreme value analysis and spatial regression techniques. J. Appl. Meteorol. Climatol. 2006, 45, 108–124. [Google Scholar] [CrossRef]
- Chen, H.; Wang, J. Regression analyses for the minimum intensity-duration conditions of continuous rainfall for mudflows triggering in Yan’an, northern Shaanxi (China). Bull. Eng. Geol. Environ. 2014, 73, 917–928. [Google Scholar] [CrossRef]
- Marra, F.; Destro, E.; Nikolopoulos, E.I.; Zoccatelli, D.; Creutin, J.D.; Guzzetti, F.; Borga, M. Impact of rainfall spatial aggregation on the identification of debris flow occurrence thresholds. Hydrol. Earth Syst. Sci. 2017, 21, 4525–4532. [Google Scholar] [CrossRef]
- Wilkinson, G.N.; Rogers, C.E. Symbolic description of factorial models for analysis of variance. J. R. Stat. Soc. Ser. C Appl. Stat. 1973, 22, 392–399. [Google Scholar] [CrossRef]
- Koenker, R.; Bassett, G., Jr. Regression quantiles. Econom. J. Econom. Soc. 1978, 46, 33–50. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).